2. 广西卡斯特动漫有限公司 南宁 530003
2. Guangxi Cast Animation Limited Company Nanning 530003
基于视频的目标跟踪用来估计视频中运动目标的位置,被广泛应用于视频监控、人机交互及视频分析等领域。尽管目前目标跟踪的精度得到了很大的提高,但是由于光照变化、部分遮挡、背景成簇及视点变化等因素使得可靠地跟踪运动目标仍然面临很多困难。
目标跟踪算法大致分为生成式跟踪算法及判别式跟踪算法两类。生成式跟踪算法假定被跟踪的目标可以由一定的生成模型来描述,因而跟踪相当于在所有的候选目标中找到最可能的跟踪目标[1]。生成式跟踪算法的关键在于目标的外观表示。为了简洁地表示运动目标,稀疏表示被应用于目标跟踪,这些方法将目标表示为模板空间中模板稀疏线性组合[2, 3, 4, 5]。为了提高目标跟踪的鲁棒性,跟踪一般在贝叶斯推理框架下执行(如粒子滤波)。判别式跟踪算法将目标看作二值分类问题,其基本思想是在视频序列的每一帧中应用分类器对目标进行分类,并将每帧分类结果组合成一个运动轨迹作为最终的跟踪结果。代表算法包括:online AdaBoost[6]、multiple instance learning[7]。判别式跟踪算法由于采用了有效的目标视觉表示,在简单的跟踪环境下能够取得较好的跟踪效果。而生成式跟踪算法在遮挡等复杂环境能够鲁棒地跟踪目标,因为其考虑了背景信息。
最近深度学习在特征提取领域取得了较好的效果,通过在大规模训练数据库学习可以得到目标的高效表示[8, 9, 10]。本文提出一种结合特征点匹配及深度神经网络检测的目标运动跟踪算法,其目的是为了利用目标检测(基于目标视觉先验知识)及目标跟踪(基于目标的在线信息)的优点,对目标进行高精度鲁棒性跟踪。本文的创新点在于:1) 利用特征点匹配及深度神经网络检测可以防止跟踪漂移及跟踪丢失;2) 利用深度神经网络对目标特征表示的高效性,提高目标跟踪的精度。
1 算法概述本文提出的目标运动跟踪算法如图 1所示,包括两大部分:1) 目标的先验视觉模型离线训练,训练稀疏自编码深度神经网络在图像集上得到通用的目标视觉先验。2) 目标在线跟踪,首帧时根据标识的跟踪目标位置提取正负样本,在目标的先验视觉模型基础上训练深度神经网络得到目标的专用视觉特征表示模型;其他帧中采用粒子滤波对目标进行跟踪,为了防止跟踪漂移,运动模型由上下两帧间匹配的SIFT特征计算得到。
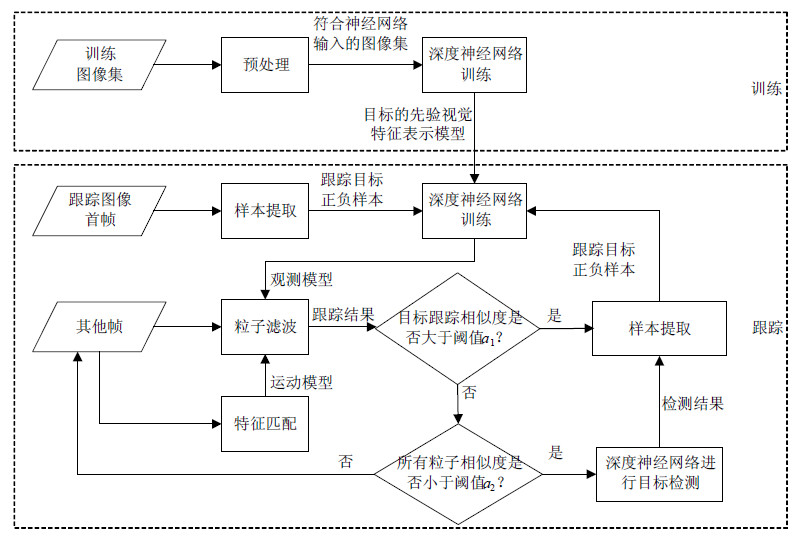 |
| 图1 算法概述 |
由于深度学习结构具有强大的函数表达能力,能有效地从少数样本中学习多变函数的本质。故本文采用稀疏自编码深度神经网络在通用训练样本的基础上学习得到目标的先验视觉表示。
2.1 训练数据集采用VOC2010及Caltech101数据集作为离线训练的样本集。为了与其他算法比较,将所有训练图像都预先转换成灰度图像。另外,由于神经网络输入层的数据维数固定,需要根据输入层数据的大小对训练数据进行尺寸变换(采用下采样或插值)。
2.2 栈式稀疏自编码神经网络栈式自编码神经网络是一个由多层稀疏自编码器组成的神经网络,其前一层自编码器的输出作为其后一层自编码器的输入[11]。本文采用的栈式自编码神经网络结构如图 2所示,共分5层,第1层为输入层,最后一层为softmax分类器,中间3层为稀疏自编码器。训练采用逐层贪婪训练法分两步进行,第一步依次训练网络的每一层,第二步在第一步计算的每层初始权值的基础上对整个网络进行微调。
 |
| 图2 栈式稀疏自编码神经网络结构 |
第一步训练:稀疏自编码器尝试逼近一个恒等函数,从而使得输出${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }$接近于输入x。以特征层1为例说明稀疏自编码器的结构(见图 3)及训练过程。
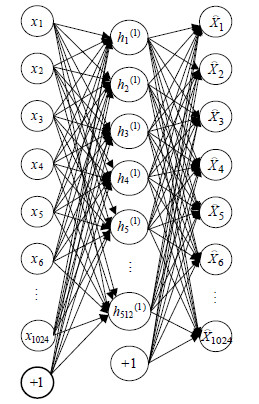 |
| 图3 特征层1稀疏自编码结构 |
设第i层样本为${x_i}$,${\bf{W}},{\bf{W'}},{\bf{b}},{\bf{b'}}$分别为输入层与隐含层及隐含层与输出层之间的权值矩阵及偏置向量。输入层(${{\bf{x}}_i} = {\left[ {{x_1}^{(i)},{x_2}^{(i)}, \cdots ,{x_{1024}}^{(i)},1} \right]^{\rm{T}}}$),隐含层(${{\bf{h}}_i} = {\left[ {h{{_1^i}^{(1)}},h{{_2^i}^{(1)}}, \cdots ,h{{_{512}^i}^{(1)}},1} \right]^{\rm{T}}}$,$h_j^{{i^{(1)}}}$为第i样本下隐含层神经元j的激励输出)及输出层(${{\bf{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}_i} = {\left[ {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_1}^{(i)},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_2}^{(i)}, \cdots ,{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_{1024}}^{(i)}} \right]^{\rm{T}}}$)具有以下关系:
| ${{\bf{h}}_i} = f({\bf{W}}{{\bf{x}}_i} + {\bf{b}}),{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} _i} = f({\bf{W'}}{{\bf{h}}_i} + {\bf{b'}})$ | (1) |
式中,$f( \cdot )$为logistic sigmoid函数。
建立稀疏自编码器的目标函数为:
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;{J_{{\rm{sparse}}}}({\bf{W}},{\bf{W'}},{\bf{b}},{\bf{b'}}) = \\ J({\bf{W}},{\bf{W'}},{\bf{b}},{\bf{b'}}) + \beta \sum\limits_{j = 1}^m {\left[ {{\rm{KL}}(\rho ||{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } }_j})} \right]} \end{array}$ | (2) |
式中,$\beta $控制稀疏性惩罚因子的权重;$\beta \sum\limits_{j = 1}^m {\left[ {{\rm{KL(}}\rho ||{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } }_j}{\rm{)}}} \right]} $为稀疏约束项,其中m为隐含层神经元的数量,$\rho $为稀疏性参数,通常是一个接近于0的较小的值。${\rm{KL(}}\rho ||{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } _j}{\rm{)}}$为$\rho ,{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } _j}$之间的交叉熵,定义为:
| ${\rm{KL(}}\rho ||{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } _j}{\rm{) = }}\rho \log \frac{\rho }{{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } }_j}}} + (1 - \rho )\log \frac{{1 - \rho }}{{1 - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } }_j}}}$ | (3) |
式中,${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } _j}$为隐含层神经元j的平均激励,${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } _j} = \frac{1}{n}\sum\limits_{i = 1}^n {h{{_j^i}^{(1)}}} $,n为样本数。
$J({\bf{W}},{\bf{W'}},{\bf{b}},{\bf{b'}})$为代价函数,定义如下:
| $ \begin{array}{l} J({\bf{W}},{\bf{W'}},{\bf{b}},{\bf{b'}}) = \left[ {\frac{1}{n}\sum\limits_{i = 1}^n {\left( {\frac{1}{2}{{\left\| {{{{\bf{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}}_i} - {{\bf{x}}_i}} \right\|}^2}} \right)} } \right] + \\ \;\;\;\frac{\lambda }{2}\left[ {\sum\limits_{i = 1}^{512} {\sum\limits_{j = 1}^{1024} {{{({w_{ij}})}^2}} + \sum\limits_{i = 1}^{1024} {\sum\limits_{j = 1}^{512} {{{(w{'_{ij}})}^2}} } } } \right] \end{array} $ | (4) |
式中,${w_{ij}},{w'_{ij}}$分别为权值矩阵${\bf{W}},{\bf{W'}}$中的分量;n为样本数;式中的第一项为平方和误差项,第二项为正则项,$\lambda $为正则项系数,用来控制两项的权值比重。
稀疏自编码器为求解使式(2)最小化的参数,即:
| ${\bf{W}},{\bf{W'}},{\bf{b}},{\bf{b'}} = \arg {\rm{ }}\mathop {\min }\limits_{{\bf{W}},{\bf{W}}',{\bf{b}},{\bf{b}}'} ({J_{{\rm{sparse}}}}({\bf{W}},{\bf{W'}},{\bf{b}},{\bf{b'}}))$ | (5) |
上式采用神经网络的反向传播算法可以求得。如果已求得特征层1的稀疏自编码器,计算在样本下其隐含层${{\bf{h}}^{(1)}}$的输出作为计算特征层2的稀疏自编码器时的输入,这样依次训练可以求得所有稀疏自编码器的权值。
第二步微调:在第一步训练过程中,由于训练每一层参数时,会固定其他各层参数保持不变,为得到更好的结果,上述预训练过程完成之后,可以通过反向传播算法同时调整所有层的参数以改善结果。
为了提高算法抵抗局部遮挡的能力,除了训练一个整体目标自编码深度神经网络,同时将目标分成4个不重叠的子目标(上半部分,下半部分,左半部分及右半部分)分别训练一个自编码深度神经网络,由于尺寸减少一半,因而这4个子目标对应的自编码深度神经网络的输入层的大小都为512。在局部遮挡下目标部分区域可见,利用部分可见区域进行目标相似性度量可以提高算法的可靠性。
3 基于粒子滤波的目标跟踪粒子滤波作为目标跟踪中的一种常用方法,具有非线性非高斯系统建模功能。由于粒子滤波能够处理多模式问题,因而它相对其他单模式跟踪算法鲁棒性更好,具体算法请参考文献[12]。粒子滤波跟踪的精度依赖于状态模型及观测模型的可靠性,下面说明这两个模型在本文算法中的构建。
3.1 状态模型本文以向量${{\bf{x}}_t} = {(x_t^1,y_t^1,x_t^2,y_t^2,x_t^3,y_t^3,x_t^4,y_t^4)^{\rm{T}}}$表示目标状态,$(x_t^i,y_t^i)$分别为目标在图像中4个角的坐标。采用的状态模型如下:
| $p({x_t}|{x_{t - 1}}) = g({x_{t - 1}}) + {v_{t - 1}},{v_{t - 1}} \sim N(0,\sum )$ | (6) |
式中,$N(0,\sum )$为零向量均值多元高斯函数;$\sum $为对角矩阵;$g({{\bf{x}}_{t - 1}})$为运动模型。采用六参数仿射变换定义如下:
| $\left\{ {\begin{array}{*{20}{c}} {{x_t} = {a_1}{x_{t - 1}} + {a_2}{y_{t - 1}} + {a_0}}\\ {{y_t} = {a_4}{x_{t - 1}} + {a_5}{y_{t - 1}} + {a_3}} \end{array}} \right.$ | (7) |
式中,${a_0},{a_1},{a_2},{a_3},{a_4},{a_5}$为运动模型参数,采用以下方法可计算得到。
由上式定义误差函数为:
| ${\bf{E}}({\bf{p}};{\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {{x_t} - {a_1}{x_{t - 1}} - {a_2}{y_{t - 1}} - {a_0}}\\ {{y_t} - {a_4}{x_{t - 1}} - {a_5}{y_{t - 1}} - {a_3}} \end{array}} \right]$ | (8) |
式中,${\bf{p}} = {({a_0},{a_1},{a_2},{a_3},{a_4},{a_5})^{\rm{T}}}$;${\bf{x}} = ({x_t},{y_t},{x_{t + 1}},{y_{t + 1}})$为两匹配SIFT特征点在图像上的坐标。最小化下式可以求得运动模型参数:
| ${{\bf{p}}^*} = \arg {\rm{ min}}\left\{ {\sum\limits_x {{\bf{E}}{{({\bf{p}};{\bf{x}})}^{\rm{T}}}{\bf{E}}({\bf{p}};{\bf{x}})} } \right\}$ | (9) |
采用Gauss-Newton迭代法来优化上式。假定第$(k + 1)$次迭代时已知${{\bf{p}}_k}$的估计值,则求得p的增量$\Delta {\bf{p}}$使下式最小化:
| $\Delta p = \arg \mathop {\min }\limits_{\Delta {\bf{p}}} \sum\limits_x {{\bf{E}}{{({{\bf{p}}_k} + \Delta {\bf{p}};x)}^{\rm{T}}}{\bf{E}}({{\bf{p}}_k} + \Delta {\bf{p}};x)} $ | (10) |
然后更新p的估计值${{\bf{p}}_{k + 1}} \leftarrow {{\bf{p}}_k} + \Delta {\bf{p}}$,重复以上两步直至收敛。
${\bf{E}}({{\bf{p}}_k} + \Delta {\bf{p}};{\bf{x}})$利用一阶泰勒展开式线性化为:
| ${\bf{E}}({{\bf{p}}_k} + \Delta {\bf{p}};{\bf{x}}) = {\bf{E}}({{\bf{p}}_k};{\bf{x}}) + {\bf{J}}({{\bf{p}}_k})\Delta {\bf{p}}$ | (11) |
式中,J为雅克比矩阵。将式(11)代入式(9),得:
| $\begin{array}{c} \Delta p = \arg \mathop {\min }\limits_{\Delta {\bf{p}}} \sum\limits_x {({\bf{E}}({{\bf{p}}_k};{\bf{x}}) + } \\ {\bf{J}}({{\bf{p}}_k})\Delta {\bf{p}}{)^{\rm{T}}}({\bf{E}}({{\bf{p}}_k};{\bf{x}}) + {\bf{J}}({{\bf{p}}_k})\Delta {\bf{p}}) \end{array}$ | (12) |
将上式对$\Delta {\bf{p}}$求偏导并等于零,有:
| $\begin{array}{*{20}{l}} {\;\;\;\;\;\;\sum\limits_x {\left[ {2{{\bf{J}}^{\rm{T}}}{\bf{E}}({{\bf{p}}_k};{\bf{x}}) + 2{{\bf{J}}^{\rm{T}}}{\bf{J}}\Delta {\bf{p}}} \right]} = 0}\\ { \Rightarrow \Delta {\bf{p}} = {{(\sum\nolimits_x {\left[ {{{\bf{J}}^{\rm{T}}}{\bf{J}}} \right]} )}^{ - 1}}\left( {\sum\limits_x { - {{\bf{J}}^{\rm{T}}}\left[ {{\bf{E}}({{\bf{p}}_k};{\bf{x}})} \right]} } \right)} \end{array}{\rm{ }}$ | (13) |
以深度神经网络的输出作为粒子的相似度,由于共有5个深度神经网络,故粒子的相似度结合目标及子目标的深度神经网络输出定义如下:
| $p({{\bf{z}}_{\rm{t}}}|{{\bf{x}}_{\rm{t}}}) \propto {\theta _1}c_t^f + {\theta _2}\max (c_{\rm{t}}^t,c_{\rm{t}}^b,c_{\rm{t}}^l,c_{\rm{t}}^r)$ | (14) |
式中,${\theta _1},{\theta _2}$为相似度系数,满足${\theta _1} + {\theta _2} = 1$,其值根据实验调整设置;$c_{\rm{t}}^f$为目标深度神经网络的输出,$c_{\rm{t}}^t,c_{\rm{t}}^b,c_{\rm{t}}^l,c_{\rm{t}}^r$分别为4个子目标深度神经网络的输出。
3.3 目标跟踪待跟踪的目标由用户在首帧中标注得到,并且提取待跟踪目标图像区域中的SIFT特征。在首帧中提取目标的正负样本对离线训练得到的栈式稀疏自编码深度神经网络进行再训练,得到目标的视觉专用表示模型。正样本集由选定目标区域根据以下变换方程得到:
| $\left( {\begin{array}{*{20}{c}} {x'}\\ {y'} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }\\ { - \sin \theta }&{\cos \theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1&s\\ s&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right) $ | (15) |
式中,${(x,y)^{\rm{T}}}$为选定目标区域中的像素点坐标;${(x',y')^{\rm{T}}}$为变换后的区域像素点坐标;$\theta ,s$为变换参数,$\theta $为变换角度,$\theta \in \left[ { - {\rm{\pi }}/4,{\rm{\pi }}/4} \right]$,s为变换尺度,$s \in \left[ {0.8,1.2} \right]$。随机选择一组$(\theta ,s)$值,根据式(15)将目标模板进行变换作为一个训练正样本,负样本集则以选定目标区域之外的图像区域作为数据源,以不同的尺度及位置从这些数据源中提取负样本。
目标在线跟踪算法流程如图 1所示。在本算法中设定两个阈值${a_1},{a_2}$,且${a_1} > {a_2}$,a1用来判定当前跟踪结果是否可靠,如果可信度超过该阈值,则将跟踪结果作为一个新的正样本,并从该区域以外的图像区域选择负样本,重新训练深度神经网络;a2用来判定粒子滤波跟踪是否发生漂移,如果所有粒子的相似度都低于该阈值,则表明跟踪器失效,需要由深度神经网络扫描整个图像进行目标检测,并根据检测结果进行粒子滤波器重新初始化。
4 实验本文在公开测试数据集上进行实验验证算法的有效性,实验所用计算机CPU为酷睿i3(2.1GHz)处理器,内存为4GB。参数设置为:$\rho = 0.05,\beta = 0.3,\lambda = 0.01,{\theta _1} = 0.5,{\theta _2} = 0.5,{a_1} = 0.9,{a_2} = 0.6$。实验中粒子数为300,跟踪目标由首帧手工标注得到。
4.1 定量比较采用7种具有一定挑战的视频进行跟踪比较实验,这些视频都存在不同的跟踪困难因素:遮挡、不规则运动、姿态变化、光照变化、背景成簇等。用作比较的最新跟踪算法包括:VTD[13]、MIL[14]、IVT[1],为了比较公平,使用作者提供的代码在相同的目标初始值下进行实验。
采用两种评价标准来比较跟踪结果。第一种为跟踪正确帧率,正确跟踪的标准采用PASCAL VOC竞赛中目标跟踪的评价准则[15]。某帧当其跟踪结果满足$\frac{{{\rm{area}}({R_{\rm{T}}} \cap {R_{\rm{G}}})}}{{{\rm{area}}({R_{\rm{T}}} \cup {R_{\rm{G}}})}} > 50\% $被认为是正确跟踪,其中${R_{\rm{T}}}$为跟踪到的目标区域,${R_{\rm{G}}}$为真实的目标区域。第二种为中心点跟踪误差,该误差为跟踪到的目标中心点与真实目标中心点的像素间欧氏距离。比较结果见表1,表中各项中的括号外数字为正确跟踪到的帧率,括号内数字为中心点跟踪误差。由表可知,在大多数视频中本文算法的跟踪结果都优于其他跟踪算法。本文算法对所有视频的跟踪速率平均为12帧/s,基本上达到实时跟踪的要求。
| 表1 正确跟踪帧率及中心点误差 |
图 4为各跟踪算法在7个视频上的部分帧跟踪比较结果。不同跟踪困难因素下本文算法的跟踪结果分析如下。
 |
| 图4 不同视频跟踪结果对比 |
遮挡:图 4a及图 4b为严重遮挡及部分遮挡下的视频跟踪结果。本文算法可以较精确地跟踪目标,在遮挡后没有出现跟踪漂移及跟踪丢失现象,主要得益于特征点匹配及子目标相似度量。其他跟踪算法在遮挡后都出现不同的跟踪漂移现象。
不规则运动:图 4c及图 4d为跟踪目标在快速无规则运动下的跟踪结果。在这两个视频中跟踪目标都进行了剧烈无规则的运动,剧烈运动造成的运动模糊使得精确跟踪目标比较困难。由跟踪结果可知本文算法跟踪效果较好,其原因在于深度学习得到的目标视觉先验以及在线跟踪策略,使得跟踪算法能够最大限度地捕捉目标的外观变化。
姿态变化:图 4e为电路板旋转的视频跟踪结果。由于本文采用了六参数的仿射模型,因此在粒子滤波中可以产生更多具有旋转变化的粒子,这些粒子能够更好地表示目标的运动状态。由跟踪结果观察可知,IVT不能正确跟踪目标的尺度变化及旋转变化。
光照变化:图 4f为具有强烈光照变化的视频跟踪结果。由于深度神经网络在线训练,使得分类器能够考虑视频过程中的光照变化,取得了较好的跟踪效果。所有算法基本上都能跟踪到运动目标,但是由于MIL不支持尺度变化,因此,跟踪效果不理想。
背景成簇:图 4g为复杂背景下的视频跟踪结果。由于本文建立的目标视觉先验是在大规模现实图像库下的训练结果,目标视觉先验不仅考虑了目标信息,同时也综合了不同背景下的信息,因此该目标视觉先验具有较强的鉴别性。另外,SIFT特征的高效鉴别性也增强了本文算法在复杂背景下的目标跟踪能力。
5 结 论深度学习得到的目标视觉先验可以精简地表示目标的外观变化,利用该优点,本文提出了一种结合特征点匹配及深度神经网络检测的目标运动跟踪算法。利用粒子滤波进行目标跟踪,跟踪过程中观测模型以训练后的深度神经网络输出作为相似度量,以匹配SIFT特征点对计算得到的运动模型建立状态模型。在7种测试视频上与其他3种跟踪算法的比较实验结果表明,本文算法的跟踪精度更高,具有抗漂移、抗遮挡能力。本文所采用的深度神经网络最后一层为softmax分类器,该分类器为线性分类器,在样本状态空间为非线性分布情况下识别精度会降低。在以后的研究中,将尝试在网络最后一层使用非线性分类器来进一步提高算法的鲁棒性。
| [1] | ROSS D, LIM J, LIN R, et al. Incremental learning for robust visual tracking[J]. International Journal of Computer Vision, 2008, 77(1): 125-141. |
| [2] | ZHANG T, GHANEM B, LIU S, et al. Low-rank sparse learning for robust visual tracking[C]//European Conference on Computer Vision. Firenze, Italy: Springer-Verlag, 2012. |
| [3] | BAO C, WU Y, LING H, et al. Real time robust L1 tracker using accelerated proximal gradient approach[C]//IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA: IEEE, 2012. |
| [4] | MEI X, LING H. Robust visual tracking using l1 minimization[C]//IEEE International Conference on Computer Vision. Kyoto, Japan: IEEE, 2009. |
| [5] | WANG Q, CHEN F, YANG J, et al. Transferring visual prior for online object tracking[J]. IEEE Transactions on Image Processing, 2012, 21(7): 3296-3305. |
| [6] | GRABNER H, GRABNER M, BISCHOF H. Real-time tracking via on-line boosting[C]//British Machine Vision Conference. Edinburgh, UK: Springer-Verlag, 2006. |
| [7] | BABENKO B, YANG M, BELONGIE S. Robust object tracking with online multiple instance learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1619-1632. |
| [8] | KRIZHEVSKY A, SUTSKEVER I, HINTON G. ImageNet classification with deep convolutional neural networks[C]//Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: MIT, 2012. |
| [9] | 郑胤, 陈权崎, 章毓晋. 深度学习及其在目标和行为识别中的新进展[J]. 中国图象图形学报, 2014, 19(2): 175-184. ZHENG Yin, CHEN Quan-qi, ZHANG Yu-jin. Deep learning and its new progress in object and behavior recognition[J]. Journal of Image and Graphics, 2014, 19(2): 175-184. |
| [10] | 李帅, 许悦雷, 马时平, 等. 一种深度神经网络SAR遮挡目标识别方法[J]. 西安电子科技大学学报(自然科学版), 2015, 42(3): 170-177. LI Shuai, XU Yue-lei, MA Shi-ping, et al. New method for SAR occluded targets recognition using DNN[J]. Journal of Xidian University, 2015, 42(3): 170-177. |
| [11] | VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11: 3371-3408. |
| [12] | ARULAMPALAM M S, MASKELL S, GORDON N. A tutorial on particle filters for online non-linear/non-Gaussian Bayesian tracking[J]. IEEE Transaction on Signal Processing, 2002, 50(1): 174-188. |
| [13] | KWON J, LEE K. Visual tracking decomposition[C]//IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, USA: IEEE, 2010. |
| [14] | BABENKO B, YANG M, BELONGIE S. Robust object tracking with online multiple instance learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1619-1632. |
| [15] | EVERINGHAM M, VAN GOOL L, WILLIAMS C, et al. The Pascal visual object classes (voc) challenge[J]. International Journal of Computer Vision, 2010, 88(2): 303-338. |
 2016, Vol. 45
2016, Vol. 45
