目标跟踪是计算机视觉的重要领域,具有重要的研究意义和良好应用前景。但在实际的运动目标跟踪过程中,随着时间的推移目标表观往往会出现遮挡、旋转、尺度等各种复杂变化,对跟踪算法的稳定性和准确性均带来了极大的挑战,因此需要寻求一种跟踪精度高且适用多场景的目标跟踪算法[1]。
针对该需求,许多学者开展了深入的研究,粒子滤波由于跟踪精度高、不受系统线性与噪声高斯假设的限制,受到了越来越多关注。在该框架下,文献[2]通过在线数据学习建立子空间表观模型,比典型方法更能适应目标表观的真实变化。文献[3, 4]找到了在线表观模型合适的表示方式,并进一步提高了模型更新效率。文献[5]成功将高阶张量理论引入到目标跟踪领域。文献[6]结合多重线性空间理论,提出的模型增量更新方式可更好地描述目标表观的动态变化。以上方法使用的是单视图的目标表观模型,难以应对目标姿态、尺度等多种表观变化,并容易导致跟踪漂移。
本文以灰度共生(GLCM)与三阶张量理论为基础,通过三维表观模型、双线性空间下的增量学习更新及粒子滤波下的二级联合跟踪最终锁定目标。该算法可以在保证跟踪精度的基础上有效应对遮挡、旋转、尺度变化等多种复杂场景下的目标跟踪。
1 基于GLCM的三维在线表观模型与跟踪领域的其他方法不同,本文利用灰度共生矩阵对目标区域的高区分度特征进行二元超分描述,进一步提高表观模型的稳定性,并结合三阶张量的理论优势,集成目标的多视图信息,同时借助双线性空间理论,提出在线增量学习的模型更新方法,以更好地描述跟踪过程中表观的动态变化。
1.1 二元GLCM特征超分提取构建表观模型,应选取稳定性好、辨识度高的特征,灰度特征运算方便且可较好地描述目标表观,但在光照变化时对目标与背景的区分度明显下降。但纹理特征受光线变化影响较小,且GLCM可通过多种角度对目标的纹理特征进行描述,分别从方向、相邻间隔、变化幅度等多方面对目标进行描述,同时兼具了灰度特征运算方便的优点。
GLCM表示图像在方向$\theta $上相距s的灰度像素对$(i,j)$共同出现的概率分布,用${P_{\theta ,s}}$表示,包含角二阶矩、熵、对比度、逆差矩、相关度等统计量特征。文献[7]证明了熵ENT与对比度CON为相关度最低、分辨能力最好的统计量特征,其中参数s根据不同需要一般从$\{ 1,2,4,8,16,32\} $中进行取值[8],该环节需要在获得稳定纹理描述的同时保持较低的运算复杂度,经大量实验表明,s通常取值为4满足该条件[9],此时最精细的超分窗口为$(5 \times 5)$。$p(i,j)$代表${P_{\theta ,s}}$的元素,目标区域定义为$(N \times M)$,定义如下:
| ${\rm{ENT}} = - \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {p(i,j)\log p(i,j)} } $ | (1) |
| ${\rm{CON}} = \sum\limits_{ij} {{{(i - j)}^2}p(i,j)} $ | (2) |
式中,ENT为图像信息量的随机性度量,代表纹理的复杂程度;CON为图像纹理的清晰程度,其值越大纹理越清晰。本文通过超分窗口$(5 \times 5)$,将目标超分为若干像素块,并通过ENT和CON特征进行描述,得到超分特征矩阵${{\bf{P}}_{{\rm{ENT}}}}$与${{\bf{P}}_{{\rm{CON}}}}$。步骤如下:
1) 首先对目标区域$(N \times M)$进行标定,并通过超分窗口$(5 \times 5)$进行细分;
2) 对细分后的像素块分别提取灰度信息,通过运算得到其灰度共生矩阵GLCM,并进行归一化;
3) 通过归一化后的GLCM,经计算得到二维超分矩阵${{\bf{P}}_{{\rm{ENT}}}}$与${{\bf{P}}_{{\rm{CON}}}}$。
4) 当N/5,M/5余数不足5时,即图像边缘像素块,令余数为k,采取如下策略:
| $\left\{ {\begin{array}{*{20}{c}} {3 \le k < 5}&{空缺像素以最邻近像素补齐}\\ {1 \le k \le 2}&{舍弃对该像素块的超分运算} \end{array}} \right.$ |
为了更多地挖掘目标表观的有效线索信息,利用三阶张量来对跟踪序列图像中的目标进行表述,该模式的优势是既能保留目标区域的几何空域信息,并易集成目标区域的其他线索。因此三维表观模型可由特征矩阵与时域多视图信息建立。目标区域的特征信息由超分特征矩阵表示,组成模型的前两个数据模式;结合目标区域有限时刻的连续多视图观测信息,建立模型的第三个线索,时域视图模式。
令共选取K种线索特征对目标进行建模,并将相应第k条线索的帧视图数据记为${X^k} \in {R^{{I_1} \times {I_2}}}$,取连续n帧图像获得连续视图观测数据,可表示为三阶张量形式${\chi ^k} = \{ X_1^k,X_2^k, \cdots ,X_n^k\} \in {R^{{I_1} \times {I_2} \times {I_3}}}$,${I_3} = n$,即可相应建立起三维在线表观模型,关于熵ENT和对比度CON的三维表观模型示意如图 1所示。
 |
| 图1 三维在线表观模型 |
引入多维线索建立的三维表观模型会带来运算量的大幅提升,为缓解该不足,利用双线性空间[9]理论展开表观模型,并对其进行增量更新。
1) 双线性空间展开。实际场景中的目标表观变化在有限时间内可认定其服从线性变化理论,可引入双线性空间对目标模型进行展开,其示意图如图 2所示,可利用线性空间的正交基对模型进行特征表示。同时对线性空间展开进行如下改进:首先通过对样本观测数据去均值化,能凸显样本观测数据的变化,即$\bar \chi = \{ {X_1} - \bar X,{X_1} - \bar X, \cdots ,{X_n} - \bar X\} $,然后对其进行模型数据展开,得到两个模式${{\bf{\bar \chi }}_1} \in {R^{{I_1} \times (n{I_2})}}$,${{\bf{\bar \chi }}_2} \in {R^{{I_2} \times (n{I_1})}}$。正交基的表示形式为${{\bf{V}}_{(i)}} = [V_{(i)}^1,V_{(i)}^2, \cdots ,$ $V_{(i)}^{{P_{(i)}}}] \in $${R^{{I_{(i)}} \times {P_{(i)}}}}$,为便于对训练样本中的数据变化信息进行表示,可以对样本均值${{\bf{\bar \chi }}_{(i)}}$的奇异值递推分解(RSVD)[4]获知其子模式的正交基,通过其前${P_{(i)}}$个最大值对应的数据集$\{ \zeta _{(i)}^1,\zeta _{(i)}^2, \cdots ,\zeta _{(i)}^{{P_{(i)}}}\} $对正交基进行描述。其中,${P_{(i)}}$的个数代表线性空间模型的维度数,其取值利用式(3)判定:
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{P_{(i)}} = \\ \arg \mathop {\min }\limits_k \left\{ {k|k = 1,2, \cdots ,{I_i},\sum\limits_{j = 1}^K \zeta _{(i)}^j/\sum\limits_{j = 1}^{{I_i}} \zeta _{(i)}^j \ge \lambda } \right\} \end{array}$ | (3) |
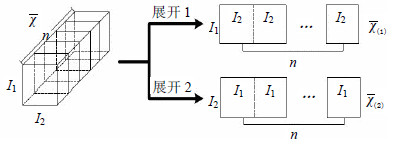 |
| 图2 观测数据双线性空间展开 |
式(3)中,阈值$\lambda $依据经验确定($0 \le \lambda \le 1$),为使$\lambda $的取值能在保存最大数据变异信息的同时使运算量保持在一个合适范围内,经实验验证,取值0.85时可取得较理想的结果。同时,通过投影降维可降低模型表示的运算量对线性空间的子模型进行投影降维,可降低模型描述的计算量[5],如式(4):
| $Y = X \times {}_1{\bf{V}}_{(1)}^{\rm{T}} \times {}_2{\bf{V}}_{(2)}^{\rm{T}}$ | (4) |
式中,${}_1{\bf{V}}_{(1)}^{\rm{T}}$和${}_2{\bf{V}}_{(2)}^{\rm{T}}$分别表示展开1模式和2模式下的相应子空间的正交基。
2) 增量学习更新。常规模型更新需要保留较多的目标观测数据,且由于多维线索表观模型的引入按常规更新方式运算量明显加大,但可结合跟踪过程中的新增观测信息来更新目标表观模型[10]优化模型的表示,故特别提出结合双线性空间的学习更新方法。它以连续n帧包含跟踪目标的视图为基础,通过紧跟$\Delta t$时间内新增的m帧视图信息对模型进行学习更新。令$\chi _t^k = \{ X_1^k,X_2^k, \cdots ,X_n^k\} $为t时刻基于第k条线索下的双线性空间模型的有效观测数据,$\chi _{\Lambda t}^k = \{ X_{n + 1}^k,X_{n + 2}^k, \cdots ,X_{n + m}^k\} $为间隔$\Delta t$后新录入的m帧视图观测信息,则$t + \Delta t$时刻模型可表示为$\chi _{t + \Lambda t}^k = \{ X_1^k,X_2^K, \cdots ,X_n^k,X_{n + 1}^k,X_{n + 2}^k, \cdots ,X_{n + m}^k\} $,该环节问题则转化为对$t + \Delta t$时刻模型进行表示的问题,即增量模型的数据均值和正交基的求解问题。实施方式如下:
① 求取已有样本数据集的均值$\bar X_t^k = \frac{1}{n}\sum\limits_{i = 1}^n {X_i^k} $,新增样本数据的均值$\bar X_{\Delta t}^k = \frac{1}{m}\sum\limits_{i = n + 1}^{n + m} {X_i^k} $;
② 引入新增样本后对模型均值进行更新(h为消逝系数),$\bar X_{t + \Delta t}^k = \frac{m}{{hn + m}}\bar X_{\Delta t}^k + \frac{{hn}}{{hn + m}}\bar X_t^k$;
③ 为避免直接引入样本均值对数据即时变化信息的影响,先对新增样本去均值处理:$\bar \chi _{\Delta t}^k = \{ X_{n + 1}^k - \bar X_{\Delta t}^k, \cdots ,X_{n + m}^k - \bar X_{\Delta t}^k\} $,然后对模型再进行双线性展开,可得$\{ \bar \chi _{\Delta t(i)}^k|i = 1,2\} $;
④ 求解$\bar G_{(i)}^k = [\bar \chi _{t(i)}^k,\sqrt {\frac{{nm}}{{n + m}}} (\bar X_{t(i)}^k - \bar X_{\Delta t(i)}^k)],$ $i = 1,2$,其中$\bar X_{t(i)}^k$与$\bar X_{\Delta t(i)}^k$分别为已有样本数据集均=值和新增样本均值的线性空间展开;
⑤ 结合RSVD[4]方法,可得到新模型的正交基。
常规模型更新通常直接进行数据学习,空域复杂度是$\Delta ({I_i}{(n + m)^2})$,结合增量学习更新后空域复杂度变为$\Delta ({I_i}(P_{(i)}^k + m))$;常规模型更新方法的时域复杂度是$\Delta ({I_i}{(n + m)^2})$,结合增量学习更新后时域复杂度变为$\Delta ({I_i}{m^2})$。可见运算量并未随数据的增长而增多,运算复杂度总体较低。
2 二级联合跟踪粒子滤波作为算法的跟踪框架,主要包括动态模型与观测模型,观测模型$p({z_t}|{s_t})$是保证跟踪效果的关键,需重点改进:1) 以建立的三维表观模型为基础,结合当前时刻信息分别进行在线权重估计,进而建立自适应观测模型,因连续的目标帧视图代表的表观变化通常较小,可通过自适应观测模型的自身调整克服;2) 以真实目标视图为基准,建立目标的静态观测模型,防止长时跟踪过程中误差累积出现跟踪漂移;3) 通过两个模型的联合匹配,实现对目标的稳定跟踪。
2.1 自适应观测模型假定有K条线索对目标模型进行描述,利用式(5)能得到目标的观测模型并实现线索的融合[11]:
| $p({z_t}|{s_t}) = \sum\limits_{k = 1}^K {\lambda _t^kp(z_t^k|{s_t})} $ | (5) |
式中,$z_t^k$表示第k条独立线索的样本观测数据;$\lambda _t^k$表示第k条线索的置信度。因$p(z_t^k|{s_t}) \propto $$\exp (\frac{{{\rm{HF}}_t^k}}{{{\sigma ^2}}})$,且${\sigma ^2}$为预设方差,${\rm{HF}}_t^k$表示新增数据的重构残差值,因此通过${\rm{HF}}_t^k$值便可得到观测模型$p(z_t^k|{s_t})$的取值。为便于后续在线线索融合的实现,可选取相应数目的新增粒子来动态估计各线索的权值[12],同时为使权重的更新更接近表观线索的真实变化,引入消逝系数更新权重$\lambda _t^{k*} = f\lambda _{t - 1}^k + (1 - f)\lambda _t^k$,其中f为消逝系数,权值更新越快,f越小,即旧样本数据对权值的影响越小,各线索之间便可起到相互补充的效果。
2.2 静态观测模型模型更新过程中会出现场景突变,容易导致跟踪漂移。在滤波理论跟踪下首帧视图是唯一的目标真实信息,对其他时刻状态的预测均存在一定的误差,以首帧真实目标视图为基准,建立静态观测模型。具体步骤:1) 标定初始化首帧图像中的目标视图,提取特征信息${P_{{\rm{EN}}{{\rm{T}}_{\rm{0}}}}}$与${P_{{\rm{CO}}{{\rm{N}}_{\rm{0}}}}}$;2) 以连续n张目标首帧视图信息为原型,建立目标首帧视图的三维表观模型;3) 以首帧视图的表观模型为基础,建立目标的静态观测模型$p{}_0({z_t}|{s_t})$。
3 实验分析 3.1 评价指标与测试视频运动目标跟踪算法评价体系中平均跟踪误差(ATE)与跟踪框重合率(AOR)是非常具有代表性的评价指标。平均跟踪误差由${\rm{AT}}{{\rm{E}}_X}$与${\rm{AT}}{{\rm{E}}_Y}$两个指标决定;以A表示跟踪算法的跟踪框,以B表示测试视频的真实边界框,则计算方式如下:
| ${\rm{ATE}} = \frac{{{\rm{AT}}{{\rm{E}}_X} + {\rm{AT}}{{\rm{E}}_Y}}}{2}$ | (6) |
| ${\rm{AOR}} = A \cap B/A \cup B$ | (7) |
测试视频选取的是目标跟踪数据集Tracker BBenchmark v1.0中的序列视图[10],如表 1所示。
| 表1 对比测试视频 |
为了有针对性地对本文算法进行测试,选取如下算法对照实验:多线索融合的目标跟踪算法(MAPF),增量对数线性空间学习的跟踪算法(IRST)与增量线性空间学习的跟踪算法(IVT)。对比算法均以粒子滤波为跟踪框架,且均采用相同的目标运动模型。
图 3a中CarScale场景下,小车快速运动,存在明显的尺度变化与树木的遮挡,仅本文算法做到了该视频场景下的尺度自适应跟踪,其他跟踪算法偏差较大,验证了本文基于三维表观模型的多线索目标联合优化跟踪算法处理复杂场景的鲁棒性。图 3b为旋转扰动遮挡场景下的Tiger1视频。图 3bi帧中,算法均可以准确的跟踪,图 3bii与图 3biii目标发生旋转与形变,表观发生较大变化,MAPF算法逐渐跟丢目标难以适应该场景,IRST算法由于基于对数线性空间建模,对目标表观变化更加敏感优于IVT算法,而本文算法由于引入目标连续视图建立表观模型,能较好适应目标表观的大幅变化,且由于引入了二级联合跟踪机制,避免了跟踪漂移的出现。
 |
| 图3 多种表观变化场景实验对比 |
图 3c的Soccer视频为由于相机运动与背景大幅突变造成运动模糊的场景。与图 3b类似,初始阶段,几种算法均可较准确的捕捉到目标,区别较小,但随着庆祝场面升级,相机需要快速运动以捕捉Soccer造成视图严重模糊,由图 3cii与图 3ciii可见,3种对比算法由于视图严重模糊无法跟踪目标,均出现了跟踪漂移现象,只有本文算法均成功捕捉到了跟踪目标。图 3d的Car4场景下,目标表观存在明显的光线突变。MAPF算法因为结合LBP线索,跟踪精度显著优于IVT算法;IVT算法在光线突变后,目标被跟丢,表明仅利用灰度建模稳定性欠佳;IRST算法在小车刚进入桥下时,存在漂移现象,但在表观稳定后又找回了目标,表明仅利用COV建模对场景突变鲁棒性较差;但本文方法由于采用的线索间可相互动态补充,能有效应对该跟踪场景。
为了定量验证算法的跟踪效果,通过ATE与AOR两个指标作为评估依据,可看出本文算法相比对照算法有了较大进步,具有较高的跟踪精度,跟踪误差平均保持小于9像素;表 2所示数据表明,本文算法亦可较好地适应目标的尺度变化,进一步验证了本文的模型及其更新方法对提高跟踪效率的良好效果;同时算法对视频的处理速度也相应提高,有效保证了跟踪的实时性。
| 表2 算法定量对比评估 |
本文针对视频跟踪过程中目标表观存在的复杂变化,提出了一种基于灰度共生的多线索目标联合优化跟踪算法。以灰度共生理论为基础,利用高辨识度特征对目标区域分别进行超分提取,从空域和时域角度分别对跟踪目标进行三维表观建模;通过双线性空间的在线增量学习更新方式对模型进行动态更新,提高了算法的运算效率;同时二级联合跟踪能有效避免跟踪漂移,保证跟踪的精度。实验表明,该算法在多种包含剧烈表观变化的跟踪环境中可取得良好的跟踪效果。
| [1] | YANG H, SHAO L, ZHENG F, et al. Recent advances and trends in visual tracking: A review[J]. Neurocomputing, 2011, 74(18): 3823-3831. |
| [2] | HO J, LEE K C, YANG M H, et al. Visual tracking using learned linear subspaces[C]//Proceedingsof IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]: IEEE, 2012. |
| [3] | LEE K C, KRIEGMAN D. Online learning of probabilistic appearance manifolds for video-based recognition and tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]: IEEE, 2013. |
| [4] | ROSS D, LIM J, LIN R S, et al. Incremental learning for robust visual tracking[J]. International Journal of Computer Vision, 2013, 77(1-3): 125-141. |
| [5] | LATHAUWER L, MOOR B, VANDEWALLE J. On the best rank-1 and rank-(R1, R2,..., Rn) approximation fhigherorder tensors[J]. SIAM Journal of Matrix Analysis and Applications, 2000, 21(4): 1324-1342. |
| [6] | LI X, HU W, ZHANG Z, et al. Visual tracking via incremental Log-Euclidean Riemannian sub-space learning [C]//IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]: IEEE, 2013. |
| [7] | LI X, HU W, ZHANG Z, et al. Robust visual tracking based on incremental tensor subspace learning[C]//International Conference on Computer Vision. [S.l.]: [s.n.], 2012. |
| [8] | 薄华, 马缚龙, 焦李成. 图像纹理的灰度共生矩阵计算问题的分析[J]. 电子学报, 2014, 34(1): 155-158. BO Hua, MA Fu-long, JIAO Li-cheng. Research on computation of GLCM of image texture[J]. Acta Electronica Sinica, 2014, 34(1): 155-158. |
| [9] | CLAUSI D A, HUANG D. Design-based texture feature fusion using Gabor filters and co-occurrence probabilities[J]. IEEE Trans on Image Processing, 2013, 14(7): 925-936. |
| [10] | WU Y, LIM J, YANG M H. Object tracking benchmark[J]. Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. |
| [11] | KHAN Z H, GU I Y H. Online domain-shift learning and object tracking based on nonlinear dynamic models and particle filters on Riemannian manifolds[J]. Computer Vision and Image Understanding, 2014, 125: 97-114. |
| [12] | CHENG X, LI N, ZHOU T, et al. Object tracking via collaborative multi-task learning and appearance model updating[J]. Applied Soft Computing, 2015, 31: 81-90. |
 2016, Vol. 45
2016, Vol. 45
