多摄像机环境下跟踪目标的跨摄像机再识别是一个急需解决的关键性问题,是指如何利用前一摄像机获得的目标信息,在下一摄像机中识别出该目标。这是多摄像机实现目标接力跟踪的关键。目标的跨机再识别主要有两类方法,一类是基于摄像机之间的三维几何关系,这需要相邻摄像机有重叠的视场,如基于三维信息的目标交接[1, 2, 3]。这类方法通过坐标匹配识别目标,对摄像机的布局、安装乃至标定均有一定要求;另一类是基于目标的特征匹配,这不需要相邻摄像机有重叠视场,灵活方便,切合视频监控的实际需要,但难点在于找到一种既具有较强目标识别能力又具有较高跨机鲁棒性的目标特征。如人体跟踪常用的颜色特征,在单机跟踪时效果较好,但在跨机时就不够可靠[4],即使通过跨机颜色校正有所改善[5],但离实用也还有相当距离。为此,许多研究将目光投向目标表面的结构性特征,如纹理特征。表面结构性特征的一个重要分析工具是频谱。如对目标图像进行Gabor或小波变换[6, 7],但这往往需要使用多尺度、多方向的模板进行多次滤波,再用滤波的结果构造特征向量,用时过长。相对于Gabor或小波变换,傅里叶变换则简便、快速,常见的形式是傅里叶描述子[8, 9],用于描述目标的轮廓;二维情况下傅里叶频谱特征的典型构造是,将频谱图分为扇形或环形区域,使用各区域频谱幅度的均值及方差组成特征向量进行匹配[10]。但由于傅里叶频谱高低频的幅度差别极大,这种特征构造方式会使高频信号淹没于低频信号之中,并且频谱原有的空间信息损失严重,影响特征的目标识别能力。为此,本文提出一种直接使用傅里叶频谱进行匹配的改进方法,最大程度地保留和使用频谱信息,提高目标的识别能力。
1 傅里叶频谱随图像灰度的变化图像的离散傅里叶变换如下:
| $\begin{array}{c} F(u,v) = \\ \frac{1}{{MN}}\sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{N - 1} {f(x,y)\exp } } \left[ { - {\rm{j}}2{\rm{\pi }}(\frac{{ux}}{M} + \frac{{vy}}{N})} \right]\\ u = 0,1, \cdots ,M - 1,v = 0,1, \cdots ,N - 1 \end{array}$ | (1) |
式中,M、N为图像$f(x,y)$的宽与高;$F(u,v)$即图像的傅里叶频谱。
目标跨摄像机时,由于光照及摄像机参数变化,目标图像的灰度会发生变化。根据摄像机光电信号转换规律[11, 12],在不考虑光照几何条件的情况下,变化后的灰度值为:
| ${f'_k}(x,y) = {G_k}^{\frac{1}{\gamma }}{f_k}(x,y) k = r,g,b $ | (2) |
式中,${G_k}$为k颜色通道光照强度和摄像机增益的综合变化倍率;$\gamma $为摄像机的gamma值。由式(1)和式(2)易知,跨机时,目标图像的灰度和傅里叶频谱在各空域点和频域点均是等倍率变化的。另外,由于亮度是各通道的线性组合,且不受摄像机白平衡调节的影响,故只要光照色温不变或变化较小,亮度通道的频谱变化也是各频点等倍率的。
式(2)所示灰度变化模型是理论上的理想情况。实际上,由于$\gamma $值的不完全一致[13, 14],光照几何条件引起的自阴影以及某些摄像头内置的图像增强算法带来的一定的灰度值的非线性映射[15],实际的灰度和频谱变化会在等倍率的基础上有所波动。
2 非刚性目标的频谱变化非刚性体可看作多个相对刚性的子部分组成的变形体。如图 1所示的人体,头部、小臂及小腿本身内部的纹理结构可视为不变的(刚性子部分),人体姿态的变化可分解为头部相对于躯干发生了平移,小臂和小腿发生了不同角度的旋转。从视频监控的实际看,一般的非刚性目标中,相对刚性的子部分的像素占大多数甚至绝大多数,而完全非刚性变化部分的像素只占少数,如图 1中大臂和小臂连接处、大腿和小腿连接处等。根据傅里叶变换的叠加性质,在灰度水平相当的情况下,刚性子部分对傅里叶频谱的贡献为主要的,而刚性子部分之间的少量像素的贡献则是次要的。因此,通过分析各刚性子部分频谱的变化及其叠加,即可近似整体频谱的变化。
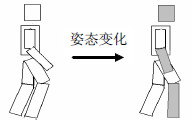 |
| 图1 非刚性目标的刚性分解 |
这样,非刚性目标整体的频谱可近似分解为:
| $F(u,v) = \sum\limits_i {Fi(u,v)} $ | (3) |
式中,$Fi(u,v)$为各刚性子部分的傅里叶频谱。但由于式(3)是复数相加,整体的频谱幅值变化不能分解为各刚性子部分频谱幅值的简单相加。以两个子部分为例,叠加后的总频谱幅值为:
| ${\rm{|}}F(u,v){{\rm{|}}^2} = {\rm{|}}{F_1}{{\rm{|}}^2} + {\rm{|}}{F_2}{{\rm{|}}^2} + 2{\rm{|}}{F_1}{\rm{||}}{F_2}{\rm{|}}\cos ({\theta _1} - {\theta _2})$ | (4) |
由式(4)可见,整体频谱幅值与子部分频谱相位差$({\theta _1} - {\theta _2})$关系很大。由于非刚性体子部分之间极易发生相对位移或其他仿射变化,相位差会剧烈变动,故频谱幅值极不稳定,无法用于频谱的直接匹配。
为获得稳定可比的频谱特征,本文在频谱图各点对式(4)做小范围平均。由于自然图像频谱的相位随频点变化很快,可视作是随机分布的,相位差$({\theta _1} - {\theta _2})$也呈随机分布,故有:
| $\overline {{\rm{|}}F(u,v){{\rm{|}}^2}} = \overline {{\rm{|}}{F_1}{{\rm{|}}^2}} + \overline {{\rm{|}}{F_2}{{\rm{|}}^2}} $ | (5) |
式中,$2{\rm{|}}{F_1}(u,v){\rm{|}}\;{\rm{|}}{F_2}(u,v){\rm{|}}\cos ({\theta _1} - {\theta _2})$的平均值为0。对于多个子部分,式(5)显然可以推广为:
| $\overline {{\rm{|}}F(u,v){{\rm{|}}^2}} = \overline {{\rm{|}}{F_1}{{\rm{|}}^2}} + \overline {{\rm{|}}{F_2}{{\rm{|}}^2}} + \cdots + \overline {{\rm{|}}{F_n}{{\rm{|}}^2}} $ | (6) |
这样,整体的频谱幅值平方即可分解为各子部分频谱幅值平方的简单相加。为节省计算开销,本文直接对幅值进行局部平均处理。整体的频谱幅值即可近似分解为各子部分频谱幅值的简单相加。下面据此分析各子部分频谱变化对整体频谱变化的影响。
根据人体姿态变化特点,其刚性子部分可能的变化主要为:平移、旋转以及少量的错切和横竖不等比缩放(来源于立体目标视角的变化)。这些变化对应的频谱幅值图变化如图 2所示。由图可见,除平移的频谱幅值图不变外,其他变化仅会使原频谱幅值图产生类似的几何变化。因此,如果在目标图像取样时适当限制,使得各子部分的变化在较小范围之内,则整体频谱幅值的变化就不大。因此,本文使用视频帧中目标去除阴影后的最窄外接矩形区域(高宽比最大)作为目标图像的取样窗口。这样,在视角变化不大的情况下,各主要刚性子部分及其遮挡变化就不大,平均化处理后的目标整体频谱幅值分布结构就会大致不变。另外由图 2可见,子部分变化时频谱的低频段(靠近中心)变化远小于高频段,故整体的频谱幅值图在低频段更加稳定。
 |
| 图2 图像的仿射变化及其频谱变化 |
为尽量减少信息损失,本文采用高斯滤波来对频谱幅值图进行局部平均化处理。高斯卷积模板如下:
| $G = \exp [ - (\Delta {u^2} + \Delta {v^2})/(2{\sigma ^2})]$ | (7) |
式中,$\sigma $为标准差;模板宽度为$\Delta u \Delta v \in [ - 3\sigma , + 3\sigma ]$。由于参加比较的两个频谱图使用相同卷积核,故卷积核前的系数统一为1。$\sigma $对局部平均的效果影响很大,$\sigma $取值过大,则频谱图原有信息丢失过多,影响对目标的区分;$\sigma $取值过小,则频谱图的对比就不够稳定。$\sigma $的取值最终由实验确定。
3.2 频谱的比较和相似性度量根据傅里叶频谱的变化规律,考虑到自然图像的频谱能量强烈集中于直流和低频的特点,为避免高频细节信息被直流和低频信息所淹没,本文提出如下频谱对点相除的比较方法。
首先考虑两个具有相同窗口尺寸的目标图像。设F1、F2为经过了高斯滤波的待比较幅值频谱图,将两频谱中心点(即直流点)及坐标轴对准,则在两图的重叠区域MN内,各点幅值对点相除结果D为:
| $\begin{array}{*{20}{c}} {D(u,v) = \left\{ \begin{array}{l} {F_2}/{F_1} {\rm{ if }} {F_1} \ge T \cap {F_2} \ge T\\ {F_2}/T {\rm{if }} {F_1} {\rm{ < }}T \cap {F_2} \ge T\\ 不纳入统计 {\rm{if }} {F_1} {\rm{ < }}T \cap {F_2} < T \end{array} \right.}\\ {u = 0,1, \cdots ,M - 1,v = 0,1, \cdots ,N - 1} \end{array}$ | (8) |
式中,$T = \alpha \max (|{F_1}|)$,为频谱的统计阈值,$\alpha $为阈值系数,$0 \le \alpha < < 1$,取值由实验确定。设置该阈值的原因是,幅值过小的频点,如高频频点,更易受跨机变化的干扰。
对点相除结果D反映了两个目标频谱图在对应频点的幅值变化倍率,目标图像越相似,则变化倍率越趋于一致,亦即D的离散程度反映了两个目标图像的相似性。为更好地排除亮度的影响,本文使用D的归一化标准差S作为两个目标图像的相似性距离,有:
| $S = \frac{1}{{\overline D }}{\rm{sqrt}}\left( {\frac{1}{{(MN)'}}\sum\limits_{(u,v)} {(D - \overline D } {)^2}} \right)$ | (9) |
式中,$(MN)'$为MN中纳入统计的点数,$\overline D $为纳入统计的D的平均值。按照式(9),两个图形越相似,则其间的相似性距离S就越小,完全一样时S为0。
如果两个目标图像的窗口尺度亦即解析尺度不一样,根据式(1)容易证明,只需将其中一个谱图沿着宽度方向适当伸缩,使其与另一个频谱图高宽比一致,在中心和坐标轴对准的情况下,在两图的重叠区域按式(8)和式(9)计算即可,如图 3所示。
 |
| 图3 不同尺度窗口图像的频谱比较 |
由上可见,解析尺度不同时,小尺度图像的频谱全部纳入了比较范围,而大尺度图像中体现更多细节的高频信息则无法参与对比。因此,使用本文方法时,目标图像的匹配效果主要决定于小图像的尺度。小图像尺度越小,可供匹配的线索就越少,匹配的效果就会降低。
4 实验与分析实验首先在不变场景中考察不同目标尺度及少量视角变化下本文方法的目标识别能力,旨在验证本文方法的原理。然后在变化场景下进行跨摄像机的目标识别实验,并与纹理识别常用的方法进行比较,考察本文方法的实际应用效果。实验中,频谱平均化处理的高斯卷积核标准差为:$\sigma {\rm{ = }}1.5$,频谱幅值纳入统计的阈值系数为:$\alpha {\rm{ = }}0.005$。视频拍摄时摄像机的增益、曝光和白平衡均处于自动状态。
4.1 不变场景下的目标识别选择同一场景连续拍摄的视频,排除光照和摄像机参数差异的影响。视频中两目标身高类似,将摄像机分别置于5种不同距离,从而使目标具有不同的解析尺度,如图 4所示,图中左起分别为目标1和目标2。
 |
| 图4 同一场景处于不同解析尺度的目标 |
为使每个目标在5个解析尺度下各获得3张最窄目标图像,并使视角尽量一致,排除视角差异的影响。将两目标共30张目标图像按尺度分组,每组中每个目标有3张目标图像,组内目标进行两两交叉比较,计算相似性距离,结果列于表 1,表中解析尺度为目标的窗高,用像素个数表示。
| 表1 不同解析尺度下的识别能力(亮度通道) |
可以看到,在大尺度时,不同目标之间的最小相似性距离显著大于同目标之间的最大相似性距离,目标识别能力强。目标尺度变小时,目标识别能力开始下降。解析尺度降至150像素时,不同目标之间的最小相似性距离已与同目标之间的最大相似性距离接近,此时对目标的区分就不够可靠了。
下面考察少量视角差异下的识别能力。与上类似,获取同一场景连续视频中的两个目标在相同解析尺度下的各5个窗口图像,窗口高度约为300像素,分成A、B两组,各组内从第1至第5图视角差异逐渐加大,如下图 5所示。考察第1图与后续图的相似性距离变化,结果如表 2所示(亮度通道)。
 |
| 图5 少量视角差异下的目标图像 |
| 表2 不同视角差异下的相似性距离 |
可以看到,相同目标之间的相似性距离随着视角差异的加大有所增加,但仍明显小于不同目标间(25种对比组合)的最小相似性距离0.39。这说明在一定范围内,只要目标相对于摄像机的暴露面没有大的变化,视角差异对目标识别的影响是有限的。
上述两个实验过程中,视频均为同一场景连续拍摄,可以认为此过程中没有光照变化和摄像机参数变化,而只有多次图像取样时目标的非刚性形变和视角变化。因此,实验结果说明,本文方法对于非刚性目标的频谱变化分析是合理的,通过最窄取样窗口的限定和频谱的局部平均化处理,可以使非刚性目标的频谱变化控制在较小范围。
4.2 跨场景下的目标识别在图 4的第2、3、4幅图所示的3个不同尺度中为目标1、2任选最窄窗口图像各1张,共6张,作为第一摄像机的目标图像。另外使用6个不同目标(包含目标1、2)各自分别在5个不同场景中拍摄共30段视频,目标尺度均不小于第一摄像机目标图像中的最大尺度,从中为每个目标在每种场景中截取最窄窗口图像1张,6个目标共30张目标图像,作为第二摄像机的目标图像,5个场景光照条件均不同,如图 6所示,图中行人为目标2,其他目标在此5种场景中的图像与此类似,不重复列出。
 |
| 图6 目标2在5种不同场景 |
按本文方法分别计算第一与第二摄像机目标图像的相似性距离,共有180个结果,将结果按第一摄像机目标图像的3个尺度分组计算均值和最值,分列于表 3,其中后两组(尺度为190和150像素)为跨尺度比较。另外,为考察本文方法的有效性,使用目前纹理描述常用的特征做同样的相似性距离计算,结果列于表 3中供比较。
| 表3 不同解析尺度下的分辨能力(亮度通道) |
表 3中,经典傅里叶分区方法(Fourier)[10]将频谱幅值图分成6个扇形区(0~180°),使用各区内的幅度均值及标准差组成归一化特征向量;Gabor方法[6, 7]使用4个波长尺度(以目标窗高为统一折算单位)和6个方向(0~180°)的Gabor模板对目标图像进行滤波,使用各次滤波的幅度均值及标准差组成归一化特征向量;LBP方法[16]使用具有旋转不变性的等价LBP值组成归一化特征向量。Fourier和Gabor特征使用Canberra距离,LBP特征使用Bhatacharyya距离。
对于各种方法的目标区分能力使用Q值评价,Q值越高区分能力越强,公式如下:
| $Q = \frac{{不同目标间最小距离-相同目标间平均距离}}{{相同目标间最大距离-相同目标间平均距离}}$ | (10) |
式中,如分子小于或等于0,则Q=0。另外,不同目标间的最小距离采用一个尺度数据组内居前5位(占该组数据总数的10%)最小距离的平均值,以排除异常数据影响。
从表 3可以看到,在跨场景的情况下,本文方法能较好地识别相同或不同目标,对光照亮度、色温及摄像机变化有较强的鲁棒性,与使用Gabor特征的效果类似。由于频谱信息损失小,本文方法的目标识别能力比经典傅里叶分区方法有所提高。在跨尺度比较时,本文方法受到的影响比LBP小。另外从表 3中还可以看到,作为基于表面结构性信息的特征,上述各种方法的目标识别效果均与目标尺度有关,尺度变小时识别效果普遍降低。
4.3 本文方法的运行速度本文方法使用Matlab2010b编程,在32位Windows XP下运行,硬件环境为:64位双核AMD Athlon II CPU,主频3.1GHz,一级缓存128 KB×2,二级缓存2 MB,内存3.25 GB。完成两幅285*90尺寸的图像比较用时仅为0.047 6s,已接近实时速度,这远快于使用Gabor特征的速度,对于目标的跨机再识别已经足够了。简单分析看,本文方法只需对视频帧中的目标区域使用高效的FFT算法做一次傅里叶变换,再对谱图进行必要的拉伸和高斯滤波即可用于匹配,匹配时只需对幅值足够大的一小部分重点频点(前面实验中纳入统计的重点频点个数均未超过窗口像素个数的20%)进行一次除法运算,再统计标准差,计算开销不大。如对程序加以优化,速度还会有较大提升空间。因此本文方法略作简化也可用于单机跟踪,比如与颜色特征融合使用。
5 结 束 语本文方法的实质是将图像转至频域进行模板匹配。由于转至了频域,解决了非刚性形变情况下空域模板匹配的对准问题。而通过对频谱做局部平均化处理和取样窗口的最窄限定,则使得频域模板匹配得以稳定可靠进行。由于频域模板最大程度地保留了图像信息,因此本文方法相对于几种常用的纹理特征方法有一定的改进,对于跟踪目标的跨机再识别有一定的实用价值。作为一种基于结构性信息的方法,本文方法对于跨摄像机时的光照变化和摄像机参数变化有一定的鲁棒性,但对目标的解析尺度和视角变化幅度有一定要求,容差能力还需进一步提高。此外,本文对光照方向变化引起的自阴影未做针对性处理。下一步还需研究目标表面结构性信息的丰富程度对本文方法影响,包括如何评价结构性信息的丰富程度并合理分配权重,从而使该方法能够更好地与其他特征融合使用。
| [1] | BLACK J, ELLIS T. Multiple camera image tracking[C]//Proceedings of the second International Workshop on Performance Evaluation of Tracking and Surveillance. Hawaii, USA: [s.n.], 2001: 68-75. |
| [2] | IBISCH A, HOUBEN S, MICHAEL M, et al. Arbitrary object localization and tracking via multiple-camera surveillance system embedded in a parking garage[C]//Proc SPIE 9407, Video Surveillance and Transportation Imaging Applications 2015. San Francisco, California, USA: SPIE, 2015: 94070G. |
| [3] | FEI YIN, MAKRIS D, VELASTIN S A, et al. Calibration and object correspondence in camera networks with widely separated overlapping views[J]. Computer Vision, IET, 2015, 9(3): 354-367. |
| [4] | WANG Xiao-gang. Intelligent multi-camera video surveillance: a view[J]. Pattern Recognition Letters, 2013(34): 3-19. |
| [5] | SOORI U, YUEN P W, HAN J W, et al. Target recognitions in multiple-camera closed-circuit television using color constancy[J]. Optical Engineering, 2013, 52(4): 602-614. |
| [6] | 闫允一, 姜帅, 郭宝龙. 结合稳定兴趣点和Gabor小波的图像检索[J]. 西安电子科技大学学报, 2014, 41(5): 118-123. YAN Yun-yi, JIANG Shuai, GUO Bao-long. Image retrieval using stable interest points and gabor wavelet[J]. Journal of Xidian University, 2014, 41(5): 118-123. |
| [7] | 朱明忠. 多尺度Gabor小波变换在图像检索中的应用[J]. 电子科技, 2011, 24(8): 61-69. ZHU Ming-zhong. Application of multi-scale Gaborwavlet transform in image retrieval[J]. Electronic Sci & Tech, 2011, 24(8): 61-69. |
| [8] | MENNESSONA J, JEANB C S, MASCARILLA L. Color fourier-mellin descriptors for image recognition[J]. Pattern Recognition Letters, 2014, 40: 27-35. |
| [9] | ALTANTSETSEG E, KATSUTSUGU M Y, KOUICHI K. Pairwise matching of 3D fragments using fast fourier transform[J]. The Visual Computer, 2014, 30(6-8): 929-938. |
| [10] | 闫晶莹, 王成儒. 一种新的纹理特征提取算法[J]. 西安邮电学院学报, 2011, 16(1): 49-53. YAN Jing-ying, WANG Cheng-ru. A new method for texture feature extraction[J]. Journal of Xi'an University of Posts and Telecommunications, 2011, 16(1): 49-53. |
| [11] | 彭国福, 林正浩. 图像处理中Gamma校正的研究和实现[J]. 电子工程师, 2006, 32(2): 30-36. PENG Guo-fu, LIN Zheng-hao. The study and implementation of Gamma correction in image processing [J]. Electronic Engineer, 2006, 32(2): 30-36. |
| [12] | CAO Yuan, PAN Xiao-fang, ZHAO Xiao-jin, et al. An analog gamma correction scheme for high dynamic range CMOS logarithmic image sensors[J]. Sensors(Basel), 2014, 14(12): 24132-24145. |
| [13] | KAUR K, KANWAL N, BHULLAR J S. A technique for enhancement of gray image using local Gamma correction [J]. International Journal of Computer Applications, 2014, 105(5): 36-39. |
| [14] | 储清翠, 王华彬, 陶亮. 图像的局部自适应Gamma校正[J]. 计算机工程与应用, 2015(7): 189-193. CHU Qing-cui, WANG Hua-bin, TAO Liang. Local adaptive Gamma correction method[J]. Computer Engineering and Applications, 2015(7): 189-193. |
| [15] | SINGH K, KAPOOR R. Image enhancement using exposure based sub image histogram equalization[J]. Pattern Recognition Letters, 2014(36): 10-14. |
| [16] | 刘丽, 谢毓湘, 魏迎梅, 等. 局部二进制模式方法综述[J].中国图象图形学报, 2014, 19(12): 1696-1720. LIU Li, XIE Yu-xiang,WEI Ying-mei, et al. Survey of local binary pattern method[J]. Journal of Image and Graphics, 2014, 19(12): 1696-1720. |
 2016, Vol. 45
2016, Vol. 45
