2. 中电集团第39研究所 西安 710065
2. No.39 Research Institute, CETC Xi'an 710065
网络蠕虫是一种无须用户干预即可独立运行的攻击程序或恶意代码[1]。如CodeRed和Slammer等蠕虫都可在很短的时间内主动攻击网络上具有相应漏洞的大量主机,其大规模爆发会造成巨大的经济损失,因而被认为是Internet上最大的安全威胁之一[2]。
为了减轻蠕虫的危害,人们提出了多种蠕虫建模、检测及遏制方法[3, 4, 5, 6, 7, 8, 9, 10]。目前,针对蠕虫的遏制技术主要包括加固技术、隔离围堵技术和良性蠕虫对抗技术等。加固技术仅针对已知漏洞或缺陷,却无法防范未知蠕虫。隔离围堵技术是为了减缓蠕虫的传播速度,并控制其感染范围,但算法较为复杂,如文献[11]对Chord进行扩展,提出一种被称为Verme的协议,即将系统节点按照其弱点类型进行分组,每一个组称为一个Island,具有相同弱点的Islands彼此不会相邻;文献[12]提出了一个专门的di-jest系统帮助节点选择邻居,在建立连接前,di-jest服务器使用一定的评估方法计算两个节点是否具有足够的差异性,从而避免脆弱性相同的节点相邻,延缓蠕虫传播,但并没有对节点差异性进行量化分析。良性蠕虫对抗技术对爆发的蠕虫进行动态的主动防御,是目前较有效的蠕虫遏制方法之一;文献[13]针对主动对抗技术、被动对抗技术及简单混合对抗技术存在的缺陷,提出了分而治之混合对抗技术;文献[14]提出实时混合对抗技术,但这两种方法对网络资源消耗较大。
针对现有蠕虫遏制技术存在的以上问题,本文提出基于节点异质度分析的蠕虫遏制方法。以自传播蠕虫为研究对象,对节点异(同)质度和拓扑区隔度进行量化;在此基础上,提出了两种新颖、实用的蠕虫遏制方法;采用Matlab7.0对以上方法进行有效性验证,并对仿真结果进行理论分析。
1 节点异质度及拓扑区隔度分析本节分析了蠕虫传播的行为特性,然后给出节点异质度、节点同质度和拓扑区隔度的定义,并对它们进行量化分析。
1.1 蠕虫传播行为特性自传播蠕虫利用主机的安全漏洞或策略缺陷,通过网络进行自传播的程序。这种蠕虫往往利用主机在操作系统、应用软件、数据库等方面存在的漏洞进行攻击。为了感染更多的主机系统,蠕虫一般会采用多种技术(如多线程、选择性随机扫描、DNS扫描和完全扫描等),最大限度地发现可攻击的目标,并在探测到多个弱点主机以后进行自传播,从而入侵大量的目标。蠕虫的传播模式如图 1所示。
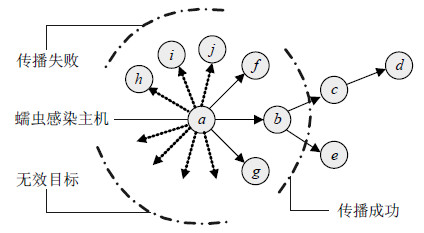 |
| 图1 自传播蠕虫活动模式 |
图 1中,蠕虫感染主机a进行目标探测一般会出现3种情形:1) “无效目标”,由于蠕虫采用选择性随机扫描或完全扫描策略,因此产生很多无效的扫描目标;2)“传播失败”,部分不具备蠕虫攻击所需漏洞条件的主机(如h、i和j等),虽被探测到,但无法被蠕虫感染;3)“传播成功”,部分弱点主机(如b、f和g等)被探测到后,蠕虫利用其漏洞获取系统权限,将自身传播出去,并形成感染链路,如链路a→b→c→d或a→b→e。
1.2 节点异质度、同质度的探测及量化方法由以上分析表明,节点a与b(或f、g)的同质性较强,即它们之间具有相同弱点的可能性较大,因此易受同一蠕虫的攻击;而节点a与h(或i、j)的异质性较强,即它们之间的差异性相对较大,从而不利于同一蠕虫的传播。为了描述节点间的这种关系,给出节点异质度、节点同质度和拓扑区隔度的定义如下:
节点异质度:指节点在操作系统、应用软件(或服务)、数据库和防御措施4个方面的差异性。
节点同质度:指节点在以上4个方面的相似性。
拓扑区隔度:指网络拓扑中所有相邻节点之间的平均异质度。
1) 节点异质度的探测及量化算法可分为:
① 确定异质度的评价指标并分级量化
由节点异质度定义可确定4个评价指标:O—操作系统类型及其漏洞;S—应用服务类型及其配置策略;D—数据库类型及其漏洞;F—安全防护措施。它们的分级量化如表 1所示。
| 表1 评价指标的分级量化表 |
② 利用漏洞扫描、安全检测和人工审计等方式,探测集群内每个节点在以上4个指标方面的准确信息,然后依据表 1对每一对节点进行分析比较,如针对节点i、j,则给出评价指标的等级量化值为$O(i,j)$、$S(i,j)$、$D(i,j)$和$F(i,j)$。
③ 采用权重系数${\omega _1}$、${\omega _2}$、${\omega _3}$和${\omega _4}$,用于反映以上4个评价指标对蠕虫传播的影响程度,则节点i、j的异质度为:
| $d(i,j) = {\omega _1}O(i,j) + {\omega _2}S(i,j) + {\omega _3}D(i,j) + {\omega _4}F(i,j)$ | (1) |
式中,${\omega _1} + {\omega _2} + {\omega _3} + {\omega _4} = 1$,具体取值由专家根据经验给出。
2) 节点同质度的探测及量化算法
根据节点同质度的定义,节点i、j的同质度$l(i,j)$为:
| $l(i,j) = 1 - d(i,j)$ | (2) |
将网络拓扑Net抽象为有向图$G(V,E)$来表示,其中顶点集合(代表网络节点)和边的集合(代表节点间存在物理或逻辑连接)分别用$V(G)$和$E(G)$表示。若Net拥有n个节点、m条边,则Net的拓扑区隔度量化计算为:
| $d({\rm{Net}}) = \frac{1}{m} \times \sum\limits_{e(i,j) \in E(G)}^m {d(i,j)} $ | (3) |
式中,$\forall i,j \in V(G)$;$e(i,j)$为边;$d(i,j)$为节点i和j之间的异质度。网络拓扑区隔度的大小反映了节点在拓扑中的差异化分布情况,其值越大表明拓扑中同质度较高的节点分布越分散,越有利于抑制蠕虫的传播,否则相反。
2 基于节点异质度分析的蠕虫遏制方法考虑到节点异(同)质度对蠕虫传播行为的影响,首先提出基于拓扑区隔度优化的蠕虫遏制方法,旨在增大拓扑区隔度以达到抑制蠕虫传播速度的目的;其次对传统的蠕虫主动对抗技术进行改进,提出基于网络监测的良性蠕虫主动对抗技术。
2.1 基于拓扑区隔度优化的蠕虫遏制方法增大网络拓扑区隔度,降低蠕虫感染率,能够实现对蠕虫传播的有效抑制。为此,在网络设计与规划阶段,在满足实际网络应用的前提下,可为重要节点设计异质度相对较大的邻居节点,或使同质度较大且易受蠕虫攻击的节点分散开来,避免集中分布,以阻断感染链路的形成;在网络建成并投入运行后,拓扑结构相对稳定,对其进行区隔度优化受到一定程度的条件限制,但仍可采用一些辅助手段来增大其区隔度,如节点调换、系统重装或服务重配置等。由以上分析可见,该方法既实用又可行。
针对网络设计与规划阶段,本文设计了一种拓扑区隔度优化方法,通过科学部署网络节点在拓扑中的位置,达到增大拓扑区隔度的目的,其主要步骤如下:
1) 将网络拓扑结构表示为图$G(V,E)$。
2) 依据拓扑结构图计算得到多组分布不同的拓扑区隔位,其算法如图 2所示。拓扑区隔位是指一组特殊的顶点集合,其中任意两顶点不存在物理(或逻辑)连接。
 |
| 图2 生成Net的拓扑区隔位置集 |
3) 对节点进行蠕虫感染风险评估及同、异质度分析,然后选取那些风险度和同质度均较大的节点,使它们分布于步骤2)得到的某一组或几组拓扑区隔位上,以达到风险分散的目的。
4) 对重要节点及其邻居节点进行漏洞加固、系统重装和服务重配置等,以使相邻节点间的异质度最大化。
拓扑区隔位生成算法实现如下:
Algorithm: 拓扑区隔位生成算法
Input: 网络拓扑结构图G(V,E),顶点集元烽|V(G)|=n,边集元数|E(G)|=m
Output: 输出该网络拓扑对应的一组区隔位置集S
BEGIN
i=1; //网络拓扑顶点集V(G)的元素标识,i∈{1,2,…,n}
k=0; //所生成区隔位置集S的元数|S|
S=Φ; //区隔位置集,初值为空集
L=V(G); //L为从V(G)中删除当前集合S及其邻居顶点后的剩余顶点集do
{ 1 从集合L中任取一个顶点v(i);
2 获取v(i)的甩有邻居顶点集N(i);
3 将顶点v(i)存入集合S中;
4 更新集合L,令L=L-N(i)-v(i),即从L中删除v(i)及N(i);
} while (|L|>0); //|L|为剩余顶点集L的元数
k=|S|;
输出拓扑区隔位置集S;
END
以一个拥有13个顶点的网络拓扑Net为例,可生成3组不同的区隔位置集S1、S2和S3,如图 2所示。
为了反映拓扑区隔度变化对蠕虫感染率的影响,在此给出考虑拓扑区隔度的蠕虫传播模型为:
| $\frac{{{\rm{d}}I(t)}}{{{\rm{d}}t}} = \frac{\lambda }{N}{e^{ - d(\Delta )}}I(t)[N - I(t)]$ | (4) |
式中,$d(\Delta ) = d({\rm{Net}}*) - d({\rm{Net}})$,$d({\rm{Net}})$为原拓扑区隔度,$d({\rm{Net}}*)$为优化后的拓扑区隔度;$I(t)$是t时刻被感染的主机数;N是网络主机总数;$\lambda $是蠕虫感染率;${e^{ - d(\Delta )}}$用于反映拓扑区隔度变化对蠕虫感染率的影响。这一模型能较好地描述扫描机制一致的蠕虫,尤其在传播初期没有人工干预的情况下,能较好刻画蠕虫的传播特性。
2.2 基于网络监测的良性蠕虫主动对抗方法将网络中的主机分为4类:1) 易感类S,该类主机既没有被蠕虫感染也没有被良性蠕虫感染,但具有被蠕虫感染的可能性;2) 感染类I,该类主机被蠕虫感染但没有被良性蠕虫感染;3) 良性感染类U,该类主机被良性蠕虫感染;4) 恢复类R,该类主机既不会被蠕虫感染也不会被良性蠕虫感染。
借助于医学界以毒攻毒的思想,良性蠕虫可以像蠕虫一样传播,给有漏洞的主机打补丁或清除被感染的主机上的蠕虫病毒,或者同时具有以上2个功能。文献[13, 14]中采用良性蠕虫主动扫描、感染所有易感主机,而没有考虑当易感主机与感染主机之间的异质度较大时,其实易感主机是很难被感染主机感染成功的。为此,本文对传统的良性蠕虫对抗方式进行改进,提出一种基于网络监测的良性蠕虫主动对抗方法,其实现机制如图 3所示。
 |
| 图3 基于网络监测的良性蠕虫对抗方法 |
图 3主要包含4个步骤:1) 当网络检测到蠕虫后,立即读取“网络节点信息数据库”,查找感染主机的IP、OS和相关配置信息等,同时触发良性蠕虫主动攻击新发现的感染主机;2) 分析感染主机与所有易感主机的差异性,并量化计算其异(同)质度。该计算过程是提前完成的,且随着网络变化而不断更新其计算结果;3) 依据步骤2)中的计算结果,将同质度较大(或异质度较小)的主机作为高危易感主机;4) 调整良性蠕虫的扫描策略,由默认的完全扫描策略调整为有针对性的部分扫描策略,即仅限于主动扫描和感染步骤3)中确定的高危易感主机群。此步能有效地控制良性蠕虫的扫描范围,提高其遏制蠕虫传播的有效性,且降低了网络资源消耗。
对蠕虫传播进行建模,该模型中用到的参数的含义及初始值见表 2。
| 表2 模型的参数及其初始值 |
主机间的状态转换如图 4所示。
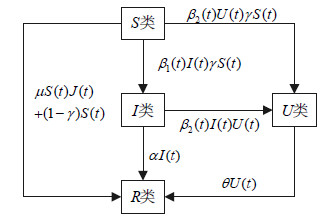 |
| 图4 主机间的状态转换图 |
根据主机间的状态转换图,可建立蠕虫的传播模型为如下微分方程组:
| $\left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}U(t)}}{{{\rm{d}}t}} = {\beta _2}(t)U(t)[\gamma S(t) + I(t)] - \theta U(t)}\\ {\frac{{{\rm{d}}I(t)}}{{{\rm{d}}t}} = {\beta _1}(t)I(t)\gamma S(t) - {\beta _2}(t)I(t)U(t) - \alpha I(t)}\\ {\frac{{{\rm{d}}J(t)}}{{{\rm{d}}t}} = {\beta _1}(t)I(t)\gamma S(t)}\\ {\frac{{{\rm{d}}R(t)}}{{{\rm{d}}t}} = \mu S(t)J(t) + (1 - \gamma )S(t) + \alpha I(t) + \theta U(t)}\\ {S(t) = N - I(t) - U(t) - R(t)} \end{array}} \right.$ | (5) |
随着蠕虫及良性蠕虫的不断传播,网络会被经常阻塞并且破坏网络中的设备,这样就减小了蠕虫的感染速度,因此得到蠕虫的感染率为:
| ${\beta _1}(t) = {\beta _1}(0){\left( {1 - \frac{{I(t) + U(t)}}{N}} \right)^{{\eta _1}}}$ | (6) |
同理可得良性蠕虫的感染率为:
| ${\beta _2}(t) = {\beta _2}(0){\left( {1 - \frac{{I(t) + U(t)}}{N}} \right)^{{\eta _2}}}$ | (7) |
为了验证本文的蠕虫遏制方法的有效性,采用Matlab7.0软件对蠕虫传播模型进行仿真,对比分析蠕虫传播变化曲线。为了叙述简便,方法1为基于拓扑区隔度优化的蠕虫遏制方法,方法2为基于网络监测的良性蠕虫主动对抗方法。
3.1 方法1对式(4)所示的蠕虫传播模型进行仿真,假设网络主机总数为$N = 1 \times {10^6}$,原拓扑的蠕虫感染率为$\lambda = 0.08$;第一次优化后,拓扑区隔度增大0.1,即$d({\Delta _1}) = 0.1$,第二次优化后对应$d({\Delta _2}) = 0.2$,第三次优化后对应$d({\Delta _3}) = 0.3$,对这3次拓扑区隔度优化后的蠕虫传播情况进行仿真,如图 5所示。
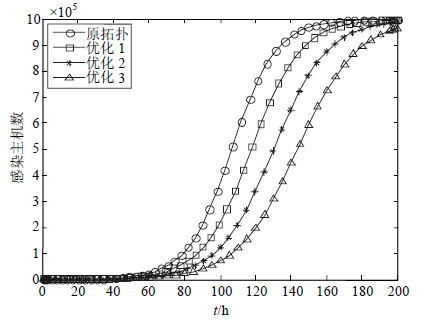 |
| 图5 蠕虫遏制有效性对比图 |
由图 5可知,对拓扑区隔度进行优化有利于遏制蠕虫的传播,且拓扑区隔度越增大,其对蠕虫的遏制效果就越好。
3.2 方法2为了有效比较方法2与文献[13, 14]中的主动对抗技术,除了增加参数$\gamma $以外,其余模型参数及其初值均相同。根据表 2所示的模型参数及其初值,可得方法2条件下的蠕虫传播情况,如图 6所示。
 |
| 图6 方法2条件下的蠕虫传播情况图 |
由图 6可知,在实施方法2条件下,随着良性感染主机数$U(t)$的逐渐增加,蠕虫感染主机数$I(t)$在$T \approx 18h$时达到峰值,随后便逐渐减少,直到$T \approx 70h$时减少为0,因此表明方法2具有较好的蠕虫遏制效果。
为了进一步证明方法2相对于文献[13, 14]中传统的主动对抗技术的优势,本文从遏制有效性、网络资源消耗两个方面进行比较分析。
1) 遏制有效性对比分析
参数$\gamma $表示高危易感主机占所有易感主机的百分比,即说明t时刻存在数目为$(1 - \gamma )S(t)$的易感主机与感染主机之间异质度相对较大,这部分易感主机并不会被蠕虫感染,因此将这部分易感主机暂时视为隔离主机是完全可行的。文献[13, 14]中的主动对抗技术就是$\gamma = 1$的情形,本文将其与参数$\gamma $取不同值时(95%、90%和85%)的蠕虫传播情况进行对比分析,如图 7所示。
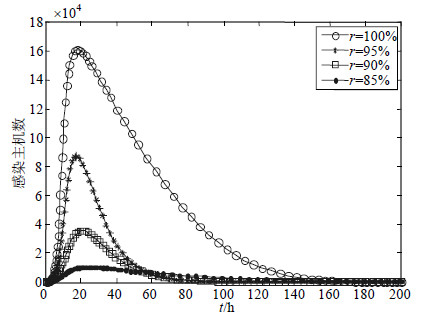 |
| 图7 遏制有效性对比分析 |
由图 7可知,在文献[13, 14]的传统对抗技术下($\gamma = 100\% $),其蠕虫感染主机数的峰值约为160 000;相比之下,方法2条件下($\gamma < 100\% $)的蠕虫感染主机数峰值小很多。因此,从遏制蠕虫爆发峰值的能力来看,方法2更能有效地抑制蠕虫的传播。
2) 网络资源消耗对比分析
蠕虫在传播过程中对网络的资源消耗与网络中的主动探测蠕虫(包括网络蠕虫和良性蠕虫)数量成正比。在主动对抗技术下,良性蠕虫和网络蠕虫均主动扫描网络中的漏洞主机,即主动探测蠕虫数量为感染主机$I(t)$和良性感染主机$U(t)$的数量之和。在参数取值同图 7的情况下,其主动探测蠕虫数量的对比变化情况如图 8所示。
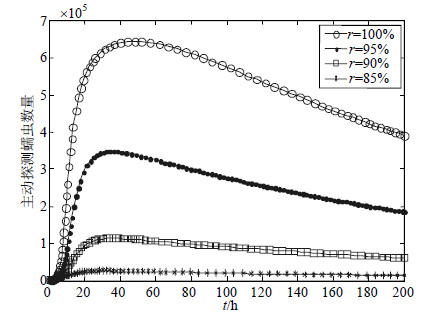 |
| 图8 网络资源消耗对比分析 |
由图 8可知,在文献[13, 14]的传统对抗技术下($\gamma = 100\% $),其主动探测蠕虫数量的峰值超过600 000;而在方法2条件下($\gamma < 100\% $),其主动探测蠕虫数量的峰值要小得多;另外,随着参数$\gamma $取值的减小,其主动探测蠕虫数量也减小。因而,采用方法2将节省更多的网络资源,更有利于缓解蠕虫攻击条件下的网络拥塞问题。
4 结 束 语本文分析了自传播蠕虫的行为特性,定义、量化了节点异(同)质度及网络拓扑区隔度;在此基础上提出了两种蠕虫遏制方法,即基于拓扑区隔度优化的蠕虫遏制方法和基于网络监测的良性蠕虫主动对抗方法;采用Matlab7.0软件对以上方法进行仿真验证,方法1的仿真结果表明,网络拓扑区隔度越大越有利于抑制蠕虫的传播速度;方法2对比仿真结果表明,方法2具有较好的蠕虫遏制效果,且能更好地满足遏制有效性和网络资源消耗低的双重要求。下一步工作是研究拓扑相关蠕虫的传播模型及其遏制方法。
| [1] | MOORE D, PAXSON V, SAVAGE S, et al. Inside the slammer worm[J]. IEEE Magazine of Security and Privacy, 2003, 1(4): 33-39. |
| [2] | HATAHET S, BOUABDALLAH A, YACINE C. A new worm propagation threat in bit torrent: Modeling and analysis[J]. Telecommunication Systems, 2010, 45(2-3): 95-109. |
| [3] | STEPHENSON B, SIKDAR B. A quasi-species model for the propagation and containment of polymorphic worms[J]. IEEE Transactions on Computers, 2009, 58(9): 1289-1296. |
| [4] | 严博, 吴晓平, 廖巍, 等. 基于随机进程代数的P2P网络蠕虫对抗传播特性分析[J]. 电子学报, 2012, 40(2): 293-299. YAN Bo, WU Xiao-ping, LIAO Wei, et al. Propagation characteristics analysis of worm-anti-worm in P2P network based on stochastic process algebra[J]. Acta Electronica Sinica, 2012, 40(2): 293-299. |
| [5] | 梁广民, 任安. 车载蠕虫传播建模与仿真[J]. 电子科技大学学报, 2013, 42(2): 277-282. LIANG Guang-min, REN An. Modeling and simulating epidemics of vehicular worms[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(2): 277-282. |
| [6] | 和亮, 冯登国, 王蕊, 等. 基于MapReduce的大规模在线社交网络蠕虫仿真[J]. 软件学报, 2013, 24(7): 1666-1682. HE Liang, FENG Deng-guo, WANG Rui, et al. Map reduce-based large-scale online social network worm simulation[J]. Journal of Software, 2013, 24(7): 1666-1682. |
| [7] | 冯朝胜, 秦志光, 袁丁, 等. P2P网络中被动型蠕虫传播与免疫建模[J]. 电子学报, 2013, 41(5): 884-889. FENG Chao-sheng, QIN Zhi-guang, YUAN Ding, et al. Modeling propagation and immunization of passive worms in peer-to-peer networks[J]. Acta Electronica Sinica, 2013, 41(5): 884-889. |
| [8] | 张伟, 王汝传, 李鹏. 基于云安全环境的蠕虫传播模型[J]. 通信学报, 2012, 33(4): 17-24. ZHANG Wei, WANG Ru-chuan, LI Peng. Worm propagation modeling in cloud security[J]. Journal on Communications, 2012, 33(4): 17-24. |
| [9] | 冯朝胜, 袁丁, 卿昱, 等. P2P网络中激发型蠕虫传播动态建模[J]. 电子学报, 2012, 40(2): 300-307. FENG Chao-sheng, YUAN Ding, QING Yu, et al. Dynamic modeling of reactive worm propagation in P2P networks[J]. Acta Electronica Sinica, 2012, 40(2): 300-307. |
| [10] | 汪洁, 王建新, 刘绪崇. 基于近邻关系特征的多态蠕虫防御方法[J]. 通信学报, 2011, 32(8): 150-158. WANG Jie, WANG Jian-xin, LIU Xu-chong. Novel approach based on neighborhood relation signature against polymorphic internet worms[J]. Journal on Communications, 2011, 32(8): 150-158. |
| [11] | FREITAS F, RODRIGUES R, RIBEIRO C, et al. VERME: Worm containment in peer-to-peer overlays[C]//IPTPS'07: Proceeding of the 6th International Workshop on Peer-to-Peer Systems. Sellevae: [s.n.], 2007. |
| [12] | MCILWRAITH D, PQAUIER M. Di-jest: Autonomic neighbor management for worm resilience in P2P systems [C]//WoWMoM'08: International Symposium World of Wireless, Mobile and Multimedia Networks. [S.l.]: IEEE, 2008. |
| [13] | 周翰逊, 赵宏, 闻英友. 分而治之的混合型良性蠕虫的建模与分析[J]. 计算机研究与发展, 2009, 46(7): 1110-1116. ZHOU Han-xun, ZHAO Hong, WEN Ying-you. Modeling and analysis of divide and rule hybrid benign worms[J]. Journal of Computer Research and Development, 2009, 46(7): 1110-1116. |
| [14] | 秦拯, 李军群, 欧露, 等. 实时混合对抗蠕虫的建模和分析[J]. 湖南大学学报(自然科学版), 2011, 38(5): 74-78. QIN Zheng, LI Jun-qun, OU Lu, et al. Modeling and analysis of real-time hybrid anti-worms[J]. Journal of Hunan University(Natural Sciences), 2011, 38(5): 74-78. |
 2016, Vol. 45
2016, Vol. 45

