全球定位系统 (global positioning system,GPS)作为基于导航卫星的分布式测距/距离、全球定位/导航系统,已在电力行业得到了较为广泛的应用[1]。该系统的组成包括:空间部分(24颗导航卫星)、地面控制部分(主控站、地面天线、监测站)和用户设备(GPS接收机、卫星天线)三部分构成。通常,用户通过卫星天线和GPS接收机,就能在地球上的任何地点实施定位与测时[2, 3]。目前,电力行业对GPS应用较多,如:故障测距、系统运行实时监测、电网调度自动化同步时间、故障录波器时间同步、雷电定位系统、自动控制与调节的标准时间等。因而带有GPS坐标的电力设备分布较广。从目前的诸多研究成果来看,GPS系统在导航系统中的应用还存在较多问题;首先,GPS作为非自主式的、我国没有自主知识产权的定位导航系统,它的应用往往受到国外政策等非技术因素的制约[2];其次,由于电力系统所处环境错综复杂,其中的桥梁、林区、坑道、密集建筑等地形地貌,都将对GPS系统的应用构成影响,特别是复杂电磁环境中,GPS系统的通信中断时常发生。因此,结合GPS系统与电子地图中的残存数据,实现容灾导航,进行自动寻路,已成为当前研究人员钻研的热点和难点之一[2]。由于现有的研究成果仅仅依托孤立的电子地图中残存的道路和坐标信息进行容灾[4, 5, 6],因此少有成功应用。目前国外较为先进的解决方案(如GPS-discovery)存在下列问题[3]:首先是用于电力系统维护的交通工具数量较多,分布较广,如果这些导航系统中的坐标“残迹”无法共享,则会带来极大的信息浪费[7, 8, 9];其次,尽管大量的电力设备具有GPS坐标,但仅自身的“残迹”信息和静态地图,在复杂多变的电网环境中,进行道路选择等容灾工作是极为困难的[10, 11]。针对上述问题,利用电力设施的坐标残迹,本文提出了一种新型容灾导航算法(disaster-tolerant navigation algorithm,DTNA)。
本文首先分析了当前系统存在的问题,给出了详细的解决思路;其次对算法的模型结构和电力设备GPS坐标“残迹”数据结构进行了详述,并给出算法流程;最后对比了算法的仿真性能,并分析其应用前景。
1 算法分析 1.1 问题分解目前广泛应用的GPS+电子地图导航模式,在面对各种灾难时存在下列3个问题:
1) 大量既有的电力设备坐标和资源被忽视和浪费。目前已投入应用的分布式容灾导航算法主要采用集中信息处理模式,即:大量的导航节点通过中心控制站或集中调度系统实现数据融合与信息交换,而节点间并不进行直接的数据交换与共享,诸如系统中已有的道路信息、电力设备的变更、GPS坐标等数据均无法实现多节点共享;此种容灾模式、在实际应用中问题较多,不但在处理性能方面存在中心瓶颈问题,而且当中心控制站出现通信故障或宕机时,整个导航系统将无法引导各节点[10, 11, 12]。与之形成鲜明对比的是:目前普遍装备的导航计算机系统(节点)往往具有较强的计算和存储能力,却不能物尽其用;较之远程通信,当节点相遇或并行时,存储在其中的电力设备残迹数据却不能共享,整个系统的容灾性能很差。
2) 大量已生成的导航信息利用率低下。尽管电子地图中往往包含有大量电力设备的GPS坐标,并在车辆行进过程中生成了较多的道路数据,但这些数据都属于“点”类型,数据表述的连续性较差,且具有用后即丢弃的“瞬态”特性;尽管电子地图等导航设备的存储空间较大,但缺少对应的通路存储备用机制,因此当出现通信灾难时,节点与GPS系统失联,无法获取路途中的坐标信息,也无法通过其他节点进行更新,经过一段时间后,既有的导航信息将消耗殆尽[13, 14, 15]。
3) 目前的组合导航系统中,由于相对于电子地图中的坐标,GPS信息是动态的,这主要体现在:相同道路上的不同节点接收到的可行道路GPS坐标,由于时间和位置不同而不完全相同;所以,一旦出现GPS通信灾难,电子地图将不得不根据节点自身的运行轨迹和残存坐标来代替GPS定位导航,而目前的容灾系统均缺少可行道路识别与匹配的相关算法,因而可行性较差[16, 17]。
1.2 解决方案针对第一个问题,本文算法改变了原有的信息集中共享模式,并充分利用了节点中残存的电力设备坐标“残迹”;要求各节点从临近的其他节点中尽可能获取“残迹”数据,从而保证自身在寻路过程中的数据自主性和全面性,但该算法避免节点间的中继通信,以降低系统的电力和通信开销,仅在节点彼此“相遇”时进行信息交换。
针对第二个问题,本文算法在导航系统中构建了“残迹”用于容灾导航的数据结构。但由于电力设备网络结构复杂,节点数量庞大,而电子地图和导航系统的存储容量通常比较有限[18, 19],因此算法严格限制了此类数据的种类和容量,并采用了最优淘汰机制进行数据更新。由于电力施工和维护过程往往需要车辆进入陌生地域,而在GPS出现灾难的情况下,导航系统中没有相关信息,因此不但需要特定的信息共享协议,实现电子地图的信息交换,以便实现陌生地域的导航与选路;而且需要构建与之对应的数据结构和处理算法进行高效的匹配与选择操作。
针对第三个问题,由于电力设备网络结构较为复杂,其中的道路可行性又呈现较为明显的随机性。此外,由于电力设备网络中的道路状态构成的描述空间相当复杂,难以通过普通的数值计算方法进行匹配和选择。我国的科研人员立足现有硬件设备,广泛采用了“以软件算法弥补硬件性能”的做法,并取得了一定的成功[20, 21, 22]。本文算法基于前人研究成果采用了FCM聚类算法进行道路聚类与匹配,通过实验发现效果良好。
1.3 算法模块与数据结构本文算法的处理单元与基本流程如图 1所示。由于车载电子地图等系统的处理能力较为有限,因此必须充分利用既有的电力设备坐标残迹,并采用精简算法模型,故而从结构上看,本文算法较为精炼。
 |
| 图1 DTNA算法结构域与流程 |
首先是残迹管理单元。该单元主要通过两种方式进行残迹数据收集:1) 灾难发生前,根据本节点所在位置(如未标注的电力设备或道路关键点等)定时或定点进行残迹生成;2) 在节点相遇时,彼此从对方的车载电子地图中共享相关数据。上述数据将在预处理后,保存在电子地图中的存储单元里,并可以通过1.5节中的算法进行搜索或匹配。此外,该单元还用于容灾导航过程中的自我纠偏,如:当节点经过若干有GPS坐标的电力设备时,该单元将电子地图中自身现存的位置和这些事前验证过的坐标进行数据融合,从而发现导航偏差,并予以纠正。
其次是容灾导航单元。该单元可以在GPS灾难时,通过实时跟踪行车路线(通过节点的速度和方向等参数累计求得)对节点的当前位置进行计算,并根据当前位置和目的地之间的残迹自动实现道路选择。由于导航误差,同一条道路往往在电子地图中被标注为多条不同的道路。同时,地图上的任意两点之间可能存在多条可通行。为对上述问题进行辅助决策,本单元采用了1.5节中的处理方法实施道路的评估和预测(匹配),从中找出匹配程度最高、最为适宜的道路。
最后是双向接口单元。第一种接口用于残迹管理单元与电子地图的数据通信,该接口上传递的数据主要是“道路关键点/残迹队列”;第二种接口用于残迹管理单元与容灾导航单元之间的通信,该单元向上接收用户提交的导航需求,向下接收整合后的残迹数据,将选路辅助决策信息,通过电子地图提供给用户,实现“道路信息-寻路需求”匹配查找。
本文算法中的外来数据与自生成数据量较大,为统一进行数据管理,采用了循环链表结构来保存电力设备的坐标残迹以及道路的关键点信息,以便在GPS灾难发生时进行道路辅助选择。尽管本文算法以残迹作为基本的数据支撑,但考虑到数据结构的包容性,因此选择了信息量较大的“道路标志信息”记录作为主元素,从而构成链表。该链表以残迹管理单元的信息生成顺序和信息提供节点的ID为master/slave索引),与其他简单链表不同,该链表的所有元素均以嵌入方式,链接了新链表,从而保存和管理该道路上的对应数据,主要是道路标志信息与残迹数据。这些元素以GPS定位的产生时间和坐标数据为master/slave索引。通过采用这种嵌入式链表结构,算法能够从横向上管理对每条道路中包含的“残迹”和关键点。从纵向上能够以时间为依据,以相遇的每辆车的ID作为“道路标志信息”的索引,同时能够区分同路的不同节点生成的“不同道路”,从而为容灾导航提供了良好的数据基础。算法通过该链表,可以实现道路的检索和匹配操作,具体实现参见1.5节。
1.4 算法流程本文算法的处理流程主要分为3段,如图 1所示:
1) 各节点通过两种方式收集导航坐标。一方面在行进途中,人工或自动记录和保存各种电力设备的GPS坐标,另一方面对行驶过的道路进行关键点数据采集,以便在GPS灾难发生时使用。在此阶段,当节点能够彼此直接通信时(例如平行或错车时),算法将通过直接通信方式交换两类容灾数据:当前自身信息(如:根据多坐标测量算法生成的当前所在位置坐标),及电子地图中目前存在的道路“残迹”数据(包括道路上各关键点的坐标、路况等数据)。
2) 自动容灾导航阶段。当GPS灾难发生时,算法将从嵌入电子地图的残迹二维叠加空间中提取数据,加载于电子地图的坐标图层;同时,算法将道路标志信息通过人机接口模块,一方面标注于坐标图层,另一方面在节点通过这些坐标附近时,提醒驾驶员进行核对和验证,通过上述操作,算法一方面能对车辆自身所在位置进行纠偏,另一方面为驾驶员进行道路选择提供辅助决策。
3) 人机交互阶段。节点需要进行自动容灾导航时,电子地图接收到寻路的任务信息(如:源点、目标点、当前方向等),算法将根据电子地图中的残迹数据,提供将任务信息在二维叠加空间进行搜索,选择其中最优的道路残迹,并通过电子地图展示给驾驶员,以供选择参考。
1.5 残迹数据处理算法针对上述需求,本文提出了基于信息融合的残迹数据处理方法,可以假设两条道路向量分别为Vi和Vj,两条道路中的关键信息点数量分别为li和lj,其中相近点(分布式导航标准为两点间距离50米)共有l个,则这两条道路的相似度(也可用于“道路信息-寻路需求”匹配查找)可描述为:
| $T({{\bf{V}}_i},{{\bf{V}}_j}) = \left\{ \begin{array}{l} \frac{l}{{{l_i} + {l_j} - l}}\begin{array}{*{20}{c}} {}&{} \end{array}当l \ge k\\ \begin{array}{*{20}{c}} {}&{} \end{array}0\begin{array}{*{20}{c}} {}&{}&{} \end{array}当l < k \end{array} \right.$ | (1) |
式中,T∈[0,1],而k为道路相近点控制阈值,需根据具体情况配置。基于上述相似度表述,本文算法采用FCM算法实现了基于划分的道路聚类子算法,该算法的核心思想是同一类道路之间的相似度最高。相对于其他算法对于道路相似的划分而言,FCM算法是柔性的、模糊的划分,因而适于处理残迹点数不同、相近点交错出现的道路数据。该算法的主要处理过程可以表述为:在道路选择或匹配过程中,通过迭代选优,刷新各道路的“残迹”中心,以及相关的隶属度矩阵中的数据,直到相关道路数据接近准则函数的极小值:
| ${J_m}(U,{\bf{V}}) = \sum\limits_{j = 1}^N {\sum\limits_{i = 1}^c {u_{ij}^m} } d_{ij}^2$ | (2) |
式中,V={v1,v2,…,vc},为道路以某一残迹wi为中心的矢量;相关权重可表述为:$m \in (1,\infty )$;$d_{ij}^2 = ({x_j} - {v_i}){\bf{A}}({x_j} - {v_i})$,A为正定矩阵,当${\bf{A}} = I$时,dij是欧氏距离$\left\| {{x_j}} \right. - \left. {{v_i}} \right\|$。式(2)的相关约束条件设定为$\sum\limits_{i = 1}^c {{u_{ij}}} = 1$$\left| {{\forall _j}} \right.$,此时,使用拉格朗日乘数算法进行处理,得到下列无约束准则:
| $F = \sum\limits_{j = 1}^N {\sum\limits_{i = 1}^c {u_{ij}^m} } d_{ij}^2 - \sum\limits_{j = 1}^N {{\lambda _{\rm{j}}}} \left( {\sum\limits_{i = 1}^c {{u_{ij}}} - 1} \right)$ | (3) |
式(3)达到极小值的必要条件为:
| $\partial F/{\partial _{uij}} = mu_{ij}^{m - 1}d_{ij}^2 - {\lambda _j} = 0$ | (4) |
| $\partial F/\partial {\lambda _J} = - \left( {\sum\limits_{i = 1}^c {{u_{ij}}} - 1} \right) = 0$ | (5) |
根据上述两个条件,综合式(3)则有:
| ${u_{ij}} = {({\lambda _j}/md_{ij}^2)^{\frac{1}{{m - 1}}}}$ | (6) |
将(6)引入上式(5)可得:
| $\sum\limits_{i = 1}^c {{u_{ij}}} = {\left( {\frac{{{\lambda _j}}}{m}} \right)^{\frac{1}{{m - 1}}}}{\sum\limits_{i = 1}^c {\left( {\frac{1}{{d_{ij}^2}}} \right)} ^{\frac{1}{{m - 1}}}} = 1$ | (7) |
由此可得:
| ${\left( {\frac{{{\lambda _j}}}{m}} \right)^{\frac{1}{{m - 1}}}} = \frac{1}{{\sum {{{\left( {\frac{1}{{d_{kj}^2}}} \right)}^{\frac{1}{{m - 1}}}}} }}$ | (8) |
将式(8)引入式(6),可得:
| ${u_{ij}}\frac{1}{{\sum\limits_{k = 1}^c {{{\left( {\frac{{{d_{ij}}}}{{{d_{kj}}}}} \right)}^{\frac{2}{{m - 1}}}}} }}$ | (9) |
由于${d_{ij}}$存在0值;则对于${\forall _j}$可以将集合${I_j}$和${\bar I_j}$定义为:${I_j} = \{ i\left| {{d_{ij}}} \right. = 0\} $,以及${\bar I_j} = \{ 1,2, \cdots ,3\} - {I_j}$,此时,如果${I_j} = \Phi $,将有:
| ${u_{ij}} = \frac{1}{{\sum\limits_{k = 1}^c {{{\left( {\frac{{{d_{ij}}}}{{{d_{kj}}}}} \right)}^{\frac{2}{{m - 1}}}}} }}$ | (10) |
当${I_j} \ne \Phi $时,则${\forall _i} \in \overline {{I_j}} $,此时,需要进行如下设置:${u_{ij}} = 0$,以及$\sum\limits_{i \in {I_j}} {{u_{ij}}} = 1$;进一步,可以得出道路聚类中心的更新公式,由$\partial J(U,V)/{\partial _{{v_i}}} = 0$时,有:
| $\begin{array}{c} \sum\limits_{j = 1}^N {u_{ij}^m} \frac{\partial }{{\partial {v_i}}}[({x_j} - {v_i}){\bf{A}}({x_j} - {v_i})] = \\ \sum\limits_{J = 1}^N {u_{ij}^m} [ - 2{\bf{A}}({x_j} - {v_i})] = 0 \end{array}$ |
由式(10)引出:
| ${v_i} = \sum\limits_{j = 1}^N {u_{ij}^m} {x_j}/\sum\limits_{j = 1}^N {u_{ij}^m} $ | (11) |
根据上述推导,结合道路匹配和选择的实际需求,可以得出本算法中的道路聚类算法步骤。
1) 首先确定需要进行聚类的类数$c(2 \le c < N)$、阈值m、道路矩阵A和误差阈值$\varepsilon > 0$;
2) 生成初始FCM算法的模糊分类矩阵${U^{(0)}}$,其中以式(2)为表述,${u_{ij}}$表征其中的元素,并设置s=0;
3) 对${U^{(s)}}$的$\{ v_i^{(s)}\} $集合进行计算,有:
| $v_i^{(s)} = \sum\limits_{j = 1}^N {u_{ij}^m} {x_j}/\sum\limits_{j = 1}^N {u_{ij}^m} {\rm{ }}i = 1,2, \cdots ,c$ |
4) 以下列算式刷新${U^{(s)}}$为${U^{(s + 1)}}(j = 1$~$N)$,$N)$和${\bar I_j}$${I_j} = \{ i\left| {{d_{ij}}} \right. = 0\} $,${\bar I_j} = \{ 1,2, \cdots ,c\} - {I_j}$,刷新xj的隶属度。当${I_j} = \Phi $时,有${u_{ij}} = \frac{1}{{\sum\limits_{k = 1}^c {{{\left( {\frac{{{d_{ij}}}}{{{d_{kj}}}}} \right)}^{\frac{2}{{m - 1}}}}} }}$;如不为空,则有${u_{ij}} = 0$,${\forall _i} \in {\bar I_j}$设置$\sum\limits_{i \in {I_j}} {{u_{ij}}} = 1$。
5) 判断是否有$\left\| {{U^{(s)}} - } \right.\left. {{U^{(s + 1)}}} \right\| < \varepsilon $,如果满足该条件,则停止递归;反之,则有s=s+1,循环至步骤3)继续。
2 性能实验与分析为验证算法的性能,将其与目前常见的GPS- discovery算法进行了基于仿真实验的平行对比[2]。GPS-discovery算法是一种常见于车载导航系统中的通用容灾算法,主要应用于CAN车载现场总线系统中。由于其性能优良,已有多款智能导航系统中嵌入了该算法,实践证明该算法具有一定的容灾能力,但在精度和时耗上还需要进一步提高。仿真实验中模拟了20个节点(电力施工/维护车辆)在20 km×20 km(其中带有GPS坐标的电力设备数量为100~300个,设备间最小间距为100 m)的地幅内遭遇GPS通信灾难的场景,设定车辆间的数据传输距离为200m,节点间采用全双向(通讯速率为64 K/s),车辆的速度设定为10 km/h~60 km/h随机生成。分别通过两种算法记录其仿真过程来度量其性能;仿真地图中共设置了12条通路,同时,模拟的车载电子地图中随机预设了2~5条已知坐标序列的道路,并至少包含一条正在生成的道路残迹序列。
从宏观上看,图 2展示的是两种算法在仿真实验中克服GPS灾难,同效果容灾(达到相同的容灾程度)引导区域中所有车辆脱困所需的平均时耗。如图 2所示,采用本算法的分布式导航系统,节点间能够充分共享和融合电力设备的坐标残迹,因而较之目前常用的GPS-Discovery算法能够更快地引导车辆寻找可行的道路,到达目的地。
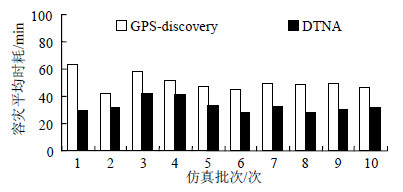 |
| 图2 两种容灾算法的时耗对比 |
图 3展示了在历次仿真实验中,虚拟节点中的两种算法为完成容灾各自消耗的系统资源。电子地图系统中最重要的是计算资源和存储资源,尽管本算法数据结构较为复杂,并且存在节点间“残迹”共享操作,但该算法所需的存储资源与GPS-discovery算法相比,并不存在明显差别,因此未在图中罗列(运行本算法的虚拟节点平均所需的存储空间较之运行GPS-discovery算法的节点所需,相差在±4%以内)。而本算法所需的计算资源远少于GPS-discovery算法所需,因而更加适用于计算能力有限的电子导航系统。
 |
| 图3 两种容灾算法的计算资源消耗对比 |
从微观上看,DTNA算法也具有较高的导航精度,如图 4所示。从两次实验中各随机选取了5台虚拟车辆作为导航精度的监测记录对象,其中DTNA算法为A组,而GPS-Discovery算法为B组。如图 4所示,DTNA的导航精度全面(平均超过25%以上)超过了GPS-Discovery算法,而且在达到精度峰值之后,精度下降趋势也较为平缓,保持了较高的个体导航精度,体现了算法较好的稳定性。
 |
| 图4 两种容灾算法的个体导航精度对比 |
从仿真实验结果来看,DTNA算法的道路选择和匹配子算法的精度尚可,但对广幅地域中海量残迹数据的存储和处理方法需要进一步研究。此外,为充分利用驾驶员的经验,还将进一步研究容灾导航算法中的人机交互信息共享方法与技术,从而提高算法的适应性和可用性。该算法的适用性改造包括以下两个方面:首先是算法运行环境的适用性改造,需要因地制宜的根据不同的运行环境调整算法,从而发挥其最大功效,如:当前嵌入式系统的存储器大大增加,该算法可以适当以存储换计算,扩大残迹的存储量,从而提高算法的运行速度和精度;其次是算法的跨平台适应性改造,该算法当前采用C语言开发,未来可以考虑采用JAVA改造,从而实现多平台一体化,保证算法的可移植性,使得不同平台上的导航系统能在发生灾难时,相互提供容灾信息。
| [1] | 刘雯静, 张童飞, 胡志珍, 等. 基于超声和无线组网的超高树障在线监测装置[J]. 电力系统自动化, 2013, 37(10): 98-103. LIU Wen-jing, ZHANG Tong-Fei, HU Zhi-zhen, et al. A transmission line monitoring device based on ultrasonic and wireless networking technologies[J]. 2013, 37(10): 98-103. |
| [2] | 张佳琳, 赵琳. 基于残迹融合的高可用分布式导航算法[J]. 四川大学学报(工程科学版), 2011, 43(3): 118-123. ZHANG Jia-lin, ZHAO Lin. A high available distributed navigation algorithm based on access vestige fusion[J]. Journal of Sichuan University(Engineering Science Edition), 2011, 43(3): 118-123. |
| [3] | 沈迪, 李建华, 朱瑞. 军事信息系统容灾备份策略仿真研究[J]. 计算机仿真, 2013, 30(1): 23-27. SHEN Di, LI Jian-hua, ZHU Rui. Simulation and researching of disaster backup strategy of military information system[J]. Computer Simulation, 2013, 30(1): 23-27. |
| [4] | 李佩娟, 徐晓苏, 王立辉, 等. 水下无源组合导航系统智能容错方法设计[J]. 中国惯性技术学报, 2013, 21(2): 221-225. LI Pei-juan, XU Xiao-su, WANG Li-hui, et al. Design of intelligent fault-tolerant to passive underwater integrated navigation sys-tem[J]. Journal of Chinese Inertial Technology, 2013, 21(2): 221-225. |
| [5] | 曲法义, 王小刚, 崔乃刚, 等. 基于惯导/GPS/视觉的无人机容错相对导航方法[J]. 中国惯性技术学报, 2013, 21(5): 781-786. QU Fa-yi, WANG Xiao-gang, CUI Nai-gang, et al. Fault-tolerance relative navigation approach based on SINS/GPS/Vision for UAV[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 781-786. |
| [6] | GURKAN T, BILEL N, GIANPAOLO C. Unmanned aerial vehicle-aided communications system for disaster recovery[J]. Journal of Network and Computer Applications, 2014, 41(1): 27-36. |
| [7] | BRANDON P S. Extreme management in disaster recovery[J]. Procedia Engineering, 2011, 14(3): 84-94. |
| [8] | TUNA G, MUMCU T V, GULEZ K. Unmanned aerial vehicle-aided wireless sensor network deployment system for post-disaster monitoring[C]//The 8th International Conference on Intelligent Computing (ICIC). Huangshan, China: [s.n.], 2012, 304(1): 298-305. |
| [9] | XU T, CHUDLEY J, SUTTON R. A fault tolerant multi-sensor navigation system for an unmanned surface vehicle[J]. Fault Detection, Supervision and Safety of Technical Processes, 2012, 12(3): 1503-1508. |
| [10] | YANG Feng, CHENG Cheng, PAN Quan, et al. Practical integrated navigation fault detection algorithm based on sequential hypothesis testing[J]. Journal of Systems Engineering and Electronics, 2011, 22: 146-149. |
| [11] | LI Xu, ZHANG Wei-gong. An adaptive fault-tolerant multisensor navigation strategy for automated vehicles[J]. IEEE Transactions on Vehicular Technology, 2010, 59(6): 2815-2829. |
| [12] | LI Wen, LI Qing-dong, REN Zhang. On air data assisted INS/GPS fault-tolerant integrated navigation system[C]//The 2014 33rd of Control Conference (CCC). Beijing, China: [s.n.], 2014: 3282-3286. |
| [13] | LIANG Yue-qian, JIA Ying-min, MATSUNO F. A fault-tolerant integrated navigation for UAV systems using time-variant vector distribution coefficients[C]//American Control Conference (ACC). Portland, OR, USA; IEEE, 2014: 678-683. |
| [14] | PORTUGAL D, ROCHA R P. Scalable, fault-tolerant and distributed multi-robot patrol in real world environments [C]//International Conference on Intelligent Robots and Systems (IROS). Tokyo: IEEE, 2013: 4759-4764. |
| [15] | USHAQ M, FANG Jian CHENG. A fault tolerant integrated navigation scheme realized through online tuning of weighting factors for federated kalman filter[J]. Applied Mechanics and Materials, 2014, 446(2): 1078-1085. |
| [16] | LI Dan-yong, SONG Yong-duan, HUANG Dong, et al. Model-independent adaptive fault-tolerant output tracking control of 4WS4WD road vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 169-179. |
| [17] | ZHAO Bo, SKJETNE ROGER, BLANKE MOGENS, et al. Particle filter for fault diagnosis and robust navigation of underwater robot[J]. IEEE Transactions on Control Systems Technology, 2014, 32(9): 1372-1381. |
| [18] | USHAQ M, Fang Jian CHENG, ALI J. An adaptive & fault tolerant sins/gps integrated navigation scheme robustified against slowly growing errors in gps updates[J]. Applied Mechanics and Materials, 2013, 390(5): 500-505. |
| [19] | ZENG Jing, GUO Xiao-song, ZHANG Guo-liang. Study on fault-tolerant method of mobile robot integrated navigation[J]. Applied Mechanics and Materials, 2013, 301(1): 468-474. |
| [20] | 吴有龙, 王晓鸣, 曹鹏, 等. 一种改进的故障检测算法在组合导航中的应用[J]. 北京理工大学学报, 2015, 35(5): 494-499. WU You-long, WANG Xiao-ming, CAO Peng, et al. A novel fault detection algorithm for integrated navigation system[J]. Transactions of Beijing Institute of Technology, 2015, 35(5): 494-499. |
| [21] | 柳明. GPS失效下的无人机组合导航系统[J]. 济南大学学报, 2014, 29(2): 129-132. LIU Ming. UAV integrated navigation system under GPS failure[J]. Journal of University of JiNan, 2014, 29(2): 129-132. |
| [22] | 王融, 刘建业, 熊智, 等. 基于序贯概率映射的组合导航自适应容错算法[J]. 控制与决策, 2014, 29(10): 1861-1865. WANG Rong, LIU Jian-ye, XIONG Zhi, et al. Adaptive fault-tolerant algorithm based on sequential probability mapping for integrated navigation[J]. Control and Decision, 2014, 29(10): 1861-1865. |
 2016, Vol. 45
2016, Vol. 45
