2. 成都信息工程大学控制工程学院 成都 610225;
3. 上海交通大学软件学院 上海 闵行区 200030
2. School of Control Engineering, Chengdu University of Information Technology Chengdu 610225;
3. School of Software, Shanghai Jiaotong University Minhang Shanghai 200030
在提倡节能减排的当今世界,用电设备尤其是科学计算设备的能耗问题日益突出,越来越受到软硬件开发商、科研机构和政府的重视[1, 2]。
在工业界有一句名言“如果你不能度量它,那么你就不能改进它”,这句话蕴含了度量是后续工作的基础[2]。能耗度量方式主要有间接和直接两种方式。间接方式是利用能耗模型、利用硬件性能计数器或硬件事件和能耗之间的关联模型进行估测软件运行能耗。文献[3, 4]基于部件访问率提出了一种功率模型,用来估测部件的功率和整个程序的功率消耗;文献[5, 6]通过估算指令能耗提出了嵌入式软件能耗计算方法和操作系统内核能耗估算模型;文献[7]基于神经网络的训练结果提出了GPU的功耗模型。间接方式方便了用户获得功率或能耗数据,但这些数据通常误差较大且在硬件环境改变的情况下模型的参数必须重新进行训练。软件能耗测量最直接的方式是使用功率测量仪器,但它在能耗测量上存在和设备连接困难的缺点。目前,利用内置传感器进行功率采集测量已经成为一种趋势,如NVIDIA的Tesla系列显卡[1, 8]。内置传感器测量方式带来了很大的方便,同时也引起了诸如功率迟滞、程序能耗受其启动时间影响等问题[9, 10]。文献[9]通过引入经验参数进行解决,但它的计算需要显卡内部电路器件组成,要求较高。为此,本文提出了一种无需了解显卡内部电路器件组成的基于逼近函数的数据采集矫正方法。通过实验验证,该方法能够很好地解决此类问题。
1 问题描述使用内置功率传感器采集功耗数据时会产生功率迟滞、程序能耗受其启动时间影响等问题[9, 10]。这些问题影响了程序能耗测量的准确性以及破环了软件功耗不受启动时间影响的特性。
1) 传感器采集功率迟滞问题。功率迟滞问题表现为内置功率传感器在程序运行阶段和结束阶段采集的功率数据未能实时地反映设备实际功率使用情况,采集的功率往往迟滞于GPU内核程序驱动硬件活动状况。它们所表现出的共同特征是传感器采集的数据逐渐接近真实功率。迟滞问题会造成在程序运行时间内对功率数据的积分所得到软件能耗数据不准确。由于无法明确迟滞时间,且迟滞时间难以在采集到的功率曲线中体现出来,因此通过延长采样时间的方法来获得程序真实能耗的方法是不可行的。用量化的方式来描述这种现象即为:
| $E_{({t_1},{t_2},{\text{Sw}})}^{{\text{Sensor}}} < E_{({t_1},{t_2},{\text{Sw}})}^{{\text{Actual}}}$ | (1) |
2) 程序能耗受启动时间影响。上述迟滞现象所造成的另一个问题是两个相同程序在相差一段时间内运行,后者所消耗的能耗显著增加,即程序启动时间间隔影响其后程序的能耗。从软件能耗产生本质原因来看,两个相同的程序在相同的硬件上运行的能耗是相同的或由于程序运行的局部性原理而造成的后者能耗的降低;并且软件能耗与软件的启动时间无关,但由于迟滞现象的出现使得相同程序所消耗的能耗和启动的时间相关。这种现象明显与软件能耗产生的本质[2, 4]不符。用量化的方式来描述这种现象即为:
| $E_{({t_1},{t_2},{\text{Sw}})}^{{\text{Sensor}}} \ne E_{({t_{\text{2}}}{\text{ + }}\Delta t,2{t_2}{\text{ + }}\Delta t - {t_1},{\text{Sw}})}^{{\text{Sensor}}}$ | (2) |
式(1)和式(2)中的E表示软件能耗;三元组下标$({t_1},{t_2},{\text{Sw)}}$分别表示程序开始时间、程序结束时间、运行的软件;Δt为两个程序启动时间间隔;上标Sensor和Actual分别表示使用功率传感器测得的能耗和设备实际消耗能耗情况。
2 基于逼近函数的能耗矫正方法由于内置功率传感器内部的硬件组成细节、硬件驱动实现以及其使用的功率计算算法厂商未被提供,所以本文通过采集传感器的大量数据,以及观测相关现象进而分析上述问题产生的原因主要在于:
1) 观测传感器所采集的大量数据发现它们具有连续性,推测传感器可能使用了与温度相关的算法来计算功率。
2) 从传感器在程序运行阶段和结束阶段采集的数据所表现出的共有特征,推测功率传感器可能使用了一类电容或电感效应的电路。
上述原因使得传感器采集到的数据在程序运行阶段和结束阶段不能真实反映软件在运行时设备的功率使用情况。软件能耗和硬件能耗之间的关系[2, 5]、问题产生的原因以及传感器采集的数据逐渐接近真实功率的现象[9, 10],启发本文根据软件运行时长进行数据矫正。内置传感器采集运行时间短的程序所得到的功耗数据是趋向性数据,对其进行拟合能够对趋向性数据进行矫正。对于运行时间长的程序,由于传感器采集的数据是逐渐逼近的真实数据,本文采用基于误差方向的逼近函数进行矫正。
对传感器采集的大量数据进行观测发现如果程序运行时间或并行程序中的分阶段运行的线程时间在小于tp内,那么在这个时间段内传感器测得的数据是趋向性数据,这段程序所消耗的真实功率可以利用位于tp后的功率数据来表示。tp是内置功率传感器数据趋于真实数据时的时间,它的取值为内置功率传感器从产生功耗数据开始得出的功耗数据和文献[7]中直接功率测量方法得到的数据相差3%时所经历的时间。不同型号的GPU有不同的tp值。为了减少误差可以通过采集一定数量软件的功耗数据获得。由于程序运行时间在tp内,测得的数据是趋向性数据。利用函数拟合方法能够使采集到的趋向性数据逼近软件运行时的实际功率数据,因此采用函数拟合方法对软件运行时的功率进行逼近。首先利用函数拟合方法将采集到的数据拟合成函数${f_{{P_{{\text{meas}}}}}}{t_i}$,然后再求得${f_{{P_{{\text{meas}}}}}}({t_p} + {t_i})$来逼近表示时刻ti下的真实功率数据,为了提高准确度,本文取时刻ti-△t、时刻ti以及时刻ti+△t下功率数据的平均作为逼近表示时刻ti下的真实功率数据。因此运行时间在tp内程序的功率数据使用如式(3)进行矫正:
| $\begin{align} & {{P}_{\text{real}}}({{t}_{i}})=\text{Avg}({{f}_{{{P}_{\text{meas}}}}}({{t}_{i-\Delta t}}+{{t}_{P}}), \\ & {{f}_{{{P}_{\text{meas}}}}}({{t}_{i}}+{{t}_{P}}),{{f}_{{{P}_{\text{meas}}}}}({{t}_{i+\Delta t}}+{{t}_{P}})) \\ \end{align}$ | (3) |
对于运行时间大于${t_P}$部分的程序,由于传感器所采集到的数据逐渐逼近于真实数据且利用误差方向可以逼近于真实数据,因此采用误差方向为判断标准的逼近函数能够很好地逼近于程序的实际功耗并可以得到理想的效果。误差方向用K表示,是传感器采集数据的逼近方向。在逼近方向范围内使用逼近值对实际功耗数据进行表示。采用式(4)对运行时间大于${t_P}$部分的软件功耗数据进行矫正表示:
| ${{P}_{\text{real}}}({{t}_{i}})=\left\{ \begin{align} & Avg(P_{\text{meas}}^{K}({{t}_{i-\Delta t}}),P_{\text{meas}}^{K}({{t}_{i}}),P_{\text{meas}}^{K}({{t}_{i\text{+}\Delta t}}))K\ge 0 \\ & \text{Min}(P_{\text{meas}}^{K})K\text{} < 0 \\ \end{align} \right.$ | (4) |
| $K = \frac{{{P_{{\text{meas}}}}({t_{i + \Delta t}}) - {P_{{\text{meas}}}}({t_{i - \Delta t}})}}{{{t_{i + \Delta t}} - {t_{i - \Delta t}}}}$ |
在程序运行结束后,内置传感器会产生尾滞能耗现象[9, 10, 11]。它由两部分组成,一部分是传感器采集每个程序都有的常数能耗部分,常数部分是测量所有程序都表现出来的不随所测程序改变而改变的恒定能耗部分;另一部分能耗是根据软件运行时间不同的可变部分,它是程序运行结束后设备保持活动空闲时的功率。因此对于尾滞能耗的可变部分不能作为软件运行时的能耗。为了使尾滞能耗的可变部分能更好地表现出程序结束时设备的功率情况,根据能耗产生的本质[2, 5],只需将尾滞能耗的可变部分矫正为空闲状态时的功率即可;常数能耗部分为程序无关的且是恒定的,所以不需要矫正。
综上,经过上述方法得到程序运行时的实际功率数据,利用式(5)将上述矫正后的数据在程序运行的时间段内进行积分就可以得到程序的真实能耗数据:
| $E_{({t_{{\text{start}}}},{t_{{\text{end}}}},{\text{Sw}})}^{{\text{Actual}}} = \int_{{\text{ }}{t_{{\text{start}}}}}^{{\text{ }}{t_{{\text{end}}}}} {{P_{{\text{real}}}}({t_i}){\text{d}}t} $ | (5) |
在带有内置传感器的平台中,K20系列GPU运算速度快、应用范围广且所带的功率传感器成为测量功耗的一种典型配置。为此本文选取了具有代表性的K20系列(K20c、K20m和K20X)GPU为实验平台,验证所提出方法的有效性。K20c和K20m有13个streaming multiprocessors(SMX,2496个processing elements)和5GB显存。K20x拥有6GB显存和14个streaming multiprocessors(SMX,2688个processing elements)。它们的区别在于散热方式,K20c使用主动散热方式,K20m使用被动散热方式。实验平台所使用的CUDA开发环境是VS2010,编译环境是NVCC5.5。本文使用程序通过NVML接口查询GPU的功率数据,并且查询出的数据都带有时间标记。
实验程序使用两种不同算法实现模拟重力感应引起的多个恒星运动程序。第一种算法实现的程序执行精确的双向力计算,这种算法在规模为N的情况下复杂度为O(n2),简称为NBody。第二种算法使用Barnes-Hut算法执行近似计算作用力的实现程序,算法的思想是把N个恒星周围的体积层次划分成有次序小正方体直到最里面的每个小正方体只有一个星体。结果被记录在一个非平衡八叉树的层次结构中。这种层次结构使算法的复杂性降为O(nlogn)[12],将这种方法简称为BHut。
3.2 单内核程序实验图 1为使用NBody方法在N=700 000时的功率曲线和使用本文提出的方法得到的功率数据。图中曲线部分表示传感器采样得到的功率数据,虚线部分表示使用本文矫正方法中的式(4)得到GPU功率曲线。图中t1、t2、t3分别表示程序开始时间、程序结束时间、常数能耗消耗开始时间。
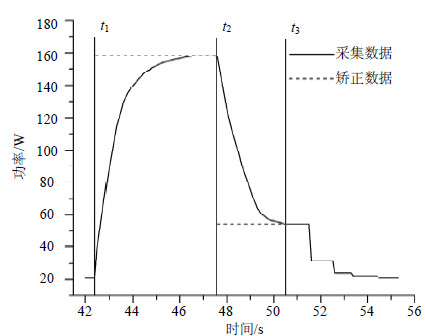 |
| 图1 N=700 000采集功率曲线图和矫正后的功率曲线图 |
通过观察图中矫正后的功率数据可以看出,矫正后的数据能够有效地逼近真实功耗数据,并且当程序运行结束时立即到达尾滞能耗空闲状态功耗数值,矫正后的数据满足软件能耗产生的实质并能够反映GPU运行时的真实功率。当程序在t1和t2之间执行,矫正后的数据能够和采样得到的稳定数据重合,间接验证了本文方法的正确性。对于K20c系列GPU,活动空闲功率为54.2 W左右,因此在使用本文方法后将程序运行结束时的能耗到常数能耗之间的功率数据置为54.2 W,即为软件结束后的真实功率。软件实际能耗利用式(5)在t1和t2时间段积分即可得到。
由图 1可以看出使用本文提出的方法可以消除由传感器自身因素所带来的迟滞问题;而它所带来的一个问题是程序能耗受其启动时间影响。图 2为使用NBody方法在N=350 000,启动间隔时间为1.1 s的两个相同程序的功率曲线和使用式(3)矫正后的功率数据。图中t1、t3分别表示第一个和第二个程序开始时间,t2、t4分别为第一个和第二个程序结束时间,t5是常数能耗开始时间。从图中可以看到:1) 未矫正前两个相同的程序能耗明显不同;2) 使用本文方法矫正后的曲线在两个程序运行期间是相同的,且都在程序运行结束时处于活动空闲状态。相同的实验在N=350 000,间隔0.4 s的情况下得到的矫正曲线和间隔1.1 s得到的矫正曲线情况相同。由图中矫正后的结果可以看出使用本文方法能够很好地解决程序能耗受启动时间影响的问题且得到的功率数据与何时运行程序无关,这个特性使得功率传感器在测量程序能耗时无需等待传感器数据达到空闲功率后启动下一个程序的功率测量。
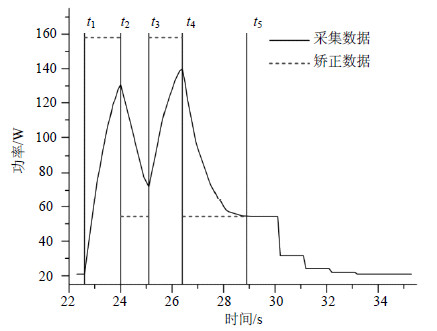 |
| 图2 启动间隔时间为1.1s,N=350 000的两个相同程序的功率曲线和矫正后的功率曲线图 |
为了确保所提出的方法具有通用性,本文使用K20m、K20x和不同驱动版本下的实验情况。图 3a、图 3b分别为N=700 000时,K20m、K20x传感器采集功率曲线图和使用式(4)矫正后的功率曲线图。由图中的曲线可以看出K20m和K20c对于同一程序而言具有几乎相同的功率曲线,所不同的是K20m的功率比K20c的功率要高出10 W左右。图 3b中的曲线显示了K20x中的功率传感器采集的数据和K20c、K20m采集的数据曲线明显不同,K20x中的传感器尽最大努力得到GPU的真实功率,这种现象也从侧面验证了本文所提出的方法的正确性。在不同驱动版本下的功率数据曲线与矫正后的曲线和图 3表现现象类似,在此不再赘述。由图 3矫正后的数据可以看出使用本文提出的方法可以较好地解决由传感器测量功耗时所产生的问题。由于迟滞问题在K20m和K20x上被解决,因此程序能耗受启动时间影响的问题也就不存在了。通过实验结果也验证了利用本文所提出的方法解决式(2)所描述的问题,在此由于篇幅有限,就不再展示在K20m和K20x平台上程序能耗受其启动时间影响的实验结果。
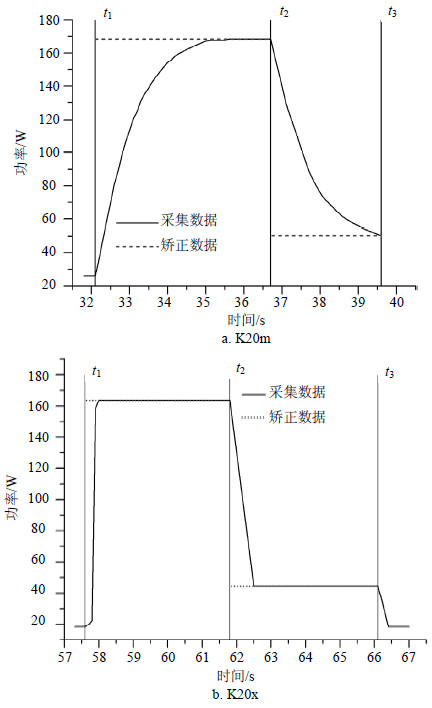 |
| 图3 N=700 000在K20m、K20x上的采集功率曲线图和矫正后的功率曲线图 |
图 4是使用BHut方法在规模N=22 000 000所得到的功率曲线和矫正后的功率曲线图。由图中可以看出BHut方法最高功率(128.2 W)低于NBody方法最高功率(158.4 W),并且BHut方法在程序结束前功率出现下降现象,这点不同于NBody方法。原因在于使用BHut方法使得GPU硬件利用情况没有NBody方法高,并且在程序结束前硬件出现负载非均衡的情况,使得GPU中的一些SM不再参与作用力计算。
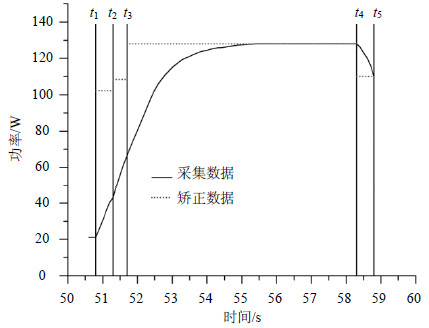 |
| 图4 N=22 000 000采集功率曲线图和矫正后的功率曲线图 |
通过本文提出的方法得到的功率曲线和NBody曲线有别,主要表现在t1和t2、t2和t3、t4和t5阶段。t1和t2阶段与t2和t3阶段主要是BHut方法建立的数据结构和对数据进行处理等工作,处理这些工作的内核程序非均衡地利用GPU中SM。这些工作使得功率数据不同于t3和t4阶段的作用力计算。由于t1和t2阶段与t2和t3阶段运行时间小于tp,因此使用式(3)进行矫正。在t3和t4阶段内核函数运行时间大于tp,因此使用式(4)进行矫正。在t4和t5阶段一些SM不再参与计算,因此GPU的功率出现下降,利用逼近函数较好地得到了真实功率数据。通过分析程序和观察图中的曲线,可以看出本文提出的方法能够很好地跟踪GPU硬件功率的变化情况而不仅仅给出一个恒定的值。
4 结果比较文献[9]也提出了一种解决这个问题的方法,表 1展示了在利用传感器计算程序能耗时两种方法在上述实验环境下的结果对比。
| 表1 结果对比 |
可以看出:1) 本文的方法与文献[9]的方法得出的结果具有很大的相似性,最大误差不超过1%,表明本文方法能够很好地解决此类问题。2) 对比文献[9]中使用的经验参数方法,本文方法使用逼近函数的方法也能得到较好的效果,说明了本文方法具有很好的通用性和可靠性。
5 结束语本文提出了一种矫正内置功率传感器数据的方法。使用该方法可以较好地解决传感器测量能耗所存在的功率迟滞、程序能耗受其启动时间影响等问题,同时具有较好的准确性与通用性。本文选取典型的K20系列GPU为实验平台进行验证,通过实验表明该方法适用于解决传感器测量能耗存在的问题。该方法较准确地获得软件在设备中运行的能耗,为以后的程序能耗优化奠定了基础。下一步研究内容包括程序能效比优化和能耗评估,以进一步提高能量的利用率,为绿色计算的深入应用打下坚实的基础。
| [1] | Top 500 Supercomputer Site. The green lists[EB/OL]. [2014-11]. http://www.green500.org/greenlists. |
| [2] | 郭兵, 沈艳, 邵子立. 绿色计算的重定义与若干探讨[J]. 计算机学报, 2009, 32(12): 2311-2319. GUO Bing, SHEN Yan, SHAO Zi-li. The redefinition and some discussion of green computing[J]. Chinese Journal of Computers, 2009, 32(12): 2311-2319. |
| [3] | HONG S, KIM H. An integrated GPU power and performance model[C]//ACM SIGARCH Computer Architecture News. [S.l.]: ACM, 2010, 38(3): 280-289. |
| [4] | ISCI C, MARTONOSI M. Runtime power monitoring in high-end processors: Methodology and empirical data[C]//Proceedings of the 36th annual IEEE/ACM International Symposium on Microarchitecture. [S.l.]: IEEE Computer Society, 2003: 93. |
| [5] | 刘啸滨, 郭兵, 沈艳, 等. 基于ARM处理器的嵌入式软件能耗统计模型[J]. 电子科技大学学报, 2012, 41(5): 770-774. LIU Xiao-bin, GUO Bing, SHEN Yan, et al. ARM-based embedded software statistical energy model[J]. Journal of University of Electronic Science And Technology of China. 2012, 41(5): 770-774. |
| [6] | 赵霞, 郭耀, 雷志勇, 等. 基于模拟器的嵌入式操作系统能耗估算与分析[J]. 电子学报, 2008, 36(2): 209-215. ZHAO Xia, GUO Yao, LEI Zhi-yong, et al. Estimation and analysis of embedded operating system energy consumption [J]. ACTA Electronica Sinica, 2008, 36(2): 209-215. |
| [7] | SONG S, SU C, ROUNTREE B, et al. A simplified and accurate model of power-performance efficiency on emergent gpu architectures[C]//2013 IEEE 27th International Symposium on Parallel & Distributed Processing (IPDPS). [S.l.]: IEEE, 2013: 673-686. |
| [8] | NVIDIA Corporation. “NVIDIA's next generation CUDA compute architecture: Kelper GK110/210” White paper V1.1[EB/OL]. (2012-03-17). http://www.nvidia.com. |
| [9] | BURTSCHER M, ZECENA I, ZONG Z. Measuring GPU power with the K20 built-in sensor[C]//Proceedings of Workshop on General Purpose Processing Using GPUs. [S.l.]: ACM, 2014: 28. |
| [10] | PATHAK A, HU Y C, ZHANG M, et al. Fine-grained power modeling for smartphones using system call tracing[C]//Proceedings of the sixth conference on Computer systems. [S.l.]: ACM, 2011: 153-168. |
| [11] | PATHAK A, HU Y C, ZHANG M. Where is the energy spent inside my app?: Fine grained energy accounting on smartphones with eprof[C]//Proceedings of the 7th ACM European Conference on Computer Systems. [S.l.]: ACM, 2012: 29-42. |
| [12] | BARNES J, HUT P. A Hierarchical O(nlogn) force-calculation algorithm[J]. Nature, 1986, 324(4): 446-449. |
 2016, Vol. 45
2016, Vol. 45
