从14世纪的黑死病到SARS、H1N1,以及最近的埃博拉病毒(Ebola),流行病的传播时刻威胁着人类的生命安全,同时也给社会发展带来了巨大的经济损失[1, 2, 3, 4]。一直以来,来至各个领域的专家和学者都致力于研究流行病传播机制、预警和防控[5, 6, 7, 8]。其中,及时准确地预警流行病传播是控制流行病大规模爆发的关键。针对流行病的特有传播途径、传播速率、潜伏期和行为响应等性质建立恰当的传播模型是预警流行病传播的第一步。如易感态-感染态(SI)模型可以描述艾滋病和埃博拉病毒这类爆发突然且尚缺有效治疗手段的流行病,易感态-感染态-恢复态(SIR)模型用以描述水痘和麻疹这类患者能完全康复并获得终身免疫力的流行病,易感态-感染态-易感态(SIS)模型则可以描述感冒和淋病这类康复患者可能再次被感染的传染病[9]。这些经典的传播模型只能在一定程度上反应真实流行病的内在特性,更准确地描述模型需要在此基础上考虑个体的年龄、性别、行为特性以及心理变化等因素所带来的影响。在现代流行病建模过程中,学者们利用复杂网络来描述传播路径底层结构。其中,节点表示个体,连边表示个体之间的各种关系。研究发现中心节点的存在导致许多实际网络并不存在流行病爆发阈值[10, 11, 12]。借助复杂网络来研究流行病的内在传播机制开启了现代流行病传播的新纪元[12, 13, 14, 15]。
在现代流行传播研究中,大多数学者采用理论分析和计算机模拟相结合的方法揭示流行病传播机制、预警及其控制。他们从网络的宏观结构(如网络结构异质性)[10, 11, 12, 17, 18, 19, 20]、中尺度结构(如社区结构)[21, 22, 23]以及微观结构角度(如节点度、边权大小)[24, 25, 26, 27]出发分析不同结构特性对流行病传播速度[24, 28]、传播可预测性[29, 30]、传播范围[17, 25]和爆发阈值[31, 32, 33, 34]的影响,并确定影响传播的关键节点[35, 36, 37, 38, 39],进一步还原流行病传播路径,寻找流行病传播源[40, 41]等。对于全球范围的流行病爆发,学者们发现现代交通网络起着至关重要的作用。最近,文献[42]发现全球流行病传播到达时间并不是取决于两地的实际距离,而关键在于两地之间的有效距离长度。在流行病的控制研究中,学者们从网络的全局和局域结构出发设计有效的流行病免疫策略[43]。例如,根据网络全局结构提出的目标免疫[44],基于网络局域结构信息的熟人免疫[45]以及信息驱动的免疫[46, 47, 48]等策略在控制疾病传播方面都有较好的效果。
值得注意的是,关于流行病传播的理论分析方法通常会涉及一些基本假设。例如,异质平均场理论假设度相同的节点之间不存在任何差异,并且相邻节点的状态是相互独立的[10]。这些基本假设将直接导致理论预测与实际传播过程之间存在一定的差异,甚至得到截然不同的结论。面对错综复杂的流行病传播过程,这些基本假设极大地制约了理论方法的广泛运用。因此,经典的理论方法很难描述真实的流行病传播,进而阻碍了人们对真实流行病传播的认识。幸运的是,计算机模拟方法很大程度上能够弥补理论分析过程中的这些不足。一方面,在利用计算机模拟流行病传播时无需做出多余的假设,从而保证了流行病传播过程的准确性;另一方面,计算机模拟可以更适用于结构复杂、规模庞大的社会系统,并能够综合考虑实际社会因素对流行病传播的影响。正是由于这些优点,计算机模拟方法已成为研究流行病传播不可替代的手段。
同步更新(synchronous updating method)和异步更新(asynchronous updating method)是动力学研究中两种最为常用的计算机模拟方法。然而,对于同一动力学过程,这两种模拟方法在更新节点状态时的差异性可能会导致动力学过程在定量和定性上的差异[49, 50, 51]。例如,文献[52]发现运用同步方法来更新元胞自动机囚徒困境博弈模型会导致网格中的合作与背叛交替出现,但采用异步更新方法则不会出现合作个体。现有研究中,已有许多文献致力于介绍如何利用各种理论方法来分析流行病传播动力学[16, 53, 54, 55],对于计算机模拟流行病传播过程却甚少提及,使得人们对如何准确地模拟流行病传播缺乏必要的认识和理解。鉴于此,本文将首先基于SIS和SIR传播模型详细介绍同步更新方法和异步更新方法的具体实现步骤,继而讨论两种更新方法对流行病传播动力学的影响,并对两种方法之间的区别与联系进行分析。最后,对本文进行总结和展望。
1 计算机模拟方法同步更新和异步更新的差异性源于人们看待实际动力学过程的角度有所不同[50]。若从一个长时间尺度上来观察事物的动态变化,不难发现所有个体都在同时地更改自己的状态,这也就蕴含着事物的状态改变是同步更新的。换个角度,若关注于连续时间变化,并且每个瞬间只允许一个事件发生,就会发现不同节点的状态更新是异步进行的。实际生活中,所有事物的状态演化都发生在同一时间尺度上,即同步更新。但并不是所有事物的状态都在某个时刻发生改变,这就意味着异步更新是连续时间的离散近似。本文将以经典的SIS和SIR流行病传播模型为例来详细阐述同步更新和异步更新方法在流行病传播模型中的应用。
对于SIS流行病传播模型,节点在每个时刻只能处于易感态(S)或感染态(I)。易感态节点表示未被流行病感染的个体,且可能被感染;感染态节点表示已经被流行病感染且具有传播能力。每一时间步内,每个感染态节点以概率$\lambda $尝试感染它的所有易感态邻居节点,然后以概率$\gamma $恢复成易感态。
对于SIR流行病传播模型,任意时刻节点只能处于易感态(S)或感染态(I)或恢复态(R)。易感态节点表示未被流行病感染的个体,且可能被感染;感染态节点表示已经被流行病感染且具有传播能力;恢复态节点则表示曾感染流行病且完全康复。与SIS模型类似,每一时间步内,每个感染态节点以概率$\lambda $尝试感染它的邻居易感态节点,并以概率$\gamma $变为恢复态。
1.1 同步更新方法同步更新方法主要思想是:每个节点根据它们自己及其邻居节点的上一步状态来更新自己的当前状态,所有节点的状态更新过程都在单位时间内同时完成[10, 11, 12]。对于SIS流行病传播,初始时刻随机选择或按照某种策略选择${\rho _0}$比例的节点作为感染态节点,其余节点都处于易感态。用队列${Q_1}$存放当前步具有感染能力的节点(即上一时间步的未恢复感染节点及其感染节点),队列${Q_2}$存放当前步新感染的节点。首先,将初始时刻感染的所有节点存放在队列${Q_1}$中。接下来,每一时间步的传播过程按以下步骤进行:
1) 遍历队列${Q_1}$中的感染态节点,每个感染态节点以概率$\lambda $尝试感染它的所有易感态邻居节点。若成功感染它的易感态邻居,则将新感染的易感态节点存放到队列${Q_2}$中;
2) 以概率$\gamma $恢复队列${Q_1}$中的节点,并将恢复成功的节点从队列${Q_1}$中移除;
3) 将队列${Q_2}$中的节点存放至队列${Q_1}$中,表示它们在下一个时刻具有感染能力,并清空队列${Q_2}$中的所有元素;
4) 更新系统时间$t \to t + 1$,并重复步骤1)~4)直到$t = {t_{\max }}$或者系统中没有感染态节点为止。
SIR传播模型同步更新方法与SIS完全类似,更新过程终止的条件是系统中不再有感染态节点。
关于同步更新方法的时空复杂度,除了需要$O(N + E)$空间存储图的邻接表外,模拟SIS或SIR流行病传播过程还需要$O(N)$的额外空间来存储队列${Q_1}$和${Q_2}$。其中,$N$和$E$分别表示网络中的节点和边数量。因此,同步更新方法的空间复杂度为$O(N + E)$,模拟过程中需要额外空间大小为$O(N)$。单位时间内(即平均访问所有节点一次所需时间),遍历队列${Q_1}$及其邻居节点的所需时间为$O(\left\langle k \right\rangle N)$。然而,大多数实际网络都是稀疏网络,即网络平均度$\left\langle k \right\rangle \ll N$,从而单位时间内感染过程的时间复杂度近似为$O(E)$。对于恢复过程和更新感染节点状态,需要的时间复杂度为$O(N)$。综合来看,利用同步更新单位时间步的时间复杂度为$O(E)$。
1.2 异步更新方法在异步更新方法的实现过程中,节点独立地更新其状态,并且它的邻居节点在其更新状态时能观察到它的新状态[53]。异步更新方法广泛地运用于各种动力学模拟,包括投票模型、博弈、阈值模型和传播模型等。Gillespie算法是异步更新方法中典型的代表方法,模拟了生物化学中的有效反应过程,以及马尔科夫动力学过程和泊松过程[56, 57, 58]。在实现Gillespie算法的过程中,最为重要的就是如何给每个时间步赋予发生过程和时间更新步长。假设系统中有$N$个独立的随机离散过程,每个过程发生的概率为${\beta _i}$,$i = 1,2, \cdots ,N$。对于泊松过程,在t时刻发生事件i的概率为:
| ${\prod _i} = \frac{{{\beta _i}}}{{N\bar \beta }}$ | (1) |
本文以经典的SIS传播动力学为例,具体介绍Gillespie算法。首先,指定队列${Q_1}$和队列${Q_2}$。队列${Q_1}$用于存放所有感染态节点,队列${Q_2}$用于存放活跃边。活跃边是指感染态节点与易感态节点相连的边。然后,在每一时刻按照以下步骤模拟SIS传播过程。
1) 在队列${Q_1}$和队列${Q_2}$中,根据事件发生概率${\prod _i}$选择一个事件的发生。对于SIS传播模型,恢复事件发生的概率为$\gamma $,活跃边发生传播的概率为$\lambda $,则事件i发生的概率${\prod _i} = \frac{{{\beta _i}}}{{\gamma {N_{\text{A}}}(t) + \lambda {N_{\text{E}}}(t)}}$。其中,${N_{\text{A}}}(t)$和${N_{\text{E}}}(t)$分别表示在t时刻系统中感染态节点数和活跃边数。
2) 若选择发生的事件是恢复节点i,则:从队列${Q_1}$中移除节点i;从队列${Q_2}$中移除节点i所连接的活跃边;在队列${Q_2}$中添加节点i现连接的活跃边,即添加节点i和它的感染态邻居节点j的连边到队列${Q_2}$中。
若选择发生的事件是感染节点i,则:在队列${Q_1}$中添加节点i;从队列${Q_2}$中移除节点i所连接的活跃边;在队列${Q_2}$中添加节点i现连接的活跃边,即添加节点i和它的易感态邻居节点j的连边到队列${Q_2}$中。
3) 更新系统中每个过程的时间为$t \to t + \tau $,其中,$\tau = \frac{1}{{\gamma {N_{\text{A}}}(t) + \lambda {N_{\text{E}}}(t)}}$[60]。重复步骤1)~3)直到时间t达到${t_{\max }}$或者系统中没有感染态节点为止。
SIR模型的异步更新方法也是类似地进行,模拟结束条件是网络中不再有感染态节点。
异步更新方法需要$O(E)$的额外存储空间来暂储模拟过程中节点和活跃边状态的改变。在单位时间内(指的是网络中的每个节点平均更新一次状态的时间),平均来看网络中的每个感染态节点和活跃边都会遍历一次,所需时间为$O(N + E)$。访问每个感染态节点或活跃边时都需要更新队列${Q_1}$和${Q_2}$这一操作所需时间也是$O(N + E)$。因此,异步更新方法在单位时间内的时间复杂度为$O[{(N + E)^2}]$。
1.3 参数设置对于SIS模型,同步更新方法和异步更新方法都涉及到时间参数${t_{\max }}$,${t_{\max }}$的设置直接影响最终的传播结果。这是因为,SIS传播模型存在一个临界传播概率${\lambda _{\text{c}}}$。当传播率$\lambda \leqslant {\lambda _{\text{c}}}$时,感染态节点随时间呈指数快速衰减,系统处于吸收态;当传播概率$\lambda > {\lambda _{\text{c}}}$时,系统中将一直存在感染态的节点,系统处于活跃态。然而,网络的淬火无序结构会导致在临界点附近感染范围呈广延指数或幂律衰减形式,即系统中将长时间存在感染态节点[61, 62, 63, 64, 65]。若设置${t_{\max }}$太小,系统仍然处于弛豫态;若设置${t_{\max }}$过大,系统更容易进入吸收态,导致只有少许模拟过程处于活跃态[66]。因此,在实现SIS传播过程,设置时间${t_{\max }}$至关重要。根据不同的研究需要,将最大时间设置为104~1010不等(具体设置与$N$和$E$相关)。在流行病传播动力学中,国内外学者在设置${t_{\max }}$采取了不同的方法。例如,设置${t_{\max }} = $1 000[67],或设置${t_{\max }} = {10^7}$[64]。
在计算网络中稳态感染节点平均比例只统计那些存活的模拟过程[59],即系统没有到达吸收态。随着时间t增加,系统处于活跃的概率也就越小,意味着需要更多的模拟实验实现次数。尤其在临界点附近,系统处于活跃的概率更小。如何防止系统频繁地陷入吸收态,只用少量的实验模拟便能得到比较准确的稳态值呢?这一难题在亚稳态方法(quasistationary state)中[60, 68]得到了很好的解决。亚稳态方法的主要思想是让系统一直处于活跃态,利用它曾经经历的状态替换当前状态。值得注意的是,更新节点状态时既可以运用同步更新方法也可以运用异步更新方法。在实现过程中需要用队列$Q$保存$M$个活跃的演化过程。在某一个时间步,若系统转变为吸收态,则从队列$Q$中随机选择一个活跃过程替换当前过程。此外,还需要以概率${p_{{\text{rep}}}}$更新队列$Q$中的过程。经历弛豫时间${t_{\text{r}}}$后,在${t_{\text{a}}}$个时间步内求均值得到系统中有n个感染态节点的概率${\bar P_n}$。进一步得出感染密度为$\rho = \frac{1}{N}\sum\limits_n {n{{\bar P}_n}} $。一般来说,在模拟过程中队列$Q$的长度取值$M = 400$,替换概率${p_{{\text{rep}}}}$取为10-2到10-4不等(网络越大,${p_{{\text{rep}}}}$越小),弛豫时间${t_{\text{r}}} = {10^6}$,平均时间长度${t_{\text{a}}} = {10^7}$。
文献[69, 70, 71, 72]在模拟过程中不允许网络中最后一个感染态节点恢复来防止系统进入吸收态。这种简单的处理虽然改变了SIS传播模型,但是对系统的稳态密度影响很小[70]。利用这种简单的模拟方法,对SIS传播[71, 72] 、非马尔科夫流行病传播[69, 70]都做了系统的研究,最近,又发现这种模拟方法改变了两个互斥SIS传播动力学过程(即某一时刻节点只能被两个流行病中的一个感染):基于单个网络的两个互斥SIS传播模型中,该模拟方法会使得两个动力学交替占主导地位[73],而传统模拟方法导致稳态时最多只有一个动力学存活[74, 75]。由此可见,选择合适的模拟方法对流行病传播动力学的分析至关重要。
2 两种更新方法之间的联系与区别在计算机模拟过程中,节点状态更新都是离散时间步骤。在模拟过程中,若每一时间步选择$f$比例的节点更新其状态,$1/N \leqslant f \leqslant 1$,同步更新方法和异步更新方法便对应于两种极端的情形[53, 76]。若$f = 1.0$,即每个时间步更新所有节点的状态,则与同步更新过程相同。若$f = 1/N$,即每个时间步平均随机更新一个节点的状态,则与异步更新过程相同。
从表 1不难看出,同步更新方法的时空复杂度都比异步更新方法更低。同步更新方法的优势在于能快速模拟动力学过程(即每个时间步同时改变所有节点状态),且易于编写程序;异步更新方法需要逐个更新系统中节点的状态(即每个时间步只有一个节点改变其状态),程序实现较复杂。对现有文献进行不完全统计,发现若研究只关注于稳态时的感染密度,往往选择快速、简单的同步更新方法;若研究关注于动力学演化过程(如局域现象),往往选择系统状态改变缓慢的异步更新方法更为合适[16]。
| 表1 单位时间步内,同步更新和异步更新方法的时空复杂度 |
本文利用前面所介绍的同步更新和异步更新方法来模拟SIS和SIR流行病传播模型,进一步分析这两种方法对传播所带来的影响。在图 1和图 2中,在平均度$\left\langle k \right\rangle = 10$的ER网络中运用两种方法模拟SIS和SIR传播,其中,恢复概率为1。发现两种模拟方法在更新节点状态时的微妙差异导致传播动力学在定性和定量上都有很大的差异。当$\lambda $较小时,感染密度也较小。对于同步更新,每一时间步,所有感染态节点尝试感染其所有易感态邻居后才可能会恢复;而对于异步更新,活跃边发生感染和感染态节点恢复这两种事件是按某种概率随机出现的。这种不同导致异步更新情况下会有部分感染态节点还未尝试感染易感态邻居之前就已恢复,而同步更新情况下将产生更多的新感染态节点,因此具有较小的爆发阈值。当$\lambda $较大时,感染密度较大。对于同步更新而言,因$\gamma = 1$的限制,SIS模型的感染密度会逐渐趋于0.5的上限[10]。然而对于异步更新,感染态节点的增加会产生更多的活跃边,因而感染事件具有更大的发生概率而更可能先发生,导致新感染态节点的逐渐增加。相比于SIS模型,SIR的感染态节点恢复不会减少最终的感染规模,也不能限制同步更新中感染先发生的优势,从而具有更大的最终爆发规模。由此可见,两种模拟方法对流行病的爆发阈值和最终感染密度所带来的定量影响也是不容忽视的,尤其是在发展和提出新理论方法的过程中需慎重考虑模拟方法所带来的影响。
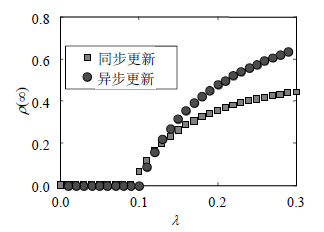 |
| 图1 在ER网络上同步更新和异步更新模拟SIS模型,稳态时传播范围随传播率的变化 |
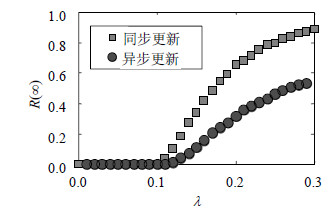 |
| 图2 在ER网络上同步更新和异步更新模拟SIR模型,稳态时传播范围随传播率的变化 |
针对不同的流行病传播模型,设计出快速、准确的模拟方法对揭示传播机制,以及预警和控制起着不可替代的作用。本文以SIS和SIR流行病传播动力学为例,详细地介绍如何运用同步更新和异步更新两种常用方法来进行计算机模拟,分析了两种模拟方法的时空复杂度,并阐述了两种模拟方法之间的联系与区别,举例讨论了它们对流行病传播范围和爆发阈值的影响。理清同步更新方法和异步更新方法不仅仅能加深对动力学本身的认识,还有助于提出和发展一些更加准确的理论分析方法。此外,可以将两种更新方法可以推广到其他流行病传播模型(如SI,SEIR模型等),以及其他动力学模型(如阈值模型,投票模型,博弈等)的实验模拟。
两种方法在模拟过程中的细微差异对流行病最终传播范围和爆发阈值会造成定量上的影响。更值得深思的问题是,对于同一流行病传播模型,不同的模拟方法是否会对临界值、临界指数和局域现象等一系列问题有定性或者定量的影响?网络结构包括度分布异质性、平均度、集群系数、度-度关联、社区等,也包括退火网络和时序网络等是否会增加或减小两种模拟方法定量上的差异?亟待更为系统地探究这两种模拟方法对动力学过程所带来的影响,尤其是对非平衡动力学过程所带来的影响。
本文研究工作得到电子科技大学优秀博士生学术支持计划(YXBSZC20131065)的资助,在此表示感谢。
| [1] | MEYERS L A, POURBOHLOUL B, NEWMAN M E J, et al. Networktheory and SARS: Predicting outbreak diversity[J]. J TheorBiol, 2005(232): 71-81. |
| [2] | LEROY E M, ROUQUET P, FORMENTY P, et al. Multiple Ebola virustransmission events and rapid decline of central africanwildlife[J]. Science, 2004(303): 387-390. |
| [3] | MILLER J C, DANON L, O'HAGAN J J, et al. Student behavior during a school closure caused by pandemic influenza A/H1N1[J]. PLoS ONE, 2010(5): e10425. |
| [4] | 马知恩, 周义仓, 王稳地, 等. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004. MA Zhi-en, ZHOU Yi-chang, WANG Wen-di, et al. Mathematical modeling and study of infectious diseasedynamics[M]. Beijing: Science Press, 2004. |
| [5] | KEELING M, ROHANI P. Modeling infectious diseases in humans and animals[M]. Princeton: Princeton University Press, 2007. |
| [6] | ANDERSON R M, MAY R M. Infectious diseases in humans[M]. Oxford: Oxford University Press, 1992. |
| [7] | ANDERSSON H, BRITTON T. Stochastic epidemic models and theirstatistical analysis, lecture notes in statistics[M]. New York: Springer, 2000. |
| [8] | KEELING M, POHANI P. Modeling infectious diseases in humansand animals[M]. Princeton: Princetion University Press, 2007. |
| [9] | KERMACK W O, MCKENDRICK A G. A contribution to the math-ematical theory of epidemics[J]. Proc R SocLond A, 1927(115): 700-721. |
| [10] | PASTOR-SATORRAS R, VESPIGNANI A. Epidemic spreading in scale-Free networks[J]. Phys Rev Lett, 2001(86): 3200-3203. |
| [11] | PASTOR-SATORRAS R, VESPIGNANI A. Epidemic dynamics in finite size scale-free networks[J]. Phys Rev E, 2002(65): 035108(R). |
| [12] | PASTOR-SATORRAS R, VESPIGNANI A. Epidemic dynamics and endemic states in complex networks[J]. Phys Rev E, 2001(63): 066117. |
| [13] | 周涛, 傅忠谦, 牛永伟, 等. 复杂网络上传播动力学研究综述[J]. 自然科学进展, 2005, 15(5): 513-517. ZHOU Tao, FU Zhong-qian, NIU Yong-wei, et al. Summary of research on propagation dynamics on complex networks[J]. Progress in Natural Science, 2005, 15(5): 513-517. |
| [14] | 李翔, 刘宗华, 汪秉宏. 网络传播动力学[J]. 复杂系统与复杂性科学, 2010, 7(2): 33-37. LI Xiang, LIU Zong-hua, WANG Bing-hong. On spreading dynamics on networks[J]. Complex Systems and Complexity Science, 2010, 7(2): 33-37. |
| [15] | WANG L, LI X. Spatial epidemiology of networked metapopulation: an overview[J]. Chin Sci Bull, 2014, 59(28): 3511-3522. |
| [16] | PASTOR-SATORRAS R, CASTELLANO C, MIEGHEM P V, et al. Epidemic processes in complex networks[J]. Rev Mod Phys, 2015(87): 925-979. |
| [17] | NEWMAN M E J. The spread of epidemic disease on networks[J]. Phys Rev E, 2002(66): 016128. |
| [18] | YANG Z, ZHOU T. Epidemic spreading in weighted networks: an edge-based mean-field solution[J]. Phys Rev E, 2012(85): 056106. |
| [19] | YAN G, ZHOU T, WANG J, et al. Epidemic spread in weightedscale-free networks[J]. Chin PhysLett, 2005(22): 510. |
| [20] | SUN Y, LIU C, ZHANG C X, et al. Epidemic spreading on weighted complex networks[J]. PhysLett A, 2014, 378(7): 635-640. |
| [21] | WANG R S, ALBERT R. Effects of community structure on the dynamics of random threshold networks[J]. Phys Rev E, 2013(87): 012810. |
| [22] | MIN Y, JIN X, GE Y, et al. The role of community mixingstyles in shaping epidemic behaviors in weighted networks[J]. PLOS ONE, 2013, 8(2): e57100. |
| [23] | NEWMAN M E J. Random graphs with clustering[J]. Phys Rev E, 2009(103): 058701. |
| [24] | BARTHELEMY M, BARRAT A, PASTOR-SATORRAS R, et al. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks[J]. Phys Rev E, 2004(92): 178701. |
| [25] | WANG W, TANG M, ZHANG H F, et al. Epidemic spreading oncomplex networks with general degree and weight distributions[J]. Phys Rev E, 2014(90): 042803. |
| [26] | XU E H W, WANG W, XU C, et al. Suppressed epidemics in multirelationalnetworks[J]. Phys Rev E, 2015(92): 022812. |
| [27] | LI R Q, TANG M, HUI P M. Epidemic spreading on multi-relational networks[J]. ActaPhys Sin, 2013, 62(16): 168903. |
| [28] | CUI A X, WANG W, TANG M, et al. Efficient allocation of heterogeneous response times in information spreading process[J]. Chaos, 2014(24): 033113. |
| [29] | SHU P, TANG M, GONG K, et al. Effects of weak ties on epidemicpredictability on community networks[J]. Chaos, 2012, 22(4): 043124. |
| [30] | ZHAO Z D, LIU Y, TANG M. Epidemic variability in hierarchicalgeographical networks with human activity patterns [J]. Chaos, 2012, 22(2): 023150. |
| [31] | BOGUNA M, PASTOR-SATORRAS R, VESPIGNANI A. Absence of epidemic threshold in scale-free networks with degree correlations[J]. Phys Rev E, 2003(90): 028701. |
| [32] | BOGUNA M, CASTELLANO C, PASTOR-SATORRAS R. Nature of theepidemic threshold for the susceptible-infected-susceptible dynamics in networks[J]. Phys Rev Lett, 2013, 111(6): 068701. |
| [33] | CASTELLANO C, PASTOR-SATORRAS R. Thresholds for epidemic spreading in networks[J]. Phys Rev Lett, 2010 (105): 218701. |
| [34] | SHU P, WANG W, TANG M. Numerical identification of epidemic thresholds for susceptible-infected-recovered model on finite-size networks[J]. Chaos, 2015(25): 063104. |
| [35] | KITSAK M, GALLOS L K, HAVLIN S, et al. Identification of influential spreaders in complex networks[J]. Nat Phys, 2010(6): 888-893. |
| [36] | LIU Y, TANG M, ZHOU T, et al. Core-like groups resulting in invalidation of k-shell decomposition analysis[EB/OL]. (2014-09-18). http://arXiv.org/abs/1409.5187. |
| [37] | CHEN D B, LU L Y, SHANG M S, et al. Identifying influentialnodes in complex networks[J]. Physica A, 2002, (391): 1777-1787. |
| [38] | LIU J G., REN Z M, GUO Q. Ranking the spreading influence incomplex networks[J]. Physica A, 2013(392): 4154-4159. |
| [39] | PEI S, MAKSE H A. Spreading dynamics in complexnetworks[J]. Journal of Statistical Mechanics: Theory and Experiment, 2013(13): P12002. |
| [40] | PINTO P C, THIRAN P, VETTERLI M. Locating the sourceof diffusion in large-scale networks[J]. Phys Rev Lett, 2012,109(6): 068702. |
| [41] | CHEN D B, XIAO R, ZENG A. Predicting the evolution of spreading oncomplex networks[J]. Sci Rep, 2014(4): 6108. |
| [42] | BROCKMANN D, HELBING D. The hidden geometry of complex, network-driven contagion phenomena[J]. Science, 2013(342): 1337-1442. |
| [43] | 王伟, 杨慧, 龚凯, 等. 复杂网络上的局域免疫研究[J]. 电子科技大学学报,2013, 42(6): 817-830. WANG Wei, YANG Hui, GONG Kai, et al. Local immunization algorithm on complex networks[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(6): 817-830. |
| [44] | PASTOR-SATORRAS R, VESPIGNANI A. Immunization of complex networks[J]. Phys Rev E, 2002(65): 036104. |
| [45] | COHEN R, HAVLIN S, BEN-AVRAHAM D. Efficient immunization strategies for computer networks and populations[J]. Phys Rev Lett, 2003, 91(24): 247901. |
| [46] | YANG H, TANG M, ZHANG H F. Efficient community-basedcontrol strategies in adaptive networks[J]. New J Phys, 2012(14): 123017. |
| [47] | LIU H K, YANG H, TANG M, et al. Local transient-based quarantine strategy in adaptive networks[J]. Scientia Sinica Physica, Mechanica&Astronomica, 2013, 43(2): 1-10. |
| [48] | WANG W, TANG M, YANG H, et al. Asymmetrically interactingspreading dynamics on complex layered networks[J]. Sci Rep, 2014(4): 5097. |
| [49] | WU Z X, RONG Z. Boosting cooperation by involving extortion in spatial Prisoner's dilemma[J]. Phys Rev E, 2014(90): 062102. |
| [50] | SCHONFISCH B, DE ROOS A. Synchronous and asynchronous updating in cellular automata[J]. BioSystems, 1999(51): 123-143. |
| [51] | WOLFRAM S. Statistical mechanics of cellular automata[M]. Rev Mod Phys, 1983(55): 601-644. |
| [52] | HUBERMAN B A, GLANCE N S. Evolutionary games and computer simulations[J]. Proc Natl Acad Sci USA, 1993(90): 7716-7781. |
| [53] | PORTER MA, GLEESON J P. Dynamical systems on networks: atutoria[EB/OL]. (2014-03-29). http://arXiv.org/abs/1403.7663. |
| [54] | VOLZ E M, MILLER J C, GALVANI A, et al. Effects of heterogeneousand clustered contact patterns on infectious disease dynamics[J]. PloS Comput Biol, 2013(7): e1002042. |
| [55] | FU X C, SMALL M, CHEN G R. Propagation dynamics on complex networks: Models, methods and stability analysis[M]. BeiJing: High Education Press, 2014. |
| [56] | GILLESPIE D. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions[J]. Journal of Computational Physics, 1976(22): 403G. |
| [57] | GILLESPIE D. Exact stochastic simulation of coupled chemicalreactions[J]. Journal of Physical Chemistry, 1977(81): 2340-2361. |
| [58] | GILLESPIE D. Approximate accelerated stochastic simulation ofchemically reacting systems[J]. Journal of Chemical Physics, 2001(115): 1716-1733. |
| [59] | MARRO J, DICKMAN R. Nonequilibrium phase transition in latticemodels[M]. London: Cambridge University Press, 1999. |
| [60] | FERREIRA S C, CASTELLANO C, PASTOR-SATORRAS R. Epidemic thresholds of the susceptible-infected-susceptible model on networks: a comparison of numerical and theoretical results[M]. Phys Rev E, 2012(86): 041125. |
| [61] | GOLTSEV A V, DOROGOVTSEV S N, OLIVEIRA J G, et al. Localizationand spreading of diseases in complex networks[J]. Phys Rev Lett, 2012(109): 128702. |
| [62] | VOJTA T. Rare region effects at classical, quantum and nonequilibrium phase transitions[J]. J Phys A Math Gen, 2006(39): 143-205. |
| [63] | ODOR G. Spectral analysis and slow spreading dynamics oncomplex networks[J]. Phys Rev E, 2013, 88(3): 032109. |
| [64] | MUNOZ M A, JUHASZ R, CASTELLANO C, et al. Griffiths phases oncomplex networks[J]. Phys Rev Lett, 2010, 105(12): 128701. |
| [65] | MORETTI P, A. MUNOZ M. Brain architecture, griffiths phases,and the stretching of criticality[J]. Nat Commu, 2013(4): 2521. |
| [66] | FERREIRA R S, FERREIRA S C. Critical behavior of the contact process on small-world networks[J]. EurPhys J B, 2013(86): 462. |
| [67] | WU Q, FU X, SMALL M, et al. The impact of awareness on epidemic spreading in networks[J]. Chaos, 2012(22): 013101. |
| [68] | DE OLIVEIRA M M, DICKMAN R. How to simulate the quasistationary state[J]. Phys Rev E, 2005(71): 016129. |
| [69] | MIEGHEM P V, DE BOVENKAMP R. Non-Markovian infection spread dramatically alters the susceptible infected-susceptible epidemic threshold in networks[J]. Phys Rev Let-t, 2013(110): 108701. |
| [70] | CATOR E, DE BOVENKAMP R, MIEGHEM P V. Susceptible-infected-susceptible epidemics on networks with general infection andcure times[J]. Phys Rev E, 2013(87): 062816. |
| [71] | CATOR E, MIEGHEM P V. Susceptible–infected-susceptible epidemics on the complete graph and the star graph: Exact analysis[J]. Phys Rev E, 2013(87): 012811. |
| [72] | LI C, DE BOVENKAMP R, MIEGHEM P V. Susceptible infected-susceptible model: a comparison of N-intertwined and heterogeneous mean-field approximations[J]. Phys Rev E, 2012(86): 026116. |
| [73] | DE BOVENKAMP R, KUIPERS F, MIEGHEM P V. Domination-timedynamics in susceptible-infected-susceptible virus competitionon networks[J]. Phys Rev E, 2014(89): 042818. |
| [74] | WANG Y, XIAO G, LIU J. Dynamics of competing ideas in complex social systems[J]. New J Phys, 2012(14): 013015. |
| [75] | SAHNEH F D, SCOGLIO C. Competitive epidemic spreading overarbitrary multilayer networks[J]. Phys Rev E, 2014(89): 062817. |
| [76] | HARRIS K D, DANFORTH C M, DODDS P S. Dynamical influenceprocesses on networks: General theory and applications to social contagion[J]. Phys Rev E, 2013(88): 022816. |
 2016, Vol. 45
2016, Vol. 45
