随着德国低轨卫星-地面站(LEO-GOS 5.6Gbps)和低轨卫星间(LEO-LEO 5.6 Gbps)相干激光通信实验的成功，相干通信成为卫星激光链路首选方案。未来德国低轨卫星-同步轨道卫星(LEO-GEO 1.8 Gbps)激光链路和美国的激光通信中继实验(2.88 Gbps)以及日本的下一代激光通信终端(2.5 Gbps)均采用相干技术^{[1, 2]}。考虑到卫星相干光通信要求的强抗空间抗辐照能力、低功率损耗和大范围的多普勒补偿能力，目前日趋成熟的基于DSP技术的光纤相干接收技术并不适用于卫星激光通信^[3]，基于OPLL的相干接收技术仍是星间和星地激光链路的第一选择^{[4, 5, 6]}。

因为卫星激光链路无法进行中继和再生，因此高灵敏度相干接收机是卫星光通信的关键技术之一，而高性能的OFE是实现高灵敏度接收的关键。在过去的研究中，由于通信码速率比较低，仅将OFE作为理想的器件进行考虑^{[5, 6, 7]}，而更多的是关注相干接收机的结构设计及相位噪声的抑制^{[8, 9]}。理想的OFE要求平衡接收支路上信号功率和传输时间严格相等。但混频器内各支路上的分光不均和平衡探测器上两光探测器响应的不一致造成了两支路间的功率失配^{[10, 11]}，同时光混频器内各支路光程差引起的传输时间差别和两光电探测器响应时间的不一致产生了传输时间失配。两种失配降低了前端对相对强度噪声(RIN)的抑制和差分信号的放大。随着通信速率的上升，失配带来的影响更加明显，成为制约高灵敏度接收的重要因素。

本文针对星地20Gbps BPSK的相干接收机中，OFE中功率失配和传输失配对数据接收和相位锁定的影响进行了分析，并进行参数优化将失配带来的接收机性能恶化降低到最小，为接收前端的设计和通信链路裕量提供设计参考。

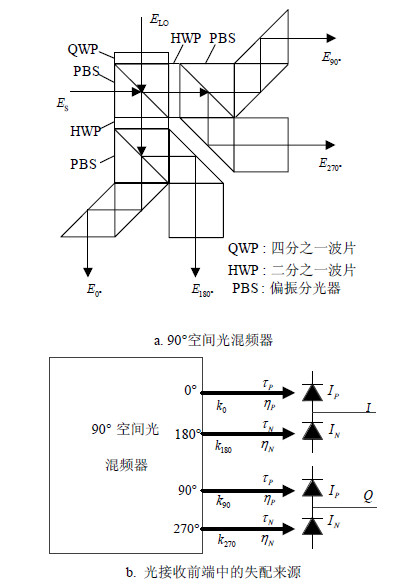
1 光学接收前端的失配及共模抑制比

理想的平衡探测器可以消除本振激光器带来的RIN噪声，其对RIN噪声的抑制能力用共模抑制比(CMRR)表示^[12]，同样将OFE的CMRR定义为：

$\text{CMRR}=10\log {{\left( \frac{\left| {{I}_{P}}-{{I}_{N}} \right|}{{{I}_{P}}+{{I}_{N}}} \right)}^{2}}$

(1)

如图 1所示，${{I}_{P}}$、${{I}_{N}}$分别为平衡探测器中两光电探测器的输出电流。对OFE的CMRR产生影响的除了I和Q支路内部分光不等(${{k}_{0}}\ne {{k}_{180}}$，${{k}_{90}}\ne {{k}_{270}}$)和平衡探测器的响应度的不一致(${{\eta }_{P}}\ne {{\eta }_{N}}$)外，两支路上的时间失配(${{\tau }_{P}}\ne {{\tau }_{N}}$)同样产生影响。CMRR在频域内可表示为^[10]：

$\text{CMRR}=10\log {{\left| \frac{{{\eta }^{2}}-{{\text{e}}^{\text{j}2\pi f\tau }}}{{{\eta }^{2}}+1} \right|}^{2}}$

(2)

式中，$\eta ={{\eta }_{\text{Hybrid}}}{{\eta }_{\text{BR}}}$，${{\eta }_{\text{Hybrid}}}$和${{\eta }_{\text{BR}}}$分别为光混频内两支路间的分光比和平衡探测器内两光电探测器响应度之比；$\tau ={{\tau }_{P}}-{{\tau }_{N}}={{\tau }_{\text{Hybrid}}}+{{\tau }_{\text{BR}}}$为两支路间时间差，包含光混频器光程不等引起的时延${{\tau }_{\text{Hybrid}}}$和两光探测器的时延${{\tau }_{\text{BR}}}$。对于$\eta $和$\tau $其取值范围分别为：$0\le \left| 10\log \eta \right|\le \left| 10\log {{\eta }_{\text{Hybrid}}} \right|+\left| 10\log {{\eta }_{\text{Balance}}} \right|$，$0\le \left| \tau \right|\le $ $\left| {{\tau }_{\text{Hybrid}}} \right|+\left| {{\tau }_{\text{BR}}} \right|$。

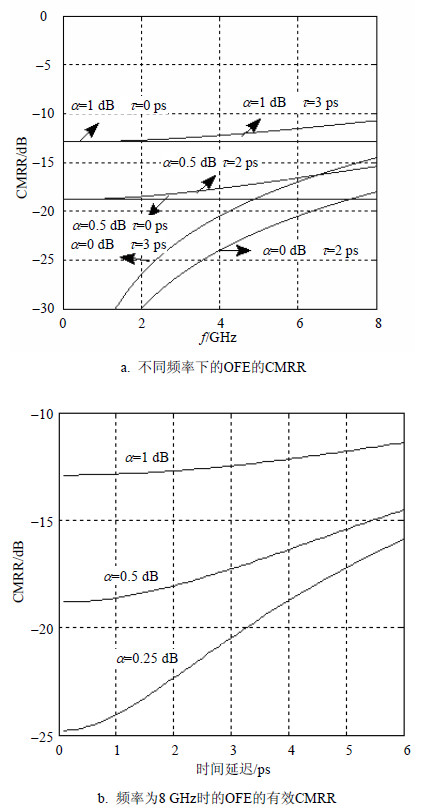
在空间光混频器内分光误差主要来自于二分之一波片的安装误差和PBS的偏振分光误差^[13]。二分之一波片2.5mrad的旋转将带来0.08 dB的分光误差^[13]；对于一个典型的PBS其P光S光的透射率和反射率分别为：${{T}_{\text{P}}}>95%$，${{R}_{\text{P}}}<5%$和${{T}_{\text{S}}}<1%$，${{R}_{\text{S}}}>99%$，其将带来约0.35 dB的分光误差。在平衡探测器内，两探测器的响应度最大有0.5 dB的误差，此时$\eta $的最大值达到0.93 dB。$\tau $一般为几个皮秒。图 2给出了在$\eta $和$\tau $影响下，接收前端的CMRR随频率变换的曲线。

通过图 2a可以看出，CMRR受分功率失配和时间失配影响，在低频段主要是受功率失配的影响，而在高频段时间失配的影响增大。图 2给出了频率为8 GHz时，不同功率失配下，有效CMRR^[10]随时间失配的变化趋势。该频率对应20 Gbps BPSK接收机的接收带宽。可以看出，如果$\eta $和$\tau $取值分别为0.25dB和2 ps，CMRR取值为-22.35 dB；如果两者增加到1 dB和3 ps，那么将CMRR增大到-12.47 dB。CMRR的取值表征了光接收前端对于LO带来的RIN噪声的抑制能力。CMRR值增加使接收机中的RIN噪声增加，同时降低数据接收的信噪比和OPLL的输入信噪比，影响OPLL性能。

2 失配对光锁相环路性能的影响 2.1 失配对相位跟踪的影响

图 3为基于COSTAS光锁相环的BPSK接收机原理图。对于I支路，信号光和本振光分别表示为：

${{E}_{S}}\equiv \sqrt{(1-\alpha ){{P}_{S}}}\cos \left[ {{\omega }_{S}}t+{{\phi }_{S}}(t)+{{\phi }_{D}}(t) \right]$

(3)

${{E}_{\text{LO}}}\equiv \sqrt{{{{P}_{\text{LO}}}}/{2}\;}\cos [{{\omega }_{\text{LO}}}t+{{\phi }_{\text{LO}}}(t)+{{\phi }_{C}}(t)]$

(4)

式中，${{P}_{S}}$、${{P}_{\text{LO}}}$，${{\omega }_{S}}$、${{\omega }_{\text{LO}}}$和${{\phi }_{S}}(t)$、${{\phi }_{\text{LO}}}(t)$分别为接收信号光和本振光的功率、频率和初始相位；${{\phi }_{D}}(t)$为相位调制信号，取值为0或$\text{ }\!\!\pi\!\!\text{ }$；${{\phi }_{C}}(t)$为LO输出的控制信号；$\alpha $为信号光分到正交支路(Q支路)的分光比。LO功率在4条支路上均匀分光。

那么I支路的输出电流信号可以表示为：

$\begin{align} & {{I}_{0}}=\frac{\text{e}{{k}_{0}}{{\eta }_{P}}}{2hv}\left[ \alpha {{P}_{S}}+{{{P}_{\text{LO}}}}/{2}\; \right.+ \\ & \left. {{K}_{\text{PDI}}}\cos (\Delta \phi (t)+{{\phi }_{D}}(t)-{{\phi }_{C}}(t)+\Delta {{\phi }_{0}}) \right] \\ \end{align}$

(5)

$\begin{align} & {{I}_{180}}=\frac{\text{e}{{k}_{180}}{{\eta }_{N}}}{2hv}\left[ \alpha {{P}_{S}}+{{{P}_{\text{LO}}}}/{2}\; \right.- \\ & \left. {{K}_{\text{PDI}}}\cos (\Delta \phi (t+\tau )-{{\phi }_{C}}(t+\tau )+{{\phi }_{D}}(t+\tau )) \right] \\ \end{align}$

(6)

式中，${{K}_{\text{PDI}}}=2\sqrt{{\alpha {{P}_{S}}{{P}_{\text{LO}}}}/{2}\;}$；$\Delta \phi (t)={{\phi }_{S}}(t)-{{\phi }_{\text{LO}}}(t)$，$\tau $约为几个皮秒，而激光器相位噪声起伏的频率最大值低于兆赫兹。因此有：${{\phi }_{S}}(t)\approx {{\phi }_{S}}(t+\tau )$，${{\phi }_{\text{LO}}}(t)\approx {{\phi }_{\text{LO}}}(t+\tau )$，且${{k}_{0}}$、${{k}_{180}}\approx 1$，${{\eta }_{P}}$、${{\eta }_{N}}\approx 1$，那么获得I支路的电流可以表示为：

$\begin{align} & {{I}_{I}}=\frac{\text{e}}{hv}\left[ \frac{{{k}_{0}}{{\eta }_{P}}-{{k}_{180}}{{\eta }_{N}}}{2}\left( \alpha {{P}_{S}}+\frac{{{P}_{\text{LO}}}}{2} \right) \right.+ \\ & {{K}_{\text{PDI}}}\sqrt{\frac{\alpha {{P}_{S}}{{P}_{\text{LO}}}}{2}}(\cos (\Delta \phi (t)+{{\phi }_{D}}(t)-{{\phi }_{C}}(t))+ \\ & \left. \frac{{}}{{}}\text{ }\cos (\Delta \phi (t)-{{\phi }_{C}}(t)+{{\phi }_{D}}(t+\tau ))) \right] \\ \end{align}$

(7)

因为${{k}_{0}}{{\eta }_{P}}\ne {{k}_{180}}{{\eta }_{N}}$，此时剩余的电流约为$(({{k}_{0}}{{R}_{P}}-{{k}_{180}}{{R}_{N}}){{P}_{\text{LO}}})/4\ne 0$，而信号光功率非常小，故可忽略不计。交流项可以表示为：

$\begin{align} & \cos \left( \Delta {{\phi }_{\text{rand}}}(t)+\frac{{{\phi }_{D}}(t)+{{\phi }_{D}}(t+\tau )}{2} \right)\times \\ & \cos \left( \frac{{{\phi }_{D}}(t)-{{\phi }_{D}}(t+\tau )}{2} \right) \\ \end{align}$

(8)

其中，$\Delta {{\phi }_{\text{rand}}}(t)=\Delta \phi (t)-{{\phi }_{C}}(t)$为相位跟踪残差，${{\phi }_{D}}(t)=0$,$\text{ }\!\!\pi\!\!\text{ }$，在$\tau $的时间内式(8)取值为0，此时相当于产生了一个矩形脉冲的干扰信号。对于5 ps的矩形脉冲，其能量主要分布在200 GHz的带宽内，而锁相环路的带宽仅为兆赫兹量级，引入环路的能量非常小，因此可忽略不计。那么获得的相位误差信号可以表示为：

$\begin{matrix} V={{R}^{2}}\sqrt{\alpha }(1-\alpha ){{P}_{\text{LO}}}{{P}_{S}}\sin (2(\Delta \phi (t)-{{\phi }_{C}}(t))+2{{\phi }_{D}}(t))= \\ 2{{K}_{\text{PD}}}\sin (2(\Delta \phi (t)-{{\phi }_{C}}(t)))\approx \\ 2{{K}_{\text{PD}}}(\Delta \phi (t)-{{\phi }_{C}}(t)) \\ \end{matrix}$

(9)

式中，$R={\text{e}{{\eta }_{P}}}/{hv}\;={\text{e}{{\eta }_{N}}}/{hv}\;$；${{K}_{\text{PD}}}={{K}_{\text{PDI}}}{{K}_{\text{PDQ}}}$为光电探测器的增益；$2{{\phi }_{D}}(t)=0$或$2\text{ }\!\!\pi\!\!\text{ }$；$\Delta \phi (t)-{{\phi }_{C}}(t)$取值非常小，因此$\sin (2(\Delta \phi (t)-{{\phi }_{C}}(t)))\approx 2(\Delta \phi (t)-{{\phi }_{C}}(t))$。通过分析看出，锁相环路具有的低通窄带特性屏蔽掉时间延迟的影响。

2.2 失配对OPLL环路相位噪声的影响

环路中的相位噪声主要来自于信号光激光器和本振激光器的相位噪声以及进入环路内的强度噪声，主要包括散粒噪声、RIN噪声和热噪声，而在以往的研究中将OFE认为是理想器件，完全将RIN噪声消除而不予考虑，但失配降低对RIN噪声的抑制能力，在高性能的接收中必须进行考虑。

激光器相位噪声的功率谱密度(PSD)为^{[8, 9]}：

${{S}_{\text{PN}}}(f)={(\Delta {{f}_{S}}+\Delta {{f}_{\text{LO}}})}/{2\text{ }\!\!\pi\!\!\text{ }}\;$

(10)

式中，$\Delta {{f}_{S}}$、$\Delta {{f}_{\text{LO}}}$分别为信号光与本振光激光器的线宽。I和Q支路总的散粒噪声、热噪声和剩余的RIN噪声分别为^[10]：

${{S}_{\text{Shot}}}=2qR{{{P}_{\text{LO}}}}/{2}\;(K_{\text{PDI}}^{2}+K_{\text{PDQ}}^{2})=2q{{R}^{3}}{{P}_{S}}P_{\text{LO}}^{2}$

(11)

同理^[10]，有：

${{S}_{\text{TIA}}}=2i_{\text{TIA}}^{2}{{R}^{2}}{{P}_{S}}{{P}_{\text{LO}}}$

(12)

${{S}_{\text{RIN}}}={{R}^{4}}P_{\text{LO}}^{3}(\text{RIN})\ \text{CMRR}{{{P}_{S}}}/{2}\;$

(13)

式中，${{i}_{\text{TIA}}}$为前置放大器的噪声电流密度。环路锁相后相位噪声可以表示为^{[5, 6, 7, 8]}：

$\begin{matrix} \sigma _{\text{TOT}}^{2}=E\left[ \phi _{\text{PN}}^{2}(t) \right]+E\left[ \phi _{\text{SN}}^{2}(t) \right]= \\ \int_{\ -\infty }^{\ \infty }{{{S}_{\text{PN}}}(f){{\left| 1-H(f) \right|}^{2}}\text{d}f}+\int_{\ -\infty }^{\ \infty }{{{S}_{\text{SN}}}(f){{\left| H(f) \right|}^{2}}}= \\ \frac{\Delta {{f}_{S}}+\Delta {{f}_{\text{LO}}}}{2\text{ }\!\!\pi\!\!\text{ }}{{\int_{\ -\infty }^{\ \infty }{\left| \frac{1-H(f)}{f} \right|}}^{\text{2}}}\text{d}f+ \\ \frac{q+{i_{\text{TIA}}^{2}}/{(R{{P}_{\text{LO}}})}\;+{R{{P}_{\text{LO}}}(\text{RIN})\text{CMRR}}/{4}\;}{2R\alpha (1-\alpha ){{P}_{S}}}\int_{\ -\infty }^{\ \infty }{{{\left| H(f) \right|}^{2}}}\text{d}f \\ \end{matrix}$

(14)

在优化带宽下，相位噪声为^[8]：

$\sigma _{\text{TOT}}^{2}=\sqrt{\frac{(\Delta {{f}_{S}}+\Delta {{f}_{\text{LO}}})(q+{i_{\text{TIA}}^{2}}/{(R{{P}_{\text{LO}}})}\;+{R{{P}_{\text{LO}}}(\text{RIN})\ \text{CMRR}}/{4}\;)}{\text{ }\!\!\pi\!\!\text{ }R\alpha (1-\alpha ){{P}_{S}}}}$

(15)

通过式(15)可以看出，在优化的带宽下，总的相位噪声是一个与LO功率和OFE的CMRR相关的量，可以进一步对通过对LO功率优化来降低相位噪声。

通过本振优化，那么此时总的相位噪声可以表示为：

$\sigma _{\text{TOT}}^{2}=\sqrt{\frac{\Delta {{f}_{S}}+\Delta {{f}_{\text{LO}}}}{\text{ }\!\!\pi\!\!\text{ }}\frac{q+\sqrt{(\text{RIN})\ \text{CMRR}i_{\text{TIA}}^{2}}}{R\alpha (1-\alpha ){{P}_{S}}}}$

(16)

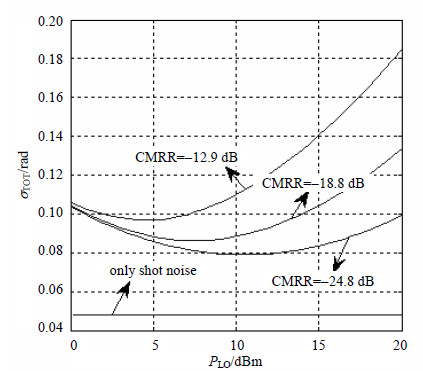
相位噪声随LO功率的变化如图 4所示，通过仿真看出，CMRR增加将使得整体的相位噪声增加，OPLL的带宽仅为兆赫兹量级，因此引起相位噪声增加主要来至于接收前端内功率失配的影响。同时在一定的CMRR下，总相位噪声随本振功率的增加发生变化，并存在一个最优值。在CMRR=-12.8，18.8，-12.5 dB时，最小的相位噪声对应的本振光分别为：10.5、7.5、4.5 dBm。此时，$\Delta {{f}_{S}}+\Delta {{f}_{\text{LO}}}$=200kHz，$R=0.65$ A/W，${{P}_{S}}=-43$dBm。图 4同样给出了仅考虑散粒噪声情况下相位噪声值。在最优的本振功率下，相对于仅考虑散粒噪声的情况，相位噪声分别增加了2.4、3.9、5.9 dB。

2.3 存在环路延迟下的相位噪声

在锁相环路中，环路的延迟是不能消除的，其值影响环路的稳定性。在考虑到环路延迟下的相位噪声可以表示为^[14]：

$\sigma _{\text{PN}}^{2}=\frac{\text{ }\!\!\pi\!\!\text{ }\sqrt{2}(\Delta {{f}_{S}}+\Delta {{f}_{\text{LO}}})}{2{{\omega }_{n}}}\frac{36+36\gamma -30{{\gamma }^{2}}+6{{\gamma }^{3}}-{{\gamma }^{4}}}{36-72\gamma +6{{\gamma }^{2}}-{{\gamma }^{4}}}$

(17)

$\begin{align} & \sigma _{\text{SN}}^{2}=\frac{3{{\omega }_{n}}(q+\sqrt{(\text{RIN})\ \text{CMRR}i_{\text{TIA}}^{2}})}{4\sqrt{2}R\alpha (1-\alpha ){{P}_{S}}}\times \\ & \frac{36+12\gamma -18{{\gamma }^{2}}+6{{\gamma }^{3}}-{{\gamma }^{4}}}{36-72\gamma +6{{\gamma }^{2}}-{{\gamma }^{4}}} \\ \end{align}$

(18)

式中，$\gamma ={{{\tau }_{D}}{{\omega }_{n}}}/{(2\xi )}\;={\tau {{\omega }_{n}}}/{\sqrt{2}}\;$；${{\tau }_{D}}$为锁相环路的环路延迟；${{\omega }_{n}}$为环路的固定频率。

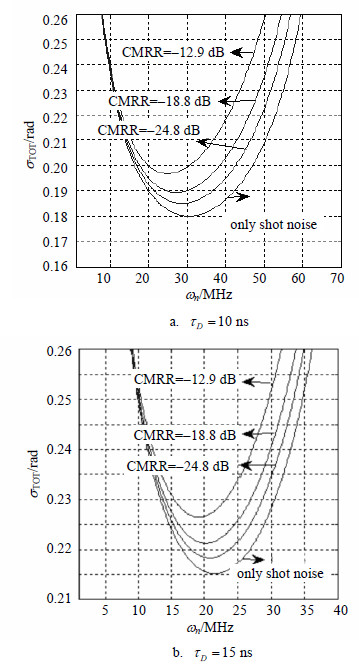
图 5给出了不同的延迟和固定频率下的相位噪声。可以看出在最优的环路带宽下的相位噪声除了取决于延迟外，还受到失配的影响。失配越严重，剩余相位噪声越大，并且失配带来的相位噪声的增加无法通过优化环路带宽和LO功率来消除。为保证稳定的相位跟踪，要求${{\sigma }_{\text{TOT}}}\le 0.18$rad^[8]。在10 ns和15 ns的环路延迟下，相位噪声均大于此值，需要减小激光器的线宽消除影响。对于15 ns的延迟，对应CMRR=-12.9，-18.8，-24.8 dB，$\Delta {{f}_{S}}+\Delta {{f}_{\text{LO}}}$依次减小到116、126、132 kHz以下。

3 失配对相干接收机灵敏度的影响

通过上面的分析可以看出，接收前端的功率失配增大降低了对RIN噪声的抑制能力，噪声增加，降低数据接收的信噪比。在LO功率优化下，此时信噪比可以表示为：

$\text{SNR}=\frac{2R(1-\alpha ){{P}_{S}}}{q\Delta f+\sqrt{2i_{\text{TIA}}^{\text{2}}\text{RIN}\cdot \ \text{CMRR}\cdot }\Delta f}$

(19)

那么此时接收机的误码率可以表示为^[15]：

$\begin{matrix} {{P}_{e}}= \\ \frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\sigma _{\text{TOT}}^{2}}}\int_{\ -\text{ }\!\!\pi\!\!\text{ }}^{\ \text{ }\!\!\pi\!\!\text{ }}{Q}(\text{SNR}\left[ 1-4Q(\sqrt{2\text{ }\!\!\pi\!\!\text{ }}{{f}_{g}}T) \right]\times \\ \cos (\Delta {{\phi }_{\text{rand}}}(t)))\exp \left( -\frac{{{(\Delta {{\phi }_{\text{rand}}}(t))}^{2}}}{2\sigma _{\text{TOT}}^{2}} \right)\text{d}(\Delta {{\phi }_{\text{rand}}}) \\ \end{matrix}$

(20)

采用高斯基带滤波器时，${{f}_{g}}T\approx 0.79$。

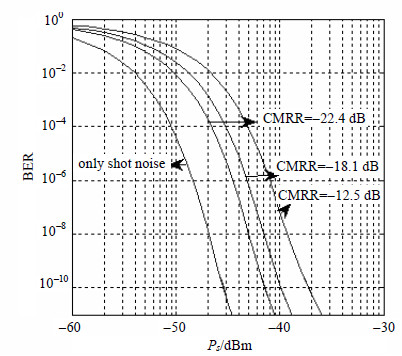
图 6给出受失配影响的接收机的误码性能的仿真。此时保证相位噪声为$\sigma =0.18$rad，相对于散粒噪声极限的接收灵敏度下降1 dB，其中0.5 dB来自于信号光的分光，0.5 dB来自于相位噪声。可以看出，当CMRR=-22.4，-18.1，-12.5 dB时，失配将接收灵敏度进一步减小4.0、5.2、7.3 dB。此时若想通过进一步减小激光器的线宽来改善误码性能意义不大，当CMRR=-24.8 dB，若进一步线宽减半，即66 kHz，灵敏度仅改善0.7 dB。因为此时相位噪声已经很小，造成灵敏度下降的主要因素为接收信噪比的下降。为保证接收机具有优于-40 dBm的接收灵敏度，即将失配带来的灵敏度下降小于5.5 dB，此时OFE的CMRR=-17.2 dB，综合考虑功率失配和时间传输失配控制的难度，应保证OFE内功率失配小于0.5 dB，时间传输失配小于3 ps。

4 结论

本文讨论了OFE内功率失配和传输时间失配的来源和失配对接收机灵敏度的影响。OFE内的功率失配和传输时间失配降低了平衡接收对RIN噪声的抑制，使得接收机信噪比下降，锁相环路的相位噪声增加。在锁相环路中通过本振优化和带宽优化可以将相位噪声的增加量最小化。对于失配的影响表现出频率特性使得锁相环路仅受到功率失配的影响，而数据接收同时受功率失配和时间失配的影响。为保证接收机具有优于-40 dBm的接收灵敏度，要求OFE功率失配小于0.5 dB，传输失配小于3 ps。