试验模态分析(experimental modal analysis,EMA)是一种通过实验方法获取结构输入输出数据,并借助系统识别理论利用相关识别算法求解结构模态参数的方法[1]。识别算法是获取结构模态参数的关键,可分为时域算法和频域算法。频域识别算法因其可靠性较高而广泛使用。文献[2]利用传递函数的有理分式模型,通过基函数进行曲线拟合,但该方法在阶次较高时容易出现计算不收敛。文献[3]提出一种基于自回归滑动(auto-regressive moving average,ARMA)模型的频域多输入多输出(multiple input multiple output,MIMO)参数识别方法,可用于改善正交多项式在高阶计算时不易收敛的问题。文献[4]提出一种基于正交多项式的频响函数拟合方法,该方法最初只能用于单输入单输出(single input single output,SISO)识别,被扩展到了MIMO。但已有的多参考点识别方法在系数矩阵估计中需进行多次转换,造成精度损失和计算量成倍增加。
针对该问题,本文以传递函数有理分式模型为基础,借助正交多项式频响函数拟合方法,提出一种改进的模态参数识别方法;并给出算法实现流程和模态参数的稳定图校验方法,构建了模态参数识别平台,并验证了改进后的识别算法的有效性。
1 基于传递函数有理分式的模态参数识别方法根据黏性阻尼的多自由度(multi-degree-of- freedom,MDOF)系统振动的微分方程[5]和零初始条件拉氏变换,并利用阻抗矩阵和伴随矩阵,可导出传递函数矩阵H(s),其任意一个元素可表示为:
| $\begin{align} & {{H}_{ef}}(s)=\frac{{{\alpha }_{0}}+{{\alpha }_{1}}(j\omega )+\cdots +{{\alpha }_{2n-2}}{{(j\omega )}^{2n-2}}}{1+{{\beta }_{1}}(j\omega )+\cdots +{{\beta }_{2n}}{{(j\omega )}^{2n}}} \\ & e,f=1,2,\cdots ,n \\ \end{align}$ | (1) |
为解决式(1)中计算数值解的奇异性问题,文献[6]提出利用正交多项式代替原有的有理分式,得到以正交多项式表示的频响函数模型,有:
| $\mathbf{H}(j\omega )=\frac{\sum\limits_{i=0}^{2N}{{{c}_{i}}{{p}_{i}}(j\omega )}}{\sum\limits_{i=0}^{2N}{{{d}_{i}}{{q}_{i}}(j\omega )}}=\frac{\mathbf{C}(j\omega )}{\mathbf{D}(j\omega )}$ | (2) |
设在某结构的其中一个测点上共测试L个频率点。引入负频率概念,即频率范围由原来的k=1,2,…,L扩展到k=-L,…, -1, -2,1,2,…,L。此时,取${\omega _{ - k}} = $$-{{\omega }_{k}}$。负频率$-{{\omega }_{k}}$的频响函数定义为$H(j{{\omega }_{-k}})=$$H(-j{{\omega }_{k}})=$${{H}^{*}}(j{{\omega }_{k}})$。
设实测频响函数的值为${{\tilde{H}}_{k}}$,仍然满足上述关系,即${{\tilde{H}}_{-k}}=\tilde{H}_{k}^{*}$。定义误差函数${{\tilde{e}}_{k}}=H(j{{\omega }_{k}})-{{\tilde{H}}_{k}}$,令${{d}_{2N}}=1$,引入加权误差函数${{e}_{k}}$,则有:
| ${{e}_{k}}=\sum\limits_{i=0}^{2N}{{{c}_{i}}{{p}_{i}}(j\omega )}-{{\tilde{H}}_{k}}\left[ \sum\limits_{i=0}^{2N}{{{d}_{i}}{{q}_{i}}(j\omega )}+{{q}_{2N}}(j{{\omega }_{k}}) \right]$ | (3) |
当k从-L~L变化,可得到2L个误差函数。将这些误差函数写成矩阵形式可表达为$\{\mathbf{e}\}=[\mathbf{P}]\{\mathbf{c}\}-[\mathbf{Q}]\{\mathbf{d}\}-\{\mathbf{\omega }\}$。
构造目标函数$E={{\{e\}}^{\text{T}}}\{e\}$,要使实测频响函数是真实频响函数的最佳拟合,可通过计算目标函数的极值获得。目标函数取得极值的条件为:
| $\frac{\partial E}{\partial \{c\}}=\{0\}\ \text{ }\frac{\partial E}{\partial \{d\}}=\{0\}$ | (4) |
式(4)经化简可得:
| $\left[ \begin{matrix} \text{ }\!\![\!\!\text{ }\mathbf{C}\text{ }\!\!]\!\!\text{ } & [\mathbf{B}] \\ {{\text{ }\!\![\!\!\text{ }\mathbf{B}\text{ }\!\!]\!\!\text{ }}^{\text{T}}} & \text{ }\!\![\!\!\text{ }\mathbf{D}\text{ }\!\!]\!\!\text{ } \\ \end{matrix} \right]\left\{ \begin{matrix} \text{ }\!\!\{\!\!\text{ }\mathbf{c}\text{ }\!\!\}\!\!\text{ } \\ \text{ }\!\!\{\!\!\text{ }\mathbf{d}\text{ }\!\!\}\!\!\text{ } \\ \end{matrix} \right\}=\left\{ \begin{matrix} \text{ }\!\!\{\!\!\text{ }\mathbf{g}\text{ }\!\!\}\!\!\text{ } \\ \text{ }\!\!\{\!\!\text{ }\mathbf{f}\text{ }\!\!\}\!\!\text{ } \\ \end{matrix} \right\}$ | (5) |
| $(\text{ }\!\![\!\!\text{ }{{\mathbf{I}}_{2}}\text{ }\!\!]\!\!\text{ }-{{\text{ }\!\![\!\!\text{ }\mathbf{B}\text{ }\!\!]\!\!\text{ }}^{\text{T}}}\text{ }\!\![\!\!\text{ }\mathbf{B}\text{ }\!\!]\!\!\text{ })\text{ }\!\!\{\!\!\text{ }\mathbf{d}\text{ }\!\!\}\!\!\text{ }=-{{\text{ }\!\![\!\!\text{ }\mathbf{B}\text{ }\!\!]\!\!\text{ }}^{\text{T}}}\text{ }\!\!\{\!\!\text{ }\mathbf{g}\text{ }\!\!\}\!\!\text{ }$ | (6) |
| $\text{ }\!\!\{\!\!\text{ }\mathbf{c}\text{ }\!\!\}\!\!\text{ }=\text{ }\!\!\{\!\!\text{ }\mathbf{g}\text{ }\!\!\}\!\!\text{ }-\text{ }\!\![\!\!\text{ }\mathbf{B}\text{ }\!\!]\!\!\text{ }\!\!\{\!\!\text{ }\mathbf{d}\text{ }\!\!\}\!\!\text{ }$ | (7) |
设在K个测点均测得频响函数,令:
| ${{U}_{k}}=\text{ }\!\![\!\!\text{ }{{\mathbf{I}}_{2}}\text{ }\!\!]\!\!\text{ }-{{\text{ }\!\![\!\!\text{ }\mathbf{B}\text{ }\!\!]\!\!\text{ }}^{\text{T}}}[\mathbf{B}]{{V}_{k}}=-{{[\mathbf{B}]}^{\text{T}}}\text{ }\!\!\{\!\!\text{ }g\text{ }\!\!\}\!\!\text{ }$ |
| ${{U}_{k}}{{D}_{k}}={{V}_{k}}$ | (8) |
一个结构的固有频率和模态阻尼与测点位置无关,因而不同测点拟合出的有理分式传递函数分母系数Dk相差一个常数因子。为此采用最小二乘法求解式(8)可表示为:
| $\left( \sum\limits_{k=1}^{K}{U_{k}^{\text{T}}{{U}_{k}}} \right){{D}_{k}}=\sum\limits_{k=1}^{K}{U_{k}^{\text{T}}{{V}_{k}}}$ | (9) |
通过式(9)得到系数向量D后,再利用式(7)计算系数向量C及其他参数。该方法可避免在进行多参考点测量时,重复构造转换矩阵,减少转换过程带来的拟合误差,同时一次性拟合可使计算过程简化。
得到向量C、D后,利用式(1),令:
| $\mathbf{D}(s)=1+{{\beta }_{1}}s+...+{{\beta }_{2n}}{{s}^{2n}}=0$ | (10) |
求解可得n对复根${{s}_{i}}$和$s_{i}^{*}$,又有:
| $\left\{ \begin{align} & {{s}_{i}}=-{{\zeta }_{i}}{{\omega }_{i}}+j{{\omega }_{i}}\sqrt{1-\zeta _{i}^{2}} \\ & s_{i}^{*}=-{{\zeta }_{i}}{{\omega }_{i}}-j{{\omega }_{i}}\sqrt{1-\zeta _{i}^{2}} \\ \end{align} \right.$ | (11) |
故可通过下式求出固有频率与阻尼比:
| ${{\omega }_{i}}=\sqrt{{{s}_{i}}s_{i}^{*}}$ | (12) |
| ${{\zeta }_{i}}=\frac{{{s}_{i}}+s_{i}^{*}}{2{{\omega }_{i}}}$ | (13) |
用于频响函数曲线拟合的正交式有多种,如Forsythe正交多项式、Legendre多项式、向量正交多项式等,文献[7, 8]均采用Forsythe正交多项式,但其递推阶段计算量较大,影响整体的识别速度。为改善这种情况,本文采用Chebyshev正交多项式,其递推公式为${{T}_{n+1}}(x)=2x{{T}_{n}}(x)-{{T}_{n-1}}(x)$,规定${{T}_{0}}(x)=1,$ ${{T}_{1}}(x)=x$,递推可得:
| $\left\{ \begin{align} & {{T}_{1}}(x)=x \\ & {{T}_{2}}(x)=2{{x}^{2}}-1 \\ & {{T}_{3}}(x)={{2}^{2}}{{x}^{3}}-3x \\ & ... \\ \end{align} \right.$ | (14) |
本文采用Labview实现算法程序,若识别不能在一个频段内一次完成,可采用分段识别方式重复该过程。具体流程如图 1所示。
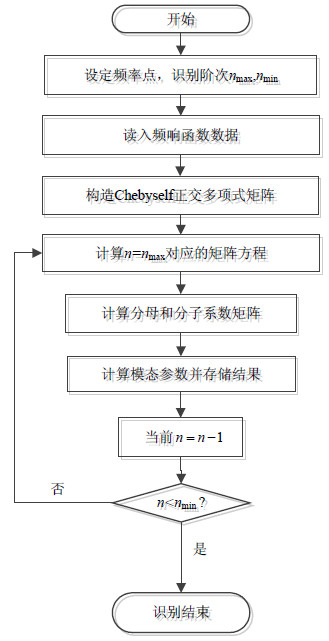 |
| 图1 算法实现流程图 |
模态定阶是参数识别的重要步骤,常借助稳定图来完成[9]。由于系统真实模态是系统的物理极点,它出现的位置不会随阶次改变而改变,而计算极点出现的位置则随阶次的改变而不同[10, 11]。稳定图极点的标示过程(以第n阶极点为例)为:
1) 设第n阶的模态频率为${{f}_{n}}$,阻尼比为${{\xi }_{n}}$;
2) 在第n-1阶寻找与之最接近的极点及其对应的参数${{f}_{n}}$和${{\xi }_{n}}$;
3) 根据下式判断相对变化量,有:
| $\left\{ \begin{gathered} \left| {\frac{{{f_n} - {f_{n - 1}}}}{{{f_{n - 1}}}}} \right| \times 100\% < {C_f}{\text{ (15a)}} \hfill \\ \left| {\frac{{{\xi _n} - {\xi _{n - 1}}}}{{{\xi _{n - 1}}}}} \right| \times 100\% < {C_\xi }{\text{ (15b)}} \hfill \\ \end{gathered} \right.$ |
4) 若式(15)均不满足,则以符号o标示为新出现的极点;若只满足式(15a)而不满足式(15b),则以符号f标示为频率稳定极点;若式(15a)、式(15b)均满足,则以符号d标示为稳定极点。
4 实验验证为验证改进算法的有效性,本文构建了多模态参数识别平台,如图 2所示。主要包括力锤、传感器、数据采集与分析系统。
 |
| 图2 实验测试平台 |
实验中吊臂尺寸为180mm×40mm× 25mm,厚度为2mm,实物图如图 3所示。实验中支撑方式为固定支撑,采用轮点激励、多点采集方式进行数据采集。实验采样频率为4kHz,采样点数214。为降低实验过程中的偶然误差,实验中对5次实验数据取平均值作为拟合数据样本。
 |
| 图3 吊臂零件 |
图 4所示为测试所得吊臂的所有频响曲线的幅值叠加谱。由图 4可看出,在响应峰值附近其信号受噪声的影响较小。
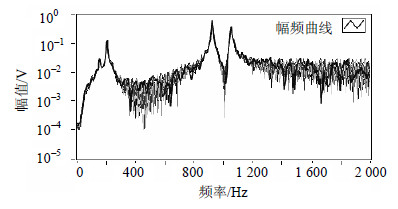 |
| 图4 吊臂零件的幅值叠加谱 |
根据叠加谱选定阶次及拟合区间,运用改进算法得到的结果如图 5所示。根据图 5的频响函数,设定Cf≤1%、Cξ≤5%进行稳定图校验(计算到8阶),结果如图 6所示。从图 6可看出,试件有3阶模态频率。
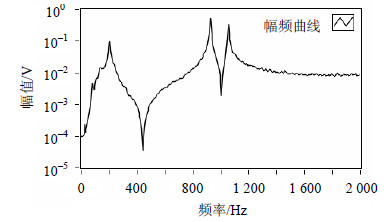 |
| 图5 吊臂零件拟合后的频响函数 |
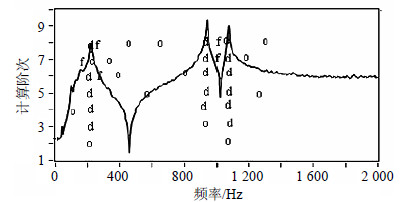 |
| 图6 吊臂零件的稳定图校验 |
为验证改进方法在模态参数识别方面的优越性,本文分别比较了采用有限元法、改进方法和原方法对吊臂的固有特性进行分析的结果。表 1列出了3种情况下吊臂零件的模态参数识别结果。
| 表1 吊臂零件识别结果比较 |
由表 1可得,改进方法的识别结果与有限元结果在第一、第二和第三阶固有频率方面的相对识别误差分别是0.453%、0.313%和0.265%;原方法的相对识别误差是0.994%、0.442%和0.341%。而改进方法在第一、第二和第三阶阻尼比方面的识别结果与理论值的相对误差分别是:10.6%、28.5%和2.00%;原方法的相对误差则为7.00%、29.9%和11.0%。
因此,通过比较可得出,改进方法在频率识别精度方面优于原方法,而在阻尼比识别方面,阶次越高,改进方法在识别精度上的优势比原方法明显。此外,本文提出的改进方法简化了识别过程中的繁琐计算过程,识别所需时间较短,可更好地用于实时识别过程,加速识别进程。
5 结束语本文通过对基于传递函数有理分式识别模态参数方法的分析,提出了一种基于传递函数有理分式的简化模态参数识别算法,并通过实验验证了改进方法在参数识别方面的准确性和高效性。实验结果表明,改进算法可快速有效地识别动态参数。本文得到的结论如下:1) 利用传递函数有理分式模型,在原有正交多项式识别方法基础上,提出一种改进方法。该方法采用一次性拟合,有效地避免多次求解中矩阵转换过程,计算过程简化。2) 利用文中所述极点标示方法建立稳定图,可较好地校验模型的参数识别结果。3) 实验结果表明,改进方法能有效地提高模态参数的识别的精度。
| [1] | 李东旭. 高等结构动力学[M]. 北京:科学出版社, 2010. LI Dong-xu. Advanced structural dynamics[M]. Beijing: Science Press, 2010. |
| [2] | CLOUGH R W, PENZIEN J. 结构动力学[M]. 王光远译. 北京: 高等教育出版社, 2006. CLOUGH R W, PENZIEN J. Structural dynamics[M]. Translated by WANG Guang-yuan. Beijing: Higher Education Press, 2006. |
| [3] | SHIH C Y, TSUEI Y G. Complex mode indication function and its applications to spatial domain parameter estimation[C]//Proceedings of the 7th International Modal Analysis Conference. Las Vegas, USA: Society for Experimental Mechanics, 1989. |
| [4] | RICHARDSON M H. Global frequency & damping estimates from frequency response measurements[C]//Proceedings of the 4th International Modal Analysis Conference. Los Angeles, USA: Society for Experimental Mechanics, 1986. |
| [5] | 张力. 模态分析与实验[M]. 北京:清华大学出版社, 2011. ZHANG Li. Modal analysis and experiment[M]. Beijing: Tsinghua University Press, 2011. |
| [6] | CHEN K F, JIAO Q Y, SHEN Y H. On the frequency mapping of modal parameters identification[J]. Mechanical Systems and Signal Processing, 2010, 21(4): 1667-1673. |
| [7] | 王彤, 张令弥. 运行模态分析的频域空间域分解法及其应用[J] . 航空学报, 2006, 27(1): 62-66. WANG Tong, ZHANG Ling-mi. Frequency and spatial domain decomposition for operational modal analysis and its application[J]. Journal of Aeronautics, 2006, 27(1): 62-66. |
| [8] | PINTELON R. Frequency-domain subspace system identification using non parametric noise models[J]. Automatica, 2008, 38(8): 1295-1311. |
| [9] | GUILLAUME P, VERBOTEN P, VAN LANDUIT S, et al. A poly-reference implementation of the least-squares complex frequency domain estimator[C]//Proceedings of the International Modal Analysis Conference. Kissimmee, FL, USA: Society for Experimental Mechanics, 2003. |
| [10] | 郭胜利. 模态参数识别方法与模块开发[D]. 南京: 南京航空航天大学, 2007. GUO Sheng-li. Modal parameter identification method and development of module[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007. |
| [11] | VERBOYEN P, GUILLAUME P, CAUGERGHE B, et al. A comparison of frequency-domain transfer function model estimator formulations for structural dynamics modeling [J]. Journal of Sound and Vibration, 2005, 27(9): 775-798. |
 2016, Vol. 45
2016, Vol. 45
