-
随着无线通信与物联网技术的发展,车辆因特网(Internet of vehicles, IoV)应运而生,IoV可以为旅客提供许多新的服务,如语音识别、在线视频以及虚拟现实游戏等[1-2]。这些新的服务需要消耗较多的计算资源并且具有严格的时延约束,但是用户的终端设备往往计算能力有限,无法处理这些应用。为了解决车载用户终端计算能力不足的问题,有学者提出了车辆边缘计算(vehicular edge computing, VEC),它可以根据业务的需求,灵活地分配资源。
VEC在提高系统资源利用率的同时,还能够有效提升计算密集业务的用户体验。但是与传统的云服务器相比,当考虑到经济成本以及部署的灵活性时,VEC服务器的计算能力往往有限[3]。为了进一步提高系统的资源利用率需要一种新的动态资源分配策略。
目前,针对VEC的资源管理主要有以下研究。为了同时最小化车辆和VEC服务器的消耗,文献[4]在车辆侧提出了一种联合任务迁移和本地计算资源分配策略。同时在VEC侧提出了一种联合无线与计算资源分配策略。在智慧城市的车联网中,为了支持更多的时延敏感业务,同时减少网络的负载,文献[5]提出了一种联合无线与计算资源分配方案。文献[6]在车联网中研究了高能效的任务迁移问题,提出了一种基于交替方向乘子法的低复杂度分布式算法。以上所有研究都假设任务在迁移过程中信道状态是固定不变的。但在实际中,任务的迁移时延与车辆信道的相干时间并不在同一个时间级别。例如,当车辆速度为100 km/h,载频为1.8 GHz时,信道的相干时间约为2.5 ms,而任务的迁移时延可达到数十毫秒至数百毫秒,对于某些时延不敏感的业务,任务的迁移时延可达到数秒。如果不考虑信道的快速时变特性,会使得资源利用率降低,任务的迁移时延也无法得到满足[3-7]。因此,在VEC系统中进行资源分配时需要考虑信道的时变特性。
信道的快速时变特性是车联网的一个重要特点,本文主要研究在VEC系统中,信道的快速时变特性对资源分配策略的影响。构建一个在系统计算资源和信道容量有限以及任务QoS约束下的车载用户终端能耗最小化问题。由于车联网场景中多是视距场景,并且车辆的位置可以预测,因此可以利用路径损耗信息替代信道状态信息(channel state information, CSI)。通过利用李雅普诺夫随机优化理论,可以将原问题转化为两个子问题。由于计算资源分配子问题是一个单变量的优化问题,因此很容易求解。而无线资源分配子问题是一个混合整数规划问题,通过将该问题转换为单变量的优化问题进行求解。基于以上两个子问题的结果,提出一种联合无线与计算资源分配(joint radio and computation resource allocation, JRCRA)算法,并通过仿真结果验证JRCRA算法的有效性。
本文的主要贡献包括以下3点:
1) 本文在考虑车辆快速时变信道的特性下,提出一种联合无线与计算资源分配算法来减少车载用户的能量消耗。仿真结果显示,当数据包平均到达速率从20个/时隙增加到40个/时隙时,提出的算法性能相较于传统的贪婪算法能耗降低了48.85%。
2) 利用李雅普诺夫随机优化理论,通过调整控制参数V,可以实现车载用户能量消耗与任务处理时延的均衡。
3) 针对分解后的无线资源分配子问题,提出了一种有效算法来求解该混合整数规划问题。
-
本节首先给出VEC的系统模型,接着给出任务的传输队列和计算队列。
-
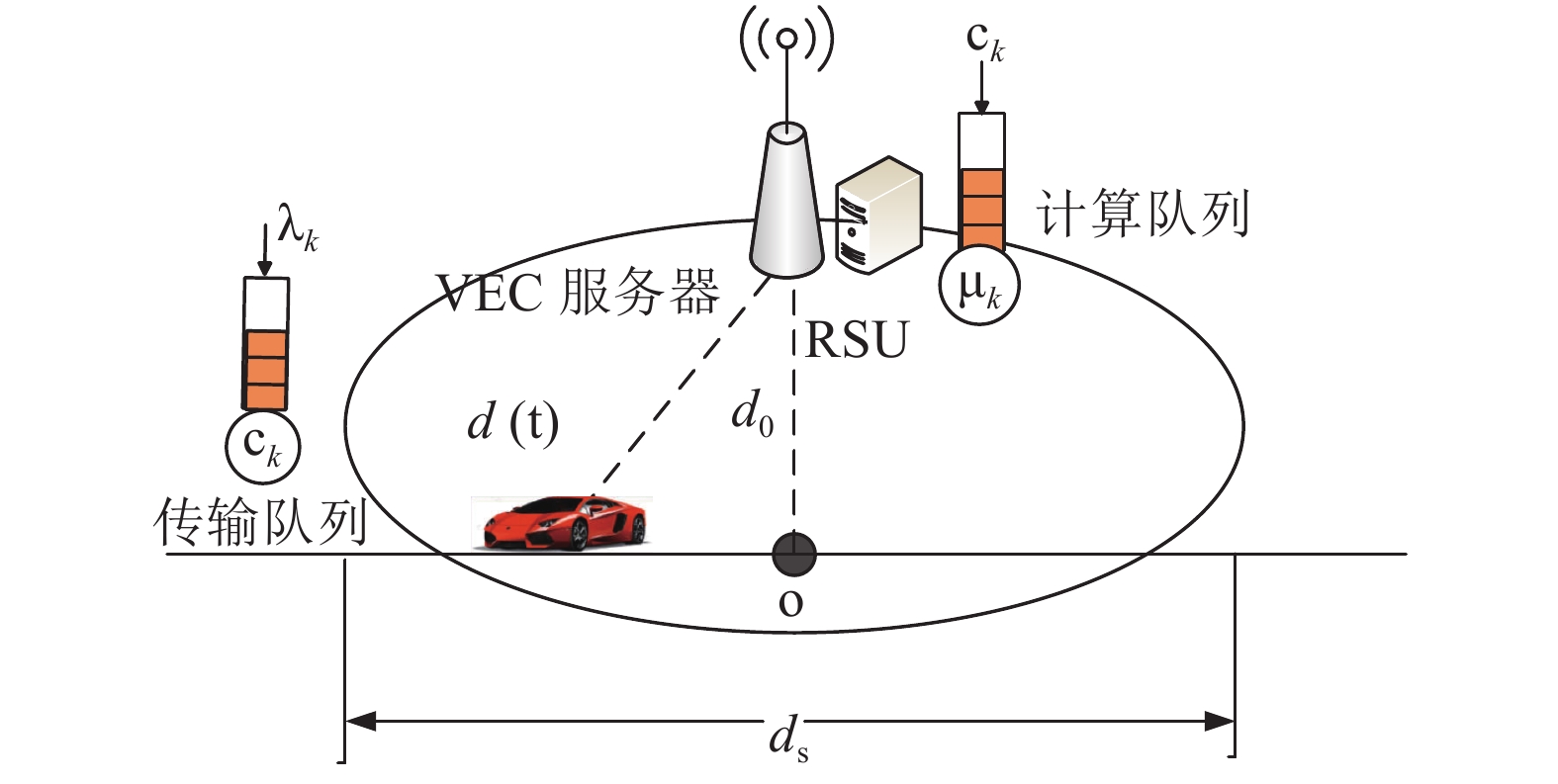
如图1所示,考虑一条单向道路,部署在路旁的路边单元(road side unit, RSU)均配备有VEC服务器,为用户提供无线服务。车辆用户终端需要将所有任务传输至VEC服务器进行计算。RSU距离道路的垂直距离为
${d_0}$ ,每个RSU的覆盖直径为${d_s}$ 。当车速为$v$ 时,车辆穿越RSU覆盖的小区所消耗的时间为$T = \dfrac{{{d_s}}}{v}$ 。当车辆到达O点时,令$t = 0$ 。定义$h\left( t \right)$ 为$t$ 时刻的信道增益。在车联网中,获取车辆的CSI极其困难,但是由于车辆的运动轨迹已知,因此可以利用可预测的路径损耗信息代替准确的CSI。则$t$ 时刻的路径损耗可以表示为:$$ h(t) = \frac{1}{{{{(d_0^2 + {{(vt)}^2})}^{\frac{\alpha }{2}}}}}\;\;- \frac{{{d_s}}}{{2v}} \leqslant t \leqslant \frac{{{d_s}}}{{2v}} $$ (1) 式中,
$\alpha $ 为路径损耗因子。由于小区的信道变化是可预测的,并且每个小区内的信道变化是对称的,因此本文只需要研究半个小区内的资源分配策略[8]。定义
$P\left( t \right)$ 为车载用户终端在时刻的发射功率。此时,车辆与RSU之间的无线传输速率为:$$ R(t) = W{\log _2}(1 + h(t)P(t)) $$ (2) 式中,
$W$ 是系统带宽。假设数据包的大小相同,均为$L$ 比特,则链路容量可以定义为能够传输的最大数据包数量为$C(t) = \left\lfloor {R(t)/L} \right\rfloor $ [9]。 -
在本文中,用两类队列模型来表示任务由车载用户终端到VEC服务器的处理过程。如图1所示,任务的处理过程被分为两个阶段,一是任务的传输阶段,二是任务在VEC服务器中的计算阶段。这两个阶段可以分别被建模为任务的传输队列和计算队列。
对于任务传输队列,车载用户终端将K个独立的任务迁移至VEC服务器。定义任务集合为
${{K}} = \left\{ {1,2, \cdots ,K} \right\}$ 。定义${{H}}(t) = \left[ {{H_1}(t),{H_2}(t),\cdots,{H_k}(t)} \right]$ 为传输队列积压向量,其中${H_k}\left( t \right)$ 为第$k$ 个任务在$t$ 时刻的传输队列积压。定义
${{A}}(t) = [A_{1}(t),A_{2}(t),\cdots,A_{k}(t)] $ 为任务所产生的数据包向量,其中$A_{k}(t)$ 为第$k$ 个任务在$t$ 时刻所产生的数据包。任务数据包的产生速度满足均值为${\lambda _k} = {{E}}\left[ {{A_k}(t)} \right]$ 的独立同分布过程,并且第$k$ 个任务在每一时隙所能产生的最大数据包为${B_k}$ 。定义${c_k}(t) \in [0,{H_k}(t)]$ 为第$k$ 个任务在$t$ 时刻所迁移的数据包。因此,第$k$ 个任务的传输队列可以表示为:$$ H_{k}(t+1)= \max [H_{k}(t)-c_{k}(t),0]+A_{k}(t) $$ (3) 为了保证任务的QoS需求,从长期平均的角度来看,平均的迁移数据包不应小于
${q_{_k}}$ 。对于任务计算队列,任务由VEC服务器进行计算。定义
${{Q}}(t) = [{Q_1}(t),{Q_2}(t),\cdots,{Q_k}(t)]$ 为VEC服务器的计算队列积压向量,其中${Q_k}\left( t \right)$ 为第$k$ 个任务在$t$ 时刻的计算队列积压。定义${\mu _k}(t) \in [0,{Q_k}(t)]$ 为第$k$ 个任务在$t$ 时刻所计算的数据包。因此,第$k$ 个任务的计算队列可以表示为:$$ {Q_k}(t + 1) = \max [{Q_k}(t) - {\mu _k}(t),0] + {c_k}(t) $$ (4) -
本节首先在VEC系统中构造一个联合无线与计算资源分配问题,该问题是在保证任务QoS要求下实现车载用户终端能耗最小化。然后利用随机动态优化理论对该问题进行重构。
-
为了避免丢包,所有的队列应该保持稳定。对于任意变量
$z$ ,定义长期平均期望为:$$ \bar z: = \mathop {\lim }\limits_{t \to \infty } \frac{1}{t}\sum\limits_{\tau = 0}^{t - 1} {\bf{E}} [z(\tau )] $$ (5) 基于长期时间平均期望,队列稳定需要满足如下条件[10]:
1) 如果
$\mathop {\lim }\limits_{t \to \infty } \dfrac{{{\bf{E}}\{ |H(t)|\} }}{t} = 0$ 成立,那么队列$H\left( t \right)$ 是平均速率稳定的。2) 如果
$\bar H < \infty $ 成立,那么队列$H\left( t \right)$ 是强稳定的。基于以上队列稳定的定义,联合无线与计算资源分配的问题可以建模为:
$$\tag{6a} {\min _{\{ {c_k}(t)\} ,\{ {\mu _k}(t)\} ,P(t)}}\bar P $$ (6a) $$\tag{6b} {\rm{s}}{\rm{.t}}{\rm{.}}\;{\bar c_k} \geqslant {q_{_k}} $$ $$\tag{6c} {\bar H_k} < \infty ,\quad{\bar Q_k} < \infty $$ $$\tag{6d} \sum\limits_{k = 1}^K {{c_k}} (t) \leqslant C(t) $$ $$\tag{6e} \sum\limits_{k = 1}^K {{\mu _k}} (t) \leqslant {\mu _{{\rm{total}}}} $$ $$\tag{6f} 0 \leqslant {c_k}(t) \leqslant {H_k}(t) $$ $$\tag{6g} 0 \leqslant {\mu _k}(t) \leqslant {Q_k}(t) $$ 式中,
${\mu _{{\rm{total}}}}$ 为VEC服务器的总计算资源。约束式(6b)表示每个任务的QoS要求;约束式(6c)确保队列稳定;约束式(6d)为信道容量约束;约束式(6e)为VEC服务器总计算资源约束;约束式(6f)和式(6g)分别表示迁移数据包和计算数据包约束。由于式(6)是一个非凸问题,难以求解,因此需要对该问题进行重构。 -
由于式(6)存在时间平均,因此难以求解。本小节采用随机动态优化理论将约束式(6b)重新构建为单个时间平均的函数[9]。引入虚拟队列
${Z_k}(t)$ ,可以表示为:$$ {Z_k}(t + 1) = \max [{Z_k}(t) - {c_k}(t),0] + {q_{_k}} $$ (7) 其初始条件为
${Z_k}(0) = 0$ 。对于虚拟队列${Z_k}(t)$ ,${c_k}(t)$ 可以看作是每个虚拟队列所处理的数据包,${q_{_k}}$ 可以看作是虚拟队列${Z_k}(t)$ 的到达数据包。基于虚拟队列
${Z_k}(t)$ ,式(6)可以被重构为:$$\tag{8a} {\min _{\{ {c_k}(t)\} ,\{ {\mu _k}(t)\} ,P(t)}}\bar P $$ $$\tag{8b} {\rm{s}}{\rm{.t}}{\rm{.}}\;{\bar H_k} <\infty ,\;{\bar Q_k} < \infty ,\;{\bar Z_k} <\infty $$ $$\tag{8c} (6{\rm d}) - (6{\rm g}) $$ 式(8)仍然难以求解,下一节利用动态随机优化算法来求解该问题。
-
本节利用动态随机优化理论来求解式(8)。首先,利用李雅普诺夫随机优化理论将式(8)分解为两个独立的子问题。然后通过对两个子问题进行求解,提出动态无线与计算资源分配算法。
-
定义
${{Z}}(t)$ 为虚拟队列${Z_k}(t)$ 所组成的向量。${{\varTheta }}(t)$ 为虚拟队列和实际队列所组成的向量,可以表示为:$$ {{\varTheta }}(t) = {[{{{H}}^{\rm T}}(t),{{{Q}}^{\rm T}}(t),{{{Z}}^{\rm T}}(t)]^{\rm T}} $$ (9) 二阶李雅普诺夫函数可以表示为:
$$ L({{\varTheta }}(t)) = \frac{1}{2}\sum\limits_{k = 1}^K {({H_k}(} t{)^2} + {Q_k}{(t)^2} + {Z_k}{(t)^2}) $$ (10) 李雅普诺夫漂移可以表示为:
$$ \Delta ({{\varTheta }}(t)) = {\bf{E}}[L({{\varTheta }}(t + 1)) - L({{\varTheta }}(t))\mid {{\varTheta }}(t)] $$ (11) 由于
$\Delta ({{\varTheta }}(t))$ 难以求解,因此下面对$\Delta ({{\varTheta }}(t))$ 的上界进行分析。定理 1 在t时刻,对于任意队列状态,在任意接入控制与资源分配策略下,
${{\varTheta }}(t)$ 应满足以下不等式:$$ \Delta ({{\varTheta }}(t)) \leqslant D + {\bf{E}}[G(t)\mid {\bf{\varTheta }}(t)] $$ (12) 式中,
$$ D = \frac{1}{2}\sum\limits_{k = 1}^K {\left[ {3{C^2} + \mu _{\rm {total}}^2 + B_k^2 + q_k^2} \right]} $$ (13) $$ \begin{split} &\qquad\qquad G(t) = \sum\limits_{k = 1}^K {{H_k}} (t)[{A_k}(t) - {c_k}(t)]+\\ & \quad\;\; \sum\limits_{k = 1}^K {{Q_k}} (t)[{c_k}(t) - {\mu _k}(t)]+\sum\limits_{k = 1}^K {{Z_k}} (t)[{q_k} - {c_k}(t)] \end{split} $$ (14) 相关证明见文献[11]。
-
上一小节得到了李雅普诺夫漂移
$\Delta ({{\varTheta }}(t))$ 的上界。本小节利用漂移惩罚因子理论来最小化“漂移惩罚因子”,其表达式为:$$ \min {\bf{E}}[G(t) + VP(t)] $$ (15) 式中,
$V \geqslant 0$ 是一个控制参数,表示用户发射功率最小化的权重。通过调整控制参数V,可以实现传输功率消耗与任务传输队列与计算队列之和的总队列时延的均衡。根据李雅普诺夫随机优化理论,问题目标是最小化李雅普诺夫漂移
$\Delta ({{\varTheta }}(t))$ ,可以通过在每一时隙最小化$\Delta ({{\varTheta }}(t)) \leqslant D + {\bf{E}}[G(t)\mid {{\varTheta }}(t)]$ 的右式来求得。右式可被分解为一系列子问题,可以在每一时隙利用实际队列与虚拟队列进行求解。对于式(15),可以被分解为两个独立的子问题。从式(15)中分解出
${c_k}(t)$ 和$P(t)$ ,可以得到无线资源分配子问题:$$\tag{16a} {{{\max }_{\left\{ {{c_k}(t)} \right\},P(t)}}\sum\limits_{k = 1}^K {\left[ {\left( {{H_k}(t) - {Q_k}(t)} \right.} \right.} }{\left. {\left. { + {Z_k}(t)} \right){c_k}(t) - VP(t)} \right]} $$ $$\tag{16b} {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\sum\limits_{k = 1}^K {{c_k}} (t) \leqslant C(t) $$ $$\tag{16c} 0 \leqslant {c_k}(t) \leqslant {H_k}(t) $$ 同理,从式(15)中分解出
${\mu _k}(t)$ ,可以得到计算资源分配子问题:$$\tag{17a} {\max _{\{ {\mu _k}(t)\} }}\sum\limits_{k = 1}^K {{Q_k}} (t){\mu _k}(t) $$ $$\tag{17b} {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\sum\limits_{k = 1}^K {{\mu _k}} (t) \leqslant {\mu _{\rm {total}}} $$ $$\tag{17c} 0 \leqslant {\mu _k}(t) \leqslant {Q_k}(t) $$ -
当给定
${\mu _{{\rm{total}}}}$ 时,式(17)的最优解是计算资源按照任务所需计算资源的降序分配给每个任务。将所有的任务按照${Q_k}$ 的降序进行排列,并定义所排序的集合为$\{ {k_1},{k_2},\cdots,{k_K}\} $ 。对于$m = 0,1,\cdots,K$ ,定义${f_1}(m) = \displaystyle\sum\limits_{n = 0}^m {{Q_{{k_n}}}} $ ,其中${Q_{{k_0}}} = 0$ 。基于以上分析,问题(17)的最优解为:$$ {\mu _{{k_n}}} = \left\{ {\begin{aligned} & {{Q_{{k_n}}}}\qquad\qquad\quad\;\,{1 \leqslant n < m}\\ & {{\mu _{{\rm{total}}}} - {f_1}(n - 1)}\;\;\;{n = m}\\ & {0}\qquad\qquad\qquad\;\,{m < n \leqslant K} \end{aligned}} \right. $$ (18) -
无线资源分配子问题可表示为:
$$\tag{19a} \begin{split} & {{{\max }_{\left\{ {{c_k}(t)} \right\},P(t)}}M(t) \buildrel \Delta \over = \sum\limits_{k = 1}^K {\left[ {\left( {{H_k}(t)} \right)} \right.} } - {Q_k}(t) +\\ & \qquad\qquad\quad {Z_k}(t) ){c_k}(t) - VP(t) ] \end{split} $$ $$\tag{19b} {\rm{s}}{\rm{.t}}{\rm{.}}\sum\limits_{k = 1}^K {{c_k}} (t) \leqslant C(t) = \left\lfloor {\frac{{W{{\log }_2}(1 + h(t)P(t))}}{L}} \right\rfloor $$ $$\tag{19c} 0 \leqslant {c_k}(t) \leqslant {H_k}(t) $$ 由于
${c_k}(t)$ 是一个整数变量,式(19)是一个混合整数规划问题,因此难以求解。接下来通过将式(19)转换为一个单变量问题,提出一种无线资源分配策略。为了简化方便,下面省略时间标号t。从式(19a)中可以看出,如果
${H_k} + {Z_k} \leqslant {Q_k}$ ,那么问题的最优解是${c_k} = 0$ ,$P = 0$ 。当
${H_k} + {Z_k} > {Q_k}$ 时,首先忽略C的整数特性,当取得最优的无线资源分配策略时,约束式(19b)可以写为:$$ \sum\limits_{k = 1}^K {{c_k}} = C = \frac{W}{L}{\log _2}(1 + hP) $$ (20) 式(20)成立是因为对于任意的可行解
$c_{k} $ 都可以通过减少C和P在满足约束式(19b)、式(19c)的情况下进一步增大。对于式(20),功率消耗可以表示为:$$ P = \frac{1}{h}({2^{C\frac{L}{W}}} - 1) $$ (21) 约束式(19c)可以进一步写为:
$$ 0 \leqslant C \leqslant \sum\limits_{k = 1}^K {{H_k}} $$ (22) 其次,考虑C的整数特性,无线资源分配的式(19)可以重新被构建为一个单变量优化问题:
$$\tag{23a} {\max _{C \in {\mathbb{N}}}}\hat M(C) \buildrel \Delta \over = {g_1}(C) - {g_2}(C) $$ $$\tag{23b} {\rm{s}}{\rm{.t}}{\rm{.}}\;\text{式}(22) $$ 式中,
$$\tag{24a} {g_1}(C) \buildrel \Delta \over = {\max _{\{ {c_k}\} }}\;\sum\limits_{k = 1}^K {({H_k} + {Z_k} - {Q_k})} {c_k} $$ $$\tag{24b} {\rm{s}}{\rm{.t}}{\rm{. }}\;\sum\limits_{k = 1}^K {{c_k}} = C $$ $$\tag{24c} 0 \leqslant {c_k} \leqslant {H_k} $$ $$ {g_2}(C) \buildrel \Delta \over = VP = \frac{V}{h}({2^{C\frac{L}{W}}} - 1) $$ (25) 由于式(24)和式(17)有着相同的形式,因此可以采用相同的方法进行求解。当式(24)给定C时,信道容量将按照任务队列积压的降序分配给每个任务。将所有的任务按照
${H_k}$ 的降序进行排列,并定义所排序的集合为$\{ {k_1},{k_2},\cdots,{k_K}\} $ 。对于$m = 0,1,\cdots,K$ ,定义${f_2}(m) = \displaystyle\sum\limits_{n = 0}^m {{H_{{k_n}}}} $ ,其中${H_{{k_0}}} = 0$ 。基于以上分析,式(24)的最优解为:$$ {c_{{k_n}}} = \left\{ {\begin{split} & {{H_{{k_n}}}}\qquad\qquad\;\;{1 \leqslant n < m}\\ & {C - {f_2}(n - 1)}\quad{n = m}\\ & {0}\qquad\qquad\quad\;\;\;{m < n \leqslant K} \end{split}} \right. $$ (26) 为了求解式(23),首先给出以下定理:
定理 2 函数
$\hat M(C)$ 在$[0,f(K)]$ 范围内是关于C的单峰函数。证明:一方面,由于
$\Delta {g_1}(C) = {g_1}(C + 1) -$ $ {g_1}(C) = {H_{{K_m}}}$ ,$\Delta {g_1}(C)$ 是C的单调非增函数。另一方面,由于$\Delta {g_2}(C) = \dfrac{V}{h}({2^{\frac{L}{W}}} - 1){2^{\frac{L}{W}C}}$ ,$\Delta {g_2}(C)$ 是C的单调增函数。因此$\hat M(C) = {g_1}(C) - {g_2}(C)$ 是C的单调递减函数,意味着$\hat M(C)$ 是一个凹函数。根据文献[12],如果$\hat M(C)$ 是一个凹函数,那么其在$[0,f(K)]$ 范围内是单峰函数。基于定理2,提出一种无线资源分配算法如算法1所示。
算法1 无线资源分配算法
1) 初始化
${c_k} = 0$ ;$\hat M(0) = 0$ ;$C = 0$ 2) 将任务按照
${H_k} + {Z_k} - {Q_k}$ 降序排列,得到排列集合$\{ {k_1},{k_2}, \cdots ,{k_K}\} $ 3) for n=1 to K do
4) for
${c_{{k_n}}} = 1$ to${H_{{k_n}}}$ do5)
$C: = C + 1$ 6) 计算
$\hat M(C)$ 7) if
$\hat M(C) < \hat M(C - 1)$ 或违反约束式(22) then8)
${c_{{k_n}}}: = {c_{{k_n}}} - 1$ ,$C: = C - 1$ 9) 跳至步骤13)
10) end if
11) end for
12) end for
13) 通过式(21),得到
$P$ 和${c_k}$ -
基于以上两个独立的子问题,本小节提出JRCRA算法如算法2所示。首先初始化所有的系统参数,在每一时隙根据式(18)和算法1求解计算资源分配和无线资源分配两个子问题。在每一时隙结束时,队列向量
${{\varTheta }}(t + 1)$ 通过式(3),式(4)和式(7)来进行更新。在每一时隙重复该算法。算法2 JRCRA算法
1) 初始化系统参数;
2) while
$t \in [0,T]$ do3) for
$k = 1$ to K do4) 通过式(18)得到
${\mu _k}(t)$ 5) 通过求解子式(19)得到
${c_k}(t)$ 和$P(t)$ 6) 通过式(3),式(4)和式(7)更新
${H_k}(t)$ ,${Q_k}(t)$ 和${Z_k}(t)$ 7) end for
8) end while
-
本节验证提出的JRCRA算法性能。仿真参数如表1所示。
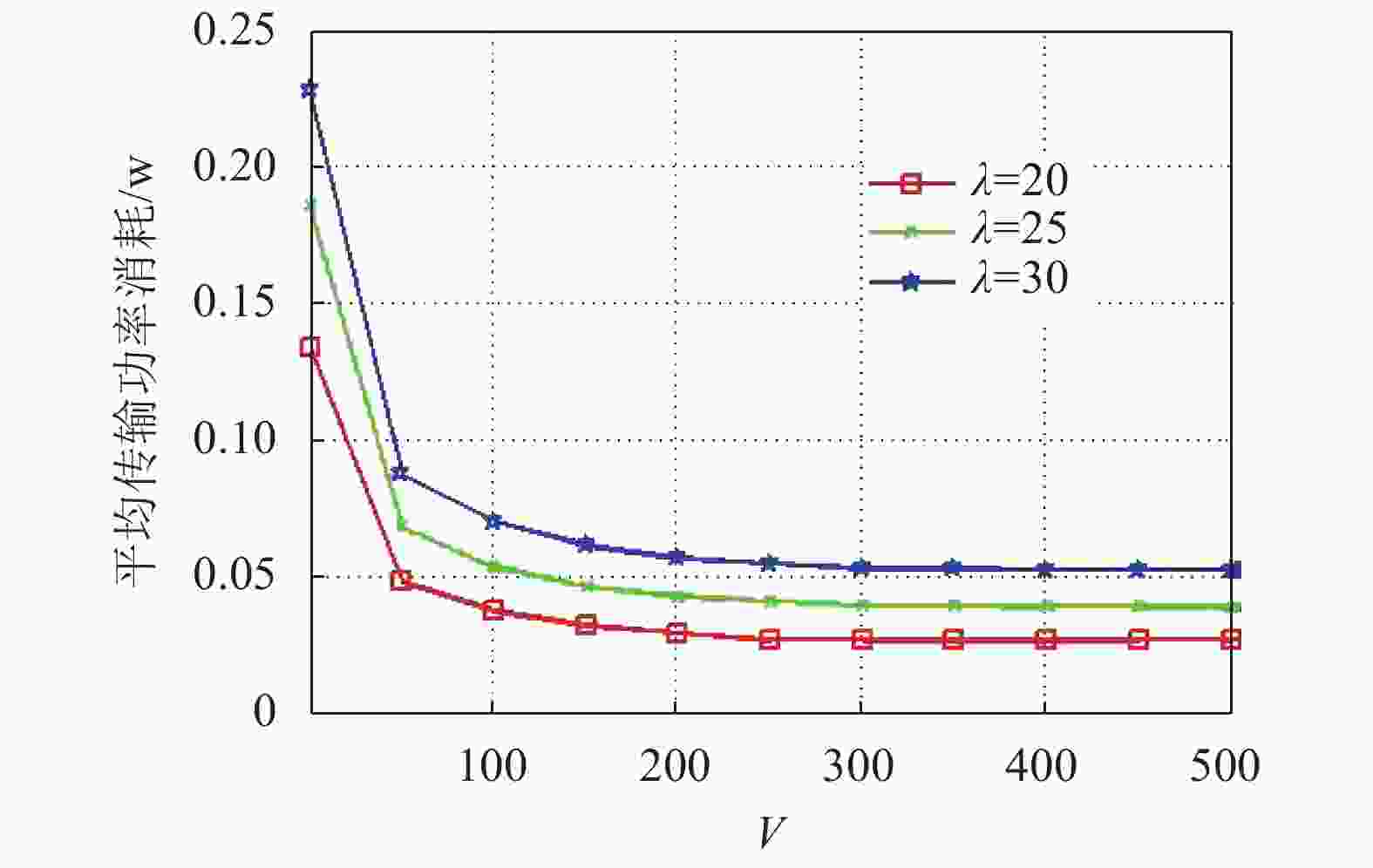
图2为不同控制参数V对总平均功率消耗的影响。从该图中可以看出,总平均功率消耗随着参数V的增加而下降,并且当V足够大时,会收敛至最优的功率消耗。图3为不同控制参数V对总平均队列积压的影响。从该图中可以看出,总平均队列积压随着V线性增加。从图2和图3可以看出,总平均功率消耗和队列积压可以通过调整控制参数V以实现均衡。另外,随着数据包到达速度的增加,平均功率消耗和队列积压都有明显的增加。
表 1 仿真参数
参数描述 值 信道带宽/MHz 5 数据包大小/bits 240 时隙/s 0.5 路损因子 4 车速/m·s−1 20 小区半径/m 500 RSU距公路距离/m 20 任务数目 6 噪声功率/dBm −142 任务迁移数据包要求/个·时隙−1 20 为了证明提出的JRCRA算法的有效性,本文将JRCRA算法与贪婪算法进行比较。贪婪算法是按顺序一个接一个的处理任务,只有处理完一个任务才会处理下一个任务。
图4为不同算法下数据包平均到达速率对平均功率消耗的影响。所有的任务QoS要求相同并且控制参数V为200。从该图中可以看出当数据包平均到达速率增大时,贪婪算法所消耗的功率大于JRCRA算法所消耗的功率。当数据包平均到达速率从20个/时隙增加到40 个/时隙时,提出的JRCRA算法相较于传统的贪婪算法能耗降低了48.85%。这是因为对于贪婪算法来说,如果一个任务要被处理,那么必须要等该任务之前的所有任务都已处理完毕。这样可能会导致在信道条件较差的情况下,有大量的数据包需要被迁移至服务器。为了确保任务的QoS需求,用户则需要增加发射功率。
-
本文在VEC系统中研究了车辆快速时变信道对资源分配策略的影响。首先构建了一个联合无线与计算资源分配使得车载用户终端能量消耗最小化的问题,并利用车辆信道的可预测特性和李雅普诺夫随机优化理论,将原问题分解为两个子问题。然后通过对两个子问题进行求解,提出了JRCRA算法。最后仿真结果显示,当数据包平均到达速率从20个/时隙增加到40个/时隙时,此算法性能相较于传统的贪婪算法能耗降低了48.85%。 本文仅研究了一个VEC 服务器的迁移与资源分配问题。后续可以接着从多VEC服务器选择方面进行研究。当网络中存在大量VEC服务器时,车载用户可以通过选择计算资源更为丰富的VEC服务器来进行迁移计算,进一步降低时延,减少能耗。
本文的研究还得到兰州市科技局项目(2018-3-9)和甘肃政法学院校级科研项目(GSZF2018XQNLW10, GSZF2017XQNLW02)的支持,在此表示感谢!
User Energy Minimization Resource Allocation in Vehicular Edge Computing
-
摘要: 考虑车辆时变信道对资源分配策略的影响,构建在保证任务QoS要求下的车载用户终端能量消耗最小化问题。利用车辆信道可预测特性以及李雅普诺夫随机优化理论将原问题分解为计算资源分配和无线资源分配两个子问题。由于计算资源分配子问题是单变量优化问题,因此可以直接得到解决方案。而对于无线资源分配子问题,通过将其转换为单变量优化问题进行求解。基于两个子问题的结果,提出一种联合无线与计算资源分配算法。仿真结果显示,当数据包平均到达速率从20个/时隙增加到40个/时隙时,该算法能耗相较于传统的贪婪算法能耗降低了48.85%。
-
关键词:
- 联合无线与计算资源分配 /
- 李雅普诺夫 /
- 时变信道 /
- 车辆边缘计算
Abstract: Considering the effect of time-varying channel on the resource allocation scheme, a vehicle user power minimization problem with task QoS requirement constraints is formulated. By utilizing the vehicle channel predictability and Lyapunov theory, the original problem is reformulated as two sub-problems of a single variable, which can be solved easily. Thus an algorithm is proposed to solve these two sub-problems of resource allocation and then a joint radio and computation resource allocation scheme is formed according to the two sub-problems solutions. The simulation results show that the power consumption of the proposed algorithm is decreased by 48.85% compared with traditional greedy algorithm when the data average arrival rate grows from 20 packets/slot to 40 packets/slot. -
表 1 仿真参数
参数描述 值 信道带宽/MHz 5 数据包大小/bits 240 时隙/s 0.5 路损因子 4 车速/m·s−1 20 小区半径/m 500 RSU距公路距离/m 20 任务数目 6 噪声功率/dBm −142 任务迁移数据包要求/个·时隙−1 20 -
[1] 闵丽娟, 卢捍华, 吴瑞雯. 物制系统综述[J]. 南京邮电大学学报(自然科学版), 2017, 37(2): 68-73. MIN Li-juan, LU Han-hua, WU Rui-wen. Survey of internet of things control system[J]. Journal of Nanjing University of Posts and Telecommunications (Natural Science Edition), 2017, 37(2): 68-73. [2] 孙其博, 刘杰, 黎羴, 等. 物联网: 概念、架构与关键技术研究综述[J]. 北京邮电大学学报, 2010, 33(3): 1-9. doi: 10.3969/j.issn.1007-5321.2010.03.001 SUN Qi-bo, LIU Jie, LI Shan, et al. Internet of things: summarize on concepts, architecture and key technology problem[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(3): 1-9. doi: 10.3969/j.issn.1007-5321.2010.03.001 [3] LI S, ZHANG N, LIN S, et al. Joint admission control and resource allocation in edge computing for Internet of things[J]. IEEE Network, 2018, 32(1): 72-79. doi: 10.1109/MNET.2018.1700163 [4] DU J, YU F R, CHU X, et al. Computation offloading and resource allocation in vehicular networks based on dual-side cost minimization[J]. IEEE Transactions on Vehicular Technology, 2018, 68(2): 1079-1092. [5] SHAH S S, ALI M, MALIK A W, et al. vFog: A vehicle-assisted computing framework for delay-sensitive applications in smart cities[J]. IEEE Access, 2019, 7: 34900-34909. doi: 10.1109/ACCESS.2019.2903302 [6] ZHOU Z, FENG J, CHANG Z, et al. Energy-efficient edge computing service provisioning for vehicular networks: A consensus ADMM approach[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 5087-5099. doi: 10.1109/TVT.2019.2905432 [7] ZHANG K, MAO Y, LENG S, et al. Mobile-edge computing for vehicular networks: A promising network paradigm with predictive off-loading[J]. IEEE Vehicular Technology Magazine, 2017, 12(2): 36-44. doi: 10.1109/MVT.2017.2668838 [8] LI S, ZHU G, LIN S, et al. Energy-efficient power allocation in cloud radio access network of high-speed railway[C]//Proceedings of IEEE Vehicular Technology Conference. Piscataway, USA: IEEE, 2016: 1-5. [9] XU S, ZHU G, SHEN C, et al. Utility-based resource allocation in high-speed railway wireless networks[J]. EURASIP Journal on Wireless Communications and Networking, 2014, 2014(1): 68. doi: 10.1186/1687-1499-2014-68 [10] NEELY M J. Stochastic network optimization with application to communication and queueing systems[M]. Williston, VT, USA: Morgan and Claypool Pubilshers, 2010. [11] LI S, WANG Q, KOU W, et al. Joint remote radio heads and baseband units pool resource scheduling for delay-aware traffic in cloud radio access networks[J]. Telecommunication Systems, 2019, 71(1): 77-91. doi: 10.1007/s11235-018-0506-5 [12] BERTIN E M, THEODORECU R. Some characterizations of discrete unimodality[J]. Statistics & probability letters, 1984, 2(1): 23-30. -


 ISSN
ISSN 




 下载:
下载: