-
辐射源无源定位是雷达[1]、声纳[2]、无线通信网络[3]以及电子对抗[4]等领域中的一个基本问题。针对某一外源辐射源,多平台协同无源定位通常可以采用基于到达角(AOA)的定位体制[5-6]、基于到达时间差(TDOA)的定位体制[7],以及基于AOA-TDOA联合的定位体制[8-9]。当源辐射源运动或者协同平台运动时,到达频率差(FDOA)通常也被加入无源定位算法以提高定位精度[10-12]。另一方面,由于上述几类观测量与辐射源位置成非线性关系,因此辐射源无源定位问题不是一个简单的问题。近年来涌现了多种算法试图解决辐射源无源定位问题,如基于泰勒展开的迭代搜索算法[13]、闭合解定位算法[6-12]等。虽然闭合解定位算法的定位精度容易受到传感器位置误差的影响,但是由于其具有不需要辐射源位置的先验知识且回避了迭代搜索算法常遇到的迭代发散问题的优点,因而备受关注。本文同样将焦点聚于移动辐射源无源定位闭合解算法。
现有的很多无源定位闭合解算法能直接用于电子对抗领域中针对敌方移动辐射源无源定位的问题。文献[8]所提的基于AOA-TDOA的联合定位闭合解算法忽视了传感器位置误差所带来的影响;而文献[9]所提的基于AOA-TDOA的联合定位闭合解算法虽然考虑了传感器位置误差的影响,但所提算法只针对双平台协同定位这一特例;文献[7]所提的基于TDOA的定位闭合解算法以及文献[10-12]所提基于TDOA-FDOA的联合定位闭合解算法,虽然都考虑了协同平台的位置误差,但均要求参与定位任务的我方协同平台的个数不小于5个。这一要求限制了上述几种算法在实际作战场景中的应用范围。针对上述问题,在建立移动辐射源位置与各种观测量以及各个传感器位置的近似等式关系的基础上,本文提出一种新的AOA-TDOA-FDOA联合定位闭合解算法。所提算法在保持闭合解框架不变的前提下,不仅考虑了传感器位置误差所带来的影响,同时还能将参与定位的我方平台个数减小至3个。进一步对所提算法进行理论分析,在观测噪声及传感器位置误差均为高斯噪声并且噪声强度适中时,所提算法的定位误差均方根能达到克拉美罗(CRLB)界。3平台协同定位仿真实验结果以及对照仿真实验结果验证了上述理论结论。
-
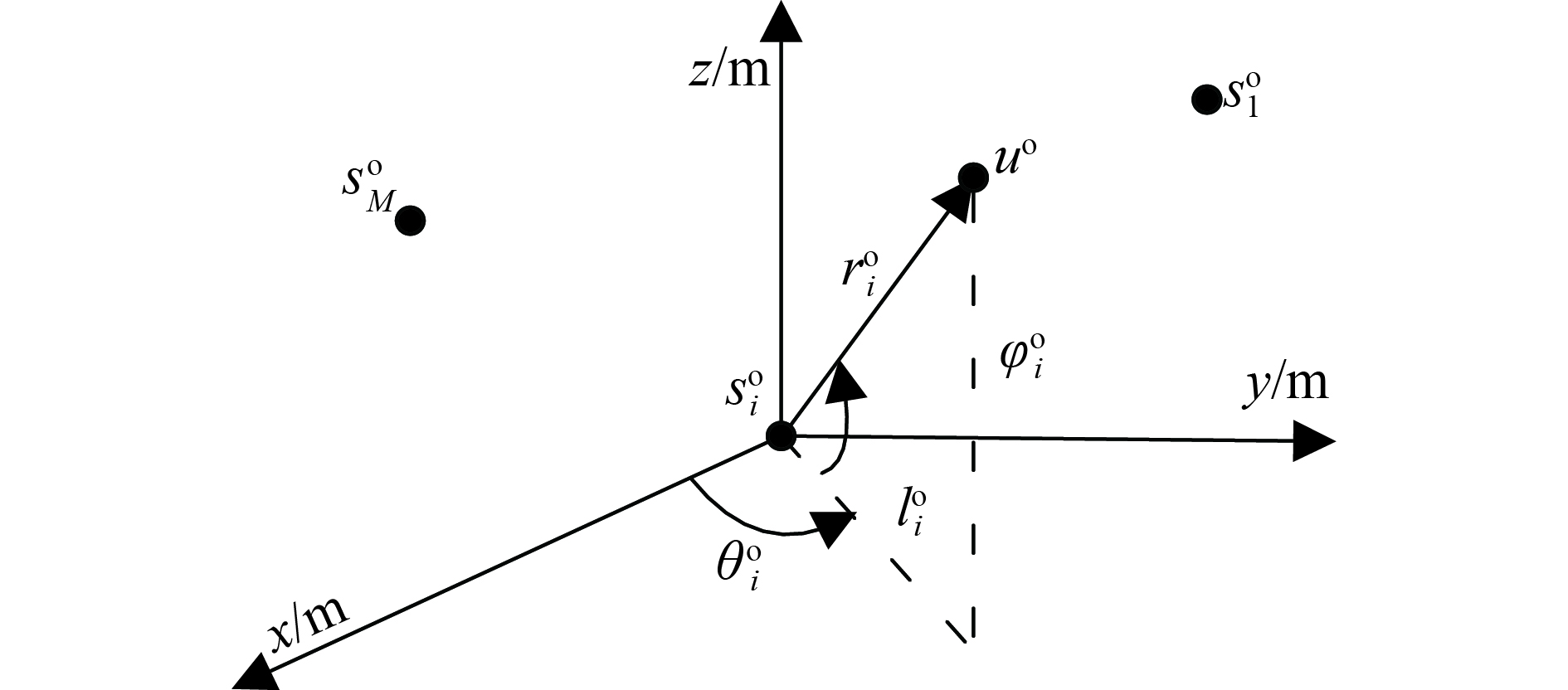
假定某时刻有M个传感器对一移动辐射源开展联合协同无源定位,定位场景如图1所示。
记移动辐射源在该时刻的三维位置向量为
${{ {u}}^o} = {[{x^o},{y^o},{z^o}]^{\rm T} }$ ,三维速度向量为${{\dot{ u}}^o} = {[{\dot x^o},{\dot y^o},{\dot z^o}]^{\rm T} }$ 。记该时刻第$i{\rm{(}}i = 1,2, \cdots ,M{\rm{)}}$ 个传感器的所在真实位置为${ {s}}_i^o = {[x_i^o,y_i^o,z_i^o]^{\rm T} }$ ,真实速度为${\dot{ s}}_i^o = {[\dot x_i^o,\dot y_i^o,\dot z_i^o]^{\rm T} }$ 。一般地,定位算法并不能获取上述传感器的真实坐标与真实速度,而只能获取传感器所在平台的导航设备提供的位置向量与速度向量。记该时刻导航设备给出的第$i$ 个传感器的所在位置为${{ {s}}_i} = {[{x_i},{y_i},{z_i}]^{\rm T} }$ ,速度为${{\dot{ s}}_i} = {[{\dot x_i},{\dot y_i},{\dot z_i}]^{\rm T} }$ 。为简便行文,将各传感器的位置向量与速度向量收集在一起,并记为
${ {\beta }} = {[{{ {s}}^{\rm T} },{{\dot{ s}}^{\rm T} }]^{\rm T} }$ ,其中${ {s}} = {[{ {s}}_1^{\rm T} , { {s}}_2^{\rm T} , \cdots ,}$ ${{ {s}}_M^{\rm T} ]^{\rm T} }$ ;${\dot{ s}} = {[{\dot{ s}}_1^{\rm T} , {\dot{ s}}_2^{\rm T} , \cdots ,{\dot{ s}}_M^{\rm T} ]^{\rm T} }$ 。若记传感器位置误差向量为$\Delta { {\beta }}$ ,那么$\Delta { {\beta }}\! =\! { {\beta }} - {{ {\beta }}^o} \!=\! {{\rm{[}}\Delta {{ {s}}^{\rm{T}}},\Delta {{\dot{ s}}^{\rm{{\rm T}}}}{\rm{]}}^{\rm{{\rm T}}}}$ ,其中,$\Delta { {s}}= $ ${[\Delta { {s}}_1^{\rm T} ,\Delta { {s}}_2^{\rm T} , \cdots ,\Delta { {s}}_M^{\rm T} ]^{\rm T} }$ ;$\Delta {\dot{ s}} = {[\Delta {\dot{ s}}_1^{\rm T} ,\Delta {\dot{ s}}_2^{\rm T} , \cdots ,\Delta {\dot{ s}}_M^{\rm T} ]^{\rm T} }; \Delta {{ {s}}_i} = {{ {s}}_i} - $ ${ {s}}_i^o$ ;$\Delta {{\dot{ s}}_i} = {{\dot{ s}}_i} - {\dot{ s}}_i^o$ 。一般地,$\Delta { {\beta }}$ 通常认为是零均值的高斯向量,其协方差矩阵为${{ {Q}}_{ {\beta }}}$ 。记
$\theta _i^o$ 与$\phi _i^o$ 分别表示该时刻辐射源相对于第$i{\rm{(}}i = 1,2, \cdots ,M{\rm{)}}$ 个传感器的方位角与高低角的真实值,表示为:$$ \;\theta _i^o = {\tan ^{ - 1}}\left(\frac{{{y^o} - y_i^o}}{{{x^o} - x_i^o}}\right){\rm{ }}\phi _i^o = {\tan ^{ - 1}}\left(\frac{{{z^o} - z_i^o}}{{\sqrt {{{({x^o} - x_i^o)}^2} + {{({y^o} - y_i^o)}^2}} }}\right) $$ (1) 式中,
$\theta _i^o \in \left( { - {\text π} ,{\text π} } \right)$ ;$\phi _i^o \in \left( {{{ - {\text π} } / {2,}}{{\text π} / 2}} \right)$ 。在实际中,所观测到的方位角与高低角均带有测量噪声,即有${ {\theta }} = {{ {\theta }}^o} + {{ {n}}_\theta }$ 与${ {\phi }} = {{ {\phi }}^{\rm{o}}} + {{ {n}}_\phi }$ 。记上式中的${ {\theta }} = {[{\theta _1}, {\theta _2}, }$ $ \cdots ,{\theta _M}]^{\rm T}$ 与${ {\phi}} = {{\rm{[}}{\phi _1}, {\phi _2}, \cdots ,{\phi _M}{\rm{]}}^{\rm{T}}}$ 分别表示该时刻方位角与高低角的测量向量,而${{ {\theta }}^o} = {[\theta _1^o, \theta _2^o,\cdots ,\theta _M^o]^{\rm T} }$ 与${{ {\phi}} ^{\rm{o}}} = {{\rm{[}}\phi _1^o, \phi _2^o, \cdots ,\phi _M^o{\rm{]}}^{\rm{T}}}$ 分别表示该时刻方位角与高低角的真实值向量,以及${{ {n}}_\theta } = {[{n_{\theta 1}}, {n_{\theta 2}},\cdots ,{n_{\theta M}}]^{\rm T} }$ 与${{ {n}}_\phi } = {[{n_{\phi 1}}, {n_{\phi 2}}, \cdots ,{n_{\phi M}}]^{\rm T} }$ 为对应的零均值高斯噪声向量,其协方差阵分为记为${{ {Q}}_\theta }$ 、${{ {Q}}_\phi }$ 。并且假设测量噪声${{ {n}}_\theta }$ 与${{ {n}}_\phi }$ 跟传感器位置误差向量$\Delta { {\beta }}$ 统计独立。设1号传感器为参考传感器,那么该时刻则有M−1个TDOA观测量作为无源定位算法的输入。
${r_{i1}}$ 为第$i{\rm{(}}i = 2,3, \cdots ,M{\rm{)}}$ 个传感器与第1个传感器之间的TDOA观测量。一般地,${r_{i1}} = r_{i1}^o + {n_{i1}}$ ,其中${n_{i1}}$ 为测量噪声,$r_{i1}^o$ 为第i个传感器与第1个传感器之间的TDOA真值,并且有$r_{i1}^o = r_i^o - r_1^o$ ,其中$r_k^o = $ $ \left\| {{{ {u}}^o} - { {s}}_k^o} \right\|$ 代表该时刻移动辐射源与第$k{\rm{(}}k = 1,2, \cdots ,M{\rm{)}}$ 个传感器之间的欧氏距离。记在该时刻M−1个TDOA观测向量为${ {r}} = {{\rm{[}}{r_{21}}, {r_{31}},\cdots ,{r_{M1}}{\rm{]}}^{\rm{T}}}$ ,则${ {r}} = {{ {r}}^o} + {{ {n}}_t}$ ,其中${{ {r}}^o} = {\rm{[}}r_{21}^o, r_{31}^o,\cdots ,$ $r_{M1}^o{{\rm{]}}^{\rm{T}}}$ 为TDOA真实值向量,${{ {n}}_t} = {\rm{[}}{n_{21}}, {n_{31}},\cdots , $ ${n_{M1}}{\rm{]}}^{\rm{T}}$ 为对应的观测噪声向量。假设噪声向量${{ {n}}_t}$ 为零均值、协方差矩阵为${{ {Q}}_t}$ 的高斯分布向量,并且与传感器位置误差向量$\Delta { {\beta }}$ 、方位角噪声向量${{ {n}}_\theta }$ 以及高低角噪声向量${{ {n}}_\phi }$ 统计独立。同样地,设1号传感器为参考传感器,那么该时刻则有M−1个FDOA观测量作为无源定位算法的输入。
${{\dot r}_{i1}}$ 为第$i{\rm{(}}i = 2,3, \cdots ,M{\rm{)}}$ 个传感器与第1个传感器之间的FDOA观测量。一般地,${{\dot r}_{i1}} = {\dot r}_{i1}^o + {\dot n_{i1}} = {\dot r}_i^o - {\dot r}_1^o + {\dot n_{i1}}$ ,其中${\dot n_{i1}}$ 为测量噪声,${\dot r}_{i1}^o$ 为第i个传感器与第1个传感器之间的FDOA真值,并且有${\dot r}_k^o = {{{{{\rm{(}}{{ {u}}^o} - { {s}}_k^o{\rm{)}}}^{\rm{T}}}{\rm{(}}{{{\dot{ u}}}^o} - {\dot{ s}}_k^o{\rm{)}}} / {r_k^o}}$ ,$k = 1,2, \cdots ,M $ 。记在该时刻M−1个FDOA观测向量为${\dot{ r}} = {{\rm{[}}{{\dot r}_{21}}, {{\dot r}_{31}},\cdots ,{{\dot r}_{M1}}{\rm{]}}^{\rm{T}}}$ ,则${\dot{ r}} = {{\dot{ r}}^o} + {{ {n}}_\nu }$ ,${{\dot{ r}}^o} = {{\rm{[}}{\dot r}_{21}^o, {\dot r}_{31}^o,\cdots ,{\dot r}_{M1}^o{\rm{]}}^{\rm{T}}}$ 为FDOA真实值向量,${{ {n}}_\nu } = {{\rm{[}}{\dot n_{21}}, {\dot n_{31}},\cdots ,{\dot n_{M1}}{\rm{]}}^{\rm T}}$ 为对应的观测噪声向量。假设噪声向量${{ {n}}_\nu }$ 为零均值、协方差矩阵为${{ {Q}}_\nu }$ 的高斯分布向量,并且与传感器位置误差向量$\Delta { {\beta }}$ 、方位角噪声向量${{ {n}}_\theta }$ 、高低角噪声向量${{ {n}}_\phi }$ 以及TDOA噪声向量${{ {n}}_t}$ 统计独立。需要说明的是,许多文献(如文献[12])在定义TDOA表达式时将光速c也包含在内,在定义FDOA表达式时同时将光速c和辐射源信号载频
${f_o}$ 也包含在内。而这两类定义在已知辐射源信号载频${f_o}$ 时没有本质区别。因此,本文不特意区分上述两类定义,其含义可由上下文得到。综上,为简化算法推导,将上述3类观测量汇集起来。记
${ {\alpha }} = {[{{ {\theta }}^{\rm{T}}},{{ {\phi}} ^{\rm{T}}},{{ {r}}^{\rm{T}}},{{\dot{ r}}^{\rm{T}}}]^{\rm{T}}}$ 为该时刻的AOA、TDOA及FDOA测量值向量,$\Delta { {\alpha }} = {{\rm{[}}{ {n}}_\theta ^{\rm{T}},n_\phi ^{\rm{T}},{ {n}}_t^{\rm{T}},{ {n}}_\nu ^{\rm{T}}{\rm{]}}^{\rm{T}}}$ 为对应的观测噪声向量。一般地,观测噪声向量$\Delta { {\alpha }}$ 被建模为零均值、协方差矩阵${{ {Q}}_\alpha }$ 为高斯向量,其中${{ {Q}}_\alpha }$ 的定义为:$${{ {Q}}_\alpha } = {\rm E}{\rm{[}}\Delta { {\alpha }}\Delta {{ {\alpha }}^{\rm{T}}}{\rm{]}} = {\rm{diag}}{\rm{\{ }}{{ {Q}}_\theta },{{ {Q}}_\phi },{{ {Q}}_t},{{ {Q}}_\nu }{\rm{\} }}$$ (2) 那么,移动辐射源AOA-TDOA-FDOA联合无源定位算法所涉问题为:已知某一时刻的AOA、TDOA及FDOA测量向量
${ {\alpha }}$ 与传感器位置向量${ {\beta }}$ ,以及二者对应的噪声/误差向量的协方差矩阵${{ {Q}}_\alpha }$ 与${{ {Q}}_{ {\beta }}}$ ,尽可能准确地估计该时刻的移动辐射源位置${{ {u}}^o}$ 。 -
移动辐射源AOA-TDOA-FDOA联合定位算法采用两阶段估计流程。第一阶段,首先建立起移动辐射源位置参数
${{ {u}}^o}$ 、${{\dot{ u}}^o}$ 与观测向量${ {\alpha }}$ 及传感器位置向量${ {\beta }}$ 的伪线性关系,进而得到${{ {u}}^o}$ 与${{\dot{ u}}^o}$ 粗略估计值;第二阶段,修正第一阶段的粗估计值,从而精确估计出某时刻移动辐射源的位置。 -
方位角
$\theta _i^o$ 、高低角$\phi _i^o$ 与移动辐射源位置参数${{ {u}}^o}$ 的伪线性关系可以通过以下代数变换推导得出。由式(1)可知,对观测真值$\theta _i^o$ 取正切运算,有:$$0 = \sin \theta _i^o{\rm (}{x^o} - x_i^o{\rm )} - \cos \theta _i^o{\rm (}{y^o} - y_i^o{\rm )}$$ (3) 式中,
$\theta _i^o$ 、$x_i^o$ 以$y_i^o$ 及均为真实值,实际中并不可得,用带噪值或带误差值代替上述各量,则式(3)变为:$${\eta _{\theta i}} = \sin {\theta _i}{\rm (}{x^o} - {x_i}{\rm )} - \cos {\theta _i}{\rm (}{y^o} - {y_i}{\rm )}$$ (4) 式中,
${\eta _{\theta i}}$ 为测量噪声${n_{\theta i}}$ 以及传感器位置误差$\Delta {{ {s}}_i}$ 带来的近似误差。记${{ {g}}_{\theta i}} = {{\rm{[}} - \sin {\theta _i},\cos {\theta _i},0{\rm{]}}^{\rm{T}}}$ ,那么式(4)可以等价表达为:$${\eta _{\theta i}} = { {g}}_{\theta i}^{\rm{T}}{{ {s}}_i} - { {g}}_{\theta i}^{\rm{T}}{{ {u}}^o}$$ (5) 当测量噪声
${n_{\theta i}}$ 很弱时,$\cos \left( {{n_{\theta i}}} \right) \approx 1$ 及$\sin \left( {{n_{\theta i}}} \right) \approx $ $ {n_{\theta i}}$ ,$\sin {\theta _i} \approx \;\sin \theta _i^o + {n_{\theta i}}\cos \theta _i^o$ 及$\cos {\theta _i} \approx \cos \theta _i^o -$ $ {n_{\theta i}}\sin \theta _i^o$ 。将上述两近似等式以及${x_i} = x_i^o + \Delta {x_i},{y_i} = y_i^o + $ $ \Delta {y_i}$ 带入式(4),有${\eta _{\theta i}} = \cos \theta _i^o\Delta {y_i}- \sin \theta _i^o\Delta {x_i} + {\rm{\{ (}}{x^o} - x_i^o{\rm{)}}\cos \theta _i^o{\rm{ + }}$ $ ({y^o} - y_i^o{\rm{)}}\sin \theta _i^o{\rm{\} }}{n_{\theta i}}$ 。再利用图1中的一个几何关系式${\rm{(}}{x^o} \!-\! x_i^o{\rm{)}}\cos \theta _i^o \!+\! {\rm{(}}{y^o} \!-\! y_i^o{\rm{)}}\sin \theta _i^o = l_i^o{\cos ^2}\theta _i^o + l_i^o{\sin ^2}\theta _i^o =$ $ l_i^o = r_i^o\cos \phi _i^o$ ,并定义${ {g}}_{\theta i}^o = {{\rm{[}} - \sin \theta _i^o,\cos \theta _i^o,0{\rm{]}}^{\rm{T}}}$ ,那么有:$${\eta _{\theta i}} = {n_{\theta i}}r_i^o\cos \phi _i^o + { {g}}_{\theta i}^{o{\rm{T}}}\Delta {{ {s}}_i}$$ (6) 式(5)与式(6)分别建立了向量
${{ {u}}^o}$ 与方位角${\theta _i}$ 之间的近似等式关系,以及近似误差${\eta _{\theta i}}$ 与测量噪声${n_{\theta i}}$ 及传感器位置误差$\Delta {{ {s}}_i}$ 之间的函数关系。同样地,对式(1)中的观测真值
$\phi _i^o$ 取正切运算,并用${\theta _i},{\phi _i},{x_i},{y_i},{z_i}$ 分别代替其真实值,有:$${\eta _{\phi i}} = { {g}}_{\phi i}^{\rm{T}}{{ {s}}_i} - { {g}}_{\phi i}^{\rm{T}}{{ {u}}^o}$$ (7) 式中,
${{ {g}}_{\phi i}} = {{\rm{[}} - \sin {\phi _i}\cos {\theta _i}, - \sin {\phi _i}\sin {\theta _i},\cos {\phi _i}{\rm{]}}^{\rm{T}}}$ ;${\eta _{\phi i}}$ 为测量噪声${n_{\phi i}}$ 以及传感器位置误差$\Delta {{ {s}}_i}$ 带来的近似误差。当测量噪声${n_{\phi i}}$ 很弱时,$\sin {\phi _i} = \sin \phi _i^o + {n_{\phi i}}\cos \phi _i^o$ 及$\cos {\phi _i} = \cos\phi _i^o - {n_{\phi i}}\sin \phi _i^o$ 近似成立,并将上述两近似关系及${{ {s}}_i} = { {s}}_i^o + \Delta {{ {s}}_i}$ 代入式(7),忽略二阶误差项,有:$${\eta _{\phi i}} = r_i^o{n_{\phi i}} + { {g}}_{\phi i}^{o{\rm T}}\Delta {{ {s}}_i}$$ (8) 式中,
${ {g}}_{\phi i}^o = {{\rm{[}} - \sin \phi _i^o\cos \theta _i^o, - \sin \phi _i^o\sin \theta _i^o,\cos \phi _i^o{\rm{]}}^{\rm{T}}}$ 。上式推导过程中使用了图1中两个几何关系$0 = {\rm{(}}{x^o} - x_i^o{\rm{)}}\times$ $\sin \theta _i^o - {\rm{ (}}{y^o} - y_i^o{\rm{)}}\cos \theta _i^o$ 及${\rm{(}}{x^o} - \;x_i^o{\rm{)}}\cos \theta _i^o\cos \phi _i^o+ {\rm{(}}{y^o} - y_i^o{\rm{)}}\times$ $ \sin \theta _i^o\cos \phi _i^o + {\rm{(}}{z^o} - z_i^o{\rm{)}}\sin \phi _i^o = r_i^o$ 。式(7)与式(8)分别建立了向量${{ {u}}^o}$ 与高低角${\phi _i}$ 之间的近似等式关系,以及近似误差${\eta _{\phi i}}$ 与测量噪声${n_{\phi i}}$ 及传感器位置误差$\Delta {{ {s}}_i}$ 之间的函数关系。事实上,
${ {s}}_i^o - {{ {u}}^o}$ 为三维空间中的一个向量,而向量${ {g}}_{\theta i}^o$ 与向量${ {g}}_{\phi i}^o$ 是此三维空间中既彼此正交又同时与向量${ {s}}_i^o - {{ {u}}^o}$ 成正交关系。当存在测量噪声和传感器位置误差时,定位算法只能得到${{ {g}}_{\theta i}}$ 与${{ {g}}_{\phi i}}$ 。向量${{ {g}}_{\theta i}}$ 与向量${{ {g}}_{\phi i}}$ 虽然彼此正交,但却不再与向量${ {s}}_i^o - {{ {u}}^o}$ 正交,这也就是残差${\eta _{\theta i}}$ 与${\eta _{\phi i}}$ 的产生原因。 -
如文献[10-12]及文献[7]所示,TDOA观测量
${r_{i1}},$ $i{\rm{(}}i = 2,3, \cdots ,M{\rm{)}}$ 可以通过如下方式进行线性化处理。首先,对等式$r_{i1}^o + r_1^o = r_i^o$ 的两边同时取平方运算,有:$$r_{i1}^{o2} + 2r_{i1}^or_1^o = { {s}}_i^{o{\rm{T}}}{ {s}}_i^o - { {s}}_1^{o{\rm{T}}}{ {s}}_1^o - 2{{\rm{(}}{ {s}}_i^o - { {s}}_1^o{\rm{)}}^{\rm{T}}}{{ {u}}^o}$$ (9) 将上式中的
$r_{i1}^o$ 用${r_{i1}} - {n_{i1}}$ 代替,${ {s}}_i^o$ 用${{ {s}}_i} - \Delta {{ {s}}_i}$ 代替,忽略二阶误差项整理可得:$${\varepsilon _{t,i}} = r_{i1}^2 - { {s}}_i^{\rm{T}}{{ {s}}_i} + { {s}}_1^{\rm{T}}{{ {s}}_1} + 2{{\rm{(}}{{ {s}}_i} - {{ {s}}_1}{\rm{)}}^{\rm{T}}}{{ {u}}^o} + 2r_1^o{r_{i1}}$$ (10) 式中,
${\varepsilon _{t,i}}$ 代表近似误差,其定义为:$${\varepsilon _{t,i}} = 2r_i^o{n_{i1}} + 2{{\rm{(}}{{ {u}}^o} - {{ {s}}_i}{\rm{)}}^{\rm{T}}}\Delta {{ {s}}_i} - 2{{\rm{(}}{{ {u}}^o} - {{ {s}}_1}{\rm{)}}^{\rm{T}}}\Delta {{ {s}}_1}$$ (11) 借助于辅助变量
$r_1^o$ ,式(10)表征了TDOA观测量${r_{i1}}$ 与辐射源位置向量${{ {u}}^o}$ 之间的近似线性关系,同时式(11)也给出了近似误差${\varepsilon _{t,i}}$ 与测量噪声${n_{i1}}$ 及传感器位置误差$\Delta {{ {s}}_i}$ 之间的函数表达关系。对于FDOA观测量
${{\dot r}_{i1}},i{\rm{(}}i = 2,3, \cdots ,M{\rm{)}}$ 的线性化处理方式为同时对式(10)及式(11)的右端对时间求导数[10-12],即:$$ \begin{split} {\varepsilon _{\nu ,i}} =\,& r_1^o{{\dot n}_{i1}} + {\dot r}_1^o{n_{i1}} + {({{{\dot{ u}}}^o} - {\dot{ s}}_i^o)^{\rm T} }\Delta {{ {s}}_i} - {({{{\dot{ u}}}^o} - {{{\dot{ s}}}_1})^{\rm T} }\Delta {{ {s}}_1} +\\ & {({{ {u}}^o} - { {s}}_i^o)^{\rm T} }\Delta {{{\dot{ s}}}_i} - {({{ {u}}^o} - {{ {s}}_1})^{\rm T} }\Delta {{{\dot{ s}}}_1} = \\ \,& {r_{i1}}{{\dot r}_{i1}} - {\dot{ s}}_i^{\rm T} {{ {s}}_i} + {\dot{ s}}_1^{\rm T} {{ {s}}_1} + {({{{\dot{ s}}}_i} - {{{\dot{ s}}}_1})^{\rm T} }{{ {u}}^o} + \\ & {({{ {s}}_i} - {{ {s}}_1})^{\rm T} }{{{\dot{ u}}}^o} + {{\dot r}_{i1}}r_1^o + {r_{i1}}{\dot r}_1^o \end{split} $$ (12) 借助于辅助变量
$r_1^o$ 与${\dot r}_1^o$ ,式(12)不仅给出了FDOA观测量${{\dot r}_{i1}}$ 与移动辐射源位置参数${{ {u}}^o}$ 与${{\dot{ u}}^o}$ 之间的近似线性关系,同时也给出了近似误差${\varepsilon _{\nu ,i}}$ 、测量噪声${n_{i1}}$ 、${\dot n_{i1}}$ 、传感器位置误差$\Delta {{ {s}}_i}$ 和速度误差$\Delta {{\dot{ s}}_i}$ 之间的函数表达关系。 -
1)第一阶段:粗估计。
从上面的分析中可以知道,借助于辅助变量
$r_1^o$ 与${\dot r}_1^o$ ,移动辐射源位置参数${{ {u}}^o}$ 、${{\dot{ u}}^o}$ 与无源定位输入观测向量${ {\alpha }}$ 及传感器位置向量${ {\beta }}$ 之间能建立起近似线性关系,并且近似误差也有显示表达式。因此,在第一阶段可以选取${ {\varphi }}_1^o = {[{{{ {u}}^{o{\rm T}}}}, r_1^o,{{{\dot{ {u}}}^{o{\rm T}}} },{{\dot {r}}_1^o]^{\rm T}} }$ 为移动辐射源位置参数的估计参数向量。记
${ {\eta }} \;=\; {{\rm{[}}{\eta _{\theta 1}}, {\eta _{\theta 2}}, \cdots \;,{\eta _{\theta M}},\;{\eta _{\phi 1}},{\eta _{\phi 2}},\; \cdots \;,{\eta _{\phi M}}{\rm{]}}^{\rm{T}}},\;{{ {\varepsilon }}_t} = $ ${\rm{[}}{\varepsilon _{t,2}},{\varepsilon _{t,3}},\;\cdots ,{\varepsilon _{t,M}}{\rm{]}}^{\rm{T}}$ ,以及${{ {\varepsilon }}_\nu } = {[{\varepsilon _{\nu ,2}}, {\varepsilon _{\nu ,3}}, \cdots ,{\varepsilon _{\nu ,M}}]^{\rm T} }$ ,并定义${{ {\varepsilon }}_1} = {\rm{[}}{{ {\eta }}^{\rm{T}}},{ {\varepsilon }}_t^{\rm{T}},$ ${ {\varepsilon }}_\nu ^{\rm{T}}{\rm{]}}^{\rm{T}}$ ,那么联合式(5)~式(8)、式(10)~式(12),有:$${ {B}}_1^o\Delta { {\alpha }} + { {D}}_1^o\Delta { {\beta }} = {{ {\varepsilon }}_1} = {{ {h}}_1} - {{ {G}}_1}{ {\varphi }}_1^o$$ (13) 式中,
$$\begin{array}{l} {{ {h}}_1} = \left[ {\begin{array}{*{20}{c}} {{{ {h}}_{\theta \phi }}} \\ {{{ {h}}_t}} \\ {{{ {h}}_\nu }} \end{array}} \right],\;\;{{ {G}}_1} = \left[ {\begin{array}{*{20}{c}} {{{ {G}}_{\theta \phi }}} \\ {{{ {G}}_t}} \\ {{{ {G}}_\nu }} \end{array}} \right],\;\;{ {D}}_1^o = \left[ {\begin{array}{*{20}{c}} {{ {D}}_{\theta \phi }^o}&{{{ O}_{2M \times 3M}}} \\ {{{ {D}}^o}}&{{{ O}_{\left( {M - 1} \right) \times 3M}}} \\ {{{{\dot{ D}}}^o}}&{{{ {D}}^o}} \end{array}} \right],\\ { {B}}_1^o = \left[ {\begin{array}{*{20}{c}} {{ {B}}_{\theta \phi }^o}&{{{ {{ O}}}_{2M \times \left( {M - 1} \right)}}}&{{{ {{ O}}}_{2M \times \left( {M - 1} \right)}}} \\ {{{ {{ O}}}_{\left( {M - 1} \right) \times 2M}}}&{{{ {B}}^o}}&{{{ {{ O}}}_{\left( {M - 1} \right) \times \left( {M - 1} \right)}}} \\ {{{ {{ O}}}_{\left( {M - 1} \right) \times 2M}}}&{{{{\dot{ B}}}^o}}&{{{ {B}}^o}} \end{array}} \right] \\ \end{array} $$ (14) 式(14)中的矩阵
${{ O}_{i \times j}}$ 代表$i \times j$ 维的全零矩阵,矩阵${{ {h}}_{\theta \phi }},{{ {G}}_{\theta \phi }},{{ {h}}_t},{{ {h}}_\nu },{{ {G}}_t},{{ {G}}_\nu }$ 分别定义为:$$ \begin{array}{l} {{ {h}}_{\theta \phi }} = \left[ {\begin{array}{*{20}{c}} {\left( {{{ {G}}_\theta } \odot { {S}}} \right){{{\textit{1}}}_{M \times 1}}}\\ {\left( {{{ {G}}_\phi } \odot { {S}}} \right){{{\textit{1}}}_{M \times 1}}} \end{array}} \right],\;\;\;\;\;{{ {G}}_{\theta \phi }} = \left[ {\begin{array}{*{20}{c}} {{{ {G}}_\theta }}&{{{ O}_{M \times 5}}} \\ {{{ {G}}_\phi }}&{{{ O}_{M \times 5}}} \end{array}} \right] \\ \qquad\qquad {{ {h}}_t} = \left[ {\begin{array}{*{20}{c}} {r_{21}^2 - { {s}}_2^{\rm{T}}{{ {s}}_2} + { {s}}_1^{\rm{T}}{{ {s}}_1}} \\ {r_{31}^2 - { {s}}_3^{\rm{T}}{{ {s}}_3} + { {s}}_1^{\rm{T}}{{ {s}}_1}} \\ \vdots \\ {r_{M1}^2 - { {s}}_M^{\rm{T}}{{ {s}}_M} + { {s}}_1^{\rm{T}}{{ {s}}_1}} \end{array}} \right],\\ \qquad\;\;{{ {h}}_\nu } = 2\left[ {\begin{array}{*{20}{c}} {{r_{21}}{{\dot r}_{21}} - {\dot{ s}}_2^{\rm{T}}{{ {s}}_2} + {\dot{ s}}_1^{\rm{T}}{{ {s}}_1}} \\ {{r_{31}}{{\dot r}_{31}} - {\dot{ s}}_3^{\rm{T}}{{ {s}}_3} + {\dot{ s}}_1^{\rm{T}}{{ {s}}_1}} \\ \vdots \\ {{r_{M1}}{{\dot r}_{M1}} - {\dot{ s}}_M^{\rm{T}}{{ {s}}_M} + {\dot{ s}}_1^{\rm{T}}{{ {s}}_1}} \end{array}} \right] , \\ \qquad {{ {G}}_t} = - 2\left[ {\begin{array}{*{20}{c}} {{{\left( {{{ {s}}_2} - {{ {s}}_1}} \right)}^{\rm{T}}}}&{\begin{array}{*{20}{c}} {{r_{21}}}&{{{\textit{0}}}_{4 \times 1}^{\rm{T}}} \end{array}} \\ {{{\left( {{{ {s}}_3} - {{ {s}}_1}} \right)}^{\rm{T}}}}&{\begin{array}{*{20}{c}} {{r_{31}}}&{{{\textit{0}}}_{4 \times 1}^{\rm{T}}} \end{array}} \\ \vdots & \vdots \\ {{{\left( {{{ {s}}_M} - {{ {s}}_1}} \right)}^{\rm{T}}}}&{\begin{array}{*{20}{c}} {{r_{M1}}}&{{{\textit{0}}}_{4 \times 1}^{\rm{T}}} \end{array}} \end{array}} \right], \\ {{ {G}}_\nu } = - 2\left[ {\begin{array}{*{20}{c}} {{{\left( {{{{\dot{ s}}}_2} - {{{\dot{ s}}}_1}} \right)}^{\rm{T}}}}&{{{\dot r}_{21}}}&{{{\left( {{{ {s}}_2} - {{ {s}}_1}} \right)}^{\rm{T}}}}&{{r_{21}}} \\ {{{\left( {{{{\dot{ s}}}_3} - {{{\dot{ s}}}_1}} \right)}^{\rm{T}}}}&{{{\dot r}_{31}}}&{{{\left( {{{ {s}}_3} - {{ {s}}_1}} \right)}^{\rm{T}}}}&{{r_{31}}} \\ \vdots & \vdots & \vdots & \vdots \\ {{{\left( {{{{\dot{ s}}}_M} - {{{\dot{ s}}}_1}} \right)}^{\rm{T}}}}&{{{\dot r}_{M1}}}&{{{\left( {{{ {s}}_M} - {{ {s}}_1}} \right)}^{\rm{T}}}}&{{r_{M1}}} \end{array}} \right] \\ \end{array} $$ (15) 式中,
$ \odot $ 表示向量Schur乘法;${{{\textit{1}}}_{m \times 1}}$ 与${{{\textit{0}}}_{m \times 1}}$ 分别表征m维取值全1的列向量与全0的列向量;${{ {G}}_\theta } = {{\rm{[}}{{ {g}}_{\theta 1}}, {{ {g}}_{\theta 2}},\cdots ,{{ {g}}_{\theta M}}{\rm{]}}^{\rm{T}}},{{ {G}}_\phi } = {{\rm{[}}{{ {g}}_{\phi 1}}, {{ {g}}_{\phi 2}},\cdots ,{{ {g}}_{\phi M}}{\rm{]}}^{\rm{T}}} $ ;S=${\rm{[}}{{ {s}}_1}, {{ {s}}_2}, \cdots ,{{ {s}}_M}{\rm{]}}^{\rm{T}}$ 。式(14)中的矩阵
${ {B}}_{\theta \phi }^o,{ {D}}_{\theta \phi }^o$ 的定义分别为:$${ {B}}_{\theta \phi }^o = \left[ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{ {B}}_{\theta n}^o} \\ {{{ O}_{M \times M}}} \end{array}} \right]}&{\left[ {\begin{array}{*{20}{c}} {{{ O}_{M \times M}}} \\ {{ {B}}_{\phi \omega }^o} \end{array}} \right]} \end{array}} \right],\quad\;{ {D}}_{\theta \phi }^o = \left[ {\begin{array}{*{20}{c}} {{ {B}}_{\theta s}^o} \\ {{ {B}}_{\phi s}^o} \end{array}} \right]$$ (16) 式中,
$ { {B}}_{\theta s}^o\! = \!{\rm{diag}}{\rm{(}}{ {G}}_\theta ^o{\rm{); }}{ {B}}_{\phi s}^o \!=\! {\rm{diag}}{\rm{(}}{ {G}}_\phi ^o{\rm{); }}{ {B}}_{\phi \omega }^o \!\!=\! {\rm{diag}}{\rm{([}}r_1^o, r_2^o, \cdots $ $ r_M^o{\rm{]); }}{ {B}}_{\theta n}^o = {\rm{diag}}{\rm{([}}r_1^o\cos \phi _1^o, r_2^o\cos \phi _2^o, \cdots ,r_M^o\cos \phi _M^o{\rm{])}} $ 。式(14)中的矩阵
${{ {B}}^o},{{\dot{ B}}^o}$ 分别定义为:$${{ {B}}^o} = 2\left[ {\begin{array}{*{20}{c}} {r_2^o}&0&0&0 \\ 0&{r_3^o}&0&0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0&0&{r_M^o} \end{array}} \right],\;\;\;{{\dot{ B}}^o} = 2\left[ {\begin{array}{*{20}{c}} {{\dot r}_2^o}&0&0&0 \\ 0&{{\dot r}_3^o}&0&0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0&0&{{\dot r}_M^o} \end{array}} \right]$$ (17) 式(14)中的矩阵
${{ {D}}^o},{{\dot{ D}}^o}$ 分别按如下方式定义其每一行,即矩阵${{ {D}}^o},{{\dot{ D}}^o}$ 的第$i{\rm{(}}i = 1,2, \cdots ,M - 1{\rm{)}}$ 行定义为:$$\left\{ \begin{array}{l} {{ {D}}^o} = \left[\begin{array}{*{20}{c}} { - { {p}}_1^{\rm T} }&{{{\textit{0}}}_{3(i - 1) \times 1}^{\rm T} }&{{ {p}}_{i + 1}^{\rm T} }&{{{\textit{0}}}_{3(M - i - 1) \times 1}^{\rm T} } \end{array}\right] \\ {{{\dot{ D}}}^o} = \left[\begin{array}{*{20}{c}} { - {\dot{ p}}_1^T}&{{{\textit{0}}}_{3(i - 1) \times 1}^{\rm T} }&{{\dot{ p}}_{i + 1}^{\rm T} }&{{{\textit{0}}}_{3(M - i - 1) \times 1}^{\rm T} } \end{array}\right] \end{array} \right. $$ (18) 式中,
$ {{ {p}}_k} = ({{ {u}}^o} - { {s}}_k^o);{{\dot{ p}}_k} = ({{\dot{ u}}^o} - {\dot{ s}}_k^o),k = 1,2, \cdots ,M $ 。基于式(13),可以通过加权最小二乘来求解参数
${ {\varphi }}_1^o$ 。权矩阵通常选为${ {W}} = {{\rm{(}}{ {B}}_1^o{{ {Q}}_\alpha }{ {B}}_1^{o{\rm{T}}} + { {D}}_1^o{{ {Q}}_\beta }{ {D}}_1^{o{\rm{T}}}{\rm{)}}^{ - 1}}$ 。但这种构造方式需要获取各传感器位置和速度真值、各传感器相对辐射源的方位角/高低角真值、各传感器到辐射源距离与距离变化率真值,并且还需已知辐射源位置与速度等真值。然而这些量在实际工程实践中不可得。解决上述矛盾的一种折中的处理方式是采取两步加权最小二乘计算
${ {\varphi }}_1^o$ ,即:① 令权矩阵
${ {W}} = { {Q}}_\beta ^{ - 1}$ ,则有:$${\hat{ {\varphi} }}_1^o = {{\rm{(}}{ {G}}_1^{\rm{T}}{ {W}}{{ {G}}_1}{\rm{)}}^{ - 1}}{ {G}}_1^{\rm{T}}{ {W}}{{ {h}}_1}$$ (19) 那么,
$ {{\hat{ u}}^o} \!=\! {{\hat{ {\varphi} }}_1^o}\left( {1:3} \right),\;\;{{{\hat {\dot { u}}}^o}} = {\hat{ {\varphi} }}_1^o\left( {5:7} \right),\;\;{{\hat r}_i^o} = \left\| {{{{\hat{ u}}}^o} - {{ {s}}_i}} \right\|,\;\; $ ${{\hat {\dot r}}_i^o} = {{{({{{\hat{ u}}}^o} - {{{ {s}}_i})}^{\rm T}} }({{{{\hat {\dot { u}}}}^o} - {{{\dot{ s}}}_i})} / {{\hat r}_i^o}}$ 。将${{\hat{ u}}^o}$ 与${{ {s}}_i}$ 代入式(1)可得${\hat \theta} _i^o$ 与$\hat \phi _i^o$ 。将上述各真值的替代值代入式(16)、式(17)与式(18)构造矩阵${\hat{ B}}_{\theta \phi }^o,{\hat{ D}}_{\theta \phi }^o,{{\hat{ B}}^o},{{\hat {\dot { B}}}^o},{{\hat{ D}}^o},{{\hat {\dot { D}}}^o}$ ,进而可构造出矩阵${\hat{ B}}_1^o$ 与${\hat{ D}}_1^o$ 。② 选取权
${{ {W}}_1} = {{\rm{(}}{\hat{ B}}_1^o{{ {Q}}_\alpha }{\hat{ B}}_1^{o{\rm{T}}} + {\hat{ D}}_1^o{{ {Q}}_\beta }{\hat{ D}}_1^{o{\rm{T}}}{\rm{)}}^{ - 1}}$ ,则${ {\varphi }}_1^o$ 的估计值${{ {\varphi }}_1}$ 为:$${{ {\varphi }}_1} = {{\rm{(}}{ {G}}_1^{\rm{T}}{{ {W}}_1}{{ {G}}_1}{\rm{)}}^{ - 1}}{ {G}}_1^{\rm{T}}{{ {W}}_1}{{ {h}}_1}$$ (20) 根据最小二乘理论,可知第一阶段参数的估计误差协方差阵为
${\rm{ cov}} {\rm{(}}{{ {\varphi }}_1}{\rm{)}} = {{\rm{(}}{ {G}}_1^{\rm{T}}{{ {W}}_1}{{ {G}}_1}{\rm{)}}^{ - 1}}$ 。2)第二阶段:精估计。
对于第一阶段的参数估计值
${{ {\varphi }}_1}$ ,其前三维分量${{ {\varphi }}_1}(1:3)$ 是移动辐射源在某时刻的位置向量${{ {u}}^o}$ 的估计值,其第五至第七维分量${{ {\varphi }}_1}(5:7)$ 是该辐射源在该时刻的瞬时速度向量${{\dot{ u}}^o}$ 的估计值。但根据最小二乘理论,由式(20)估计得出${{ {\varphi }}_1}$ 的前提条件是$(r_1^o,{\dot r}_1^o)$ 与$({{ {u}}^o},{{\dot{ u}}^o})$ 无关,但这又与第一阶段估计参数${ {\varphi }}_1^o$ 的定义矛盾,因而按照这种方式估计出的移动辐射源的位置向量与速度向量不精确。因此,在第二阶段,本文使用第一阶段的参数估计值${{ {\varphi }}_1}(4)$ 与${{ {\varphi }}_1}(8)$ 来构建另一个最小二乘模型,以提高${{ {u}}^o}$ 与${{\dot{ u}}^o}$ 估计精度,从而实现对该时刻移动辐射源的无源定位。记向量
${{ {\varphi }}_1}$ 对应的估计误差向量为$\Delta {{ {\varphi }}_1}$ ,由于${{ {\varphi }}_1}(1:3) = {{ {u}}^o} + \Delta {{ {\varphi }}_1}(1:3)$ ,则有:$$\begin{split} & \qquad ({{ {\varphi }}_1}(1:3) - {{ {s}}_1}) \odot ({{ {\varphi }}_1}(1:3) - {{ {s}}_1}) = \\ & ({{ {u}}^o} - {{ {s}}_1}) \odot ({{ {u}}^o} - {{ {s}}_1}) + 2({{ {u}}^o} - {{ {s}}_1}) \odot \Delta {{ {\varphi }}_1}(1:3) \end{split} $$ (21) 此外,从
${ {\varphi }}_1^o$ 的定义可以得知${{ {\varphi }}_1}(4) = r_1^o + \Delta {{ {\varphi }}_1}(4) =$ $ \left\| {{{ {u}}^o} - { {s}}_1^o} \right\| + \Delta {{ {\varphi }}_1}(4)$ ,将${ {s}}_1^o = {{ {s}}_1} - \Delta {{ {s}}_1}$ 代入上式,并忽略二阶误差项,则有:$${[{{ {\varphi }}_1}(4)]^2} = \left\| {{{ {u}}^o} - {{ {s}}_1}} \right\| + 2{({{ {u}}^o} - {{ {s}}_1})^{\rm T} }\Delta {{ {s}}_1} + 2r_1^o\Delta {{ {\varphi }}_1}(4)$$ (22) 类似地,有:
$$ \begin{split} &\quad\quad({{ {\varphi }}_1}(1:3) - {{ {s}}_1}) \odot ({{ {\varphi }}_1}(5:7) - {{{\dot{ s}}}_1}) = \\ & ({{ {u}}^o} - {{ {s}}_1}) \odot ({{{\dot{ u}}}^o} - {{{\dot{ s}}}_1}) + ({{{\dot{ u}}}^o} - {{{\dot{ s}}}_1}) \odot \Delta {{ {\varphi }}_1}(1:3) + \\ &\quad\quad\quad \;({{ {u}}^o} - {{ {s}}_1}) \odot \Delta {{ {\varphi }}_1}(5:7) \\ \end{split} $$ (23) 以及:
$$\begin{split} & {{ {\varphi }}_1}(4){{ {\varphi }}_1}(8) = {({{ {u}}^o} - {{ {s}}_1})^{\rm T} }({{{\dot{ u}}}^o} - {{{\dot{ s}}}_1}) + {({{ {u}}^o} - {{ {s}}_1})^{\rm T} }\Delta {{{\dot{ s}}}_1} + \\ & \;\;\;\;\;\;\;\;\;\;\; {({{{\dot{ u}}}^o} - {{{\dot{ s}}}_1})^{\rm T} }\Delta {{ {s}}_1} + {\dot r}_1^o\Delta {{ {\varphi }}_1}(4) + r_1^o\Delta {{ {\varphi }}_1}(8) \end{split} $$ (24) 基于上面的讨论,第二阶段参数向量可选择为:
$${ {\varphi }}_2^o = {{\rm{[((}}{{ {u}}^o} - {{ {s}}_1}{\rm{)}} \odot {\rm{(}}{{ {u}}^o} - {{ {s}}_1}{\rm{)}}{{\rm{)}}^{\rm{T}}},{{\rm{((}}{{ {u}}^o} - {{ {s}}_1}{\rm{)}} \odot {\rm{(}}{{\dot{ u}}^o} - {{\dot{ s}}_1}{\rm{))}}^{\rm{T}}}{\rm{]}}^{\rm{T}}}$$ (25) 联合式(21)~式(24),有:
$${{ {\varepsilon }}_2} = {{ {h}}_2} - {{ {G}}_2}{ {\varphi }}_2^o$$ (26) 式中,
$$ \begin{split} & {{ {h}}_2} = \left[ {\begin{array}{*{20}{c}} {\;({{ {\varphi }}_1}(1:3) - {{ {s}}_1}) \odot ({{ {\varphi }}_1}(1:3) - {{ {s}}_1})} \\ {{{[{{ {\varphi }}_1}(4)]}^2}} \\ {({{ {\varphi }}_1}(1:3) - {{ {s}}_1}) \odot ({{ {\varphi }}_1}(5:7) - {{{\dot{ s}}}_1})} \\ {{{ {\varphi }}_1}(4){{ {\varphi }}_1}(8)} \end{array}} \right],\\ &\qquad{{ {G}}_2} = \left[ {\begin{array}{*{20}{c}} {{{ {I}}_{3 \times 3}}}&{{{ {{ O}}}_{3 \times 3}}} \\ {{{\textit{1}}}_{3 \times 1}^{\rm{T}}}&{{{\textit{0}}}_{3 \times 1}^{\rm{T}}} \\ {{{ {{ O}}}_{3 \times 3}}}&{{{ {I}}_{3 \times 3}}} \\ {{{\textit{0}}}_{3 \times 1}^{\rm T} }&{{{\textit{1}}}_{3 \times 1}^{\rm T} } \end{array}} \right] \end{split} $$ (27) 另一方面,针对等式误差
${{ {\varepsilon }}_2}$ ,有:$${{ {\varepsilon }}_2} = {{ {B}}_2}\Delta {{ {\varphi }}_1} + {{ {D}}_2}\Delta { {\beta }}$$ (28) 式中,矩阵
${{ {B}}_2},{{ {D}}_2}$ 的定义如下所示:$$ \begin{array}{l} \begin{array}{*{20}{c}} {{{ {B}}_2} = \left[\!\!\! {\begin{array}{*{20}{c}} {2{\tilde { B}}}&{{{ {{ O}}}_{4 \times 4}}} \\ {{\dot{\tilde { B}}}}&{{\tilde { B}}} \end{array}} \!\!\right]},\;\;{\begin{array}{*{20}{c}} {{\tilde { B}} = {\rm{diag}} \left[ {({{ {\varphi }}_1}(1:3) - {{ {s}}_1}),{{ {\varphi }}_1}(4)} \right]} \\ {{\dot{\tilde { B}}} = {\rm{diag}} \left[ {({{ {\varphi }}_1}(5:7) - {{{\dot{ s}}}_1}),{{ {\varphi }}_1}(8)} \right]} \end{array}} , \end{array} \\ \qquad {{ {D}}_2} = \left[ {\begin{array}{*{20}{c}} {{{ {{ O}}}_{3 \times 6M}}}&{}&{}&{} \\ {2{{({{ {\varphi }}_1}(1:3) - {{ {s}}_1})}^{\rm T} }}&{{{\textit{0}}}_{\left( {6M - 3} \right) \times 1}^{\rm T} }&{}&{} \\ {{{ {{ O}}}_{3 \times 6M}}}&{}&{}&{} \\ {{{({{ {\varphi }}_1}(5:7) - {{{\dot{ s}}}_1})}^{\rm T} }}&{{{\textit{0}}}_{\left( {3M - 3} \right) \times 1}^{\rm T} }\\ {\;{{({{ {\varphi }}_1}(1:3) - {{ {s}}_1})}^{\rm T} }}&{\;{{\textit{0}}}_{\left( {3M - 3} \right) \times 1}^{\rm T} } \end{array}}\!\!\!\!\!\! \right] \end{array} $$ (29) 式(28)决定了第二阶段加权最小二乘的权矩阵
${{ {W}}_2}$ 的选取形式[10],即${ {W}}_2^{ - 1} = \{ {{ {B}}_2}{\rm{cov}}({{ {\varphi }}_1}){ {B}}_2^{\rm T} + {{ {D}}_2}{{ {Q}}_\beta }{ {D}}_2^{\rm T} + $ ${{ {B}}_2}{\rm{cov}}({{ {\varphi }}_1}){ {G}}_1^{\rm T} {{ {W}}_1}{{ {D}}_1}{{ {Q}}_\beta }{ {D}}_2^{\rm T} + {{ {D}}_2}{{ {Q}}_\beta }{ {D}}_1^{\rm T} {{ {W}}_1}{{ {G}}_1}{\rm{cov}}({{ {\varphi }}_1}){ {B}}_2^{\rm T} \} $ 。那么第二阶段估计参数${ {\varphi }}_2^o$ 的加权最小二乘估计值为:$${{ {\varphi }}_2} = {({ {G}}_2^{\rm T} {{ {W}}_2}{{ {G}}_2})^{ - 1}}{ {G}}_2^{\rm T} {{ {W}}_2}{{ {h}}_2}$$ (30) 且
${ {\varphi }}_2^o$ 的估计误差为:$$\Delta {{ {\varphi }}_2} = {{ {\varphi }}_2} - { {\varphi }}_2^o = {{\rm{(}}{ {G}}_2^{\rm T} {{ {W}}_2}{{ {G}}_2}{\rm{)}}^{ - 1}}{ {G}}_2^{\rm T} {{ {W}}_2}{{ {\varepsilon }}_2}$$ (31) 对应的协方差矩阵为
${\rm{cov}} {\rm{(}}{{ {\varphi }}_2}{\rm{)}} = {{\rm{(}}{ {G}}_2^{\rm{T}}{{ {W}}_2}{{ {G}}_2}{\rm{)}}^{ - 1}}$ 。一旦得到
${{ {\varphi }}_2}$ ,那么位置向量${{ {u}}^o}$ 及速度向量${{\dot{ u}}^o}$ 的最终估计值可由以下方式计算得到,即:$${ {u}} = { {\varPi }}\sqrt {{{ {\varphi }}_2}(1:3)} + {{ {s}}_1}\quad\;\;{\dot{ u}} = {{ {\varphi }}_2}(4:6)./({ {u}} - {{ {s}}_1}) + {{\dot{ s}}_1}$$ (32) 式中,
${ {\varPi }} = {\rm{diag}}[{{ {\varphi }}_1}(1:3) - {{ {s}}_1}]$ ;“./”表示对应元素相除。矩阵${ {\varPi }}$ 的存在避免了对${{ {\varphi }}_2}$ 元素开平方时的正负符号模糊问题。式(32)最终给出了某时刻移动辐射源AOA-TDOA-FDOA的联合定位闭合解。下面给出定位解
${ {u}}$ 与${\dot{ u}}$ 对应的协方差矩阵,若记算法给出的定位解向量${ {\varTheta }} = {{\rm{[}}{{ {u}}^{\rm{T}}},{{\dot{ u}}^{\rm{T}}}{\rm{]}}^{\rm{T}}}$ ,那么对式(25)求一阶全微分有:$$\Delta {{ {\varphi }}_2} = { {\varXi }}\Delta { {\varTheta }}$$ (33) 式中,
${ {\varXi }} = \left[ {\begin{array}{*{20}{c}} {2{\rm{diag}}[{{ {u}}^o} - {{ {s}}_1}]}&{{{ {{ O}}}_{3 \times 3}}} \\ {2{\rm{diag}}[{{{\dot{ u}}}^o} - {{{\dot{ s}}}_1}]}&{2{\rm{diag}}[{{ {u}}^o} - {{ {s}}_1}]} \end{array}} \right]$ 。在第二阶段的估计过程中,
${{ {s}}_1}$ 与${{\dot{ s}}_1}$ 被视作常量,因而$\Delta {{ {s}}_1}$ 与$\Delta {{\dot{ s}}_1}$ 未出现在式(33)里。式(28)表明当噪声强度不大时,${{ {\varepsilon }}_2}$ 近似满足零均值,因此式(31)所示的$\Delta {{ {\varphi }}_2}$ 同样近似为零均值。所以,本文所提的AOA-TDOA-FDOA联合定位给出的闭合解同样近似满足零均值特性。那么,由式(33)可得定位解向量${ {\varTheta }}$ 的理论协方差矩阵为:$${\rm{cov}}({ {\varTheta }}) = {{ {\varXi }}^{ - 1}}{\rm{cov}}{\rm{(}}{{ {\varphi }}_2}{\rm{)}}{{ {\varXi }}^{ - {\rm T} }}$$ (34) 需要指出的是,文献[10-11]分析了基于TDOA与FDOA观测量的联合定位闭合解算法,其第一阶段估计参数向量与本文选取的向量
${ {\varphi }}_1^o$ 一致。${ {\varphi }}_1^o$ 是8维向量,因此文献[10-11]所提算法至少需要5个协同平台参与定位任务,才能按照式(19)及式(20)估计${ {\varphi }}_1^o$ 。而在实际的电子对抗作战过程中难以满足这一条件,本文在继承文献[10-11]所提算法框架的前提下,将AOA观测量引入定位算法,这就使得实际作战所需的协同平台个数降至3个,既节约了定位成本,也提高了无源定位闭合形式算法的战场生存能力。 -
上节详细讨论了某时刻移动辐射源AOA-TDOA-FDOA的联合定位闭合解,本节将对上述算法进行理论分析,并给出其估计误差的理论误差下界,即CRLB界。
AOA、TDOA以及FDOA测量值向量
${ {\alpha}} $ 与传感器位置和速度向量${ {\beta }}$ 均服从高斯分布,并且两者独立,因此数据向量${ {\mu }} = {{\rm{[}}{{ {\alpha }}^{\rm{T}}},{{ {\beta }}^{\rm{T}}}{\rm{]}}^{\rm{T}}}$ 与参数向量${ {\vartheta}} = {[{{ {u}}^{\rm{T}}},{{\dot{ u}}^{\rm{T}}},{{ {s}}^{\rm{T}}},{{\dot{ s}}^{\rm{T}}}]^{\rm{T}}}$ 的概率密度函数为:$$ \begin{split} &\ln f\left( {{ {\mu}} ;{ {\vartheta}} } \right) =\, {k_1} - \frac{1}{2}{({ {\alpha }} - { {\alpha }}_{}^o)^{\rm{T}}}{ {Q}}_{ {\alpha}} ^{ - 1}({ {\alpha }} - { {\alpha }}_{}^o) + \\ &\qquad {k_2} - \frac{1}{2}{({ {\beta }} - { {\beta }}_{}^o)^{\rm{T}}}{ {Q}}_{ {\beta }}^{ - 1}({ {\beta }} - { {\beta }}_{}^o) \end{split} $$ (35) 式中,
${k_1} = - {{\ln \{ {{(2{ {{\text π}}} )}^{4M - 2}}\left| {{{ {Q}}_a}} \right|\} } / 2};{k_2} = - {{\ln \{ {{(2{ {{\text π}}} )}^{6M}}\left| {{{ {Q}}_{{\beta }}}} \right|\} } / 2},$ 都是常数。那么根据定义,参数${ {\theta}} $ 的CRLB界为:$${\rm{CRLB}}\left( { {\theta}} \right) = - {\rm E}{\left[ {\frac{{{\partial ^2}\ln f\left( {{ {\mu}} ;{ {\vartheta}} } \right)}}{{\partial { {\vartheta}} \partial {{ {\vartheta }}^{\rm T} }}}} \right]^{ - 1}} \triangleq {\left[ {\begin{array}{*{20}{c}} { {X}}&{ {Y}} \\ {{{ {Y}}^{\rm T} }}&{ {Z}} \end{array}} \right]^{ - 1}}$$ (36) 式中,
$$ \left\{\!\!\!\! \begin{array}{l} { {X}} \!=\! - {\rm E}{\left[ {\dfrac{{{\partial ^2}\ln f\left( {{ {\mu}} ;{ {\vartheta}} } \right)}}{{\partial { {\varTheta}} \partial {{ {\varTheta}} ^{\rm T} }}}} \right]^{ - 1}} \!= {\left( {\dfrac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\varTheta}} }}} \right)^{\rm T} }{ {Q}}_{ {\alpha}} ^{ - 1}\left( {\dfrac{{\partial {{ {\alpha }}^o}}}{{\partial { {\varTheta}} }}} \right) \\ { {Y}} \!=\! - {\rm E}{\left[ {\dfrac{{{\partial ^2}\ln f\left( {{ {\mu}} ;{ {\vartheta}} } \right)}}{{\partial { {\varTheta}} \partial {{ {\beta}} ^{\rm T} }}}} \right]^{ - 1}}\! = {\left( {\dfrac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\varTheta}} }}} \right)^{\rm T} }{ {Q}}_{ {\alpha}} ^{ - 1}\left( {\dfrac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\beta}} }}} \right) \\ { {Z}} \!=\! - {\rm E}{\left[ {\dfrac{{{\partial ^2}\ln f\left( {{ {\mu}} ;{ {\vartheta}} } \right)}}{{\partial { {\beta}} \partial {{ {\beta}} ^{\rm T} }}}} \right]^{ - 1}} \!= {\left( {\dfrac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\beta}} }}} \right)^{\rm T} }{ {Q}}_{ {\alpha}} ^{ - 1}\left( {\dfrac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\beta}} }}} \right) + { {Q}}_{ {\beta}}^{ - 1} \!\!\!\!\!\!\!\!\!\!\!\!\!\! \end{array} \right. $$ (37) 由向量求导定义可知,式(37)中的偏导
${\partial {{ {\alpha}} ^o}} / $ ${\partial { {\varTheta}} }$ 与${{\partial {{ {\alpha}} ^o}} / {\partial { {\beta}} }}$ 实质是向量${{ {\alpha}} ^o}$ 对向量${ {u}}$ 、向量${\dot{ u}}$ 、向量${ {s}}$ 及向量${\dot{ s}}$ 求偏导,即有:$${\left( {\dfrac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\varTheta}} }}} \right)_{(4M - 2) \times 6}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\dfrac{{\partial {{ {\theta}} ^o}}}{{\partial { {u}}}}} \right)}_{M \times 3}}}&{{{\left( {\dfrac{{\partial {{ {\theta}} ^o}}}{{\partial {\dot{ u}}}}} \right)}_{M \times 3}}} \\ {{{\left( {\dfrac{{\partial {{ {\phi}} ^o}}}{{\partial { {u}}}}} \right)}_{M \times 3}}}&{{{\left( {\dfrac{{\partial {{ {\phi }}^o}}}{{\partial {\dot{ u}}}}} \right)}_{M \times 3}}} \\ {{{\left( {\dfrac{{\partial {{ {r}}^o}}}{{\partial { {u}}}}} \right)}_{(M - 1) \times 3}}}&{{{\left( {\dfrac{{\partial {{ {r}}^o}}}{{\partial {\dot{ u}}}}} \right)}_{(M - 1) \times 3}}} \\ {{{\left( {\dfrac{{\partial {{{\dot{ r}}}^o}}}{{\partial { {u}}}}} \right)}_{(M - 1) \times 3}}}&{{{\left( {\dfrac{{\partial {{{\dot{ r}}}^o}}}{{\partial {\dot{ u}}}}} \right)}_{(M - 1) \times 3}}} \end{array}} \right]$$ (38) 以及:
$${\left( {\dfrac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\beta}} }}} \right)_{(4M - 2) \times 6M}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\dfrac{{\partial {{ {\theta}} ^o}}}{{\partial { {s}}}}} \right)}_{M \times 3M}}}&{{{\left( {\dfrac{{\partial {{ {\theta}} ^o}}}{{\partial {\dot{ s}}}}} \right)}_{M \times 3M}}} \\ {{{\left( {\dfrac{{\partial {{ {\phi}} ^o}}}{{\partial { {s}}}}} \right)}_{M \times 3M}}}&{{{\left( {\dfrac{{\partial {{ {\phi}} ^o}}}{{\partial {\dot{ s}}}}} \right)}_{M \times 3M}}} \\ {{{\left( {\dfrac{{\partial {{ {r}}^o}}}{{\partial { {s}}}}} \right)}_{(M - 1) \times 3M}}}&{{{\left( {\dfrac{{\partial {{ {r}}^o}}}{{\partial {\dot{ s}}}}} \right)}_{(M - 1) \times 3M}}} \\ {{{\left( {\dfrac{{\partial {{{\dot{ r}}}^o}}}{{\partial { {s}}}}} \right)}_{(M - 1) \times 3M}}}&{{{\left( {\dfrac{{\partial {{{\dot{ r}}}^o}}}{{\partial {\dot{ s}}}}} \right)}_{(M - 1) \times 3M}}} \end{array}} \right]$$ (39) 下面逐一给出式(38)、(39)中每个偏导矩阵的具体表达式。根据定义有
${{\partial {{ {\theta}} ^o}} / {\partial {\dot{ u}}}} = {{ O}_{M \times 3}}, {{\partial {{ {\phi}} ^o}} / {\partial {\dot{ u}}}} =$ $ {{ O}_{M \times 3}}$ 以及${{\partial {{ {\theta}} ^o}}/ {\partial {\dot{ s}}}} = {{ O}_{M \times 3M}},{{\partial {{ {\phi}} ^o}}/ {\partial {\dot{ s}}}} = {{ O}_{M \times 3M}}$ 。记${{ {\lambda }}_i}, {{ {\kappa }}_i}, $ ${\rm{ (}}i = 1,2, \cdots ,\;M{\rm{)}}$ ,具有如下表达形式:$$\left\{ \begin{split} & {{ {\lambda }}_i} = {\left[ - \frac{{\sin \theta _i^o}}{{r_i^o\cos \phi _i^o}},\frac{{\cos \theta _i^o}}{{r_i^o\cos \phi _i^o}},0\right]^{\rm{T}}} \\ & {{ {\kappa }}_i} = {\left[ - \frac{{\sin \phi _i^o\cos \theta _i^o}}{{r_i^o}}, - \frac{{\sin \phi _i^o\sin \theta _i^o}}{{r_i^o}},\frac{{\cos \phi _i^o}}{{r_i^o}}\right]^{\rm{T}}} \\ \end{split} \right.$$ (40) 那么,
$ {{\partial {{ {\theta}} ^o}} / {\partial { {u}}}} = {{\rm{[}}{{ {\lambda }}_1},{{ {\lambda }}_2}, \cdots ,{{ {\lambda }}_M}{\rm{]}}^{\rm{T}}}\dot = {{ {A}}_{u1}},{{\partial {{ {\phi}} ^o}} / {\partial { {u}}}} = $ ${\rm{[}}{{ {\kappa }}_1}, {{ {\kappa }}_2}, \cdots , {{ {\kappa }}_M}{\rm{]}}^{\rm{T}}\;\dot =\;{{ {A}}_{u2}},{{\partial {{ {\theta}} ^o}} / {\partial { {s}}}} = {\rm{diag}}{\rm{(}}{{ {A}}_{u1}}{\rm{)}}\;\dot =\; {{ {A}}_{s1}},{{\partial {{ {\phi}} ^o}} / {\partial { {s}}}} =$ ${\rm{diag}}{\rm{(}}{{ {A}}_{u2}}{\rm{)}}\dot = {{ {A}}_{s2}} $ 。记
${{ {E}}_{3M \times 3}} = {\left[ {{{ {I}}_{3 \times 3}}, \cdots ,{{ {I}}_{3 \times 3}}} \right]^{\rm{T}}}$ ,并定义两个(M−1)×3M的矩阵${{ {C}}_1}$ 与矩阵${{ {C}}_2}$ ,其第$i{\rm{(}}i = 1,2, \cdots ,M - 1{\rm{)}}$ 行的定义为:$$\left\{\!\!\!\! \begin{array}{l} {{ {C}}_1}\left( {i,:} \right) = \left[ {\begin{array}{*{20}{c}} { - { {a}}_1^{\rm{T}}}&{{{\textit{0}}}_{3(i - 1) \times 1}^{\rm{T}}}&{{ {a}}_{i + 1}^{\rm{T}}}&{{{\textit{0}}}_{3(M - i - 1) \times 1}^{\rm{T}}} \end{array}} \right] \\ {{ {C}}_2}\left( {i,:} \right) = \left[ {\begin{array}{*{20}{c}} { - { {b}}_1^{\rm{T}}}&{{{\textit{0}}}_{3(i - 1) \times 1}^{\rm{T}}}&{{ {b}}_{i + 1}^{\rm{T}}}&{{{\textit{0}}}_{3(M - i - 1) \times 1}^{\rm{T}}} \end{array}} \right] \end{array} \right. \!\!\!\!\!\!\!\!\!\!\!\!\!\! $$ (41) 式中,
$ {{ {a}}_i} \!=\! ({{ {u}}^o} - { {s}}_i^o)/r_i^o;{{ {b}}_i} \!=\! ({{\dot{ u}}^o} - {\dot{ s}}_i^o)/r_i^o - {\dot r}_i^o({{ {u}}^o} - { {s}}_i^o)/r_i^{o2}$ 。那么,则有:$$ \begin{array}{l} \dfrac{{\partial {{ {r}}^o}}}{{\partial { {u}}}} = {{ {C}}_1}{ {E}},\;\dfrac{{\partial {{{\dot{ r}}}^o}}}{{\partial { {u}}}} = {{ {C}}_2}{ {E}},\;\dfrac{{\partial {{ {r}}^o}}}{{\partial {\dot{ u}}}} = {{ O}_{(M - 1) \times 3}},\;\;\;\dfrac{{\partial {{{\dot{ r}}}^o}}}{{\partial {\dot{ u}}}} = {{ {C}}_1}{ {E}}, \\ \dfrac{{\partial {{ {r}}^o}}}{{\partial { {s}}}} = - {{ {C}}_1},\;\dfrac{{\partial {{{\dot{ r}}}^o}}}{{\partial { {s}}}} = - {{ {C}}_2},\;\;\dfrac{{\partial {{ {r}}^o}}}{{\partial {\dot{ s}}}} = {{ O}_{(M - 1) \times 3M}},\;\dfrac{{\partial {{{\dot{ r}}}^o}}}{{\partial {\dot{ s}}}} = - {{ {C}}_1} \\ \end{array} $$ (42) 综合上述各个偏导矩阵,那么式(38)与式(39)所表征的偏导矩阵的具体表达形式为:
$$ \begin{split} &\left( {\frac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\varTheta}} }}} \right) = \left[ {\begin{array}{*{20}{c}} {{{ {A}}_{u1}}}&{{{ O}_{M \times 3}}} \\ {{{ {A}}_{u2}}}&{{{ O}_{M \times 3}}} \\ {{{ {C}}_{\rm{1}}}{ {E}}}&{{{ O}_{(M - 1) \times 3}}} \\ {{{ {C}}_2}{ {E}}}&{{{ {C}}_1}{ {E}}} \end{array}} \right],\\ &\left( {\frac{{\partial {{ {\alpha}} ^o}}}{{\partial { {\beta}} }}} \right) = \left[ {\begin{array}{*{20}{c}} {{{ {A}}_{s1}}}&{{{ O}_{M \times 3M}}} \\ {{{ {A}}_{s2}}}&{{{ O}_{M \times 3M}}} \\ { - {{ {C}}_1}}&{{{ O}_{(M - 1) \times 3M}}} \\ { - {{ {C}}_2}}&{ - {{ {C}}_1}} \end{array}} \right] \end{split} $$ (43) 将式(43)代入式(37),即可得6M+6维方阵
${\rm{CRLB}}\left( { {\vartheta }} \right)$ 的具体形式。由矩阵求逆引理可得移动辐射源位置及速度参数
${ {\varTheta }}$ 的CRLB界,即:$${\rm{CRLB}}\left( { {\varTheta }} \right) = {{ {X}}^{ - 1}} + {{ {X}}^{ - 1}}{ {Y}}{\left( {{ {Z}} - {{ {Y}}^T}{{ {X}}^{ - 1}}{ {Y}}} \right)^{ - 1}}{{ {Y}}^T}{{ {X}}^{ - 1}}$$ (44) 式中,
${{{X}}^{ - 1}}$ 表示当测角与时差/频差传感器不存在位置误差及速度误差时的参数${ {\varTheta }}$ 的CRLB界,因此式(44)中的第二项表征了由测角与时差/频差传感器位置及速度误差引起的参数${ {\varTheta }}$ 的CRLB界的增量部分。式(44)的迹表征了任一种多平台AOA-TDOA-FDOA联合定位算法的估计误差均方根的下界。文献[10]已证明,当TDOA与FDOA测量误差与传感器位置与速度误差都服从高斯分布并且噪声不大,并且传感器距离辐射源较远时,定位解向量
${ {\varTheta }}$ 的理论协方差矩阵${\rm{cov}}({ {\varTheta }})$ 能达到其理论误差下界。基于类似的证明过程,当无源定位算法加入AOA观测量后,本文所提算法所给出定位解向量${ {\varTheta }}$ 的理论协方差矩阵${\rm{cov}}({ {\varTheta }})$ 也能达到对应的CRLB界。由于篇幅限制,在此省略这一结论的推导过程,下面将给出仿真实验,验证本文提出算法的均方根误差在噪声不大时同样能达到CRLB界。 -
为验证本文提出的移动辐射源AOA-TDOA- FDOA联合定位闭合解算法的性能,本节首先给出一组3平台协同定位一个移动辐射源位置的仿真实例。移动辐射源初始位置为[57 891, −12 536,
$ 125{\rm{]}}^{\rm{T}}$ (单位为m,下同),初始速度为${{\rm{[}}12,30,0{\rm{]}}^{\rm{T}}}$ (单位为m/s,下同);协同平台主站初始位置为[5 000,$1\;500, \,3\;500{\rm{]}}^{\rm{T}}$ ,初始速度为${{\rm{[}}120, - 20,0{\rm{]}}^{\rm{T}}}$ ;协同平台辅站1的初始位置为${{\rm{[}}21\;500,\;15\;000,5\;800{\rm{]}}^{\rm{T}}}$ ,初始速度为${{\rm{[}}130,0,0{\rm{]}}^{\rm{T}}}$ ;协同平台辅站2的初始位置为${\rm{[}}20\;500, $ $- 45\;000,5\;800{\rm{]}}^{\rm{T}}$ ,初始速度为${{\rm{[}}110,50,0{\rm{]}}^{\rm{T}}}$ 。辐射源载波频率为$1.125 \times {10^9}$ Hz。为评价无源定位算法的定位精度,本文采用均方根误差为评价标准,其定义为:$${\rm{MSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {\left\| {{{ {u}}^o} - {{ {u}}_i}} \right\|_2^2} } $$ (45) 式中,
${\rm{MSE}}$ 为某时刻无源定位所估计的辐射源位置的均方根误差;${{ {u}}^o}$ 为该时刻移动辐射源真实位置;${{ {u}}_i}$ 为第i次独立仿真实验所估计的辐射源位置;N为独立仿真实验次数。需要指出的是,在N次独立仿真实验过程中,每次仿真中辐射源移动轨迹以及每个平台的真实运动轨迹都一致。本节后续部分将首先以此为基础给出几组仿真实例,验证本文所提算法在各种噪声强度下的定位能力;然后再给出两组对比实验,说明本文所提算法在定位精度与定位时间等方面较其他已有定位算法所具备的优势。 -
为验证本文所提算法对平台位置误差的适应能力,在这组仿真中将3架空中平台的图1中x、y、z向上的位置误差标准差变化范围同时设置为10−2~105 m,所有平台图1中x、y、z向上的速度误差标准差固定为0.2 m/s,并且将所有AOA测量噪声标准差均固定为3°,所有TDOA测量噪声标准差均固定为100 ns,以及所有FDOA测量噪声标准差均固定为100 Hz。5 000次独立仿真形成的均方根定位误差曲线如图2所示。为直观说明本文所提算法对平台位置误差的适应能力,每种设置下的定位误差理论下界(即式(44)所示的
${\rm{CRLB}}\left( { {\varTheta }} \right)$ 矩阵的前3个对角元素和的平方根)也同时绘制在图2中。图2表明当所有协同平台在图1中x、y、z这3个方向的位置误差标准差均不超过5×103 m时,本文所提算法在3平台协同定位场合下的均方根定位误差能达到对应的CRLB界。
-
为验证本文所提算法对测角噪声强度的适应能力,在这组仿真中,将每个平台的方位角测量噪声标准差变化范围同时设置为10−2°~102°,而所有平台在图1中x、y、z向的位置误差标准差都固定为5 m、速度误差标准差都固定为0.2 m/s,并且将所有高低角测量噪声标准差均固定为3°,所有TDOA测量噪声标准差均固定为100 ns,所有FDOA测量噪声标准差均固定为100 Hz。5 000次独立仿真形成的均方根定位误差曲线如图3所示。同时为直观说明本文所提算法对测角噪声强度的适应能力,每种设置下的CRLB界也同时绘制在图3中。
图3表明当所有协同平台所测得的方位角的测量误差标准差不大于20°时,本文所提算法在3平台协同定位场合下的均方根定位误差能达到对应的CRLB界。
-
为验证本文所提算法对TDOA噪声强度的适应能力,在这组仿真中,将每个TDOA测量噪声标准差变化范围同时设置为10−2~106 ns,所有平台在x、y、z向的位置误差标准差都固定为5 m,速度误差标准差都固定为0.2 m/s,并且将所有方位/高低角测量噪声标准差均固定为3°,所有FDOA测量噪声标准差均固定为100 Hz。5 000次独立仿真形成的均方根定位误差曲线如图4所示。同时为直观说明本文所提算法对TDOA测量噪声强度的适应能力,每种设置下的CRLB界也同时绘制在图4中。
图4表明当所有TDOA观测量的测量噪声标准差不大于105 ns时,本文所提算法在3平台协同定位场合下的均方根定位误差能达到对应的CRLB界。
-
为验证本文所提算法对FDOA噪声强度的适应能力,在这组仿真中,将每个FDOA测量噪声标准差变化范围同时设置为10−2~104 Hz,所有平台在x、y、z向的位置误差标准差都固定为5 m,速度误差标准差都固定为0.2 m/s,并且将所有方位/高低角测量噪声标准差均固定为3°,所有TDOA测量噪声标准差均固定为100 ns。5 000次独立仿真形成的均方根定位误差曲线如图5所示。同时为直观说明本文所提算法对FDOA测量噪声强度的适应能力,每种设置下的CRLB界也同时绘制在图5中。
图5表明当所有FDOA观测量的测量噪声标准差不大于200 Hz时,本文所提算法在3平台协同定位场合下的均方根定位误差能达到对应的CRLB界。
-
针对移动辐射源TDOA-FDOA联合无源定位闭合解算法需要至少5个协同平台参与一次定位任务的问题,本文将AOA观测量引入,提出一种新的基于AOA-TDOA-FDOA的联合定位闭合解算法。本文所提算法在兼顾平台位置不确定性以及保持代数闭合解框架不变的前提下,能将参与定位的平台个数有效地减少至3个。同时,理论分析与仿真实验结果都表明所提算法在面对工程上常见的噪声强度时,定位性能可以达到理论误差下界。这表明,本文所提算法既能拓宽算法的战场应用范围,也能提高算法的战场生存能力。
Closed-Form AOA-TDOA-FDOA Solution for Moving Source Location
-
摘要: 移动辐射源无源定位是电子对抗领域需要解决的关键问题之一。基于到达时间差(TDOA)与到达频率差(FDOA)的联合定位闭合解算法是解决上述问题的有效途径之一,但完成一次定位至少需要5个协同平台才能达到该算法的应用条件。在保持无源定位闭合解框架的前提下,为减少协同平台个数,提出了一种融合到达角(AOA)观测量、TDOA观测量以及FDOA观测量的无源定位算法。当各观测量的观察噪声及传感器位置偏差均为高斯噪声且噪声强度适中时,可建立移动辐射源位置与各观测量及传感器位置的近似代数表达式,并由此形成AOA-TDOA-FDOA联合定位闭合解算法。进一步的理论分析表明,该算法的定位误差能达到克拉美罗界,数值仿真结果与理论分析结论吻合。Abstract: The location of a moving emitting source is a key problem in the field of electronic countermeasures. One of the effective solutions to solve this problem is the passive location closed-form algorithm based on the time difference of arrival (TDOA) and frequency difference of arrival (FDOA) measurements. However, in order to satisfy the requirement of the above algorithm, at least 5 nodes need to collaborate to complete a location task. Given the closed-form frame of passive location algorithm, by combining the angle of arrival (AOA), TDOA and FDOA measurements, a novel location algorithm is proposed to reduce the number of collaborative platforms. The approximate algebraic relationships are derived between the moving source position and the measurements with platform positions. According to the aforementioned conditions, the closed formed expressions can be calculated by joint AOA-TDOA-FDOA mechanism. The theoretical analysis demonstrates that solution accuracy of the proposed location algorithm can achieve the Cramér–Rao lower bound (CRLB), some numerical simulation results coincide with the theoretical results.
-
Key words:
- AOA /
- closed-form algorithm /
- FDOA /
- passive moving source location /
- TDOA
-
[1] TUYSUZ B. A new target radar cross section based passive radar surveillance receiver positioning algorithm on real terrain maps[J]. Radioengineering, 2018, 27(3): 891-898. doi: 10.13164/re.2018.0891 [2] BHARATHI B M R, MOHANTY A R. Underwater sound source localization by EMD-base maximum likelihood method[J]. Acoustics Australia, 2018, 46(2): 193-203. doi: 10.1007/s40857-018-0129-8 [3] ZHANG L, GAO Q, MA X, et al. DeFi: Robust training-free device-free wireless localization with WiFi[J]. IEEE Trans on Vehicular Technology, 2018, 67(9): 8822-8831. doi: 10.1109/TVT.2018.2850842 [4] THARMARASA R, SUBRAMANIAM M, NADARAJAH N, et al. Multitarget passive coherent location with transmitter-origin and target-altitude uncertainties[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(3): 2530-2550. doi: 10.1109/TAES.2012.6237607 [5] JEAN O, WEISS A. Geolocation by direction of arrival using arrays with unknown orientation[J]. IEEE Trans on Signal Process, 2014, 62(12): 3135-3142. doi: 10.1109/TSP.2014.2321109 [6] WANG Y, HO K C. An asymptotically efficient estimator in closed-form for 3-D AOA localization using a sensor network[J]. IEEE Trans on Wireless Communications, 2015, 14(12): 6524-6535. doi: 10.1109/TWC.2015.2456057 [7] LIU Y, GUO F, YANG L, et al. An improved algebraic solution for TDOA localization with sensor position errors[J]. IEEE Trans on Communications Letters, 2015, 19(12): 2218-2221. doi: 10.1109/LCOMM.2015.2486769 [8] YIN J, WAN Q, YANG S, et al. A simple and accurate TDOA-AOA localization method using two stations[J]. IEEE Trans on Signal Processing Letters, 2016, 23(1): 144-158. doi: 10.1109/LSP.2015.2505138 [9] ZHAO Y, LI Z, HAO B, et al. Bias reduced method for TDOA and AOA localization in the presence of sensor errors[C]//IEEE International Conference on Communications. Paris, France: IEEE, 2017: 1-6. [10] HO K C, LU X, KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution[J]. IEEE Trans on Signal Processing, 2007, 55(2): 684-696. doi: 10.1109/TSP.2006.885744 [11] SUN M, HO K C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J]. IEEE Trans on Signal Processing, 2011, 59(7): 3434-3440. doi: 10.1109/TSP.2011.2131135 [12] YU H, HUANG G, GAO J, et al. An efficient constrained weighted least squares algorithm for moving source location using TDOA and FDOA measurements[J]. IEEE Trans on Wireless Communications, 2012, 11(1): 44-47. doi: 10.1109/TWC.2011.102611.110728 [13] FOY W H. Position-location solution by Taylor-series estimation[J]. IEEE Trans on Aerospace and Electronic Systems, 1976, 12(2): 187-194. doi: 10.1109/TAES.1976.308294 -


 ISSN
ISSN 




 下载:
下载: