留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

姓名
邮箱
手机号码
标题
留言内容
验证码

Multi-Strategy Dynamic Fruit Fly Optimization Algorithm for Continuous Optimization Problems

SHI Jian-ping,  LI Pei-shen,  LIU Guo-pin,  LIU Peng

downloadPDF
文章导航 > 电子科技大学学报  > 2020 >  49(5): 718-731
石建平, 李培生, 刘国平, 刘鹏. 求解连续优化问题的多策略动态果蝇优化算法[J]. 电子科技大学学报, 2020, 49(5): 718-731. doi: 10.12178/1001-0548.2019088
引用本文: 石建平, 李培生, 刘国平, 刘鹏. 求解连续优化问题的多策略动态果蝇优化算法[J]. 电子科技大学学报, 2020, 49(5): 718-731. doi: 10.12178/1001-0548.2019088
shu
SHI Jian-ping, LI Pei-shen, LIU Guo-pin, LIU Peng. Multi-Strategy Dynamic Fruit Fly Optimization Algorithm for Continuous Optimization Problems[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(5): 718-731. doi: 10.12178/1001-0548.2019088
Citation: SHI Jian-ping, LI Pei-shen, LIU Guo-pin, LIU Peng. Multi-Strategy Dynamic Fruit Fly Optimization Algorithm for Continuous Optimization Problems[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(5): 718-731. doi: 10.12178/1001-0548.2019088
shu

求解连续优化问题的多策略动态果蝇优化算法

doi: 10.12178/1001-0548.2019088
  • 1.

    南昌大学机电工程学院　南昌　330031

  • 2.

    贵阳学院电子与通信工程学院　贵阳　550005

  • 3.

    河北地质大学宝石与材料工艺学院　石家庄　050031

详细信息

  • 中图分类号: TP301.6

Multi-Strategy Dynamic Fruit Fly Optimization Algorithm for Continuous Optimization Problems

  • 1.

    School of Mechanical & Electrical Engineering, Nanchang University　Nanchang　330031

  • 2.

    School of Electronic & Communication Engineering, Guiyang University　Guiyang　550005

  • 3.

    School of Gems and Materials Technology, Hebei GEO University　Shijiazhuang　050031

Funds: National Natural Science Foundation of China (51566012); Joint Foundation of Guizhou Province (LH [2015]7302)
More Information
    Author Bio:

    SHI Jian-ping was born in 1981, male, PhD, associate professor, his research interests include intelligent optimization algorithm

    Corresponding author: LI Pei-shen, E-mail: lps20150331@163.com

  • 摘要: 果蝇优化算法(FOA)是一种新的全局优化算法，其灵感源于果蝇的嗅觉和视觉觅食行为，该算法具有很强的连续优化问题的解决能力。然而，FOA存在算法候选解不能取负值、种群多样性差、局部搜索能力弱等缺点。为了克服上述不足，该文提出了一种基于多策略进化和动态更新种群最优信息的改进果蝇优化算法(MDFOA)。算法引入了一种有效的多策略候选解生成方法和一个新的控制参数，较好的平衡了算法的全局搜索和局部搜索能力。此外，还设计了全局最优信息的实时更新机制，提高了算法的收敛速度，采用29个复杂的基准测试函数来检验该算法的有效性。实验结果表明，该算法的优化性能优于FOA、6种改进的FOA及另外两种智能优化算法。
    Abstract: Fruit fly optimization algorithm (FOA) is a new global optimization algorithm inspired by the osphresis and vision behaviors of the fruit flies, which has been shown to have a strong capacity for solving continuous optimization problems. However, the candidate solutions of FOA could not take values those are negative, and the basic FOA is also faced with the challenges of poor diversity of the swarm and weak local search ability. To overcome these limitations synthetically, this study presents an improved FOA based on multi-strategy evolution and dynamic updating of swarm optimal information (MDFOA), aiming at well balancing the global search and local search abilities. In the proposed MDFOA, an effective candidate solution generating method and a new control parameter are introduced to improve the convergence performance. Moreover, a real-time update mechanism of the global optimal information is designed to further improve the convergence speed of the algorithm. 29 complex continuous benchmark functions are used to test the effectiveness of the proposed method. Numerical results show that the proposed MDFOA is superior to several other algorithms, such as the basic FOA, six variants of FOA, and two state-of-the-art intelligent optimization algorithms.

  • Figure  1.  Average convergence curves on some 30-dimensional functions

    下载: 全尺寸图片 幻灯片

    Figure  2.  Average convergence curves on some 60-dimensional functions

    下载: 全尺寸图片 幻灯片

    Figure  3.  Average convergence curves on some high-dimensional functions

    下载: 全尺寸图片 幻灯片

    Table  1.   Comparison with other algorithms on 30-dimensional functions

    FUN* PAR** FOA LGMS-FOA AE-LGMS-FOA MFOA IFFO SFOA IFOA PSO DE MDFOA
    F1 Mean 2.654 91×10−2 2.041 98×10−5 1.324 37×10−5 4.102 41×10−1 3.610 37×10−11 2.581 60×10−3 7.871 24×10−3 2.400 35×10−1 6.811 56×10−5 0
    Std. 3.550 92×10−4 5.081 24×10−6 1.878 10×10−5 1.898 06×10−1 1.357 91×10−11 9.434 37×10−6 1.120 16×10−4 8.512 01×10−2 3.130 28×10−5 0
    F2 Mean 1.055 87 6.670 69×10−1 6.670 30×10−1 1.307 85 1.926 01 9.816 44×10−1 8.585 17×10−1 5.467 75 1.082 54 8.791 79×10−2
    Std. 2.224 28×10−1 6.147 25×10−4 3.629 64×10−4 4.773 88×10−1 1.314 89 3.292 52×10−3 7.326 63×10−2 2.471 65 2.358 78×10−1 2.803 54×10−2
    F3 Mean −9.990 37×10−1 −1.000 00 −1.000 00 −9.857 76×10−1 −1.000 00 −9.999 12×10−1 −9.997 14×10−1 −9.994 74×10−1 −1.00000 −1
    Std. 1.684 04×10−5 1.530 34×10−16 1.716 12×10−15 4.136 78×10−3 3.253 46×10−13 2.311 06×10−7 3.372 79×10−6 2.104 87×10−4 5.993 22×10−8 0
    F4 Mean 4.984 86×10 3.894 99×103 4.000 10×103 4.803 63×102 3.509 88×104 8.390 06 4.449 66×10 6.862 43×103 2.124 92×10 0
    Std. 8.449 54×10−1 2.483 79×103 3.183 33×103 1.969 34×102 2.893 41×104 4.017 54×10−1 1.21355 3.130 06×104 8.929 25 0
    F5 Mean 2.772 91×10−2 9.358 51×10−2 2.877 09×10−2 3.626 63×10−2 1.025 32×10−1 2.064 39×10−3 2.450 96×10−5 3.514 76×10−2 1.507 72×10−1 1.108 24×10−4
    Std. 3.966 91×10−3 3.501 61×10−2 1.381 61×10−2 1.710 53×10−2 4.397 10×10−2 2.936 93×10−4 1.890 84×10−5 5.612 26×10−3 3.118 76×10−2 1.269 48×10−4
    F6 Mean 2.899 37×10 2.812 60×10 2.829 60×10 3.085 33×10 2.678 31×102 2.873 03×10 2.832 83×10 3.526 96×102 2.349 55×102 0
    Std. 1.047 93×10 4.748 08×10−1 3.352 01×10−1 7.376 63×10−1 5.276 92×102 3.387 44×10−2 2.135 70×10−1 1.763 42×102 2.296 57×102 0
    F7 Mean 5.530 27×10−1 1.576 23 3.482 54×10−1 2.058 93×10−1 1.239 53×104 7.063 14×10−5 1.660 15×10−1 6.181 79×102 3.134 29×104 0
    Std. 1.097 98×10−2 1.584 46 3.319 02×10−1 1.028 48×10−1 4.383 64×103 1.307 40×10−5 1.967 17×10−3 1.953 47×102 8.085 59×103 0
    F8 Mean 3.219 55×10−2 9.028 51×10−2 1.658 90×10−1 7.931 00×10−2 1.846 25×10 2.267 00×10−3 1.730 55×10−3 4.404 56 6.766 26 0
    Std. 4.239 52×10−3 4.011 35×10−2 3.418 84×10−2 1.143 54×10−2 7.605 24 3.517 88×10−5 7.246 46×10−5 5.282 62×10−1 4.440 89×10−15 0
    F9 Mean 7.492 10×10−1 1.098 82×10−2 1.663 30×10−3 7.492 10×10−1 6.861 83×10−6 7.137 58×10−2 1.305 76×10−1 8.996 87×10−1 2.197 13×10−2 0
    Std. 2.501 46×10−3 1.209 39×10−2 3.022 21×10−3 1.323 44×10−1 9.776 98×10−7 1.294 22×10−4 8.151 27×10−4 1.424 08×10−1 5.625 55×10−3 0
    F10 Mean 1.926 99×10−3 1.025 40×10−17 1.861 35×10−11 2.902 97×10−2 6.245 67×10−12 1.302 18×10−4 5.724 17×10−4 1.151 13×10 4.249 09×10−3 0
    Std. 4.166 31×10−5 2.095 22×10−18 1.758 86×10−11 8.543 35×10−3 2.574 07×10−12 3.003 52×10−6 8.368 76×10−6 4.260 17 1.484 47×10−3 0
    F11 Mean 6.666 67×10−2 0 0 0 0 0 0 1.410 00×10 0 0
    Std. 2.494 44×10−1 0 0 0 0 0 0 5.088 22×10 0 0
    F12 Mean 4.004 91×10−6 2.113 60×10−8 1.054 94×10−8 2.334 20×10−5 1.643 22×10−13 2.564 74×10−6 1.078 08×10−6 4.573 30×10−15 2.620 34×10−16 0
    Std. 1.163 77×10−7 3.413 93×10−8 1.620 98×10−8 2.776 45×10−5 4.084 76×10−13 1.442 21×10−8 1.877 82×10−8 1.078 50×10−14 4.216 74×10−16 0
    F13 Mean 2.704 89×10−2 3.358 10×10−4 6.628 20×10−4 3.922 97×10−1 5.133 96×10−11 2.552 92×10−3 8.043 28×10−3 1.329 84 5.167 88×10−4 0
    Std. 6.358 33×10−4 5.096 28×10−4 1.233 19×10−3 1.048 78×10−1 1.851 94×10−11 9.986 68×10−6 1.240 80×10−4 6.507 06×10−1 2.066 19×10−4 0
    F14 Mean −4.499 98×102 −4.500 00×102 −4.500 00×102 −4.499 71×102 −4.500 00×102 −4.500 00×102 −4.499 99×102 −4.384 71×102 −4.499 96×102 −450
    Std. 3.833 95×10−5 7.696 64×10−14 1.252 34×10−11 1.002 04×10−2 1.721 21×10−12 2.426 35×10−6 8.649 19×10−6 4.034 65 1.272 64×10−3 0
    F15 Mean −4.494 49×102 −4.487 77×102 −4.492 05×102 −4.497 95×102 1.093 15×104 −4.500 00×102 −4.498 34×102 1.394 04×102 4.964 17×104 −450
    Std. 9.923 08×10−3 1.971 83 1.506 04 9.182 83×10−2 3.608 17×103 1.859 08×10−5 2.400 25×10−3 1.758 61×102 9.514 77×103 0
    F16 Mean 3.558 46×10−2 7.435 78×1010 8.409 12×10−7 1.715 34×10−1 1.539 58×10−6 9.473 78×10−3 1.852 58×10−2 1.829 05 1.936 80×10−2 8.881 78×10−16
    Std. 3.999 38×10−4 8.738 05×10−11 4.461 98×10−7 3.960 04×10−2 2.815 81×10−7 4.110 99×10−5 1.373 32×10−4 4.526 29×10−1 3.154 29×10−3 0
    F17 Mean 2.122 33×10−3 1.184 89×10−19 1.055 98×10−13 3.207 58×10−2 8.989 09×10−6 1.870 46×10−4 6.321 09×10−4 2.096 03×10−1 2.091 90 0
    Std. 4.239 32×10−5 2.228 42×10−20 1.191 64×10−13 1.284 36×10−2 3.660 72×10−6 6.420 60×10−7 7.743 16×10−6 8.953 58×10−2 2.073 22 0
    F18 Mean 1.529 48×10 1.721 17×10 1.458 87×10 1.016 53×10 4.355 33×10 5.656 14 1.664 12 4.279 37×10 2.721 49×10 0
    Std. 1.009 66 2.695 98 2.811 01 9.574 89×10−1 2.353 51×10 7.199 90×10−1 2.424 83×10−2 5.089 76 3.360 34 0
    F19 Mean 7.432 97×10−2 7.586 52×10−17 2.400 65×10−11 5.170 78×10−2 4.617 33 2.594 14×10−4 1.146 10×10−3 9.668 09 1.219 98×10 0
    Std. 1.182 12×10−1 1.573 25×10−16 2.851 05×10−11 1.517 25×10−2 1.057 06 6.023 38×10−6 1.648 03×10−5 6.900 02×10−1 2.100 12×10−1 0
    F20 Mean 1.710 92 4.780 38×10−2 6.911 40×10−3 4.469 23×10−3 6.022 69×10−14 1.557 39 1.688 02 5.602 23×10−2 9.140 49×10−3 0
    Std. 3.731 78×10−2 8.697 80×10−2 2.586 01×10−2 1.679 26×10−3 3.689 89×10−14 2.158 01×10−2 1.136 68×10−4 3.974 16×10−2 7.843 11×10−3 0
    F21 Mean 9.928 65×10−5 4.271 25×10−3 3.040 00×10−3 1.485 75×10−3 2.470 93×10−2 2.929 70×10−6 2.960 96×10−5 1.095 31 4.316 43×10−2 0
    Std. 1.820 64×10−6 5.686 99×10−3 6.019 96×10−3 5.010 67×10−4 2.238 19×10−2 3.109 89×10−7 5.233 10×10−7 4.570 23×10−2 6.753 52×10−2 0
    F22 Mean −2.841 88×10 −2.900 00×10 −2.900 00×10 −2.841 88×10 −2.102 67×10 −2.899 78×10 −2.898 89×10 −1.832 46×10 −7.860 84 −29
    Std. 1.850 64 6.678 09×10−15 2.733 39×10−11 3.566 31×10−1 1.706 06 5.770 50×10−5 1.470 70×10−4 1.155 69 5.554 64×10−1 0
    F23 Mean 4.990 09 −6.318 77×102 −7.347 31×102 −4.361 41×102 1.914 46×104 2.989 93×10 1.148 48×10 4.723 30×103 8.654 97×104 −4.922 99×103
    Std. 3.259 43 7.624 73×10 8.727 69×10 2.339 31×10 1.385 17×104 2.052 26×10−2 2.159 12 3.200 87×103 3.658 90×104 6.301 71
    F24 Mean 2.234 19 5.942 91 5.818 03 7.979 67×10−2 2.673 34 1.504 58×10−2 9.747 19×10−5 5.216 97 5.816 07 1.384 15×10−14
    Std. 8.152 19×10−1 2.778 01×10−1 1.669 68×10−1 6.409 98×10−2 4.467 16×10−1 8.099 43×10−2 3.647 13×10−6 2.422 29×10−1 8.428 15×10−2 7.425 11×10−14
    F25 Mean 1.328 27×10 6.927 79×10−15 7.903 25×10−12 8.625 40 7.661 18 3.432 01×10−2 1.130 56×10−1 4.658 48×10 1.547 93×102 0
    Std. 1.532 45×10 3.846 95×10−15 8.580 86×10−12 6.858 25 3.137 41 1.041 57×10−4 2.009 60×10−3 1.383 97×10 9.403 70 0
    F26 Mean 2.241 52 6.158 04×10−15 6.478 37×10−12 6.358 95 5.833 33 3.440 58×10−2 1.139 38×10−1 4.334 66×10 1.268 37×102 0
    Std. 3.618 81 3.362 07×10−15 6.437 30×10−12 4.481 49 2.001 39 5.648 66×10−4 3.001 51×10−3 9.232 60 1.447 52×10 0
    F27 Mean 1.032 07×10−1 9.198 73×10−1 6.598 73×10−1 9.988 07×10−2 1.719 87 3.703 75×10−3 9.987 34×10−2 9.595 61×10−1 1.031 19 0
    Std. 1.795 06×10−2 1.796 29×10−1 1.254 33×10−1 7.605 82×10−6 3.208 32×10−1 6.500 75×10−5 1.230 66×10−8 1.107 18×10−1 8.918 04×10−2 0
    F28 Mean 3.804 73×10 1.054 23 4.950 60×10−1 1.972 56×10 4.085 76×10−1 4.551 62×10 3.562 42 3.294 62 2.469 66×10 4.263 26×10−14
    Std. 1.898 20 3.155 78×10−1 2.042 02×10−1 2.800 02 6.633 84×10−1 1.597 30 8.810 73×10−2 8.555 10×10−1 2.724 82 0
    F29 Mean 7.066 57×102 6.050 03×102 5.837 67×102 4.692 89×102 1.072 16×102 4.166 18×102 4.153 27×102 1.003 79×106 1.205 26×104 0
    Std. 3.537 12×10 6.860 47×10 5.681 38×10 7.557 70×10 6.957 96×10 1.027 39×10 2.966 08×10−2 9.593 76×105 1.406 34×104 0
    　　* is for functions; ** is for parametric
    下载: 导出CSV

    Table  2.   Comparison with other algorithms on 60-dimensional functions

    FUN* PAR** FOA LGMS-FOA AE-LGMS-FOA MFOA IFFO SFOA IFOA PSO DE MDFOA
    F1 Mean 2.032 34×10−1 4.723 39×10−3 1.759 10×10−3 2.747 05 1.944 46×10 1.116 20×10−2 6.122 21×10−2 2.192 39×10 1.856 62×10 0
    Std. 3.808 53×10−3 2.424 00×10−3 8.994 76×10−4 5.041 69×10−1 2.212 21×10 2.372 33×10−5 7.609 33×10−4 4.280 44 4.029 84 0
    F2 Mean 2.077 32 7.853 24×10−1 7.498 69×10−1 3.841 57 9.030 56×102 1.000 97 8.446 87×10−1 2.333 47×102 7.130 63×103 1.131 94×10−1
    Std. 8.033 99×10−1 5.061 00×10−2 2.443 84×10−2 6.012 81×10−1 1.290 03×103 2.827 07×10−3 8.925 15×10−2 8.305 94×10 2.007 67×103 6.477 52×10−2
    F3 Mean −9.962 88×10−1 −1.000 00 −1.000 00 −9.498 43×10−1 −1.000 00 −9.998 09×10−1 −9.988 76×10−1 −9.851 90×10−1 −9.837 26×10−1 −1
    Std. 6.508 06×10−5 4.720 03×10−8 6.396 99×10−10 1.068 67×10−2 1.262 42×10−11 3.407 99×10−7 1.351 89×10−5 2.554 46×10−3 3.304 03×10−3 0
    F4 Mean 1.774 84×102 1.388 39×104 7.985 99×103 2.262 75×103 7.992 24×106 1.749 69×10 1.590 45×102 3.396 37×105 1.731 10×106 0
    Std. 2.681 01 8.368 48×103 4.079 95×103 8.473 96×102 3.937 53×106 5.482 24×10−1 3.392 98 3.942 34×105 4.821 07×105 0
    F5 Mean 7.719 70×10−2 2.693 44×10−1 9.139 36×10−2 1.072 93×10−1 8.906 98×10−1 2.074 06×10−3 2.801 41×10−5 1.177 58×10−1 7.924 44×10−1 1.311 06×10−4
    Std. 1.004 96×10−2 7.601 88×10−2 5.040 13×10−2 4.155 52×10−2 2.915 67×10−1 4.804 90×10−4 2.746 35×10−5 2.052 97×10−2 1.483 24×10−1 1.108 38×10−4
    F6 Mean 6.072 93×10−1 5.808 55×10 5.813 86×10 6.787 49×10 1.203 68×105 5.848 49×10 5.798 18×10 1.390 77×104 7.781 39×105 0
    Std. 2.657 87 4.263 81×10−1 3.178 53×10−1 2.328 08 1.259 52×105 4.916 70×10−2 2.241 68×10−1 4.413 45×103 2.808 27×105 0
    F7 Mean 8.208 58 2.302 33×10 1.097 07×10 1.241 99 6.575 32×104 2.663 81×10−4 2.495 70 9.693 97×103 2.935 33×105 0
    Std. 1.586 55×10−1 2.752 09×10 1.106 64×10 9.063 90×10−1 1.272 55×104 1.259 43×10−4 4.026 86×10−2 2.523 51×103 4.212 24×104 0
    F8 Mean 7.700 65×10−2 2.925 18×10−1 3.354 07×10−1 1.104 88×10−1 5.856 78×10 2.362 07×10−2 1.541 76×10−3 1.156 03×10 1.907 67×10 0
    Std. 1.033 12×10−2 3.042 21×10−2 3.565 00×10−2 1.526 45×10−2 5.340 20 2.389 64×10−5 6.006 50×10−5 1.125 88 7.105 43×10−15 0
    F9 Mean 6.588 54×10−1 2.123 29×10−1 6.005 55×10−2 2.002 57 5.694 88 1.489 80×10−1 3.649 34×10−1 8.427 86 4.255 15×10 0
    Std. 6.185 54×10−3 6.329 88×10−2 3.821 81×10−2 1.953 68×10−1 6.722 16 1.751 92×10−4 2.188 42×10−3 1.082 61 1.576 22×10 0
    F10 Mean 7.455 67×10−3 1.768 46×10−4 1.765 27×10−5 1.086 56×10−1 1.240 33×103 2.813 39×10−4 2.251 74×10−3 2.967 98×102 3.144 57×102 0
    Std. 1.415 21×10−4 2.528 11×10−4 1.277 68×10−5 1.903 35×10−2 8.659 78×102 3.796 54×10−6 2.713 63×10−5 6.279 39×10 5.895 67×10 0
    F11 Mean 3.333 33×10−2 0 0 0 1.448 07×103 0 0 3.053 67×102 3.162 33×102 0
    Std. 1.795 05×10−1 0 0 0 1.022 01×103 0 0 6.367 91×10 5.779 20×10 0
    F12 Mean 4.059 77×10−6 1.533 68×10−8 1.298 43×10−8 2.294 69×10−5 5.229 28×10−13 2.561 84×10−6 1.122 20×10−6 1.710 89×10−13 1.527 03×10−2 0
    Std. 1.314 60×10−7 2.352 55×10−8 2.689 12×10−8 3.580 26×10−5 8.709 00×10−13 1.717 23×10−8 7.066 42×10−8 2.961 39×10−13 4.616 90×10−2 0
    F13 Mean 2.044 34×10−1 1.992 20×10−2 9.146 90×10−3 2.768 07 1.244 17×102 1.098 70×10−2 6.140 42×10−2 8.499 14×10 8.127 80×10 0
    Std. 3.592 55×10−3 1.253 57×10−2 5.517 95×10−3 5.683 49×10−1 7.711 15×10 2.977 78×10−5 8.726 19×10−4 1.937 99×10 1.771 44×10 0
    F14 Mean −4.499 93×102 −4.499 99×102 −4.500 00×102 −4.499 03×102 1.078 35×103 −4.500 00×102 −4.499 98×102 −1.333 49×102 −1.055 29×102 −450
    Std. 1.251 37×10−4 6.418 47×10−4 1.183 33×10−5 2.001 44×10−2 9.562 91×102 5.017 55×10−6 3.209 91×10−5 5.646 64×10 6.530 85×10 0
    F15 Mean −4.418 35×102 −4.272 13×102 −4.366 35×102 −4.488 77×102 6.647 77×104 −4.500 00×102 −4.475 06×102 8.600 60×103 2.958 22×105 −450
    Std. 1.316 36×10−1 2.863 23×10 1.582 78×10 3.767 07×10−1 1.074 04×104 1.021 11×10−4 3.527 37×10−2 2.269 27×103 3.715 73×104 0
    F16 Mean 5.079 46×10−2 2.500 37×10−3 7.173 44×10−4 2.591 56×10−1 5.813 44 9.881 17×10−3 2.655 14×10−2 4.384 56 4.967 09 8.881 78×10−16
    Std. 5.999 59×10−4 1.996 14×10−3 2.295 39×10−4 3.950 88×10−2 2.826 31 3.830 14×10−5 2.025 18×10−4 2.536 87×10−1 2.713 66×10−1 0
    F17 Mean 9.813 47×10−2 3.548 59×10−6 2.393 37×10−7 5.949 83×10−2 1.809 90×10−3 4.066 97×10−4 2.490 85×10−3 5.430 13 5.131 37×10 0
    Std. 2.714 64×10−1 5.947 76×10−6 1.857 89×10−7 2.439 58×10−2 2.841 31×10−3 9.761 84×10−7 4.092 81×10−5 1.414 45 4.223 80 0
    F18 Mean 3.221 46×10 3.852 05×10 3.468 89×10 2.175 68×10 2.836 05×102 1.099 73×10 3.909 86 1.750 74×102 2.990 67×102 0
    Std. 1.674 12 3.116 64 3.994 06 1.622 61 2.692 19×10 1.671 09 1.849 99×10−1 1.942 14×10 1.656 79×10 0
    F19 Mean 3.086 87×10−1 3.705 07×10−4 4.729 22×10−5 2.203 13×10−1 1.713 54×10 5.591 80×10−4 4.487 93×10−3 2.347 29×10 2.714 48×10 0
    Std. 4.612 59×10−1 3.630 33×10−4 4.626 38×10−5 3.527 79×10−2 1.013 33 1.002 52×10−5 7.014 91×10−5 1.064 31 2.152 44×10−1 0
    F20 Mean 1.469 30 1.066 87×10−1 2.227 22×10−4 8.887 61×10−3 1.436 33×10 1.339 92 1.448 69 2.763 18 5.247 73×105 0
    Std. 4.387 05×10−4 5.720 45×10−2 4.975 31×10−4 1.745 68×10−3 1.004 84×10 7.734 09×10−3 1.450 98×10−4 8.313 99×10−1 5.046 76×105 0
    F21 Mean 2.093 40×10−4 8.116 12×10−2 1.493 35×10−2 2.912 92×10−3 3.396 21×10 3.443 86×10−6 6.335 42×10−5 3.739 77 3.849 90 0
    Std. 4.279 14×10−6 4.125 07×10−2 7.380 88×10−3 7.351 80×10−4 1.458 63×10 4.195 28×10−7 9.245 16×10−7 4.379 75×10−1 6.081 39×10−1 0
    F22 Mean −5.222 17×10 −5.899 99×10 −5.900 00×10 −5.713 38×10 −3.114 33×10 −5.899 49×10 −5.895 59×10 −3.326 66×10 −8.961 09 −59
    Std. 6.392 02 8.694 19×10−5 1.582 49×10−6 7.743 99×10−1 2.644 81 1.029 75×10−4 8.153 19×10−4 2.733 93 6.860 83×10−1 0
    F23 Mean 2.137 22×10 −6.939 75×102 −7.803 90×102 −7.374 65×102 7.235 13×106 5.995 22×10 3.049 83×10 6.324 05×105 3.383 72×107 −3.484 64×104
    Std. 4.850 19 3.631 43×102 2.687 89×102 4.120 47×10 2.451 36×106 9.290 76×10−3 2.444 14 1.277 45×105 7.578 94×106 1.181 81×103
    F24 Mean 9.291 36 1.303 87×10 1.293 54×10 2.829 25×10 7.780 55 1.826 87×10−2 7.394 35×10−4 1.233 58×10 1.303 55×10 6.948 02×10−18
    Std. 2.239 11 3.282 71×10−1 3.663 42×10−1 1.391 79×10−1 6.854 58×10−1 6.845 72×10−2 4.938 15×10−5 2.554 25×10−1 1.130 98×10−1 3.739 49×10−17
    F25 Mean 7.082 010×10 1.955 54×10−4 8.255 59×10−6 2.465 99×10 1.144 53×102 7.462 94×10−2 4.356 71×10−1 1.666 98×102 4.924 83×102 0
    Std. 4.927 44×10 2.554 75×10−4 4.499 40×10−6 9.116 73 2.114 60×10 1.586 75×10−4 9.308 18×10−3 2.939 72×10 1.820 84×10 0
    F26 Mean 3.667 74×10 1.496 42×10−4 8.835 24×10−6 2.481 13×10 9.010 00×10 7.460 46×10−2 4.451 01×10−1 1.303 63×102 4.627 48×102 0
    Std. 5.574 01×10 2.602 87×10−4 5.364 21×10−6 8.851 01 1.705 94×10 1.678 25×10−4 2.981 61×10−2 2.372 50×10 1.895 75×10 0
    F27 Mean 1.865 40×10−1 1.026 54 9.598 73×10−1 9.989 02×10−2 1.420 99×10 6.241 88×10−2 9.987 33×10−2 2.817 32 5.822 70 0
    Std. 3.399 35×10−2 4.493 95×10−1 4.579 67×10−1 3.129 82×10−5 1.553 14 2.806 12×10−1 6.169 16×10−9 2.078 65×10−1 3.856 29×10−1 0
    F28 Mean 7.676 34×10 3.078 95 2.020 90 4.190 64×10 1.052 73×10 9.708 75×10 7.775 32 1.715 21×10 7.605 32×10 1.421 09×10−13
    Std. 2.922 57 3.716 20×10−1 3.570 58×10−1 2.972 62 2.947 27 2.996 63 9.914 09×10−2 1.982 57 2.079 59 0
    F29 Mean 3.070 80×103 2.773 58×103 2.659 67×103 2.230 40×103 6.001 25×1013 1.660 32×103 1.665 77×103 1.319 56×1010 1.103 47×1016 0
    Std. 1.319 50×102 1.750 67×102 1.487 93×102 1.518 05×102 8.120 58×1013 1.664 96×10 4.163 24×10−1 6.880 91×109 8.076 19×1015 0
    下载: 导出CSV

    Table  3.   High-dimensional benchmark functions optimization results of MDFOA

    FUN* PAR** n=100 n=200 n=300 n=400
    F1 Mean 0 0 0 0
    Std. 0 0 0 0
    F2 Mean 1.707 04×10−1 1.900 13×10−1 2.270 63×10−1 2.137 6×10−1
    Std. 3.619 35×10−2 6.831 70×10−2 1.236 30×10−1 1.250 05×10−1
    F3 Mean −1 −1 −1 −1
    Std. 0 0 0 0
    F4 Mean 0 0 0 0
    Std. 0 0 0 0
    F5 Mean 1.209 81×10−4 1.108 13×10−4 1.060 77×10−4 1.456 90×10−4
    Std. 1.059 54×10−4 9.601 13×10−5 1.053 27×10−4 1.570 89×10−4
    F6 Mean 0 0 0 0
    Std. 0 0 0 0
    F7 Mean 0 0 0 0
    Std. 0 0 0 0
    F8 Mean 0 0 0 0
    Std. 0 0 0 0
    F9 Mean 0 0 0 0
    Std. 0 0 0 0
    F10 Mean 0 0 0 0
    Std. 0 0 0 0
    F11 Mean 0 0 0 0
    Std. 0 0 0 0
    F12 Mean 0 0 0 0
    Std. 0 0 0 0
    F13 Mean 0 0 0 0
    Std. 0 0 0 0
    F14 Mean −450 −450 −450 −450
    Std. 0 0 0 0
    F15 Mean −450 −450 −450 −450
    Std. 0 0 0 0
    F16 Mean 8.881 78×10−16 8.881 78×10−16 8.881 78×10−16 8.881 78×10−16
    Std. 0 0 0 0
    F17 Mean 0 0 0 0
    Std. 0 0 0 0
    F18 Mean 0 0 0 0
    Std. 0 0 0 0
    F19 Mean 0 0 0 0
    Std. 0 0 0 0
    F20 Mean 0 0 0 0
    Std. 0 0 0 0
    F21 Mean 0 0 0 0
    Std. 0 0 0 0
    F22 Mean −99 −199 −299 −399
    Std. 0 0 0 0
    F23 Mean −1.167 73×105 −4.845 14×105 −1.033 58×106 −1.741 83×106
    Std. 1.002 56×104 5.355 32×104 1.497 21×105 2.543 10×105
    F24 Mean 9.805 84×10−16 6.404 25×10−15 5.685 00×10−15 2.500 11×10−15
    Std. 4.352 40×10−15 2.492 30×10−14 1.472 99×10−14 7.664 45×10−15
    F25 Mean 0 0 0 0
    Std. 0 0 0 0
    F26 Mean 0 0 0 0
    Std. 0 0 0 0
    F27 Mean 0 0 0 0
    Std. 0 0 0 0
    F28 Mean 2.842 17×10−13 6.252 78×10−13 9.094 95×10−13 1.250 56×10−12
    Std. 0 0 0 0
    F29 Mean 0 0 0 0
    Std. 0 0 0 0
    下载: 导出CSV
  • [1] DE MAGALHÃES C S, ALMEIDA D M, BARBOSA H J C, et al. A dynamic niching genetic algorithm strategy for docking highly flexible ligands[J]. Information Sciences, 2014, 289: 206-224. doi:  10.1016/j.ins.2014.08.002
    [2] WANG L, GENG H, LIU P, et al. Particle swarm optimization based dictionary learning for remote sensing big data[J]. Knowledge-Based Systems, 2015, 79: 43-50. doi:  10.1016/j.knosys.2014.10.004
    [3] LIAO T, SOCHA K, DE OCA M A M, et al. Ant colony optimization for mixed-variable optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 503-518. doi:  10.1109/TEVC.2013.2281531
    [4] TANG L, ZHAO Y, LIU J. An improved differential evolution algorithm for practical dynamic scheduling in steelmaking-continuous casting production[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(2): 209-225. doi:  10.1109/TEVC.2013.2250977
    [5] KIRAN M S, HAKLI H, GUNDUZ M, et al. Artificial bee colony algorithm with variable search strategy for continuous optimization[J]. Information Sciences, 2015, 300: 140-157. doi:  10.1016/j.ins.2014.12.043
    [6] PAN W T. A new fruit fly optimization algorithm: Taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69-74. doi:  10.1016/j.knosys.2011.07.001
    [7] WANG L, ZHENG X, WANG S. A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem[J]. Knowledge-Based Systems, 2013, 48: 17-23. doi:  10.1016/j.knosys.2013.04.003
    [8] PAN W T. Mixed modified fruit fly optimization algorithm with general regression neural network to build oil and gold prices forecasting model[J]. Kybernetes, 2014, 43(7): 1053-1063. doi:  10.1108/K-02-2014-0024
    [9] PAN Q K, SANG H Y, DUAN J H, et al. An improved fruit fly optimization algorithm for continuous function optimization problems[J]. Knowledge-Based Systems, 2014, 62: 69-83. doi:  10.1016/j.knosys.2014.02.021
    [10] HU R, WEN S, ZENG Z, et al. A short-term power load forecasting model based on the generalized regression neural network with decreasing step fruit fly optimization algorithm[J]. Neurocomputing, 2017, 221: 24-31. doi:  10.1016/j.neucom.2016.09.027
    [11] LI H, GUO S, ZHAO H, et al. Annual electric load forecasting by a least squares support vector machine with a fruit fly optimization algorithm[J]. Energies, 2012, 5(11): 4430-4445. doi:  10.3390/en5114430
    [12] HAN J, WANG P, YANG X. Tuning of PID controller based on fruit fly optimization algorithm[C]//2012 IEEE International Conference on Mechatronics and Automation. [S.l.]: IEEE, 2012: 409-413.
    [13] LIU Y, WANG X, LI Y. A modified fruit-fly optimization algorithm aided PID controller designing[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation. [S.l.]: IEEE, 2012: 233-238.
    [14] ZHENG X L, WANG L, WANG S Y. A novel fruit fly optimization algorithm for the semiconductor final testing scheduling problem[J]. Knowledge-Based Systems, 2014, 57: 95-103. doi:  10.1016/j.knosys.2013.12.011
    [15] WANG L, SHI Y, LIU S. An improved fruit fly optimization algorithm and its application to joint replenishment problems[J]. Expert Systems with Applications, 2015, 42(9): 4310-4323. doi:  10.1016/j.eswa.2015.01.048
    [16] WANG L, LIU R, LIU S. An effective and efficient fruit fly optimization algorithm with level probability policy and its applications[J]. Knowledge-Based Systems, 2016, 97: 158-174. doi:  10.1016/j.knosys.2016.01.006
    [17] KANARACHOS S, GRIFFIN J, FITZPATRICK M E. Efficient truss optimization using the contrast-based fruit fly optimization algorithm[J]. Computers & Structures, 2017, 182: 137-148.
    [18] DU T S, KE X T, LIAO J G, et al. DSLC-FOA: Improved fruit fly optimization algorithm for application to structural engineering design optimization problems[J]. Applied Mathematical Modelling, 2018, 55: 314-339. doi:  10.1016/j.apm.2017.08.013
    [19] DARVISH A, EBRAHIMZADEH A. Improved fruit-fly optimization algorithm and its applications in antenna arrays synthesis[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(4): 1756-1766. doi:  10.1109/TAP.2018.2800695
    [20] SHEN L, CHEN H, YU Z, et al. Evolving support vector machines using fruit fly optimization for medical data classification[J]. Knowledge-Based Systems, 2016, 96: 61-75. doi:  10.1016/j.knosys.2016.01.002
    [21] WU L, LIU Q, TIAN X, et al. A new improved fruit fly optimization algorithm IAFOA and its application to solve engineering optimization problems[J]. Knowledge-Based Systems, 2018, 144: 153-173. doi:  10.1016/j.knosys.2017.12.031
    [22] PAN W T. Using modified fruit fly optimisation algorithm to perform the function test and case studies[J]. Connection Science, 2013, 25(2-3): 151-160. doi:  10.1080/09540091.2013.854735
    [23] SHAN D, CAO G H, DONG H J. LGMS-FOA: An improved fruit fly optimization algorithm for solving optimization problems[J]. Mathematical Problems in Engineering, 2013, 2013(7): 1256-1271.
    [24] YUAN X, DAI X, ZHAO J, et al. On a novel multi-swarm fruit fly optimization algorithm and its application[J]. Applied Mathematics and Computation, 2014, 233: 260-271. doi:  10.1016/j.amc.2014.02.005
    [25] MITIĆ M, VUKOVIĆ N, PETROVIĆ M, et al. Chaotic fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2015, 89: 446-458. doi:  10.1016/j.knosys.2015.08.010
    [26] NIU J, ZHONG W, LIANG Y, et al. Fruit fly optimization algorithm based on differential evolution and its application on gasification process operation optimization[J]. Knowledge-Based Systems, 2015, 88: 253-263. doi:  10.1016/j.knosys.2015.07.027
    [27] WU L, XIAO W, ZHANG L, et al. An improved fruit fly optimization algorithm based on selecting evolutionary direction intelligently[J]. International Journal of Computational Intelligence Systems, 2016, 9(1): 80-90. doi:  10.1080/18756891.2016.1144155
    [28] ZHANG Y, CUI G, WU J, et al. A novel multi-scale cooperative mutation fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2016, 114: 24-35. doi:  10.1016/j.knosys.2016.09.027
    [29] BABALIK A, İŞCAN H, BABAOĞLU İ, et al. An improvement in fruit fly optimization algorithm by using sign parameters[J]. Soft Computing, 2018, 22(22): 7587-7603. doi:  10.1007/s00500-017-2733-1
    [30] LV S X, ZENG Y R, WANG L. An effective fruit fly optimization algorithm with hybrid information exchange and its applications[J]. International Journal of Machine Learning and Cybernetics, 2018, 9(10): 1623-1648. doi:  10.1007/s13042-017-0669-5
    [31] HAN X, LIU Q, WANG H, et al. Novel fruit fly optimization algorithm with trend search and co-evolution[J]. Knowledge-Based Systems, 2018, 141: 1-17. doi:  10.1016/j.knosys.2017.11.001
    [32] WU L, ZUO C, ZHANG H. A cloud model based fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2015, 89: 603-617. doi:  10.1016/j.knosys.2015.09.006
    [33] ZHANG Y, CUI G, ZHU E, et al. AFOA: An adaptive fruit fly optimization algorithm with global optimizing ability[J]. International Journal on Artificial Intelligence Tools, 2016, 25(6): 1650032. doi:  10.1142/S0218213016500329
    [34] SHI Y, EBERHART R. A modified particle swarm optimizer[C]//1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational intelligence. [S.l.]: IEEE, 1998: 69-73.
    [35] SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation-CEC99. [S.l.]: IEEE, 1999, 3: 1945-1950.
    [36] STORN R, PRICE K. Differential evolution–A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. doi:  10.1023/A:1008202821328
  • [1] LI Peng, HU Jiang-ping, ZHANG Yu-ping.  Design and Analysis of Distributed Optimization Algorithm for Economic Dispatch Problem of Energy-Water Hybrid Networks . 电子科技大学学报, 2020, 49(5): 652-659, 665. doi: 10.12178/1001-0548.2020238
    [2] Jie-fu CHEN, Hua CHEN, Xing XU, Yan-li JI, Li-jiang CHEN.  Learning to Write Multi-Stylized Chinese Characters by Generative Adversarial Networks . 电子科技大学学报, 2019, 48(5): 674-678. doi: 10.3969/j.issn.1001-0548.2019.05.003
    [3] Fang-yuan YU.  A New Alternating Iteration Recovery Algorithm for Compressed Channel Estimation with Basis Mismatch . 电子科技大学学报, 2018, 47(4): 491-496. doi: 10.3969/j.issn.1001-0548.2018.04.003
    [4] Yan LI, Bu-ning TIAN, Feng YANG.  Optimization Algorithm of the Beam Direction Calibration for a Small Antenna Array . 电子科技大学学报, 2017, 46(5): 692-696. doi: 10.3969/j.issn.1001-0548.2017.05.009
    [5] 闫钧华, 张焕春, 经亚枝.  基于Multi-Agent的分布式测控系统任务调度算法 . 电子科技大学学报, 2006, 35(1): 62-65.
  • 加载中
WeChat 点击查看大图
图(3) / 表(3)
计量
  • 文章访问数:  4923
  • HTML全文浏览量:  1171
  • PDF下载量:  29
  • 被引次数: 0
出版历程
  • 收稿日期:  2019-04-06
  • 修回日期:  2020-05-20
  • 网络出版日期:  2020-09-29
  • 刊出日期:  2020-09-23

Multi-Strategy Dynamic Fruit Fly Optimization Algorithm for Continuous Optimization Problems

doi: 10.12178/1001-0548.2019088
  • 1. 南昌大学机电工程学院　南昌　330031
  • 2. 贵阳学院电子与通信工程学院　贵阳　550005
  • 3. 河北地质大学宝石与材料工艺学院　石家庄　050031
    • 基金项目:  National Natural Science Foundation of China (51566012); Joint Foundation of Guizhou Province (LH [2015]7302)
    作者简介:

    SHI Jian-ping was born in 1981, male, PhD, associate professor, his research interests include intelligent optimization algorithm

    通讯作者: LI Pei-shen, E-mail: lps20150331@163.com
  • 收稿日期: 2019-04-06
  • 修回日期: 2020-05-20
  • 网络出版日期: 2020-09-29
  • 刊出日期: 2020-09-23

  • 中图分类号: TP301.6

摘要: 果蝇优化算法(FOA)是一种新的全局优化算法，其灵感源于果蝇的嗅觉和视觉觅食行为，该算法具有很强的连续优化问题的解决能力。然而，FOA存在算法候选解不能取负值、种群多样性差、局部搜索能力弱等缺点。为了克服上述不足，该文提出了一种基于多策略进化和动态更新种群最优信息的改进果蝇优化算法(MDFOA)。算法引入了一种有效的多策略候选解生成方法和一个新的控制参数，较好的平衡了算法的全局搜索和局部搜索能力。此外，还设计了全局最优信息的实时更新机制，提高了算法的收敛速度，采用29个复杂的基准测试函数来检验该算法的有效性。实验结果表明，该算法的优化性能优于FOA、6种改进的FOA及另外两种智能优化算法。

English Abstract

石建平, 李培生, 刘国平, 刘鹏. 求解连续优化问题的多策略动态果蝇优化算法[J]. 电子科技大学学报, 2020, 49(5): 718-731. doi: 10.12178/1001-0548.2019088
引用本文: 石建平, 李培生, 刘国平, 刘鹏. 求解连续优化问题的多策略动态果蝇优化算法[J]. 电子科技大学学报, 2020, 49(5): 718-731. doi: 10.12178/1001-0548.2019088
shu
SHI Jian-ping, LI Pei-shen, LIU Guo-pin, LIU Peng. Multi-Strategy Dynamic Fruit Fly Optimization Algorithm for Continuous Optimization Problems[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(5): 718-731. doi: 10.12178/1001-0548.2019088
Citation: SHI Jian-ping, LI Pei-shen, LIU Guo-pin, LIU Peng. Multi-Strategy Dynamic Fruit Fly Optimization Algorithm for Continuous Optimization Problems[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(5): 718-731. doi: 10.12178/1001-0548.2019088
shu

    全文HTML

  • Optimization problems are often encountered in the fields of scientific research, engineering technology, and management decision. How to obtain the optimal solution or suboptimal solution of these problems at the minimum cost has been one of the hot topics for researchers. In recent years, swarm intelligent optimization algorithms, such as the genetic algorithm[1], the particle swarm optimization[2], the ant colony algorithm[3], the differential evolution algorithm[4], and the artificial bee colony algorithm[5] are widely used to solve the above-mentioned optimization problems. In most cases, the swarm intelligence optimization algorithm can achieve more satisfactory results than traditional optimization methods, so it has attracted more and more attention from scholars.

    Inspired by the foraging behavior of fruit flies, Ref.[6] proposed a novel swarm intelligence-based meta-heuristic algorithm, namely the fruit fly optimization algorithm (FOA). Compared with other swarm intelligence-based algorithms, FOA has a simple algorithmic framework with a few tuned parameters, which makes it easily understood and implemented. As a novel method for finding global optimum, FOA technique has been obtained much attention and widely applied in real-world problems, such as the financial distress model solving[6], the multidimensional knapsack problem[7], neural network training[8], continuous mathematical function optimization problems[9], power loads forecasting[10-11], PID controller parameters tuning[12-13], semiconductor final testing[14], joint replenishment problems[15-16], as well as many other problems in scientific and engineering fields[17-21].

    However, FOA also has its own shortcomings. Particularly, the taste concentration judgment value cannot be taken a negative value, so FOA cannot deal with the optimization problem with negative decision variables. In addition, with the iteration of algorithm, the diversity of the swarm is rapidly lost, making the algorithm easy to fall into local optimum. Furthermore, the weak local search ability of FOA leads to low convergence accuracy of the FOA algorithm. To improve the convergence performance of FOA, a series of improvement studies have been carried out by many scholars at home and abroad. Ref.[22] proposed an improved FOA by adding an escaping parameter to the taste concentration judgment value, and the fruit fly individual in this algorithm is searched in three-dimensional space. Ref.[23] used a linear generation mechanism to generate candidate solutions, instead of nonlinear generation mechanism in basic FOA, and a new improved fruit fly algorithm based on a linear mechanism was proposed. Ref.[24] presented a novel multi-swarm fruit fly optimization algorithm, and the performance of the algorithm was greatly improved by employing the multi-swarm behavior. By introducing a new control parameter and an effective solution generating method, Ref.[9] also proposed an improved fruit fly optimization algorithm for solving continuous optimization problems. Ref.[25] introduced a novel parameter integrated with chaos into the basic FOA and put forward a chaotic fruit fly algorithm. Ref.[26] modified the expression of the smell concentration judgment value in FOA, and a differential vector was introduced to replace the stochastic search mechanism. Ref.[27] proposed an improved fruit fly optimization algorithm based on selecting evolutionary direction intelligently. Ref.[28] introduced a multi-scale cooperative mutation mechanism and proposed a multi-scale cooperative mutation fruit fly optimization algorithm. Ref.[29] added two sign parameters into the original FOA for dealing with not only the positive side of the search space, but also the whole. In order to better balance the global search and local search abilities, Ref.[30] proposed an improved FOA based on the hybrid location information exchange mechanism. By embedding the trend search strategy into the original FOA and combining with the co-evolution mechanism, Ref.[31] developed a novel fruit fly optimization algorithm. Ref.[16] proposed an improved fruit fly optimization algorithm with a level probability policy and a new mutation parameter aiming at expanding search space and skipping local optima. Ref.[32] introduced a normal cloud model into fruit fly osphresis foraging and proposed a normal cloud model based FOA. According to historical memory and elite strategy mechanism, Ref.[33] proposed an adaptive fruit fly optimization algorithm.

    The afore-mentioned variants of FOA are all based on a single evolutionary strategy. However, this single evolutionary model often lacks an effective mechanism for maintaining diversity of the swarm, and it is difficult to reasonably balance the global exploration and local exploitation of the algorithm, so the optimization process is prone to fall into premature convergence. In addition, according to the foraging behavior of the actual fruit fly swarm, the visual foraging behavior of each individual fruit fly should follow its olfactory foraging behavior. In order to overcome the shortcomings mentioned above, this article presents an improved FOA based on multi-strategy evolution and dynamic updating of swarm optimal information (MDFOA). The MDFOA is applied to various standard optimization problems and compared with the original FOA, six variants of the FOA, and two state-of-the-art algorithms.

    The rest of the paper is organized as follows. In Section 1, the basic FOA is introduced. The MDFOA is described in detail in Section 2. Experimental design and comparisons are illustrated in Section 3. Finally, Section 4 gives the concluding remarks.

    • 1.   Basic FOA

    • The basic FOA is a swarm intelligence-based meta-heuristic algorithm inspired by the foraging behavior of fruit flies. The fruit fly itself is superior to other species in osphresis and vision. The osphresis organs of fruit flies can sense odors floating in the air even 40 km far away from them. During hunting for food, they use their olfactory sense and find direction to the food source. Then, after they get close to the food location, they fly toward the food source by using their visual senses. The procedure of basic FOA can be described as follows[6]:

      1) Initialize relate parameters, including population size, the maximum number of iterations, and the location of fruit fly swarm ( $X\_{\rm{axis}}$ , $Y\_{\rm{axis}}$ ).

      2) For each fly in the swarm, a random fly direction and distance are provided, and the new location is generated by using Eq. (1):

      $$\left\{ \begin{aligned} & {X_i} = X\_{\rm{axis}} + {\rm{RandomValue}} \\ & {Y_i} = Y\_{\rm{axis}} + {\rm{RandomValue}} \end{aligned} \right.$$ (1)

      where i is the ith fly in the swarm. RandomValue represents the fly range parameter.

      3) Given the unknown food source, calculate the distance between each fly and the origin by using Eq. (2). Calculate the smell concentration judgment value by using Eq. (3):

      $${\rm{Dis}}{{\rm{t}}_i} = \sqrt {{X_i}^2 + {Y_i}^2} $$ (2)
      $${S_i} = \frac{1}{{{\rm{Dis}}{{\rm{t}}_i}}}$$ (3)

      4) Substitute the smell concentration judgment value ( ${S_i}$ ) into smell concentration judgment function (or called fitness function) and the smell concentration value is calculated by using Eq. (4):

      $${\rm{Smel}}{{\rm{l}}_i} = {\rm{Fitness}}({S_i})$$ (4)

      5) Identify the best smell concentration value in the fruit fly swarm (finding the minimum value) by using Eq. (5):

      $$[{\rm{bestSmell}}\;\;{\rm{bestIndex}}] = \min ({\rm{Smel}}{{\rm{l}}_i})$$ (5)

      6) Keep the best smell concentration value and the corresponding X and Y coordinates, and at this moment, the fruit fly swarm moves toward the location by using their vision:

      $$\left\{ \begin{aligned} &{\rm{Smellbest = bestSmell}} \\ &X\_{\rm{axis}} = X({\rm{bestIndex}}) \\ &Y\_{\rm{axis}} = Y({\rm{bestIndex}}) \\ \end{aligned} \right.$$ (6)

      7) Repeat step 2)～6). Stop when the iterative number reaches the maximum iterative number.

    2.   Improved FOA

    • Due to its simple evolutionary mechanism, FOA is unable to effectively balance the global search and local search abilities of the algorithm, which makes it difficult to achieve the ideal optimization results in dealing with complex optimization problems. Inspired by other state-of-the-art swarm intelligence-based algorithms, such as particle swarm optimization algorithm (PSO)[34-35] and differential evolution algorithm (DE)[36], an improved version of FOA (MDFOA) is developed in this study. We detail the MDFOA as follows.

      • 2.1.   Multi-Strategy Evolution

    • Multi-strategy evolution refers to selecting one strategy from a strategy base as an iterative equation for the current individual olfactory search of fruit flies. Different fly individuals of the same generation may have different evolutionary strategies, so that the diversity of the swarm is improved, and the global search ability of the algorithm is also enhanced. The selection of strategies is a key factor that affects the optimization performance of algorithm. The more strategies in the strategy base, the more powerful the algorithm is in solving complex optimization problems. With fewer strategies in the strategy base, it may be difficult for the algorithm to achieve the expected convergence quality. After repeated numerical simulation experiments, the strategy base consists of the following strategies in this study:

      $$X_i^{k + 1} = {X_{\min }} + ({X_{\max }} - {X_{\min }}){r_1}$$ (7)
      $$X_i^{k + 1} = X_i^k + \omega {\rm{(}}X_{r1}^k - X_{r2}^k{\rm{)}}$$ (8)
      $$X_i^{k + 1} = P_g^k + \omega (P_{r1}^k - P_{r2}^k{\rm{)}}$$ (9)
      $$X_i^{k + 1} = P_g^k + \omega ({l_1} - 0.5)P_g^k$$ (10)
      $$x_{ij}^{k + 1} = \left\{\!\!\!\! \begin{array}{l} \left\{\!\!\!\! {\begin{array}{*{20}{l}} {p_{gj}^k + \omega ({l_2} - 0.5)}&{j = m,m + 1, \cdots ,n}\\ {x_{ij}^k}&{{\rm{others}}} \end{array}} \right.\begin{array}{*{20}{l}} {}&\!\!\!\!\!{{r_2} < 0.5} \end{array}\\ \left\{\!\!\!\! {\begin{array}{*{20}{l}} {p_{gj}^k + \omega ({l_2} - 0.5)}&{j = m}\\ {x_{ij}^k}&{{\rm{others}}} \end{array}} \right.\begin{array}{*{20}{l}} {}&{{r_2} \geqslant 0.5} \end{array} \end{array} \right.$$ (11)

      where $X_i^{k + 1} = (x_{i,1}^{k + 1},x_{i,2}^{k + 1},...,x_{i,n}^{k + 1})$ denotes the (k+1)th generation position vectors of the ith fly; n is the dimensionality of the problem; ${X_{\max }}$ and ${X_{\min }}$ are the upper and lower boundary vectors of the search space, respectively; Indices r1 and r2 are random and mutually different integers generated in the range [1, ${\rm{ps}}$ ]( ${\rm{ps}}$ presents the population size), and they are different from the position vector’s index i and g; $P_{r1}^k$ and $P_{r2}^k$ are the best historical position vectors of the r1th and r2th flies, respectively; $P_g^k = (p_{g,1}^k,p_{g,2}^k,...,p_{g,n}^k)$ is the global historical best position vector of fruit fly swarm; l1, l2, ${r_1}$ and ${r_2}$ are random variables uniformly distributed on the interval [0,1]; m is a random integer generated in the range [1, n]; $\omega $ is a scaling factor that controls the search radius.

      The five evolutionary strategies of Eq.(7)～(11) focus on the global search and local search of the algorithm, respectively. According to Eq.(7), the position vector of the ith fly is reinitialized randomly within the search space, in this way, the fly is given the ability to escape from the local optimum. In Eq.(8), the current position of the ith fly is taken as the reference vector, and the difference vector ${\rm{(}}X_{r1}^k - X_{r2}^k{\rm{)}}$ is used to randomly disturb the reference vector, this strategy makes full use of the difference information among individuals in the swarm to search in local neighborhoods. In Eq.(9), the optimal position vector of current fruit fly swarm is taken as the reference vector, and the vector $(P_{r1}^k - P_{r2}^k{\rm{)}}$ is used as the disturbance vector of the reference vector. Like Eq.(9), the optimal position vector of current fruit fly swarm is the reference vector and the vector $({l_1} - 0.5)P_g^k$ is the disturbance vector in Eq.(10). Eqs.(9) and (10) learn from the historical optimal solution in different ways to further improve the convergence accuracy of the solution and accelerate the convergence speed of the algorithm. To mine potential better solutions, we randomly choose one position variant or (n−m+1) position variants, and a new solution is generated by using Eq.(11).

      • 2.2.   A New Parameter and Dynamic Updating Mechanism

    • In the basic FOA, the search radius is fixed and cannot be changed during iterations. This leads to a low convergence speed and a tendency to fall into a local optimal solution. In the early iterations, the fruit fly swarm location is usually far from the optimal solution, so the perturbation component should be valued in a larger range to find a promising region. In the final generations, the swarm location is close to the optimal solution, and the perturbation component should be taken in a small scope to further improve the convergence accuracy of the algorithm. Therefore, the parameter $\omega $ in the above evolutionary strategies is changed dynamically with iterations as the following:

      $$\omega = \alpha \exp \left( - \beta \frac{{{\rm{Iteration}}}}{{{\rm{Iteratio}}{{\rm{n}}_{\max }}}}\right)$$ (12)

      where $\alpha $ and $\beta $ are two adjustment coefficients. For the sake of simplicity, we take the same value in this paper, that is, $\alpha = \beta $ . Iteration is the iteration number. ${\rm{Iteratio}}{{\rm{n}}_{\max }}$ is the maximum iteration number.

      In the basic FOA, the visual search of fly is based on the premise that the olfactory search of the fruit fly swarm has been completed, which lags the update of the optimal position information of the swarm, thus reducing the convergence speed of the algorithm. To solve this problem, we propose a mechanism of real-time dynamic updating in this paper, that is, after the fly completes the olfactory search, the new position is immediately evaluated. If the new position is better than the current optimal position of swarm, the optimal location and its corresponding information will be updated, so the purpose of updating swarm information in real time can be achieved.

      • 2.3.   Implement of MDFOA

    • The detailed steps of implementing the MDFOA are described as follows.

      1) Initialize relate parameters, including population size ps, the maximum number of iterations ${\rm{Iteratio}}{{\rm{n}}_{\max }}$ , and adjustment coefficients $\alpha $ and $\beta $ . The position of each fruit fly is randomly generated and evaluated, and the optimal position is selected as the current optimal position of the swarm.

      2) For the ith fly, a strategy selected from equations (7)～(11) is used as an evolutionary strategy for its olfactory search, and the value of parameter $\omega $ is calculated by using Eq.(12).

      3) According to Eq.(13) and Eq.(14), the best historical position of the fly individual and the best historical position of the fruit fly swarm are updated in real time, respectively. Here, we abandon the calculation of the distance ${\rm{Dis}}{{\rm{t}}_i}$ , and directly take the position vector ${X_i}$ as the smell concentration judgment value, i.e., ${S_i} = {X_i}$ , which solves the shortcoming that ${S_i}$ cannot take a negative value in the basic FOA:

      $$P_i^{k + 1} = \left\{ \begin{array}{l} X_i^{k + 1}\begin{array}{*{20}{c}} {}&{{\rm{Fitness}}(X_i^{k + 1}) \leqslant {\rm{Fitness}}(P_i^k)} \end{array} \\ P_i^k{\rm{ }}\begin{array}{*{20}{c}} {}&{{\rm{Fitness}}(X_i^{k + 1}) > {\rm{Fitness}}(P_i^k)} \end{array} \\ \end{array} \right.{\rm{ }}$$ (13)
      $$P_g^{k + 1} = \left\{ \begin{array}{l} X_i^{k + 1}\begin{array}{*{20}{c}} {}&{{\rm{Fitness}}(X_i^{k + 1}) \leqslant {\rm{Fitness}}(P_g^k)} \end{array} \\ P_g^k\begin{array}{*{20}{c}} {}&{{\rm{Fitness}}(X_i^{k + 1}) > {\rm{Fitness}}(P_g^k)} \end{array}{\rm{ }} \\ \end{array} \right.{\rm{ }}$$ (14)

      4) If all flies of the current generation complete the evolution operation, the next step is executed; otherwise return to step 2).

      5) If the iterative number reaches the maximum iterative number, the algorithm ends; otherwise return to step 2).

    3.   Experiments and Comparisons

    • For the purpose of verifying the performance of MDFOA, 29 well-known benchmark functions are considered in this test. For a detailed description of these benchmark functions, please refer to ref.[9]. Among these test functions, the first 15 problems are unimodal functions and the remaining 14 problems are multimodal functions. The effectiveness of the algorithm is evaluated on these benchmark functions with varying dimensions as 30, 60, 100, 200, 300, and 400. The results of the MDFOA are compared with those of the basic FOA, LGMS-FOA[23], AE-LGMS-FOA[19], MFOA[22], IFFO[9], SFOA[29], IFOA[15], PSO and DE. All the proposed algorithms are coded in MATLAB R2013a. The computation is conducted on a personal computer (PC) with Intel (R) Core(TM) i7-7700, 3.6 GHz CPU, 16 GB RAM, and Windows 10 Operational System.

      • 3.1.   Parameter Setting

    • The experimental parameters of the other nine algorithm are set according to the corresponding papers. The parameters setting of different algorithms are described below.

      In LGMS-FOA, we set ${\omega _0} = 1$ , $\alpha = 0.95$ , and $n = 0.005$ . The parameters of AE-LGMS-FOA are $p = 0.005$ , ${\omega _0} = 1$ , and $n = 10$ , and 80% of the best population are used to generate ${X_{Av}}$ . For FOA and MFOA, the random initialization fruit fly swarm location zone is [0,10], the random direction and distance of iterative fruit fly food searching is [−1,1]. The parameters of IFFO are ${\lambda _{{\rm{max}}}} = ({\rm{UB}} - {\rm{LB}})/2$ and ${\lambda _{{\rm{min}}}} = {10^{ - 5}}$ , where UB and LB are the upper and lower bounds of independent variables, respectively. In IFOA, 50% of the individuals in a swarm fly toward local optimal solution and the others fly randomly, and the perturbation amplification factor ( $\omega $ ) is 0.3. For PSO, ${\omega _{{\rm{max}}}} = 0.9$ , ${\omega _{{\rm{min}}}} = 0.4$ , ${c_1} = {c_2} = 2$ , and ${v_{{\rm{max}}}}$ is set to be 20% of ${x_{{\rm{max}}}}$ . The mutation operator of DE is best/1, and the differentiation factor(F) and crossover probability (Cr) are 0.5, 0.5, respectively. The parameters of MDFOA are $\alpha = \beta = 6$ . The population size of each algorithm is set to 50, and the number of iterations is set to 500 times.

      • 3.2.   Comparison of MDFOA with Other Algorithms

    • In this section, we present the optimization results of different algorithms.

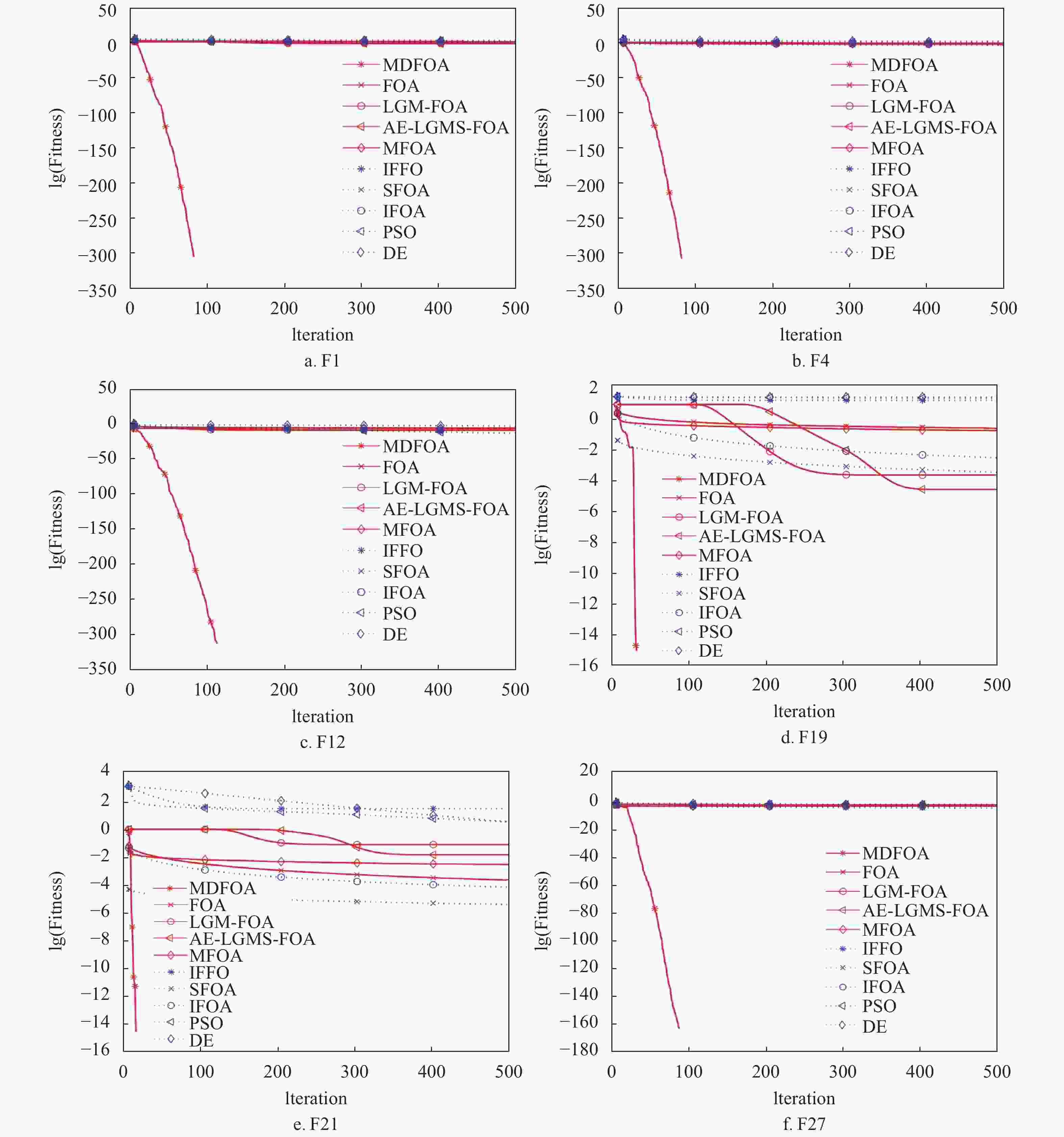
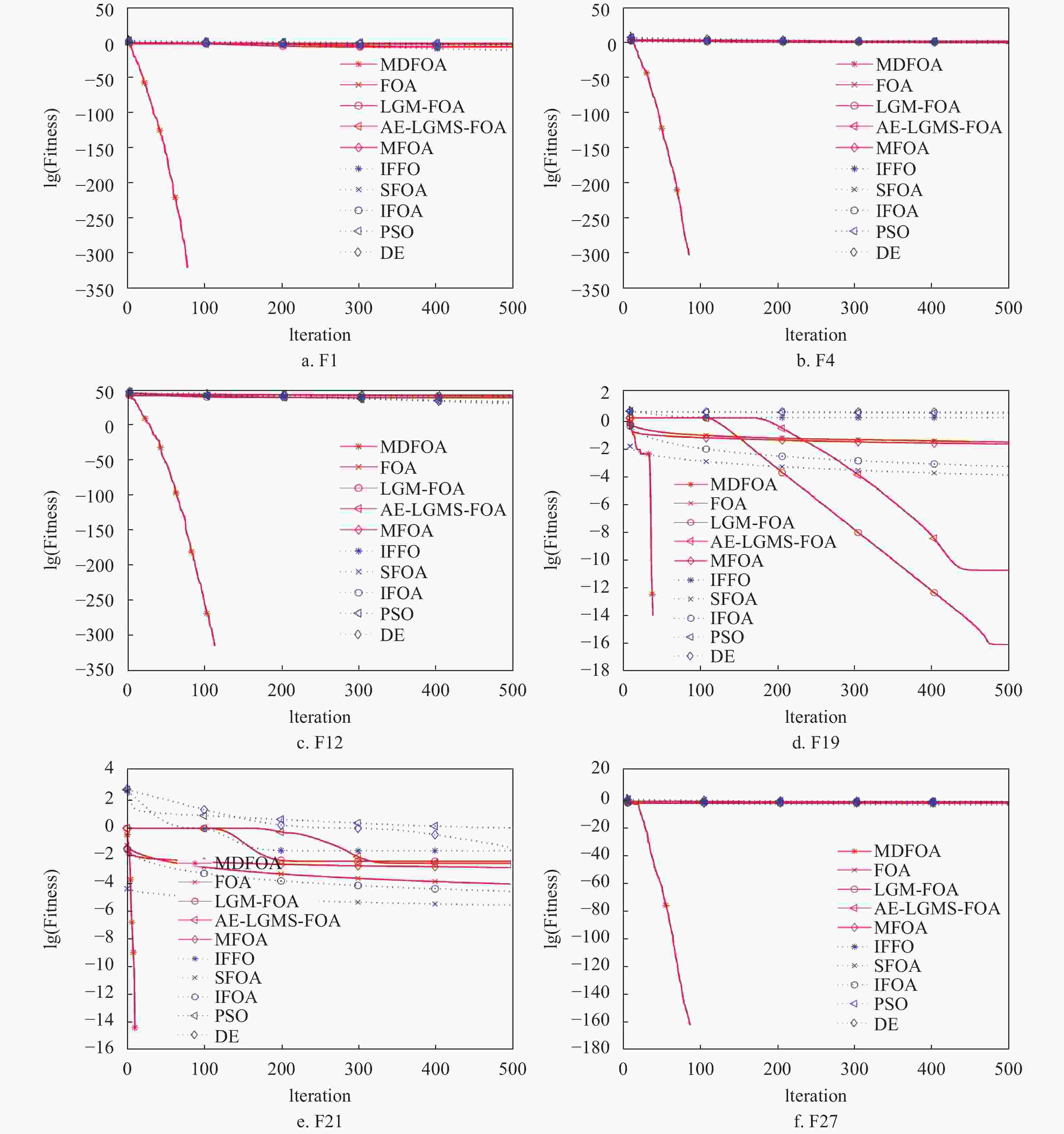
      In order to show the reliability, stability, and robustness of the results, each function is optimized over 30 independent runs, and the mean value (Mean) and standard deviation (Std) are reported in Tables 1 and 2 for all functions with dimensions equal to 30 and 60, respectively. The average convergence curves of the optimization processes for some typical functions by different algorithms are illustrated in Fig.1 and Fig.2 (To facilitate evaluate and observation, the fitness of the objective function in the graph is a logarithm with the base of 10).

      Figure 1.  Average convergence curves on some 30-dimensional functions

      From Table 1 and 2, we can find that MDFOA outperforms other algorithms in many respects:

      1) For unimodal functions (F1-F15), MDFOA obtains almost all the best mean results (except F5). In terms of algorithm stability, MDFOA gets 13 best results (except for F2, F5). For F2 with dimensions equal to 30, AE-LGMS-FOA gets the smallest standard deviation. While for F2 with dimensions equal to 60, SFOA gets the smallest standard deviation. For F5 with dimensions equal to 30 and 60, IFOA obtains the best mean result and the smallest standard deviation, followed by MDFOA. Eight algorithms including LGMS-FOA, AE-LGMS-FOA, MFOA, IFFO, SFOA, IFOA, DE and DMDFOA can converge to the theoretical optimal value of function F11 with dimensions equal to 30. When the dimensions are increased to 60, six algorithms including LGMS-FOA, AE-LGMS-FOA, MFOA, SFOA, IFOA and DMDFOA can converge to the theoretical optimal value of function F11.

      Figure 2.  Average convergence curves on some 60-dimensional functions

      2) For multimodal functions (F16-F29), MDFOA obtains all the best mean results. In terms of algorithm stability, MDFOA also gets 13 best results (except F23). For F23 with dimensions equal to 30 and 60, SFOA obtains the smallest standard deviation.

      3) The increment of the problem dimension has little effect on the convergence performance of MDFOA. While the convergence performance of other algorithms decreases obviously with an increase in the dimension of the problem.

      Table 1.  Comparison with other algorithms on 30-dimensional functions

      FUN* PAR** FOA LGMS-FOA AE-LGMS-FOA MFOA IFFO SFOA IFOA PSO DE MDFOA
      F1 Mean 2.654 91×10−2 2.041 98×10−5 1.324 37×10−5 4.102 41×10−1 3.610 37×10−11 2.581 60×10−3 7.871 24×10−3 2.400 35×10−1 6.811 56×10−5 0
      Std. 3.550 92×10−4 5.081 24×10−6 1.878 10×10−5 1.898 06×10−1 1.357 91×10−11 9.434 37×10−6 1.120 16×10−4 8.512 01×10−2 3.130 28×10−5 0
      F2 Mean 1.055 87 6.670 69×10−1 6.670 30×10−1 1.307 85 1.926 01 9.816 44×10−1 8.585 17×10−1 5.467 75 1.082 54 8.791 79×10−2
      Std. 2.224 28×10−1 6.147 25×10−4 3.629 64×10−4 4.773 88×10−1 1.314 89 3.292 52×10−3 7.326 63×10−2 2.471 65 2.358 78×10−1 2.803 54×10−2
      F3 Mean −9.990 37×10−1 −1.000 00 −1.000 00 −9.857 76×10−1 −1.000 00 −9.999 12×10−1 −9.997 14×10−1 −9.994 74×10−1 −1.00000 −1
      Std. 1.684 04×10−5 1.530 34×10−16 1.716 12×10−15 4.136 78×10−3 3.253 46×10−13 2.311 06×10−7 3.372 79×10−6 2.104 87×10−4 5.993 22×10−8 0
      F4 Mean 4.984 86×10 3.894 99×103 4.000 10×103 4.803 63×102 3.509 88×104 8.390 06 4.449 66×10 6.862 43×103 2.124 92×10 0
      Std. 8.449 54×10−1 2.483 79×103 3.183 33×103 1.969 34×102 2.893 41×104 4.017 54×10−1 1.21355 3.130 06×104 8.929 25 0
      F5 Mean 2.772 91×10−2 9.358 51×10−2 2.877 09×10−2 3.626 63×10−2 1.025 32×10−1 2.064 39×10−3 2.450 96×10−5 3.514 76×10−2 1.507 72×10−1 1.108 24×10−4
      Std. 3.966 91×10−3 3.501 61×10−2 1.381 61×10−2 1.710 53×10−2 4.397 10×10−2 2.936 93×10−4 1.890 84×10−5 5.612 26×10−3 3.118 76×10−2 1.269 48×10−4
      F6 Mean 2.899 37×10 2.812 60×10 2.829 60×10 3.085 33×10 2.678 31×102 2.873 03×10 2.832 83×10 3.526 96×102 2.349 55×102 0
      Std. 1.047 93×10 4.748 08×10−1 3.352 01×10−1 7.376 63×10−1 5.276 92×102 3.387 44×10−2 2.135 70×10−1 1.763 42×102 2.296 57×102 0
      F7 Mean 5.530 27×10−1 1.576 23 3.482 54×10−1 2.058 93×10−1 1.239 53×104 7.063 14×10−5 1.660 15×10−1 6.181 79×102 3.134 29×104 0
      Std. 1.097 98×10−2 1.584 46 3.319 02×10−1 1.028 48×10−1 4.383 64×103 1.307 40×10−5 1.967 17×10−3 1.953 47×102 8.085 59×103 0
      F8 Mean 3.219 55×10−2 9.028 51×10−2 1.658 90×10−1 7.931 00×10−2 1.846 25×10 2.267 00×10−3 1.730 55×10−3 4.404 56 6.766 26 0
      Std. 4.239 52×10−3 4.011 35×10−2 3.418 84×10−2 1.143 54×10−2 7.605 24 3.517 88×10−5 7.246 46×10−5 5.282 62×10−1 4.440 89×10−15 0
      F9 Mean 7.492 10×10−1 1.098 82×10−2 1.663 30×10−3 7.492 10×10−1 6.861 83×10−6 7.137 58×10−2 1.305 76×10−1 8.996 87×10−1 2.197 13×10−2 0
      Std. 2.501 46×10−3 1.209 39×10−2 3.022 21×10−3 1.323 44×10−1 9.776 98×10−7 1.294 22×10−4 8.151 27×10−4 1.424 08×10−1 5.625 55×10−3 0
      F10 Mean 1.926 99×10−3 1.025 40×10−17 1.861 35×10−11 2.902 97×10−2 6.245 67×10−12 1.302 18×10−4 5.724 17×10−4 1.151 13×10 4.249 09×10−3 0
      Std. 4.166 31×10−5 2.095 22×10−18 1.758 86×10−11 8.543 35×10−3 2.574 07×10−12 3.003 52×10−6 8.368 76×10−6 4.260 17 1.484 47×10−3 0
      F11 Mean 6.666 67×10−2 0 0 0 0 0 0 1.410 00×10 0 0
      Std. 2.494 44×10−1 0 0 0 0 0 0 5.088 22×10 0 0
      F12 Mean 4.004 91×10−6 2.113 60×10−8 1.054 94×10−8 2.334 20×10−5 1.643 22×10−13 2.564 74×10−6 1.078 08×10−6 4.573 30×10−15 2.620 34×10−16 0
      Std. 1.163 77×10−7 3.413 93×10−8 1.620 98×10−8 2.776 45×10−5 4.084 76×10−13 1.442 21×10−8 1.877 82×10−8 1.078 50×10−14 4.216 74×10−16 0
      F13 Mean 2.704 89×10−2 3.358 10×10−4 6.628 20×10−4 3.922 97×10−1 5.133 96×10−11 2.552 92×10−3 8.043 28×10−3 1.329 84 5.167 88×10−4 0
      Std. 6.358 33×10−4 5.096 28×10−4 1.233 19×10−3 1.048 78×10−1 1.851 94×10−11 9.986 68×10−6 1.240 80×10−4 6.507 06×10−1 2.066 19×10−4 0
      F14 Mean −4.499 98×102 −4.500 00×102 −4.500 00×102 −4.499 71×102 −4.500 00×102 −4.500 00×102 −4.499 99×102 −4.384 71×102 −4.499 96×102 −450
      Std. 3.833 95×10−5 7.696 64×10−14 1.252 34×10−11 1.002 04×10−2 1.721 21×10−12 2.426 35×10−6 8.649 19×10−6 4.034 65 1.272 64×10−3 0
      F15 Mean −4.494 49×102 −4.487 77×102 −4.492 05×102 −4.497 95×102 1.093 15×104 −4.500 00×102 −4.498 34×102 1.394 04×102 4.964 17×104 −450
      Std. 9.923 08×10−3 1.971 83 1.506 04 9.182 83×10−2 3.608 17×103 1.859 08×10−5 2.400 25×10−3 1.758 61×102 9.514 77×103 0
      F16 Mean 3.558 46×10−2 7.435 78×1010 8.409 12×10−7 1.715 34×10−1 1.539 58×10−6 9.473 78×10−3 1.852 58×10−2 1.829 05 1.936 80×10−2 8.881 78×10−16
      Std. 3.999 38×10−4 8.738 05×10−11 4.461 98×10−7 3.960 04×10−2 2.815 81×10−7 4.110 99×10−5 1.373 32×10−4 4.526 29×10−1 3.154 29×10−3 0
      F17 Mean 2.122 33×10−3 1.184 89×10−19 1.055 98×10−13 3.207 58×10−2 8.989 09×10−6 1.870 46×10−4 6.321 09×10−4 2.096 03×10−1 2.091 90 0
      Std. 4.239 32×10−5 2.228 42×10−20 1.191 64×10−13 1.284 36×10−2 3.660 72×10−6 6.420 60×10−7 7.743 16×10−6 8.953 58×10−2 2.073 22 0
      F18 Mean 1.529 48×10 1.721 17×10 1.458 87×10 1.016 53×10 4.355 33×10 5.656 14 1.664 12 4.279 37×10 2.721 49×10 0
      Std. 1.009 66 2.695 98 2.811 01 9.574 89×10−1 2.353 51×10 7.199 90×10−1 2.424 83×10−2 5.089 76 3.360 34 0
      F19 Mean 7.432 97×10−2 7.586 52×10−17 2.400 65×10−11 5.170 78×10−2 4.617 33 2.594 14×10−4 1.146 10×10−3 9.668 09 1.219 98×10 0
      Std. 1.182 12×10−1 1.573 25×10−16 2.851 05×10−11 1.517 25×10−2 1.057 06 6.023 38×10−6 1.648 03×10−5 6.900 02×10−1 2.100 12×10−1 0
      F20 Mean 1.710 92 4.780 38×10−2 6.911 40×10−3 4.469 23×10−3 6.022 69×10−14 1.557 39 1.688 02 5.602 23×10−2 9.140 49×10−3 0
      Std. 3.731 78×10−2 8.697 80×10−2 2.586 01×10−2 1.679 26×10−3 3.689 89×10−14 2.158 01×10−2 1.136 68×10−4 3.974 16×10−2 7.843 11×10−3 0
      F21 Mean 9.928 65×10−5 4.271 25×10−3 3.040 00×10−3 1.485 75×10−3 2.470 93×10−2 2.929 70×10−6 2.960 96×10−5 1.095 31 4.316 43×10−2 0
      Std. 1.820 64×10−6 5.686 99×10−3 6.019 96×10−3 5.010 67×10−4 2.238 19×10−2 3.109 89×10−7 5.233 10×10−7 4.570 23×10−2 6.753 52×10−2 0
      F22 Mean −2.841 88×10 −2.900 00×10 −2.900 00×10 −2.841 88×10 −2.102 67×10 −2.899 78×10 −2.898 89×10 −1.832 46×10 −7.860 84 −29
      Std. 1.850 64 6.678 09×10−15 2.733 39×10−11 3.566 31×10−1 1.706 06 5.770 50×10−5 1.470 70×10−4 1.155 69 5.554 64×10−1 0
      F23 Mean 4.990 09 −6.318 77×102 −7.347 31×102 −4.361 41×102 1.914 46×104 2.989 93×10 1.148 48×10 4.723 30×103 8.654 97×104 −4.922 99×103
      Std. 3.259 43 7.624 73×10 8.727 69×10 2.339 31×10 1.385 17×104 2.052 26×10−2 2.159 12 3.200 87×103 3.658 90×104 6.301 71
      F24 Mean 2.234 19 5.942 91 5.818 03 7.979 67×10−2 2.673 34 1.504 58×10−2 9.747 19×10−5 5.216 97 5.816 07 1.384 15×10−14
      Std. 8.152 19×10−1 2.778 01×10−1 1.669 68×10−1 6.409 98×10−2 4.467 16×10−1 8.099 43×10−2 3.647 13×10−6 2.422 29×10−1 8.428 15×10−2 7.425 11×10−14
      F25 Mean 1.328 27×10 6.927 79×10−15 7.903 25×10−12 8.625 40 7.661 18 3.432 01×10−2 1.130 56×10−1 4.658 48×10 1.547 93×102 0
      Std. 1.532 45×10 3.846 95×10−15 8.580 86×10−12 6.858 25 3.137 41 1.041 57×10−4 2.009 60×10−3 1.383 97×10 9.403 70 0
      F26 Mean 2.241 52 6.158 04×10−15 6.478 37×10−12 6.358 95 5.833 33 3.440 58×10−2 1.139 38×10−1 4.334 66×10 1.268 37×102 0
      Std. 3.618 81 3.362 07×10−15 6.437 30×10−12 4.481 49 2.001 39 5.648 66×10−4 3.001 51×10−3 9.232 60 1.447 52×10 0
      F27 Mean 1.032 07×10−1 9.198 73×10−1 6.598 73×10−1 9.988 07×10−2 1.719 87 3.703 75×10−3 9.987 34×10−2 9.595 61×10−1 1.031 19 0
      Std. 1.795 06×10−2 1.796 29×10−1 1.254 33×10−1 7.605 82×10−6 3.208 32×10−1 6.500 75×10−5 1.230 66×10−8 1.107 18×10−1 8.918 04×10−2 0
      F28 Mean 3.804 73×10 1.054 23 4.950 60×10−1 1.972 56×10 4.085 76×10−1 4.551 62×10 3.562 42 3.294 62 2.469 66×10 4.263 26×10−14
      Std. 1.898 20 3.155 78×10−1 2.042 02×10−1 2.800 02 6.633 84×10−1 1.597 30 8.810 73×10−2 8.555 10×10−1 2.724 82 0
      F29 Mean 7.066 57×102 6.050 03×102 5.837 67×102 4.692 89×102 1.072 16×102 4.166 18×102 4.153 27×102 1.003 79×106 1.205 26×104 0
      Std. 3.537 12×10 6.860 47×10 5.681 38×10 7.557 70×10 6.957 96×10 1.027 39×10 2.966 08×10−2 9.593 76×105 1.406 34×104 0
      　　* is for functions; ** is for parametric

      Table 2.  Comparison with other algorithms on 60-dimensional functions

      FUN* PAR** FOA LGMS-FOA AE-LGMS-FOA MFOA IFFO SFOA IFOA PSO DE MDFOA
      F1 Mean 2.032 34×10−1 4.723 39×10−3 1.759 10×10−3 2.747 05 1.944 46×10 1.116 20×10−2 6.122 21×10−2 2.192 39×10 1.856 62×10 0
      Std. 3.808 53×10−3 2.424 00×10−3 8.994 76×10−4 5.041 69×10−1 2.212 21×10 2.372 33×10−5 7.609 33×10−4 4.280 44 4.029 84 0
      F2 Mean 2.077 32 7.853 24×10−1 7.498 69×10−1 3.841 57 9.030 56×102 1.000 97 8.446 87×10−1 2.333 47×102 7.130 63×103 1.131 94×10−1
      Std. 8.033 99×10−1 5.061 00×10−2 2.443 84×10−2 6.012 81×10−1 1.290 03×103 2.827 07×10−3 8.925 15×10−2 8.305 94×10 2.007 67×103 6.477 52×10−2
      F3 Mean −9.962 88×10−1 −1.000 00 −1.000 00 −9.498 43×10−1 −1.000 00 −9.998 09×10−1 −9.988 76×10−1 −9.851 90×10−1 −9.837 26×10−1 −1
      Std. 6.508 06×10−5 4.720 03×10−8 6.396 99×10−10 1.068 67×10−2 1.262 42×10−11 3.407 99×10−7 1.351 89×10−5 2.554 46×10−3 3.304 03×10−3 0
      F4 Mean 1.774 84×102 1.388 39×104 7.985 99×103 2.262 75×103 7.992 24×106 1.749 69×10 1.590 45×102 3.396 37×105 1.731 10×106 0
      Std. 2.681 01 8.368 48×103 4.079 95×103 8.473 96×102 3.937 53×106 5.482 24×10−1 3.392 98 3.942 34×105 4.821 07×105 0
      F5 Mean 7.719 70×10−2 2.693 44×10−1 9.139 36×10−2 1.072 93×10−1 8.906 98×10−1 2.074 06×10−3 2.801 41×10−5 1.177 58×10−1 7.924 44×10−1 1.311 06×10−4
      Std. 1.004 96×10−2 7.601 88×10−2 5.040 13×10−2 4.155 52×10−2 2.915 67×10−1 4.804 90×10−4 2.746 35×10−5 2.052 97×10−2 1.483 24×10−1 1.108 38×10−4
      F6 Mean 6.072 93×10−1 5.808 55×10 5.813 86×10 6.787 49×10 1.203 68×105 5.848 49×10 5.798 18×10 1.390 77×104 7.781 39×105 0
      Std. 2.657 87 4.263 81×10−1 3.178 53×10−1 2.328 08 1.259 52×105 4.916 70×10−2 2.241 68×10−1 4.413 45×103 2.808 27×105 0
      F7 Mean 8.208 58 2.302 33×10 1.097 07×10 1.241 99 6.575 32×104 2.663 81×10−4 2.495 70 9.693 97×103 2.935 33×105 0
      Std. 1.586 55×10−1 2.752 09×10 1.106 64×10 9.063 90×10−1 1.272 55×104 1.259 43×10−4 4.026 86×10−2 2.523 51×103 4.212 24×104 0
      F8 Mean 7.700 65×10−2 2.925 18×10−1 3.354 07×10−1 1.104 88×10−1 5.856 78×10 2.362 07×10−2 1.541 76×10−3 1.156 03×10 1.907 67×10 0
      Std. 1.033 12×10−2 3.042 21×10−2 3.565 00×10−2 1.526 45×10−2 5.340 20 2.389 64×10−5 6.006 50×10−5 1.125 88 7.105 43×10−15 0
      F9 Mean 6.588 54×10−1 2.123 29×10−1 6.005 55×10−2 2.002 57 5.694 88 1.489 80×10−1 3.649 34×10−1 8.427 86 4.255 15×10 0
      Std. 6.185 54×10−3 6.329 88×10−2 3.821 81×10−2 1.953 68×10−1 6.722 16 1.751 92×10−4 2.188 42×10−3 1.082 61 1.576 22×10 0
      F10 Mean 7.455 67×10−3 1.768 46×10−4 1.765 27×10−5 1.086 56×10−1 1.240 33×103 2.813 39×10−4 2.251 74×10−3 2.967 98×102 3.144 57×102 0
      Std. 1.415 21×10−4 2.528 11×10−4 1.277 68×10−5 1.903 35×10−2 8.659 78×102 3.796 54×10−6 2.713 63×10−5 6.279 39×10 5.895 67×10 0
      F11 Mean 3.333 33×10−2 0 0 0 1.448 07×103 0 0 3.053 67×102 3.162 33×102 0
      Std. 1.795 05×10−1 0 0 0 1.022 01×103 0 0 6.367 91×10 5.779 20×10 0
      F12 Mean 4.059 77×10−6 1.533 68×10−8 1.298 43×10−8 2.294 69×10−5 5.229 28×10−13 2.561 84×10−6 1.122 20×10−6 1.710 89×10−13 1.527 03×10−2 0
      Std. 1.314 60×10−7 2.352 55×10−8 2.689 12×10−8 3.580 26×10−5 8.709 00×10−13 1.717 23×10−8 7.066 42×10−8 2.961 39×10−13 4.616 90×10−2 0
      F13 Mean 2.044 34×10−1 1.992 20×10−2 9.146 90×10−3 2.768 07 1.244 17×102 1.098 70×10−2 6.140 42×10−2 8.499 14×10 8.127 80×10 0
      Std. 3.592 55×10−3 1.253 57×10−2 5.517 95×10−3 5.683 49×10−1 7.711 15×10 2.977 78×10−5 8.726 19×10−4 1.937 99×10 1.771 44×10 0
      F14 Mean −4.499 93×102 −4.499 99×102 −4.500 00×102 −4.499 03×102 1.078 35×103 −4.500 00×102 −4.499 98×102 −1.333 49×102 −1.055 29×102 −450
      Std. 1.251 37×10−4 6.418 47×10−4 1.183 33×10−5 2.001 44×10−2 9.562 91×102 5.017 55×10−6 3.209 91×10−5 5.646 64×10 6.530 85×10 0
      F15 Mean −4.418 35×102 −4.272 13×102 −4.366 35×102 −4.488 77×102 6.647 77×104 −4.500 00×102 −4.475 06×102 8.600 60×103 2.958 22×105 −450
      Std. 1.316 36×10−1 2.863 23×10 1.582 78×10 3.767 07×10−1 1.074 04×104 1.021 11×10−4 3.527 37×10−2 2.269 27×103 3.715 73×104 0
      F16 Mean 5.079 46×10−2 2.500 37×10−3 7.173 44×10−4 2.591 56×10−1 5.813 44 9.881 17×10−3 2.655 14×10−2 4.384 56 4.967 09 8.881 78×10−16
      Std. 5.999 59×10−4 1.996 14×10−3 2.295 39×10−4 3.950 88×10−2 2.826 31 3.830 14×10−5 2.025 18×10−4 2.536 87×10−1 2.713 66×10−1 0
      F17 Mean 9.813 47×10−2 3.548 59×10−6 2.393 37×10−7 5.949 83×10−2 1.809 90×10−3 4.066 97×10−4 2.490 85×10−3 5.430 13 5.131 37×10 0
      Std. 2.714 64×10−1 5.947 76×10−6 1.857 89×10−7 2.439 58×10−2 2.841 31×10−3 9.761 84×10−7 4.092 81×10−5 1.414 45 4.223 80 0
      F18 Mean 3.221 46×10 3.852 05×10 3.468 89×10 2.175 68×10 2.836 05×102 1.099 73×10 3.909 86 1.750 74×102 2.990 67×102 0
      Std. 1.674 12 3.116 64 3.994 06 1.622 61 2.692 19×10 1.671 09 1.849 99×10−1 1.942 14×10 1.656 79×10 0
      F19 Mean 3.086 87×10−1 3.705 07×10−4 4.729 22×10−5 2.203 13×10−1 1.713 54×10 5.591 80×10−4 4.487 93×10−3 2.347 29×10 2.714 48×10 0
      Std. 4.612 59×10−1 3.630 33×10−4 4.626 38×10−5 3.527 79×10−2 1.013 33 1.002 52×10−5 7.014 91×10−5 1.064 31 2.152 44×10−1 0
      F20 Mean 1.469 30 1.066 87×10−1 2.227 22×10−4 8.887 61×10−3 1.436 33×10 1.339 92 1.448 69 2.763 18 5.247 73×105 0
      Std. 4.387 05×10−4 5.720 45×10−2 4.975 31×10−4 1.745 68×10−3 1.004 84×10 7.734 09×10−3 1.450 98×10−4 8.313 99×10−1 5.046 76×105 0
      F21 Mean 2.093 40×10−4 8.116 12×10−2 1.493 35×10−2 2.912 92×10−3 3.396 21×10 3.443 86×10−6 6.335 42×10−5 3.739 77 3.849 90 0
      Std. 4.279 14×10−6 4.125 07×10−2 7.380 88×10−3 7.351 80×10−4 1.458 63×10 4.195 28×10−7 9.245 16×10−7 4.379 75×10−1 6.081 39×10−1 0
      F22 Mean −5.222 17×10 −5.899 99×10 −5.900 00×10 −5.713 38×10 −3.114 33×10 −5.899 49×10 −5.895 59×10 −3.326 66×10 −8.961 09 −59
      Std. 6.392 02 8.694 19×10−5 1.582 49×10−6 7.743 99×10−1 2.644 81 1.029 75×10−4 8.153 19×10−4 2.733 93 6.860 83×10−1 0
      F23 Mean 2.137 22×10 −6.939 75×102 −7.803 90×102 −7.374 65×102 7.235 13×106 5.995 22×10 3.049 83×10 6.324 05×105 3.383 72×107 −3.484 64×104
      Std. 4.850 19 3.631 43×102 2.687 89×102 4.120 47×10 2.451 36×106 9.290 76×10−3 2.444 14 1.277 45×105 7.578 94×106 1.181 81×103
      F24 Mean 9.291 36 1.303 87×10 1.293 54×10 2.829 25×10 7.780 55 1.826 87×10−2 7.394 35×10−4 1.233 58×10 1.303 55×10 6.948 02×10−18
      Std. 2.239 11 3.282 71×10−1 3.663 42×10−1 1.391 79×10−1 6.854 58×10−1 6.845 72×10−2 4.938 15×10−5 2.554 25×10−1 1.130 98×10−1 3.739 49×10−17
      F25 Mean 7.082 010×10 1.955 54×10−4 8.255 59×10−6 2.465 99×10 1.144 53×102 7.462 94×10−2 4.356 71×10−1 1.666 98×102 4.924 83×102 0
      Std. 4.927 44×10 2.554 75×10−4 4.499 40×10−6 9.116 73 2.114 60×10 1.586 75×10−4 9.308 18×10−3 2.939 72×10 1.820 84×10 0
      F26 Mean 3.667 74×10 1.496 42×10−4 8.835 24×10−6 2.481 13×10 9.010 00×10 7.460 46×10−2 4.451 01×10−1 1.303 63×102 4.627 48×102 0
      Std. 5.574 01×10 2.602 87×10−4 5.364 21×10−6 8.851 01 1.705 94×10 1.678 25×10−4 2.981 61×10−2 2.372 50×10 1.895 75×10 0
      F27 Mean 1.865 40×10−1 1.026 54 9.598 73×10−1 9.989 02×10−2 1.420 99×10 6.241 88×10−2 9.987 33×10−2 2.817 32 5.822 70 0
      Std. 3.399 35×10−2 4.493 95×10−1 4.579 67×10−1 3.129 82×10−5 1.553 14 2.806 12×10−1 6.169 16×10−9 2.078 65×10−1 3.856 29×10−1 0
      F28 Mean 7.676 34×10 3.078 95 2.020 90 4.190 64×10 1.052 73×10 9.708 75×10 7.775 32 1.715 21×10 7.605 32×10 1.421 09×10−13
      Std. 2.922 57 3.716 20×10−1 3.570 58×10−1 2.972 62 2.947 27 2.996 63 9.914 09×10−2 1.982 57 2.079 59 0
      F29 Mean 3.070 80×103 2.773 58×103 2.659 67×103 2.230 40×103 6.001 25×1013 1.660 32×103 1.665 77×103 1.319 56×1010 1.103 47×1016 0
      Std. 1.319 50×102 1.750 67×102 1.487 93×102 1.518 05×102 8.120 58×1013 1.664 96×10 4.163 24×10−1 6.880 91×109 8.076 19×1015 0

      4) For most of the 29 complex benchmark functions, MDFOA can converge to the theoretical optimal value, which shows that MDFOA has strong global search and local search abilities, as well as strong algorithm stability.

      From Fig.1 and Fig.2, it can be observed that the evolution curves of the MDFOA descend much faster and reach lower level than that of other nine algorithms, indicating that MDFOA has the advantages of fast convergence speed and high convergence accuracy. The results in Fig.1 and Fig.2 also show that several other algorithms are easy to be trapped to the local optimal.

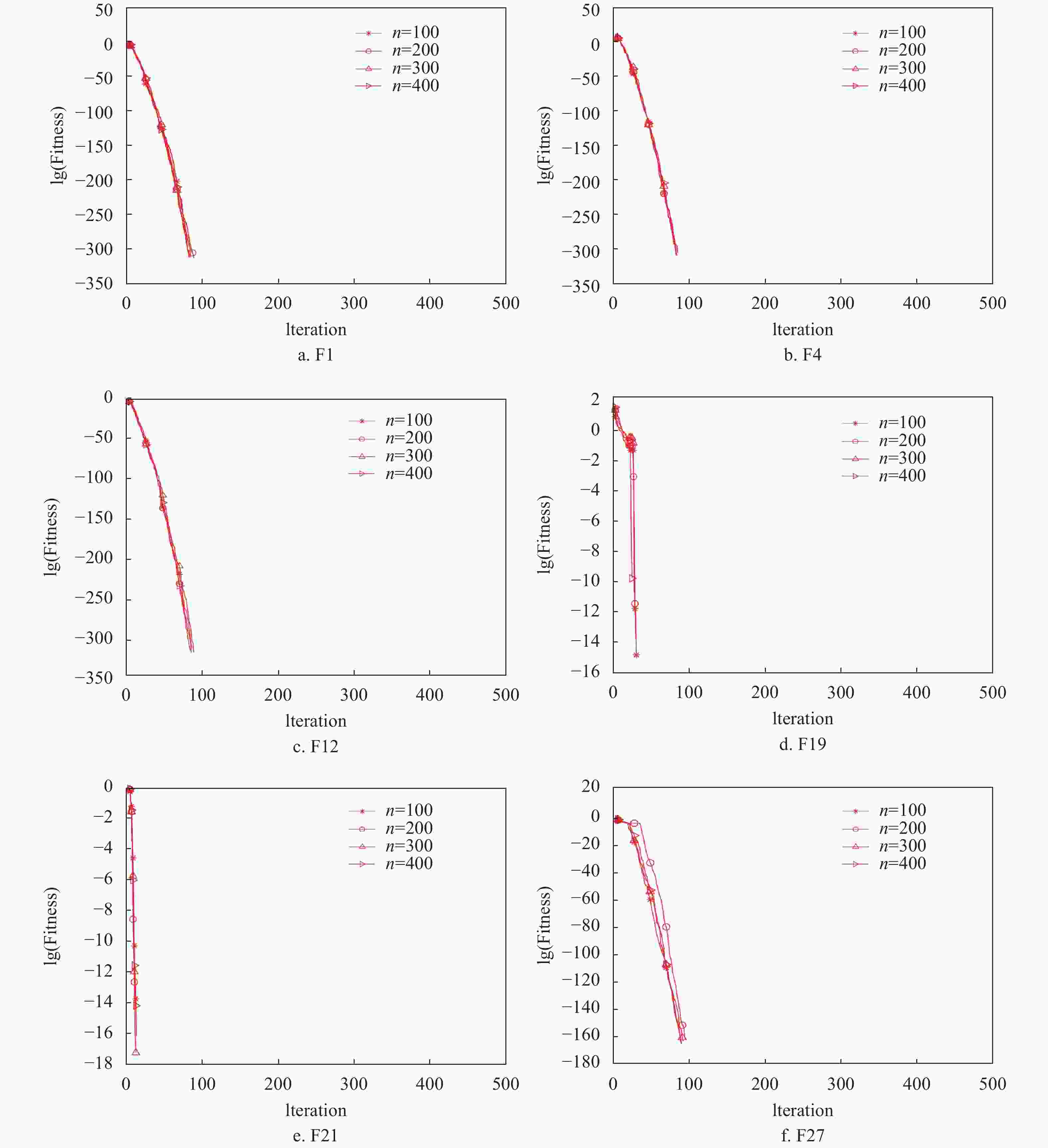
      • 3.3.   Analysis of High-Dimensional Functions

    • To test the ability of MDFOA of dealing with high-dimensional complex optimization problems, the dimensions of the benchmark functions increase to 100, 200, 300, and 400, respectively. The parameter setting and operating environment of MDFOA are kept the same as described above. The mean value and standard deviation are calculated based on the 30 independent replications, and the results are shown in Table 3. The average convergence curves of the optimization processes for some typical functions by MDFOA are illustrated in Fig.3.

      From Table 3, we can find that MDFOA is still highly effective and reliable in solving high-dimensional complex problems. The change in the dimension of the problems has little effect on the optimization performance of MDFOA. Among the 29 100-dimensional benchmark functions, MDFOA can converge to the theoretical optimal value of 23 functions. The same conclusion is reached when the dimensions increased to 200, 300, and 400. MDFOA also shows high convergence accuracy and excellent algorithm stability for benchmark functions that fail to converge to the theoretical optimal value. The above results are further verified by Fig.3. It should be noted that with an increase in the scale of the problem, the running time of the algorithm also increases.

      Table 3.  High-dimensional benchmark functions optimization results of MDFOA

      FUN* PAR** n=100 n=200 n=300 n=400
      F1 Mean 0 0 0 0
      Std. 0 0 0 0
      F2 Mean 1.707 04×10−1 1.900 13×10−1 2.270 63×10−1 2.137 6×10−1
      Std. 3.619 35×10−2 6.831 70×10−2 1.236 30×10−1 1.250 05×10−1
      F3 Mean −1 −1 −1 −1
      Std. 0 0 0 0
      F4 Mean 0 0 0 0
      Std. 0 0 0 0
      F5 Mean 1.209 81×10−4 1.108 13×10−4 1.060 77×10−4 1.456 90×10−4
      Std. 1.059 54×10−4 9.601 13×10−5 1.053 27×10−4 1.570 89×10−4
      F6 Mean 0 0 0 0
      Std. 0 0 0 0
      F7 Mean 0 0 0 0
      Std. 0 0 0 0
      F8 Mean 0 0 0 0
      Std. 0 0 0 0
      F9 Mean 0 0 0 0
      Std. 0 0 0 0
      F10 Mean 0 0 0 0
      Std. 0 0 0 0
      F11 Mean 0 0 0 0
      Std. 0 0 0 0
      F12 Mean 0 0 0 0
      Std. 0 0 0 0
      F13 Mean 0 0 0 0
      Std. 0 0 0 0
      F14 Mean −450 −450 −450 −450
      Std. 0 0 0 0
      F15 Mean −450 −450 −450 −450
      Std. 0 0 0 0
      F16 Mean 8.881 78×10−16 8.881 78×10−16 8.881 78×10−16 8.881 78×10−16
      Std. 0 0 0 0
      F17 Mean 0 0 0 0
      Std. 0 0 0 0
      F18 Mean 0 0 0 0
      Std. 0 0 0 0
      F19 Mean 0 0 0 0
      Std. 0 0 0 0
      F20 Mean 0 0 0 0
      Std. 0 0 0 0
      F21 Mean 0 0 0 0
      Std. 0 0 0 0
      F22 Mean −99 −199 −299 −399
      Std. 0 0 0 0
      F23 Mean −1.167 73×105 −4.845 14×105 −1.033 58×106 −1.741 83×106
      Std. 1.002 56×104 5.355 32×104 1.497 21×105 2.543 10×105
      F24 Mean 9.805 84×10−16 6.404 25×10−15 5.685 00×10−15 2.500 11×10−15
      Std. 4.352 40×10−15 2.492 30×10−14 1.472 99×10−14 7.664 45×10−15
      F25 Mean 0 0 0 0
      Std. 0 0 0 0
      F26 Mean 0 0 0 0
      Std. 0 0 0 0
      F27 Mean 0 0 0 0
      Std. 0 0 0 0
      F28 Mean 2.842 17×10−13 6.252 78×10−13 9.094 95×10−13 1.250 56×10−12
      Std. 0 0 0 0
      F29 Mean 0 0 0 0
      Std. 0 0 0 0

      Figure 3.  Average convergence curves on some high-dimensional functions

    4.   Conclusions and Future Research

    • In order to overcome the shortcomings of the basic FOA, such as low convergence accuracy and easy to fall into local optimum, we propose a novel improved fruit fly optimization algorithm, namely multi-strategy dynamic fruit fly optimization algorithm. A strategy randomly selected from the strategy base is used as the current evolution operator of each fruit fly individual, and different evolutionary strategies complement each other to effectively improve the overall optimization performance of the algorithm. To further improve the convergence speed of the algorithm, the algorithm employs a mechanism of dynamically updating the swarm information in real time, thus the non-evolutionary individuals of current generation can obtain the latest global optimal information in time. Tests on 29 benchmark functions indicate that the proposed MDFOA can perform better than FOA, LGMS-FOA, AE-LGMS-FOA, MFOA, IFFO, SFOA, IFOA, PSO and DE in terms of convergence accuracy, convergence speed and convergence stability. MDFOA also shows good performance in solving high-dimensional function optimization problems.

      In this paper, we choose an evolutionary strategy from the strategy base by random selection. Adaptive strategy selection may be a better choice, and it will be one of the research contents in the future. In addition, the parameters $\alpha $ and $\beta $ in Eq. (12) are two key parameters that affect the convergence performance of the algorithm, and their reasonable settings also need to be further studied in the future work.

参考文献 (36)

目录

    /

    返回文章
    返回

    期刊在线

    编辑办公

    友情链接

    版权所有 © 《电子科技大学学报》编辑部

    地址: 成都市建设北路二段四号电子科技大学主楼中350室 电话: 028-83202308,83207559 Email: xuebao@uestc.edu.cn

    本系统由 北京仁和汇智信息技术有限公司 开发