Consider a social network with n individuals denoted by an weighted undirected graph $G = \{ V,E,{{W}}\} $, where $V = \{ 1,2, \cdots ,n\} $ is the set of nodes(individuals) and $E \subseteq V \times V$ is the set of edges representing the interaction between pairs of nodes. ${{W}} = [{w_{ij}}] \in {{\mathbb{R}}^{n \times n}}$ denotes the edge weight in the graph, which is a stochastic matrix satisfying $\displaystyle\sum\limits_{j = 1}^n {{w_{ij}}} = 1$,$\forall i \in V$. If $(i,j) \in E$, then ${w_{ij}} > 0$. In an undirected graph, $(u,v) \in E$ means than $(v,u) \in E$. The neighboring set of node $i$ is denoted by ${N_i}$, i.e. ${N_i}: = \{ j \in V:(i,j) \in E\} $.

In the following, we firstly introduce the classic DeGroot model proposed in Ref.[20]. Then, we develop a dynamic evolution model of social opinion in a hostile environment, where an intruder intends to guide the network opinion into its malicious opinion.

The DeGroot model mainly explores the relationship between the opinion dynamis of individuals and internal coupling among the individuals. Each individual updates its opinion by:

where ${x_i}(k) \in {\mathbb{R}}$ is the opinion of individual $i$ at time step $k \in {\mathbb{N}}$. As Eq. (1) shows, the opinion of each individual $i$ at each time step, $\forall i \in V$, is updated by synthesizing its own opinion and its neighbors’ opinions.

Much work has been directed to the convergence analysis of the DeGroot model, such as Ref.[29-30]. In Ref.[29], a sufficient and necessary condition for the group opinion consensus is obtained.

The classic DeGroot model mainly considers the influence of system parameters and network topology on opinion evolving in an ideal environment, i.e., no extra opinion input. However, the scenario that an intruder inject malicious opinion into the individuals happens frequently, where the opinion dynamics could be much more complicated due to the intervention of other factors. In this paper, we develop a model based on the DeGroot model, considering an extra input term from the intruder describing the malicious opinion.

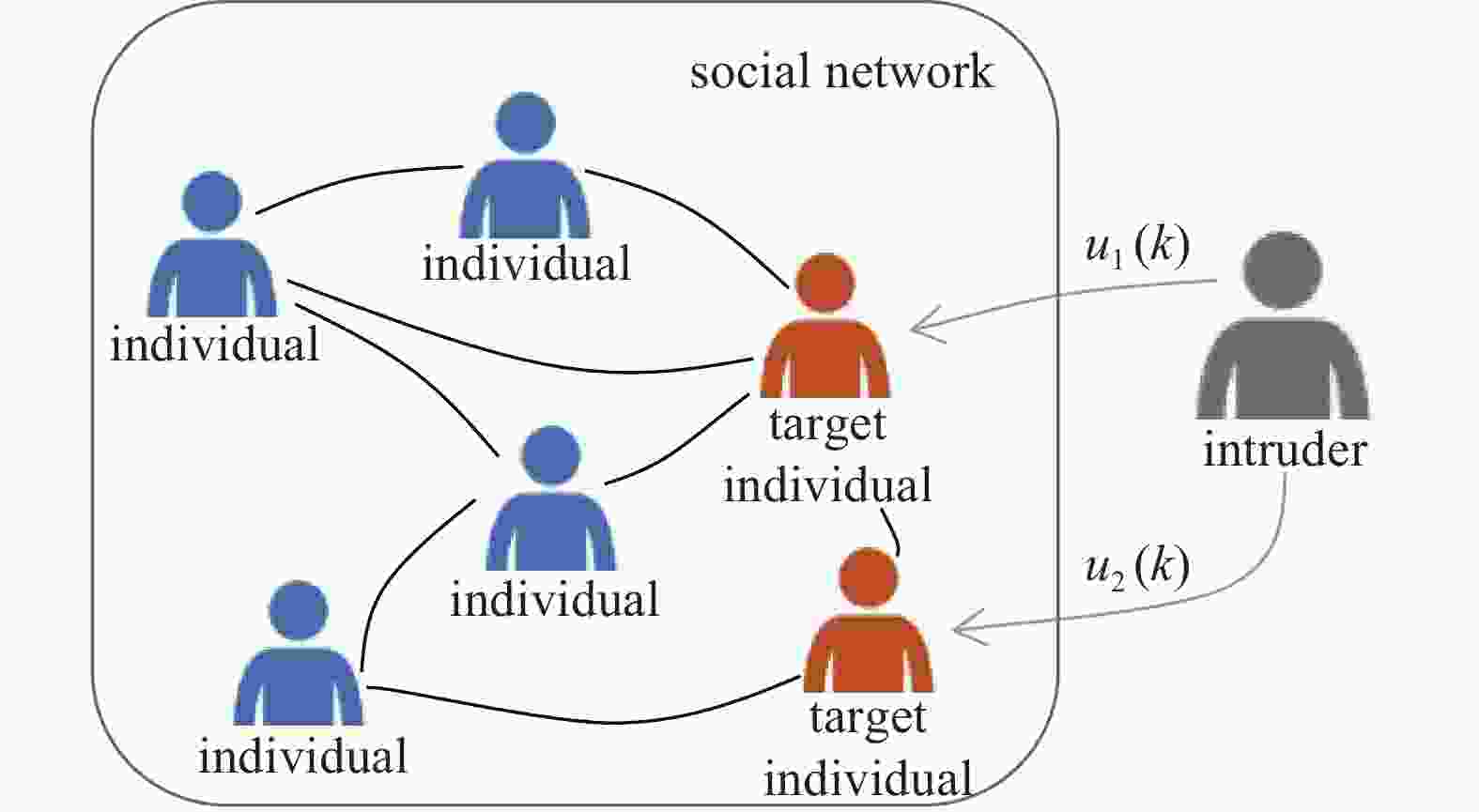
Definition 1　The intruder with hostile opinion selects a subset of individuals to be target individuals at initial time. At each time step, the intruder can obtain the opinion states of those target individuals, and disguise itself as a neighbor of target individuals with designed opinion state.

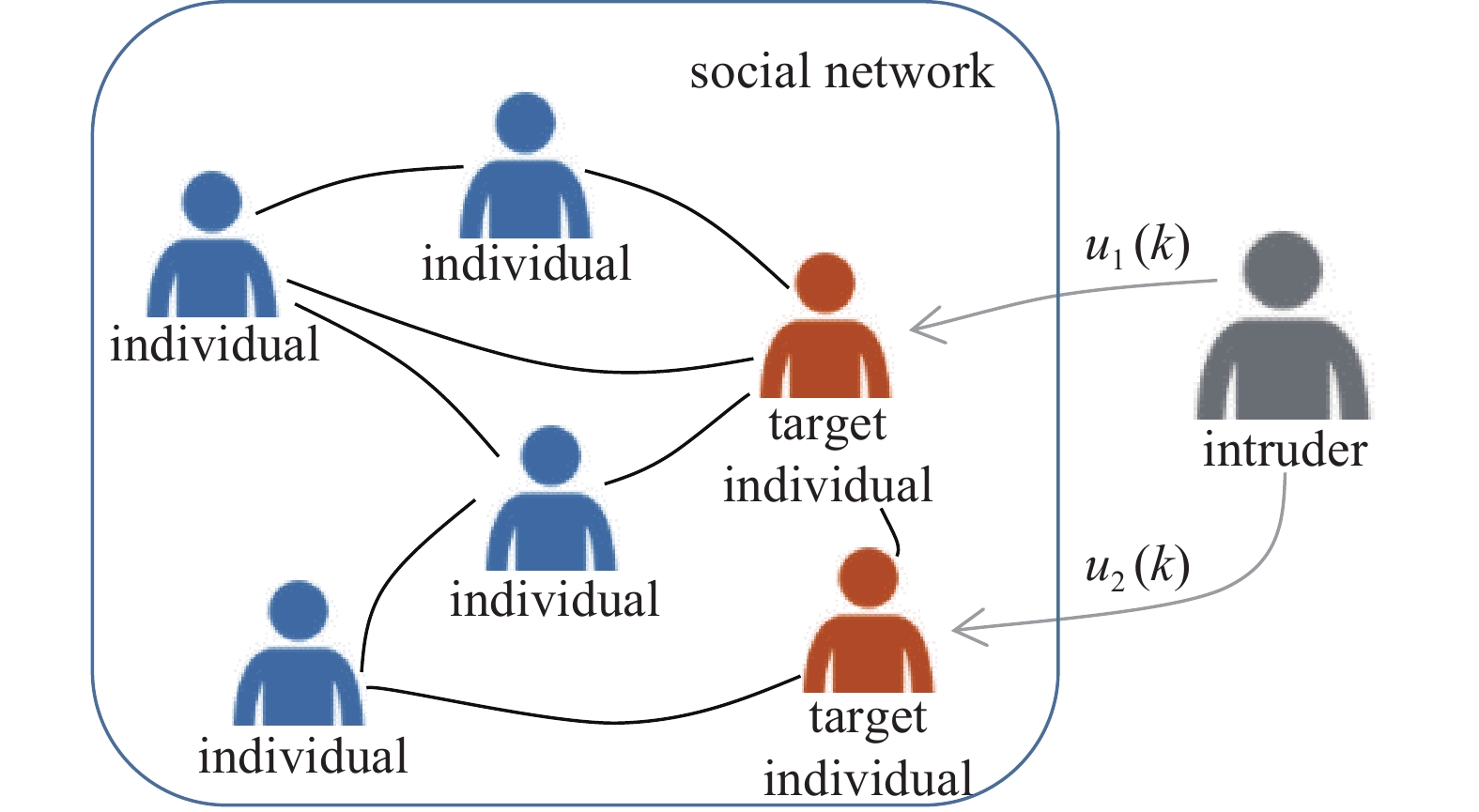
In Fig.1, the network consisting of blue and red individuals, the blue one represents the normal individual and red one represents the target individual. The intruder colored in grey is a hidden character. The intruder disguises itself as one of the neighbors of the target individuals, and sends an extra input ${u_i}(k)$ to every target individual. This effect will penetrate into the opinion of the target individuals like virus spreading in the crowd, potentially leading the normal individuals on malicious opinion. The opinion dynamics of each individual is described as:

Figure 1.  A social network in hostile environment.

and

where $0 < l < 1$ is a constant weight designed by the intruder, and $c$ is the malicious opinion of the attacker. ${\gamma _i} \in \{ 0,1\} $ denotes whether the individual $i$ is selected to be target individual or not. Let ${V_t} = \{ j:{\gamma _j} = 1,\forall j\} $ be the set of target individuals and ${V_n} = \{ j:{\gamma _j} = 0,\forall j\} $ be the set of normal individuals who are not selected by the attacker. Note that at each time step the intruder can obtain the state ${x_i}(k)$, $i \in {V_t}$ and then calculate the difference ${u_i}(k)$ between ${x_i}(k)$ and $c$. Then the intruder disguises itself as a neighboring individual of individual $i \in {V_t}$ with its opinion state equalling to ${u_i}(k)$. Moreover, if ${\gamma _i} = 0$, $\forall i \in V$, that is ${V_n} = V$, then the proposed model is degenerated into the DeGroot model. Intuitively, the designed opinion state ${u_i}(k)$ calculated by the intruder has a feedback effect on individual i’s opinion, it will lead individual i’s opinion to the malicious opinion $c$ if no defense mechanism is adopted by individuals.

Define ${{x}}(k) = {[{x_1}(k),{x_2}(k), \cdots ,{x_n}(k)]^{\rm{T}}}$, ${{\varGamma}} = {\rm{diag}}\{ {\gamma _1}, {\gamma _2}, \cdots ,{\gamma _n}\} $. By collecting all the states of individuals, we can rewrite the system (2) as the following vector form:

Apparently, with the continuously injecting input into the target individuals, the hostile opinion c of the intruder could be broadcasted to the whole network, then all the individuals’ opinion will converge to the malicious opinion.

In social networks, if a group of individuals without prejudice aggregate to reach consensus, the resulting opinion tends to synthesize the opinions of all the individuals in this group and form a moderate opinion. When some individuals in this network are potentially injected extra input from the intruder without being aware of danger and actively participate in group discussions, the entire group ultimately forms an opinion that is consistent with the intruder’s intention. Actually, these phenomena happen occasionally in real life, which motivates us to investigate the dynamic evolution of social opinion in hostile environments.

In the following, we are going to analyze the convergence of system (3), and firstly introduce some assumptions and definitions.

Assumption 1 (Connection) The network is connected and W is irreducible. i.e. there is at least one path between any two nodes in the network.

Theorem 1 (Stability) Under Assumption 1, the system (3) is stable if $0 < l < {\min _i}\{ 2{w_{ii}},1\} $.

Proof: Let ${\tilde{ W}} = {{W}} - l{{\varGamma}} $. All the eigenvalues of matrix ${\tilde{ W}} = [{\tilde w_{ij}}] \in {{\mathbb{C}}^{n \times n}}$ are in the union set of its n Gershgorin disk. The Gershgorin disk radius of matrix ${\tilde{ W}}$ is ${R_i} = \displaystyle\sum\limits_{j = 1,j \ne i}^n {\left| {{{\tilde w}_{ij}}} \right|} = 1 - {w_{ii}}$, then the $i$-th Gershgorin disk of matrix ${\tilde{ W}}$ is ${G_i} = \{ z\left| {\left| {z - {{\tilde w}_{ii}}} \right|} \right. \leqslant {R_i},z \in {\mathbb{C}}\} $. To guarantee the stability of the system (3), ${\tilde{ W}}$ should be a Schur stable matrix. The Gershgorin disk on the complex plane is analyzed, and there are three cases of ${\tilde w_{ii}} = 0$, ${\tilde w_{ii}} > 0$ and ${\tilde w_{ii}} < 0$.

1) When ${\tilde w_{ii}} = 0$, there are two situations here. If ${\gamma _i} = 0$, we got that ${w_{ii}} = 0$ and ${R_i} = 1$. The matrix ${\tilde{ W}}$ is not Schur stable due to $\rho ({\tilde{ W}}) = 1$. While ${\gamma _i} = 1$, by the conditions mention above, ${w_{ii}} = 1$ which means ${R_{ii}} = 1 - l$. To guarantee the stability, $0 \leqslant {R_{ii}} < 1$, and we have $0 < l \leqslant 1$.

2) When ${\tilde w_{ii}} > 0$ there are also two cases. If ${\gamma _i} = 0$, ${w_{ii}} > 0$. Further, ${R_i} < 1$, ${\tilde{W}}$ is Schur stable in this case. While ${\gamma _i} = 1$, to make the absolute maximum eigenvalue of matrix ${\tilde{ W}}$ less than one, the inequation of ${\tilde w_{ii}} + {R_i} < 1$ should be satisfied. We have $l > 0$ by solving the inequation.

3) When ${\tilde w_{ii}} < 0$, there is only the case of ${\gamma _i} = 1$. By the inequation of weii ${\tilde w_{ii}} - {R_i} < - 1$, we have $2{w_{ii}} > l$.

Take the intersection of all the conditions mention above, the range of parameter $l$ should be $0 < l < {\min _i}\{ 2{w_{ii}},1\} $, and the case of ${\gamma _i} = 0$ in (i) could not happen in a strict condition.

Definition 1　(Consensus) For the system (3) with any initial state ${{x}}(0)$, if there exists a constant $\chi \in {\mathbb{R}}$ such that:

then we say the system (3) achieves consensus.

Lemma 1　Under Assumption 1, if the system (3) is stable with ${\rm{tr}}({{\varGamma}} ) \geqslant 1$, all the states ${{x}}(k)$ finally reach consensus on ${{{x}}^{\dagger} } = c{{{\textit{1}}}_n}$.

Proof: From Theorem 1, we obtain $\rho ({\tilde{ W}}) < 1$. By iterations:

Since $\mathop {\lim }\limits_{k \to \infty } {({\tilde{ W}})^k}{{x}}(0) = 0$, we obtain ${{{x}}^{\dagger} } = cl{( {{{I}} - {\tilde{ W}}} )^{ - 1}} {{\varGamma}} {{{\textit{1}}}_n}$. Denote ${{\psi}} = l{({{I}} - {\tilde{ W}})^{ - 1}}{{\varGamma}} $, and rewrite the formula as:

Obviously, ${({{I}} - {{W}} + l{{\varGamma}} )^{ - 1}}({{\textit{1}}} - {{W}}){{{\textit{1}}}_n} = 0$. It means that ${{\psi}} $ is stochastic matrix, thus the steady state of ${{x}}(k)$ is ${{{x}}^{\dagger} } = c{{{\textit{1}}}_n}$.

In social networks, the intruders usually induce the public opinion to incite the individuals and use the public opinion to benefit from it. Motivated by the above phenomenon, we further investigate system (3) in an attack-defense environment with the goal of finding a way protecting public opinion in the presence of malicious opinion injection. Moreover, we are also interested into two other problems: 1) in the scenario that the intruder can only select the limited number target individuals, how to select those target individuals such that the convergence speed of achieving consensus on malicious opinion is maximized. The answer to this problem makes the efficient selection for the intruder, and also can help us adopting the defense strategy by protecting some ’key’ individuals; 2) how to design a defense mechanism for each individual in order to protect public opinion from malicious opinion?

Firstly, we try to solve the first problem, which is similar to the works in Ref.[31-32]. We formulate it as the following optimization problem:

where the object function $J({{\varGamma}} )$ characterizes the convergence speed of reaching consensus on the malicious opinion $c$, because ${{u}}(k)$ measures the gap between individual opinions and $c$ at each time step. The smaller $J({{\varGamma}} )$, the faster the convergence speed. To characterize the limited resources of the intruder, the number of target individuals is limited to $q$.

To solve the problem ${P_1}$, we derive the iteration equation of ${{u}}(k)$ as:

with ${\tilde{ W}} = {{W}} - l{{\varGamma}} $, then the objective function $J({{\varGamma}} )$ can be rewritten as:

After appropriate conversion of the first condition in ${P_1}$, we can use ${\tilde{ W}}$ to represent the range of ${\gamma _i}$, thus to make it easy for computer simulation. It should be noted that this conversion has no effect on the following results:

where ${({\tilde{ W}})_i}$ is the $i$-th row of ${\tilde{ W}}$.

The above optimization problem has been transformed into a convex optimization problem, which can be solved by some typical methods^[33].

It is NP-hard to traverse all possible results for Boolean combinatorial problems in large-scale networks. For solving the combinatorial optimization problem, ${l_1}$ norm is often used instead of ${l_0}$ norm to obtain a more flexible calculation method^[34]. Similar to the method in Ref.[35], we use an weighted ${l_1}$ norm to obtain an approximation guarantee for node selection strategy. Using all the above arguments, we implement an algorithm to solve suboptimal problem ${P_3}$ relaxed by ${P_2}$, which sacrifices a certain selection accuracy while reducing the computation complexity greatly.

Algorithm 1: Suboptimal selection algorithm

Input: input parameters ${{W}}$,$c$,$l$,$e$.

Output: selection strategy ${{\varGamma}} $ and suboptimal object function value ${{J}}$.

1) Initialization parameters: ${x_i}(0)$, ${f_i}(0)$.

2) Solve the optimization problem with interior point method and replace ${l_0}$ norm with ${l_1}$ norm:

3) Update the weights by ${f_i}(t + 1) = {({\gamma _i}(t) + e)^{ - 1}}$, here $e > 0$ is a small real number to prevent the denominator from being zero.

4) Let $t: = t + 1$, and return to step 2) until the solution of the algorithm in iteration has converged or $t$ reaches maximum.

The solution of the above algorithm could be computed in $O({n^2})$ operations. Besides, convex optimization method including active-set or stepwise quadratic programming can also solve this problem effectively.

By solving the optimization problem, we obtain a suboptimal solution due to the replacement of ${l_0}$ norm. Numerous efforts have been directed towards using the approximation method to solve the combinatorial problems including ${l_1}$-replacement with the aid of ADMM^[36]and convex relaxation^[37]. Here, we are more interested into providing a heuristic method rather than obtaining the optimal solution.

In this section, a defense mechanism is designed to resist hostile opinion from the intruder by identifying target individuals in the network so as to avoid continuous hostile opinion injection. The purpose of the intruder is to make individuals deviating from the original opinions and achieving on the hostile opinion of attacker. Generally, the malicious opinion of the intruder differs from the original weighted averaged opinion of individuals at steady state with large gap. From the perspective of the network, if it is aware of the potential attack and the attacking types of the attacker, it can implement a defense mechanism on each individual to identify the compromised opinion at each time step.

Aggressive behavior in attack-defense environ-ment often leads the individuals’ original agreement opinion to a completely different situation, which means that the intruder’s target opinion will be greatly deviat-ed from the opinion reached in the unattacked case. Assume that the opinion of the intruder is significantly different from the weighted averaged opinion of individuals in the normal situation at the steady state. Suppose that each individual is aware of the intruder lurking in the network and disguising itself as its neighboring individual with a certain probability, but the identity of the target individuals selected by the attacker is still unknown. Thus, each individual needs to identify whether it has been selected by the intruder. To solve this problem, we propose a defense mechanism, where the individual decides to stop communicating with its neighboring individuals by comparing its opinion with its neighboring individuals’ averaged opinion. The mechanism is similar to the infectious resource tracing and control in virus broadcasting area.

With this mechanism, at each time step individual $i \in V$ compares the gap of its opinion and the average opinion of its neighboring individuals with a given threshold:

with:

where ${m_i}(k) = |{{{N}}_i}(k)|$. If the gap is larger than the given threshold, individual $i$ will no longer communicate with its neighboring individuals. According to the above rule, parts of individuals stop sending data to its neighboring individuals at a certain time. Thus the neighboring set of individual $i$ is time-varying, i.e., ${{{N}}_i}(k)$, $\forall i$. Assuming that $\varepsilon (k)$ is a heterogeneous threshold, which follows:

with parameter $R$ is a non-zero positive number, and $0 < \rho < 1$.

Recall that the initial opinions of individuals are random. If the initial $\varepsilon (0)$ is sufficient small, the false alarm rate may occur and normal individuals could be isolated prematurely. Thus, the initial $\varepsilon (0)$ should not be too small. With the continuous communication of individuals, the opinions of individuals evolve with a period of time, and the gap between the various opinions gradually decreases. If $\varepsilon (k)$ is too large, the target individuals cannot be identified. Hence, we adopt an attenuated threshold. Existing work has examined the opinion dynamic with declining confidence using function (5) in Ref.[38], where parameter $R$ limits the threshold range and parameter $\,\rho $ characterizes the confidence decay of individuals. Apparently, the choice of coefficient $R$, $\rho $ have direct influences on the defense effects.

In addition, because the neighboring set of individual $i$ is time-varying, the edge weights are also recalculated at each time step, which evolves as:

In the communication network topology, if $\left| {{x_i}(k)} \right. - $$\left. {{\rm{E}}[{x_i}(k)]} \right| \leqslant \varepsilon (k)$, then the neighboring set of individual $i$ is:

with ${N_i}(0) = {N_i}$,${N_i}(k) \subseteq {N_i}$. Conversely, if individual $i$ regards itself being injected malicious opinion at time step $k$, i.e.,$\left| {{x_i}(k) - {\rm{E}}[{x_i}(k)]} \right| > \varepsilon (k)$, then ${N_i}(k + 1) = \emptyset $ and its weight ${w_{ii}} = 1$ and ${w_{ij}} = 0$, $i \ne j$.

Overall, the opinion of each individual equipped with the proposed defense mechanism is updated by:

Equipped with the above mechanism, each individual conducts a self-assessment after each round of communication, and judges whether it has been attacked. If the individual is suspicious of being target individual, then it stops communicating with its neighboring individuals. It is similar to the isolation scheme of flu virus spreading in the crowd, where the infected people are consciously away from the group to avoid group infection. Eventually, those individuals identifying themselves as target individuals turn to be the isolated in the network. Meanwhile, the normal individuals might also turn to be isolated nodes, i.e.${w_{ij}} = 0$, $\forall i$, $j \in V$, $i \ne j$ if $\varepsilon (k)$ does not fit the evolving of opinions well. With the simulation tool, we also find that most of the normal individuals achieve steady-state before turning to isolated nodes.

In the following, we begin to analyze the convergence of the Eq. (6).

Theorem 2 (Convergence) For the Eq. (6) equipped with the defense mechanism Eq. (4), the opinion ${x_i}(k)$ converges to a steady-state opinion, i.e., $x_i^ * = \mathop {\lim }\limits_{k \to \infty } {x_i}(k)$.

Proof: Let $i,j \in V$. The upper bound of opinion gap at each interval is derived by:

Let ${\Delta _{ij}}(k) = \left| {{\rm{E}}[{x_i}(k)] - {\rm{E}}[{x_j}(k)]} \right|$, then the above derivation can be rewrite as:

and both $i$ and $j$ satisfy the inequation (4) at the same time, we have:

Note that $0 < {w_{ii}}(k) \leqslant 1$. It follows that:

Then the gap between the individual’s opinions at time $k$ and $k + \tau $ is:

Let $\varPsi = 2\displaystyle\sum\limits_{s = 0}^{\tau - 1} {R{\rho ^{k + s}}} = (2R/(1 - \rho )){\rho ^k}(1 - {\rho ^\tau })$, $\varUpsilon = $$\displaystyle\sum\limits_{s = 0}^{\tau - 1} {(1 - {w_{ii}}(k + s))} (\left| {{\rm{E}}[{x_i}(k + s)] - {\rm{E}}[{x_j}(k + s)]} \right|)$ and $\varPhi = l{\gamma _i}\times \displaystyle\sum\limits_{s = 0}^{\tau - 1} {\left| {{u_i}(k + s)} \right|} $. We will consider two situa-tions next.

1) If ${\gamma _i} = 0$, Eq.(7) equals to $\left| {{x_i}(k + \tau ) - {x_i}(k)} \right|$$ \leqslant \varPsi + \varUpsilon $. As explained in Remark 5, if the network defense mechanism develops without limit, the individuals in the network will become isolated individuals at a certain moment since threshold $\varepsilon $ can’t always fit in the changes of opinions, i.e., $\mathop {\lim }\limits_{\tau \to \infty } (1 - {w_{ii}}(k + \tau )) = 0$. It’s hard to judge at which time point the individuals becomes isolated, but we can be sure that $\mathop {\lim }\limits_{\tau \to \infty } \varUpsilon = (1 + {w_{ii}}(k)){\Delta _{ij}}(k) + (1 + {w_{ii}}(k{\rm{ + }}1)) {\Delta _{ij}}(k{\rm{ + }}1) + $ $ \cdots + 0$ is limited. As $\tau $ goes to infinity, the inequality is going to be $\left| {{x_i}(k + \tau ) - {x_i}(k)} \right| \leqslant $$(2R/(1 - \rho )){\rho ^k} + \mathop {\lim }\limits_{\tau \to \infty } \varUpsilon $. Let $\varTheta = \mathop {\lim }\limits_{\tau \to \infty } \varUpsilon $, the above conclusion means that $\mathop {\lim }\limits_{k \to \infty } 1 - {w_{ii}}(k) = 0$, and $\mathop {\lim }\limits_{k \to \infty } \varTheta = 0$. In summary, $\mathop {\lim }\limits_{k \to \infty } {\rm{|}}{x_i}(k + \tau )$$ - {x_i}(k){\rm{|}} = 0$, i.e., ${x_i}(k)$ converges to steady state.

2) If ${\gamma _i} = 1$, because the weight matrix ${{W}}(k)$ is time-varying under defense mechanism, it is difficult to derive simpler form. But in extreme conditions, when all the individuals are target individuals, all the opinions eventually converge to the attacker’s opinion $c$. Thus, when ${\gamma _i} = 1$, $\forall i$, $\left| {{x_i}(k + \tau ) - {x_i}(k)} \right| \leqslant \left| {c - {x_i}(0)} \right|$ is definitely established.

In this section, we provide some numerical results to verify the derived theoretical results. Notice that the graph remains conncted in all the examples.

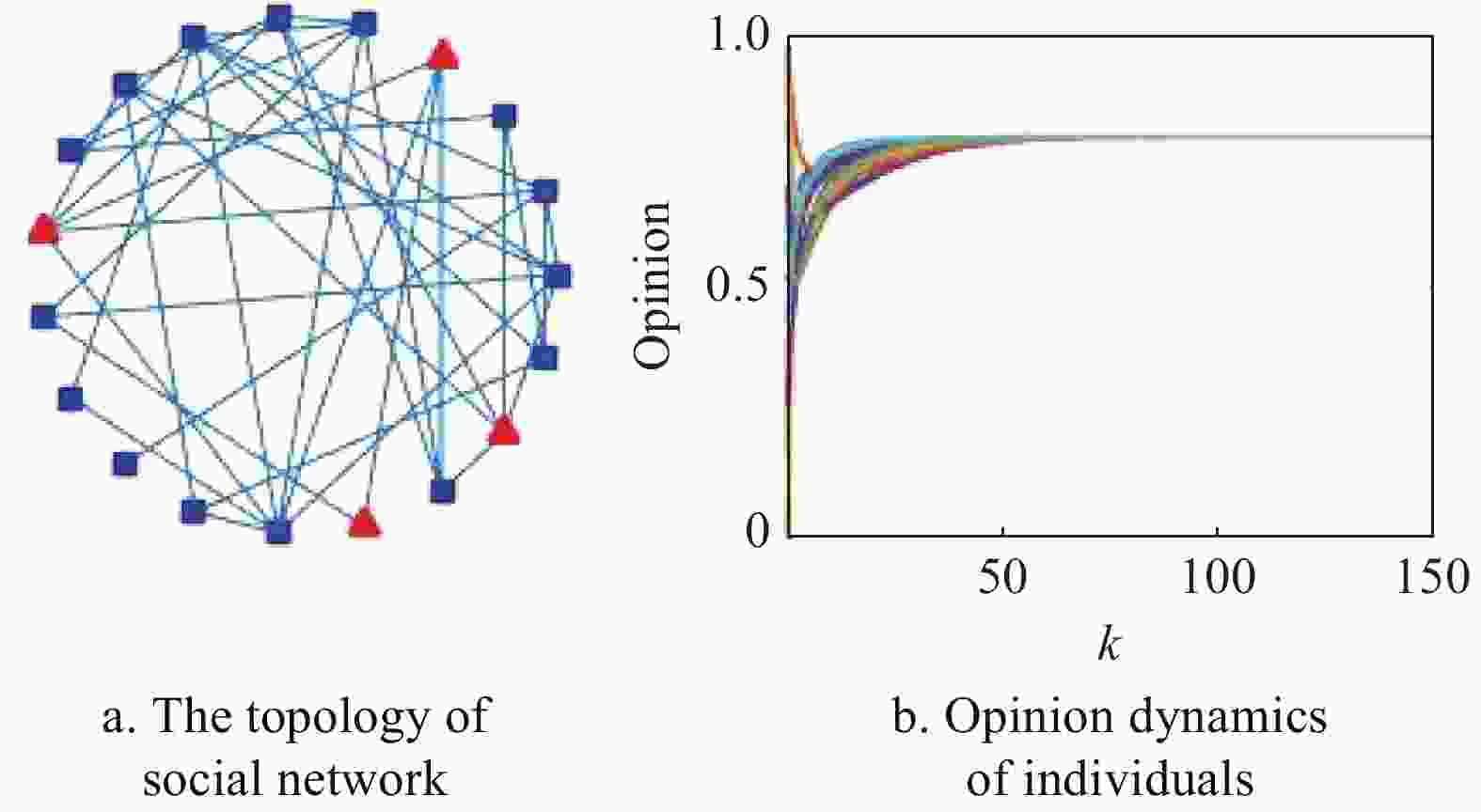
Example 1 (DeGroot model in the presence of an intruder). Consider a social network consisting of 20 individuals (see Fig. 2a. Here, the blue square represents normal individuals and the red triangle represents target individuals.), with the second largest eig-envalue of the weight matrix is ${\lambda _2}({{W}}) = 0.978\;2$ and ${\min _i}({w_{ii}}) = 0.066$. Let the malicious opinion be $c = 0.8$ and the weight be $l = 0.8 {\min _i}({w_{ii}})$. We generate ${{\varGamma}} $ with $||{{\varGamma}} |{|_0} = 10$, and choose the initial opinions ${x_i}(0) \in [0,1]$ randomly.

Figure 2.  The topology of social network and opinion dynamics in network.

The evolving of opinions of Eq. (3) is shown as Fig. 2b. Lines of different colors represent different individuals. Obviously, the individuals’ opinions converge to the malicious opinion $c$ in short time.

Example 2 (Suboptimal selection strategy). Consider the social network in Fig. 2a with identical system parameters as Example 1. Algorithm 1 returns a suboptimal selection solution for the intruder such that the aggregation speed is maximized.

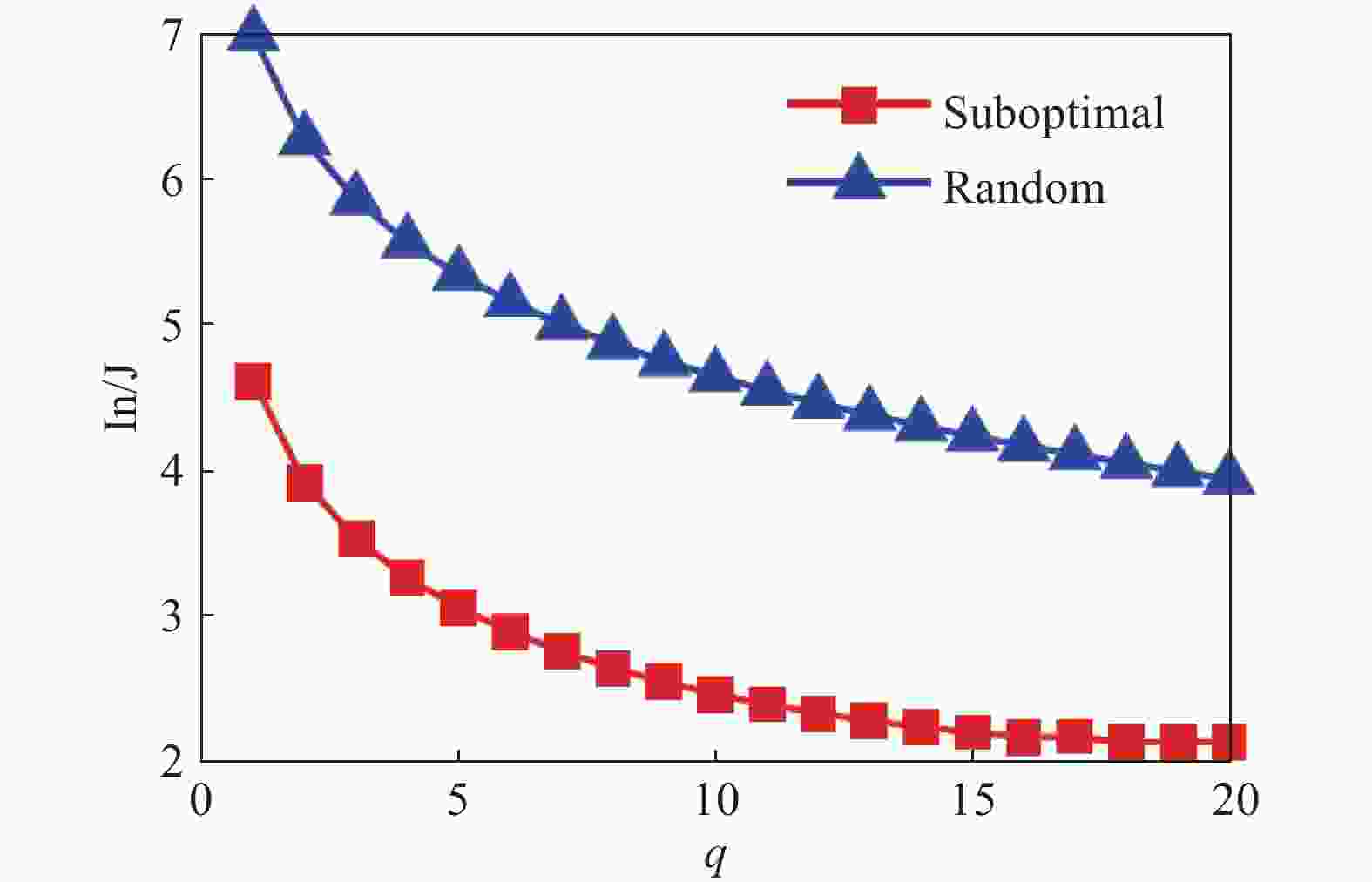
Fig. 3 shows the relationship between the objective function $J({{\varGamma}} )$ and the number $q$ under suboptimal selection strategy and random selection strategy. Obviously, the aggrega-tion speed under the former is faster than one of the latter. In addition, the aggregation speed increases as $q$ increasing, which also satisfies with the intuitive results.

In order to better understand the optimization process, we also investigate the objective function $J({{\varGamma}} )$ under two different centrality indices^[39], i.e., betweenness centrality ${C_B}$ and closeness centrality ${C_c}$, in complex networks in the case of $q = 1$. Betweenness centrality ${C_B}$ is an index to describe the importance of a node by the number of shortest paths through the node. Closeness centrality ${C_c}$ is reflected in the proximity between one node and other nodes in the network. Fig. 4 shows that individuals with higher ${C_B}$, ${C_c}$ lead to smaller $J({{\varGamma}} )$ generally. Here, the path length is represented by edge weight in the calculation of ${C_c}$. This result is obvious, the greater the influence of the nodes, the greater the contribution on the evolution of the network. It also inspires us to use network centrality to investigate target individual selection strategy from the perspective of network topology.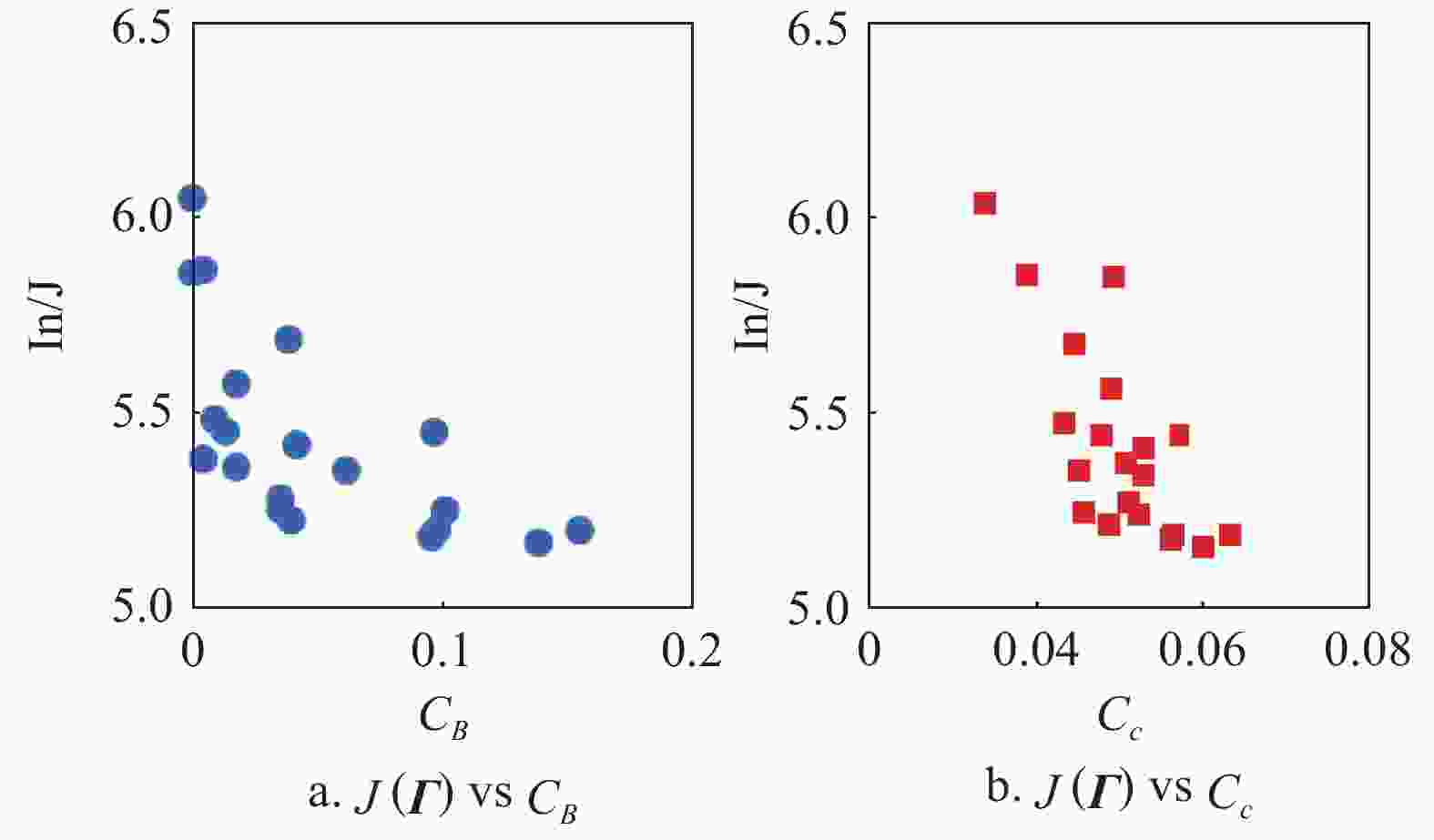

Figure 3.  $\ln (J({{\varGamma}} ))$ vs $q$ under two selection strategies.

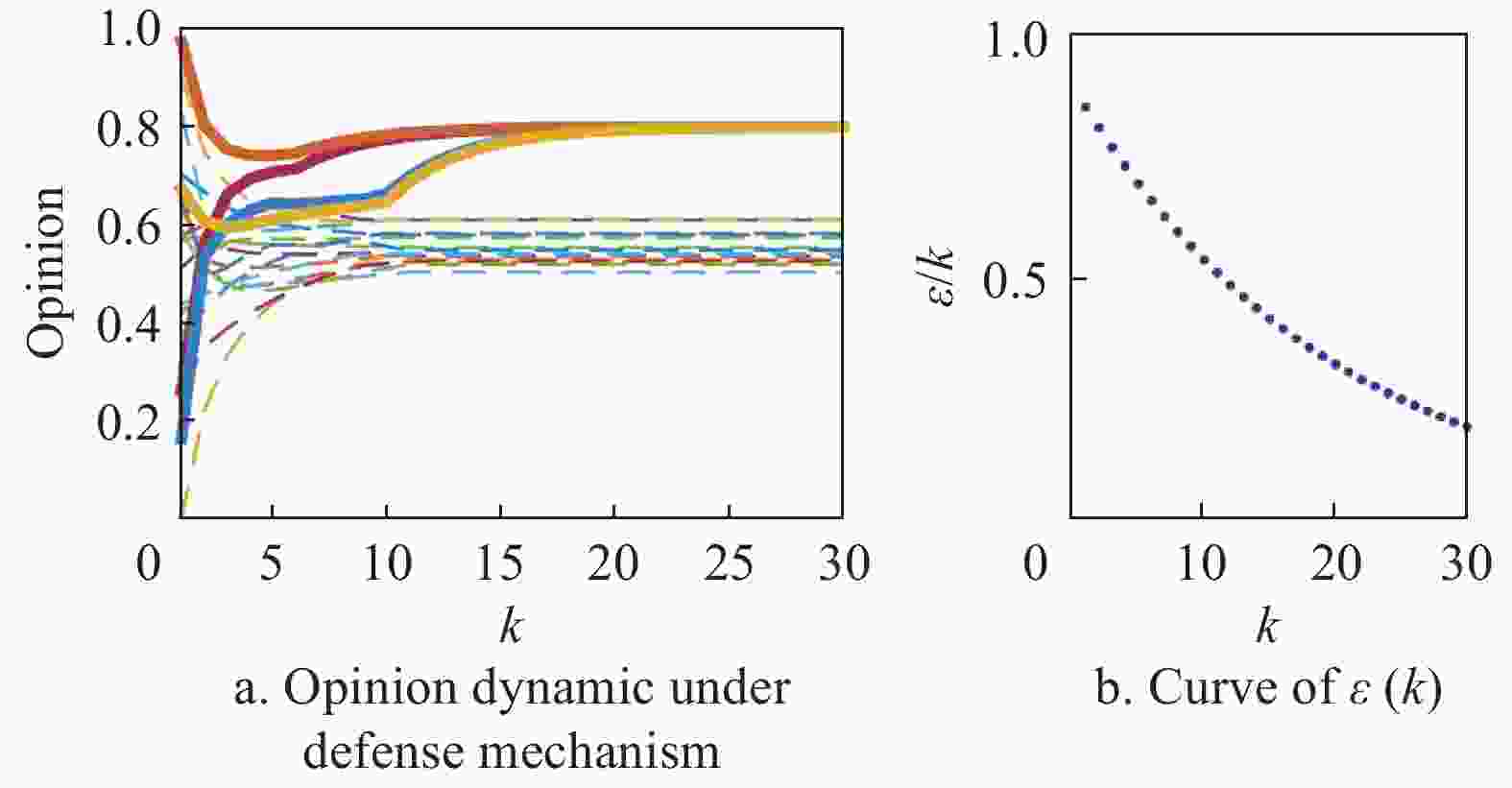
Figure 4.  The objective function $J({{\varGamma}} )$ under different indices ${C_B}$, ${C_c}$, respectively.

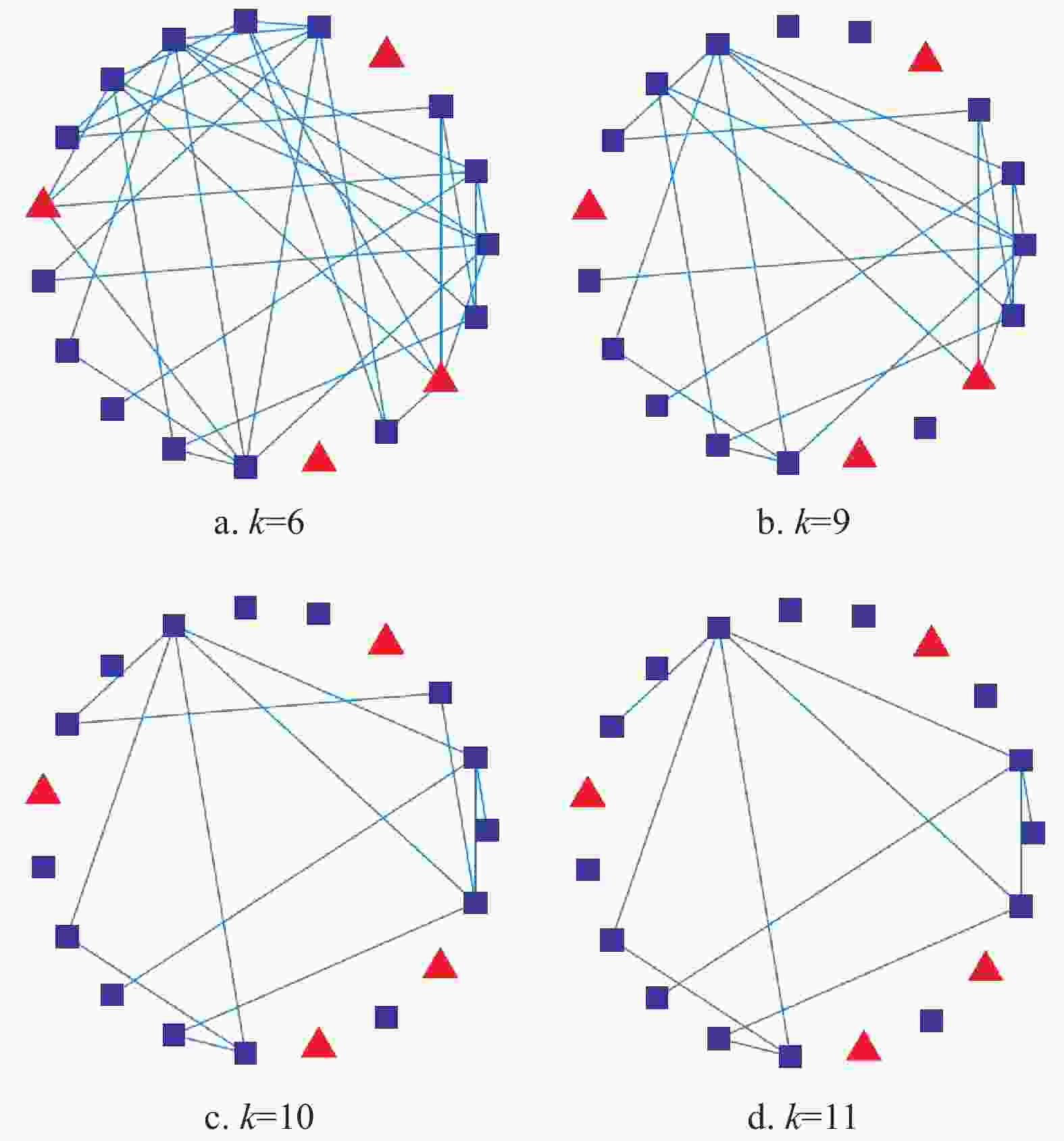
Example 3 (defense mechanism). In this example, we further study the Eq. (3) under defense mechanism with heterogeneous threshold $\varepsilon (k) = 0.9 \times {0.95^k}$. As shown in Fig. 5a, the opinions of individuals are slowly far away from the intruder’s influence, and divide into many clusters at steady state. Here, the solid line represents target individuals, and the dotted line represents normal individuals. The. In order to better understand the evolving process of opinions, Fig. 6 shows the network topology at certain time step. As the communication network topology evolves, the target individuals selected by the intruder become isolated. It is worth mentioning that the choice of parameters of threshold function has great influence on the false alarm rate, i.e., the normal individual is mistaken for target individual, or vice versa. Thus, it is key to find a suitable threshold function. However, to the best of our knowledge, few results have been obtained to the choice of the threshold. In the existing literatures, the works^[27,40] provide some heuristic algorithms to generate threshold functions which cannot be simply characterized by general explicit expressions.

Figure 5.  The dynamic evolution of opinions under defense mechanism.

Figure 6.  The evolution of networks in communication under defense mechanism.

In this paper, we have investigated the dynamic evolution of individual social opinions in an attack-defense environment, where an intruder disguises itself as one of neighboring individual of target individuals in order to guide the network opinion to a serious direction. First, we have developed a modified DeGroot model in the presence of malicious opinion injection, and have proved that all the individuals’ opinions converge to the malicious opinion of the intruder if no defense mechanism is implemented. Second, we have proposed an algorithm to obtain a suboptimal solution to select target individuals in order to maximize the convergence speed of opinion aggregation when the number of target individuals is limited. The results can help us effectively improve the defense capability of the network by protecting those ’key’ individuals. Third, we have proposed a defense mechanism using the online gap comparison to resist hostile attacks, which is similar to the self-inspecting and isolating scheme in virus spreading area. We have also analyzed the opinion convergence performance of individuals with defense mechanism. Finally, the numerical simulation have verified all the derived results and explored some performances of the proposed model.