-
车辆自组网(VANETs)是智能交通系统的核心,能够为驾驶员提供实时的交通诱导、安全及娱乐等信息,低时延、高可靠性通信是VANET的关键。然而,车辆的移动特性使得VANET的动态拓扑结构快速变化,故无法满足稳定性的通信需求。将分簇方法应用于车联网中,可以降低通信的不稳定性和复杂性。通过簇头车辆进行信息传输,可以提高交通效率,降低传输时延。目前,大多数的分簇方法是针对简单的多车道公路场景进行设计的[1]。如,文献[2]利用较低的传输延迟和网络开销获得较高的传输成功率,对停放路边和非路边车辆进行分簇。文献[3]考虑双向车道信息共享,提出基于时间划分策略和基于最优长度的分簇机制。在交叉路口,车辆会出现聚集现象,车辆的连通率会提高,但车道上每个车辆的转向不一致,车辆经过交叉路口后,簇的稳定性降低。为此,文献[4]对通过交叉路口前的车辆行为进行预测,考虑车道数,从车辆数量最多的车道方向选择簇头。文献[5]针对交通流不确定性对交叉口交通状态的影响,提出一种基于区间数据的
$k$ 均值聚类城市交叉口交通状态识别方法。文献[6]提出一种自适应分簇协议,考虑车辆节点的编号、方向、速度大小及邻居车辆节点数目,采用多目标萤火虫算法得到最优簇头。虽然簇的引入能提高车辆之间通信的稳定性,但以上文献未考虑选择有效的中继转发方式,以提高通信的可靠性[7]。基于传统的放大转发(amplify-forward, AF)和译码转发(decode-forward, DF)[8]方式,文献[9]采用单向混合译码放大转发(hybrid decode-amplify-forward, HDAF)协作方式,比AF和DF节约资源的消耗。文献[10]在VANETs系统中采用双向中继协作方式,以实现两源节点的双向信息交流,在低功耗的情况下获得高吞吐量。文献[11]针对频谱共享问题,对双向中继的选择和频谱分配进行优化,使网络速率最大化。文献[12]结合马尔可夫决策过程,采用双向中继传输模式,推导网络最优传输性能。以上文献均使用瑞利衰落信道模型。但在实际复杂的衰落环境中,NaKagami-m衰落信道模型更能体现出实际信道的衰落特性。为此,文献[13]验证了该衰落模型在车辆通信的适用性。在此基础上,基于传统AF/DF,通过最小化系统中断来提高平均频谱效率[14-15]。
综上所述,本文在NaKagami-m衰落信道条件下提出交叉路口的基于车辆权值分簇的中继转发方案。该方案包括簇的形成、簇头的选举、簇的维护及中继转发方式的选择。
-
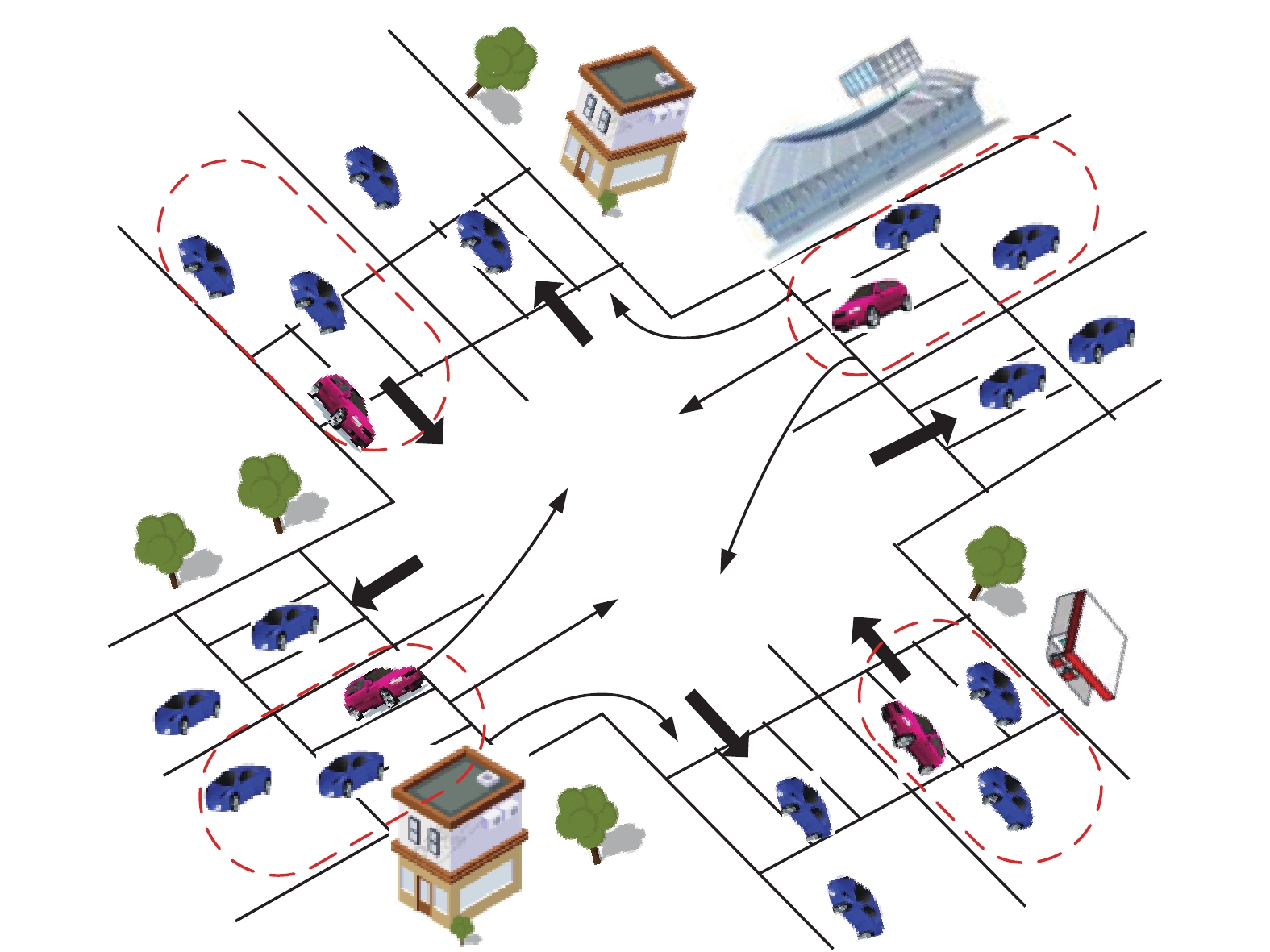
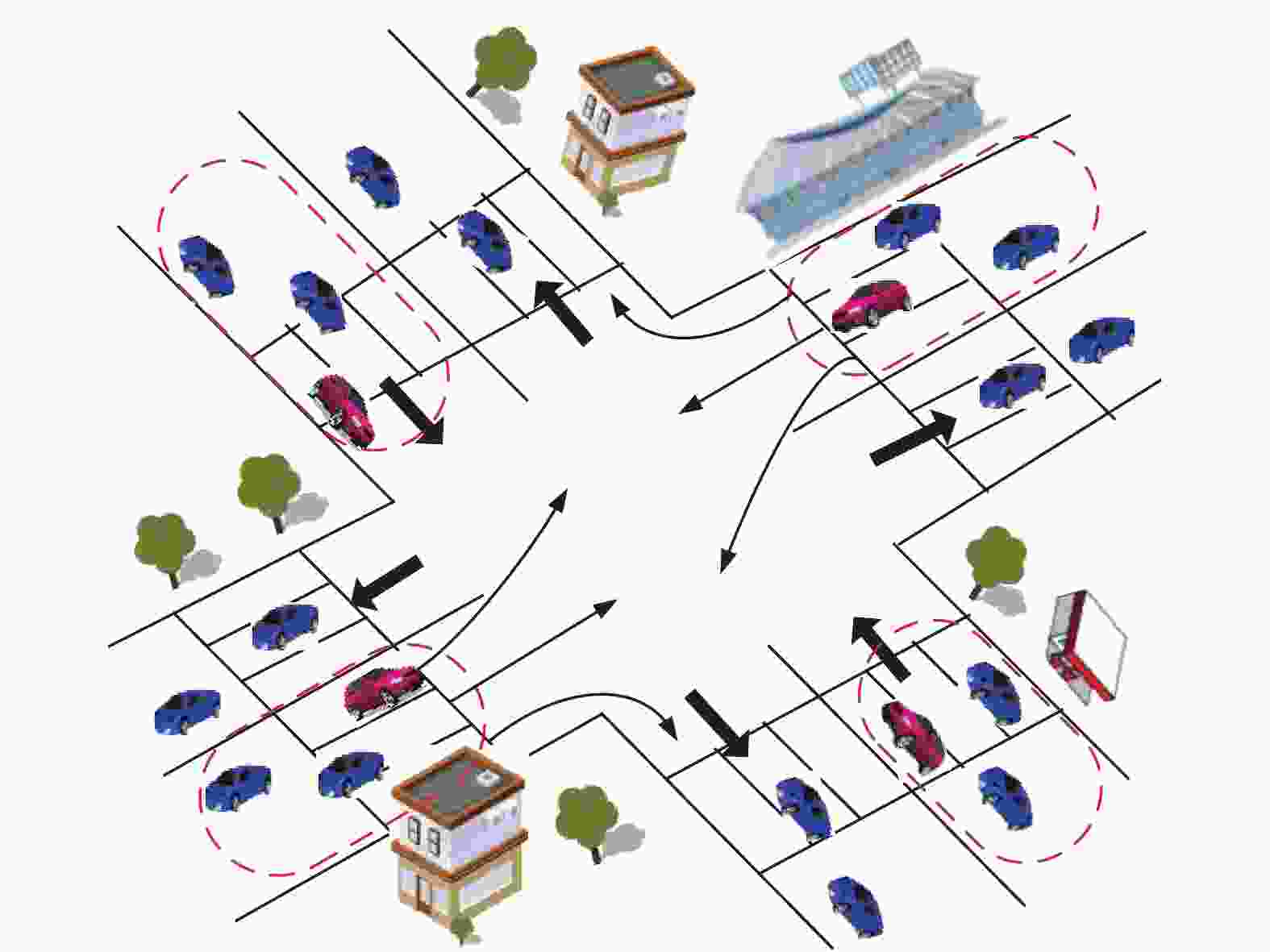
如图1所示,考虑城市道路的交叉路口场景,假设交叉路口的每条道路是双车道。交叉路口的转向最多有3个方向:左转、直行和右转。
由于在交叉口附近或者在车辆行驶的高峰期,车辆的速度和车辆之间的距离会相对稳定,变动的范围不会过大,对车辆之间的传输性能影响较小,为了简便算法可以忽略不计。由于城市道路上车流量是在不断变动的,车辆在通信过程中会产生反射、绕射和衍射等现象,这些现象导致接收车辆会收到多条不同路径到达的信号,而NaKagami-m衰落更能体现出实际信道的衰落特性,故本文考虑NaKagami-m衰落信道以表征车辆的通信信道[13]。车辆之间的交通流、相对距离以及连通率表示如下。
1)交通流
在直线公路上,车辆数服从泊松分布,设公路长度为
$l$ ,车辆的平均密度为$\rho $ (车辆数/m),那么总的车辆数为$\lambda = \rho l$ ,且公路上有$N$ 辆车的概率为:$$P(X = N) = \frac{{{\lambda ^N}{{\rm e}^{ - \lambda }}}}{{N!}} = \frac{{{{(\rho l)}^N}{{\rm e}^{ - \rho l}}}}{{N!}}$$ (1) 车辆在距离交叉路口处选择行驶方向,左转、右转和前行,即可用一个有限集合
$k$ 表示[16]:$k = \{ L,R,S\} $ ,其中,$L$ 表示左转,$R$ 表示右转,$S$ 表示前行。根据车辆的移动特性,对于不同车流量方向,车辆的权重不一样,权重公式为:
$$\varpi _i^k = \left\{ \begin{array}{l} 1\quad \quad \;\;\,k = r \\ {M_k}/M\;\quad k \ne r \\ \end{array} \right.\quad k \in (L,R,S)$$ (2) 式中,在距离交叉口处的公路上,
${ M}({ M} \leqslant { N})$ 为车辆数;${{ M}_L}$ 为左转方向的车辆数;${ M_R}$ 为右转方向的车辆数;${ M_S}$ 直行为方向的车辆数;$r$ 为车辆$i$ 的方向。2)相对距离和速度
车辆在直线公路上,车辆是不分左转、右转和前行的,则车辆
$i$ 的位置$\left( {{x_i},{y_i}} \right)$ 与其邻居之间总的相对距离和为:$$\Delta {d_1} = \sum\limits_{i = 1}^{{N_1}} {\sqrt {{{({x_i} - {x_j})}^2}{\rm{ }} + {{({y_i} - {y_j})}^2}} } $$ (3) 式中,
${N_1}$ 为车辆$i$ 的邻居数。车辆
$i$ 的速度${v_i}$ 与其相邻车辆的相对速度和为:$$\Delta {v_1} = \sum\limits_{i = 1}^{{N_1}} {\frac{{{v_i} - \bar v}}{\sigma }} $$ (4) 式中,
$\bar v$ 为所有车辆的平均速度$\bar v = \dfrac{1}{{{N_1}}}\displaystyle\sum\limits_{i = 1}^{{N_1}} {{v_i}}$ ;$\sigma $ 为标准差$\sigma = \sqrt {\dfrac{{\displaystyle\sum\limits_{i = 1}^{{N_1}} {({v_i} - \bar v)} }}{{{N_1} - 1}}}$ 。在交叉口处,车辆要进行方向的选择,车辆的相对距离为:
$$d_i^k = \sum {\varpi _i^k\Delta {d_2}} $$ (5) 式中,
$\Delta {d_2} = \left\{ \begin{array}{l} \displaystyle\sum\limits_{i = 1}^{{M_k}} {\sqrt {{{(x_{_i}^r - x_j^k)}^2}{\rm{ }} + {{(y_{_i}^r - y_j^k)}^2}} }\; \qquad k = r \\ 0\;\qquad k \ne r \\ \end{array} \right.$ 。当车辆$i$ 的方向$r$ 与邻居车辆的转向不一致时为0。相应地,车辆
$i$ 的相对速度为:$$v_i^k = \sum {\varpi _i^k\Delta {v_2}} $$ (6) 式中,
$\Delta {v_2} = \displaystyle\sum\limits_{i = 1}^{{M_k}} {\dfrac{{v_i^r - {{\bar v}_r}}}{{{\sigma _2}}}} $ ,${\bar v_r}$ 为交叉口处所有与车辆$i$ 方向相同车辆的平均速度,${\bar v_r} = \dfrac{1}{{{M_k}}}\displaystyle\sum\limits_{i = 1}^{{M_k}} {v_{_i}^r}{\text{,}}k = r{\text{;}}$ ${\sigma _2}$ 为标准差,${\sigma _2} = \sqrt {\dfrac{{\displaystyle\sum\limits_{i = 1}^{{M_k}} {(v_{_i}^r - {{\bar v}_k})} }}{{{M_k} - 1}}} {\text{,}}k = r{\text{。}}$ 3)连通率
连通率[17]代表两通信车辆间的链路质量,连通率越高,通信车辆间链路越稳定。设车辆
$i$ 为簇头车辆,通信范围为$R$ ,车辆$i$ 与邻居车辆$j$ 之间的距离$x$ 服从指数分布,车辆密度为$\rho $ ,均值为${1}/{\rho }$ ,方差为${1}/{{{\rho ^2}}}$ ,则通信车辆间的概率密度函数为$f(x) = \rho {{\rm e}^{ - \rho x}}$ ,两车辆间连通的概率为${p_x}(x \leqslant R) = 1 - {{\rm e}^{ - \rho x}}$ ,则车辆$i$ 的邻居车辆共有${N_1}$ 辆车的连通概率为:$${p_i} = \prod\limits_{i = 1}^{{N_1}} {{p_x}} = {(1 - {{\rm e}^{ - \rho x}})^{{N_1} - 1}}$$ (7) -
车辆在成簇的过程中受到多方面的影响,本文提出权值分簇算法选取各方向的最小权值作为簇头,为提高通信的可靠性采用双向AF/DF的中继转发方式进行数据传输。
-
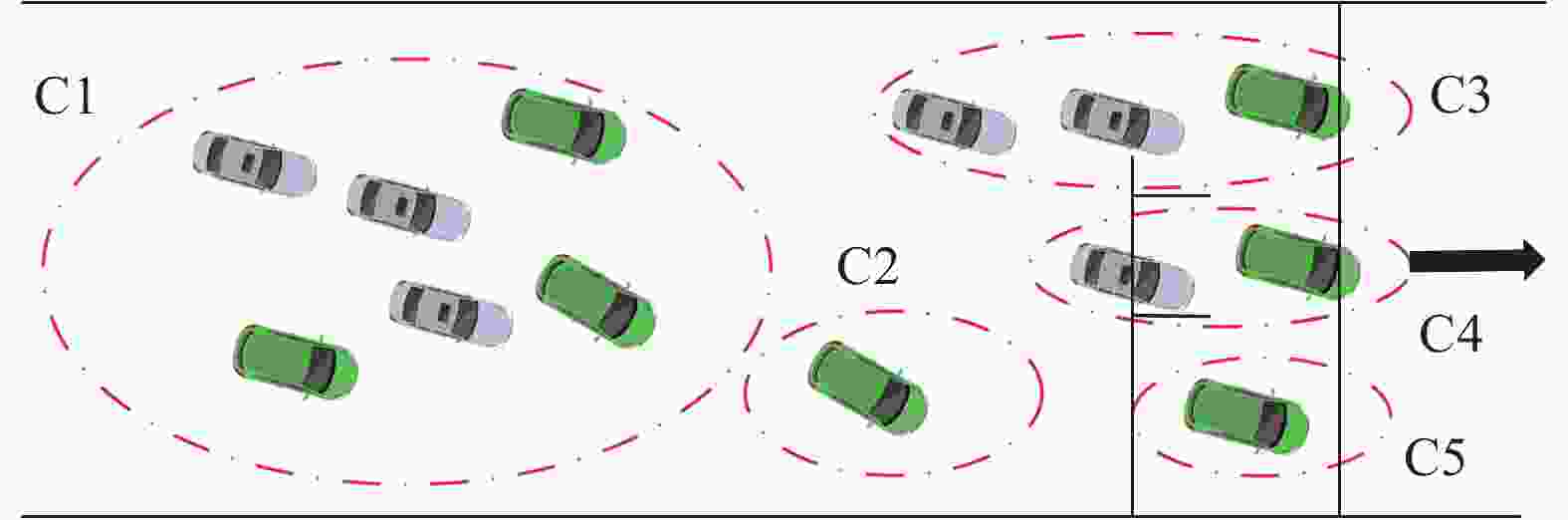
车辆可以选择3个方向通过交叉路口:前行、左转和右转。在车辆选择方向时,车辆会自觉的排列到要转同方向的队伍中,形成通信簇。
-
车辆
$i$ 在交叉口处开始向簇头(CH)车辆发送车辆的信息,包括速度、到交叉口的距离,通过交叉口的转向等。CH之间每隔一段时间进行一次信息交换,每个CH车辆接收到其簇成员(CM)的信息,在CH信息交换后,把其他簇的信息通知到其CM。C1为簇1,CH1为簇1内的CH车辆;CM1为簇1内的CM。图2为向右行驶车道上车辆分簇模型,C1内有6辆车,中间一排靠前的淡蓝色车辆为簇头CM1,通过CH1知道其他簇的信息,同时CH1把该簇内前行、向左和向右行驶的CM1车辆信息发送给相应方向的CH1车辆。C2其他向前行驶车辆形成的簇,拥有与C1簇相同的方式传递信息,该簇中向前、左转和右转的信息分别传到对应最前边(靠近交叉口)对应簇中,C3为左转车辆簇,C4为前行车辆簇,C5为右转车辆簇。其中C2~C5中绿色车辆为簇头。
C3~C5中为不同方向的车辆簇,在接近交叉口处的直线车道上,CH开始收集簇内其他车辆预行驶方向的信息,并把同一方向合成一个簇。
在每个簇内,采用多因子权值法,选出最优权值作为簇头。在直线的道路上,簇头的选择公式为:
$$ {W_i} = {w_3}{p_i}/\left( {{w_1}\Delta {d_1} + {w_2}\Delta {v_1}} \right) $$ (8) 式中,
${w_1}$ 为距离的权重;${w_1}\Delta {d_1}$ 表示距离的影响程度;${w_2}$ 为相对速度的权重;${w_2}\Delta {v_1}$ 表示速度的影响程度;${w_3}$ 为交通流的权重因子;${w_3}{p_i}$ 表示连通概率的影响程度。并将3个因素看成一个整体,即$ {w_1} + {w_2} + {w_3} = 1$ 。对式(8)求得的各用户综合权重值进行升序排序,将排序靠前的最小值用户作为簇头。由于交叉口处的车辆比直线道路上多,且一个簇内的车辆在交叉路口会有大幅度的调整,簇内许多车辆的运行方向不同,很容易造成簇的分离。所以,本文在交叉路口附近车辆进行不同方向的运动前,把直线道路上距离交叉路口近且不是簇内的车辆,根据预备相同转向车辆分为一簇,并从中提前选好簇头。同理,根据相同转向车辆的相对距离及速度的影响程度,选择综合权重最小值作为簇头,公式为:
$$ W_i^k = {w_1}d_i^k + {w_2}v_i^k\;\qquad k = r $$ (9) -
根据元胞自动机模型[18]预测两车辆间的距离,车辆
$i$ 与车辆$j$ 在$t$ 时刻的初始位置为${X_i}\left(\; t \;\right)$ 和${x_j}\left( \;t\; \right)$ ,速度和加速度分别为${v_i}\left(\; t\; \right)$ 、${v_j}\left(\; t\; \right)$ 和${a_i}$ 、$ {a_j}$ (当$a > 0$ 为加速,$a < 0$ 为减速),在$t + 1$ 时刻车辆$i$ 和车辆$j$ 的速度为:$$\left\{ \begin{aligned} & {v_i}(t + 1) = {v_i}(t) + {a_i} \\ & {v_j}(t + 1) = {v_j}(t) + {a_j} \\ \end{aligned} \right.$$ (10) 车辆的速度范围在0~vmax。
$t + 1$ 时刻两车间的速度差为:$$\Delta {v_{i,j}}(t + 1) = |{v_i}(t + 1) - {v_j}(t + 1)|$$ (11) $t + 1$ 时刻两车间的距离差为:$$\Delta {x_{i,j}}(t + 1) = \Delta {x_{i,j}}(t) + \Delta {v_{i,j}}(t + 1)$$ (12) 式中,
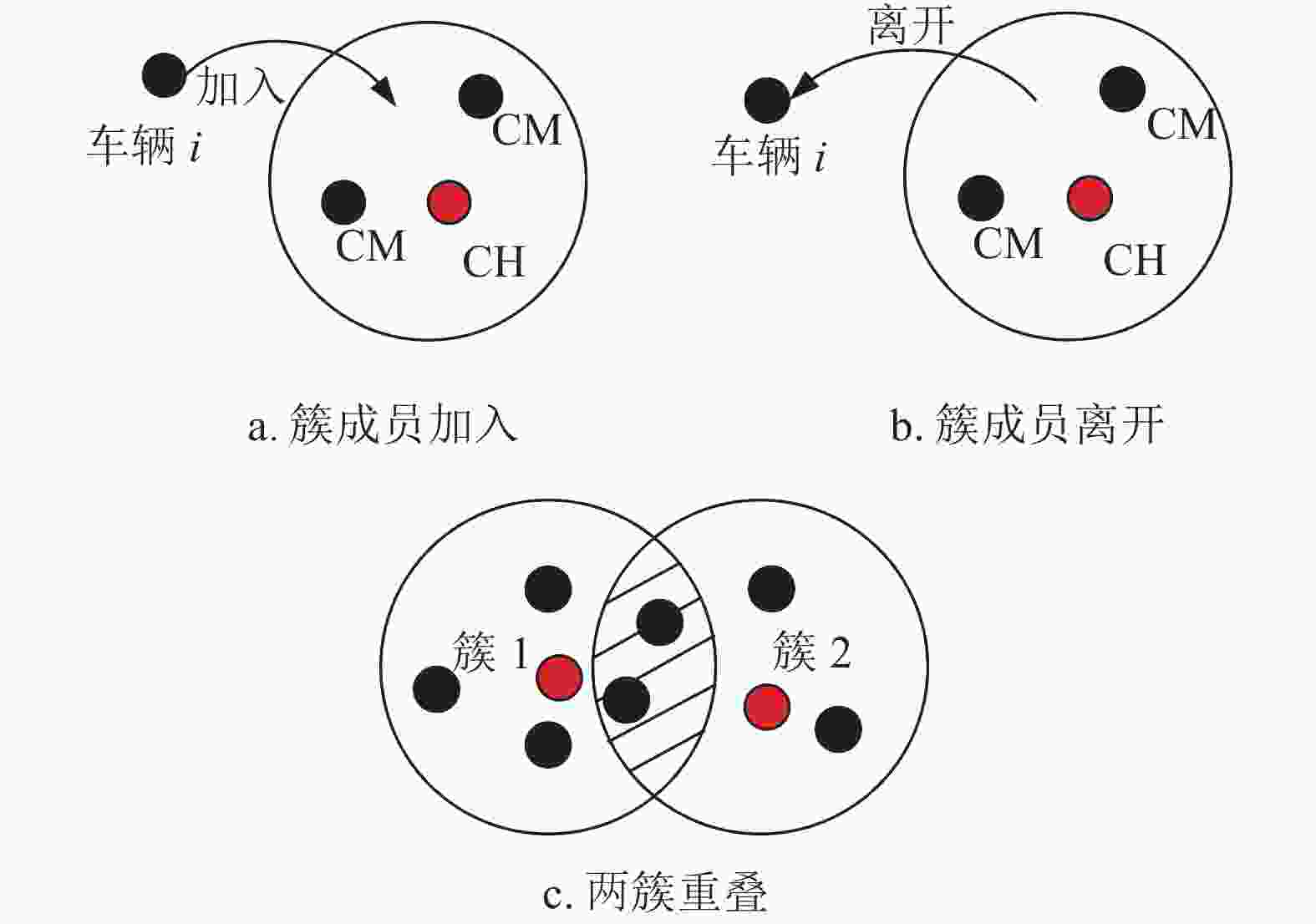
$ \Delta {x_{i,j}}(t) = |{x_i}(t) - {x_j}(t)|$ 图3中红色圆表示簇头车辆,黑色圆表示簇成员车辆。
1)簇成员加入
①车辆
$i$ 向四周发送信号,若收到一个簇头车辆的回复,则加入该簇内;②若收到大于一个簇头车辆的回复,则比较此车辆与各簇头车辆的预测距离,选择距离近的簇头并加入该簇内,簇头更新成员列表,并通知其他簇成员此车辆加入该簇;
③若在
$T$ 时间内,没有收到任何簇头的消息,则在其邻居范围内查看是否有邻居簇成员,且在邻居簇成员的通信范围内。若在其通信范围内,则加入簇,成为簇外成员,若不在通信范围内,则继续向四周发送信号,在$T$ 时间内仍未收到任何簇头或邻居簇成员信息,则自己成为簇头,如图3a所示。2)簇成员离开
车辆从某个簇内离开之前,先向四周发送hello消息,若在
$T$ 时间内未收到任何消息,车辆向簇头发送离开信息,并继续向四周发送hello消息,${T_1}$ 时间后,收到簇头消息,加入簇,未收到消息自己成为临时簇头;若在$T$ 时间内收到其他簇头消息,车辆先向自己所在簇的簇头发送离开信息,收到其他簇头的信息,直接加入簇,收到大于一个簇首信息,按照预测距离小的,加入簇,如图3b所示。3)两簇重叠
当车辆在行驶的过程中,簇1与簇2之间的簇成员重叠的部分小于等于簇1(或簇2)成员的一半,则保持原状;若大于簇1(或簇2)的一半,则重新分簇,只比较两个簇头的
$W$ 值,选取$W$ 值小的作为新的簇头,如图3c所示。 -
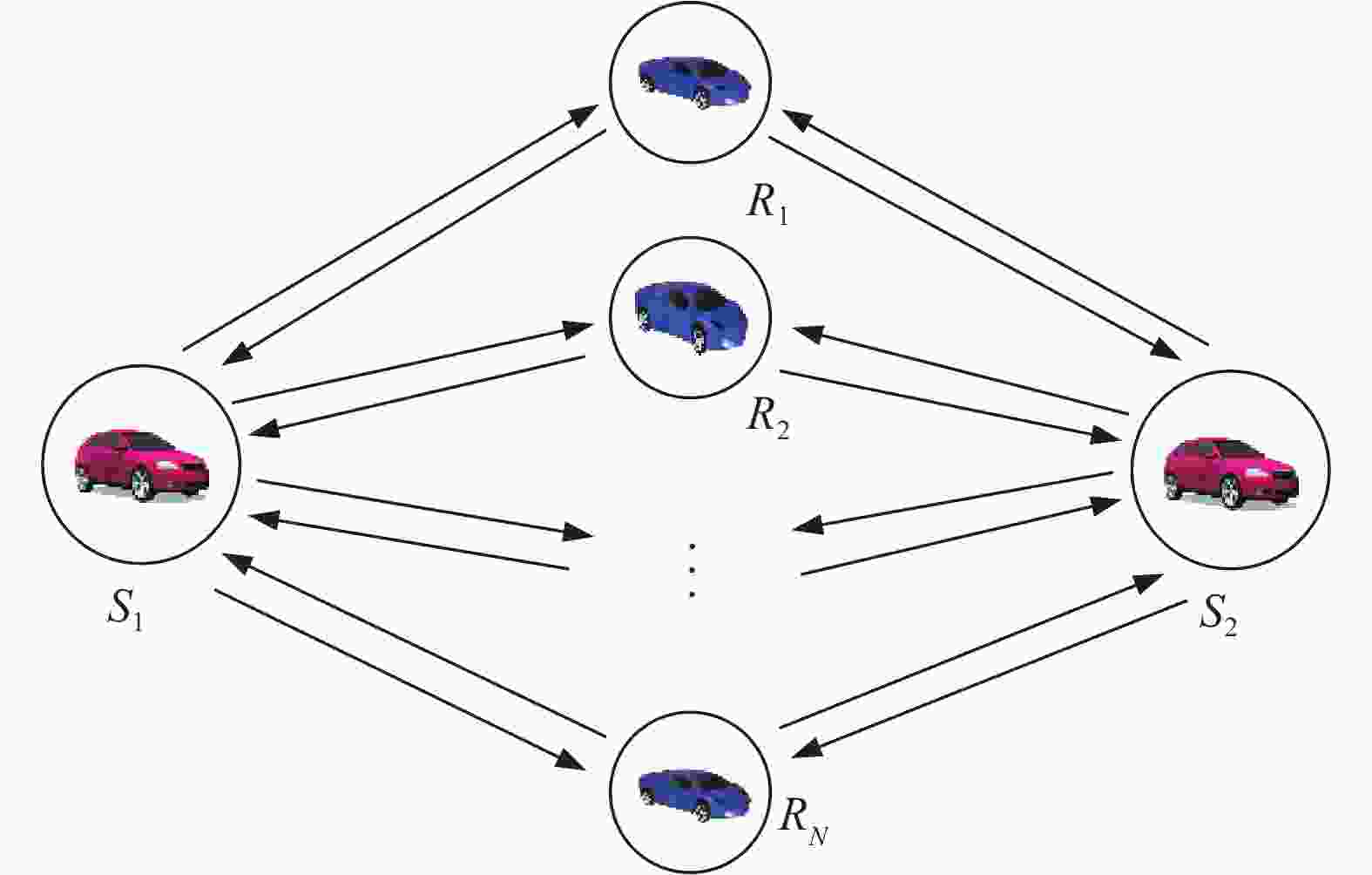
簇头车辆具有簇内广播和簇间通信的中继功能,负责簇内的传输调度和信道分配,且支持不同簇之间的通信。
当每两个簇内的簇头之间要进行簇间通信,采用双向中继系统模型如图4所示。簇头1和簇头2分别为两个源节点
${S_1}$ 和${S_2}$ ,有$N$ 个中继节点车辆$({R_i},i = 1,2,\cdots,N)$ ,假设两个源节点之间没有直接传输的信道,在NaKagami-m衰落信道下,通过AF或DF进行协助通信,则需要在两个时隙内完成通信:第一时隙,${S_1}$ 和${S_2}$ 同时向中继节点传送信息;第二时隙,且${R_i}$ 把收到的信息放大(或解码)转发给源节点。令${S_1}{\text{、}}{S_2}$ 和$ R_i$ 信号的功率分别${P_1}{\text{、}}{P_2}$ 和${P_3}$ ,且${P_1} = {P_2} = {P_3} = P{\text{,}}{N_0} = 1$ ,${S_1} \leftrightarrow {R_i}$ 和${S_2} \leftrightarrow {R_i}$ 的信道衰落系数分别为${h_{{S_1}{R_i}}}$ 和${h_{{S_2}{R_i}}}$ 。 -
考虑高信噪比的情况,假设总的传输功率为
$P$ ,且${P_{{S_1}}} = {P_{{S_2}}} = P$ 。若采用AF进行放大转发,先选用第$i$ 条中继进行转发,则${S_2}$ 信号接收到的信噪比近似为[19]:$$ \begin{split} \gamma _{{S\!_1}{R_i}{S\!_2}}^{\rm AF} =\,& \dfrac{{\dfrac{{{P_{{S\!_1}}}|{h_{{S\!_1}{R_i}}}{|^2}}}{{{N_0}}} \dfrac{{{P_{{R_i}}}|{h_{{R_i}{S\!_2}}}{|^2}}}{{{N_0}}}}}{{\dfrac{{{P_{{S\!_1}}}|{h_{{S\!_1}{R_i}}}{|^2}}}{{{N_0}}} + \dfrac{{({P_{{R_i}}} + {P_{{S\!_2}}})|{h_{{S\!_2}{R_i}}}{|^2}}}{{{N_0}}} + 1}} \approx\\ & \min \left[\dfrac{P}{{{N_0}}}|{h_{{S\!_1}{R_i}}}{|^2},\dfrac{P}{{{N_0}}}|{h_{{S\!_2}{R_i}}}{|^2}\right] \end{split} $$ (13) ${S_1}$ 信号接收到经过第$i$ 条中继信噪比近似为[19]:$$\begin{split} \gamma _{{S\!_2}{R_i}{S\!_1}}^{\rm AF} =\,& \dfrac{{\dfrac{{{P_{{S\!_2}}}|{h_{{S\!_2}{R_i}}}{|^2}}}{{{N_0}}} \dfrac{{{P_{{R_i}}}|{h_{{R_i}{S\!_1}}}{|^2}}}{{{N_0}}}}}{{\dfrac{{{P_{{S\!_2}}}|{h_{{S\!_2}{R_i}}}{|^2}}}{{{N_0}}} + \dfrac{{({P_{{R_i}}} + {P_{{S\!_1}}})|{h_{{S\!_1}{R_i}}}{|^2}}}{{{N_0}}} + 1}}\approx \\ & \min \left[\dfrac{P}{{{N_0}}}|{h_{{S\!_1}{R_i}}}{|^2},\dfrac{P}{{{N_0}}}|{h_{{S\!_2}{R_i}}}{|^2}\right] \end{split} $$ (14) ${S_1}$ 和${S_2}$ 信号接收到的信息量分别为:$$ \left\{\begin{split} & {I_{{S\!_1}{R_i}{S\!_2}}} = \frac{1}{2}{\log _2}(1 + {\gamma _{_{{S\!_1}{R_i}{S_2}}}}) \\ & {I_{{S\!_2}{R_i}{S\!_1}}} = \frac{1}{2}{\log _2}(1 + {\gamma _{_{{S\!_2}{R_i}{S\!_1}}}}) \end{split} \right. $$ (15) 假设各信道幅度服从NaKagami-m分布,且相互独立。随着
$m$ 参数的改变,NaKagami-m分布能够建模多种衰落特性的信道,当$m = 0.5$ 时,NaKagami-m分布变成单侧高斯分布,当$m = 1$ 时,变成瑞利分布。在NaKagami-m信道下,节点$i$ 到节点$j$ 的信道功率增益${g_{ij}}$ 服从Gamma分布,其概率密度函数和累计分布函数可以分别表示为[20]:$$ \left\{\begin{split} & {f_{{g_{ij}}}}(x) = \frac{{{m^m}{x^{m - 1}}}}{{\Gamma (m)}}{{\rm{e}}^{ - mx}}\;\qquad x \geqslant 0 \\ & {F_{{g_{ij}}}}(x) = \frac{{\Gamma (m,mx)}}{{\Gamma (m)}}\;\qquad x \geqslant 0 \\ \end{split} \right. $$ (16) 式中,
$\Gamma (a,ax)$ 为不完全Gamma函数;$\Gamma (a)$ 为完全Gamma函数。定义端到端的瞬时信噪比低于某一固定阈值
$\varpi $ 的概率,由香农公式得双向中继协作通信系统中断概率应满足$\Pr [|{h_{{s_1}{R_i}}}{|^2} < \varpi ] \Pr [|{h_{{s_2}{R_i}}}{|^2} > \varpi ]$ 或者$\Pr [|{h_{{s_1}{R_i}}}{|^2} > \varpi ] \Pr [|{h_{{s_2}{R_i}}}{|^2} < \varpi ]$ 。则总的中断概率表示为:$$P_{\rm out}^{\rm zong} = {P_{{S\!_1}{R_i}{S\!_2}}} + {P_{{S\!_2}{R_i}{S\!_1}}} - {P_{{S\!_1}{R_i}{S\!_2}}} \cap {P_{{S\!_2}{R_i}{S\!_1}}}$$ (17) 式中,
${P_{{S\!_1}{R_i}{S\!_2}}}$ 为${S\!_1} \to {R_i} \to {S\!_2}$ 通信链路的中断概率,表示为:$$ \begin{split} {P_{{S\!_1}{R_i}{S\!_2}}} = \,& P_{{\rm{out}}}^1 = \sum\limits_{I = 1}^N {\Pr [{I_{{S\!_1}{R_i}{S\!_2}}} < R]}= \\ & \sum\limits_{i = 1}^N {\Pr (\min [|{h_{{S\!_1}{R_i}}}{|^2},|{h_{{S\!_2}{R_i}}}{|^2}] < \varpi )} = \\ & \sum\limits_{i = 1}^N {(\Pr [|{h_{{S\!_1}{R_i}}}{|^2} < \varpi ]} \Pr [|{h_{{S\!_2}{R_i}}}{|^2} > \varpi ] + \\ & \Pr [|{h_{{S\!_1}{R_i}}}{|^2} > \varpi ] \Pr [|{h_{{S\!_2}{R_i}}}{|^2} < \varpi ]) \end{split} $$ (18) 式中,
$\varpi = \dfrac{{({2^{2{R_{\rm th}}}} - 1)P}}{{{N_0}}}$ ;${R_{\rm th}}$ 为传输速率。$$ \begin{split} & \Pr [|{h_{{S\!_1}{R_i}}}{|^2} < \varpi ] \Pr [|{h_{{S\!_2}{R_i}}}{|^2} > \varpi ]=\\ & \left( {1 - \dfrac{{\Gamma \left({m_{{S\!_1}{R_i}}},\dfrac{{{m_{{S\!_1}{R_i}}}}}{{{\Omega _{{S\!_1}{R_i}}}}}\varpi \right)}}{{\Gamma ({m_{{S\!_1}{R_i}}})}}} \right) \dfrac{{\Gamma \left({m_{{S\!_2}{R_i}}},\dfrac{{{m_{{S\!_2}{R_i}}}}}{{{\Omega _{{S\!_2}{R_i}}}}}\varpi \right)}}{{\Gamma ({m_{{S\!_2}{R_i}}})}} \end{split} $$ (19) $$ \begin{split} & \Pr [|{h_{{S\!_1}{R_i}}}{|^2} > \varpi ] \Pr [|{h_{{S\!_2}{R_i}}}{|^2} < \varpi ]=\\ & \dfrac{{\Gamma \left({m_{{S\!_1}{R_i}}},\dfrac{{{m_{{S\!_1}{R_i}}}}}{{{\Omega _{{S\!_1}{R_i}}}}}\varpi \right)}}{{\Gamma ({m_{{S\!_1}{R_i}}})}} \left( {1 - \dfrac{{\Gamma \left({m_{{S\!_2}{R_i}}},\dfrac{{{m_{{S\!_2}{R_i}}}}}{{{\Omega _{{S\!_2}{R_i}}}}}\varpi \right)}}{{\Gamma ({m_{{S\!_2}{R_i}}})}}} \right) \end{split} $$ (20) 令
${m_{{S\!_1}{R_i}}} = {m_{{S\!_2}{R_i}}} = {m_m}$ ,${\Omega _{{S\!_1}{R_i}}} = {\Omega _{{S\!_2}{R_i}}} = {\Omega _m}$ ,式(19)和式(20)代入式(18)中,可以简化为:$$ P_{\rm out}^1 = {\left( {2\dfrac{{\Gamma \left({m_m},\dfrac{{{m_m}}}{{{\Omega _m}}}\varpi \right)}}{{\Gamma ({m_m})}} - 2{{\left( {\dfrac{{\Gamma \left({m_m},\dfrac{{{m_m}}}{{{\Omega _m}}}\varpi \right)}}{{\Gamma ({m_m})}}} \right)}^2}} \right)^N} $$ (21) 同理,
${S\!_2}$ 信号传递给${S\!_1}$ 时的中断概率为:$$ \begin{split} & {P_{{S\!_2}{R_i}{S\!_1}}} = P_{\rm out}^2=\\ & {\left( {2\dfrac{{\Gamma \left({m_m},\dfrac{{{m_m}}}{{{\Omega _m}}}\varpi \right)}}{{\Gamma ({m_m})}} - 2{{\left( {\dfrac{{\Gamma \left({m_m},\dfrac{{{m_m}}}{{{\Omega _m}}}\varpi \right)}}{{\Gamma ({m_m})}}} \right)}^2}} \right)^N} \end{split} $$ (22) 令
$\dfrac{{\Gamma \left({m_m},\dfrac{{{m_m}}}{{{\Omega _m}}}\varpi \right)}}{{\Gamma ({m_m})}} = X$ ,把式(21)和式(22)代入式(17)中,得:$$P_{\rm out}^{\rm zong} = 2{[2(1 - X)]^N} - {[4{X^2}(1 - 2X + {X^2})]^N}$$ (23) -
若采用DF进行转发,则
${S_1} \to {R_i}$ 、${S_2} \to {R_i}$ 、${R_i} \to {S_2}{\text{、}}{R_i} \to {S_1}$ 信噪比分别为:$$ \begin{split} & {\gamma _{_{{S\!_1}{R_i}}}} = \frac{{{P_{{S\!_1}}}|{h_{{S\!_1}{R_i}}}{|^2}}}{{{N_0}}},\;{\gamma _{_{{S\!_2}{R_i}}}} = \frac{{{P_{{S\!_2}}}|{h_{{S\!_2}{R_i}}}{|^2}}}{{{N_0}}} \\ & {\gamma _{_{{R_i}{S_2}}}} = \frac{{{P_{{R_i}}}|{h_{{S\!_2}{R_i}}}{|^2}}}{{{N_0}}},\;{\gamma _{_{{R_i}{S\!_1}}}} = \frac{{{P_{{R_i}}}|{h_{{S\!_1}{R_i}}}{|^2}}}{{{N_0}}} \end{split} $$ (24) 假设选择中继
${R_i}$ 转发信息,且所有信道在信息传输时间段保持不变。${R_i}$ 分别向两个源节点传递信息的信息量为:$$ \begin{split} &{C_{{S\!_j}{R_i}}} = \frac{1}{2}{\log _2}[1 + ({\gamma _{_{{S\!_1}{R_i}}}} + {\gamma _{_{{S\!_2}{R_i}}}})]=\\ & \;\; \frac{1}{2}{\log _2}\left(1 + \frac{{P(|{h_{{S\!_1}{R_i}}}{|^2} + |{h_{{S\!_2}{R_i}}}{|^2})}}{{{N_0}}}\right) \end{split} $$ (25) $$ {C_{{R_i}{S\!_j}}} = \frac{1}{2}{\log _2}\left[1 + \dfrac{{P(|{h_{{S\!_1}{R_i}}}{|^2} + |{h_{{S\!_2}{R_i}}}{|^2})}}{{{N_0}}}\right] $$ (26) 式中,
$ j = 1,2$ 。本文假设当
$S - R$ 链路为发生中断,则$R$ 能够正确解码。由文献[21]可知,成功解码${S_1}$ 和${S_2}$ 的信号集合为$\varPhi$ 。若有$N$ 个中继,则D有${2^N}$ 个可能子集成功解码,令$D = {D_n}$ ,$\varPhi = \{ \varnothing ,{D_1},{D_2},\cdots,{D_{{2^N} - 1}}\}$ ,${D_n} = R - {\bar D_n}$ ,${\bar D_n}$ 为${D_n}$ 的补集。假设成功解码的中继为${R_i}$ ,错误解码的中继为${R_t}$ ,${R_{\rm th}}$ 为信息传输速率,则$R = \{ {R_i} \cup {R_t}|i,t = 1,2,\cdots,N\}$ 。$\varPhi =\varnothing$ 时,$$ ({C_{{S\!_1}{R_i}}} + {C_{{S\!_2}{R_i}}}) < {R_{\rm th}}\;\qquad {R_i} \in R $$ (27) $\varPhi = {D_n}$ 时,$$ \left\{ \begin{array}{l} ({C_{{S\!_1}{R_i}}} + {C_{{S\!_2}{R_i}}}) > {R_{\rm th}}\;\qquad{R_i} \in {D_n} \\ ({C_{{S\!_1}{R_t}}} + {C_{{S\!_2}{R_t}}}) < {R_{\rm th}}\;\qquad{R_t} \in {{\bar D}_n} \\ \end{array} \right. $$ (28) 根据全概率公式,当
$\varPhi = {D_n}$ 时,如果${C_{{R_i}{S_2}}}$ <${R_{\rm th}}$ ,或者$\varPhi = \varnothing$ 时,都会产生信号中断,所以,${S_1} \to {S_2}$ 中继选择的中断概率为[19]:$$ \begin{split} & {P_{{S\!_1}{R_i}{S\!_2}}} =\, P_{{{\rm{out}}}}^3 = \sum\limits_{n = 1}^{{2^N} - 1} {\Pr (\varPhi = {D_n})} \times \\ &\quad\;\Pr [{C_{{R_i}{S\!_2}}} < {R_{{\rm{th}}}}] + \Pr (\varPhi = \varnothing) \end{split} $$ (29) 式中,
$\Pr (\varPhi = {D_n})$ 的概率为:$$ \begin{split} &\qquad\qquad\qquad\qquad \Pr (\varPhi = {D_n})= \\ & \prod\limits_{{R_i} \in {D_n}} {\Pr \left[\frac{1}{2}{{\log }_2}\left(1 + \frac{{P(|{h_{{S\!_1}{R_i}}}{|^2} + |{h_{{S\!_2}{R_i}}}{|^2})}}{{{N_0}}}\right) > {R_{\rm th}}\right]} \times \\ & \prod\limits_{{R_t} \in {{\bar D}_n}} \Pr \left[\frac{1}{2}{{\log }_2}\left(1 + \frac{{P(|{h_{{S\!_1}{R_t}}}{|^2} + |{h_{{S\!_2}{R_t}}}{|^2})}}{{{N_0}}}\right) < {R_{\rm th}}\right] \end{split} $$ (30) 式(29)中,
$\Pr [{C_{{R_i}{S_2}}} < {R_{\rm th}}]$ 和$\Pr (\varPhi = \varnothing)$ 的概率可以表示为:$$ \begin{split} & \qquad\;\Pr [{C_{{R_i}{S\!_2}}} < {R_{\rm th}}]=\\ & \Pr \left[\dfrac{1}{2}{\log _2}\left(1 + \dfrac{{P|{h_{{S\!_2}{R_i}}}{|^2}}}{{{N_0}}}\right) < {R_{\rm th}}\right] \end{split} $$ (31) $$ \begin{split} &\qquad\qquad\quad\;\;\;\Pr (\varPhi =\, \varnothing )=\\ &\Pr \left[\frac{1}{2}{\log _2}\left(1 + \frac{{P(|{h_{{S\!_1}{R_i}}}{|^2} + |{h_{{S\!_2}{R_i}}}{|^2})}}{{{N_0}}}\right) < {R_{\rm th}}\right] \end{split} $$ (32) 所以,在使用Gamma函数时,把式(30)、式(31)和式(32)代入式(29)中,其中,
$\varpi = \dfrac{{({2^{2R}} - 1)P}}{{{N_0}}}$ ,令${m_{_{{S\!_1}{R_i}}}} = {m_{_{{S\!_2}{R_i}}}} = {m_m}$ ,${\Omega _{{S_1}{R_i}}} = {\Omega _{{S_2}{R_i}}} = {\Omega _m}$ ,中断概率为:$$ \begin{split} P_{\rm out}^3 =\,& {\left( {\dfrac{{\Gamma \left(2{m_m},\dfrac{{2{m_m}}}{{\Omega _{_m}^2}}\varpi \right)}}{{{\Gamma ^2}({m_m})}} \left(1 - \dfrac{{\Gamma \left({m_m},\dfrac{{{m_m}}}{{{\Omega _m}}}\varpi \right)}}{{\Gamma ({m_m})}}\right)} \right)^N}+\\ &\qquad\;\; {\left( {1 - \dfrac{{\Gamma \left(2{m_m},\dfrac{{2{m_m}}}{{\Omega _{_m}^2}}\varpi \right)}}{{{\Gamma ^2}({m_m})}}} \right)^N} \end{split} $$ (33) 同理,当
$\varPhi = {D_n}$ 时,如果${C_{{R_i}{S_1}}}$ <${R_{\rm th}}$ ,或者$\varPhi = \varnothing$ 时,信号从${S_2} \to {S_1}$ 的中断概率为:$$ \begin{split} &\qquad\qquad\qquad{P_{{S_2}{R_i}{S_1}}} = P_{_{\rm out}}^4=\\ & \sum\limits_{n = 1}^{{2^N} - 1} {\Pr (\varPhi = {D_n})} \Pr [{C_{{R_i}{S_1}}} < {R_{\rm th}}] + \Pr (\varPhi = \varnothing )=\\ &\quad {\left( {\dfrac{{\Gamma \left(2{m_m},\dfrac{{2{m_m}}}{{\Omega _{_m}^2}}\varpi \right)}}{{{\Gamma ^2}({m_m})}} \left(1 - \dfrac{{\Gamma \left({m_m},\dfrac{{{m_m}}}{{{\Omega _m}}}\varpi \right)}}{{\Gamma ({m_m})}}\right)} \right)^N}+\\ &\qquad\;\quad\;\; {\left( {1 - \dfrac{{\Gamma \left(2{m_m},\dfrac{{2{m_m}}}{{\Omega _{_m}^2}}\varpi \right)}}{{{\Gamma ^2}({m_m})}}} \right)^N} \end{split} $$ (34) 最后,令式(34)
$ = Y$ ,把式(33)与式(34)代入系统总中断式(17),有:$$P_{\rm out}^{\rm zong} = 2Y - {Y^2}$$ (35) -
本节主要从随着通信距离的增加,CH车辆的存活时间以及不同的中继转发、中继个数和信道来判断信噪比对中断概率的影响。参数设置如表1所示。
表 1 参数设置
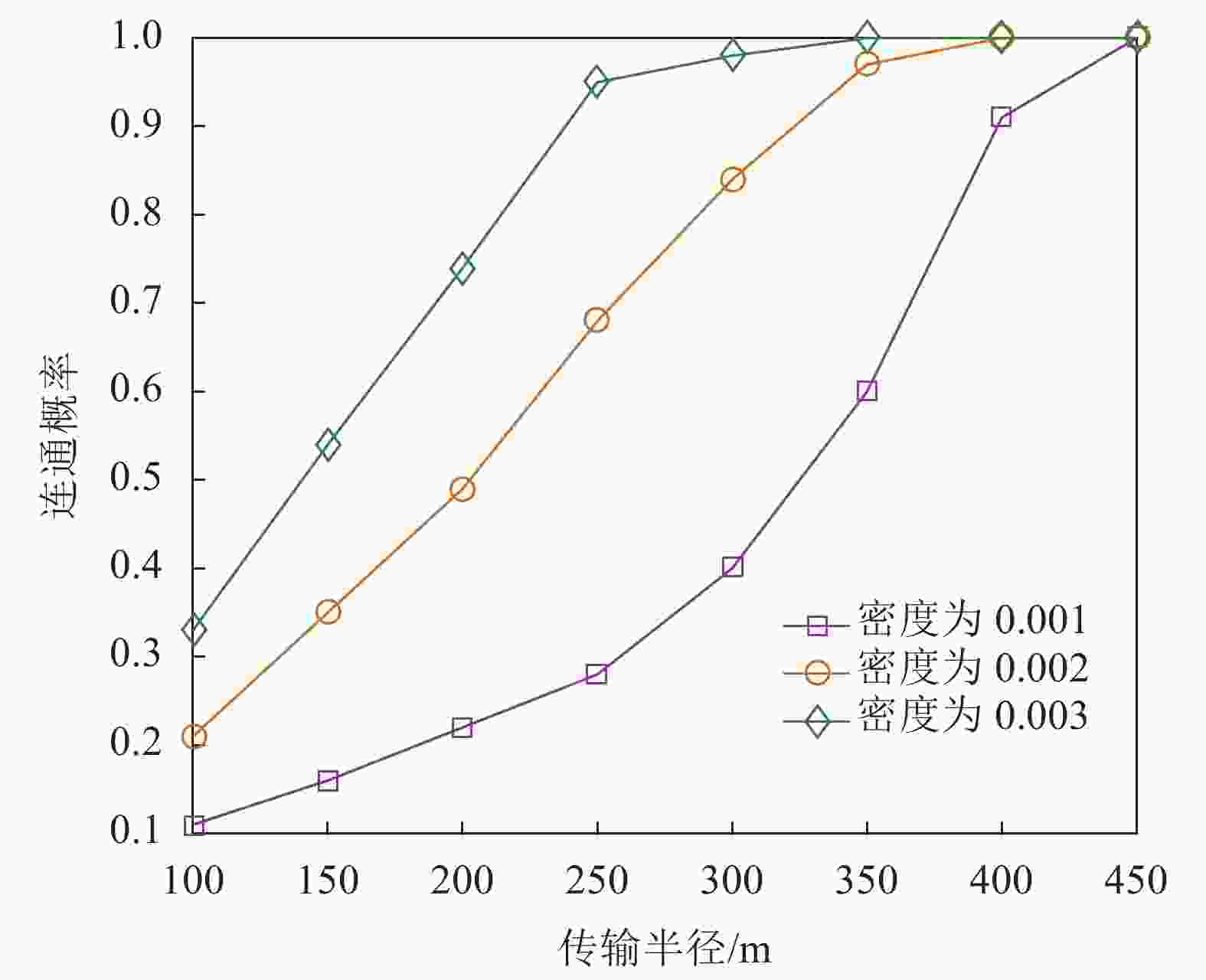
参数 数值 载波频率/ GHz 5.9 频率带宽B/MHz 20 最大传输速率阈值Rth/ bit·(s·Hz−1)−1 1 ${\Omega _m}$ 1 ${N_0}$ 1 图5为不同车辆密度下传输半径与连通率的关系。由图可以看出,随着传输半径的增大,车辆的连通率增大,车辆有机会选择不同簇头,传输稳定性得到满足。且车辆密度越大,连通率越大。
图6为簇头的存活时间。在车道上设置为60辆/km行驶的车流量密度,从图中可以看出,与基于车道的分簇算法(lane based clustering algorithm, LBC)相比,趋于稳定状态的时间提前了8 s,通信距离在不断增加,相应簇头存活时间就会相应变长。其原因是簇头车辆的覆盖面积变大,簇内的成员变多,当有车辆加入簇或者离开簇时,对簇的影响将减小。
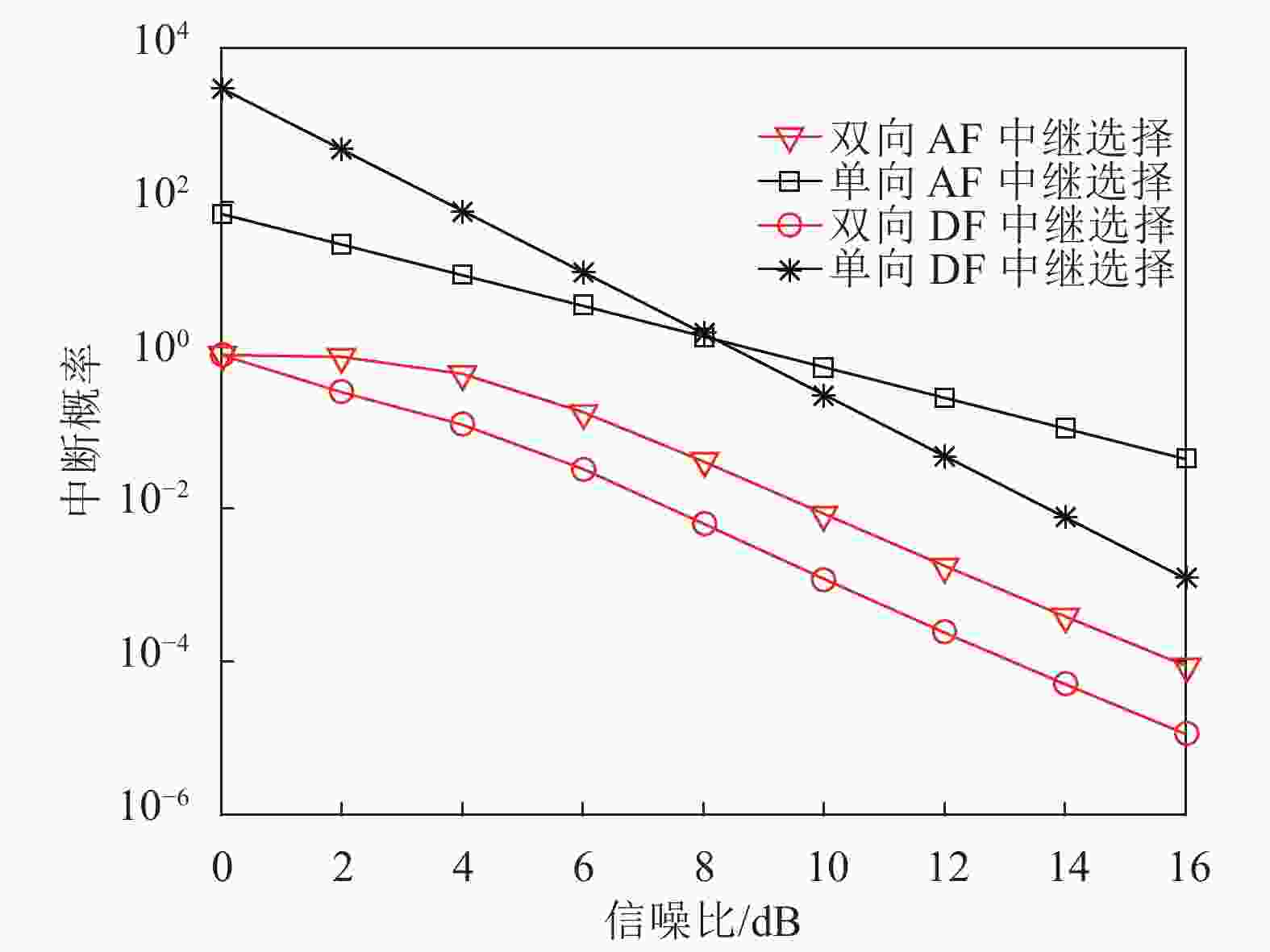
图7为不同中继选择下的中断性能。在Nakagami-m信道下且信噪比的范围设置为
$0 \sim 16\;\;\rm dB$ ,设$m = 1$ ,中继个数$N = 3$ 。从图中可以看出,在一定的范围内,随着信噪比的增加,双向AF和DF的中断概率要优于单向AF和DF的中断概率。这是由于,单向中继传输只能将源节点的信号传递单个目的节点,而双向中继传输是两个源节点的信息同时传递给对方,会减少传输时间,降低中断概率。图8为不同中继个数对双向中继的影响。设
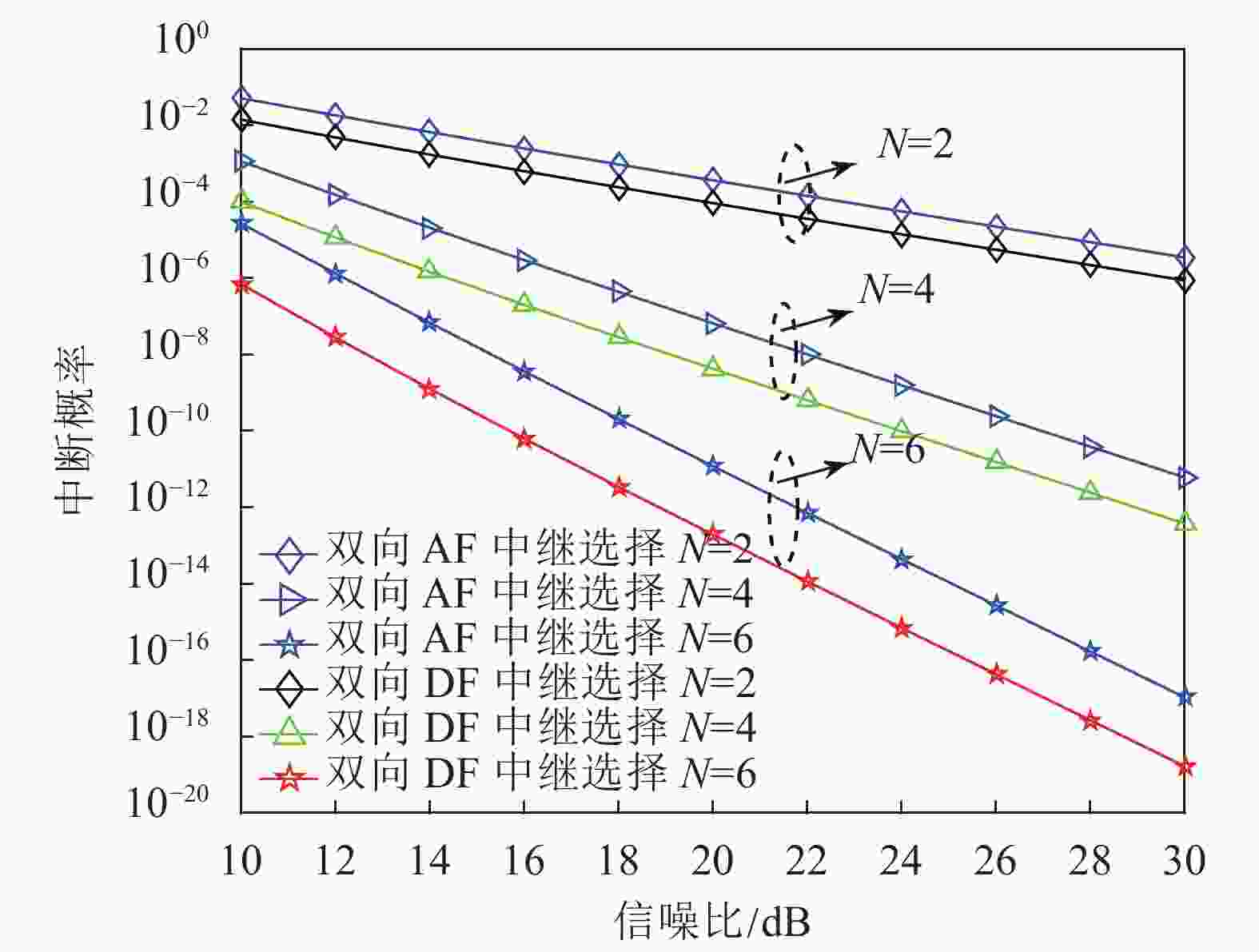
$m = 1$ ,中继个数分别为2、4、6,信噪比的范围设置为$10\sim 30\;\;\rm dB$ 。由理论分析得出,当$N$ 增加时,成功放大转发和解码的几率就会增加,中断概率会随之降低,在相同中继个数时,双向DF中继要优于双向AF中继,且图8的数值模拟与所分析的结论符合。图9为不同
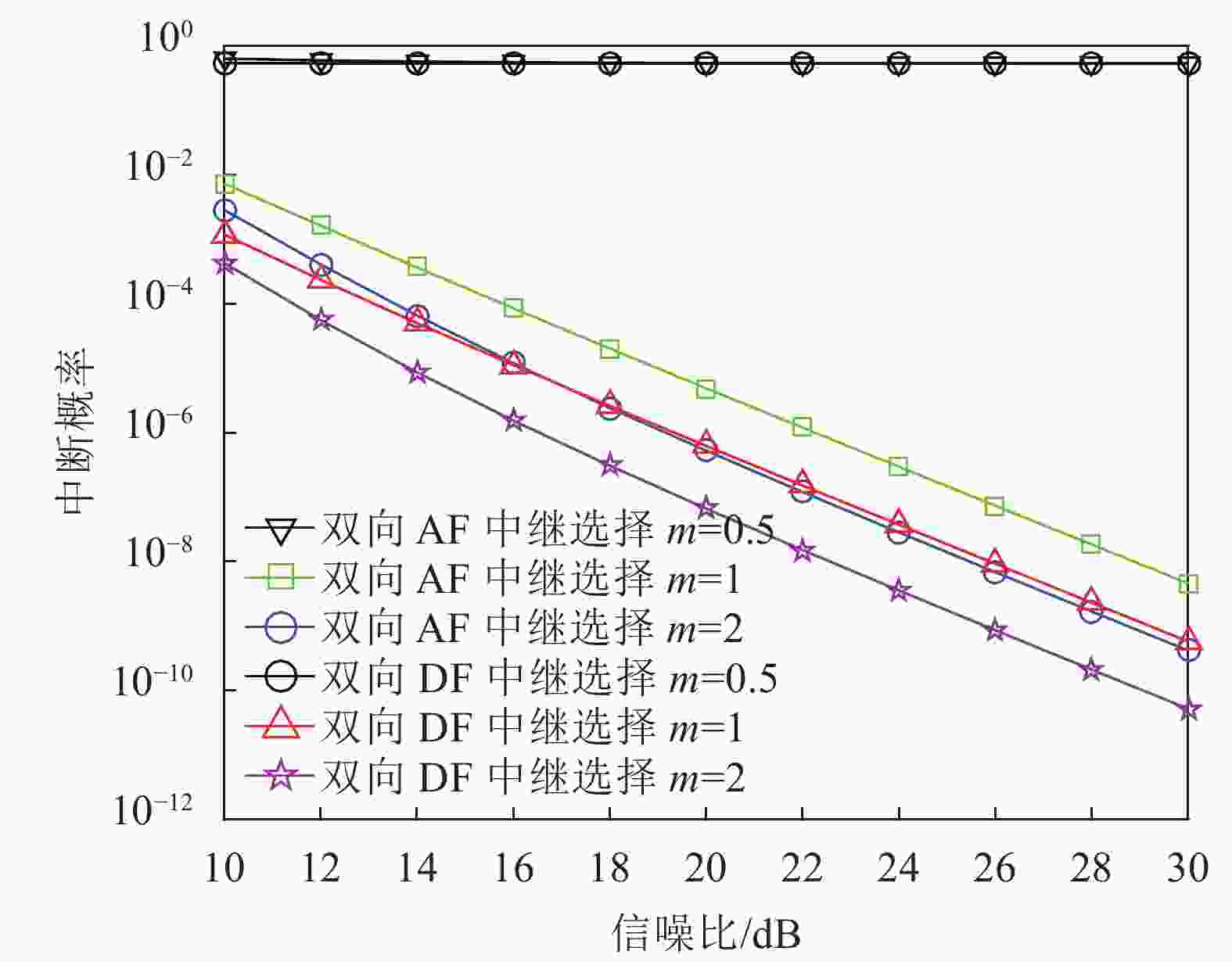
$m$ 值下对中断概率的影响。设$N = 3$ ,Nakagami信道衰落因子分别为0.5、1和2。由理论分析可知,由$m = 0.5$ 时的单侧高斯分布到$m = \infty $ 时的无衰落,随着$m$ 的增加,信道的衰落逐渐降低。图9的仿真模拟与理论分析相符合,随着信噪比与$m$ 的增加,中断概率降低,传输速率增加。 -
在城市交叉路口的场景下,为提高链路的稳定性及增强通信的可靠性,本文提出交叉路口基于车辆权值分簇的中继转发方案。仿真结果表明,所提的车辆权值分簇算法可提高链路的稳定性,且在Nakagami衰落信道条件下,采用双向DF的中继转发方式,数据传输的可靠性提高6%。
A Relay Forwarding Scheme Based on Weighted Clustering Algorithm at Cross Road
-
摘要: 针对车辆自组网(VANET)中链路不稳定与可靠性低的问题,该文提出基于车辆权值分簇的中继转发方案。该方案首先提出基于车辆权值分簇算法,提高车辆通信链路的稳定性;该算法将车辆的相对距离、相对可达速度与连通率作为分簇属性,利用升排序法找到最优簇头并将其作为中继节点,提升簇结构的稳定性。其次,在NaKagami-m衰落信道条件下,采用双向DF的中继转发方式进行数据传输以提高通信的可靠性。仿真结果表明:在相同条件下,该分簇算法与基于车道的分簇算法相比稳定性提高8 s,该双向DF中继转发方式与双向AF转发方式相比中断概率降低了6%,通信可靠性得到提高。
-
关键词:
- 交叉路口 /
- NaKagami-m衰落信道 /
- 双向中继转发 /
- 车辆分簇
Abstract: To solve the problem of unstable link and low reliability in vehicle ad hoc network (VANET), we propose a relay forwarding scheme based on weighted clustering. In the scheme, we first present the weighted cluster algorithm to improve the stability of the communication link and introduce the relative vehicular confidence distance, relative achievable rate and connectivity as clustering properties and select the optimal cluster head as a relay in the ascending order of their property weight. And then, the bidirectional DF protocol is adopted to enhance the reliability of vehicle to vehicle communication under the NaKagami-m channel. Numerical results show that the stability of the proposed algorithm cloud improve 8 seconds compared with the lane based cluster algorithm. The outage probability of bidirectional DF protocol reduces 6% compared with AF protocol.-
Key words:
- cross road /
- NaKagami-m fading channel /
- two-way relay forwarding /
- vehicle clustering
-
表 1 参数设置
参数 数值 载波频率/ GHz 5.9 频率带宽B/MHz 20 最大传输速率阈值Rth/ bit·(s·Hz−1)−1 1 ${\Omega _m}$ 1 ${N_0}$ 1 -
[1] ZHANG M S, LI C L, GUO T, et al. Cluster-based content download and forwarding scheme for highway VANETs[J]. China Communications, 2018, 15(4): 110-120. doi: 10.1109/CC.2018.8357745 [2] 朱金奇, 孙华志, 刘念伯, 等. 车载自组织网络中停放车辆合作的多媒体内容分发[J]. 电子科技大学学报, 2018, 47(4): 566-572. doi: 10.3969/j.issn.1001-0548.2018.04.015 ZHU Jin-qi, SUN Hua-zhi, LIU Nian-bo, et al. Multimedia content distribution of parked vehicles in vehicle self-organizing network[J]. Journal of University of Electronic Science and Technology of China, 2018, 47(4): 566-572. doi: 10.3969/j.issn.1001-0548.2018.04.015 [3] WANG J H, LIU K, XIAO K, et al. Dynamic clustering and cooperative scheduling for vehicle-to-vehicle communication in bidirectional road scenarios[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(6): 1913-1924. doi: 10.1109/TITS.2017.2743821 [4] RAO W M, XIA J X, LYU W T, et al. Interval data-based k-means clustering method for traffic state identification at urban intersections[J]. IET Intelligent Transport Systems, 2019, 13(7): 1106-1115. doi: 10.1049/iet-its.2018.5379 [5] MEHMOOD A, KHANAN A, MOHAMED A H, et al. ANTSC: An intelligent naïve bayesian probabilistic estimation practice for traffic flow to form stable clustering in VANET[J]. IEEE Access, 2017, 6: 4452-4461. [6] JOSHUA C, DURAISAMY R, VARADARAJAN V. A reputation based weighted clustering protocol in VANET: A multi-objective firefly approach[J]. Mobile Network & Application, 2019, 24(4): 1199-1209. [7] LI Y, SUN S L, WANG X J, et al. Optimal ad hoc power control algorithm based on outage probability[J]. International Journal of Future Generation Communication and Networking, 2016, 9(3): 111-122. doi: 10.14257/ijfgcn.2016.9.3.11 [8] BAO J R, WU J W, LIU C, et al. Optimized power allocation and relay location selection in cooperative relay networks[J]. Wireless Communications & Mobile Computing, 2017(2): 1-10. [9] LI W, KU M L, CHEN Y, et al. Performance analysis for two-way network-coded dual-relay networks with stochastic energy harvesting[J]. IEEE Transactions on Wireless Communications, 2017, 16(9): 5747-5761. doi: 10.1109/TWC.2017.2715175 [10] XIAO H, ZHANG Z S. Performance analysis of multi-source multi-destination cooperative vehicular networks with the hybrid decode-amplify-forward cooperative relaying protocol[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(9): 3081-3086. doi: 10.1109/TITS.2017.2766267 [11] BASTAMI A H, HABIBI S. Cognitive MIMO two-way relay network: Joint optimal relay selection and spectrum allocation[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 5937-5952. doi: 10.1109/TVT.2018.2803599 [12] LI W, KU M L, WANG Y C, et al. Stochastic energy harvesting and relay selection for two-way dual-relay networks[J]. IEEE Access, 2019, 7: 125323-125332. doi: 10.1109/ACCESS.2019.2938550 [13] JAMEEL F, JABEEN F, HAMID Z. Analysis of co-channel interference in VANETs under Nakagami-m fading[C]//International Conference on Frontiers of Information Technology (FIT). Islamabad: [s.n.], 2016: 153-158. [14] HWANG K S, SUNG C K. Link adaptation of two-way AF relaying network with channel estimation error over Nakagami-m fading channel[J]. IEICE Transactions on Communications, 2019, E102B(3): 581-591. [15] GUO Q, FENG W. Joint relay and eavesdropper selection strategy against multiple eavesdroppers over Nakagami-m fading channels in cooperative decode-and- forward relay networks[J]. IEEE Access, 2019, 7: 37980-37988. doi: 10.1109/ACCESS.2019.2906639 [16] LEE S, YOUNIS M, MURALI A, et al. Dynamic local vehicular flow optimization using real-time traffic conditions at multiple road intersections[J]. IEEE Access, 2019, 7: 28137-28157. doi: 10.1109/ACCESS.2019.2900360 [17] 帅建平. VANET中基于灰色系统理论的分簇算法[J]. 激光杂志, 2015, 36(8): 124-130. SHUAI Jian-ping. Clustering algorithm based on grey system theory in VANET[J]. Laser Magazine, 2015, 36(8): 124-130. [18] LI W J, NIE L. Urban rail departure capacity analysis based on a cellular automaton model[J]. Chinese Physics B, 2018, DOI: 10.1088/1674-1056/27/7/070204. [19] XIAO H L, CHEN Y H, ZHANG Q Y, et al. Joint clustering and power allocation for the cross roads congestion scenarios in cooperative vehicular networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(6): 2267-2277. doi: 10.1109/TITS.2018.2866236 [20] GAO Y, CHEN Y, HU A. Throughput and BER of wireless powered DF relaying in Nakagami-m fading[J]. Science China Information Sciences, 2017, 60(10): 102306. doi: 10.1007/s11432-016-0611-x [21] ZHU J, ZOU Y, CHAMPAGNE B, et al. Security reliability tradeoff analysis of multirelay aided decode-and-forward cooperation systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 5825-5831. doi: 10.1109/TVT.2015.2453364 -


 ISSN
ISSN 



 下载:
下载: