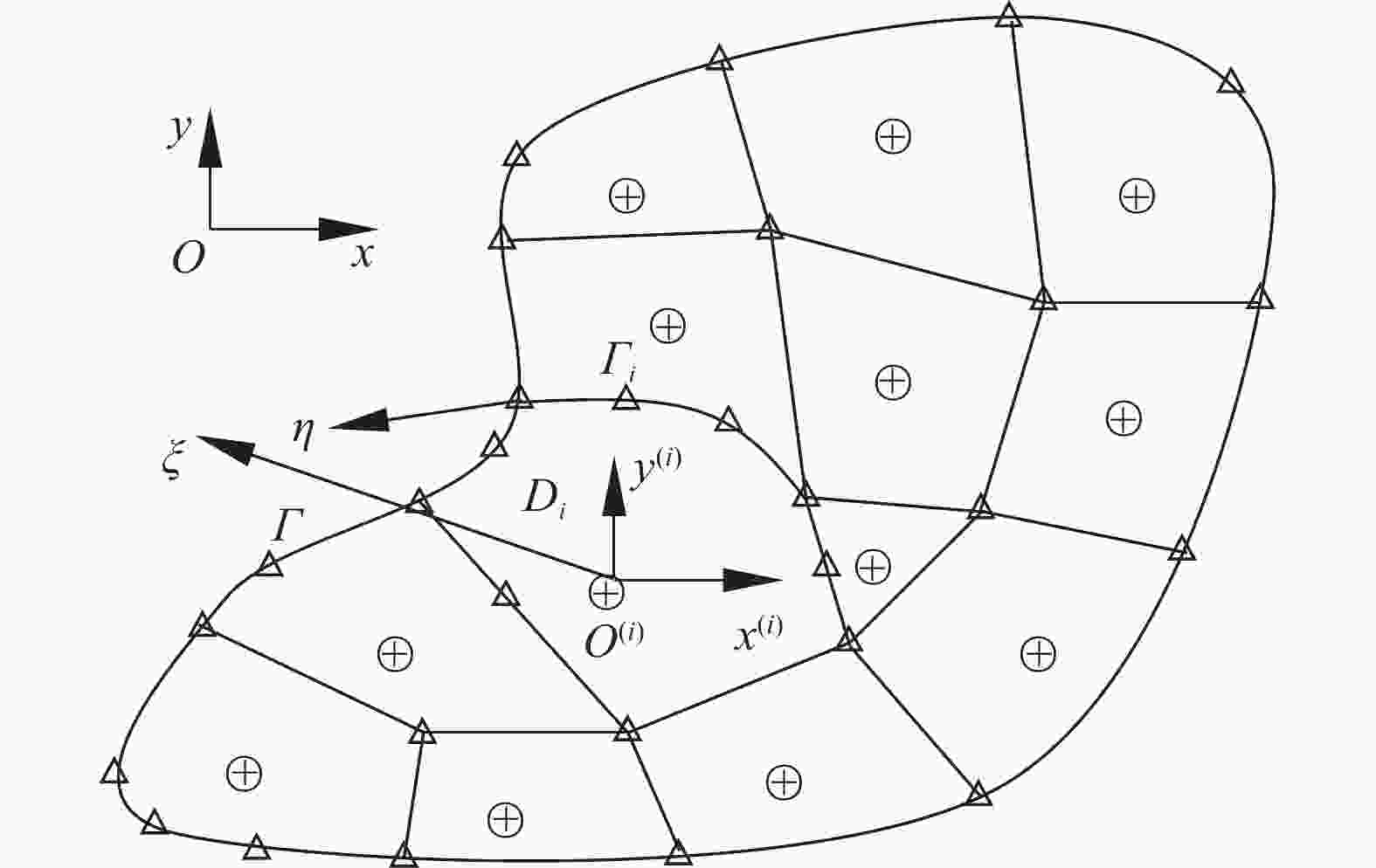
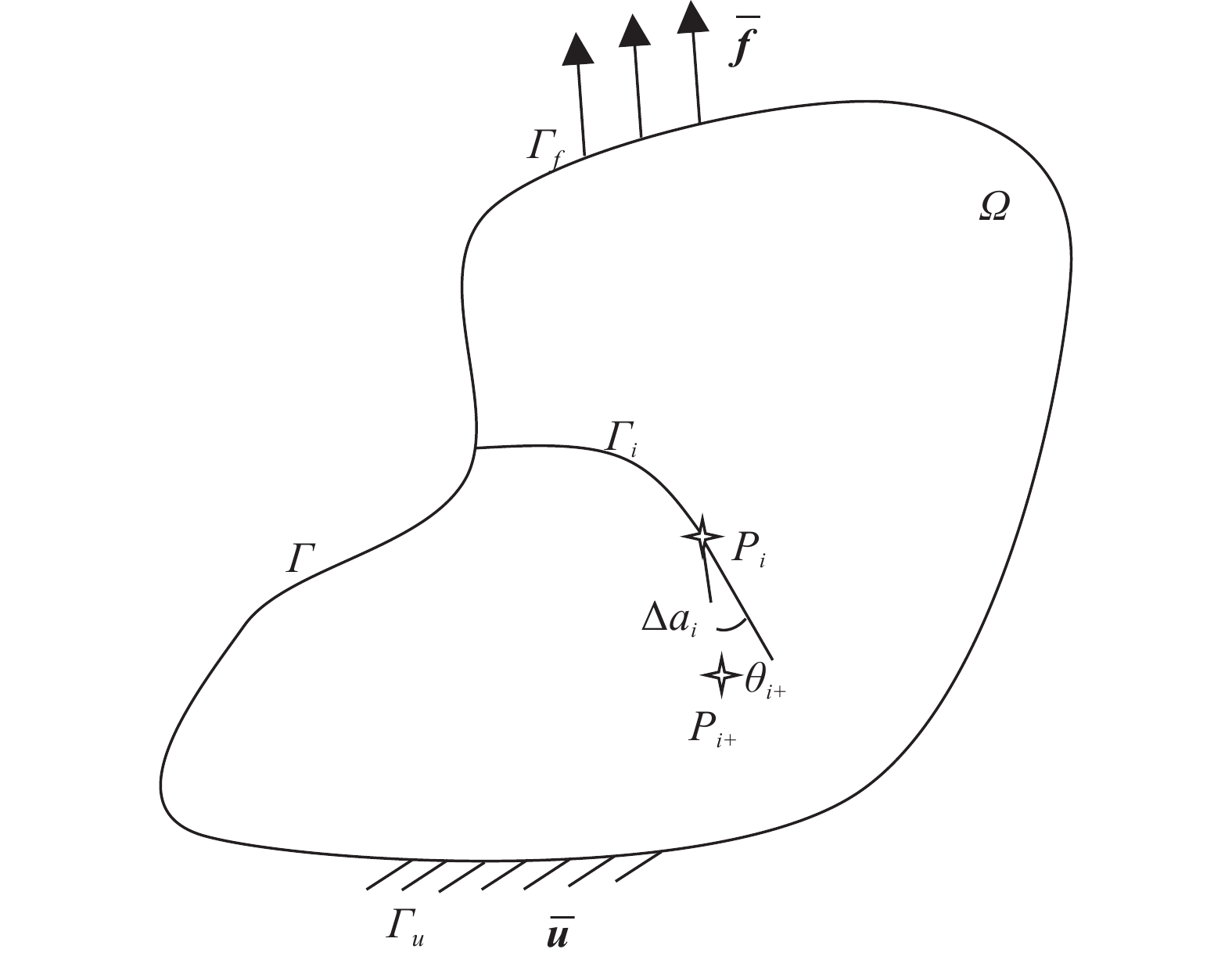
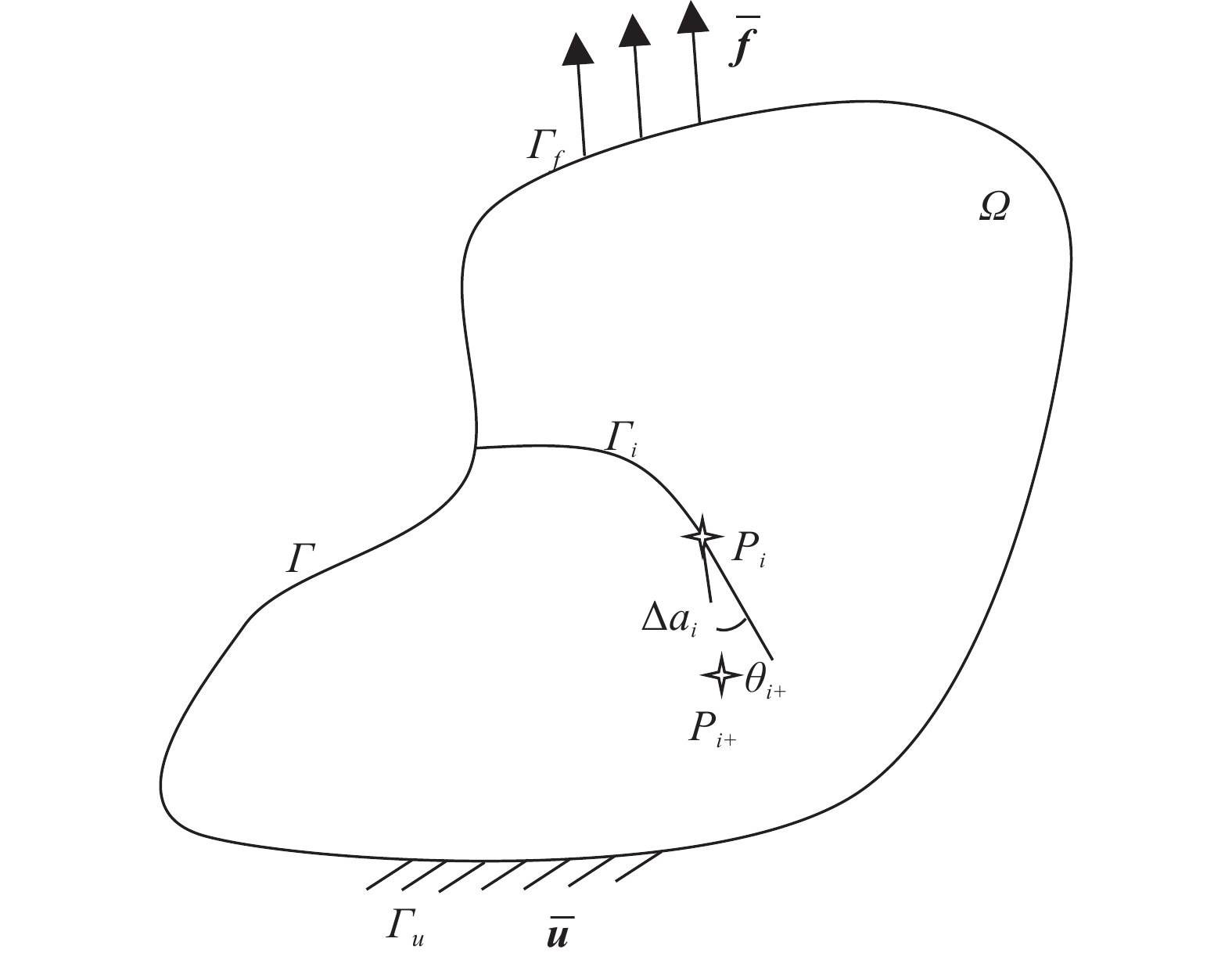
Here, we consider a 2D continum structure Ω bounded by the external boundary Γ shown in Fig. 1 as an illustration, and the boundary conditions are given as

where $\overline { u} $ and $\overline { f} $ refers to the displacement and normal traction vectors imposed on Γ_u and Γ_f, respectively. A natural fatigue crack denoted by Γ_c is embedded in Ω, and the position of the crack tip after the i-th loading cycle with i ≥1 is at the point P_i. During the (i+1)-th loading cycle, the crack Γ_c propagates in Ω with the length Δa_i+1 and the directional ange θ_i+1, and the crack tip moves to P_i+1.

Figure 1.  A 2D continum plate containing one edge crack

Experimental observations^{[4, 5, 16, 34-36]} indicate that the fatigue crack growth in practical components is affected by various factors, including the loading sequence and ratios, microdefects, specimen geometry, material properties and so forth. Many NFCG models^{[6-8, 37-40]} have been proposed thus far. In this study, the following NFCG model is adopted to characterize the fatigue crack growth rates of the whole process^{[8, 39]}.

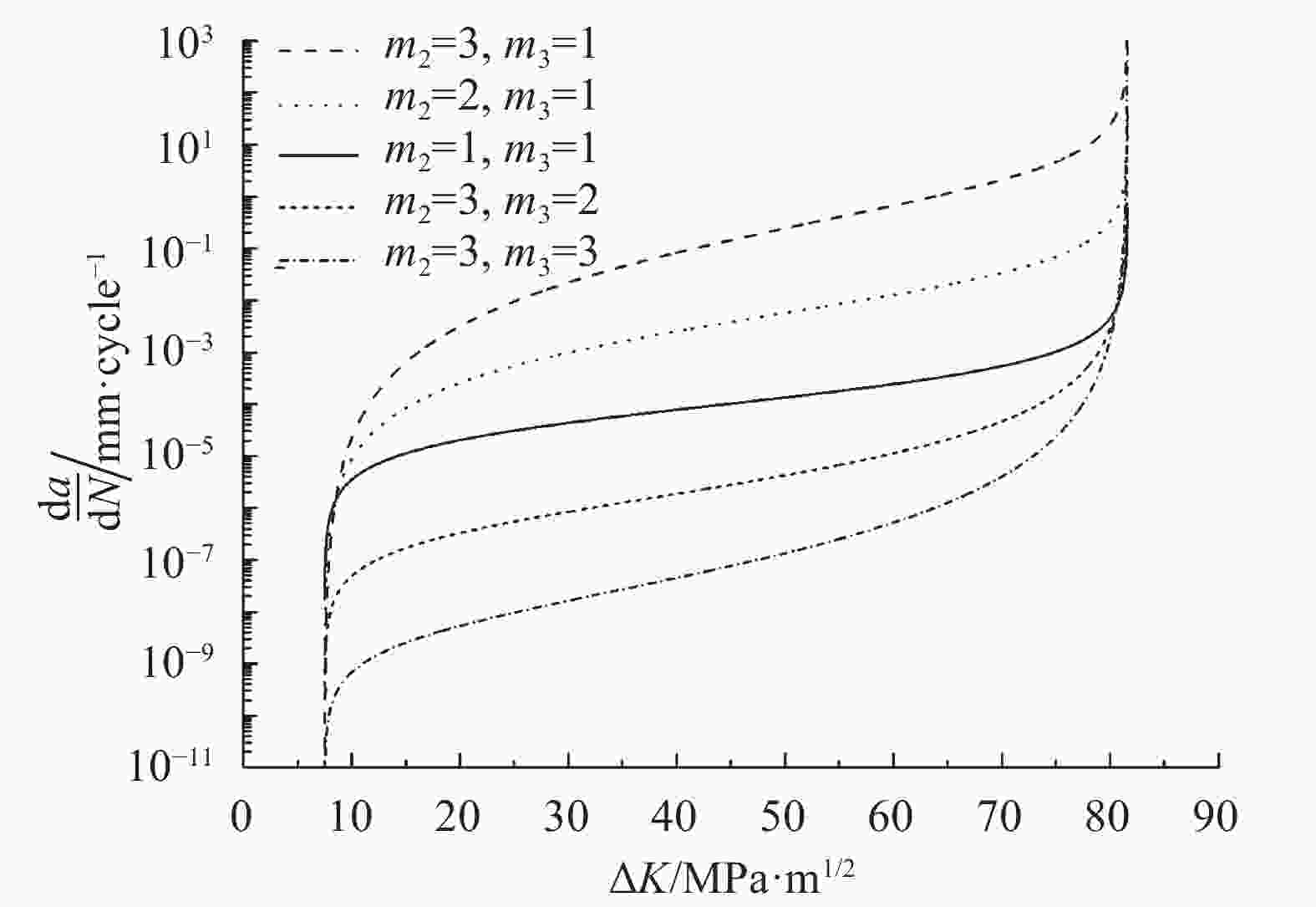
where c₁ and m₁～m₃ are the model coefficients to be determined based on the experimental data. Physically, m₂ and m₃ determine the manner of da/dN approaching the cracking threshold ΔK_th and the material fracture roughness K_IC in Fig. 2, respectively. ΔK denotes the variation of the stress intensity factor (SIF), and R is the cyclic stress ratio.

Figure 2.  Influence of the model coefficients m₂ and m₃ on da/dN

In Eq. (2), U refers to the effective stress intensity factor range ratio defined by

where γ is the crack opening ratio. To properly describe the combined effect ascribed to the loading conditions and the specimen characteristics, γ is defined in this study as^{[8, 41]}

The coefficients A₀～A₃ are evaluated by

with v the material Poisson’s ratio and t_re the relative thickness of thin-walled plates expressed as

where c is a material-property-related constant, t is the specimen thickness and k_mat is defined as

where σ_f is the material flow stress, and σ_s is the material yielding stress.

Then, the foregoing fatigue crack propagation length Δa_i+1 can be explicitly expressed as

where ΔK_i represents the variation of the mixed-mode SIF^[42] of the (i+1)-th cycle, and is further written as

with $\Delta {K_{{\rm I},(i{\rm{ + 1)}}}}$ and $\Delta {K_{{\rm {II}},(i{\rm{ + 1)}}}}$ the variation of the mode-I and mode-II SIFs, respectively.

In this study, the maximum circumferential stress criterion^[43] is adopted to characterize the fatigue crack growth direction

Here, we assume that the fatigue cracks under consideration propagate along a straight line within one loading cycle. Combining (3)～ (10), we can quantitatively determine the directional FCG velocities, the cracking direction and the location of the newly-formed crack tip P_i+1.

It is noted that the foregoing NFCG model takes explicitly account of the influence of the loading conditions by (3), the material property and specimen geometry effects by (2), (6) and (7), and the cracking physics near ΔK_th and K_IC. Hence, it is of great convenience in applying this model for specimen design, material selection, and NFCG rate and fatigue lifetime estimation in practical applications. In the following sections, the NFCG model in Eqs. (1)～(10) will be numerically implemented in the SBFEM context.

As stated previously, SBFEM shows various advantages over other strategies in simulating natural fatigue crack growth and in predicting fatigue lives due to its accurate description of SIFs at the crack tip, fewer DOFs are needed for simulation and analytical physical fields along the radial direction. In this section, a computational scheme is developed using SBFEM to simulate the NFCG process of 2D thin-walled structures.

For brevity, the 2D continum in Fig. 1 is taken again as an example. Here, the quasi-static elastic problem is addressed, and the body force of Ω is assumed to be negligible. Thus, the equilibrium equation of a point x in Ω is written as

with σ=[σ_xx, σ_yy, σ_xy]^T being the stress vector and

The stress vector σ at the point x is related to the strain vector ε= [ε_xx, ε_yy, ε_xy]^T by

where D is the second-order elastic matrix of the material forming Ω.

The strain vector ε can be rewritten in terms of the displacement vector u=[u_x,u_y]^T as

The displacement u and traction f satisfy the relations presented in Eq. (1) on the external boundary Γ and fulfill the formula below on the cracking surface Γ_i:

Equations (11)～(15) together with (1) constitute the strong governing formulation of the boundary value problem in Fig. 1. Then, the weak governing equation of the BVP in Fig. 1 is derived by using the virtual work theorem^[22] or the weighted residual formulation^{[10, 11]} as

where x_s refer to the points on the boundary Г.

Then, the whole domain Ω is discretized into polygon elements of any number of sides, e.g. Fig. 3. Simultaneously, a scaling center (e.g. O⁽ⁱ⁾) is defined for each element and specifically, the whole boundary of the element is visible from its scaling center. A local polar coordinate system is defined such that the radial axis ξ directs from the scaling center O⁽ⁱ⁾ towards the element boundary, and its value is 0 at the scaling centre and is 1 at the element boundary; the circumferential axis is denoted as η and physically represents the distance between a particular point and the origin point selected on the element boundary.

Figure 3.  Continua discretized by SBFEM

Accordingly, the displacement vector of any point (ξ, η) in the i-th subdomain D_i can be explicitly approximated by

where m_i denotes the total number of nodes on external boundary of D_i; N_k(η) is the shape function associated with the k-th node and related to the circumferential coordinate merely; u_k(ξ) is the radial displacement function associated with the k-th boundary node and defined by^{[10, 11, 22]}

where c_{k_j} is the boundary condition dependent constant and physically represent the contribution of each mode to the final solution; λ_j and φ_{k_j} are the positive eigenvalues and the associated eigenvectors of a standard eigenproblem^[43] and satisfy the internal equilibrium along the ξ direction^[42].

Combining Eqs. (12)～(18) and assembling the stiffness matrix and the loadings of all polygon subdomains together following the procedure presented in Refs.[22, 43], we finally obtain the equilibrium equation of the aforementioned BVP:

where K is the global stiffness matrix related to the geometry and the material of the BVP in question, d contains all unknows at the nodes, and F is the global external force vector.

Solving Eq. (19) delivers the nodal displacements on the element boundary. Then, invoking the relations in Eqs. (17) and (18), we can determine the resulting displacement and stress of any point in the domain by

where B¹(η) and B²(η) are the strain-displacement matrices^{[22, 43]}. Note that these two matrice are functions of the circumferential coordinate η only, which indicates that the displacement and stress solutions by SBFEM are analytical along the radial direction ξ.

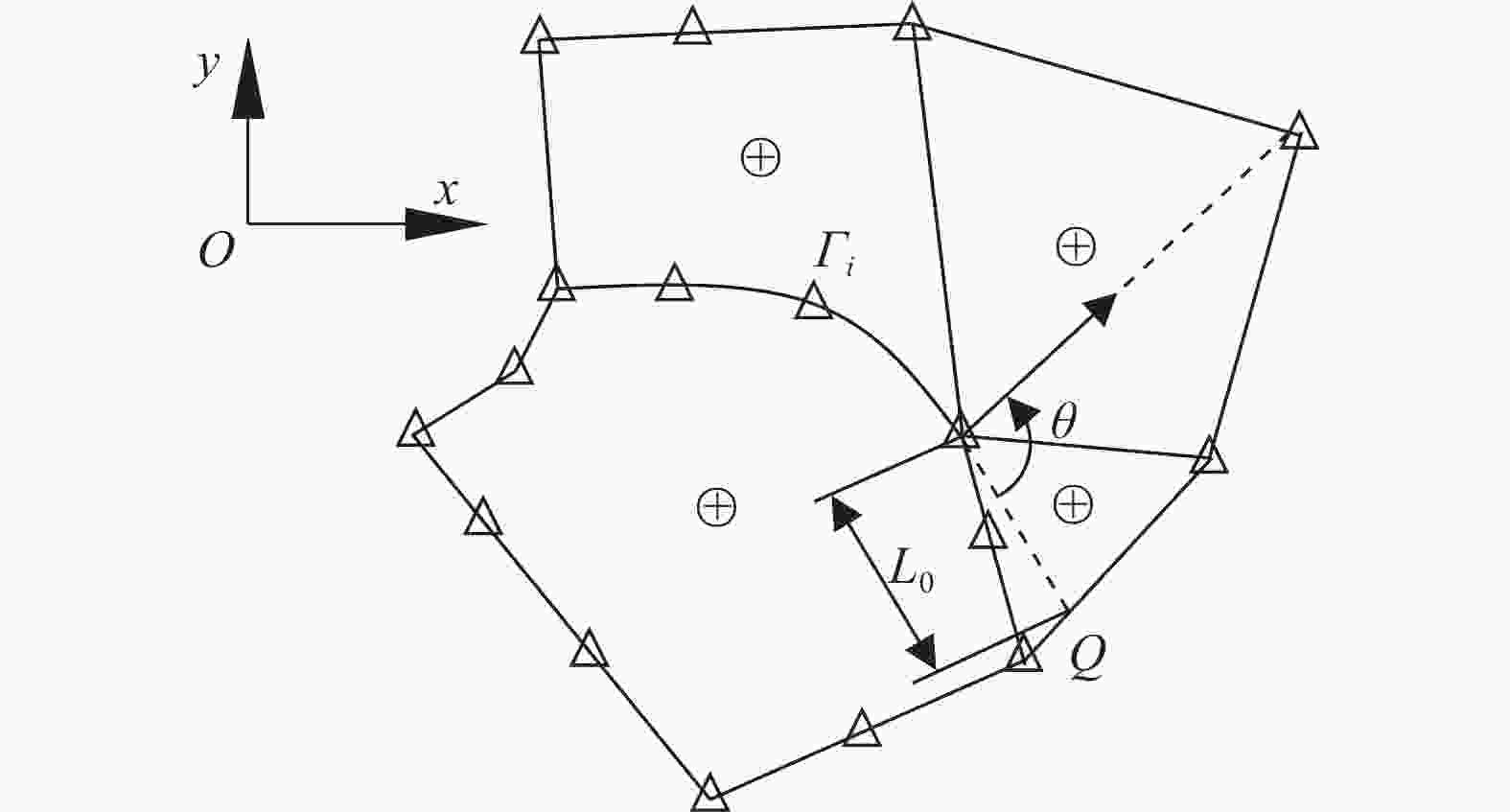
Practically, the propagation direction of natural fatigue cracks is largely influenced by the external loadings, the material property, the geometry of the structures, and the local defects. Fig. 4 visualizes the schematic diagram of a generic cracked body modelled by the SBFEM. To evaluate the SIFs of cracks of this kind, the Williams eigenfunction expansion around the crack tip^{[24, 42]} is first applied and the stresses of the point Q at the crack surface direction on the element boundary as Fig. 4 in the global. Cartesian coordinate system are then transformed to the normal stress σ_n (mode I) and the shear stress τ_n (mode II) defined on the cracking sruface plane. Finally, the mixed model SIFs are determined by

where L₀ is the distance between the crack tip and the point Q whose location doesn’t necessarily coincide any existing node. The stresses of Q can be conveniently recovered by using Eq. (20).

Figure 4.  Schematic diagram to evaluate the SIF of a generic cracked body

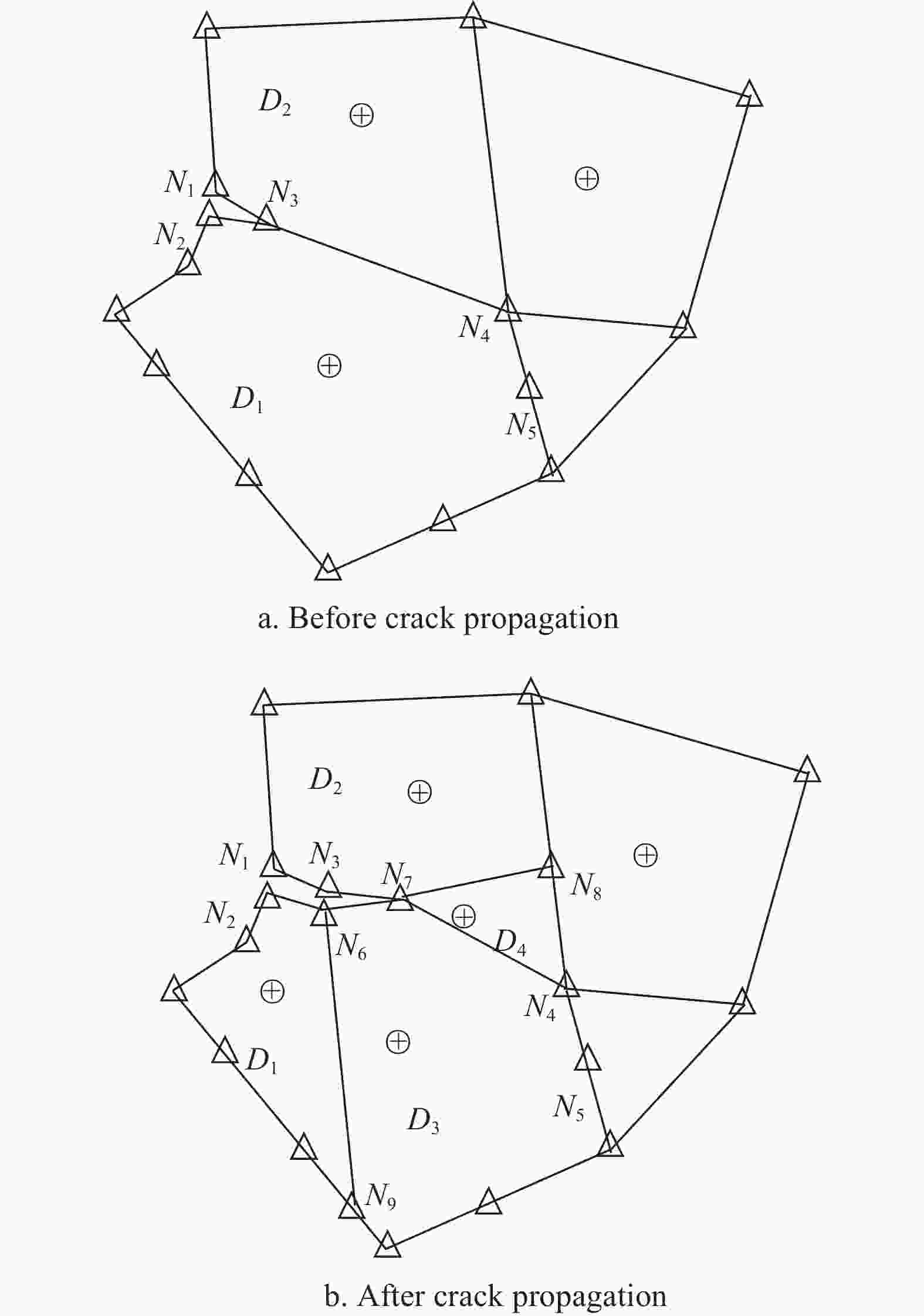
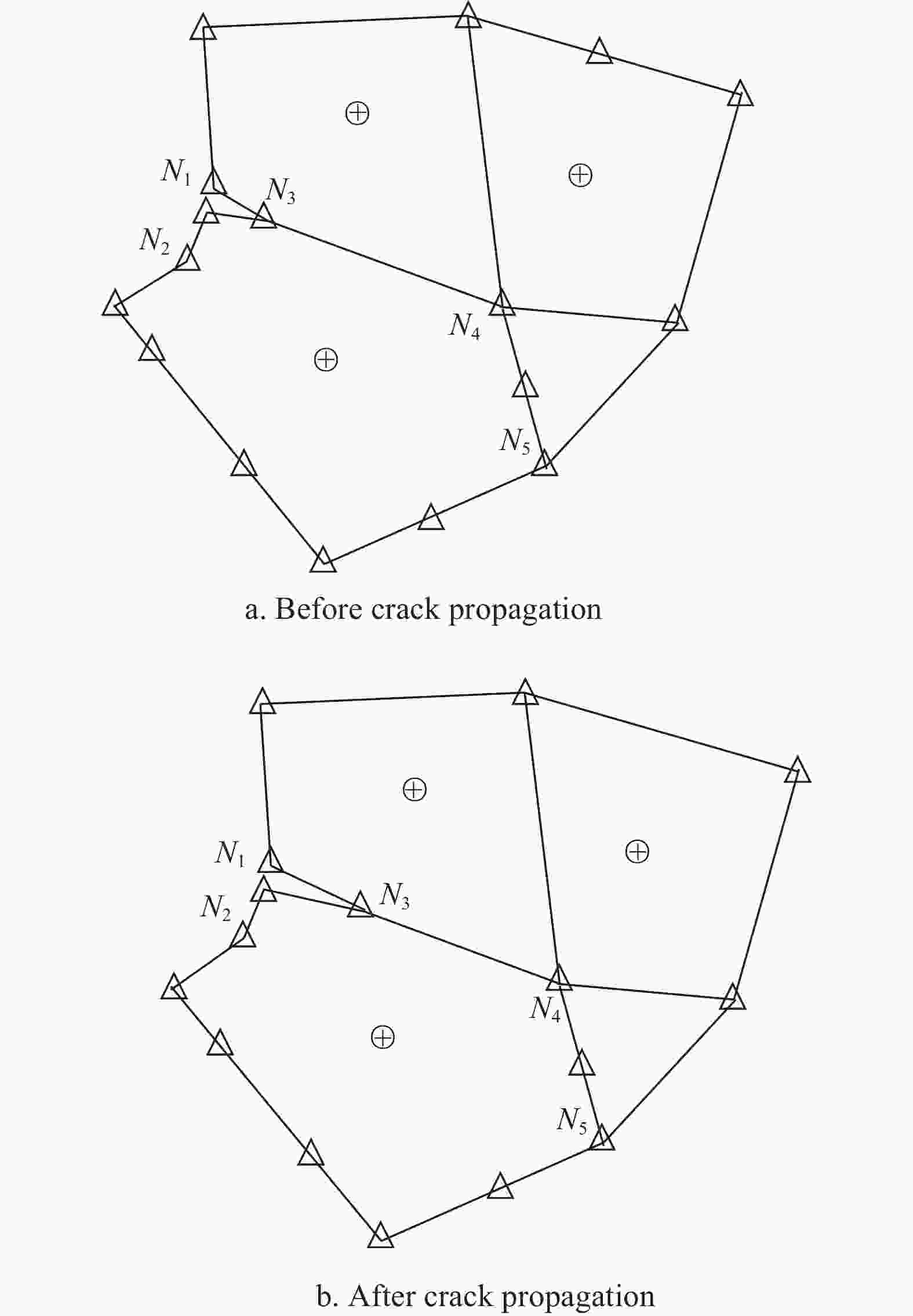
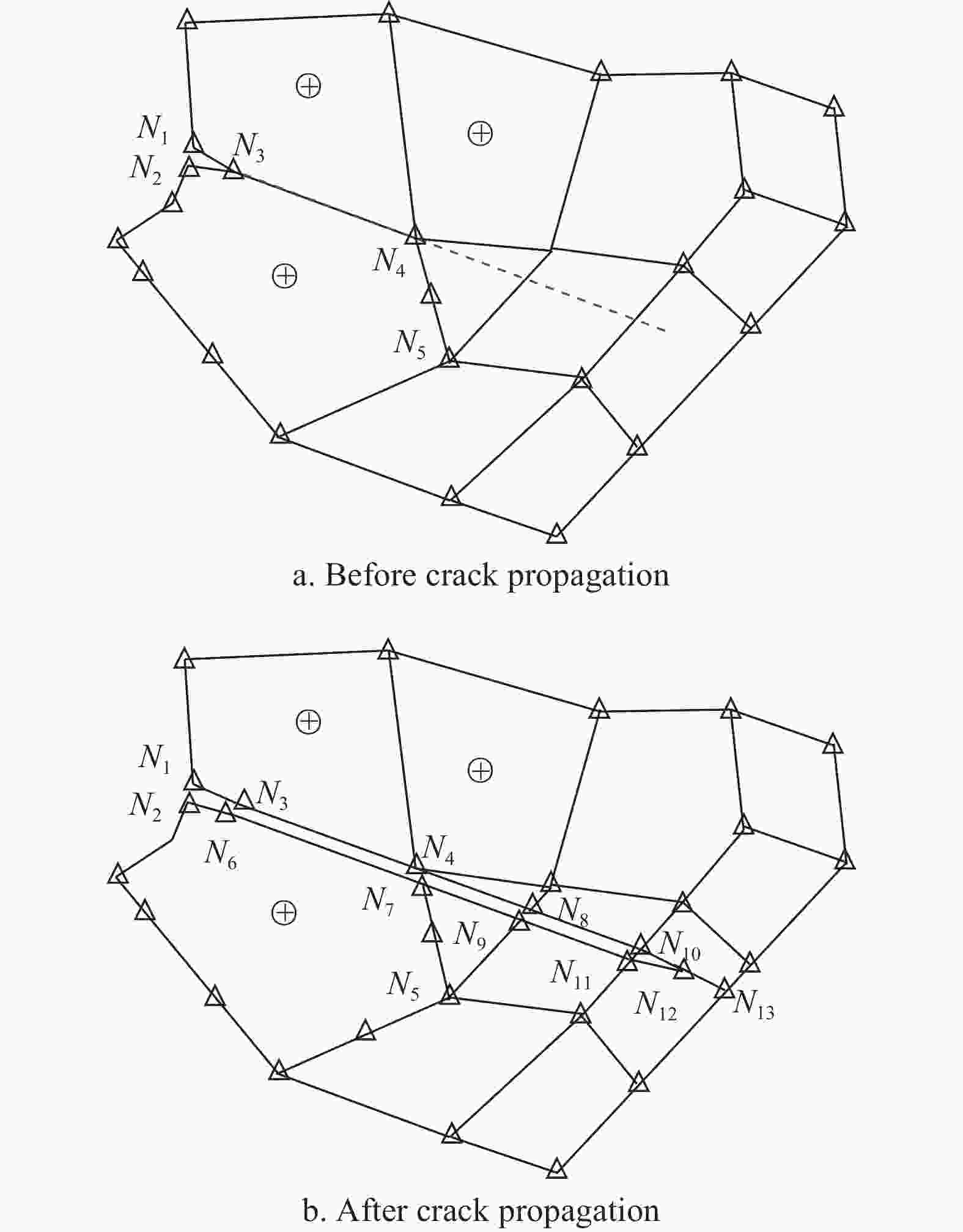
From many literatures^{[6-8, 37-41]} and experimental observations, it is known that the NFCG includes three typical stages shown in Fig. 2. The slow growth stage near the cracking threshold ΔK_th (Stage I), the steady growth stage (Stage II) and the fast fracturing stage near the fracturing point ((1−R)K_IC) (Stage III). At stage I, the fatigue crack propagation rate da/dN is so small that the crack length increment Δa during one loading cycle is much smaller compared with the side length of an subdomain. Hence, the crack of this stage is assumed to propagate within one subdomain. Two situations are considered in this study about this stage: 1) as the variation Δθ_c of θ_c computed by Eq. (10) between the current loading cycle and the former one is smaller than a critical value θ_c, say 1º, the fatigue crack is considered to propagate along the same direction and the node at the fatigue crack tip moves to a new position determined based on Eqs. (8)～(10), see Fig. 5; 2) otherwise, a new nodal point is first added at the newly-generated crack tip and two new elements are added between this point and the original crack tip. Meanwhile, a line parallel to and another one at N₆ perpendicular to the new crack segement (N₃ and N₇ in Fig. 6) are constructed to divide the original two domains into 4 parts and two new nodal points are added simultaneously at the intersection points of the subdomain boundaries as Fig. 6. Hereafter, the new line elements are added accordingly. In this study, the fatigue cracks of all instances under consideration are modeled along the element boundary, as in Fig. 3 and Fig. 4, so as to guarantee the visuality of the whole boundary of the element from it scaling center when curved cracks are involved.

Figure 6.  Remeshing strategy of NFCP of stage I with Δθ_c≥θ_c

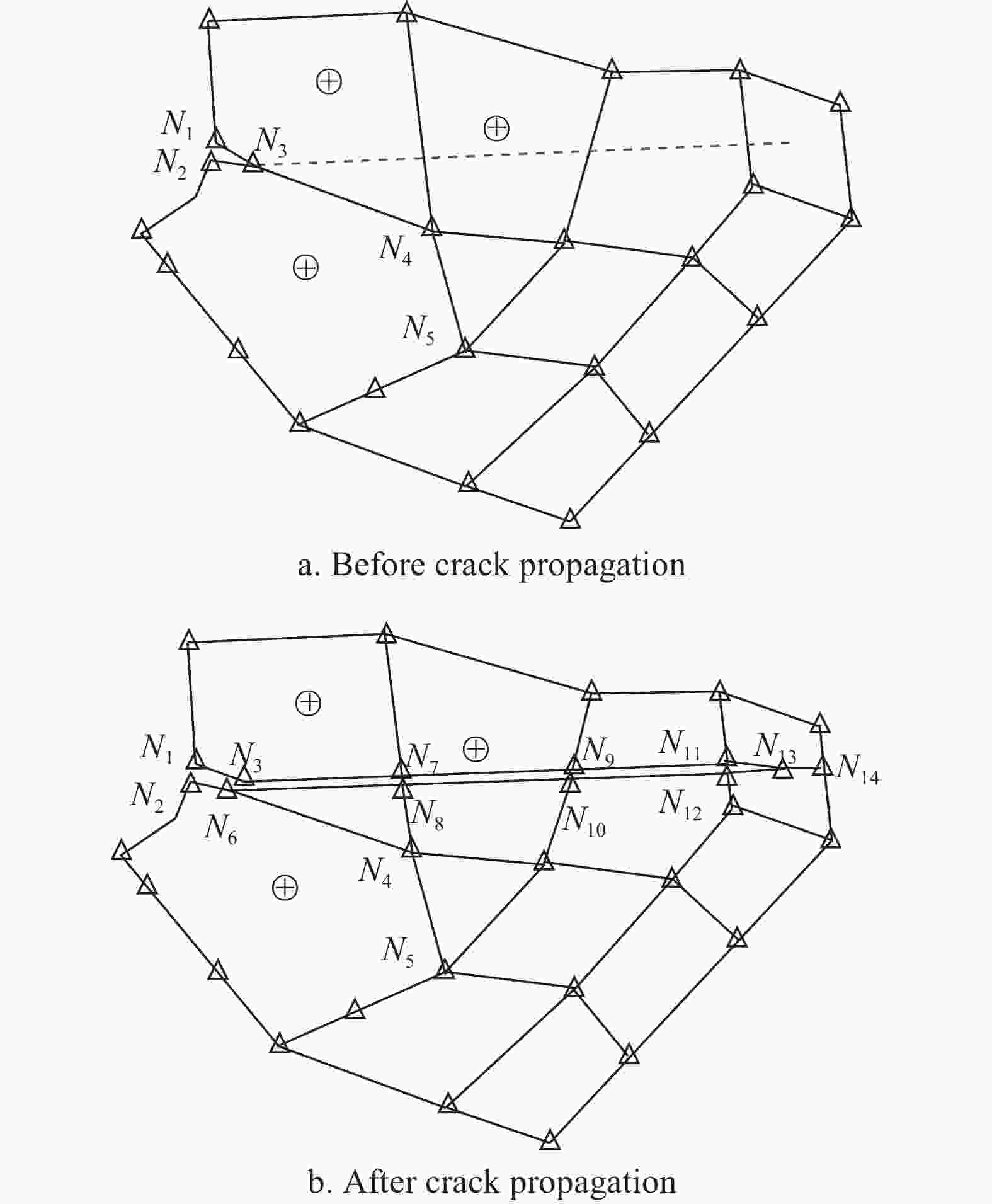
At stage II, the remeshing and optimization strategy^[43] is appropriate for modeling the fatigue crack propagations and adopted in this study. As for the last stage, nature fatigue cracks under one cyclic loading may propagate through several subdomains, see the dashed lines in Fig. 7a and Fig. 8a. To properly handle this issue, two cases are considered here and the remeshing strategies in Fig. 7b and Fig. 8b are employed to generate the discretized models for simulations with SBFEM.

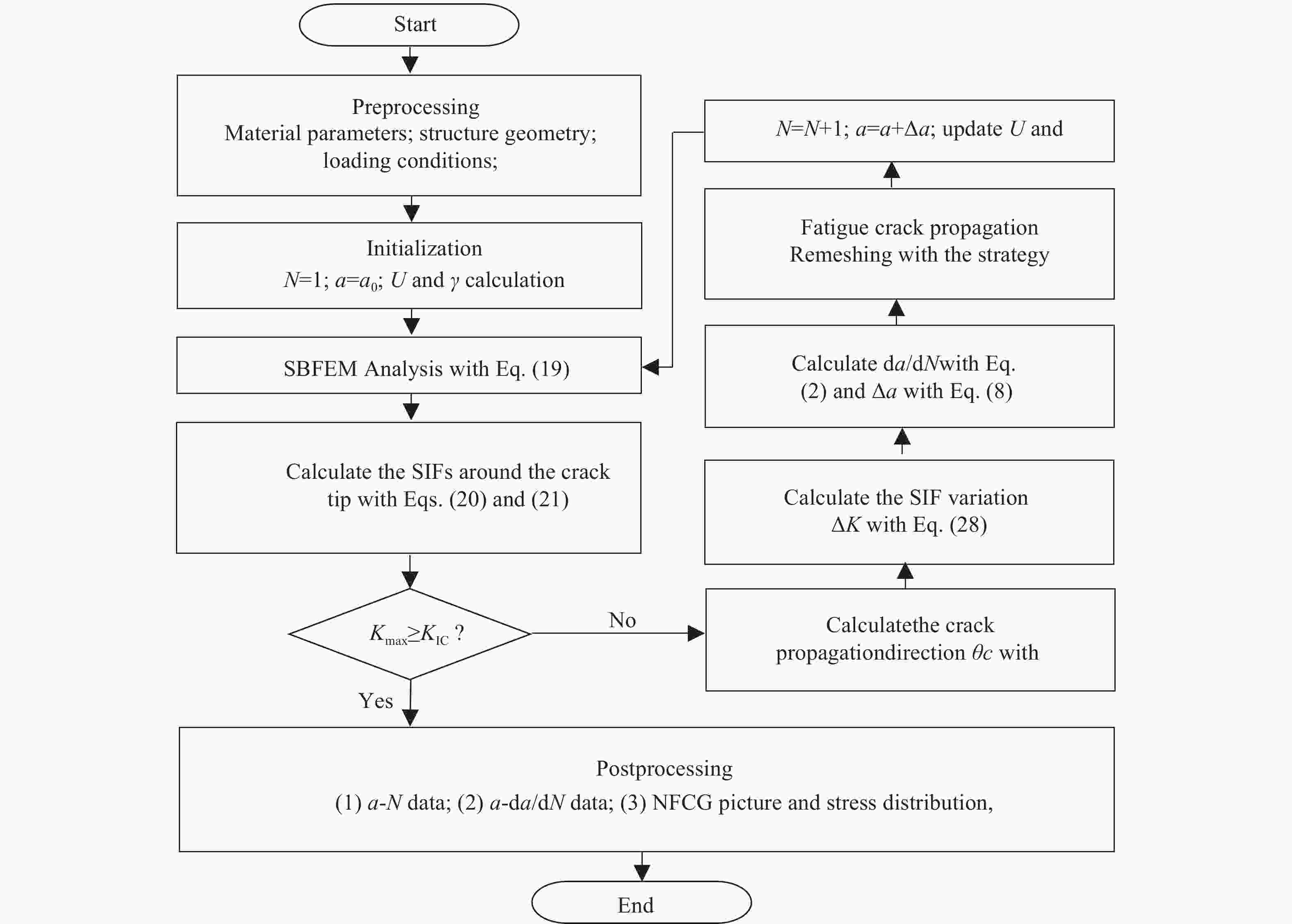
Up to now, the computational strategy using the SBFEM to numerically simulate the 2D NFCP phenomenon has been introduced completely, and an in-house package may be developed by using C++, MATLAB or others to perform the simulations. The whole process is summarized as a flow chart presented in Fig. 9.

Figure 5.  Illustration of NFCP of stage I with Δθ_c≤θ_c

Figure 7.  Remeshing strategy of NFCP of stage III (case 1)

Figure 8.  Remeshing strategy of NFCP of stage III (case 2)

Figure 9.  Flow chart of simulating NFCGs with SBFEM

In this work, we established a computational methodology framed within SBFEM to simulate the natural fatigue crack growth and to predict the fatigue lifetime of thin-walled plates considering the influence of the loading conditions and the specimen characteristics simultaneously. To be noted, the effects of loading conditions, specimen thickness and material properties could be studied with our elaborated methodology to serve as a beneficial tool for quantitatively studying the natural fatigue crack propagations and designing practical specimens.

This work was funded by the Young Scientific Innovation Team of Science and Technology of Sichuan (2017TD0017).