-
发射单一波形的相控阵雷达在目标检测、抗复杂干扰、目标参数估计等方面的性能难以满足复杂的实际需求,MIMO雷达因其具有波形分集的自由度优势,能够实现上述方面的更优性能。MIMO雷达发射方向图合成是通过设计发射波形的模值和相位,将发射能量聚焦在感兴趣的空间方向上,减少发射能量在其他方向上的分布;而随着无线通信设备(尤其是智能移动设备)的指数级增长,电磁环境中的频谱资源日益拥堵,对雷达与无线通信设备的同频相互干扰的抑制能力,亦即频谱共存能力也成为设计发射波形时必须考虑的重点。
基于MIMO雷达发射方向图拟合的波形设计方法主要分为两步法和一步法两类。
两步法即先设计发射波形的协方差阵,再在此基础上设计波形矩阵。文献[1]提出使用半定二次规划算法设计发射波形协方差阵来拟合方向图模板,能达到最优性能,但计算量很大。文献[2]提出循环算法拟合方向图模板,先设计发射波形协方差阵,再设计发射波形矩阵。文献[3]提出的算法在恒模约束和相似性约束下设计发射波形,在兼具参考波形性能的前提下具有较好的方向图拟合效果。
一步法即直接通过方向图模板匹配设计发射波形矩阵。文献[4]利用傅里叶级数分解方向图模板,进而使用无约束优化设计发射波形。文献[5]利用交替乘子算法设计恒模发射波形匹配任意形状方向图,达到了接近最优的性能,但针对大快拍数的发射波形需求,其计算量较大。文献[6]将设计波形拟合方向图的代价函数建模为
${l_p}$ 范数模型,再基于MM(majorization-minimization)算法迭代优化匹配系数与波形,得到低旁瓣、平坦的合成波束图。雷达系统频谱兼容波形设计问题一般分为两类:一类为避开无线通信系统频段的雷达波形设计,此时通信系统受干扰减少,传输速率和误码率都能得到提升,雷达系统的探测能力也会更少受到同频段通信信号干扰;另一类为雷达与无线通信系统频段共用。
文献[7]在多目标存在下,通过最小化空-频域凹陷区的波形积累能量,完成发射波形与接收滤波器联合设计,达到频谱共存的性能,计算量优于半正定松弛方法,但仍随着阵元数、采样数升高而急剧增高。文献[8]设计了模板拟合方法同时满足频谱兼容、旁瓣电平的需求,主要思路仍然是每步迭代中使用频谱模板的加载。文献[9]提出一种拉格朗日规划神经网络的方法,较好地解决加权最小二乘拟合频谱模板的问题,但收敛速率慢,计算量较大。文献[10]提出基于MM算法的频谱拟合迭代优化算法,引入频谱阻带的惩罚权向量以及设计加速收敛方法,能高效灵活地拟合频谱模板。文献[11]概述了MM算法框架,介绍了其基本原理和扩展算法,以及在信号处理、通信和机器学习应用中问题的解决方案。
总结相关文献,只有极少数文献在设计发射波形时将波束图合成与频谱塑形联系起来[12],但该方法使用矩阵求逆,运算量大。这种联合优化的工程应用价值大,既能将辐射能量投送到指定空域,又避免干扰到邻近频段的通信系统,以及降低邻近频段阻塞式干扰的影响。否则在执行雷达探测任务时,处在冲突频段的通信系统的误码率性能会受显著影响,处在冲突频段的阻塞式干扰也容易使雷达探测性能恶化。
本文针对联合优化雷达发射波形的方向图合成性能与频谱兼容能力,提出基于MM框架的迭代优化算法。首先利用空域和频域先验信息,建模波束图合成与频谱塑形联合优化的问题;迭代中,在已知上一步迭代的波形的情况下,更新当前步的匹配系数;再对均方误差代价函数进行放缩,构造替代函数;进而最小化替代函数,得到当前步迭代的最优发射波形。该算法能用较小的计算量得到接近理想的拟合效果。
-
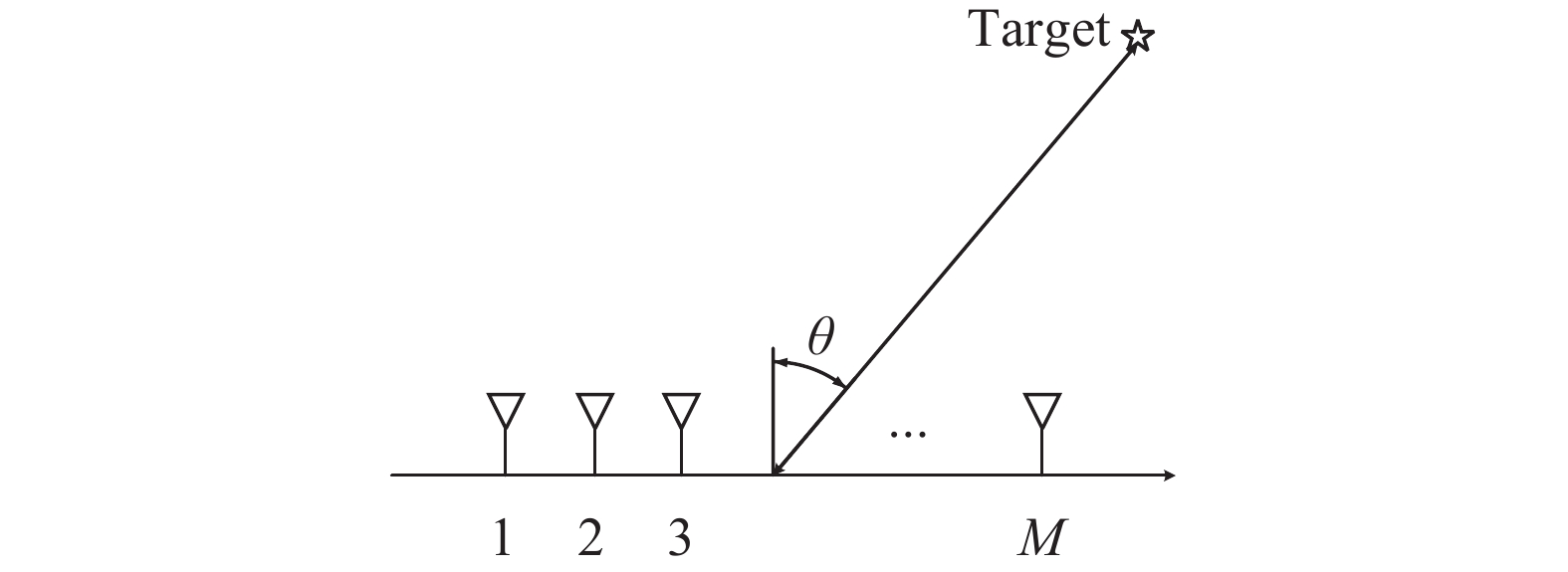
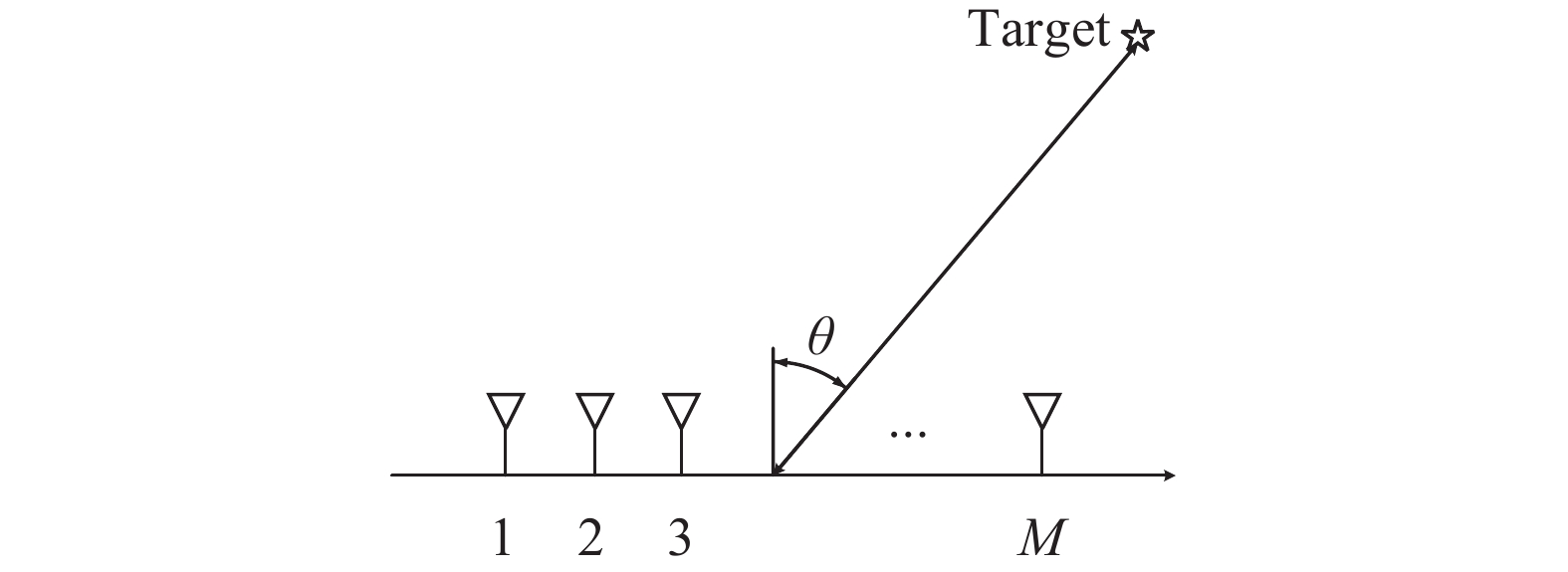
集中式MIMO雷达的M个阵元以间距为d的均匀线阵形式排列,发射场景如图1所示。
雷达的发射波形矩阵为
${{\mathit{\boldsymbol{S}}}} = \left[ {{{{\mathit{\boldsymbol{s}}}}_1},{{{\mathit{\boldsymbol{s}}}}_2}, \cdots ,{{{\mathit{\boldsymbol{s}}}}_N}} \right]$ ,波形快拍数为N,第n时刻的阵列空域波形向量为${{{\mathit{\boldsymbol{s}}}}_n} = {\left[ {{s_1}\left( n \right),{s_2}\left( n \right), \cdots ,{s_M}\left( n \right)} \right]^{\rm{T}}}$ 。远场目标位于空间角度$\theta $ 上,阵列发射导向矢量为:$${{\mathit{\boldsymbol{a}}}}(\theta ) = {\left[ {\begin{array}{*{20}{c}} 1&{{{\rm{e}}^{{\rm{j}}\frac{{2{\text{π}}}}{\lambda }d\sin \theta }}}& \cdots &{{{\rm{e}}^{{\rm{j}}\frac{{2{\text{π}} }}{\lambda }(M - 1)d\sin \theta }}} \end{array}} \right]^{\rm{T}}}$$ (1) 阵列发射波形在空间角度
$\theta $ 处合成的平均功率,亦即方向图为:$$P\left( \theta \right) = {{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}(\theta ){{\mathit{\boldsymbol{S}}}}{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{\mathit{\boldsymbol{a}}}}(\theta )$$ (2) 设空间角度格点数为G,方向图模板为
${{{\mathit{\boldsymbol{p}}}}_d} = {\left[ {{p_d}\left( 1 \right),{p_d}\left( 2 \right), \cdots ,{p_d}\left( G \right)} \right]^{\rm{T}}}$ ,空间匹配系数为$\alpha $ ,则方向图合成的问题是找到波形满足代价函数最小的优化问题,其代价函数可建模为所形成方向图与方向图模板之间的均方距离:$$\begin{split} {J_S}\left( {{{\mathit{\boldsymbol{S}}}},\alpha } \right) =& \frac{1}{G}\sum\limits_{g = 1}^G {{{\left| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{\mathit{\boldsymbol{S}}}}{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{\mathit{\boldsymbol{a}}}}({\theta _g}) - \alpha {p_d}({\theta _g})} \right|}^2}} =\\& \frac{1}{G}\sum\limits_{g = 1}^G {{{\left| {{{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{\mathit{\boldsymbol{S}}}}} \right\|}_2} - \alpha {p_d}({\theta _g})} \right|}^2}} \end{split} $$ (3) 恒定模数约束可防止功率放大器的非线性失真,从而使发射器的效率最大化。具体而言,将波形矩阵的标准化包络写为:
$$\left| {{S_{m,n}}} \right|{\rm{ = }}1\quad m = 1,2, \cdots ,M;\;n = 1,2, \cdots ,N$$ (4) 设
${q_g} = {\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{\mathit{\boldsymbol{S}}}}} \right\|_2} - \alpha {p_d}({\theta _g})$ ,空域代价函数表示为:$${J_S}\left( {\alpha ,{{\mathit{\boldsymbol{S}}}}} \right){\rm{ = }}\frac{1}{G}\sum\limits_{g = 1}^G {{{\left| {{q_g}} \right|}^2}} $$ (5) -
阵列各阵元发射时域信号,即波形矩阵S的各行的频谱为
${{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}{\left( {{{\mathit{\boldsymbol{S}}}}(m,:)} \right)^{\rm{T}}}$ ,${{\mathit{\boldsymbol{S}}}}(m,:)$ 为波形矩阵的第m行,傅里叶变换矩阵表示为:$${{\mathit{\boldsymbol{F}}}} = \left[ {\begin{array}{*{20}{c}} 1&1& \cdots &1 \\ 1&{{{\rm{e}}^{{\rm{j}}\frac{{2{\text{π}} }}{N}}}}& \cdots &{{{\rm{e}}^{{\rm{j}}\frac{{2{\text{π}} }}{N}(N - 1)}}} \\ \vdots & \vdots & & \vdots \\ 1&{{{\rm{e}}^{{\rm{j}}\frac{{2{\text{π}} }}{N}(N - 1)}}}& \cdots &{{{\rm{e}}^{{\rm{j}}\frac{{2{\text{π}} }}{N}{{(N - 1)}^2}}}} \end{array}} \right]$$ (6) 阵列发射信号为窄带带通信号,因为采样频率远远小于载频,所以不影响空域信号的窄带模型。设
${{\mathit{\boldsymbol{z}}}} \in {R^{N \times 1}}$ 为归一化的频谱模板列向量,${{\mathit{\boldsymbol{\tilde Z}}}} = {{{\mathit{\boldsymbol{1}}}}_M} \otimes {{{\mathit{\boldsymbol{z}}}}^{\rm{T}}}$ ,则理想频谱塑形的问题是找到波形满足代价函数最小的问题,其代价函数可建模为频域波形与理想频谱模板之间的均方距离:$$\begin{split} {J_F}\left( {\mu ,{{\mathit{\boldsymbol{S}}}}} \right)& = \frac{1}{N}\left\| {\sqrt {\left( {{{\mathit{\boldsymbol{S}}}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right) \circ \left( {{{{\mathit{\boldsymbol{S}}}}^*}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}}} \right)} - \mu {\bf{\tilde Z}}} \right\|_{\rm{F}}^2 \\ & = \frac{1}{N}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left| {\left| {{{\mathit{\boldsymbol{s}}}}_m^{\rm{T}}{{\mathit{\boldsymbol{f}}}}_n^*} \right| - \mu {z_n}} \right|}^2}} } \\ \end{split} $$ (7) 设
${t_{m,n}} = \left| {{{\mathit{\boldsymbol{s}}}}_m^{\rm{T}}{{\mathit{\boldsymbol{f}}}}_n^*} \right| - \mu {z_n}$ ,${{\mathit{\boldsymbol{s}}}}_m^{\rm{T}}$ 是波形矩阵${{\mathit{\boldsymbol{S}}}}$ 的第m行,频域代价函数为:$${J_F}\left( {{{\mathit{\boldsymbol{S}}}},\mu } \right){\rm{ = }}\frac{1}{N}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left| {{t_{m,n}}} \right|}^2}} } $$ (8) -
设
$\gamma $ 为调整两种代价函数的权重系数,联合代价函数是式(3)与式(5)的加权和:$$J\left( {{{\mathit{\boldsymbol{S}}}},\alpha ,\mu } \right) = \frac{\gamma }{G}\sum\limits_{g = 1}^G {{{\left| {{q_g}} \right|}^2}} + \frac{{1 - \gamma }}{N}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left| {{t_{m,n}}} \right|}^2}} } $$ (9) 联合优化的问题可以表示为:
$$\begin{split} &\qquad\qquad\qquad\; \mathop {\min }\limits_{{{\mathit{\boldsymbol{S}}}},\alpha ,\mu } J\left( {{{\mathit{\boldsymbol{S}}}},\alpha ,\mu } \right) \\ & {\rm{s.t.}}\left| {{S_{m,n}}} \right|{\rm{ = }}1\quad m = 1,2, \cdots ,M;n = 1,2, \cdots ,N \end{split} $$ (10) 问题表明需要联合考虑发射波形所形成方向图与方向图模板均方距离,以及各阵元发射波形在频域上与理想频谱模板均方距离同时达到最小。
-
代价函数在第k次迭代结果为:
$$\begin{split} J\left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}},\alpha ,\mu } \right) &= \frac{1}{G}\sum\limits_{g = 1}^G {{{\left| {{{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right\|}_2} - \alpha {p_d}({\theta _g})} \right|}^2}} + \\& \frac{1}{N}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left| {\left| {{{\mathit{\boldsymbol{s}}}}_m^{{\rm{(}}k{\rm{)T}}}{{\mathit{\boldsymbol{f}}}}_n^*} \right| - \mu {z_n}} \right|}^2}} } \end{split} $$ (11) 首先更新匹配系数,即令
$\dfrac{\partial}{{\partial \alpha }}J\left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}},\alpha ,\mu } \right) = 0$ 以及$\dfrac{\partial }{{\partial \mu }}J\left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}},\alpha ,\mu } \right) = 0$ ,可得:$${\alpha ^{(k + 1)}} = \frac{{\displaystyle\sum\limits_{g = 1}^G {{p_d}\left( {{\theta _g}} \right){{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right\|}_2}} }}{{\displaystyle\sum\limits_{g = 1}^G {p_d^2\left( {{\theta _g}} \right)} }}$$ (12) $${\mu ^{(k + 1)}} = \frac{{\displaystyle\sum\limits_{m = 1}^M {\displaystyle\sum\limits_{n = 1}^N {{z_n}\left| {{{\mathit{\boldsymbol{s}}}}_m^{(k){\rm{T}}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|} } }}{{\displaystyle\sum\limits_{m = 1}^M {\displaystyle\sum\limits_{n = 1}^N {z_n^2} } }}$$ (13) -
将式(13)、式(14)代入代价函数(9)后得到
$J\left( {{{\mathit{\boldsymbol{S}}}},{\alpha ^{(k + 1)}},}\right. \left.{{\mu ^{(k + 1)}}} \right)$ ,忽略常数项,对它进行最小化的问题可写成:$$\begin{split} & \mathop {\min }\limits_{{\mathit{\boldsymbol{S}}}} \frac{\gamma }{G}\sum\limits_{g = 1}^G {\bigg\{ \left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{\mathit{\boldsymbol{S}}}}} \right\|_2^2 - 2{\alpha ^{(k + 1)}}{p_d}({\theta _g}){{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{\mathit{\boldsymbol{S}}}}} \right\|}_2}\bigg\} } +\\ & \frac{{1 - \gamma }}{N}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\bigg\{ {{\left| {{{\mathit{\boldsymbol{s}}}}_m^{\rm{T}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|}^2} - 2{\mu ^{(k + 1)}}{z_n}\left| {{{\mathit{\boldsymbol{s}}}}_m^{\rm{T}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|\bigg\} } } \\ & {\rm{s}}{\rm{.t}}{\rm{.}}\left| {{S_{m,n}}} \right|{\rm{ = }}1\quad m = 1,2, \cdots ,M;n = 1,2, \cdots ,N \\[-10pt]\end{split} $$ (14) 设
$\;\beta _g^{(k)}= - 2{\alpha ^{(k + 1)}}{p_d}({\theta _g}) \leqslant 0$ ,$\;\tilde \beta _{m,n}^{(k)} = - 2{\mu ^{(k + 1)}}{z_n} \leqslant 0$ 。由柯西-施瓦茨不等式可得:$\;\beta _g^{(k)}{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{\mathit{\boldsymbol{S}}}}} \right\|_2} \leqslant $ $ \;\beta _g^{(k)} \dfrac{{{\rm{Re}} \left[ {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{\mathit{\boldsymbol{a}}}}({\theta _g})} \right]}}{{{{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right\|}_2}}}$ 及$\;\tilde \beta _{m,n}^{(k)}{\left| {{{\mathit{\boldsymbol{s}}}}_m^{\rm{T}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|^2} \leqslant \tilde \beta _{m,n}^{(k)}$ $\dfrac{{{\rm{Re}} \left[ {{{\mathit{\boldsymbol{s}}}}_m^{{\rm{(}}k{\rm{)T}}}{{\mathit{\boldsymbol{f}}}}_n^*{{\mathit{\boldsymbol{f}}}}_n^{\rm{H}}{{\mathit{\boldsymbol{s}}}}_m^{}} \right]}}{{\left| {{{\mathit{\boldsymbol{s}}}}_m^{{\rm{(}}k{\rm{)T}}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|}} $ 。则
$J\left( {{{\mathit{\boldsymbol{S}}}},{\alpha ^{(k + 1)}},{\mu ^{(k + 1)}}} \right)$ 的替代函数可建模为:$$\begin{split} &\qquad\;\;\; U\left( {{{\mathit{\boldsymbol{S}}}}\left| {{{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right.} \right) = \frac{\gamma }{G}\left\{ \sum\limits_{g = 1}^G {\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{\mathit{\boldsymbol{S}}}}} \right\|_2^2}\right. +\\ &\quad\;\;\; \left. \sum\limits_g {\frac{{\beta _g^{(k)}{\rm{Re}} \left[ {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{\mathit{\boldsymbol{a}}}}({\theta _g})} \right]}}{{{{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right\|}_2}}}} \right\} +\\ & \frac{{1 - \gamma }}{N}\left\{ \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left| {{{\mathit{\boldsymbol{s}}}}_m^{\rm{T}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|}^2}} } + \sum\limits_{(m,n)} {\frac{{\tilde \beta _{m,n}^{(k)}{\rm{Re}} \left[ {{{\mathit{\boldsymbol{s}}}}_m^{{\rm{(}}k{\rm{)T}}}{{\mathit{\boldsymbol{f}}}}_n^*{{\mathit{\boldsymbol{f}}}}_n^{\rm{H}}{{\mathit{\boldsymbol{s}}}}_m^{}} \right]}}{{\left| {{{\mathit{\boldsymbol{s}}}}_m^{{\rm{(}}k{\rm{)T}}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|}}} \right\} \end{split} $$ (15) 忽略常数项,替代函数寻优的问题写成:
$$\begin{split} &\qquad\qquad\;\; \mathop {\min }\limits_{{\mathit{\boldsymbol{S}}}} {f_1}({{\mathit{\boldsymbol{S}}}}) + {f_2}({{\mathit{\boldsymbol{S}}}}) \\ & {\rm{s}}{\rm{.t}}{\rm{.}}\left| {{S_{m,n}}} \right|{\rm{ = }}1\quad m = 1,2, \cdots ,M;n = 1,2, \cdots ,N \end{split} $$ (16) 其中,
$$\begin{split} & {f_1}\left( {{\mathit{\boldsymbol{S}}}} \right){\rm{ = }}\frac{\gamma }{G}\sum\limits_{g = 1}^G {\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{\mathit{\boldsymbol{S}}}}} \right\|_2^2} + \frac{{1 - \gamma }}{N}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left| {{{\mathit{\boldsymbol{s}}}}_m^{\rm{T}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|}^2}} } \\ &\;\; {f_2}\left( {{\mathit{\boldsymbol{S}}}} \right) = \frac{\gamma }{G}\sum\limits_g {\frac{{\beta _g^{(k)}{\rm{Re}} \left[ {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{\mathit{\boldsymbol{a}}}}({\theta _g})} \right]}}{{{{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right\|}_2}}}} + \\ & \quad\frac{{1 - \gamma }}{N}\sum\limits_{(m,n)} {\frac{{\tilde \beta _{m,n}^{(k)}{\rm{Re}} \left[ {{{\mathit{\boldsymbol{s}}}}_m^{{\rm{(}}k{\rm{)T}}}{{\mathit{\boldsymbol{f}}}}_n^*{{\mathit{\boldsymbol{f}}}}_n^{\rm{H}}{{\mathit{\boldsymbol{s}}}}_m^{}} \right]}}{{\left| {{{\mathit{\boldsymbol{s}}}}_m^{{\rm{(}}k{\rm{)T}}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|}}} \end{split} $$ (17) 定义
${{\mathit{\boldsymbol{A}}}}=[{{\mathit{\boldsymbol{a}}}}({\theta }_{1}),{{\mathit{\boldsymbol{a}}}}({\theta }_{2}),\cdots ,{{\mathit{\boldsymbol{a}}}}({\theta }_{G})]$ 和${\overline{\overline{{{\mathit{\boldsymbol{w}}}}}}}^{(k)}=[{\overline{\overline{w}}}_{1}^{(k)}, $ $ {\overline{\overline{w}}}_{2}^{(k)},\cdots ,{\overline{\overline{w}}}_{G}^{(k)}]$ ,其中${\bar {\bar w}}_g^{(k)} = \beta _g^{(k)}/{\left\| {{{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g}){{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right\|_2}$ ;又有${{\mathit{\boldsymbol{F}}}}=[{{{\mathit{\boldsymbol{f}}}}}_{1},{{{\mathit{\boldsymbol{f}}}}}_{2},\cdots ,{{{\mathit{\boldsymbol{f}}}}}_{N}]$ ,${{\bar{\bar {\mathit{\boldsymbol{{ \varPsi }}}}}}^{(k)}}\left( {m,n} \right) = {\bar{ \bar \varsigma }}_{m,n}^{(k)}$ ,其中${\bar{ \bar \varsigma }}_{m,n}^{(k)} = \tilde \beta _{m,n}^{(k)}/ $ $ \left| {{{\mathit{\boldsymbol{s}}}}_m^{{\rm{(}}k{\rm{)T}}}{{\mathit{\boldsymbol{f}}}}_n^*} \right|$ ;由矩阵迹的性质,可得:
$${f_1}\left( {{\mathit{\boldsymbol{S}}}} \right){\rm{ = }}\frac{\gamma }{G}{\rm{tr}}\left\{ {{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{\mathit{\boldsymbol{S}}}}} \right\} + \frac{{1 - \gamma }}{N}\left\| {{{\mathit{\boldsymbol{S}}}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right\|_{\rm{F}}^2$$ (18) $$\begin{split} & {f_2}\left( {{\mathit{\boldsymbol{S}}}} \right) = \frac{\gamma }{G}{\rm{Re}} \left[ {{\rm{tr}}\left\{ {{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{\mathit{\boldsymbol{A}}}}{\rm{diag}}\left( {\overline{\overline{{{\mathit{\boldsymbol{w}}}}}}}^{(k)} \right){{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right\}} \right] +\\ & \frac{{1 - \gamma }}{N}{\rm{Re}} \left[ {{\rm{tr}}\left\{ {{{\left[ {{{{\bar{\bar {\mathit{\boldsymbol{{ \varPsi }}}}}}}^{(k)}} \circ \left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right)} \right]}^{\rm{H}}}\left( {{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{S}}}}^{\rm{T}}}} \right)} \right\}} \right] \end{split} $$ (19) 由二阶泰勒展开,式(14)中目标函数的二次项可放缩为替代函数:
$$\begin{split} &{f_1}\left( {{\mathit{\boldsymbol{S}}}} \right) \leqslant \frac{\gamma }{G}{\rm{tr}}\left\{ {{{{\mathit{\boldsymbol{S}}}}^{(k)}}^{\rm{H}}{{\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right\} + \frac{\gamma }{G}{\rm{Re}} \Big\{ {\rm{tr}}\Big[ \left( {{{{\mathit{\boldsymbol{S}}}}^{(k){\rm{H}}}}{{\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}} \right)\times\\ & \left( {{{\mathit{\boldsymbol{S}}}} - {{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right) \Big] \Big\} + \frac{\gamma }{G}\frac{{\lambda _S^{(k)}}}{2}{\rm{Re}} \left\{ {{\rm{tr}}\left[ {{{\left( {{{\mathit{\boldsymbol{S}}}} - {{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right)}^{\rm{H}}}\left( {{{\mathit{\boldsymbol{S}}}} - {{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right)} \right]} \right\} + \\ & \frac{{1 - \gamma }}{N}\left\| {{{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right\|_{\rm{F}}^2 + \frac{{1 - \gamma }}{N}{\rm{Re}} \left\{ {{\rm{tr}}\left[ {\left( {{{{\mathit{\boldsymbol{S}}}}^{(k)*}}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}}{{{\mathit{\boldsymbol{F}}}}^*}} \right)\left( {{{\mathit{\boldsymbol{S}}}} - {{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right)} \right]} \right\} +\\ &\qquad\qquad \frac{{\lambda _F^{(k)}}}{2}\frac{{1 - \gamma }}{N}\left\| {\left( {{{\mathit{\boldsymbol{S}}}} - {{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right){{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right\|_{\rm{F}}^2 \end{split} $$ (20) Hessian矩阵被对角矩阵替代,其系数为:
$$\begin{split} & \lambda _S^{(k)} = {\lambda _{\max }}\left[ {{{{\mathit{\boldsymbol{I}}}}_N} \otimes \left( {{{\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}} \right)} \right] = {\lambda _{\max }}\left[ {{{{\mathit{\boldsymbol{I}}}}_N}} \right]{\lambda _{\max }}\left[ {{{\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}} \right] \leqslant \\ &\qquad\;\; {\rm{tr}}\left( {\sum\limits_{g = 1}^G {{{\mathit{\boldsymbol{a}}}}({\theta _g}){{{\mathit{\boldsymbol{a}}}}^{\rm{H}}}({\theta _g})} } \right) = \sum\limits_{g = 1}^G M = MG \end{split} $$ (21) $$\begin{split} & \lambda _F^{(k)} = {\lambda _{\max }}\left[ {{{{\mathit{\boldsymbol{I}}}}_N} \otimes \left( {{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}}} \right)} \right] = {\lambda _{\max }}\left[ {{{{\mathit{\boldsymbol{I}}}}_N}} \right]{\lambda _{\max }}\left[ {{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}}} \right] \leqslant \\ &\qquad\qquad\qquad\; {\rm{tr}}\left( {\sum\limits_{n = 1}^N {{{\mathit{\boldsymbol{f}}}}_n^*{{\mathit{\boldsymbol{f}}}}_n^{\rm{T}}} } \right) = {N^2} \\[-10pt]\end{split} $$ (22) 忽略常数项,
${f_1}\left( {{\mathit{\boldsymbol{S}}}} \right)$ 替代函数优化问题为:$$\begin{split} & \mathop {\min }\limits_{{\mathit{\boldsymbol{S}}}} \frac{\gamma }{G}{\rm{Re}} \left\{ {{\rm{tr}}\left[ {{{{\mathit{\boldsymbol{S}}}}^{(k){\rm{H}}}}{{\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{\mathit{\boldsymbol{S}}}}} \right]} \right\} + \frac{\gamma }{G}\frac{{\lambda _S^{(k)}}}{2}{\rm{Re}} \left\{ {{\rm{tr}}\left[ { - {{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}} - {{{\mathit{\boldsymbol{S}}}}^{(k)}}^{\rm{H}}{{\mathit{\boldsymbol{S}}}}} \right]} \right\} \\ & + \frac{{1 - \gamma }}{N}{\rm{Re}} \left\{ {{\rm{tr}}\left[ {{{{\mathit{\boldsymbol{S}}}}^{(k){\rm{H}}}}{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}}{{\mathit{\boldsymbol{S}}}}} \right]} \right\} + \frac{{\lambda _F^{(k)}}}{2}\frac{{1 - \gamma }}{N}{\rm{tr}}\left\{ { - {{\mathit{\boldsymbol{S}}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}}^{\rm{H}} - {{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}} \right\} \\ \end{split} $$ (23) 一次项为:
$$\begin{split} & {f_2}\left( {{\mathit{\boldsymbol{S}}}} \right) = \frac{\gamma }{G}{\rm{Re}} \left[ {{\rm{tr}}\left\{ {{{{\mathit{\boldsymbol{S}}}}^{(k)}}^{\rm{H}}{{\mathit{\boldsymbol{A}}}}{\rm{diag}}\left( {{{{\bar{\bf \bar {{\mathit{\boldsymbol{w}}}}}}}^{(k)}}} \right){{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{\mathit{\boldsymbol{S}}}}} \right\}} \right] + \\ &\frac{{1 - \gamma }}{N}{\rm{Re}} \left[ {{\rm{tr}}\left\{ {{{\left[ {{{{\bar{\bar {\mathit{\boldsymbol{{ \varPsi }}}}}}}^{(k)}} \circ \left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right)} \right]}^{\rm{H}}}\left( {{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{S}}}}^{\rm{T}}}} \right)} \right\}} \right] \end{split} $$ (24) ${f_1}({{\mathit{\boldsymbol{S}}}}) + {f_2}({{\mathit{\boldsymbol{S}}}})$ 的替代函数优化问题为:$$\begin{split} &\qquad\quad\;\; u\left( {{{\mathit{\boldsymbol{S}}}}\left| {{{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right.} \right) = \frac{\gamma }{G}{\rm{Re}} \Big\{ {\rm{tr}}\Big[ {{{\mathit{\boldsymbol{S}}}}^{(k){\rm{H}}}}{{\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{\mathit{\boldsymbol{S}}}} - \lambda _S^{(k)}{{{\mathit{\boldsymbol{S}}}}^{(k)}}^{\rm{H}}{{\mathit{\boldsymbol{S}}}} +\\ &\qquad\qquad\quad\;\;\;\; {{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}{{\mathit{\boldsymbol{A}}}}{\rm{diag}}\left( {{{{\bar{\bf \bar {{\mathit{\boldsymbol{w}}}}}}}^{(k)}}} \right){{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}} \Big] \Big\} +\\ &\qquad\;\;\quad \frac{{1 - \gamma }}{N}{\rm{Re}} \Bigg\{ {\rm{tr}}\Bigg[ {{{\mathit{\boldsymbol{S}}}}^{(k){\rm{H}}}}{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}}{{\mathit{\boldsymbol{S}}}} - \lambda _F^{(k)}{{{\mathit{\boldsymbol{S}}}}^{(k)}}^{\rm{H}}{{\mathit{\boldsymbol{S}}}} +\\ &\qquad\quad\;\;\quad \left\{ {{{\left[ {{{{\bar{\bar {\mathit{\boldsymbol{{ \varPsi }}}}}}}^{(k)}} \circ \left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right)} \right]}^{\rm{H}}}\left( {{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{S}}}}^{\rm{T}}}} \right)} \right\} \Bigg] \Bigg\} =\\ & \frac{\gamma }{G}{\rm{Re}} \left\{ {{\rm{tr}}\left[ {{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}\left( {{{\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}} - \lambda _S^{(k)}{{{\mathit{\boldsymbol{S}}}}^{(k)}} + {{\mathit{\boldsymbol{A}}}}{\rm{diag}}\left( {{{{\bar{\bf \bar {{\mathit{\boldsymbol{w}}}}}}}^{(k)}}} \right){{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}}} \right)} \right]} \right\} +\\ &\frac{{1 - \gamma }}{N}{\rm{Re}} \left\{ {{\rm{tr}}\left[ {{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}\left({{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}} - \lambda _F^{(k)}{{{\mathit{\boldsymbol{S}}}}^{(k)}} + [{{{\bar{\bar {\mathit{\boldsymbol{{ \varPsi }}}}}}}^{(k)}}^{\rm{H}} \circ \left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right)]{{\mathit{\boldsymbol{F}}}}} \right)} \right]} \right\} \end{split} $$ (25) 式(25)中替代优化问题写成矩阵问题:
$$\begin{split} & \mathop {\min }\limits_{{\mathit{\boldsymbol{S}}}} {\rm{Re}} \Bigg\{ {\rm{tr}}\Bigg[{{{\mathit{\boldsymbol{S}}}}^{\rm{H}}}\Bigg(\frac{\gamma }{G}{{\mathit{\boldsymbol{A}}}}{\rm{diag}}\left( {{{{{\overset{\smile}{\bar{ w} }}}}^{(k)}}} \right){{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}} + \frac{{1 - \gamma }}{N}{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}} +\\ & \frac{{1 - \gamma }}{N}\left[ {{{{\bar{\bar {\bf { \Psi }}}}}^{(k)}} \circ \left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right)} \right]{{\mathit{\boldsymbol{F}}}} - \left( {\frac{\gamma }{G}\lambda _S^{(k)} + \frac{{1 - \gamma }}{N}\lambda _F^{(k)}} \right){{{\mathit{\boldsymbol{S}}}}^{(k)}}\Bigg)\Bigg]\Bigg\} \\ & \qquad\qquad\qquad\qquad\; {\rm{s}}{\rm{.t}}{\rm{.}}\left| {{S_{m,n}}} \right| = 1 \\[-10pt]\end{split} $$ (26) 式中,
${{{\overset{\smile}{\bar{ w}} }}^{(k)}} = \left[ {\overset{\smile}{\bar w} _1^{(k)},\overset{\smile}{\bar w} _2^{(k)}, \cdots ,\overset{\smile}{\bar w} _G^{(k)}} \right]$ ,$\overset{\smile}{\bar w} _g^{(k)} = 2 + {\bar {\bar w}}_g^{(k)}$ 。上述优化问题被重构为:
$$\begin{split} & \mathop {\min }\limits_{{\mathit{\boldsymbol{S}}}} \left\| {{{\mathit{\boldsymbol{S}}}} - {{{\mathit{\boldsymbol{\varOmega }}}}^{(k)}}} \right\|_{\rm{F}}^2 \\ & {\rm{s}}{\rm{.t}}{\rm{.}}\left| {{S_{i,j}}} \right| = 1 \end{split} $$ (27) 其中,
$$\begin{split} & {{{\mathit{\boldsymbol{\varOmega }}}}^{(k)}} = \left( {\frac{\gamma }{G}\lambda _S^{(k)} + \frac{{1 - \gamma }}{N}\lambda _F^{(k)}} \right){{{\mathit{\boldsymbol{S}}}}^{(k)}} - \frac{\gamma }{G}{{\mathit{\boldsymbol{A}}}}{\rm{diag}}\left( {{{{{\overset{\smile}{\bar{ w} }}}}^{(k)}}} \right){{{\mathit{\boldsymbol{A}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{S}}}}^{(k)}} - \\ & \qquad\frac{{1 - \gamma }}{N}{{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{F}}}}^*}{{{\mathit{\boldsymbol{F}}}}^{\rm{T}}} - \frac{{1 - \gamma }}{N}\left[ {{{{\bar{\bar {\mathit{\boldsymbol{{ \varPsi }}}}}}}^{(k)}} \circ \left( {{{{\mathit{\boldsymbol{S}}}}^{(k)}}{{{\mathit{\boldsymbol{F}}}}^{\rm{H}}}} \right)} \right]{{\mathit{\boldsymbol{F}}}} \\[-10pt]\end{split} $$ (28) 考虑到恒模约束,波形矩阵更新为
${{\mathit{\boldsymbol{S}}}} = {{\rm{e}}^{{\rm{j}}\angle {{{\mathit{\boldsymbol{\varOmega }}}}^{(k)}}}}$ 。 -
总的计算复杂度包括每一步迭代中的矩阵乘法和加法,以及傅里叶变换。对N维向量做FFT的计算复杂度为
$O\left( {N\log N} \right)$ 。空间匹配系数$\alpha $ 更新的计算复杂度为$O\left( {G\left[ {N + {M^2} + 2MN} \right] + G} \right)$ ,频率匹配系数$\mu $ 更新的计算复杂度为$ O\left(MN+MN·N\mathrm{log}N\right)$ ,替代函数的参数计算复杂度为$O\left( {G + MN} \right)$ ,波形矩阵更新的计算复杂度为$O\left( {{M^2}NG + MN N\log N} \right)$ ,因此算法总的计算复杂度为:$$\begin{split} &\quad O(K\{ 2G + NG + 2MN + {M^2}G +\\ & 2MNG + {M^2}NG + 2M{N^2}\log N\} ) \end{split} $$ (29) 对于使用矩阵求逆的迭代算法,计算复杂度至少在
$O\left( {K\left\{ {{M^3}{N^3}G} \right\}} \right)$ 量级,随着阵元数、快拍数增长,计算复杂度呈几何级增长。因此本文算法的优势体现在大规模阵列、频率捷变雷达、多快拍波形的应用中。 -
本节对提出的波形设计算法进行数值算例的仿真。分别在不同场景需求下,模拟算法的方向图拟合性能与频谱拟合性能。方向图拟合的SQP算法源自文献[1]。参数设置:10阵元均匀线阵、快拍数32,方向图拟合误差占总误差比重
$\gamma = 0.5$ 。单主瓣平顶方向图主瓣为$\left[ { - 30^\circ ,30^\circ } \right]$ ,多主瓣平顶方向图主瓣为$\left[ { - 50^\circ , - 30^\circ } \right] \cup \left[ { - 10^\circ ,10^\circ } \right] \cup \left[ {30^\circ ,50^\circ } \right]$ 。第一个频谱模板的阻带归一化频率范围为$\left[ {0.2,0.5} \right]$ ,深度为−20 dB;第二个频谱模板的阻带归一化频率范围为[0, 0.061 7] ∪ [0.098 8, 0.246 9] ∪ [0.259 3, 0.284 0] ∪ [0.308 6, 0.382 7] ∪ [0.407 4, 0.493 8] ∪ [0.518 5, 0.555 6] ∪ [0.938 3, 1],深度为−20 dB。 -
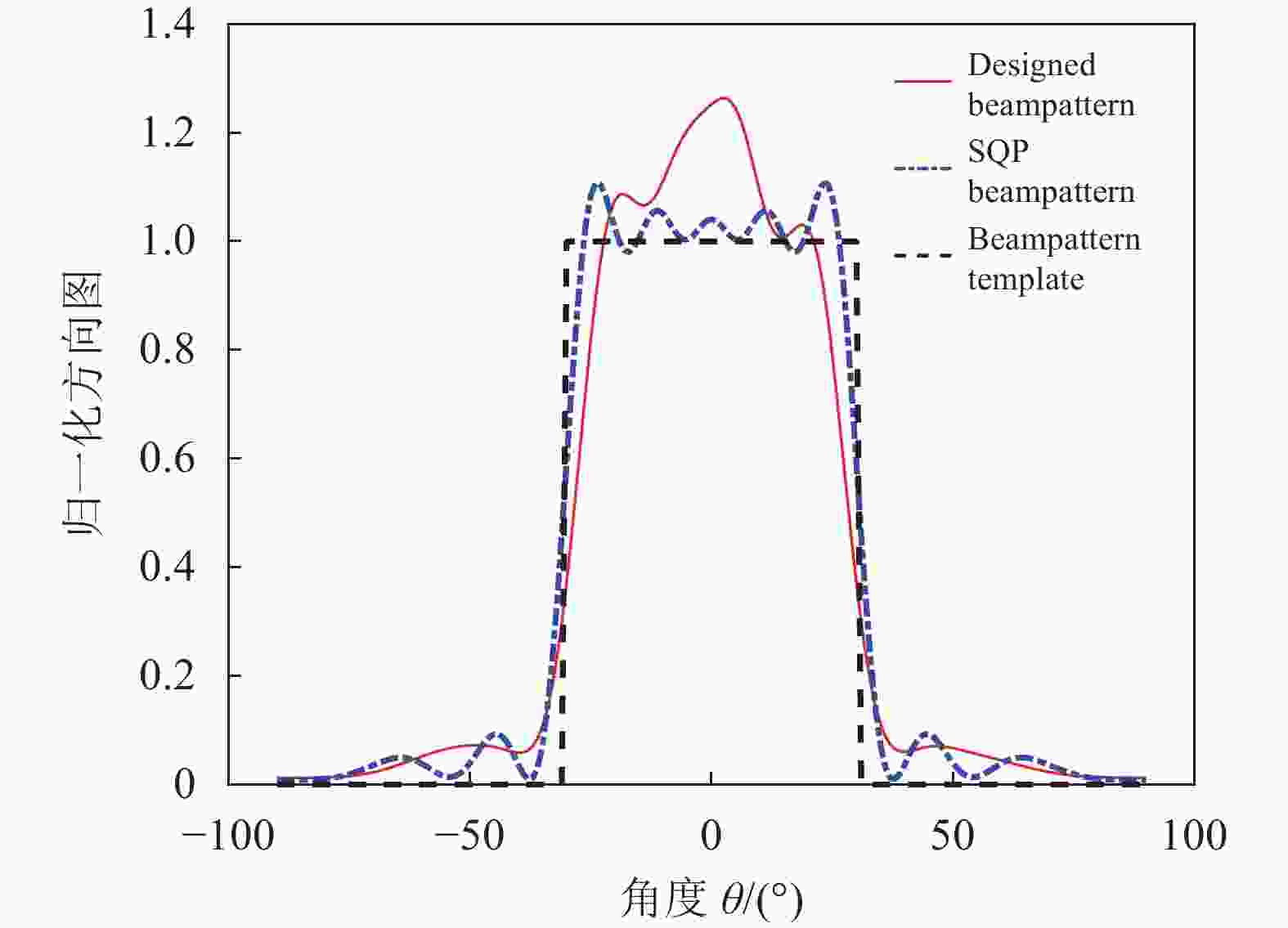
单主瓣平顶方向图应用场景:空间能量聚焦目标区域为DOA相对集中的慢变空间范围。
拟合方向图的曲线如图2所示,本文算法设计的波形合成的方向图与SQP算法合成的方向图贴近,且本文算法不需要求逆运算,计算量较小,对于频率捷变MIMO雷达这类需要不断重新计算的应用具有优势。
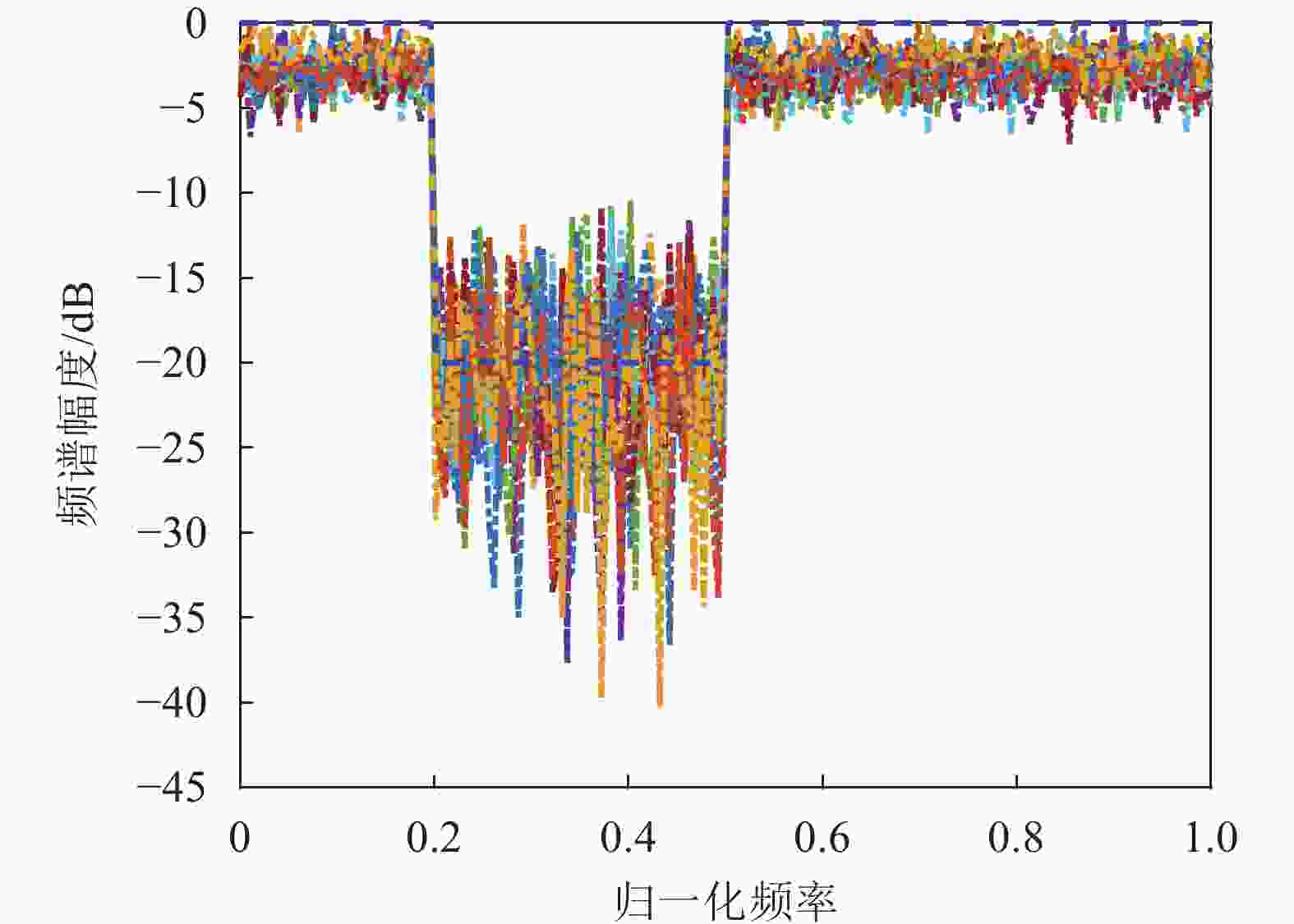
频谱拟合的曲线如图3所示,蓝色虚线为频谱模板,其他颜色为各阵元发射波形的频谱。各阵元发射波形的频谱在通带贴近模板,且波纹较小;阻带电平最浅处达到−13 dB,最深处超过−30 dB,能够有效地避免对邻近无线通信频段形成干扰。
-
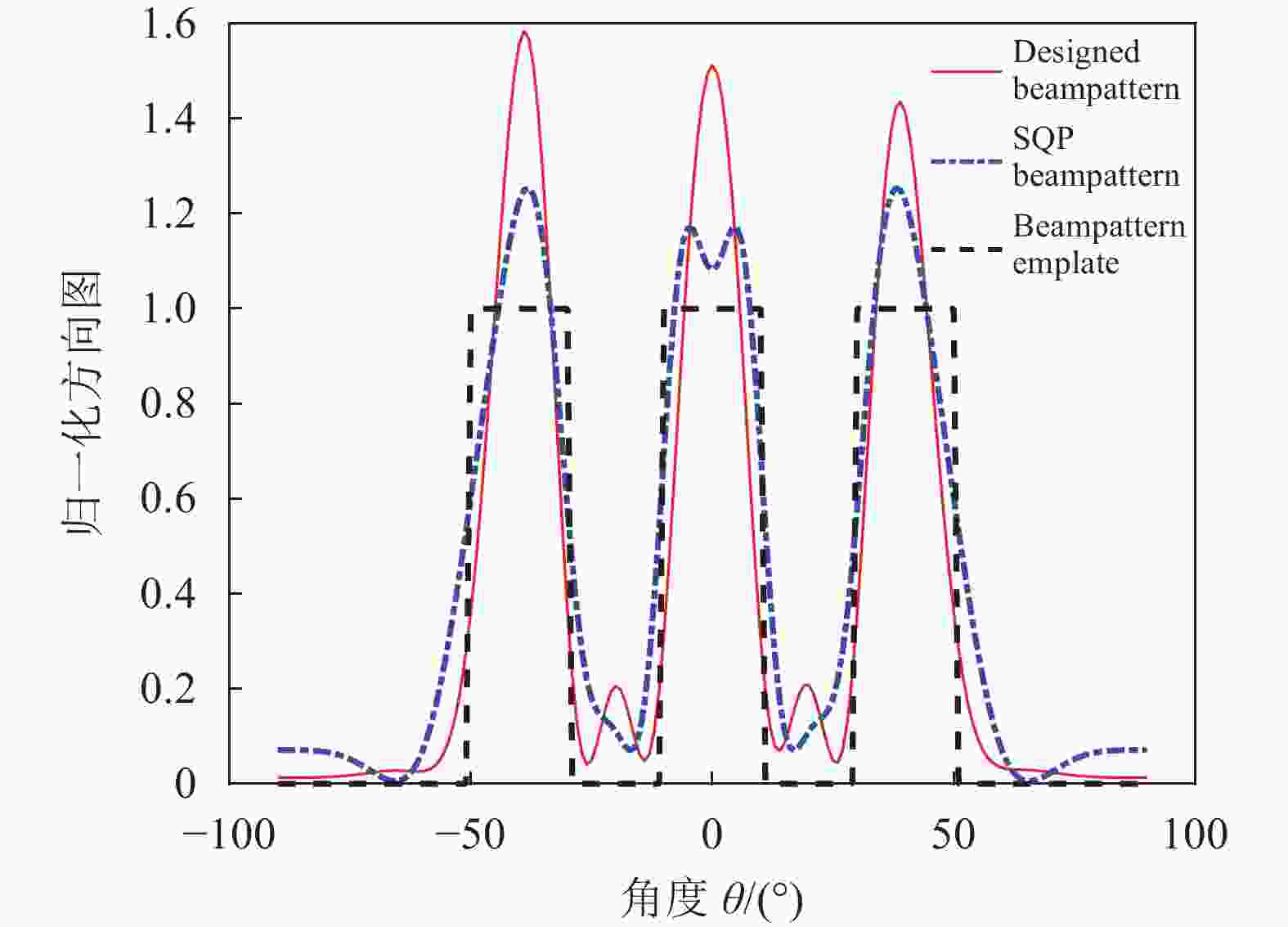
多主瓣平顶方向图应用场景:空间能量聚焦目标区域为DOA相对分散的多个空间范围。
拟合方向图的曲线如图4所示,本文算法设计的波形合成的方向图与SQP算法合成的方向图贴近,旁瓣电平更低,且不需要求逆运算,计算量较小,对于频率捷变MIMO雷达这类需要不断重新计算的应用具有优势。
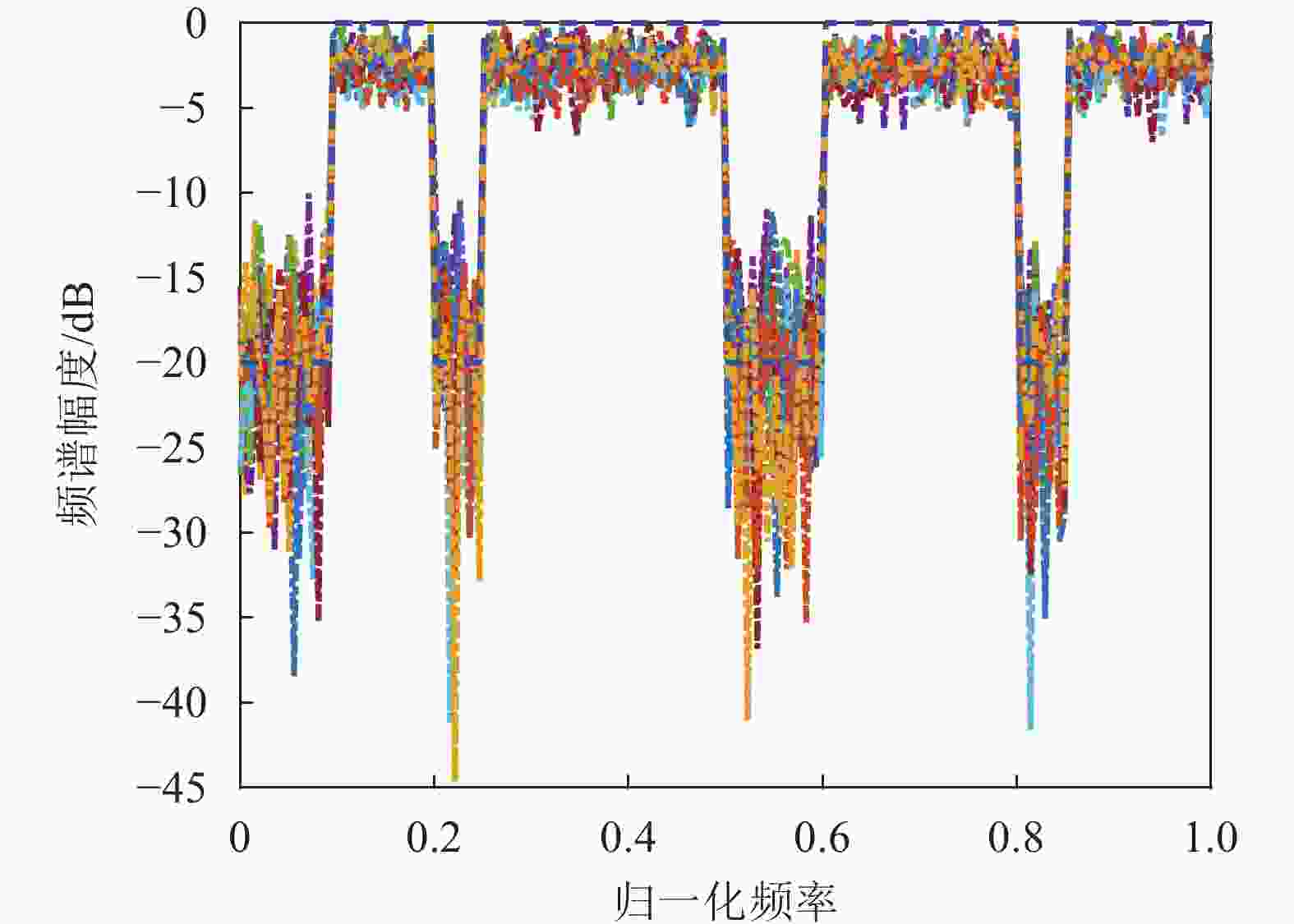
频谱拟合的曲线如图5所示,蓝色虚线为频谱模板,各阵元发射波形的频谱在通带贴近模板,且几乎没有波纹;阻带电平最浅处达到−10 dB,最深处超过−30 dB。灵活多变的频谱模板设置,使得雷达能够有效地避免对处于模板阻带频段的无线通信系统形成干扰,也能降低处于模板阻带频段的阻塞式干扰对雷达探测性能的影响。
-
本文提出的算法设计MIMO雷达发射波形,联合优化方向图合成性能和频谱塑形性能。联合优化问题被建模为加权均方误差代价函数,优化问题是非凸非平滑的。首先对优化问题的模型进行建模,再对均方误差代价函数进行放缩,构造替代函数;进而优化替代函数,得到较小代价函数值对应的波形。本文提出的迭代优化算法,具有接近理想的方向图拟合性能与频谱拟合性能,且运算量小。多个应用场景下的仿真和数值结果证明了所提方法的有效性。
未来的工作会着重关注雷达波形的探测性能,例如自相关性能、多普勒性能等,将这些性能与方向图拟合、频谱拟合联合考虑。
MIMO Radar Transmit Waveform Design for Joint Optimizing Beampattern Synthesis and Spectral Compatibility
-
摘要: 多发射-多接收雷达发射方向图合成是当前波形设计和合成问题的热点,其目的在于实现将发射能量聚焦在感兴趣的空域方向上。而在复杂的电磁环境中,还必须兼顾考虑在拥堵频段上的频谱兼容性和灵活性,避免影响邻近频段通信系统传输性能。该文提出算法设计MIMO雷达发射波形向目标空域聚焦能量的同时,避开拥堵频段的频率范围。即针对发射波形在空域、频域两类要求而联合优化。联合优化问题被建模为加权均方误差代价函数,优化问题是非凸非平滑的。在算法的每一步迭代优化中,首先更新当前步骤的匹配系数,再对均方误差代价函数进行放缩,构造替代函数;进而优化替代函数,得到较小代价函数值对应的波形。该文提出的迭代优化算法,具有接近理想的方向图合成性能与频谱塑形性能,且运算量小。仿真和数值结果证明了该方法的有效性。Abstract: This paper investigates joint optimization of beampattern synthesis and spectral compatibility of multiple-input multiple-output (MIMO) radar transmit waveform under constant modulus constraint. In complex electromagnetic environments, it is necessary to consider the spectrum compatibility and flexibility in the congested frequency band to avoid poor transmission performance of the communication system in the adjacent frequency band. In this paper, the joint optimization problem is modeled as a weighted mean square error cost function constrained by constant modulus, which is non-convex and non-smooth. In each step of the iterative optimization algorithm, firstly update the matching coefficient of the current step and scale the cost function to construct a majorization function. Next, the majorization function is optimized to obtain a waveform correspond to a smaller cost function value. The performance of the proposed algorithm has a good performance on beampattern synthesis and spectrally compatibility, it also has a small amount of calculation. Simulation and numerical results prove the effectiveness of the proposed method.
-
Key words:
- beampattern synthesis /
- MIMO radar /
- spectrally compatibility /
- waveform design
-
[1] STOICA P, LI Jian, XIE Yao. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151-4161. doi: 10.1109/TSP.2007.894398 [2] STOICA P, LI Jian, ZHU Xu-min. Waveform synthesis for diversity-based transmit beampattern design[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2593-2598. doi: 10.1109/TSP.2007.916139 [3] YU Xian-xiang, CUI Guo-long, ZHANG Tian-xian, et al. Constrained transmit beampattern design for collocated MIMO radar[J]. Signal Processing, 2018, 144: 145-154. doi: 10.1016/j.sigpro.2017.10.010 [4] ZHANG Xiao-jun, HE Zi-shu, LEZ R B, et al. MIMO radar transmit beampattern matching design[J]. IEEE Transactions on Signal Processing, 2015, 63(8): 2049-2056. doi: 10.1109/TSP.2015.2398841 [5] CHENG Zi-yang, HE Zi-shu, ZHANG Sheng-miao, et al. Constant modulus waveform design for MIMO radar transmit beampattern[J]. IEEE Transactions on Signal Processing, 2017, 65(18): 4912-4923. doi: 10.1109/TSP.2017.2718976 [6] FAN Wan, LIANG Jun-li, YU Guo-yong, et al. MIMO radar waveform design for quasi-equiripple transmit beampattern synthesis via weighted l p-minimization[J]. IEEE Transactions on Signal Processing, 2019, 67(13): 3397-3411. doi: 10.1109/TSP.2019.2917871 [7] CHENG Zi-yang, LIAO Bin, HE Zi-shu, et al. Spectrally compatible waveform design for MIMO radar in the presence of multiple targets[J]. IEEE Transactions on Signal Processing, 2018, 66(13): 3543-3555. doi: 10.1109/TSP.2018.2833818 [8] GE Peng, CUI Guo-long, KARBASI S M, et al. A template fitting approach for cognitive unimodular sequence design[J]. Signal Processing, 2016, 128: 360-368. doi: 10.1016/j.sigpro.2016.05.008 [9] LIANG Jun-li, SO H C, LEUNG C S, et al. Waveform design with unit modulus and spectral shape constraints via lagrange programming neural network[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1377-1386. doi: 10.1109/JSTSP.2015.2464178 [10] TANG Bo, LIANG Jun-li. Efficient algorithms for synthesizing probing waveforms with desired spectral shapes[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(3): 1174-1189. doi: 10.1109/TAES.2018.2876585 [11] SUN Ying, BABU P, PALOMAR D. Majorization-minimization algorithms in signal processing, communications, and machine learning[J]. IEEE Transactions on Signal Processing, 2017, 65(3): 794-816. doi: 10.1109/TSP.2016.2601299 [12] CHENG Zi-yang, HAN Chun-lin, LIAO Bin, et al. Communication-aware waveform design for MIMO radar with good transmit beampattern[J]. IEEE Transactions on Signal Processing, 2018, 66(21): 5549-5562. doi: 10.1109/TSP.2018.2868042 -


 ISSN
ISSN 



 下载:
下载: