-
航天器要完成空间探测、开发空间等特定的飞行任务,对姿态控制提出了各种要求。其中对地观测卫星在轨运行和对地观测中要求卫星在一定的干扰下实现高精度的对地指向,更需要高精度的姿态控制。近年来,卫星姿态控制领域取得了许多成果,如经典的PID控制[1-2]、最优控制[3]、鲁棒控制[4-5]、自适应控制[6-7]、滑模控制[8]、模糊控制等。
其中滑模控制本质是一类特殊的非线性控制,在控制过程中,系统的状态沿着滑动模态运动,由于滑动模态可以设计且与系统参数变化和外界扰动无关,因而具有很好的鲁棒性。但在实际系统中,状态轨迹一般不会完全沿着滑模面运动,而是在滑模面两侧来回穿越,产生抖动。对航天器来说,这种抖动不仅会影响系统的控制精度,增加航天器的能量消耗,也有可能会激发系统的高频未建模动态,使系统产生振荡甚至失稳。国内外许多学者从不同的角度提出了解决的方法。文献[9]改进了滑模切换函数,提出了边界层的概念,在边界层外采用滑模切换函数,而在边界层内使用饱和函数替代切换函数,通过减少切换增益来减小抖振。然而在系统存在参数不确定性和外界存在扰动时,边界层的方法会产生稳态误差。同时传统的滑模控制中系统的相轨迹分为到达段和滑模段,系统只有处于滑模段时,才表现出对于参数变化和干扰的鲁棒性。基于此,文献[10-11]将积分项引入了滑模面的设计中,利用积分滑模的积分特性和全局滑模特性消除稳态误差和缩短到达滑模时间。
上述控制方法仅使系统渐进稳定,即闭环系统状态要在时间趋于无穷大时才能收敛为零。有限时间控制是近年来新兴的热门控制方法,相比传统的控制方法,闭环系统状态可以在有限时间收敛到零,同时具有更快的收敛特性,在工程应用中具有发展前景。文献[12]针对不存在和存在扰动力矩的两种情况设计了两种基于修正罗德里格斯参数(MRP)描述刚体航天器姿态的有限时间控制律。文献[13]基于欧拉角描述的航天器姿态模型,设计了使闭环控制系统具有负齐次性的有限时间控制律,该方法针对系统扰动和不确定性具有一定的鲁棒性。
本文综合有限时间控制和滑模控制的特点,在滑模面的设计中加入有限时间控制算法,同时应用自适应方法设计了动态滑模切换函数增益,提出了一种有限时间自适应积分滑模控制方法。该方法相较于常规滑模控制方法,系统状态收敛更快,而相较于常规有限时间方法,鲁棒性更好。数值仿真表明了该方法的有效性。
-
建立四元数表示的航天器姿态跟踪模型如下[14]:
$$\begin{split} & {J\dot \omega } = - {({\omega } + {C}{{\omega }_{{d}}})^ \times }{J}({\omega } + {C}{{\omega }_{{d}}})+\\ & \;\; {J}[({{\omega }^ \times }{C}{{\omega }_{{d}}} - {C}{{\dot{ \omega }}_{{d}}})] + {{u}_{{c}}} + {{u}_{{d}}} \end{split}$$ (1) $$\left\{ {\begin{split} & {{{{ \dot q}}_{{v}}} = \frac{1}{2}[{q_4}{{I}_3} + {q}_{{v}}^ \times ]{\omega }}\\ & {{{\dot q}_4} = - \frac{1}{2}{q}_{{v}}^{\rm{T}}{\omega }} \end{split}} \right.$$ (2) 式中,
${J} \in {\bf{R}^{3 \times 3}}$ 为航天器转动惯量阵;${\omega } \in {\bf{R}^3}$ 为航天器本体系到期望坐标系的姿态角速度误差;${{\omega }_d} \in {\bf{R}^3}$ 为航天器期望跟踪的姿态角速度;${C}$ 为从航天器本体坐标系到期望坐标系的转换矩阵,${C} = (q_4^2 - {q}_\nu ^{\rm{T}}{{q}_\nu }){{I}_3} + $ $ 2{q}_\nu ^{\rm{T}}{{q}_\nu } - 2{q_4}{q}_\nu ^ \times $ ,且满足$\left\| {C} \right\| = 1$ ,${{C}^{\rm{T}}}{C} = 1$ ,$\det ({C}) = 1$ ,$\dot{ C} = - {{\omega }^ \times }{C}$ ;${({q}_\nu ^{\rm{T}},{q_4})^{\rm{T}}}$ 表示航天器本体系到期态坐标系的姿态四元数;${{q}_\nu } = {[\begin{array}{*{20}{l}}{{q_1}}&{{q_2}}&{{q_3}}\end{array}]^{\rm{T}}}$ ,满足${q}_\nu ^{\rm{T}}{{q}_\nu } + $ $ q_4^2 = 1$ ;上标$ {( \cdot )}^{\times }$ 表示斜对称矩阵算子。对任意向量${x} = [\begin{array}{*{20}{l}}{{x_1}}&{{x_2}}&{{x_3}}\end{array}]$ ,有:$${{x}^ \times } = \left[ {\begin{array}{*{20}{c}} 0&{ - {x_3}}&{{x_2}} \\ {{x_3}}&0&{ - {x_1}} \\ { - {x_2}}&{{x_1}}&0 \end{array}} \right]$$ ${{u}_{{c}}} \in {\bf{R}^3}$ 和${{u}_{{d}}} \in {\bf{R}^3}$ 分别为控制力矩向量和有界干扰向量,考虑到航天器转动惯量的不确定性,将${J}$ 分成确定$\hat {{J}}$ 和不确定$\Delta {J}$ 两部分,令${J} = \hat{ J} + \Delta {J}$ ,代入式(1)、式(2),可得:$$\begin{split} & {\hat J \dot \omega } = - {({\omega } + {C}{{\omega }_{{d}}})^ \times }\hat{ J}({\omega } + {C}{{\omega }_{{d}}}) +\\ & \;\;\, \hat{ J}[({{\omega }^ \times }{C}{{\omega }_{{d}}} - {C}{{\dot{ \omega }}_{{d}}})] + {{u}_{{c}}} + {d} \end{split}$$ (3) $$\left\{ {\begin{aligned} & {{{\dot{ q}}_\nu } = \frac{1}{2}[{q_4}{{I}_3} + {q}_\nu ^ \times ]{\omega }}\\ & {{{\dot q}_4} = - \frac{1}{2}{q}_\nu ^{\rm{T}}{\omega }} \end{aligned}} \right.$$ (4) 式中,
${d} = {{u}_{{d}}} - {({\omega } + {C}{{\omega }_{{d}}})^ \times }\Delta {J}({\omega } + {C}{{\omega }_{{d}}}) - \Delta {J\dot \omega } + \Delta {J}\times $ $ [({{\omega }^ \times }{C}{{\omega }_{{d}}} - {C}{{\dot{ \omega }}_{{d}}})]$ 为将转动惯量不确定和外界干扰合并的总干扰,并假设${\left\| {d} \right\|_\infty }$ 有界。 -
定义 1(强稳定性)[15] 考虑非线性系统:
$$\dot{ x} = {f}({x}),\;{x} \in {{\bf{R}}^n},\;{f}(0) = 0$$ (5) 式中,
${f}:{D} \to {{\bf{R}}^n}$ 是定义在${D}$ 上取值于${n}$ 维空间${{\bf{R}}^n}$ 的连续函数。若对$\forall {\bf{\alpha }} > 0$ 和$\forall {\varepsilon } > 0$ ,存在函数${B}:(0, + \infty ) \to (0, + \infty )$ 和${T}:(0, + \infty ) \times (0, + \infty ) \to (0, + \infty )$ ,其中${B}$ 为单调递增的且满足$\mathop {\lim }\limits_{{s} \to {{0}}} {B}({s}) = 0$ ,使得系统(5)定义在$[0,{{t}_1}),0 < {{t}_1} \leqslant + \infty $ 及$\left\| {{x}(0)} \right\| \leqslant {\alpha }$ 上的每一个解,都存在一个对应的定义在$[0, + \infty )$ 上的解${z}({t})$ 满足:$$\begin{array}{l} 1)\;{z}({t}) = {x}({t})\quad\;\;\forall {t} \in [0,{{t}_1})\\ 2)\;\left\| {{z}({t})} \right\| \leqslant {B}({\alpha })\quad\;\;\forall {t} \geqslant 0\\ 3)\;\left\| {{z}({t})} \right\| < {\varepsilon }\quad\;\;\forall {t} \geqslant {T}({\alpha },{\varepsilon }) \end{array}$$ 则
${x} = {{0}}$ 为系统(5)的强稳定平凡解,当${D} = {{\bf{R}}^n}$ 时,系统为全局强稳定。定义 2(有限时间稳定)[16] 考虑非线性系统:
$$\dot{ x} = {f}({x}),\;\;{x} \in {U} \subseteq {{\bf{R}}^n},\;\;{f}(0) = 0$$ (6) 式中,
${f}:{U} \to {{\bf{R}}^n}$ 为开区域${U}$ 上对${x}$ 连续的函数,且开区域${U}$ 包含原点。系统的解${x} = {{0}}$ 为有限时间稳定的,当且仅当系统是强稳定的且为有限时间收敛的。有限时间收敛指:对$\forall {{x}_0} \in {{U}_0} \subset {{\bf{R}}^n}$ ,存在一个连续函数${T}({x}):{{U}_0}\backslash \{ 0\} \to (0, + \infty )$ ,使得系统(6)的解${x}({t},{{x}_0})$ 满足:当${t} \in [0,{T}({{x}_0}))$ 时,${{x}}({t},{{x}_0}) \in {{U}_0}\backslash \{ 0\} $ 和$\mathop {\lim }\limits_{{t} \to {T}({{x}_0})} {x}({t},{{x}_0}) = 0$ ;当${t} > {T}({{x}_{{0}}})$ 时,有${x}({t},{{x}_{{0}}}) = {{0}}$ 。若${U} = {{U}_0} = {{\bf{R}}^n}$ ,则系统(6)为全局有限时间稳定。定义 3(向量函数齐次性)[17] 考虑如下向量函数,
${f}({x}) = {({{f}_1}({x}),{{f}_2}({x}), \cdots ,{{f}_{{n}}}({x}))^{\rm{T}}}:{{\bf{R}}^n} \to {{\bf{R}}^n}$ ,若对任意的${\varepsilon } > 0$ ,存在$({{r}_1},{{r}_2}, \cdots ,{{r}_{{n}}}) \in {{\bf{R}}^n}$ ,其中${{r}_{{i}}} > 0$ ,${i} = 1,2, \cdots ,{n} $ ,使得${f}({x})$ 满足:$${{f}_{{i}}}({{\varepsilon }^{{{r}_1}}}{{x}_1}, \cdots ,{{\varepsilon }^{{{r}_{{n}}}}}{{x}_{{n}}}) = {{\varepsilon }^{{k} + {{r}_i}}}{{f}_{{i}}}({x})\quad\;\;{i} = 1,2, \cdots ,{n}$$ 式中,
${k} > - \min \{ {{r}_{{i}}},{i} = 1,2, \cdots ,{n}\} $ ,则称${f}({x})$ 关于$({{r}_1}, $ $ {{r}_2}, \cdots , {{r}_{{n}}})$ 具有齐次度${k}$ ,其中$({{r}_1}, {{r}_2}, \cdots ,{{r}_{{n}}})$ 称为扩张。定义 4(标量函数齐次性)[18] 考虑如下连续函数,
${V}({x}):{{\bf{R}}^n} \to {\bf{R}}$ ,若对任意的${\varepsilon } > 0$ ,存在${\sigma } > 0$ 和扩张$({{r}_1},{{r}_2}, \cdots ,{{r}_{{n}}}) \in {{\bf{R}}^n}$ ,其中${{r}_{{i}}} > 0$ ,${i} = 1,2, \cdots ,{n} $ ,使得:$${V}({{\varepsilon }^{{{r}_1}}}{{x}_1},{{\varepsilon }^{{{r}_1}}}{{x}_2}, \cdots ,{{\varepsilon }^{{{r}_{{n}}}}}{{x}_{{n}}}) = {{\varepsilon }^{{\sigma }}}{V}({x})\;\;\;\;\forall {x} \in {{\bf{R}}^n}$$ 则称
${V}({x})$ 关于$({{r}_1}, {{r}_2},\cdots ,{{r}_{{n}}})$ 具有齐次度${\sigma }$ 。引理 1[19] 对于非线性系统(6),若该系统是全局渐进稳定的且具有负的齐次度,那么该系统是全局有限时间稳定的。
-
不考虑外界干扰和转动惯量不确定性的标称航天器姿态跟踪动力学方程为:
$$\begin{split} & \hat{ J\dot \omega } = - {({\omega } + {C}{{\omega }_{{d}}})^ \times }\hat{ J}({\omega } + {C}{{\omega }_{{d}}})+\\ & \;\; \hat{ J}[({{\omega }^ \times }{C}{{\omega }_{{d}}} - {C}{{\dot{ \omega }}_{{d}}})] + {u}_{{c}}^* \end{split}$$ (7) $$\left\{ {\begin{aligned} & {{{\dot{ q}}_{{v}}} = \frac{1}{2}[{q_4}{{I}_3} + {q}_{{v}}^ \times ]{\omega }}\\ & {{{\dot q}_4} = - \frac{1}{2}{q}_{{v}}^{\rm{T}}{\omega }} \end{aligned}} \right.$$ (8) 式中,
${u}_{{c}}^* \in {{\bf{R}}^3}$ 为标称姿态跟踪控制律。引入状态
${x}$ 和控制输入${u}_{{c}}^*$ 如下:$$\begin{split} & {x} = {[\begin{array}{*{20}{l}} {{{q}_1}}&{{{q}_2}}&{{{q}_3}}&{{{\omega }_{{x}}}}&{{{\omega }_{{y}}}}&{{{\omega }_{{z}}}} \end{array}]^{\rm{T}}}\\ & \qquad\;{u}_{{c}}^* = {[\begin{array}{*{20}{l}} {{{t}_1}}&{{{t}_2}}&{{{t}_3}} \end{array}]^{\rm{T}}} \end{split}$$ 则系统(7)和系统(8)可改写成如下形式:
$$\left( {\begin{array}{*{20}{c}} {{{\dot{ q}}_v}}\\ {\dot{ \omega }} \end{array}} \right) = \left( {\begin{aligned} & \qquad\qquad{\frac{1}{2}[{q_4}{{I}_3} + {q}_\nu ^ \times ]{\omega }}\\ & {{{\hat{ J}}^{ - 1}}( - {{({\omega } + {C}{{\omega }_{{d}}})}^ \times }\hat{ J}({\omega } + {C}{{\omega }_{{d}}})}+\\ & \qquad{ \hat{ J}[({{\omega }^ \times }{C}{{\omega }_{{d}}} - {C}{{\dot{ \omega }}_{{d}}})])} \end{aligned}} \right) + \left( {\begin{array}{*{20}{c}} \bf{0}\\ {{{\hat{ J}}^{ - 1}}} \end{array}} \right){u}_{{c}}^*$$ (9) 为方便控制律的设计和证明,对式(9)进行坐标变换。定义新的状态变量如下:
$${z} = {[\begin{array}{*{20}{l}} {{{q}_1}}&{{{q}_2}}&{{{q}_3}}&{{{\dot{ q}}_1}}&{{{\dot{ q}}_2}}&{{{\dot{ q}}_3}} \end{array}]^{\rm{T}}}$$ 令:
$${P} = [{q_4}{{I}_3} + {q}_{{v}}^ \times ]$$ (10) 则有:
$${\dot {{q}}_{{v}}} = \frac{1}{2}{P}{\omega }$$ (11) 对上式移项并对
${\omega }$ 求导,可得:$$\dot{ \omega } = 2{\dot{ P}^{ - 1}}{\dot{ q}_{{v}}} + 2{{P}^{ - 1}}{{\ddot q}_{{v}}}$$ (12) 将式(12)代入式(9),得:
$$\begin{aligned} & \left( {\begin{array}{*{20}{c}} {{{{\dot q}}_v}}\\ {2{{P}^{ - 1}}{{{\ddot q}}_v}} \end{array}} \right) = \left( {\begin{aligned} & \qquad\qquad\qquad{{{{\dot q}}_v}}\\ & {{{\hat{ J}}^{ - 1}}( - {{({\omega } + {C}{{\omega }_{{d}}})}^ \times }\hat{ J}({\omega } + {C}{{\omega }_{{d}}})}+\\ &\qquad { \hat{ J}[({{\omega }^ \times }{C}{{\omega }_{{d}}} - {C}{{{\dot \omega }}_{{d}}})])} \end{aligned}} \right)+\\ &\qquad\qquad\;\; \left( {\begin{array}{*{20}{c}} \bf{0}\\ {{{\hat{ J}}^{ - 1}}} \end{array}} \right){u}_{{c}}^* - \left( {\begin{array}{*{20}{c}} \bf{0}\\ {2{{\dot{ P}}^{ - 1}}{{\dot{ q}}_v}} \end{array}} \right) \end{aligned}$$ (13) 对上式进行变换如下:
$$\begin{split} & \left( {\begin{array}{*{20}{c}} {{{{\dot q}}_v}}\\ {{{{\ddot q}}_v}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {E}&\bf{0}\\ \bf{0}&{\dfrac{1}{2}{P}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{{\dot q}}_v}}\\ {2{{P}^{ - 1}}{{{\ddot q}}_v}} \end{array}} \right)= \\ & \left( {\begin{array}{*{20}{c}} {{{{\dot q}}_v}}\\ {G} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} \bf{0}\\ {\dfrac{1}{2}{P}{{\hat{ J}}^{ - 1}}} \end{array}} \right){u}_{{c}}^* \end{split}$$ (14) 式中,
$$\begin{split} &\qquad\qquad\quad {G} = {[\begin{array}{*{20}{l}} {{g_1}}&{{g_2}}&{{g_3}} \end{array}]^{\rm{T}}}=\\ & \frac{1}{2}{P}({{\hat{ J}}^{ - 1}}( - {(2{{P}^{ - 1}}{{\dot{ q}}_v} + {C}{{\omega }_{{d}}})^ \times }\hat{ J}(2{{P}^{ - 1}}{{\dot{ q}}_v} + {C}{{\omega }_{{d}}})+\\ &\;\;\;\; \hat{ J}[({(2{{P}^{ - 1}}{{\dot{ q}}_v})^ \times }{C}{{\omega }_{{d}}} - {C}{{\dot{ \omega }}_{{d}}})]) - 2{{\dot{ P}}^{ - 1}}{{\dot{ q}}_v}) \end{split}$$ 定理 1 针对坐标变换后的系统(14),标称姿态控制律
${u}_{{c}}^*$ 设计为:$${u}_{{c}}^* = 2\hat{ J}{{P}^{ - 1}}( - {G} - {{k}_1}{\rm{si}}{{\rm{g}}^{{{\alpha }_1}}}({{q}_v}) - {{k}_2}{\rm{si}}{{\rm{g}}^{{{\alpha }_2}}}({\dot{ q}_v}))$$ (15) 式中,
${{k}_1} > 0;\;{{k}_2} > 0;\;0 < {{\alpha }_1} < 1;\;{{\alpha }_2} = \dfrac{{2{{\alpha }_1}}}{{1 + {{\alpha }_1}}}$ 。若${\eta } = ({\eta _1},{\eta _2},{\eta _3})$ ,${\rm{si}}{{\rm{g}}^{{\alpha }}}({\varepsilon }) = {({\rm{si}}{{\rm{g}}^{{\alpha }}}({\eta _1}),{\rm{si}}{{\rm{g}}^{{\alpha }}}({\eta _2}),{\rm{si}}{{\rm{g}}^{{\alpha }}}({\eta _3}))^{\rm{T}}}, $ $ {\rm{si}}{{\rm{g}}^{{\alpha }}} ({\eta _i}) = {\rm{sign}}({\eta _i}){\left| {{\eta _i}} \right|^{{\alpha }}}$ ,则标称系统(14)是全局有限时间稳定的。证明:将控制律式(15)带入式(14),得:
$$\begin{split} & \left( {\begin{array}{*{20}{c}} {{{{\dot q}}_v}}\\ {{{{\ddot q}}_v}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{\dot{ q}}_v}}\\ { - {{k}_1}{\rm{si}}{{\rm{g}}^{{{\alpha }_1}}}({{q}_v}) - {{k}_2}{\rm{si}}{{\rm{g}}^{{{\alpha }_2}}}({{\dot{ q}}_v})} \end{array}} \right)=\\ & \qquad\qquad\qquad \left( {\begin{array}{*{20}{c}} {{{f}_1}({{\dot{ q}}_v})}\\ {{{f}_2}({{q}_v},{{\dot{ q}}_v})} \end{array}} \right) \end{split}$$ (16) 考虑备选Lyapunov函数:
$${V}({z}) = \frac{1}{{{{\alpha }_1} + 1}}{{k}_1}\sum\limits_{i = 1}^3 {{{\left| {{{q}_{{i}}}} \right|}^{{{\alpha }_1} + 1}}} + \frac{1}{2}\sum\limits_{{i} = 1}^3 {\dot{ q}_{{i}}^2} $$ (17) 不难验证
${V}({z})$ 是正定的,且当${z} \ne 0$ 时是连续可微的,${V}({z})$ 沿闭环系统(16)的解对时间的导数为:$$\begin{split} & \dot{ V}({z}) = {{k}_1}\sum\limits_{{i} = 1}^3 {{\rm{sgn}}({{q}_{{i}}}){{\left| {{{q}_{{i}}}} \right|}^{{{\alpha }_1}}}} {{\dot{ q}}_{{i}}} + \sum\limits_{i = 1}^3 {{{\dot{ q}}_{{i}}}} {{{\ddot q}}_{{i}}}=\\ & \sum\limits_{{i} = 1}^3 {{{\dot{ q}}_{{i}}}} ( - {{k}_1}{\rm{sgn}}({{q}_{{i}}}){\left| {{{q}_{{i}}}} \right|^{{{\alpha }_1}}} - {{k}_2}{\rm{sgn}}({{\dot{ q}}_{{i}}}){\left| {{{\dot{ q}}_{{i}}}} \right|^{{{\alpha }_2}}})+\\ & {{k}_1}\sum\limits_{{i} = 1}^3 {{\rm{sgn}}({{q}_{{i}}}){{\left| {{{q}_{{i}}}} \right|}^{{{\alpha }_1}}}} {{\dot{ q}}_{{i}}} =- {{k}_2}\sum\limits_{{i} = 1}^3 {{{\left| {{{\dot{ q}}_{{i}}}} \right|}^{{{\alpha }_2} + 1}}} \end{split}$$ (18) 显然
$\dot {{V}}({z})$ 关于${z}$ 是半负定的,闭环系统(16)是Lyapunov意义下稳定的。根据式(18)可知$\dot {{V}}({z}) = 0$ ,等价于${\dot {{q}}_1} = {\dot {{q}}_2} = {\dot {{q}}_3} = 0$ ,定义集合:$${L} = \{ {z} \in {{\bf{R}}^6},\sum\limits_{{i} = 4}^6 {\left| {{{z}_{{i}}}} \right|} = 0\} $$ (19) 由闭环系统(16)可得,集合L中所包含的最大不变集为系统的平衡点
${z} = 0$ 。因此,由LaSalle不变性原理可知闭环系统(16)是渐进稳定的。容易验证:$${{f}_1}({{\varepsilon }^{{{r}_2}}}{\dot{ q}_v}) = {{\varepsilon }^{{{r}_2}}}{\dot{ q}_v} = {{\varepsilon }^{{{r}_2} - {{r}_1} + {{r}_1}}}{\dot{ q}_v}$$ (20) $$\begin{split} & {{f}_2}({{\varepsilon }^{{{r}_1}}}{{q}_v},{{\varepsilon }^{{{r}_2}}}{{\dot{ q}}_v}) = - {{k}_1}{\rm{si}}{{\rm{g}}^{{{\alpha }_1}}}({{\varepsilon }^{{{r}_1}}}{{q}_v}) - {{k}_2}{\rm{si}}{{\rm{g}}^{{{\alpha }_2}}}({{\varepsilon }^{{{r}_2}}}{{\dot{ q}}_v}) = \\ &\quad\qquad - {{k}_1}{{\varepsilon }^{{{r}_1}{{\alpha }_1}}}{\rm{si}}{{\rm{g}}^{{{\alpha }_1}}}({{q}_v}) - {{k}_2}{{\varepsilon }^{{{r}_2}{{\alpha }_2}}}{\rm{si}}{{\rm{g}}^{{{\alpha }_2}}}({{\dot{ q}}_v})= \\ &\qquad\qquad {{\varepsilon }^{{{r}_1}{{\alpha }_1}}}{{f}_2}({{q}_v},{{\dot{ q}}_v}) = {{\varepsilon }^{{{r}_1}{{\alpha }_1} - {{r}_2} + {{r}_2}}}{{f}_2}({{q}_v},{{\dot{ q}}_v}) \end{split}$$ (21) 式中,
${{r}_1}{{\alpha }_1} = {{r}_2}{{\alpha }_2}$ ,取${{r}_1}{{\alpha }_1} - {{r}_2} = {{r}_2} - {{r}_1}$ ,对于${{r}_1} = 1$ ,则有${{r}_2} = \dfrac{{1 + {{\alpha }_1}}}{2}$ ,$0 < {{\alpha }_1} < 1 $ ,${{\alpha }_2} = \dfrac{{2{{\alpha }_1}}}{{1 + {{\alpha }_1}}}$ ,系统的齐次度为${k} = {{r}_2} = \dfrac{{{{\alpha }_1} - 1}}{2} < 0$ 。由引理1可知,系统(14)为全局有限时间稳定。即状态${z} = {[{{q}_v},{\dot{ q}_v}]^{\rm{T}}}$ 能在有限时间收敛到零。又因为${\dot{ q}_\nu } = \dfrac{1}{2}{P\omega }$ ,所以状态${x} = {[\begin{array}{*{20}{l}}{{{q}_{{v}}}}&{\omega }\end{array}]^{\rm{T}}}$ 也为有限时间收敛。对式(15)的控制律进行变换,得到以状态${x}$ 表示的控制律${u}_{{c}}^*$ 如下:$$\begin{split} &\;\; {u}_{{c}}^* = {({\omega } + {C}{{\omega }_{{d}}})^ \times }\hat{ J}({\omega } + {C}{{\omega }_{{d}}}) -\\ & \; \hat{ J}[({{\omega }^ \times }{C}{{\omega }_{{d}}} - {C}{{\dot{ \omega }}_{{d}}})] + \hat{ J}{{\dot{ P}}^{ - 1}}{P\omega }+\\ & 2\hat{ J}{{P}^{ - 1}}\left( - {{k}_1}{\rm{si}}{{\rm{g}}^{{{\alpha }_1}}}({{q}_v}) - {{k}_2}{\rm{si}}{{\rm{g}}^{{{\alpha }_2}}}\left(\frac{1}{2}{P\omega }\right)\right) \end{split}$$ (22) -
上述有限时间控制器的设计分析仅针对无聚合扰动情况,针对有聚合扰动,扰动上界存在且已知的情况,设计有限时间积分滑模控制器。首先考虑如下的积分滑模函数:
$${s} = {\omega } + {Z}$$ (23) 式中,
${s} \in {\bf{R}^3}$ 为积分滑模函数;${Z} \in {\bf{R}^3}$ 为积分项。令$\dot {{Z}}$ 和控制律${u}_{{c}}^*$ 分别为:$$\dot{ Z} = - {\dot{ P}^{ - 1}}{P\omega } + 2{{P}^{ - 1}}\left({{k}_1}{\rm{si}}{{\rm{g}}^{{{\alpha }_1}}}({{q}_v}) + {{k}_2}{\rm{si}}{{\rm{g}}^{{{\alpha }_2}}}\left(\frac{1}{2}{P\omega }\right)\right)$$ (24) $${{u}_{{c}}} = {u}_{{c}}^* + {{u}_{\rm{sw}}}$$ (25) 式中,
${u}_{{c}}^*$ 如式(22)所示,${{u}_{\rm{sw}}}$ 设计为:$${{u}_{\rm{sw}}} = - {{d}_{{c}}}{\mathop{\rm sgn}} ({s}) - k{s}$$ (26) 式中,
${{d}_{{c}}}$ 为常值标量,且取${{d}_{{c}}} > {\left\| {d} \right\|_\infty }$ ,使其能克服有界聚合扰动;${k} > 0$ 且为常值。定理 2 式(25)所示控制律能够使得系统(3)和系统(4)的状态有限时间收敛。
证明:首先证明式(26)设计的控制律能够使得系统状态在有限时间到达滑模面式(23)。
对式(23)求导,并将式(24)、式(25)和式(3)代入,可得:
$$\begin{split} & \dot{ s} = \dot{ \omega } + \dot{ Z} = {{\hat{ J}}^{ - 1}}( - {({\omega } + {C}{{\omega }_{{d}}})^ \times }\hat{ J}({\omega } + {C}{{\omega }_{{d}}}) +\\ &\quad \hat{ J}[({{\omega }^ \times }{C}{{\omega }_{{d}}} - {C}{{\dot{ \omega }}_{{d}}})] + {{u}_{{c}}} + {d}) + \dot{ Z} =\\ &\quad\quad\quad {{\hat{ J}}^{ - 1}}( - {{d}_{{c}}}{\mathop{\rm sgn}} ({s}) - k{s} + {d}) \end{split}$$ (27) 设计如下Lyapunov函数:
$${V}({s}) = \frac{1}{2}{{s}^{\rm{T}}}\hat{ Js}$$ (28) 沿闭环系统轨迹求导,得到:
$$\begin{split} & \dot{ V}({s}) = {{s}^{\rm{T}}}\hat{ J\dot {{s}}} = {{s}^{\rm{T}}}( - {{d}_{{c}}}{\mathop{\rm sgn}} ({s}) - {ks} + {d})=\\ & \quad\quad - {{d}_{{c}}}{\left\| {s} \right\|_1} - {k}{\left\| {s} \right\|_2} + {{s}^{\rm{T}}}{d} \leqslant 0 \end{split}$$ (29) 满足可达条件,系统能在有限时间收敛到滑模面。当
${s} = {{0}}$ 时,等价于$\dot{ s} = {{0}}$ ,因此,有:$$\begin{split} &\qquad \dot{ s} = \dot{ \omega } + \dot{ Z}=\dot{ \omega } - {{\dot{ P}}^{ - 1}}{P\omega } + \\ & 2{{P}^{ - 1}}\left({{k}_1}{\rm{si}}{{\rm{g}}^{{{\alpha }_1}}}({{q}_v}) + {{k}_2}{\rm{si}}{{\rm{g}}^{{{\alpha }_2}}}\left(\frac{1}{2}{P\omega }\right)\right) = {{0}} \end{split}$$ (30) 将式(11)、式(12)代入式(30),可得:
$$2{{P}^{ - 1}}{{\ddot q}_v} + 2{{P}^{ - 1}}({{k}_1}{\rm{si}}{{\rm{g}}^{{{\alpha }_1}}}({{q}_v}) + {{k}_2}{\rm{si}}{{\rm{g}}^{{{\alpha }_2}}}({\dot{ q}_v})) = 0$$ (31) 由3.1节的证明可知,系统状态沿滑模面有限时间收敛。
选取
${Z}$ 的初值如下:$${Z}(0) = - {\omega }(0)$$ (32) 即初始时刻
${s} = {{0}}$ ,消除系统的滑模到达段,提高了系统的鲁棒性。 -
在3.2节的控制器中应用自适应方法,设计如下的姿态控制律:
$${{u}_{{c}}} = {u}_{{c}}^* - \hat{ d}{\mathop{\rm sgn}} ({s}) - k{s}$$ (33) 式中,
${u}_{{c}}^*$ 保持不变,$\hat{ d}$ 为扰动上限${\left\| {d} \right\|_\infty }$ 的估计值,且$\hat{ d} = {c}\int_0^{{t}} {{{\left\| {s} \right\|}_1}} {\rm{d}}t$ ,有如下定理成立。定理 3 在聚合扰动上限未知的情况下,式(33)所示控制律能够使得系统状态有限时间收敛。
证明:考虑如下Lyapunov函数:
$${V}({s}) = \frac{1}{2}{{s}^{\rm{T}}}\hat{ J{{s}}} + \frac{1}{{2{c}}}{(\hat{ d} - \bar{ d})^2}$$ (34) 式中,
$\bar{ d}{\rm{ > }}{\left\| {d} \right\|_\infty }$ ;$\hat{ d}$ 为$\bar{ d}$ 的估计值;${c} > 0$ 用于控制自适应速率。沿闭环系统轨迹求导,得:
$$\begin{split} & \qquad\;\dot{ V}({s}) = {{s}^{\rm{T}}}\hat{ J\dot {{s}}} + \frac{1}{{c}}\dot{ {\hat d}}(\hat{ d} - \bar{ d})=\\ & {{s}^{\rm{T}}}( - \hat{ d}{\rm{sign}}({s}) - {ks} + {d}) + {\left\| {s} \right\|_1}(\hat{ d} - \bar{ d})=\\ & - \hat{ d}{\left\| {s} \right\|_1} - {k}\left\| {s} \right\|_2^2 + {{s}^{\rm{T}}}{d} + \hat{ d}{\left\| {s} \right\|_1} - {\left\| {s} \right\|_1}\bar{ d}\leqslant\\ & - {\left\| {s} \right\|_1}\bar{ d} + {\left\| {s} \right\|_1}\bar{ d} - {k}\left\| {s} \right\|_2^2 = - {k}\left\| {s} \right\|_2^2 \leqslant 0 \end{split}$$ (35) 令
${\varphi } = {k}\left\| {s} \right\|_2^2$ ,对式(34)从0到${t}$ 进行积分,有:$$\left\{ \begin{split} & {\int_0^{{t}} {\dot{ V}{\rm{d}}t \leqslant } - \int_0^{{t}} {{\varphi }{\rm{d}}t} }\\ & {{V}(0) \geqslant {V}({t}) + \int_0^{{t}} {{\varphi }{\rm{d}}t} }\\ & {\int_0^{{t}} {{\varphi }{\rm{d}}t} \leqslant {V}(0)} \end{split} \right.$$ (36) 取
${t} \to \infty $ 时的极限,有:$$\mathop {\lim }\limits_{{t} \to \infty } \int_0^{{t}} {{\varphi }{\rm{d}}t} \leqslant {V}(0) < + \infty $$ 根据Barbalat引理可知:
$$\mathop {\lim }\limits_{{t} \to \infty } {\varphi } = 0$$ 由于
${k} > 0$ ,所以可知$\mathop {\lim }\limits_{{t} \to \infty } {s} ={{0}} $ ,由3.1节的分析可知,系统(3)和系统(4)的误差四元数和误差角速度是有限时间收敛的。为避免控制器中符号函数使得滑模面出现抖振,本文用连续函数
${f}({s})$ 代替符号函数${\rm{sgn}} ({s})$ ,其表达式为:$${f}({s}) = \frac{{s}}{{\left\| {s} \right\| + {a}}}$$ (37) 式中,
$\left\| {\;} \right\|$ 表示对向量求模;${a}$ 为大于0的常数。 -
为了验证本文方法的有效性,采用文献[20]的线性滑模面代替积分滑模面,设计控制律和3.1、3.3节的控制律分别进行数值仿真并比较。刚体航天器及控制律各项参数如下:
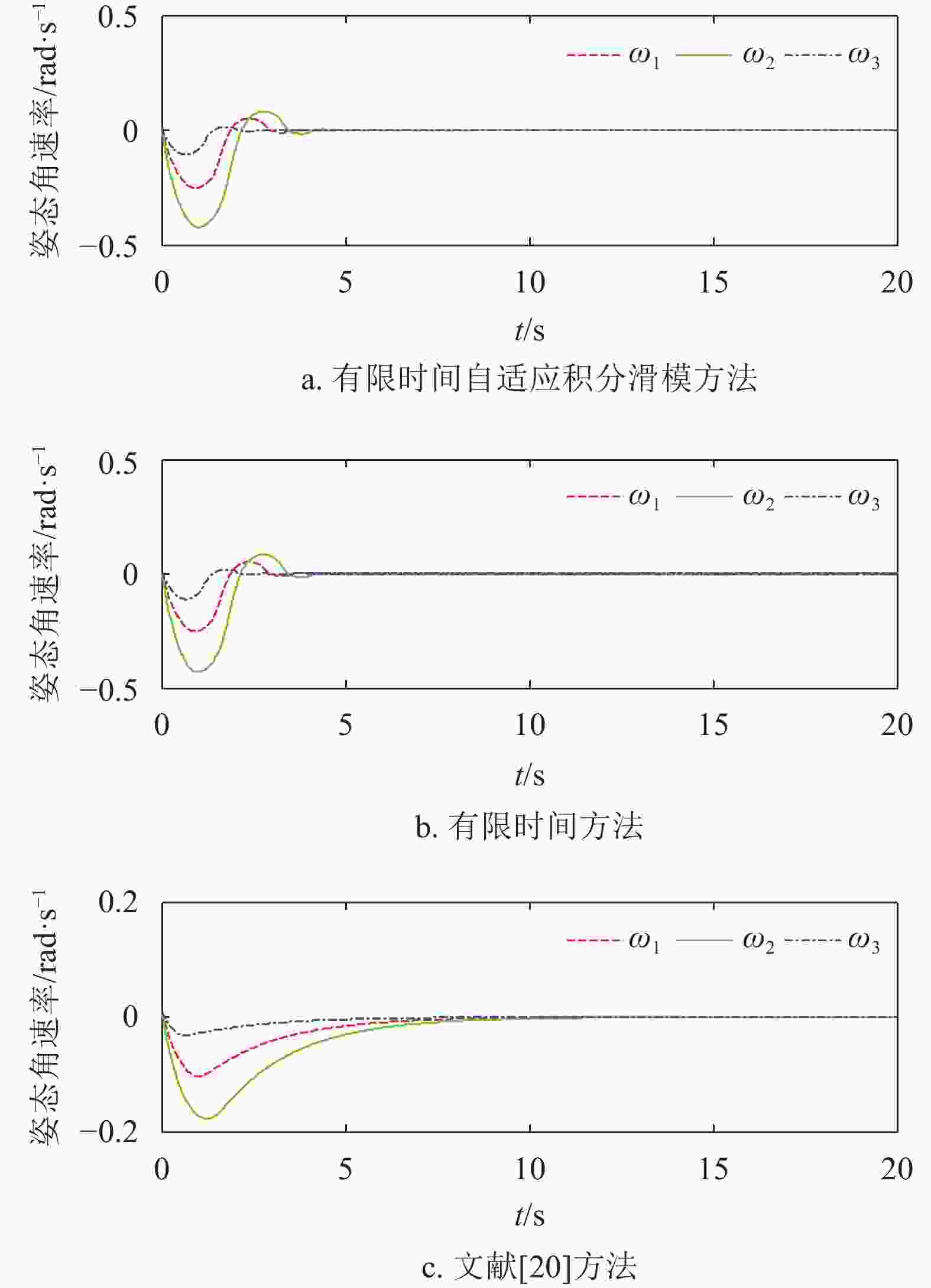
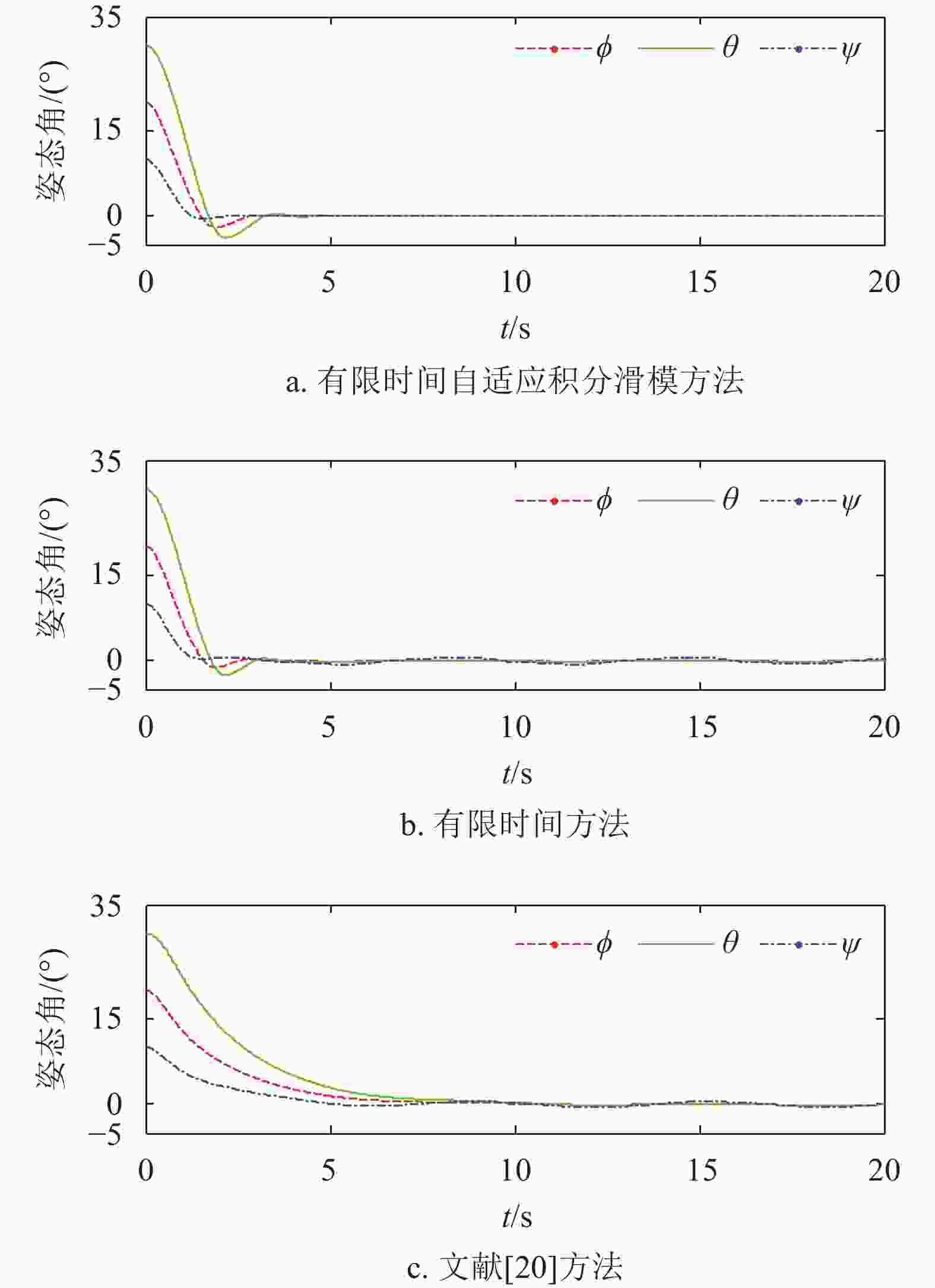
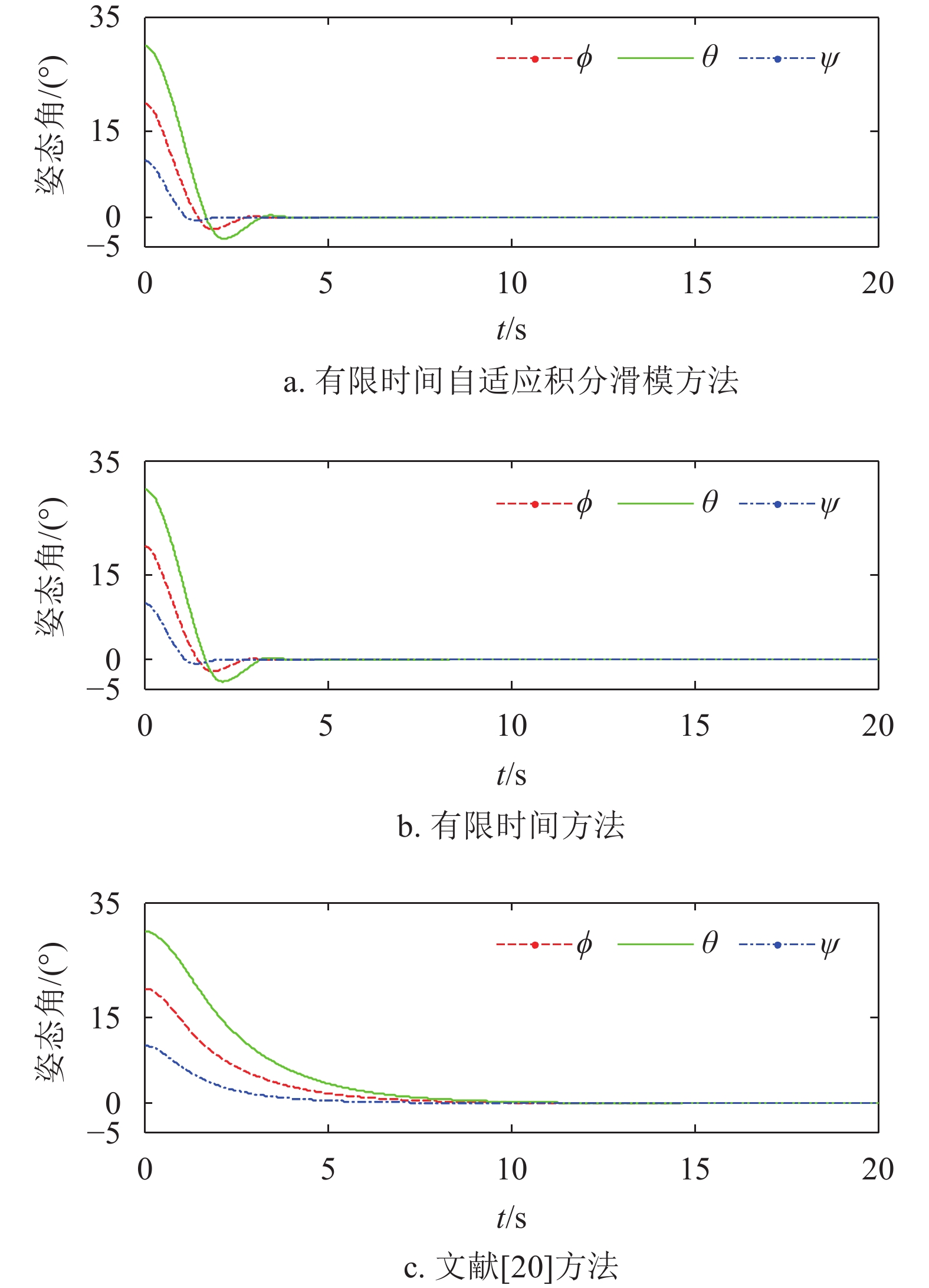
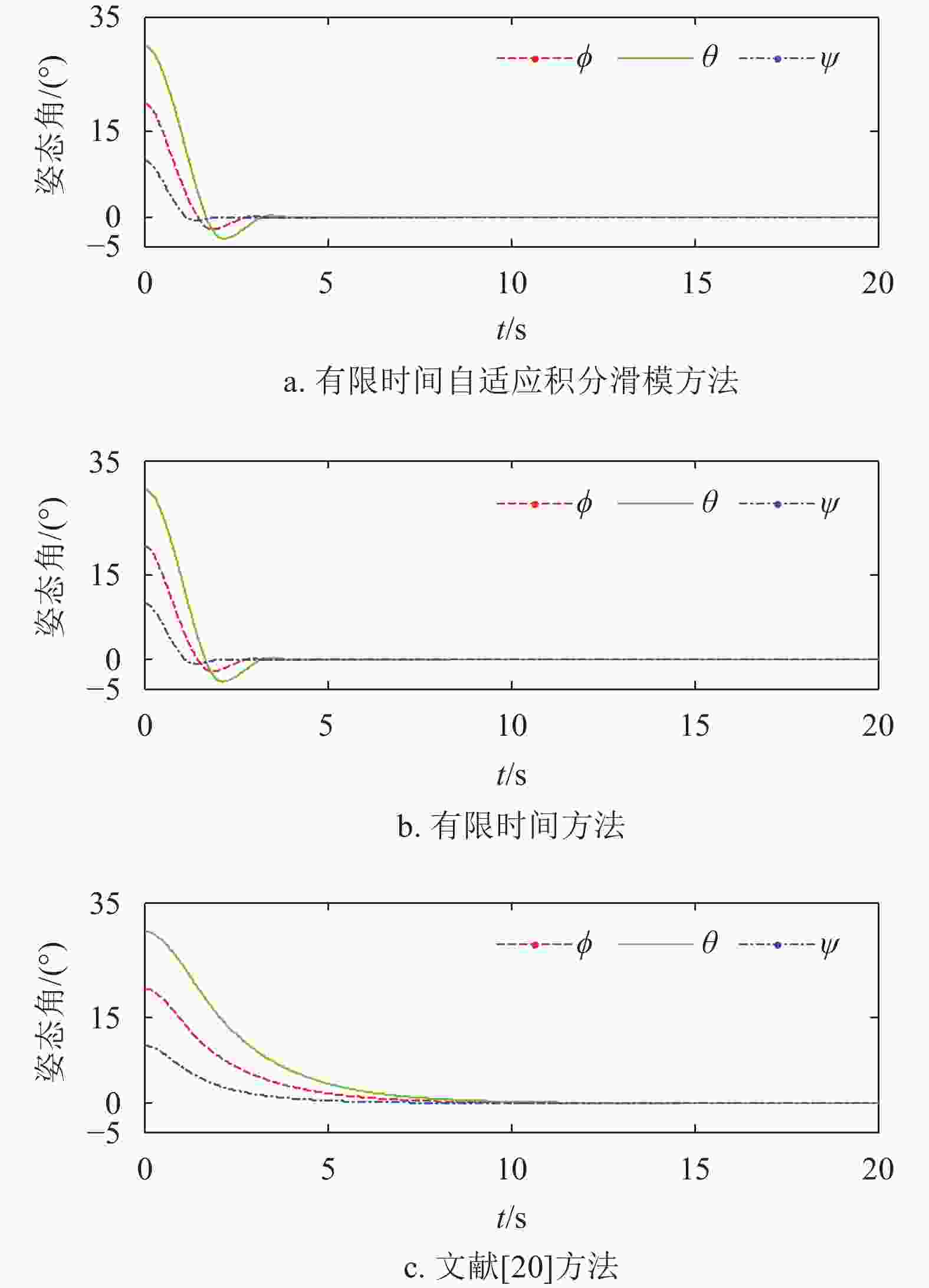
$\hat{ J} = {\rm{diag}}(900, $ $ 600,\;300)\;{\rm{kg}} \cdot {{\rm{m}}^2}$ 为惯量阵标称值,不确定性$\Delta {J}$ 取标称值的2%,外部干扰力矩${{u}_{{d}}} = (50{\rm{sin}}(0.1{t}),50{\rm{sin}}(0.5{t}), $ $ 50{\rm{sin}}{t})\;{\rm{N}} \cdot {\rm{m}}$ ,初始姿态误差四元数为${q} = [0.951\;5, $ $ 0.268\;5,\;0.144\;9,\;0.038\;1]^{\rm{T}}$ ,对应的姿态误差欧拉角为${\rm{angle}} = {[20^\circ,30^\circ,10^\circ]^{{\rm{T}}}}$ ,初始误差姿态角速度为${\omega }(0) = {[0.01,0.01,0.01]^{\rm{T}}}{\rm{rad}}/{\rm{s}}$ ,初始期望姿态四元数为${{q}_{{d}}}(0) = {[1,0,0,0]^{\rm{T}}}$ ,期望的姿态角速度为${{\omega }_{{d}}} = $ $ {[0.03\sin (0.1{t}),0.03\sin (0.1{t}),0.03\sin (0.1{t})]^{\rm{T}}}{\rm{rad}}/{\rm{s}}$ ,控制参数取${{\alpha }_1} = 0.5$ ,${{k}_1} = {{k}_2} = {k} = 1$ ,${a} = 0.01$ ,${c} = 10$ 。首先考虑无外界扰动和航天器转动惯量确定的情况,为方便比较,将误差四元数转换成按3-2-1转序得到的误差姿态角,仿真结果如图1~图3所示。
图1、图2为3种方法的误差姿态角和误差姿态角速度仿真结果,从图中可以看出,3.3节提出的有限时间自适应积分滑模方法能够使得误差姿态角和误差姿态角速度在有限时间收敛到零,在没有外界扰动和航天器转动惯量确定的情况下,与本文3.1节提出的有限时间算法结果基本相同。这是因为在积分滑模面的设计中,将有限时间控制的系统状态运动轨迹作为期望的滑动模态的导数,当系统保持在滑模面上时,状态运动轨迹便与有限时间算法相同。两种方法收敛速度均快于文献[20],原因是文献[20]使用线性滑模面,因此系统状态只能是指数收敛,在时间趋于无穷大的时候状态收敛到零。
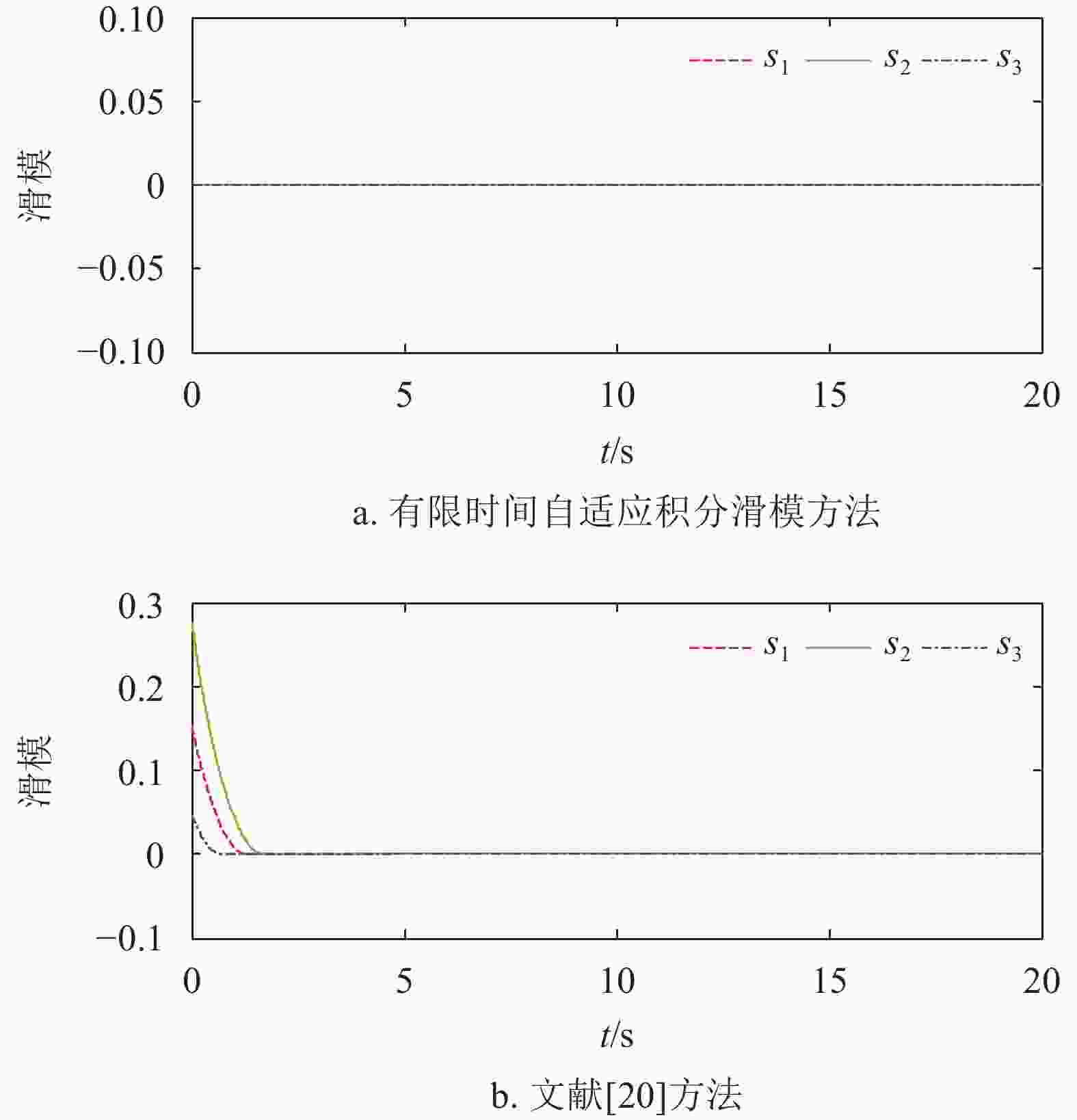
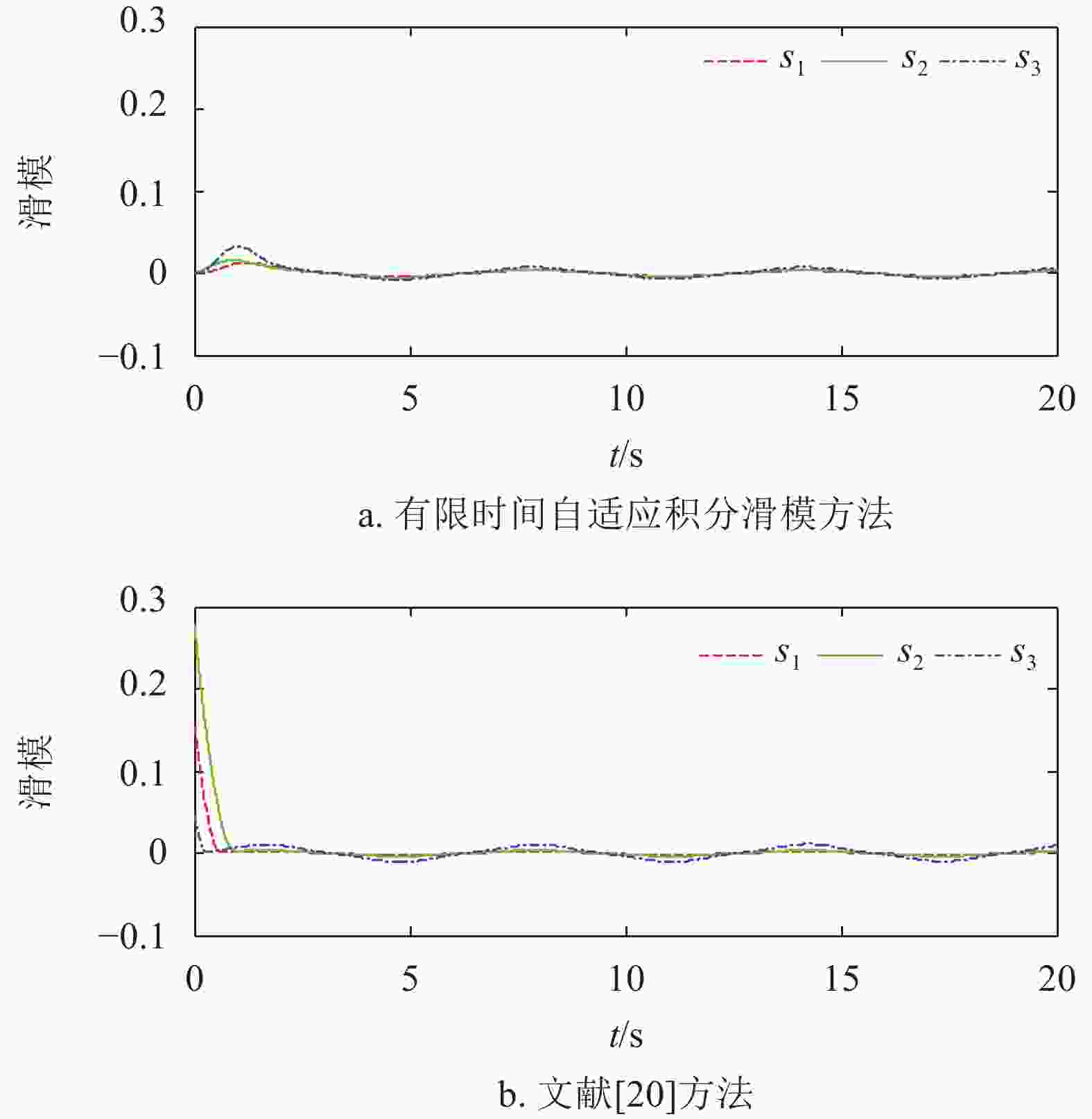
图3为本文提出的方法与文献[20]方法的滑模面仿真结果,可以看出,积分滑模具有全局滑模的特点。在无扰动的情况下,系统状态一直位于滑模面上,由于自适应参数
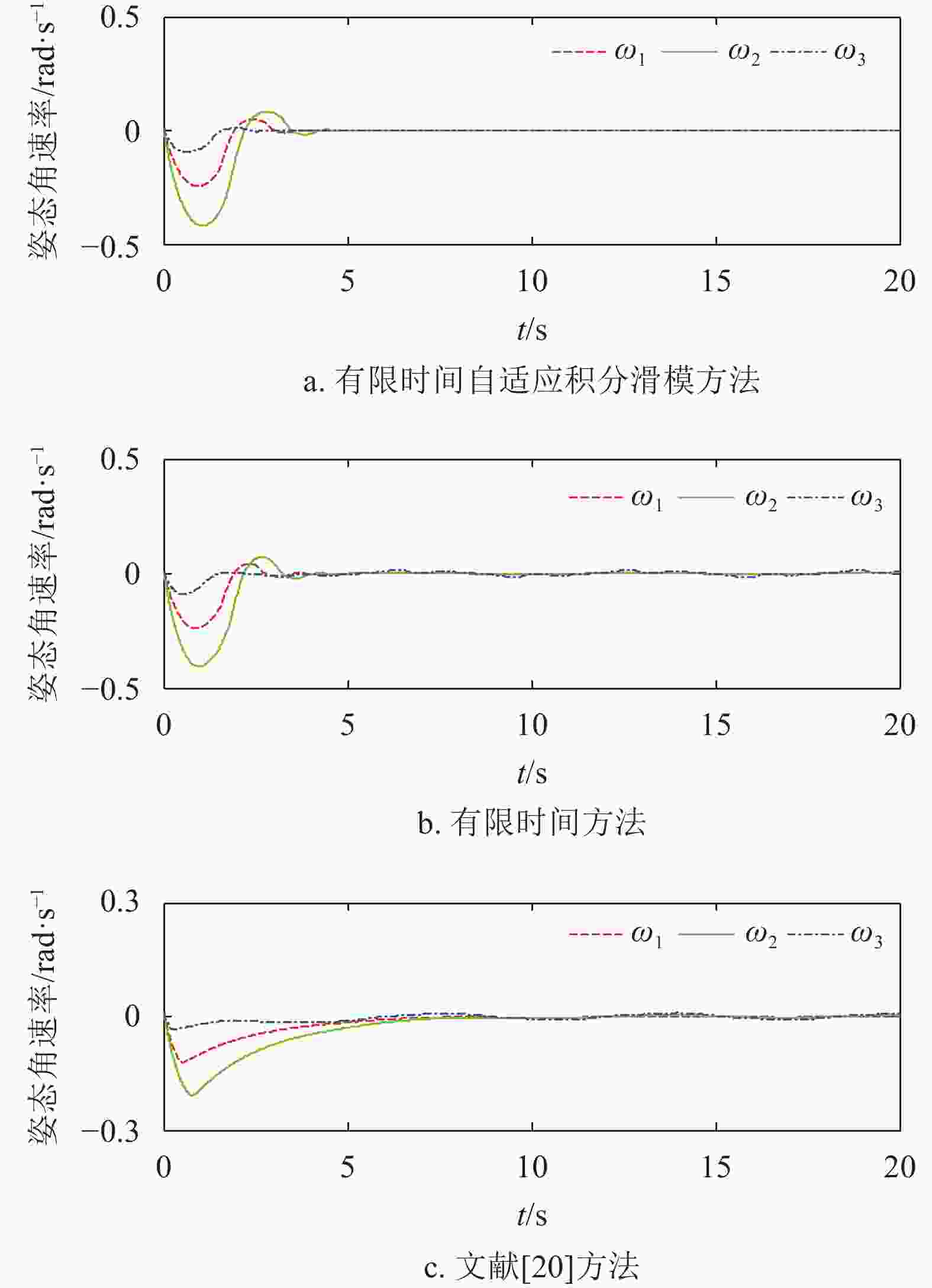
$\hat{ d}$ 中含有滑模面s的积分项,因此全局滑模可以有效避免滑模到达段可能造成的自适应参数$\hat{ d}$ 积分过大的情况。在考虑外界扰动以及航天器转动惯量存在不确定性的情况下,仿真结果如图4~图6所示。
从图4和图5中可以看出,在存在外界扰动和航天器转动惯量存在不确定性的情况下,3.3节提出的有限时间自适应积分滑模方法能够克服聚合扰动,使得误差姿态角和误差姿态角速度仍在有限时间内收敛,体现了一旦系统运行在滑动阶段,滑模控制具有对外界干扰和参数不确定的不敏感性特点。而3.1节和文献[20]的方法都只能使得误差姿态角和误差姿态角速度在零点附近波动,前者的收敛速度更快,这是因为有限时间控制方法相比线性指数控制方法具有更快的收敛性[21]。
考虑到工程上的可实现性,使用了连续函数
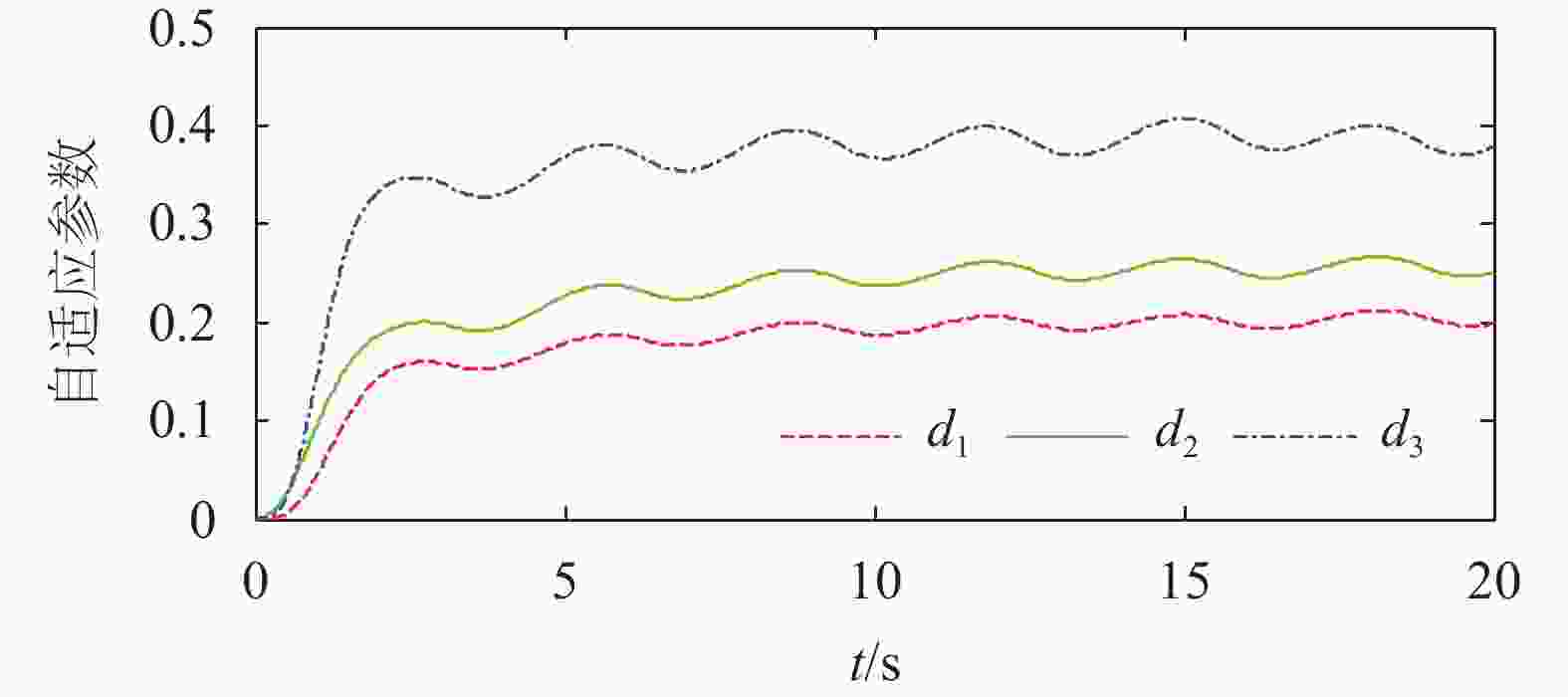
${f}({{{s}}})$ 代替切换函数${\rm{sgn}} ({{{s}}})$ 。从图6可以看出,在聚合扰动存在的情况下,传统滑模面和积分滑模面都不能收敛到零,只能收敛到边界层以内(本文仿真取边界层${a} = 0.01$ ),但积分滑模的全局滑模的特点使得积分滑模面能够迅速收敛到边界层内。由于系统状态无法严格处于滑模面上,考虑到自适应参数
$\hat{ d}$ 中含有积分项,在s不为0时会一直积分到无穷大,因此,在自适应律中引入负反馈[22],使得自适应参数最终有界,结果如图7所示。 -
考虑存在模型参数不确定和外界干扰的情况,本文建立了用四元数表示的航天器姿态跟踪数学模型,提出了一种有限时间自适应积分滑模控制方法。首先针对无参数不确定性和干扰的情况,设计了一种有限时间控制器,保证航天器姿态在有限时间跟踪上期望姿态。在考虑扰动的情况下,结合有限时间控制和滑模控制设计了一种积分滑模面,利用自适应方法动态调整切换函数增益,在线辨识聚合扰动的上界。该方法兼具有限时间控制和滑模控制的优点,可使闭环系统状态有限时间收敛并具有很好的鲁棒性。理论分析和仿真结果说明了本文方法的有效性。
Finite Time Adaptive Integral Sliding Mode Control Method for Spacecraft Attitude Tracking
-
摘要: 针对刚体航天器存在模型参数不确定性和外界干扰情况下的姿态跟踪控制问题,该文提出了一种有限时间自适应积分滑模控制方法。建立了用四元数表示的航天器姿态跟踪数学模型;在不考虑参数不确定性和干扰的情况下,基于非线性系统齐次性方法设计了一种有限时间控制算法,保证航天器姿态在有限时间内跟踪上期望姿态;当扰动存在时,为提高闭环系统的鲁棒性,结合有限时间控制和滑模控制,将有限时间控制算法应用到滑模面的设计中,设计出一种有限时间积分滑模面;最后用自适应方法设计了动态滑模切换函数增益。理论分析表明该方法兼具有限时间控制和滑模控制的优点,可使闭环系统状态有限时间收敛并具有很好的鲁棒性。仿真结果说明了该方法的有效性。Abstract: For the rigid spacecraft attitude tracking control problem with parameter uncertainties and external disturbances, a method of finite time adaptive integral sliding mode controller is proposed in this paper. A spacecraft attitude tracking model is described with quaternion. The basic principles of finite time method are introduced. Then, an integral sliding surface is designed with finite time method, which estimates bound of the disturbances and parameter uncertainties. The method has the characteristic of integral sliding mode method and finite time method. Simulation results show the fine performance of the controller.
-
[1] 李源, 吴宏悦, 吴杰. 基于遗传算法PID整定的卫星姿态控制研究[J]. 中国空间科学术, 2007(4): 66-71. LI Yuan, WU Hong-yue, WU Jie. Genetic algorithm PID self-tuning based on the satellite attitude control[J]. Chinese Space Science and Technology, 2007(4): 66-71. [2] WEN J T, KREUTZ-DELGADO K. The attitude control problem[J]. IEEE Transactions on Automatic Control, 1991, 36(10): 1148-1162. doi: 10.1109/9.90228 [3] HORRI N M, PALMER P L, ROBERTS M. Energy optimal spacecraft attitude control subject to convergence rate constraints[J]. Control Engineering Practice, 2011(19): 1297-1314. [4] 肖冰, 胡庆雷, 马广富. 航天器执行机构部分失效故障的鲁棒容错控制[J]. 控制与决策, 2011, 26(6): 801-805. XIAO Bing, HU Qing-lei, MA Guang-fu. Robust fault tolerant attitude control for spacecraft under partial loss of actuator effectiveness[J]. Control and Decision, 2011, 26(6): 801-805. [5] 邓立为, 宋申民. 基于分数阶滑模的挠性航天器姿态鲁棒跟踪控制[J]. 航空学报, 2013, 34(8): 1915-1923. DENG Li-wei, SONG Shen-min. Flexible spacecraft attitude robust tracking control based on fractional order sliding mode[J]. Aerospace Control and Application, 2013, 34(8): 1915-1923. [6] 魏静波, 刘昆, 吴锦杰. 惯性定向三轴稳定卫星姿态自适应滑模控制[J]. 控制与决策, 2013, 28(8): 1231-1234. WEI Jing-bo, LIU Kun, WU Jin-jie. Adaptive sliding mode attitude controller for satellites three-axis-stabilized in inertial frame[J]. Control and Decision, 2013, 28(8): 1231-1234. [7] 胡建, 白瑜亮, 王小刚, 等. 航天器有限时间自适应容错姿态控制[J]. 中国惯性技术学报, 2018, 26(1): 92-97. HU Jian, BAI Yu-liang, WANG Xiao-gang, et al. Finite-time adaptive fault-tolerant attitude control of spacecraft[J]. Journal of Chinese Inertial Technology, 2018, 26(1): 92-97. [8] 常雅杰, 赵晨, 段传辉. 挠性卫星姿态的有限时间终端滑模稳定控制[J]. 空间控制技术与应用, 2019, 45(3): 31-38. doi: 10.3969/j.issn.1674-1579.2019.03.005 CHANG Ya-jie, ZHAO Chen, DUAN Chuan-hui. Finite-time terminal sliding mode control of flexible satellite attitude[J]. Aerospace Control and Application, 2019, 45(3): 31-38. doi: 10.3969/j.issn.1674-1579.2019.03.005 [9] SLOTINE J J, SASTRY S S. Tracking control of nonlinear systems using sliding surfaces with application to robot manipulator[J]. International Journal of Control, 1983, 38(2): 465-492. doi: 10.1080/00207178308933088 [10] 李鹏, 马建军, 李文强, 等. 一类不确定非线性系统的改进积分型滑模控制[J]. 控制与决策, 2009, 24(10): 1463-1466. doi: 10.3321/j.issn:1001-0920.2009.10.004 LI Peng, MA Jian-jun, LI Wen-qiang, et al. Improved integral sliding mode control for a class of nonlinear uncertain systems[J]. Control and Decision, 2009, 24(10): 1463-1466. doi: 10.3321/j.issn:1001-0920.2009.10.004 [11] 丛炳龙, 刘向东, 陈振. 刚体航天器姿态跟踪系统的自适应积分滑模控制[J]. 航空学报, 2013, 34(3): 620-628. CONG Bing-long, LIU Xiang-dong, CHEN Zhen. Adaptive integral sliding mode control for rigid spacecraft attitude tracking[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(3): 620-628. [12] 李贵明, 刘良栋. 刚体卫星姿态的有限时间控制[J]. 空间控制技术与应用, 2011, 37(3): 1-8. doi: 10.3969/j.issn.1674-1579.2011.03.001 LI Gui-ming, LIU Liang-dong. Finite time stabilization method for the rigid spacecraft attitude control[J]. Aerospace Control and Application, 2011, 37(3): 1-8. doi: 10.3969/j.issn.1674-1579.2011.03.001 [13] 马克茂. 航天器连续非光滑姿态控制律设计[J]. 宇航学报, 2012, 33(6): 713-719. doi: 10.3873/j.issn.1000-1328.2012.06.005 MA Ke-mao. Design of continuous non-smooth attitude control laws for spacecraft[J]. Journal of Astronautics, 2012, 33(6): 713-719. doi: 10.3873/j.issn.1000-1328.2012.06.005 [14] 黄圳圭. 航天器姿态动力学[M]. 长沙: 国防科技大学出版社, 1997. HUANG Zhen-gui. Attitude dynamics of spacecraft[M]. Changsha: National University of Defence Technology Press, 1997. [15] KURZWEIL J. On the inversion of Lyapunov's second theorem on stability of motion[J]. American Mathematical Society Translations, 1956, 2(24): 19-77. [16] BHAT S P, BERNSTEIN D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751-766. doi: 10.1137/S0363012997321358 [17] HERMES H. Homogeneous coordinates and continuous asymptotically stabilizing feed-back controls[J]. Differential Equations, Stability and Control, 1991, 109: 249-260. [18] ROSIER L. Homogeneous Lyapunov function for homogeneous continuous vector field[J]. Systems and Control Letters, 1992, 19(6): 467-473. doi: 10.1016/0167-6911(92)90078-7 [19] BHAT S P, BERNSTEIN D S. Finite-time stability of homogeneous systems[C]//Proceedings of the American Control Conference. [S. l.]: IEEE, 1997: 2513-2514. [20] 杨宁宁, 杨照华, 余远金. 基于机械飞轮干扰补偿的小卫星自适应滑模变结构姿态控制[J]. 航天控制, 2013, 31(1): 51-57. doi: 10.3969/j.issn.1006-3242.2013.01.009 YANG Ning-ning, YANG Zhao-hua, YU Yuan-jin. The small satellite adaptive sliding mode attitude controller with mechanical flywheels disturbance compensation[J]. Aerospace Control, 2013, 31(1): 51-57. doi: 10.3969/j.issn.1006-3242.2013.01.009 [21] 李世华, 丁世宏, 都海波, 等. 非光滑控制理论与应用[M]. 北京: 科学出版社, 2013. LI Shi-hua, DING Shi-hong, DU Hai-bo, et al. Control theory and application[M]. Beijing: Science Press, 2013. [22] WHEELER G, SU C Y, STEPANENKO Y. A sliding mode controller with improved adaptation laws for the upper bounds on the norm of uncertainties[J]. Automatica, 1998, 34(12): 1657-1661. doi: 10.1016/S0005-1098(98)80024-1 -

 ISSN
ISSN 



 下载:
下载: