-
级联开关变换器因具有高可靠性、高灵活性等优点被广泛应用在新能源发电、储能、电动汽车、通信设备等场合[1-5]。在级联开关变换器中,前级变换器称为源变换器,后级变换器称为负载变换器,负载变换器的输入电压由源变换器提供,而源变换器的输出电流由负载变换器决定。这样,源变换器和负载变换器之间的相互作用将影响级联开关变换器的稳定性。
为了评估级联开关变换器的稳定性,文献[6]最早提出了基于阻抗分析的稳定性判据。根据稳定性判据可知,将两个稳定工作的开关变换器级联后,若源变换器的输出阻抗与负载变换器的输入阻抗之比满足奈奎斯特定理,则该级联开关变换器将稳定工作。随着级联开关变换器的结构变得更加多样和复杂,且考虑到稳定性判据在实际设计中较为保守,文献[7-10]提出了各种改进的稳定性判据。这些判据为级联开关变换器的设计和分析提供了很大的帮助。
上述基于阻抗分析建立的稳定性判据没有考虑级联开关变换器中各变换器的开关纹波以及它们之间的相互作用[11],尤其在级联开关变换器中,负载变换器的输入电流纹波前馈至源变换器输出电容后,重塑了源变换器输出电压的波形。源变换器的输出阻抗和负载变换器的输入阻抗即使满足了基于阻抗分析而建立的稳定性判据,级联开关变换器也会因开关纹波的相互作用而出现快标不稳定现象[12]和慢标不稳定现象[13]。此外,若负载变换器设计合适,其前馈的开关纹波还可以增大源变换器的稳定工作范围[14]。上述文献表明,精确预测级联开关变换器的稳定性需要全面考虑各开关变换器的开关纹波及其相互作用的影响。
现有文献虽指出了级联开关变换器中开关纹波相互作用的影响[11-14],但未对负载变换器前馈电流纹波时源变换器的稳定性机理进行深入研究。此外,这些文献主要分析了负载变换器前馈不连续电流纹波时源变换器的稳定性(如负载变换器采用Buck变换器[11-14]),而对负载变换器前馈连续电流纹波时源变换器的稳定性(如负载变换器采用Boost变换器[5])尚未有研究。相较于不连续电流纹波,连续电流纹波幅度变化相对较小。当源变换器采用传统电压型控制时,因用于脉冲宽度调制的锯齿波的幅度较大,负载变换器前馈连续电流纹波对稳定性的影响较小,可忽略[11]。当源变换器采用纹波控制时,该前馈电流纹波的影响却不可忽略[15]。
近年来,纹波控制技术由于控制电路简单、瞬态响应速度快等优点在开关电源中得到了广泛的关注[16-20]。纹波控制技术采用开关纹波(如输出电压纹波[16-18]、电容电流纹波[19]等)作为控制信号。相较于传统电压型控制,纹波控制开关变换器的稳定性更易受到开关纹波的影响[21]。负载变换器前馈电流纹波将对采用纹波控制的源变换器的稳定性产生显著影响。
在纹波控制中,峰值电压纹波(peak voltage ripple, PVR)控制是一种最简单、频率恒定的控制技术[15]。为此,本文选择PVR控制Buck变换器作为源变换器,同时选择峰值电流模式(peak current mode, PCM)控制Boost变换器作为负载变换器,并基于该级联开关变换器研究源变换器的稳定性机理。
-
本节将通过电路仿真展示PVR控制Buck变换器接电阻负载(独立工作)和级联PCM控制Boost变换器(作为源变换器)时的稳定性;再分析源变换器随电路参数变化时的分岔行为。
-
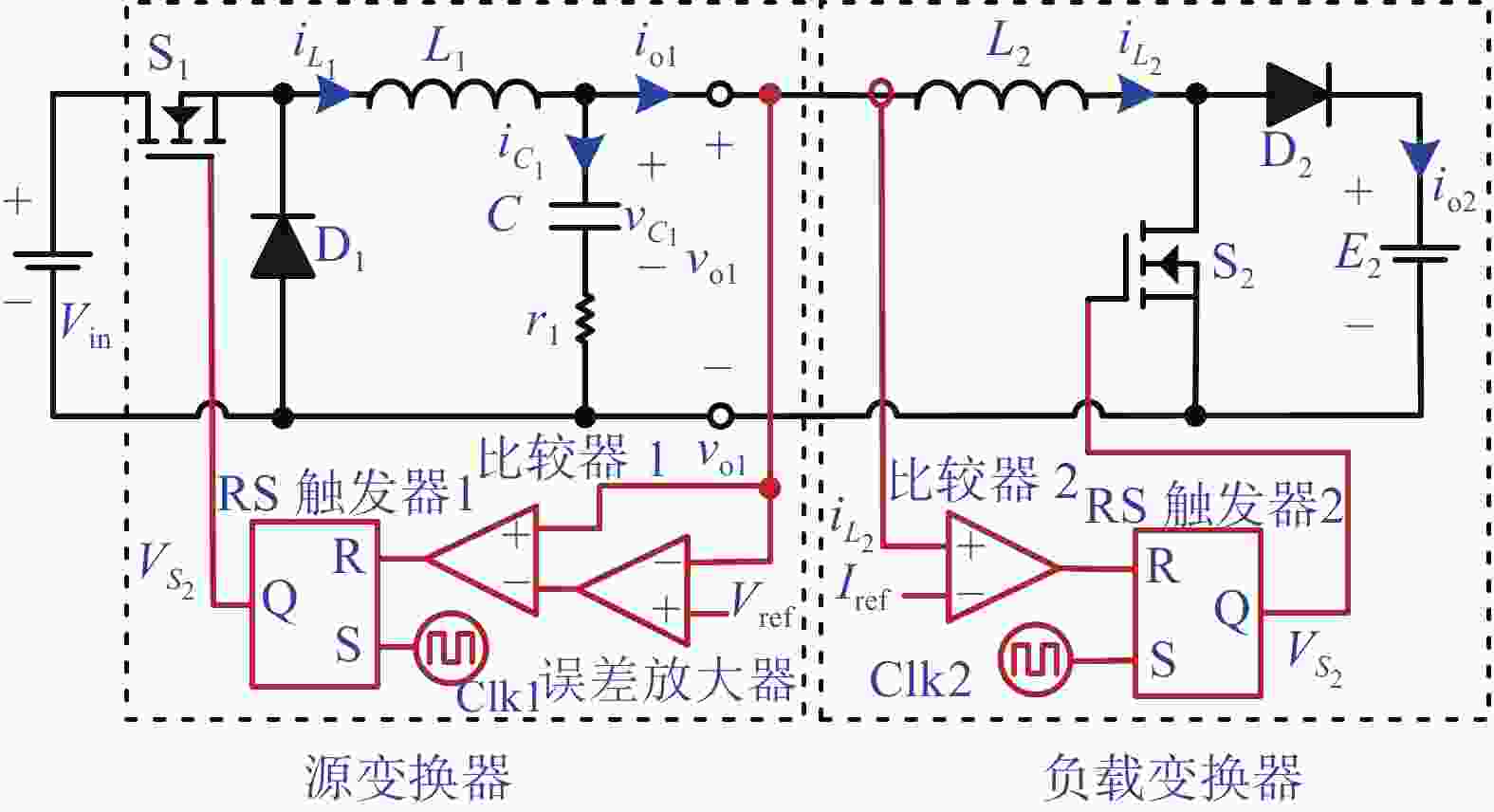
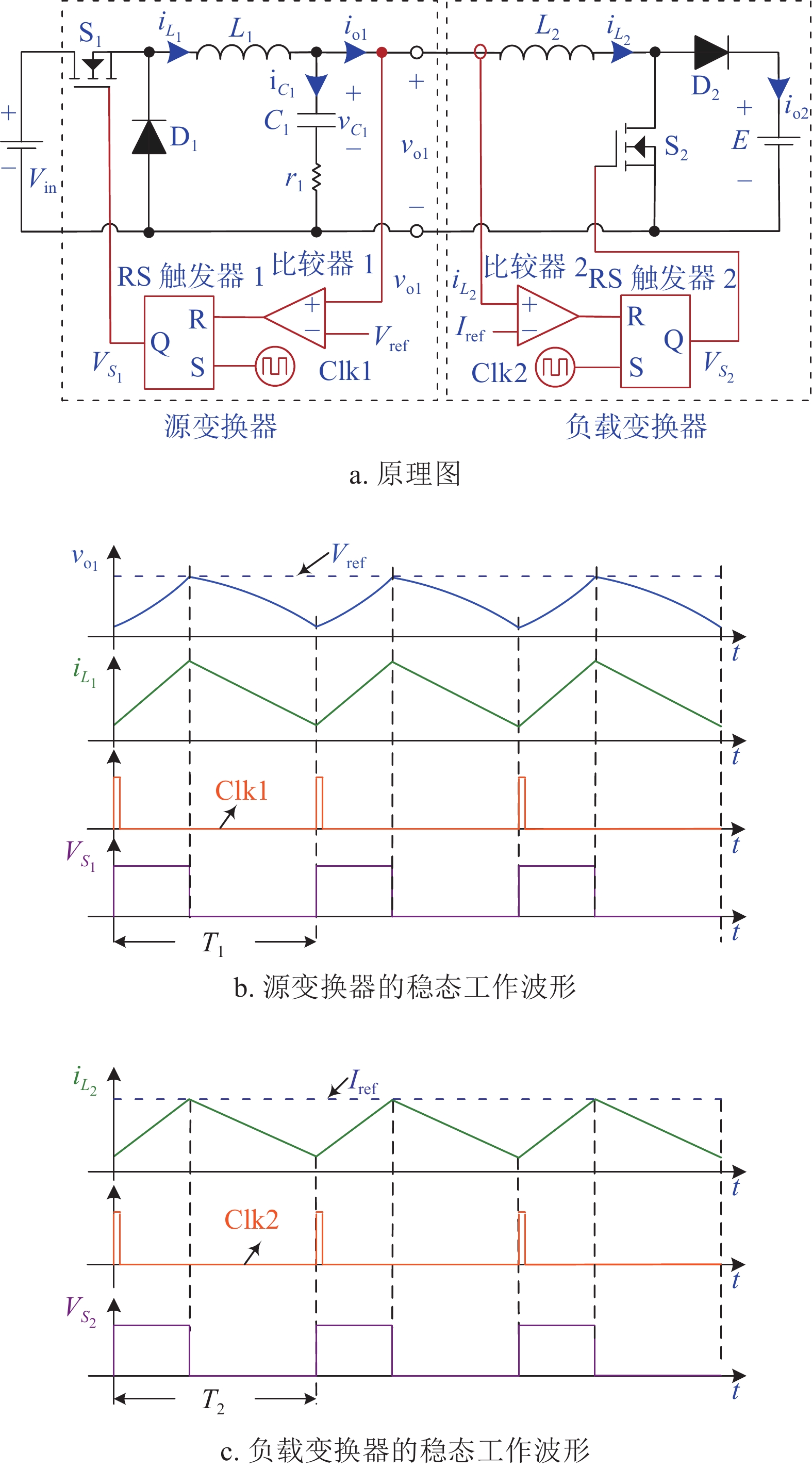
由PVR控制Buck变换器级联PCM控制Boost变换器的原理图如图1a所示,其中Vin为输入电压,S1(S2)、D1(D2)和L1(L2)分别为源(负载)变换器的开关管、二极管和电感,C1和r1为源变换器的输出电容及其等效串联电阻(equivalent series resistance, ESR),iL1(iL2)、io1(io2)、Clk1(Clk2)和VS1(VS2)分别为源(负载)变换器的电感电流、输出电流、时钟信号和控制脉冲,iC1、vC1、vo1和Vref1分别为源变换器的电容电流、电容电压、输出电压和参考电压,E和Iref分别为负载变换器的输出电压和参考电流。由于实际工作中负载变换器输出电压一般都是调节好的电压,故可近似看作输出电压恒定,用恒压源E代替。相应地,源变换器和负载变换器独立工作时的稳态工作波形分别如图1b和1c所示。
根据图1b和图1c,源变换器(负载变换器)的工作原理为:当时钟信号来临,置位RS触发器,开关管S1(S2)导通,源变换器的输出电压vo1(负载变换器的电感电流iL2)开始上升。当vo1(iL2)上升到参考电压Vref(参考电流Iref),并复位RS触发器,关断开关管S1(S2),vo1(iL2)开始下降,直至下一个开关周期来临。因此,相应的开关切换条件为:
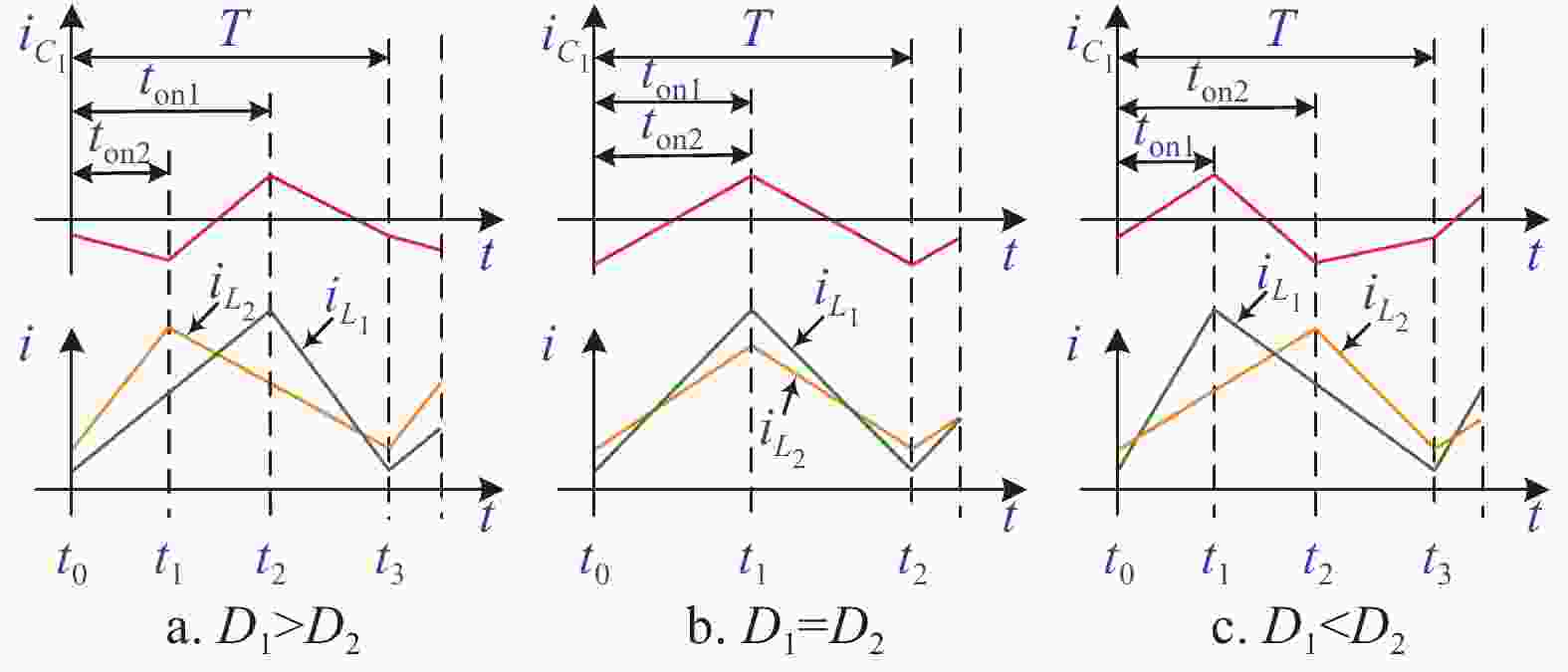
$$ {v_{{\text{o1}}}} - {V_{{\text{ref}}}} = 0 \;\;\; 或 \;\;\; {i_{L_{\text{2}}}} - {I_{{\text{ref}}}} = 0 $$ (1) 此外,在图1a中,由基尔霍夫电流定律可知, iC1=iL1–iL2,其中iC1和iL1分别为源变换器的输出电容电流和电感电流。若选择源变换器的开关频率f1与负载变换器的开关频率f2相同(设为f,即f1=f2=f),根据源变换器与负载变换器之间占空比的关系,iC1存在3种工作波形,当D1与D2的关系分别为D1>D2、D1=D2和D1<D2时,iC1、iL1和iL2的工作波形分别如图2a~图2c所示,其中D1和D2分别为源变换器和负载变换器的占空比,ton1和ton2分别为源变换器和负载变换器的导通时间,且ton1=D1/f1,ton2=D2/f2。
由图2可以看出,与独立工作时相比,负载变换器前馈电流纹波重塑了PVR控制Buck变换器的输出电容电流波形,且该重塑波形的特性与两个变换器的占空比关系密切相关。这样,PVR控制Buck变换器作为源变换器时,其稳定性将会发生显著变化。
-
下面将对比分析PVR控制Buck变换器作为源变换器和独立工作时的稳定性。由文献[15]可知,PVR控制Buck变换器独立工作且工作于电感电流连续导电模式(continuous condution mode, CCM)时的稳定工作条件为:
$$ \frac{{r}_{1}{C}_{1}}{{T}_{1}} > 0.5+\frac{{D}_{1}^{2}}{1-2{D}_{1}}\text{ }且\text{ }{D}_{1} < 0.5 $$ (2) 式中,T1为开关周期;D1为占空比。
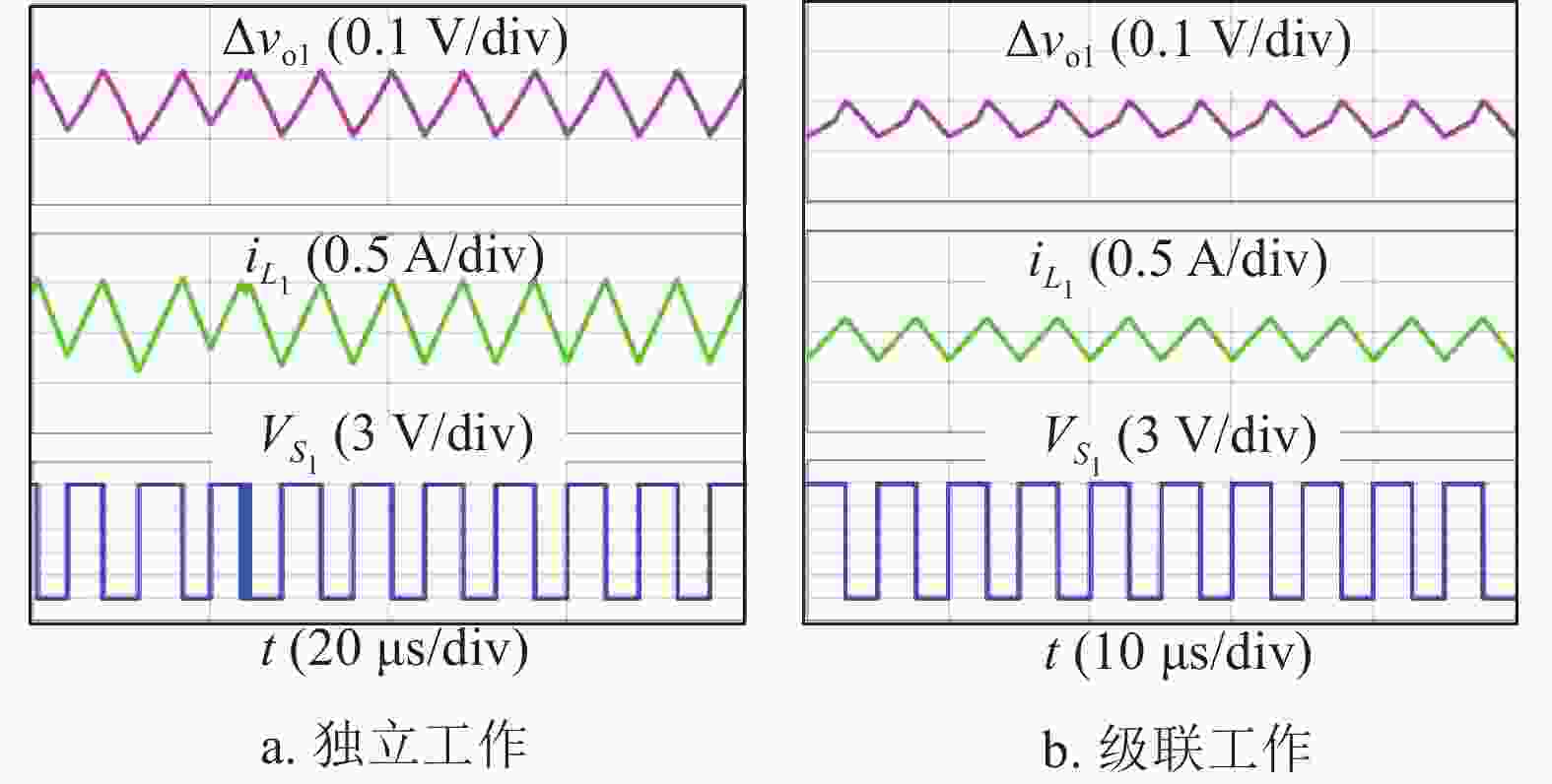
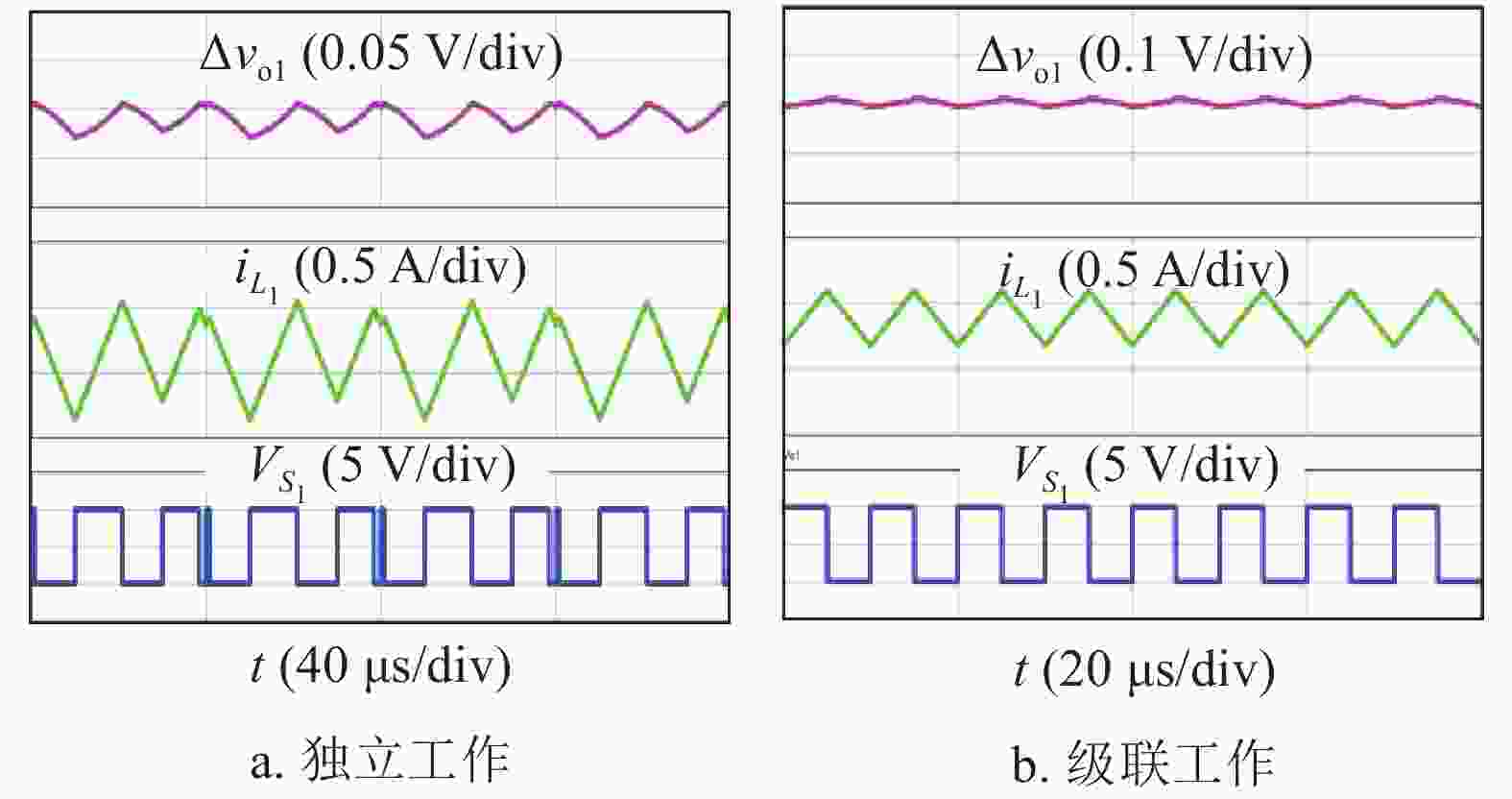
为了展示PVR控制Buck变换器独立工作时和级联工作时的稳定性,本文选取了表1所示的典型电路参数。根据式(2)的稳定条件可知,采用表1的电路参数,PVR控制Buck变换器独立工作时将工作在不稳定状态,PSIM (power simulation)仿真结果如图3a所示,其中,电阻负载R=2.35 Ω。然而,采用相同的电路参数,PVR控制Buck变换器级联工作时工作在稳定周期1状态,仿真结果如图3b所示,其中,VS1为PVR控制Buck变换器的控制脉冲。
表 1 级联开关变换器的典型电路参数
参 数 数 值 输入电压Vin/V 10 电感L1/μH 60 输出电容C1/μF 220 输出电容ESR r1/mΩ 120 基准电压Vref/V 5.5 开关频率f1/kHz 100 电感L2/μH 140 基准电流Iref/A 1 输出电压E/V 9 开关频率f2/kHz 100 -
由式(2)可知,PVR控制Buck变换器的稳定性与输出电容时间常数(r1C1)和开关周期T1之比(r1C1/T1)以及占空比D1等有关。在图1a中,由源变换器占空比D1=Vref/Vin和负载变换器占空比D2=(1−Vref/E)可知,确定Vin和E后,改变Vref即可改变D1和D2;确定输出电容容值C1和开关周期T1后,改变输出电容ESR即可改变r1C1与T1的比值。此外,电感L1的取值影响源变换器输出电容电流的斜率,进而影响输出电压纹波的斜率。为此,本文选择源变换器的参考电压Vref、输出电容ESR r1和电感L1作为可变参数来研究级联开关变换器中源变换器的稳定性机理。
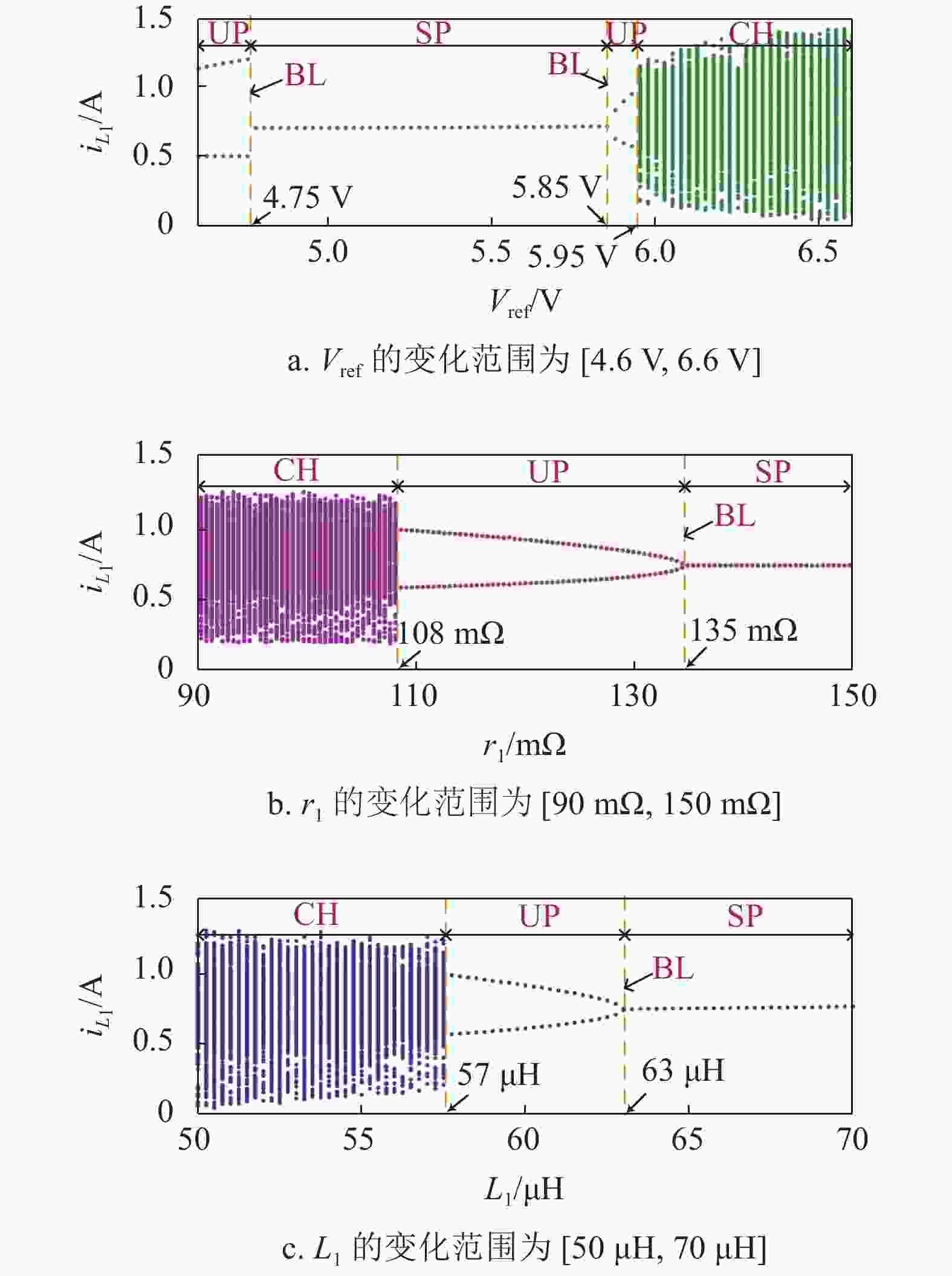
基于PSIM电路仿真所获得的数据,利用MATLAB软件可得到源变换器随Vref、r1和L1变化时的电感电流iL1分岔图分别如图4a~图4c所示。在图4中,CH表示混沌,UP表示不稳定周期2,SP表示稳定周期1,BL表示不稳定边界。需要说明的是,图4中源变换器的参数始终不满足式(2),而负载变换器始终满足稳定条件。
当Vref从4.6 V增加到6.6 V,如图4a所示,即占空比D1从0.46到0.66和D2从0.49到0.27,源变换器的运行轨迹在Vref=4.75 V处通过边界碰撞分岔由周期2进入到周期1,然后在Vref=5.85 V处通过倍周期分岔由周期1进入到周期2,然后在Vref=5.95 V处通过边界碰撞分岔由短暂的周期2进入到混沌。在第一个不稳定边界Vref=4.75 V处,源变换器和负载变换器对应的占空比分别为D1=0.475和D2=0.472;在第二个不稳定边界Vref=5.85 V处,源变换器和负载变换器对应的占空比分别为D1=0.585和D2=0.35。如图4b或图4c所示,r1从90 mΩ增加到150 mΩ或L1从50 μH增加到70 μH时,源变换器的运行轨迹在r1=108 mΩ或L1=57 μH处通过边界碰撞分岔由混沌进入到周期2,然后在r1=135 mΩ或L1=63 μH处通过逆倍周期分岔进入到周期1。在图4b和4c中,取Vref= 5.9 V,其他参数如表1所示。
分析图4可知,当Vref<4.75 V(此时D1<D2),源变换器始终工作在不稳定状态;而当Vref>4.75 V(D1>D2),源变换器可以工作在稳定状态,且稳定工作范围随输出电容ESR和电感的增大而增大。由上述分析结果表明,这些电路参数展现了与文献[11,14]不同的稳定性效应。
-
本节将建立级联开关变换器的离散映射模型,并通过研究其Jacobi矩阵的特征根来明晰级联开关变换器中源变换器的失稳机理。
-
由第1节内容可知,在本文研究的参数范围内,源变换器和负载变换器均始终工作于CCM。根据图2以及开关管Si(i=1,2)和二极管Di的工作状态,该级联开关变换器存在4种开关状态,描述为:
开关状态1:S1导通、D1截止;S2导通、D2截止;
开关状态2:S1导通、D1截止;S2关断、D2导通;
开关状态3:S1关断、D1导通;S2导通、D2截止;
开关状态4:S1关断、D1导通;S2关断、D2导通;
定义状态变量向量为x(t)=[iL1 vC1 iL2]T,则开关状态m(m=1,2,3,4)对应的状态方程为:
$$ {\boldsymbol{\dot x}}(t){\text{ = }}{{\boldsymbol{A}}_m}{\boldsymbol{x}}{\text{(}}t) + {{\boldsymbol{B}}_m} $$ (3) 式中,Am和Bm分别为状态矩阵和输入矩阵,相应的表达式分别为:
$$ {{\boldsymbol{A}}_1} = {{\boldsymbol{A}}_2} = {{\boldsymbol{A}}_3} = {{\boldsymbol{A}}_4} = \left[ {\begin{array}{*{20}{c}} { - {{{r_1}} \mathord{\left/ {\vphantom {{{r_1}} {{L_1}}}} \right. } {{L_1}}}}&{ - {1 \mathord{\left/ {\vphantom {1 {{L_1}}}} \right. } {{L_1}}}}&{{{{r_1}} \mathord{\left/ {\vphantom {{{r_1}} {{L_1}}}} \right. } {{L_1}}}} \\ {{1 \mathord{\left/ {\vphantom {1 {{C_1}}}} \right. } {{C_1}}}}&0&{ - {1 \mathord{\left/ {\vphantom {1 {{C_1}}}} \right. } {{C_1}}}} \\ {{{{r_1}} \mathord{\left/ {\vphantom {{{r_1}} {{L_2}}}} \right. } {{L_2}}}}&{{1 \mathord{\left/ {\vphantom {1 {{L_2}}}} \right. } {{L_2}}}}&{ - {{{r_1}} \mathord{\left/ {\vphantom {{{r_1}} {{L_2}}}} \right. } {{L_2}}}} \end{array}} \right] $$ $$ {{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {{{{V_{{\text{in}}}}} \mathord{\left/ {\vphantom {{{V_{{\text{in}}}}} {{L_1}}}} \right. } {{L_1}}}} \\ 0 \\ 0 \end{array}} \right] \;\;\;\; {{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} {{{{V_{{\text{in}}}}} \mathord{\left/ {\vphantom {{{V_{{\text{in}}}}} {{L_1}}}} \right. } {{L_1}}}} \\ 0 \\ { - {E \mathord{\left/ {\vphantom {E {{L_2}}}} \right. } {{L_2}}}} \end{array}} \right] $$ $$ {{\boldsymbol{B}}_3} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}} \right] \;\;\;\; {{\boldsymbol{B}}_4} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ { - {E \mathord{\left/ {\vphantom {E {{L_2}}}} \right. } {{L_2}}}} \end{array}} \right] $$ 根据式(1)的开关切换条件,PVR控制Buck级联PCM控制Boost变换器的开关切换函数为:
$$ s({\boldsymbol{x}},{\text{ }}{t_{{\text{on1}}}}) = {{\boldsymbol{K}}_1}{\boldsymbol{x}} - {V_{{\text{ref}}}} \;\;\; 或 \;\;\; s({\boldsymbol{x}},{\text{ }}{t_{{\text{on2}}}}) = {{\boldsymbol{K}}_2}{\boldsymbol{x}} - {I_{{\text{ref}}}} $$ (4) 式中,K1=[r1 1 –r1];K2=[0 0 1];toni为开关管Si的导通时间,可通过令s(·)=0求得。
-
由图2可知,在一个开关周期内,式(4)存在3种开关状态序列,分别为:
若ton1>ton2,开关状态演化方式为1→2→4,记作Z1=(1, 2, 4);
若ton1=ton2,开关状态演化方式为1→4,记作Z2=(1, 4);
若ton1<ton2,开关状态演化方式为1→3→4,记作Z3=(1,3,4)。
根据文献[22],开关状态m的起始值x(tm−1)与终止值x(tm)之间的映射关系为:
$$ \boldsymbol{x}\left(t_{m-1}\right) \rightarrow \boldsymbol{x}\left(t_{m}\right)=\boldsymbol{\phi}_{m}\left(\tau_{m}\right) \boldsymbol{x}\left(t_{m-1}\right)+\boldsymbol{\psi}_{m}\left(\tau_{m}\right) \boldsymbol{B}_{m} $$ (5) 式中,τm=tm−tm−1;
$\boldsymbol{\phi}_{m}\left(\tau _{m}\right)=\mathrm{e}^{{\boldsymbol{A}_m} {\tau_{m}}}$ ;${\boldsymbol{\psi} _m}\left( {{\tau _m}} \right) = \int_0^{{\tau _m}} {{{\rm{e}}^{{\boldsymbol{A}_m}\xi }}} {\rm{d}}\xi$ 。若矩阵Am可逆,则
$\boldsymbol{\psi}_{m}\left(\tau_{m}\right)$ 可进一步写成:$$ \boldsymbol{\psi}_{m}\left(\tau_{m}\right)={\boldsymbol{A}}_{m}^{-1}\left(\boldsymbol{\phi}_{m}\left(\tau_{m}\right)-{\boldsymbol{I}}\right) $$ (6) 定义状态变量在第n个开关周期开始时刻的值为xn=x(nT)、在第n+1个开关周期开始时刻的值为xn+1=x((n+1)T)。根据式(5)可以得到3种开关状态序列的xn+1与xn之间的映射。
对于Z1,xn+1与xn之间的映射为:
$$ \boldsymbol{x}_{n+1}=f_{1}\left(\boldsymbol{x}_{n}\right)={\boldsymbol{\varPhi}}_{1}(\tau) \boldsymbol{x}_{n}+{\boldsymbol{\varPsi}}_{1}(\tau) $$ (7) 式中,
${\boldsymbol{\varPhi}}_{1}(\tau)=\boldsymbol{\phi}_{4}\left(\tau_{4}\right) \boldsymbol{\phi}_{2}\left(\tau_{2}\right) \boldsymbol{\phi}_{1}\left(\tau_{1}\right)$ ;${\boldsymbol{\varPsi}}_{1}(\tau)=\boldsymbol{\phi}_{4}\left(\tau_{4}\right) \times $ $ \boldsymbol{\phi}_{2} \left(\tau_{2}\right) \boldsymbol{\psi}_{1}\left(\tau_{1}\right) \boldsymbol{B}_{1}+\boldsymbol{\phi}_{4}\left(\tau_{4}\right) \boldsymbol{\psi}_{2}\left(\tau_{2}\right) \boldsymbol{B}_{2}+\boldsymbol{\psi}_{4}\left(\tau_{4}\right) \boldsymbol{B}_{4}$ ;τ1=ton2;τ2=ton1–ton2;τ4=T–ton1。ton2和ton1可由式(8)求得:$$\tag{8a} {s_1}\left( {{\boldsymbol{x}_n},{t_{{\rm{on}}2}}} \right) = {\boldsymbol{K}_2}\boldsymbol{x}\left( {{t_{{\rm{on}}2}}} \right) - {I_{{\rm{ref}}}} = 0 $$ $$\tag{8b} {s_2}\left( {\boldsymbol{x}\left( {{t_{{\rm{on}}2}}} \right),{t_{{\rm{on}}1}}} \right) = {\boldsymbol{K}_1}\boldsymbol{x}\left( {{t_{{\rm{on1 }}}}} \right) - {V_{{\rm{ref }}}} = 0 $$ 对于Z2,xn+1与xn之间的映射为:
$$ \boldsymbol{x}_{n+1}=f_{2}\left(\boldsymbol{x}_{n}\right)={\boldsymbol{\varPhi}}_{2}(\tau) \boldsymbol{x}_{n}+{\boldsymbol{\varPsi}}_{2}(\tau) $$ (9) 式中,
${\boldsymbol{\varPhi}}_{2}(\tau)=\boldsymbol{\phi}_{4}\left(\tau_{4}\right) \boldsymbol{\phi}_{1}\left(\tau_{1}\right)$ ;${\boldsymbol{\varPsi}}_{2}(\tau)=\boldsymbol{\phi}_{4}\left(\tau_{4}\right) \boldsymbol{\psi}_{1}\left(\tau_{1}\right) \boldsymbol{B}_{1}+ $ $ \boldsymbol{\psi}_{4}\left(\tau_{4}\right) \boldsymbol{B}_{4}$ ;τ1=ton1=ton2;τ4=T–ton1=T–ton2。ton1和ton2可分别由式(10)求得:$$\tag{10a} {s_1}\left( {{\boldsymbol{x}_n},{t_{{\rm{on}}}}} \right) = {\boldsymbol{K}_1}\boldsymbol{x}\left( {{t_{{\rm{on}}}}} \right) - {V_{{\rm{ref}}}} = 0 $$ $$\tag{10b} {s_2}\left( {{\boldsymbol{x}_n},{t_{{\rm{on}}}}} \right) = {\boldsymbol{K}_2}\boldsymbol{x}\left( {{t_{{\rm{on}}}}} \right) - {I_{{\rm{ref }}}} = 0 $$ 对于Z3,xn+1与xn之间的映射为:
$$ \boldsymbol{x}_{n+1}=f_{3}\left(\boldsymbol{x}_{n}\right)={\boldsymbol{\varPhi}}_{3}(\tau) \boldsymbol{x}_{n}+{\boldsymbol{\varPsi}}_{3}(\tau) $$ (11) 式中,
${\boldsymbol{\varPhi}}_{3}(\tau)=\boldsymbol{\phi}_{4}\left(\tau_{4}\right) \boldsymbol{\phi}_{3}\left(\tau_{3}\right) \boldsymbol{\phi}_{1}\left(\tau_{1}\right)$ ;${\boldsymbol{\varPsi}}_{3}(\tau)=\boldsymbol{\phi}_{4}\left(\tau_{4}\right) \times $ $ \boldsymbol{\phi}_{3} \left(\tau_{3}\right) \boldsymbol{\psi}_{1}\left(\tau_{1}\right) \boldsymbol{B}_{1}+\boldsymbol{\phi}_{4}\left(\tau_{4}\right) \boldsymbol{\psi}_{3}\left(\sigma_{3}\right) \boldsymbol{B}_{3}+ \boldsymbol{\psi}_{4}\left(\tau_{4}\right) \boldsymbol{B}_{4}$ ;τ1=ton1;τ3=ton2–ton1;τ4=T–ton2。ton1和ton2可由式(12)求得:$$\tag{12a} {s_1}\left( {{\boldsymbol{x}_n},{t_{{\rm{on}}1}}} \right) = {\boldsymbol{K}_1}\boldsymbol{x}\left( {{t_{{\rm{on}}1}}} \right) - {V_{{\rm{ref}}}} $$ $$\tag{12b} {s_2}\left( {{\boldsymbol{x}_n}\left( {{t_{{\rm{on}}1}}} \right),{t_{{\rm{on2}}}}} \right) = {\boldsymbol{K}_1}\boldsymbol{x}\left( {{t_{{\rm{on}}2}}} \right) - {I_{{\rm{ref }}}} $$ 因此,可得PVR控制Buck变换器级联PCM控制Boost变换器的离散映射模型为:
$$ {{\boldsymbol{x}}_{n + 1}} = \left\{ {\begin{array}{*{20}{c}} {{f_1}\left( {{{\boldsymbol{x}}_n}} \right)}&{{t_{{\rm{col}}}} > {t_{{\rm{con}}2}}}\\ {{f_2}\left( {{{\boldsymbol{x}}_n}} \right)}&{{t_{{\rm{col}}}} = {t_{{\rm{con}}2}}}\\ {{f_3}\left( {{{\boldsymbol{x}}_n}} \right)}&{{t_{{\rm{col}}}} < {t_{{\rm{on}}2}}} \end{array}} \right.$$ (13) 式中,f1(xn)、f2(xn)和f3(xn)分别由式(7)、式(9)和式(12)表示。由上述的推导过程可知,离散映射模型式(13)是一个精确模型,但用于求解导通时间ton1和ton2的方程均是超越方程,需要采用数值求解。为了避免求解超越方程,可取eAt的近似,即
$ \mathrm{e}^{{\boldsymbol{A}} t} \approx {\boldsymbol{I}}+{{\boldsymbol{A}}t} $ (I为单位矩阵)[23],并将其代入到式(7)~式(12),可得式(13)的近似离散映射模型。 -
定义PVR控制Buck变换器级联PCM控制Boost变换器工作在稳态时的不动点为XQ=[IL1 VC1 IL2]T。基于近似离散映射模型,利用xn+1=xn=XQ可求得状态变量的不动点XQ。工作在稳态时,源变换器的输出电容电压等于其输出电压,即VC1=Vo1。从而可得:
$ {V_{{\text{o}}1}} = {V_{{\text{ref}}}},{\text{ }}{I_{L2}} = {I_{{\text{ref}}}},{\text{ }}{I_{L1}} = {I_{L2}} $ 。因此,近似离散映射模型在其不动点XQ邻域内的Jacobi矩阵可以表示为:
$$ {\boldsymbol{J}}({{\boldsymbol{X}}_{\text{Q}}}) = {\boldsymbol{\varPhi }}(\tau ) - \frac{{\partial f}}{{\partial {\boldsymbol{t}}}}{\left( {\frac{{\partial {\boldsymbol{s}}}}{{\partial {\boldsymbol{t}}}}} \right)^{ - 1}}\left( {\frac{{\partial {\boldsymbol{s}}}}{{\partial {{\boldsymbol{x}}_n}}}} \right) $$ (14) 式中,s=[s1(·) s2(·) ··· sK−1(·)]T为开关切换函数向量;t=[t1 t2 ··· tK−1]T为开关切换时刻向量,K为第K个开关状态。相应地,3个偏导数分别为:
$$ \frac{{\partial f}}{{\partial {\boldsymbol{t}}}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial f}}{{\partial {t_1}}}} \\ {\dfrac{{\partial f}}{{\partial {t_2}}}} \\ \vdots \\ {\dfrac{{\partial f}}{{\partial {t_{K - 1}}}}} \end{array}} \right] \;\text{} \frac{{\partial {\boldsymbol{s}}}}{{\partial {\boldsymbol{t}}}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {s_1}}}{{\partial {t_1}}}}&{\dfrac{{\partial {s_1}}}{{\partial {t_2}}}}& \cdots &{\dfrac{{\partial {s_1}}}{{\partial {t_{K - 1}}}}} \\ {\dfrac{{\partial {s_2}}}{{\partial {t_1}}}}&{\dfrac{{\partial {s_2}}}{{\partial {t_2}}}}& \cdots &{\dfrac{{\partial {s_2}}}{{\partial {t_{K - 1}}}}} \\ { \vdots }& \vdots & \vdots & \vdots \\ {\dfrac{{\partial {s_{K - 1}}}}{{\partial {t_1}}}}&{\dfrac{{\partial {s_2}}}{{\partial {t_{K - 1}}}}}& \cdots &{\dfrac{{\partial {s_{K - 1}}}}{{\partial {t_{K - 1}}}}} \end{array}} \right] \text{} $$ $$ \frac{{\partial {\boldsymbol{s}}}}{{\partial {{\boldsymbol{x}}_n}}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {s_1}}}{{\partial {{\boldsymbol{x}}_n}}}}&{\dfrac{{\partial {s_2}}}{{\partial {{\boldsymbol{x}}_n}}}}& \cdots &{\dfrac{{\partial {s_{K - 1}}}}{{\partial {{\boldsymbol{x}}_n}}}} \end{array}} \right] $$ 对于开关状态序列Z1,式(14)中3个偏导数中各个元素的表达式为:
$$ \partial f_{1} / \partial t_{1}=\left(\boldsymbol{I}+\boldsymbol{A}_{4} \tau_{3}\right)\left[\left(\boldsymbol{I}+\boldsymbol{A}_{2} \tau_{2}\right)\left({\boldsymbol{A}}_{1} {\boldsymbol{x}}_{n}+\boldsymbol{B}_{1}\right)-{\boldsymbol{A}}_{2} \boldsymbol{P}_{1}-{\boldsymbol{B}}_{2}\right] $$ $$ \partial f_{1} / \partial t_{2}=\left({\boldsymbol{I}}+{\boldsymbol{A}}_{4} \tau_{3}\right)\left({\boldsymbol{A}}_{1} {\boldsymbol{P}}_{1}+{\boldsymbol{B}}_{2}\right)-{\boldsymbol{A}}_{4} {\boldsymbol{P}}_{2}-{\boldsymbol{B}}_{4} $$ $$ \partial s_{1} / \partial t_{1}=\boldsymbol{K}_{2}\left(\boldsymbol{A}_{1} \boldsymbol{x}_{n}+\boldsymbol{B}_{1}\right) \;\;\;\; \partial s_{1} / \partial t_{2}=0 $$ $$ \partial s_{2} / \partial t_{1}=\boldsymbol{K}_{1}\left[\left(\boldsymbol{I}+\boldsymbol{A}_{2} \tau_{2}\right)\left(\boldsymbol{A}_{1} \boldsymbol{x}_{n}+\boldsymbol{B}_{1}\right)-\boldsymbol{A}_{2} \boldsymbol{P}_{1}-\boldsymbol{B}_{2}\right] $$ $$ \partial s_{2} / \partial t_{2}=\boldsymbol{K}_{1}\left(\boldsymbol{A}_{2} \boldsymbol{P}_{1}+\boldsymbol{B}_{2}\right) \;\;\;\; \partial s_{1} / \partial \boldsymbol{x}_{n}=\boldsymbol{K}_{2}\left(\boldsymbol{I}+\boldsymbol{A}_{1} \tau_{1}\right) $$ $$ \partial s_{2} / \partial \boldsymbol{x}_{n}=\boldsymbol{K}_{1}\left(\boldsymbol{I}+\boldsymbol{A}_{2} \tau_{2}\right)\left(\boldsymbol{I}+\boldsymbol{A}_{1} \tau_{1}\right) $$ 式中,
$ \boldsymbol{P}_{1}=\left(\boldsymbol{I}+{\boldsymbol{A}}_{1} \tau_{1}\right) {\boldsymbol{x}}_{n}+\boldsymbol{B}_{1} \tau_{1} ; \boldsymbol{P}_{2}=\left(\boldsymbol{I}+\boldsymbol{A}_{2} \tau_{2}\right) \boldsymbol{P}_{1}+ \boldsymbol{B}_{2} \tau_{2} $ 。对于开关状态序列Z2,式(14)中3个偏导数中各个元素的表达式为:
$$ \partial f_{2} / \partial t_{1}=\left(\boldsymbol{I}+\boldsymbol{A}_{4} \tau_{3}\right)\left(\boldsymbol{A}_{1} \boldsymbol{x}_{n}+\boldsymbol{B}_{1}\right)-\boldsymbol{A}_{4} \boldsymbol{P}_{1}-\boldsymbol{B}_{4} $$ $$ \partial s_{1} / \partial t_{1}=\boldsymbol{K}_{1}\left(\boldsymbol{A}_{1} \boldsymbol{x}_{n}+\boldsymbol{B}_{1}\right) \;\;\;\; \partial s_{1} / \partial \boldsymbol{x}_{n}=\boldsymbol{K}_{1}\left(\boldsymbol{I}+\boldsymbol{A}_{1} \tau_{1}\right) $$ 对于开关状态序列Z3,式(14)中3个偏导数的各个元素的表达式为:
$$ \partial f_{3} / \partial t_{1}=\left(\boldsymbol{I}+\boldsymbol{A}_{4} \tau_{3}\right)\left[\left(\boldsymbol{I}+\boldsymbol{A}_{3} \tau_{2}\right)\left(\boldsymbol{A}_{1} \boldsymbol{x}_{n}+\boldsymbol{B}_{1}\right)-\boldsymbol{A}_{3} \boldsymbol{P}_{1}-\boldsymbol{B}_{3}\right] $$ $$ \partial f_{3} / \partial t_{2}=\left(\boldsymbol{I}+\boldsymbol{A}_{4} \tau_{3}\right)\left(\boldsymbol{A}_{3} \boldsymbol{P}_{1}+\boldsymbol{B}_{3}\right)-\boldsymbol{A}_{4} \boldsymbol{P}_{3}-\boldsymbol{B}_{4} $$ $$ \partial s_{1} / \partial t_{1}=\boldsymbol{K}_{2}\left(\boldsymbol{A}_{1} \boldsymbol{x}_{n}+\boldsymbol{B}_{1}\right) \;\;\;\; \partial s_{1} / \partial t_{2}=0 $$ $$ \partial s_{2} / \partial t_{1}=\boldsymbol{K}_{1}\left[\left(\boldsymbol{I}+\boldsymbol{A}_{3} \tau_{2}\right)\left(\boldsymbol{A}_{1} \boldsymbol{x}_{n}+\boldsymbol{B}_{1}\right)-\boldsymbol{A}_{3} \boldsymbol{P}_{1}-\boldsymbol{B}_{3}\right] $$ $$ \partial s_{2} / \partial t_{2}=\boldsymbol{K}_{1}\left({\boldsymbol{A}}_{3} \boldsymbol{P}_{1}+{\boldsymbol{B}}_{3}\right) \;\;\;\; \partial s_{1} / \partial {\bf{x}}_{n}=\boldsymbol{K}_{2}\left(\boldsymbol{I}+\boldsymbol{A}_{1} \tau_{1}\right) $$ $$ \partial s_{2} / \partial {\bf{x}}_{n}=\boldsymbol{K}_{1}\left(\boldsymbol{I}+\boldsymbol{A}_{3} \tau_{2}\right)\left(\boldsymbol{I}+\boldsymbol{A}_{1} \tau_{1}\right) $$ 式中,
$\boldsymbol{P}_{3}=\left(\boldsymbol{I}+\boldsymbol{A}_{3} \tau_{2}\right) \boldsymbol{P}_{1}+\boldsymbol{B}_{3} \tau_{2}$ 。 -
通过监测离散映射模型的特征根可以判定PVR控制Buck变换器级联PCM控制Boost变换器的稳定性。离散映射模型的特征根可通过其特征根方程det[λI–J(XQ)]=0求得。
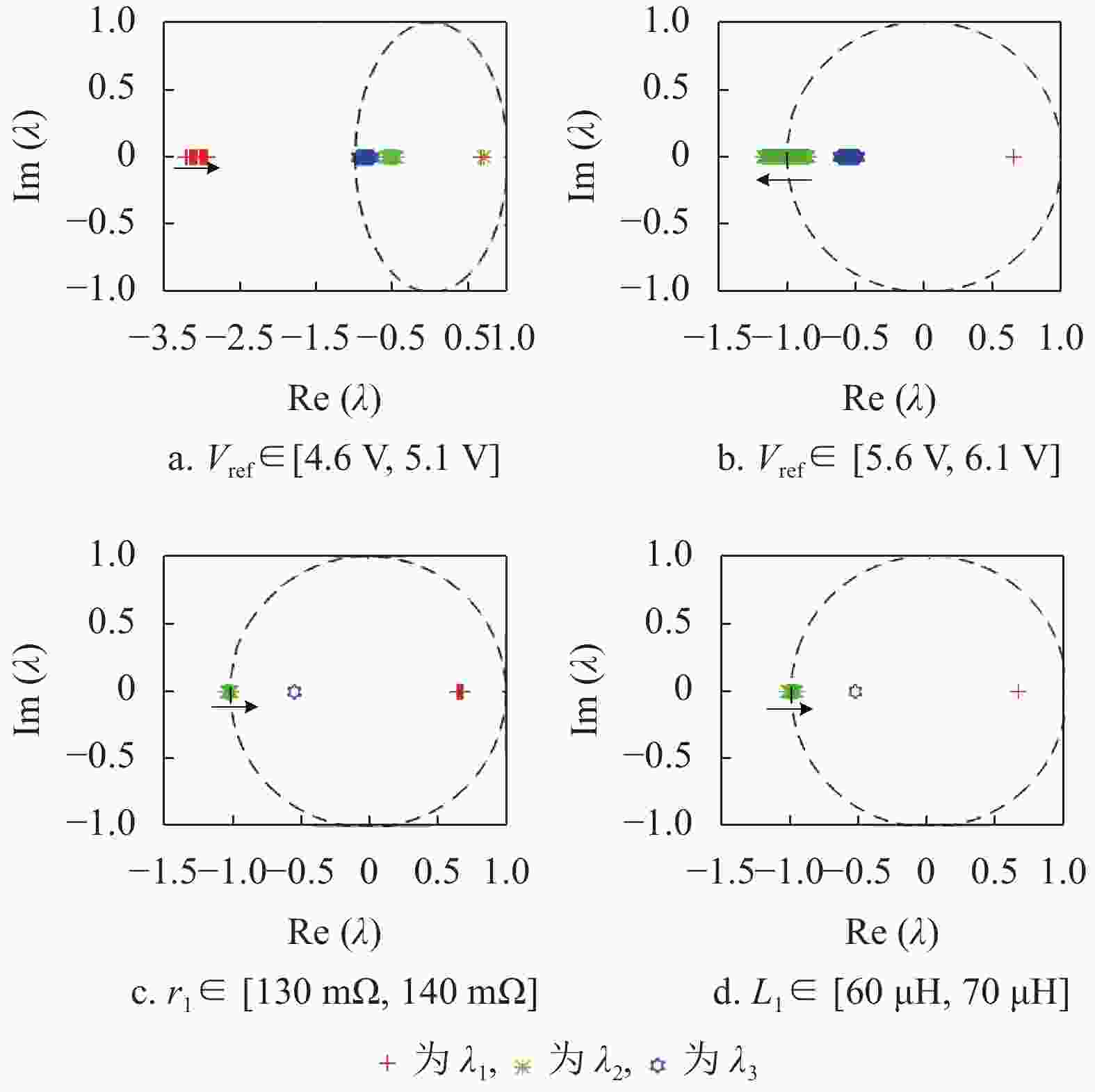
基于离散映射模型及其特征根方程,该级联开关变换器的3个特征根随源变换器Vref、r1和L1变化的运动轨迹如图5所示,相应的典型参数值对应的特征根值如表2、表3和表4所示。考虑纹波的影响,不动点XQ设定为[IL1+0.45ΔiL1 VC1 IL2]T。
由图5a和图5b以及表2可以看出,随着Vref的增大,λ1在Vref=4.74 V处突然从单位圆外跳到单位圆内,且λ2和λ3始终在单位圆内,预示着边界碰撞分岔发生;随着Vref的进一步增大,λ2在Vref=5.85 V处通过−1穿出单位圆,且λ1和λ3始终在单位圆内,预示倍周期分岔发生。由图5c和表3或由图5d和表4可以看出,随着r1或L1的增大,λ2在r1=135.7 mΩ或L1=64.4 μH处通过−1进入单位圆,预示逆倍周期分岔发生。
表 2 不同Vref的典型特征根
Vref/V 特征根(λ1, λ2, λ3) 稳定性 4.70 (−3.154, 0.691, −0.920) 不稳定 4.73 (−3.223, 0.693, −0.907) 不稳定 4.74 (0.643, −0.459, −0.909) 稳定 4.8 (0.643, −0.480, −0.886) 稳定 5.8 (0.646, −0.966, −0.563) 稳定 5.85 (0.646, −1.000, −0.549) 临界 5.86 (0.647, −1.006, −0.547) 不稳定 5.90 (0.647, −1.033, −0.536) 不稳定 表 3 不同r1的典型特征根
r1/mΩ 特征根(λ1, λ2, λ3) 稳定性 133.0 (0.679, −1.005, −0.538) 不稳定 135.0 (0.683, −1.001, −0.538) 不稳定 135.7 (0.685, −1.000, −0.538) 临界 136.0 (0.685, −0.999, −0.538) 稳定 139.0 (0.692, −0.994, −0.538) 稳定 表 4 不同L1的典型特征根
L1/μH 特征根(λ1, λ2, λ3) 稳定性 63.0 (0.646, −1.010, −0.536) 不稳定 64.0 (0.646, −1.002, −0.536) 不稳定 64.4 (0.646, −1.000, −0.536) 临界 65.0 (0.646, −0.996, −0.536) 稳定 66.0 (0.646, −0.988, −0.536) 稳定 对比图5和图4可以看出,特征根分析的动力学行为与分岔分析的动力学行为一致。此外,由图5和表2~表4也看出,与负载变换器稳定性关联的特征根λ3在所选电路参数的变化范围内始终在单位圆内,表明负载变换器始终工作在稳定的周期1状态。
-
为了说明本文研究方法的普遍性,现将研究方法拓展至V2控制Buck变换器作为源变换器的情况。相较于PVR控制,V2控制具有两个控制环路,其电压外环由误差放大器构成[24]。V2控制Buck变换器级联PCM控制Boost变换器的原理图如图6所示。
根据图6搭建其PSIM仿真电路。在仿真电路中,误差放大器采用比例积分(proportional integral, PI)补偿器,并取其反馈增益g=1,时间常数τ=100 μs。其他电路参数为:Vin=10 V,L1=60 μH,C1=220 μF,r1=40 mΩ,Vref=5.5 V,f1=100 kHz,L2=100 μH,Iref=1 A,E=9 V,f2=100 kHz。当V2控制Buck变换器独立工作时(将负载变换器替换为负载电阻R,并取值2.35 Ω),仿真波形如图7a所示;当V2控制Buck变换器级联工作时,仿真波形如图7b所示。
从图7可以看出,在相同电路参数情况下,V2控制Buck变换器独立工作时运行在不稳定状态,如图7a所示;而级联工作时运行在稳定周期1状态,如图7b所示。由此可知,V2控制Buck变换器作为源变换器时,其稳定性也受到负载变换器的影响。进一步,可采用上文的建模分析方法对V2控制Buck变换器作为源变换器时的稳定性机理进行深入研究。
-
为了验证上述理论分析和仿真分析的正确性,根据图1a所示的原理图,搭建了PVR控制Buck变换器级联PCM控制Boost变换器的实验样机,如图8所示。其中,开关管采用型号为IRF540的MOSFET,二极管采用型号为MBR2045CT的肖特基二极管,驱动芯片的型号为MCP1407,比较器型号为LM319,RS触发器由型号为74HC02的或非门芯片搭建,时钟信号由信号发生器提供,输入电压和输出电压均由稳压电源提供。
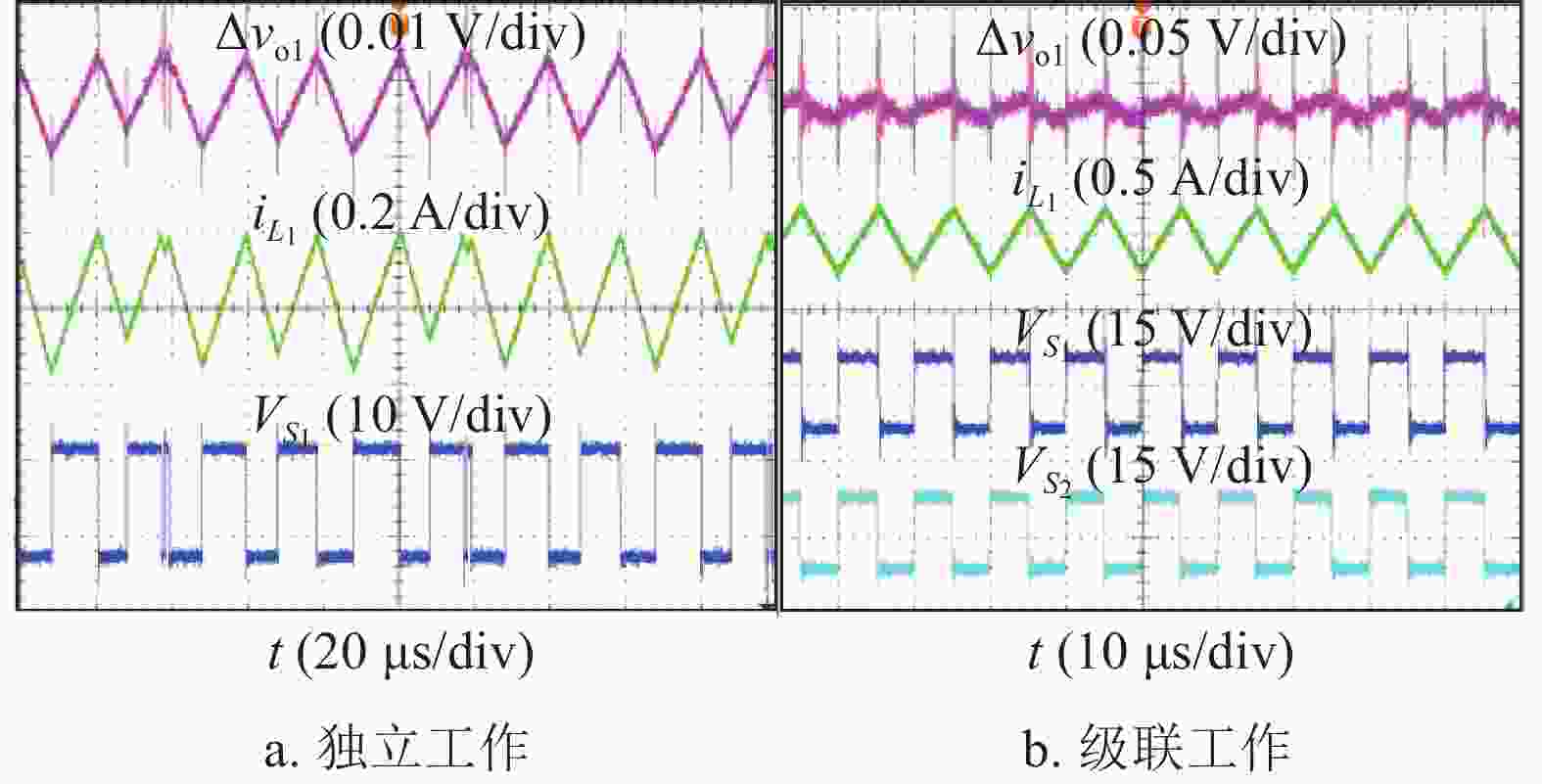
首先,基于图8的实验样机,验证图3的PSIM电路仿真波形。采用图3所使用的电路参数,得到PVR控制Buck变换器独立工作和级联工作时对应的实验结果分别如图9a和图9b所示。对比图9和图3可知,实验结果和仿真结果基本一致,即PVR控制Buck变换器独立工作时存在次谐波振荡,而级联工作时运行在稳定的周期1状态。
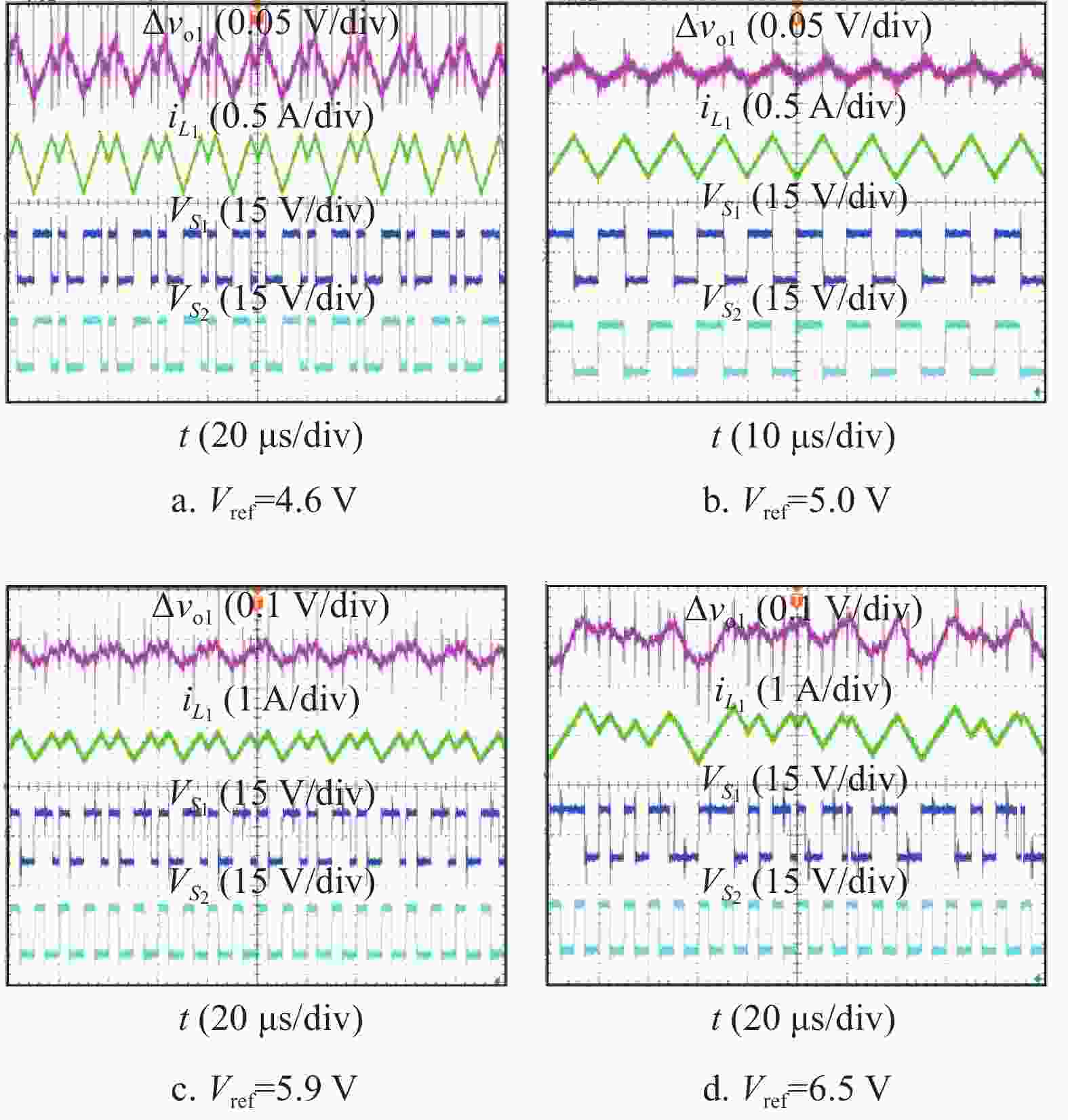
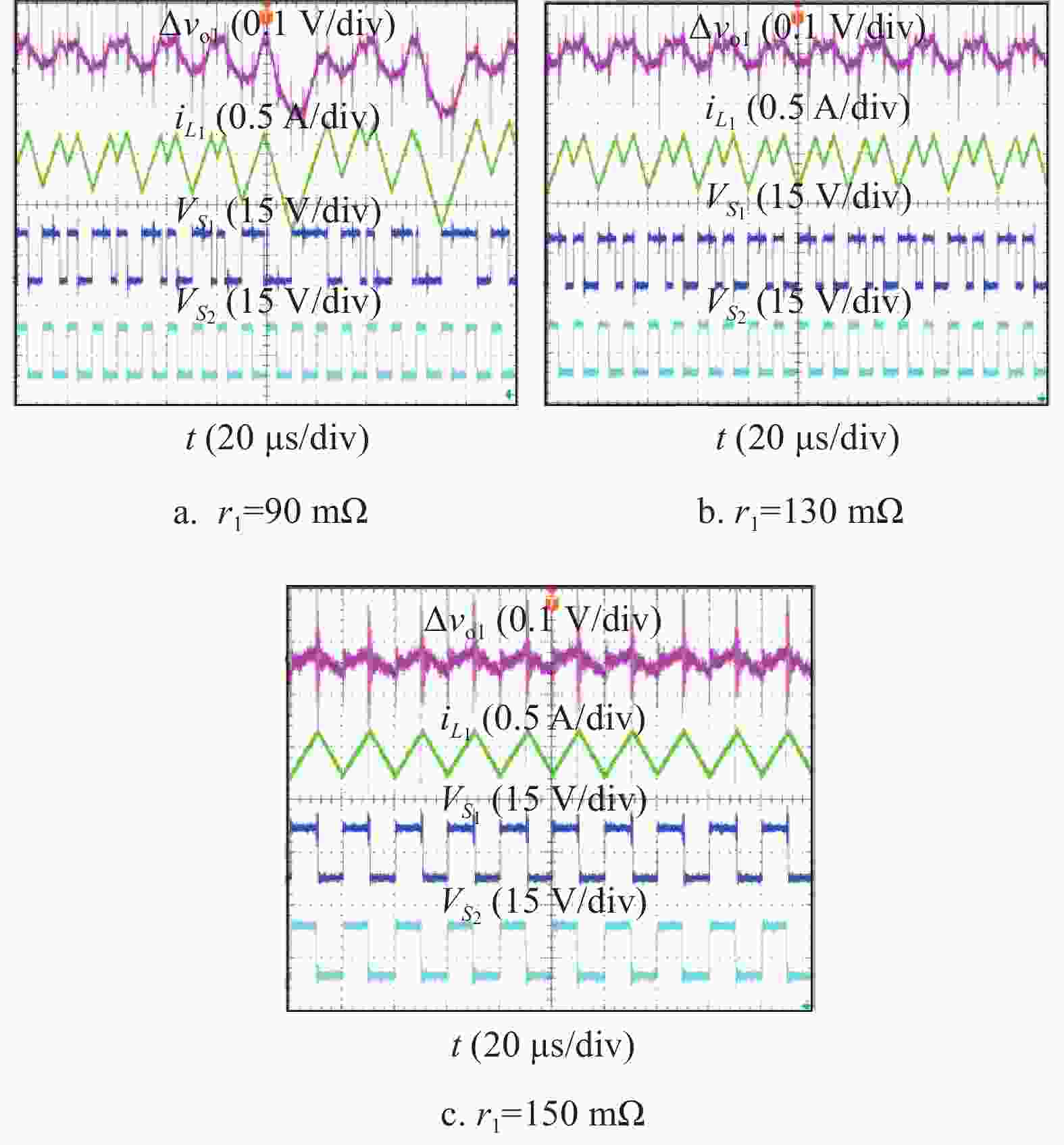
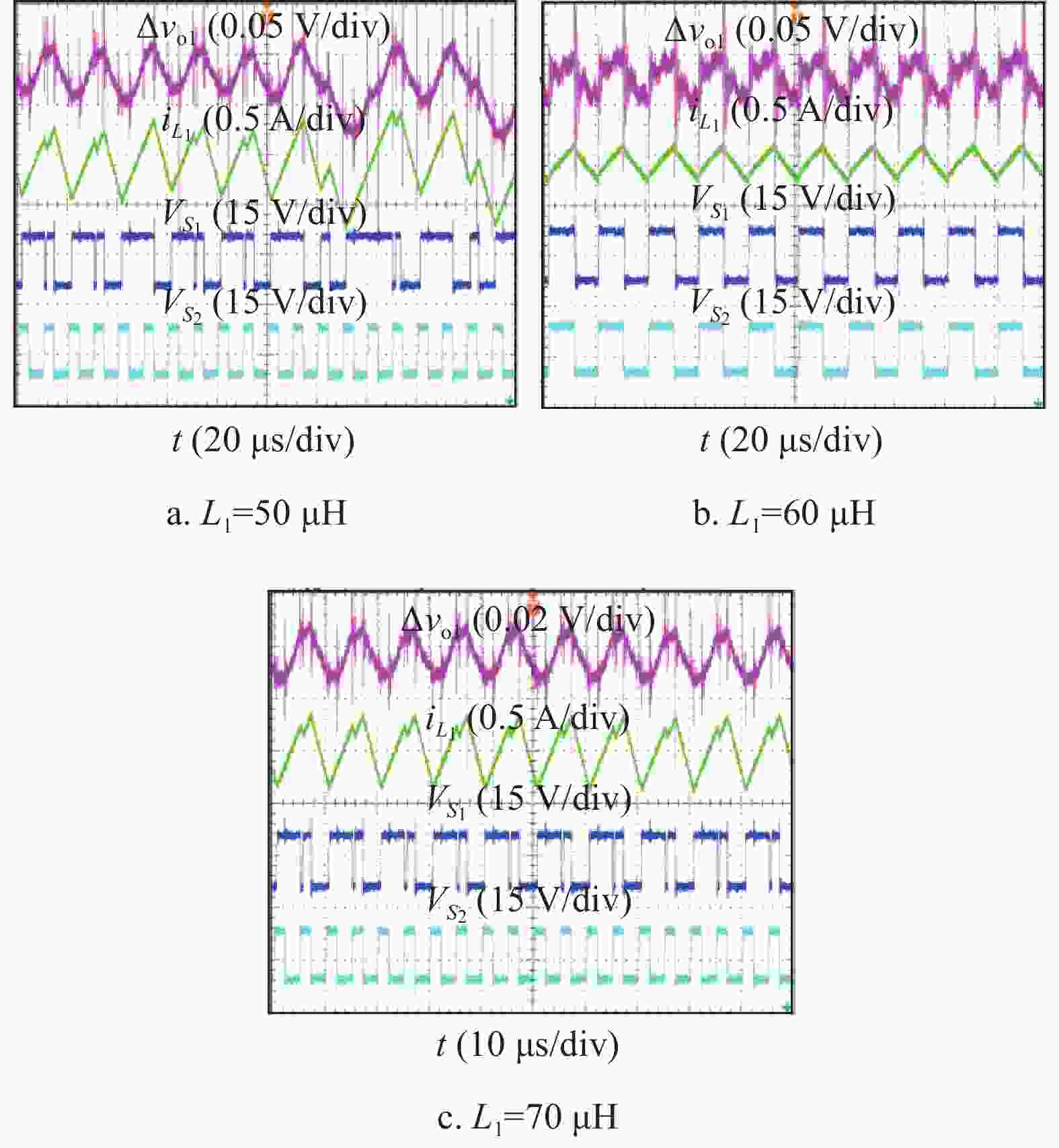
进一步,根据图4所示的分岔图,选择若干组典型电路参数验证其对源变换器稳定性的影响。根据图4a所示分岔图对应的4个工作状态区间,即周期2、周期1、周期2和混沌,分别选择Vref=4.6, 5, 5.9, 6.5 V这4组参数开展实验,相应的实验结果分别如图10a~图10d所示;根据图4b所示分岔图对应的3个工作状态区间,即混沌、周期2和周期1,分别选择r1=90, 130, 150 mΩ这3组参数开展实验,相应的实验结果分别如图11a~图11c所示。根据图4c所示分岔图对应的3个工作状态区间,即混沌、周期2和周期1,分别选择L1=50, 60, 70 μH这3组参数开展实验,相应的实验结果分别如图12a~图12c所示。
当Vref=4.6 V时,源变换器工作在不稳定的周期2状态,如图10a所示;当Vref=5 V时,源变换器工作在稳定的周期1状态,如图10b所示;当Vref=5.9 V时,源变换器工作在不稳定的周期2状态,如图10c所示;当Vref=6.5 V时,源变换器工作在混沌状态,如图10d所示。
当r1=90 mΩ或L1=50 μH时,源变换器工作在混沌状态,如图11a或图12a所示;当r1=130 mΩ或L1=60 μH时,源变换器工作在不稳定的周期2状态,如图11b或图12b所示;当r1=150 mΩ或L1=70 μH时,源变换器工作在稳定的周期1状态,如图11c或图12c所示。
-
以PVR控制Buck变换器级联PCM控制Boost变换器为例,深入研究了级联开关变换器中源变换器的稳定性机理。分析了源变换器随其参考电压、输出电容ESR和电感变化时的分岔行为。建立了级联开关变换器具有3种开关状态序列的离散映射模型,推导了其在不动点邻域内的Jacobi矩阵,并通过监测Jacobi矩阵的特征根运动轨迹,明晰了源变换器随电路参数变化的失稳机理。研究表明,增大参考电压,源变换器将通过倍周期失稳;减小参考电压,源变换器将通过边界碰撞分岔失稳。当源变换器占空比小于负载变换器占空比时,源变换器始终工作在不稳定状态;而当源变换器占空比大于负载变换器占空比时,源变换器可工作在稳定状态,且稳定工作范围随输出电容ESR和电感的增大而增大。本文的研究方法也可以拓展至V2控制Buck变换器等其他类型变换器作为源变换器的情况。
本文的研究结果和研究方法可以作为基于阻抗分析的稳定性判据的补充,可以为级联开关变换器中源变换器的参数设计提供更加精确的理论指导。
Stability Mechanism of the Source Converter in a Cascaded Switching Converter
-
摘要: 在级联开关变换器中,负载变换器前馈电流纹波可重塑源变换器的输出电压纹波,导致源变换器的稳定性发生变化。以峰值电压纹波(PVR)控制Buck变换器级联峰值电流模式(PCM)控制Boost变换器为例,研究了级联开关变换器中源变换器的稳定性机理。首先,展示了负载变换器前馈电流纹波对源变换器稳定性的影响,分析了源变换器随所选电路参数变化的分岔行为;其次,建立了级联开关变换器具有3种开关状态序列的离散映射模型,推导了其在不动点邻域内的Jacobi矩阵,通过监测Jacobi矩阵的特征根轨迹明晰了源变换器随所选电路参数变化的失稳机理;最后,实验结果验证了仿真分析和理论分析的正确性。Abstract: In cascaded switching converter, the feedforward current ripple of the load converter can reshape the output voltage ripple of the source converter, resulting in a significant change in the stability of the source converter. Take the peak voltage ripple (PVR) controlled buck converter cascading the peak current mode (PCM) controlled boost converter as an example, the stability mechanism of the source converter in cascaded switching converter is studied. Firstly, the effect of feedforward current ripple of load converter on the stability of the source converter is shown, and the bifurcation behaviors of the source converter with the variation of the chosen circuit parameters are analyzed. Secondly, a discrete-time map model of the cascaded switching converter with three switching state sequences is established, and its Jacobi matrix in neighborhood of the fixed point is derived. Then, by detecting the eigenvalues of the Jacobi matrix, the instability mechanism of the source converter with the variation of the chosen circuit parameters is clarified. Finally, the experimental results are supplied to verify the correctness of simulation and theoretical analyses.
-
表 1 级联开关变换器的典型电路参数
参 数 数 值 输入电压Vin/V 10 电感L1/μH 60 输出电容C1/μF 220 输出电容ESR r1/mΩ 120 基准电压Vref/V 5.5 开关频率f1/kHz 100 电感L2/μH 140 基准电流Iref/A 1 输出电压E/V 9 开关频率f2/kHz 100 表 2 不同Vref的典型特征根
Vref/V 特征根(λ1, λ2, λ3) 稳定性 4.70 (−3.154, 0.691, −0.920) 不稳定 4.73 (−3.223, 0.693, −0.907) 不稳定 4.74 (0.643, −0.459, −0.909) 稳定 4.8 (0.643, −0.480, −0.886) 稳定 5.8 (0.646, −0.966, −0.563) 稳定 5.85 (0.646, −1.000, −0.549) 临界 5.86 (0.647, −1.006, −0.547) 不稳定 5.90 (0.647, −1.033, −0.536) 不稳定 表 3 不同r1的典型特征根
r1/mΩ 特征根(λ1, λ2, λ3) 稳定性 133.0 (0.679, −1.005, −0.538) 不稳定 135.0 (0.683, −1.001, −0.538) 不稳定 135.7 (0.685, −1.000, −0.538) 临界 136.0 (0.685, −0.999, −0.538) 稳定 139.0 (0.692, −0.994, −0.538) 稳定 表 4 不同L1的典型特征根
L1/μH 特征根(λ1, λ2, λ3) 稳定性 63.0 (0.646, −1.010, −0.536) 不稳定 64.0 (0.646, −1.002, −0.536) 不稳定 64.4 (0.646, −1.000, −0.536) 临界 65.0 (0.646, −0.996, −0.536) 稳定 66.0 (0.646, −0.988, −0.536) 稳定 -
[1] 韦李军, 黄萌, 孙建军, 等. 带恒功率负载的光伏-储能混合发电系统非线性行为分析[J]. 电工技术学报, 2017, 32(7): 128-137. WEI L J, HUANG M, SUN J J, et al. Nonlinear analysis of photovoltaic battery hybrid power system with constant power loads[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 128-137. [2] 廖志贤, 罗晓曙, 黄国现. 两级式光伏并网逆变器建模与非线性动力学行为研究[J]. 物理学报, 2015, 64(13): 130503.1-130503.8. LIAO Z X, LUO X S, HUANG G X. Numerical modeling and research on nonlinear dynamic behaviors of two-stage photovoltaic grid-connected inverter[J]. Acta Phys Sin, 2015, 64(13): 130503.1-130503.8. [3] 黄旭程, 何志兴, 伍文华, 等. 交直流微电网中变换器级联系统稳定性分析与协同控制[J]. 中国电机工程学报, 2019, 39(5): 1432-1442. HUANG X C, HE Z X, WU W H, et al. Stability analysis of converters cascade system in the hybrid AC/DC microgrid and coordinative control[J]. Proceedings of the CSEE, 2019, 39(5): 1432-1442. [4] 周兵凯, 杨晓峰, 李继成, 等. 一种用于优化LC-DAB级联系统稳定性的虚拟阻抗控制技术[J]. 电工技术学报, 2021, DOI: 10.19595/j.cnki.1000-6753.tces.200063. ZHOU B K, YANG X F, LI J C, et al. Virtual impedance control technology for stability optimization of LC-DAB cascaded system[J]. Transactions of China Electrotechnical Society, 2021, DOI: 10.19595/j.cnki.1000-6753.tces.200063. [5] 王剑, 贾鹏宇, 李艳, 等. 优化负载变换器输入阻抗的输入电流内环控制方法[J]. 电工技术学报, 2016, 31(2): 92-101. doi: 10.3969/j.issn.1000-6753.2016.02.013 WANG J, JIA P Y, LI Y, et al. Input current inner loop control method to increase the input impedance of load converters[J]. Transactions of China Electrotechnical Society, 2016, 31(2): 92-101. doi: 10.3969/j.issn.1000-6753.2016.02.013 [6] MIDDLEBROOK R D. Input filter considerations in design and application of switching regulators[C]//IEEE Industry Applications Society Annual Meeting, Chicago: IEEE, 1976: 366-382. [7] RICCOBONO A, SANTI E. Comprehensive review of stability criteria for DC power distribution systems[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3525-3535. doi: 10.1109/TIA.2014.2309800 [8] SUN J. Impedance-based stability criterion for grid- connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078. doi: 10.1109/TPEL.2011.2136439 [9] ZHANG X, RUAN X B, TSE C K. Impedance-based local stability criterion for DC distributed power systems[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2015, 62(3): 916-925. doi: 10.1109/TCSI.2014.2373673 [10] 王伟, 宫池玉, 焦庆丽. 分布式电源级联系统稳定性分析与增强控制[J]. 电力电子技术, 2019, 53(11): 66-70. WANG W, GONG C Y, JIAO Q L. Stability analysis and enhanced control of distributed power cascaded system[J]. Power Electronics, 2019, 53(11): 66-70. [11] LI X, RUAN X B, XIONG X L, et al. Stability issue of cascaded systems with consideration of switching ripple interaction[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 7040-7052. doi: 10.1109/TPEL.2018.2876627 [12] ZHANG X, ZHONG Q, MING W. Fast scale instability problem of cascaded buck conversion system and its phase-shifted-carrier solution[C]//IEEE Energy Conversion Congress and Exposition. Montreal, QC: IEEE, 2015: 366-382. [13] DING L, WONG S C, TSC C K, et al. Bifurcation analysis of a current-mode controlled DC cascaded system and applications to design[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4): 3214-3224. doi: 10.1109/JESTPE.2020.2964818 [14] ZHOU G H, LI Y, LENG M R, et al. Stabilizing effect of load converter in cascaded system considering ripple interaction[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2021, 68(1): 296-300. doi: 10.1109/TCSII.2020.2992734 [15] REDL R, SUN J. Ripple-based control of switching regulators—An overview[J]. IEEE Transactions on Power Electronics, 2009, 24(12): 2669-2680. doi: 10.1109/TPEL.2009.2032657 [16] CORTÉS J, ŠVIKOVIĆ V, ALOU P, et al. Accurate analysis of subharmonic oscillations of V2 and V2Ic controls applied to buck converter[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 1005-1018. doi: 10.1109/TPEL.2014.2308015 [17] ZHOU G H, MAO G H, ZHOU S H, et al. Digital valley V2 control for boost converter with fast load-transient performance[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2020, 67(10): 2089-2093. doi: 10.1109/TCSII.2019.2949653 [18] 周国华, 谭伟, 周述晗, 等. V2控制Cuk变换器建模与瞬态性能分析[J]. 电工技术学报, 2021, 36(4): 820-830. ZHOU G H, TAN W, ZHOU S H, et al. Modeling and transient performance analysis of V2 controlled Cuk converter[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 820-830. [19] ZHANG X, ZHANG Z W, BAO B C, et al. Design-oriented stability of outer voltage loop in capacitor current controlled buck converters[J]. Journal of Power Electronics, 2019, 19(4): 869-880. [20] 周群, 徐懿, 张金保, 等. I2控制Buck变换器的一阶动力学分析[J]. 电子科技大学学报, 2016, 45(3): 387-392. doi: 10.3969/j.issn.1001-0548.2016.02.013 ZHOU Q, XU Y, ZHANG J B, et al. One-dimensional dynamic analysis of I2 controlled buck converter[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(3): 387-392. doi: 10.3969/j.issn.1001-0548.2016.02.013 [21] LENG M R, ZHOU G H, TIAN Q X, et al. Improved small signal model for switching converter with ripple- based control[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 222-235. doi: 10.1109/TIE.2020.2965478 [22] WANG Y, XU L M, CHEN L, et al. Discrete iterative map model-based stability analysis of capacitor current ripple-controlled SIDO CCM buck converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4): 3272-3280. doi: 10.1109/JESTPE.2020.2972651 [23] CHEN Y, TSE C K, QIU S S, et al. Coexisting fast-scale and slow-scale instability in current-mode controlled DC/DC converters: Analysis, simulation and experimental results[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2008, 55(10): 3335-3348. doi: 10.1109/TCSI.2008.923282 [24] ZHOU G H, HE S Z, ZHANG X, et al. Critical output-capacitor ESR for stability of V2 controlled buck converter in CCM and DCM[J]. Electronics Letters, 2014, 50(12): 884-886. doi: 10.1049/el.2014.0419 -


 ISSN
ISSN 



 下载:
下载: