-
全局寻优问题在工程[1-2]、金融[3]、自然科学等领域中广泛存在,求解全局寻优问题有很强的理论与现实意义。现阶段对全局寻优问题求解的重要途径是使用群体智能算法,该算法是受自然界生物的行为模式启发后设计的一类算法,旨在以更快的速度与更高的精度求解复杂的全局寻优问题。近几十年来,群体智能算法发展迅速,如蚁群算法[4-6]、粒子群优化算法[7]、蝙蝠算法[8]、灰狼算法[9]、鲸鱼算法[10]、麻雀搜索算法(sparrow search algorithm, SSA)[11]等。其中,麻雀搜索算法有收敛速度快、收敛精度高、鲁棒性强等优点[12],但同其他群体智能算法一样,它在迭代后期依然有种群多样性减少,容易陷入局部最优的问题。在提高优化算法全局寻优能力方面,文献[13]将遗传算法进行优化,通过在每一代中引入一个较低维度的活动子空间,使算法以较低的成本保证种群的多样性,提高算法的全局寻优能力。文献[14]将牛顿方法与非单调线搜索方法进行结合,当牛顿方法寻优结果不再下降时,使用非单调线搜索帮助寻优,提高算法的全局寻优能力。文献[15]在遗传算法的框架下提出了新的算法,利用历史信息帮助算法自适应地选择局部搜索与全局搜索,提出了新的“诱导”算子,提高了算法的种群多样性,帮助算法收敛至全局最优。
对于麻雀搜索算法的改进是近期群体智能算法研究的热点之一。为了解决麻雀搜索算法中存在的问题,文献[16]引入混沌理论,丰富了种群的多样性,对迭代结果进行混沌扰动,增加算法跳出局部最优的能力;文献[17]结合鸟群算法,对麻雀搜索算法的位置更新公式进行改进,提高了算法的稳定性;文献[18]使用混沌理论对麻雀搜索算法进行初始化过程的优化,并且使用危险转移策略与动态演化策略提高了算法的全局寻优能力。
Hammersley[19]序列是一种低差异序列,常被用于图像渲染等领域。在群体智能算法中,Hammersley序列可以应用于种群初始化,提高初始种群的多样性,提升算法的全局搜索能力,相较于随机数生成器与混沌序列有更好的效果,且均匀分布的初始种群可以使粗糙数据推理的论域更加完整。文献[20]介绍了一种名为粗糙数据推理的方法,该方法在数据间建立一种不明确、非确定、似存在的推理关系,与经典逻辑推理不同,粗糙数据推理的对象为数据,保证了该理论可以运用于算法优化中。文献[21]将聚类的思想与进化算法相结合,并通过实验证明了对算法种群进行合理划分,能有效提高算法的寻优能力。
为了提高麻雀搜索的全局搜索能力,加快算法的收敛速度,增加种群的多样性,本文提出一种融合粗糙数据推理的多策略改进麻雀搜索算法(sparrow search algorithm, RSSA)。首先基于Hammersley点集完成种群初始化,为粗糙数据推理提供完整的论域;其次使用粗糙数据推理,结合种群的经验建立数据间的推理关系,提高算法的收敛速度,并且增强算法跳出局部最优的能力;最后对搜索中超界的个体进行优化,保证种群多样性。
-
麻雀搜索算法主要是受自然界中麻雀觅食与反捕食行为的启发而提出,设计规则为:适应度前20%的个体为发现者,在安全值大于预警值时它们可以进行大范围的搜索,否则将飞往适应度高的安全区域;除去发现者以外的个体被称为加入者,加入者中适应度靠前的个体将与发现者争夺适应度高的位置,靠后的个体因为竞争激烈,将飞往其他地方进行搜索;同时种群中有15%的个体会触发预警机制,迅速向适应度较好的区域移动,或者随机移动以靠近其他个体。
麻雀种群及个体表示为:
$$ {\boldsymbol{X}} = {[{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2}, \cdots ,{{\boldsymbol{x}}_N}]^{\text{T}}} $$ (1) $$ {{\boldsymbol{x}}_i} = [{x_{{i}{,}{\text{1}}}},{x_{{i}{,2}}}, \cdots ,{x_{{i}{,}{D}}}] $$ (2) 式中,
$ N $ 是麻雀的种群个数;$ D $ 是麻雀个体所在解空间的最大维度。算法的适应度值矩阵表示如下:
$$ {{\boldsymbol{F}}_{\boldsymbol{x}}} = {[{f_{\text{1}}},{f_{\text{2}}}, \cdots ,{f_N}]^{\text{T}}} $$ (3) $$ {f_i} = f({{\boldsymbol{x}}_i}) $$ (4) 式中,
${f_i}$ 是个体$i$ 的适应度。在麻雀搜索算法中,适应度靠前的个体作为发现者,引领种群向食物源移动,其位置更新公式为:
$$ x_{{i}{,}{j}}^{t + {1}} = \left\{ {\begin{array}{*{20}{c}} {x_{{i}{,}{j}}^{t} \exp \left( {\dfrac{{ - i}}{{\alpha \cdot {{\rm{ite}}}{{{\rm{r}}}_{{\text{max}}}}}}} \right)}&{{R_{2}} < {\rm{ST}}} \\ {x_{{i}{,}{j}}^{t} + Q}&{{R_{2}} \geqslant {\rm{ST}}} \end{array}} \right. $$ (5) 式中,
$ t $ 为当前迭代次数;${{\rm{ite}}}{{{\rm{r}}}_{{\text{max}}}}$ 为最大迭代次数;$ i $ 为个体编号;$ j $ 为维度编号;$ x_{{i}{,}{j}}^{t} $ 则为迭代次数为$ t $ 时,第$ i $ 个麻雀在第$ j $ 维的值;$\alpha \in ({\text{0,1}}]$ 为均匀分布的随机数;$ Q $ 为正态分布的随机数;$ {R_2} \in [{\text{0,1}}] $ 、${\rm{ST}} \in [{\text{0}}{\text{.5,1}}]$ 分别代表预警值和安全值,当${R_2} < {\rm{ST}}$ ,表示附近没有天敌,将执行广泛搜索模式,如果${R_2} \geqslant {\rm{ST}}$ ,则表示附近有天敌,它们会随机飞往一个地方。加入者的位置更新公式为:
$$ x_{{i}{,}{j}}^{{t}{ + 1}} = \left\{ {\begin{array}{*{20}{c}} {Q \exp \left( {\dfrac{{{\rm{xw}}_{j}^{t} - x_{{i}{,}{j}}^{t}}}{{{i^{2}}}}} \right)}&{i > \dfrac{N}{{2}}} \\ {{\rm{xp}}_{j}^{{t}{ + 1}} + \dfrac{{1}}{D}\displaystyle\sum\limits_{{j}{\text{ = 1}}}^D {{\text{rand\{ }}{ - 1,1}{\text{\} }} {\text{(}}| {{\rm{xp}}_{j}^{t} - x_{{i}{,}{j}}^{t}} |{\text{)}}} }&{其他} \end{array}} \right. $$ (6) 式中,
$ {\rm{xw}}_j^t $ 是迭代次数为$ t $ 时麻雀种群中适应度最差的个体第$ j $ 维的值;$ {\rm{xp}}_j^{t + 1} $ 是迭代次数为$ t + {1} $ 时麻雀种群中适应度最优的个体第$ j $ 维的值;$ {{{\rm{rand}}\{ - 1,1\} }} $ 将产生一个等于−1或1的值。当$ i > N/{\text{2}} $ 时,表示适应度值较差的第$i$ 个加入者太远离食物源,需要前往别的区域觅食,以获得能量。侦查预警行为通常会在麻雀种群中选取15%的个体作为侦察预警个体,可以是发现者或加入者,其位置更新公式为:
$$ x_{{i}{,}{j}}^{{t}{ + 1}} = \left\{ {\begin{array}{*{20}{c}} {{\rm{xp}}_{j}^{t} + \beta | {x_{{i}{,}{j}}^{t} - {\rm{xp}}_{j}^{t}} |}&{{f_{i}} > {f_{g}}} \\ {x_{{i}{,}{j}}^{t} + k \left( {\dfrac{{| {x_{{i}{,}{j}}^{t} - {\rm{xw}}_{j}^{t}} |}}{{\left( {{f_{i}} - {f_{w}}} \right) + {{\text{ε}}}}}} \right)}&{{f_{i}} = {f_{g}}} \end{array}} \right. $$ (7) 式中,
$ \beta $ 是一个均值为$ {0} $ 、方差为$ {1} $ 的正态分布随机数,用于控制移动的步长;$ k \in [{{ - 1,1}}] $ 是一个随机数,既表示麻雀的运动方向,也控制麻雀运动的步长;$ {f_{i}} $ 和$ {f_{w}} $ 分别为全局最优个体适应度与最差个体适应度;$ {\varepsilon } $ 为最小常数,避免分母为$ {0} $ 的情况。当$ {f_{i}} > {f_{g}} $ 时,表明个体处于种群的边缘地带,需向种群靠近;当$ {f_{i}} = {f_{g}} $ 时,表明位于种群中间的麻雀意识到了危险,它们将向其他麻雀靠拢,以避免被捕猎。 -
文献[19]指出,在对寻优问题进行求解时,若解空间的分布未知,则个体的初始值应该在个体空间中尽量均匀地分布,这样可保证种群的多样性,而对于粗糙数据推理,分布均匀的数据集能保证论域的完整,增强粗糙数据推理的完备性。
种群初始化的常用手段有易于实现的随机数生成器和具有随机性、遍历性和规律性等特点的Tent混沌序列[17]。但在大规模寻优问题中,随机数生成器的效果很差,Tent序列在小周期点及不稳周期点有相邻点相关太强和容易迭代到不动点等缺陷。
低差异序列又称为拟蒙特卡罗序列,是一种确定性的初始化方法,低差异意味着高均匀度,而高均匀度的种群能提高群体智能算法的探索能力,且帮助算法收敛到一个更好的解。常见的低差异序列有Faure、Halton和Hammersley等,Hammersley点集在高维度,分布更均匀,更适合在算法优化中使用。Hammersley二维序列的分布如图1所示,图中的点分布非常均匀。
Hammersley序列初始化种群的方法如下:设个体取值范围为
$ [{{\boldsymbol{x}}_{\min }},{{\boldsymbol{x}}_{\max }}] $ 。由Hammersley序列产生的第i个准随机数为$ {R_i} \in [0,1] $ ,则初始种群中个体$ {{\boldsymbol{x}}_i} $ 可表示为:$$ {{\boldsymbol{x}}_i} = {{\boldsymbol{x}}_{{\text{min}}}} + {R_i} \cdot ({{\boldsymbol{x}}_{{\text{max}}}} - {{\boldsymbol{x}}_{{\text{min}}}}) $$ (8) -
粗糙集思想来源于近似理论,依托于等价关系与近似空间建立,粗糙数据推理则以粗糙集为基础。粗糙集的一些概念和定义如下。
定义 1 设
$ R $ 是数据集$ U $ 上的等价关系,令$ U/R = \{ {[x]_R}|x \in U\} $ ,即$ U/R $ 是$ U $ 中数据$ x $ 确定的$ R $ 等价类的集合,称$ U/R $ 为$ U $ 相对于$ R $ 的划分,其中$ {[x]_R} $ 为$ x $ 确定的$ R $ 等价类。结论1 设
$ U $ 是任意一数据集,则$ U $ 上等价关系的个数与$ U $ 上划分的个数相同。即$ U $ 上等价关系$ R $ 对应划分$ U/R $ ,反之$ U $ 的划分$S = \{ {S_{1}}, {S_{2}}, \cdots , {S_r} \}$ 对应等价关系$ R $ ,且$ U/R = \left\{ {{S_{1}},{S_{2}}, \cdots ,{S_r}} \right\} $ 。定义1与结论1表明
$ U $ 上的等价关系$ R $ 和$ U $ 的划分$ U/R $ 之间一一对应,而建立划分与等价关系的“桥梁”便是等价类,划分的依据是等价类。解释粗糙推理需要引入上近似的概念,首先定义近似空间。设
$ U $ 是数据集,$ R $ 是$ U $ 上的等价关系,把$ U $ 和$ R $ 构成的结构记为$ M = \left( {U,R} \right) $ ,称为近似空间,其中$ U $ 称为论域[22],由于近似空间中$ R $ 的存在可知,对于论域$ U $ 根据等价关系进行多少种划分,就可得到多少个近似空间。上下近似的定义建立在近似空间上,设
$ M = \left( {U,R} \right) $ 为近似空间,则$ U $ 的任意子集$ X $ 的上近似与下近似定义如下:$$ {R^ * }(X) = \bigcup {\left\{ {{{[a]}_R}\left| {{{[a]}_R} \in U/R\& {{[a]}_R} \cap X \ne 0} \right.} \right\}} $$ (9) $$ {R_ * }(X) = \bigcup {\left\{ {{{[a]}_R}\left| {{{[a]}_R} \in U/R\& {{[a]}_R} \subseteq X} \right.} \right\}} $$ (10) 在近似空间
$ M = \left( {U,R} \right) $ 中,$ U/R $ 是$ U $ 相对于$ R $ 的划分,上近似和下近似都是通过这个划分进行定义。其中子集$ X $ 的上近似是所有和$ X $ 的交集不是空集划分的并,子集$ X $ 的下近似是等于所有包含在$ X $ 中的划分的并。下近似从
$ X $ 内部逼近$ X $ ,上近似是从$ X $ 外部逼近,如果$ X $ 视为精确信息,则上近似包含更多信息。当上下近似空间不相等时称$ X $ 为粗糙集。 -
粗糙推理空间是对近似空间
$ M = \left( {U,R} \right) $ 的扩展。定义粗糙推理空间时,设$ U $ 是数据集,称为论域,其元素称为数据;令$ K = \left\{ {{R_{1}},{R_{2}}, \cdots ,{R_n}} \right\},\;n \geqslant 1 $ ,其中$ {R_{1}},{R_{2}}, \cdots ,{R_n} $ 是$ U $ 上$ n $ 个不同的等价关系;给定$ U $ 上的二元关系$ S \subseteq U \times U $ ,称$ S $ 为推理关系。将$ U $ 、$ K $ 和$ S $ 构成的结构记作$ W = \left( {U,K,S} \right) $ ,称为粗糙推理空间。引入粗糙推理空间是为了完善粗糙数据推理,使运作于该空间上的粗糙数据推理理论更加具体、清晰。粗糙推理空间中的$ S $ 是确定的推理关系,麻雀搜索算法中加入者向最优位置个体靠近的操作便是加入者与最优位置个体间建立了确定的推理关系。 -
数据是对象的符号表示,可以是一个数值、一个物体、或者算法的个体信息。如果把推理建立在算法优化中,由确定的位置更新公式,经过推理与演绎得出其他可行的位置更新策略,可以增加种群移动的选择,帮助算法跳出局部最优解,且增大个体收敛到理论最优位置的可能。
实际生活当中存在不明确或潜存于数据之间的粗糙数据联系,挖掘数据潜在联系,给定一些联系规则,使得这些粗糙数据联系有依据地表示,且通过一定的规则程序化粗糙数据联系,即粗糙数据推理[22]。定义粗糙数据推理时,设
$ W = \left( {U,K,S} \right) $ 为粗糙推理空间,对于$ < a,b > \in S $ 以及$ R \in K $ ,存在以下3个定义与2个引理。定义 2 设
$ b \in U $ ,如果$ b \in {R^*}([a - R]) $ ,则$ a $ 关于$ R $ 直接粗糙推出$ b $ ,记作$ a \Rightarrow {}_Rb $ 。其中$ [a - R] $ 称为后继集,其定义为:$ [a-R]=\left\{x\right|x\in U $ 且存在$z\in {[a]}_{R} $ ,使得$ < z,x > \in S\} $ 。定义 3
${b_{1}},{b_{2}}, \cdots ,{b_n} \in U$ ,如果$ a \Rightarrow {}_R{b_{1}} $ ,$ {b_{1}} \Rightarrow {}_R{b_{2}} $ ,$ {b_{2}} \Rightarrow {}_R{b_{3}} $ ,···,$ {b_{n - 1}} \Rightarrow {}_R{b_n}(n \geqslant 0) $ ,则称$ a $ 关于$ R $ 粗糙推出$ b $ ,记作$ a|{ = _R}b $ ,容易看出$ a \Rightarrow {}_Rb $ 是$ a|{ = _R}b $ 的特殊形式。定义 4 对于
$ R \in K $ ,$ a $ 关于$ R $ 直接粗糙推出或粗糙推出$ b $ 的推理称为$ W = \left( {U,K,S} \right) $ 中的关于$ R $ 的粗糙数据推理,简称为粗糙数据推理。引理1[22] 设
$ W = \left( {U,K,S} \right) $ 为粗糙推理空间,$ a,b \in U $ 且$ R \in K $ ,则$ a \Rightarrow {}_Rb $ 当且仅当$ {[b]_R} \cap [a - R] \ne \phi $ 当且仅当$ {[a]_R} \cap [a - R] \ne \phi $ 。引理2[22] 设R是U上的等价关系,如果
$ a,b \in U $ ,那么$ a \in {[b]_R} $ 当且仅当$ {[a]_R} = {[b]_R} $ 当且仅当$ b \in {[a]_R} $ 。以上3个定义确定了基于划分的粗糙数据推理,同理可定义出多种划分下的粗糙数据推理,例如
$ a|{ = _R}_{_{\text{1}}}b $ 与$ a|{ = _R}_{_{\text{2}}}b $ 。在考虑多种划分下的数据推理时可引入嵌入算法[22],该算法作用为:假设$ a|{ = _R}_{_{\text{1}}}b $ 与$ a|{ = _R}_{_{\text{2}}}b $ 都成立,若存在等价关系$ R = {R_{1}} \cap {R_{2}} $ ,嵌入算法可以判断$ a|{ = _R}b $ 是否成立。 -
传统麻雀搜索算法收敛速度较快,但从式(6)、式(7)中容易看出,加入者更新公式与预警机制中都有向全体最优靠拢的操作,这些操作导致算法容易陷入局部最优,且在算法迭代后期种群多样性将严重减少。为了改进以上缺点,本文设计了一种融合粗糙数据推理的多策略改进麻雀搜索算法,通过引入不确定、似存在的模糊关系,增大算法的搜索空间,提高算法跳出局部最优的能力。
粗糙数据推理理论基于上近似理论提出,上近似集包含的潜在联系能极大提高算法的搜索空间,进而提高算法跳出局部最优解的能力,在此证明上近似集具有包含潜在联系等模糊信息的能力。
证明1:在粗糙推理空间下,对任意的
$ x \in X $ ,由等价类的性质可知$ x \in {[x]_R} $ ,所以$ {[x]_R} \cap X \ne \phi $ 。由上近似$ {R^ * }(X) $ 的定义可知$ {[x]_R} \subseteq {R^ * }(X) $ ,于是$ x \in {R^ * }(X) $ ,因此$ X \subseteq {R^ * }(X) $ 。由证明1可知,集合的上近似集由外部逼近该集合,包含更多信息,在麻雀搜索算法中,由于发现者、加入者等个体集合的操作中包含大量靠近局部最优的操作,降低了种群多样性,使用基于上近似的粗糙数据推理理论,便可以包含更多模糊信息,扩大搜索空间,是粗糙数据推理理论能帮助算法跳出局部最优解的有力证明。
对于算法与粗糙数据推理理论结合的合理性,做出如下证明,首先证明粗糙数据推理理论能保留算法确定的收敛操作信息。
证明2:在粗糙推理空间下,对于任意由划分确立的等价关系
$ R \in K $ ,以及算法中的个体$ a,b \in U $ ,由等价类的定义可知,$ a \in {[a]_R} $ 。若存在明确的收敛信息$ < a,b > \in S $ ,由后继集的定义可知$ b \in [a - R] $ 。又因为$ [a - R] \subseteq {R^ * }([a - R]) $ (证明1),所以$ b \in {R^ * }([a - R]) $ ,因此可得$ a \Rightarrow {}_Rb $ 或$ a|{ = _R}b $ (定义2)。通过证明2可得到如下结论。
结论2 对于算法个体
$ a,b \in U $ ,若存在确定的收敛信息$ < a,b > \in S $ ,则对任意基于划分的等价关系$ R \in K $ ,有$ a \Rightarrow {}_Rb $ 或$ a|{ = _R}b $ 。该结论阐明了粗糙数据推理能保证算法确定的收敛信息不丢失,是粗糙数据推理理论可与算法相结合的先决条件。
其次证明粗糙数据推理理论能引入模糊信息,扩大算法的搜索空间。
证明3:在粗糙推理空间下,对于任意由划分确立的等价关系
$ R \in K $ ,以及算法中的个体$ a,b,u,v \in U $ ,若存在确定的$ < a,b > \in S $ ,则$ a \Rightarrow {}_Rb $ (证明2),故$ {[b]_R} \cap [a - R] \ne \phi $ (引理1)。当$ u \in {[b]_R} $ 时,由于${[u]_R} \in {[b]_R}$ (引理2),所以$ {[u]_R} \cap [a - R] \ne \phi $ ,可得$ a \Rightarrow {}_Ru $ (引理1)。同样,当$ v \in {[a]_R} $ 时易知$ v \Rightarrow {}_Rb $ 。通过证明3可得到如下结论。
结论3 设
$ W = \left( {U,K,S} \right) $ 为粗糙推理空间,如果$ R \in K $ 且$ a,b,u,v \in U $ ,则有:1)若
$ a \Rightarrow {}_Rb $ ,则当$ u \in {[b]_R} $ 时,有$ a \Rightarrow {}_Ru $ ;2)若
$ a \Rightarrow {}_Rb $ ,则当$ v \in {[a]_R} $ 时,有$ v \Rightarrow {}_Rb $ 。该结论表明,粗糙数据推理挖掘出了模糊信息,通过已有确定的收敛信息,合理的将具有粗糙联系的
$ u,v $ 引入,扩大了算法的搜索空间,帮助算法跳出局部最优解,是粗糙数据推理理论与算法结合可行的有力证明。证明2与证明3 证明了粗糙数据推理理论能与麻雀搜索算法有机结合,且能完成引入该理论的预期目标,同时也一定程度上解决了群体智能算法在优化时,改进方案多从实验与经验出发,可解释性差的问题。
定义1与结论1阐述了等价关系与划分的对应关系,所以粗糙数据推理基于等价关系建立也可称为依据划分建立。
根据麻雀搜索算法原理做以下划分:1)依照适应度划分,其对应等价关系关系记为
$ {R_{\text{1}}} $ ;2)依照高纬欧氏距离划分,其对应关系记为$ {R_{\text{2}}} $ 。高纬欧氏距离公式为:$$ {y_D}({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) = \sqrt {{{({x_{j{,1}}} - {x_{i{,1}}})}^{2}} + {{({x_{j{,2}}} - {x_{i{,2}}})}^{2}} + \cdots + {{({x_{j,d}} - {x_{i,d}})}^{2}}} $$ (11) 在麻雀搜索算法运行过程中,假设发生了加入者
$ {{\boldsymbol{x}}_i} $ 向最优个体$ {\rm{xp}} $ 靠拢的操作,即认为出现了确定推理$ < {{\boldsymbol{x}}_i},{\rm{xp}} > $ ,此为确定的$ S $ 路径,由于麻雀搜索算法的发现者−加入者模型可以认为符合适应度划分,所以该确定推理可以表示为确定路径$ {{\boldsymbol{x}}_i} \Rightarrow {}_{{R_1}}{\rm{xp}} $ ,假设种群共有$ n $ 个个体,加入者为$ m $ 个,发现者为$ n - m $ 个,则有$ {[{{\boldsymbol{x}}_i}]_{{R_{\text{1}}}}} = \{ {x_1}, \cdots ,{x_i}, \cdots ,{x_m}\} $ 和$ {[{\rm{xp}}]_{{R_{\text{1}}}}} = \{ {x_{m + 1}}, \cdots ,{x_P}, \cdots ,{x_n}\} $ ,根据等价类与划分的关系、结论2和结论3可得图2a所示的粗糙推理关系。进一步依照高纬欧氏距离进行划分,分别选取与$ {\rm{xp}} $ 、$ {{\boldsymbol{x}}_i} $ 欧式距离最近的占总体数量20%的个体,且保证所选个体互不相同,依照个体将论域划分,根据等价类与划分的关系、结论2和结论3可得图2b所示推理关系。接下来建立另一种推理关系,它由以下函数推出:
$$ y({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) = \left| {f{{({{\boldsymbol{x}}_i})}^{2}} - f{{({{\boldsymbol{x}}_j})}^{2}}} \right| {y_D}({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) $$ (12) 式中,
$ f{({{\boldsymbol{x}}_i})^{2}} - f{({{\boldsymbol{x}}_j})^{2}} $ 表示$ {{\boldsymbol{x}}_i} $ 、$ {{\boldsymbol{x}}_j} $ 个体适应度的平方差$ {y_D}({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) $ 为$ {{\boldsymbol{x}}_i} $ 、$ {{\boldsymbol{x}}_j} $ 两点间的欧式距离。该函数考虑到个体间的适应度与欧氏距离,使用式(12)对$ {{\boldsymbol{x}}_i} $ 与$ {\rm{xp}} $ 分别求出占总体数量10%的互不相同的个体,依据个体将论域划分,假设该划分对应的等价关系为$ R $ ,且已知$ R = {R_{\text{1}}} \cap {R_{\text{2}}} $ ,同样可得图2c所示的推理关系,由嵌入算法可得该推理关系成立,从而可融合粗糙数据推理理论对麻雀搜索算法进行如下改进:在$ < {{\boldsymbol{x}}_i},{\rm{xp}} > $ 成立时,记录$ {{\boldsymbol{x}}_i} $ 向$ {\rm{xp}} $ 靠近后的适应度,同时通过迭代次数与一组随机数的控制执行以下3种策略。1) 当
$ {{\boldsymbol{x}}_i} $ 向$ {\rm{xp}} $ 靠拢时,在$ {\rm{xp}} $ 的$ {R_{2}} $ 等价类中随机选择一个个体$ {{\boldsymbol{x}}_j} $ 靠拢。2) 当
$ {{\boldsymbol{x}}_i} $ 向$ {\rm{xp}} $ 靠拢时,同时在$ {\rm{xp}} $ 的$ {R_{1}} $ 等价类中随机选择一个个体$ {{\boldsymbol{x}}_{m + {1}}} $ 靠拢,依据适应度贪心选择$ {{\boldsymbol{x}}_i} $ 的靠拢对象。3) 当
$ {{\boldsymbol{x}}_i} $ 向$ {\rm{xp}} $ 靠拢时,同时在$ {\rm{xp}} $ 的$ R $ 等价类中随机选择一个个体$ {{\boldsymbol{x}}_k} $ 靠拢,依据适应度贪心选择$ {{\boldsymbol{x}}_i} $ 的靠拢对象。3种策略的推理关系如图3所示。
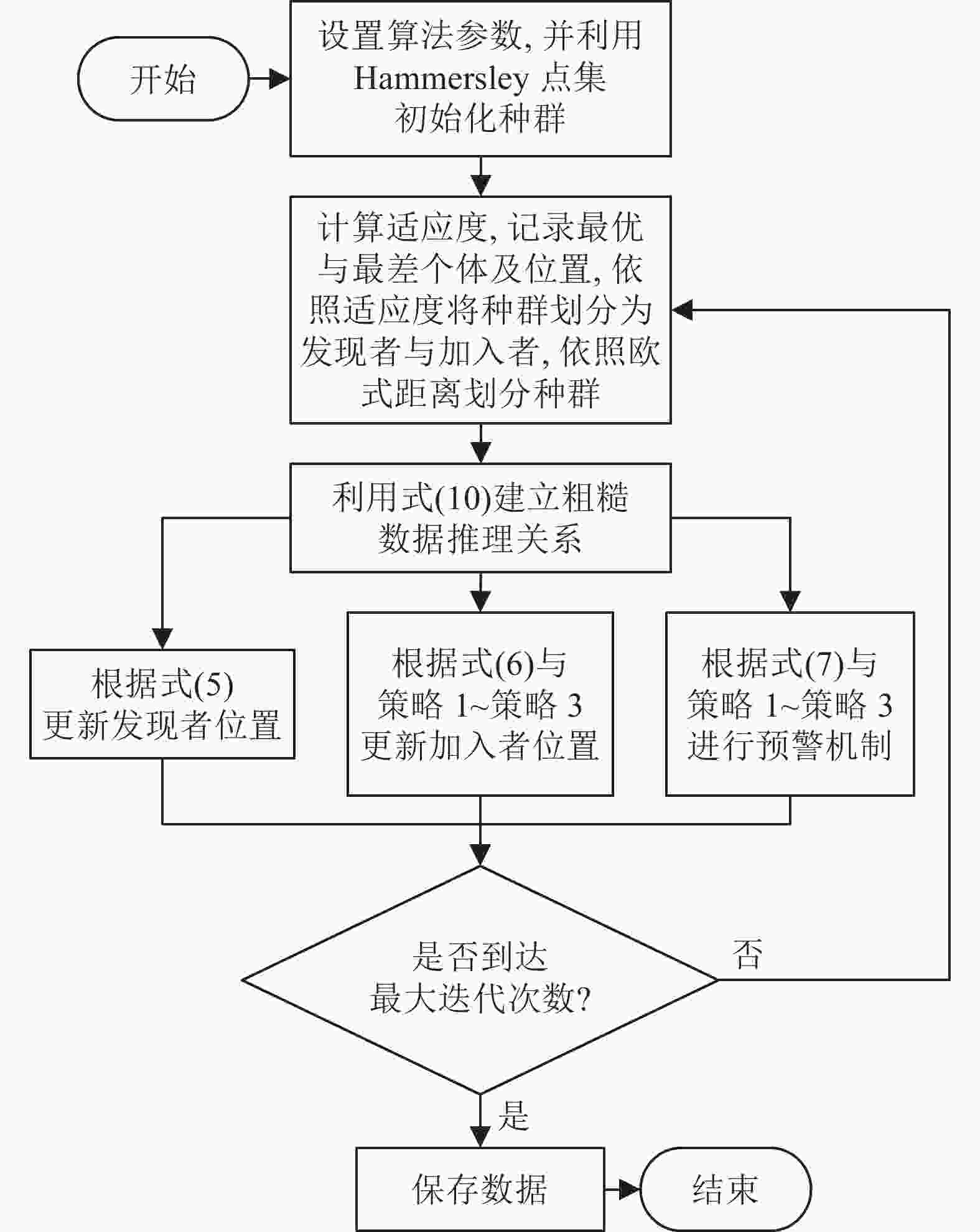
RSSA的算法流程图如图4。
-
采用正交实验分析3种策略执行概率对RSSA寻优能力的影响,测试函数如表1所示。依据当前迭代次数与最大迭代次数的比值将算法划分为前、中、后期,对应关系为前期[0, 0.15]、中期(0.15, 0.8]、后期(0.8, 1]。算法的种群个数为100,迭代次数为500,独立运行10次,求出收敛至最优值时迭代次数的平均值,若未收敛至最优则最小迭代次数取500。表2为函数F1的正交实验统计结果。
由表2可知,组合1的最优迭代次数平均值最小,所以函数F1采用组合1的执行概率,对其他函数采用同样的组合进行正交实验,得到最佳的执行概率组合结果,如表3所示。
由表3可知,函数对执行概率有敏感度,但结合表2与表3可以看出组合1对比其他组合有一定的优势,对于最优解未知函数而言,从算法普遍适用性的角度出发可以先采用组合1的执行概率,为了追求收敛速度与精度,则应对不同函数采用不同的策略执行概率组合。
表 1 待测试函数
函数类型 测试函数 范围 维度 最优值 单峰值 ${F_{\text{1} } }(x) = \displaystyle\sum\limits_{ { {i = 1} } }^{ {n} } {x_{{i} }^{\text{2} } }$ [−100,100] 30 0 ${F_{\text{2} } }(x) = \displaystyle\sum\limits_{ { {i = 1} } }^{ {n} } {\left| { {x_{{i} } } } \right|} + \displaystyle\prod\nolimits_{ { { {{i} } = 1} } }^{ {n} } {\left| { {x_{{i} } } } \right|}$ [−10,10] 30 0 ${F_{\text{3} } }(x) = {\displaystyle\sum\limits_{ { {i = 1} } }^{ {n} } {(\displaystyle\sum\limits_{ { {j = 1} } }^{ {i} } { {x_{ {j} } } } )^{\text{2} }} }$ [−100,100] 30 0 单峰值 ${F_{\text{4} } }(x) = {\max _{{i} } }\{ \left| { {x_{{i} } } } \right|,{ { - 1} } \leqslant i \leqslant n\}$ [−100,100] 30 0 ${F_{\text{5} } }(x) = \displaystyle\sum\limits_{ {{i = 1} } }^{{n} } {[100{ {({x_{ {{i + 1} } } } - x_{{i} }^{\text{2} })}^{\text{2} } } + { {({x_{{i} } } - {\text{1} })}^{\text{2} } }]}$ [−30,30] 30 0 ${F_{\text{6} } }(x) = \displaystyle\sum\limits_{ {{i = 1} } }^{{n} } { { {([{x_{{i} } } + {\text{0} }{\text{.5} }])}^{\text{2} } } }$ [−100,100] 10 0 多峰值 ${F_{\text{7} } }(x) = \displaystyle\sum\limits_{ {{i = 1} } }^{{n} } { - {x_{{i} } }\sin (\sqrt {\left| { {x_{{i} } } } \right|} )}$ [−500,500] 30 −418.9×d ${F_{\text{8} } }(x) = \displaystyle\sum\limits_{ {{i = 1} } }^{{n} } {[x_{{i} }^{\text{2} } - {\text{10} }\cos ({\text{2π} }x) + {\text{10} }]}$ [−5.12,5.12] 30 0 ${F_{\text{9} } }(x) = - {\text{20} }\exp ( - {\text{0} }{\text{.2} }\sqrt {\dfrac{ {\text{1} } }{ {{n} } }\displaystyle\sum\limits_{ {{i = 1} } }^{{n} } {x_{{i} }^{\text{2} } } } ) - \exp (\dfrac{ {\text{1} } }{ {{n} } }\displaystyle\sum\limits_{ {{i = 1} } }^{{n} } {\cos ({\text{2π} }{x_i})} ) + {{e} } + {\text{20} }$ [−32,32] 30 0 ${F_{ {\text{10} } } }(x) = \dfrac{ {\text{1} } }{ { {\text{4000} } } }\displaystyle\sum\limits_{ { {i = 1} } }^{ {n} } {x_{{i} }^{\text{2} } } - \displaystyle\prod\limits_{ { {i = 1} } }^{ {n} } {\cos (\dfrac{ { {x_{ {i} } } } }{ {\sqrt i } })} + {\text{1} }$ [−600,600] 30 0 固定维
多峰值$ {F_{{\text{11}}}}(x) = {\text{4}}x_{\text{1}}^{\text{2}} - {\text{2}}{\text{.1}}x_{\text{1}}^{\text{4}} + \dfrac{{\text{1}}}{{\text{3}}}x_{\text{1}}^{\text{6}} + {x_{\text{1}}}{x_{\text{2}}} - {\text{4}}x_{\text{2}}^{\text{2}} + {\text{4}}x_{\text{2}}^{\text{4}} $ [−5,5] 2 −1.0316 表 2 F1正交实验结果
组合 前期执行概率 中期执行概率 后期执行概率 平均值 策略1 策略2 策略3 策略1 策略2 策略3 策略1 策略2 策略3 1 0.3 0.4 0.3 0.2 0.7 0.1 0.1 0.2 0.7 167.4 2 0.3 0.4 0.3 0.2 0.7 0.1 0.2 0.2 0.6 214.8 3 0.3 0.4 0.3 0.3 0.6 0.1 0.1 0.2 0.7 206.9 4 0.3 0.4 0.3 0.3 0.6 0.1 0.2 0.2 0.6 275.4 5 0.4 0.3 0.3 0.2 0.7 0.1 0.1 0.2 0.7 212.4 6 0.4 0.3 0.3 0.2 0.7 0.1 0.2 0.2 0.6 251.3 7 0.4 0.3 0.3 0.3 0.6 0.1 0.1 0.2 0.7 283.3 8 0.4 0.3 0.3 0.3 0.6 0.1 0.2 0.2 0.6 234.9 表 3 剩余函数正交实验结果
函数名 组合 最小迭代次数均值 F2 2 370.9 F3 1 203.8 F4 1 313.6 F5 6 490.2 F6 3 498.8 F7 2 469.5 F8 1 15.7 F9 6 26.7 F10 5 196.4 F11 1 11.3 -
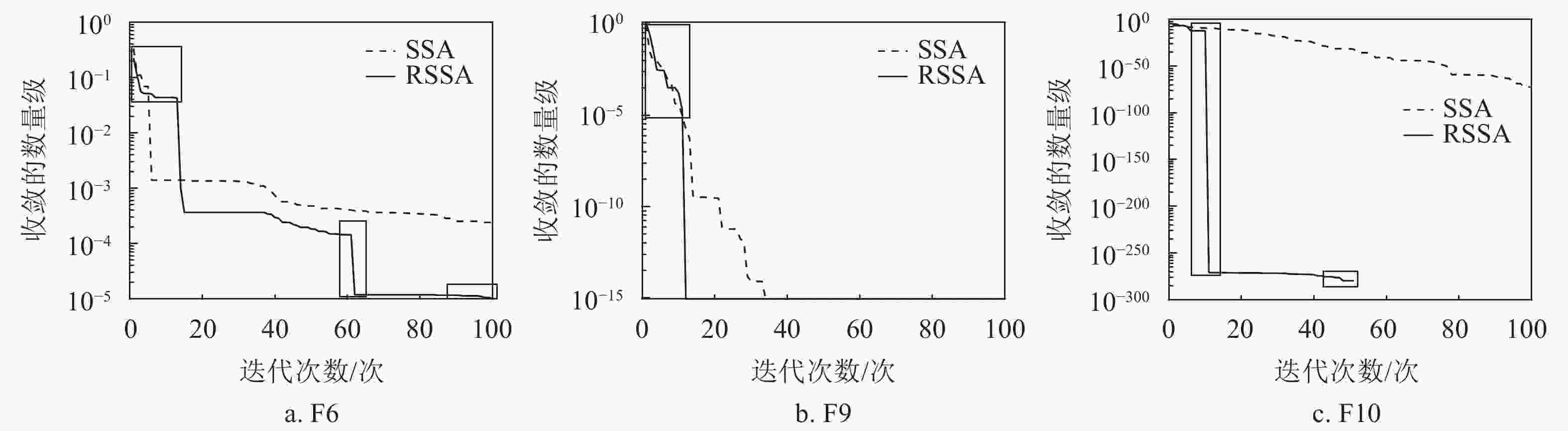
策略1使用依托高维欧氏距离的划分,增大了算法的搜索范围,使算法具有了跳出局部最优的能力;策略2使用依托适应度的划分,提高了算法的收敛速度;策略3使用式(12)推导出的划分,从高维欧氏距离与适应度两个方面同时逼近最优值,提高算法的收敛精度。为了证明以上推论,使用SSA与RSSA进行多次对比实验,选择对算法收敛能力与跳出局部最优能力要求较高的函数,如表1中的F6、F9和F10,绘制其中一次实验的收敛曲线如图5所示。对比实验的种群个数为50,迭代次数为100。
从图5a、图5b的左小框部分可以看出,在算法运行的初期由于策略1的影响,算法的收敛速度与SSA相比并不快,且有一定波动,说明算法牺牲了收敛速度扩大了搜索范围增大;从图5c的左长方形框部分可以看出,在算法运行的中期由于主要执行策略2,算法的收敛速度大幅度提升;从图5a、图5c的中间小框部分可以看出,由于3种策略的共同影响,算法具有了跳出局部最优的能力,且在跳出局部最优后能够继续向最优解收敛,或收敛至最优解;从图5a的右小框部分可以看出,在算法运行的后期策略1与策略3的共同影响下,算法的收敛速度放缓,但是精度提高,收敛曲线表明算法在迭代中后期已经陷入局部最优,但由于策略1的影响,算法最终跳出局部最优并开始向全局最优收敛。对比实验证明粗糙数据推理理论的引入达到了预期的效果。
-
时间复杂度是评价算法执行效率的重要指标。假设求解问题规模是D维,麻雀种群规模为正整数N,求解目标函数所需的时间为f(D)。文献[23]指出传统麻雀搜索算法的时间复杂度为:
$$ T = O(f(D) + D) $$ (13) 麻雀搜索算法位置更新公式的时间复杂度为:
$$ T = O(D) $$ (14) 在RSSA中,产生一个D维Hammersley序列的时间复杂度为
$ T = O(D) $ ,但基于Hammersley序列的初始化方法是一种确定性的初始化方法,在确定算法个体数N后仅需执行一次,便可作为本地信息直接调取。假设调取本地Hammersley序列所需执行时间为t1,按式(8)生成单个个体所需时间为t2,则RSSA的初始化种群时间复杂度为:$$ {T_1} = O(N({t_1} + {t_2})) = O(1) $$ (15) 策略1需要依据高维欧氏距离进行划分,假设计算一次D维欧式距离耗时为t3D,共需计算N−1次,总耗时(N−1)t3D;且需要随机选择一个个体向其靠拢,随机选择个体耗时t4,靠拢操作与具体的位置更新公式耗时相同,复杂度为O(D),所以策略1的时间复杂度为:
$$ {T_2} = O((N - 1){t_3}D + {t_4}) + O(D) = O(D) $$ (16) 策略2需要依据适应度进行划分,计算一次D维函数耗时为f(D),共需计算N−1次,总耗时(N−1)f(D);同样需要随机选择一个个体执行靠拢操作,随机选择个体耗时t5,靠拢操作复杂度为O(D),且需要进行贪心选择,即计算两次D维函数,并进行对比,该操作耗时2f(D)+t6。所以策略2的时间复杂度为:
$$ \begin{split} & {T_3} = O((N - 1)f(D) + {t_5} + 2f(D) + {t_6}) + O(D)= \\ &\qquad\qquad \qquad\quad O(f(D) + D) \end{split} $$ (17) 在计算策略3前,依照式(12)计算,需要求解两次D维函数,耗时为2f(D),且计算一次D维欧氏距离,耗时为t7D,式(12)的时间复杂度为:
$$ {T_4} = O(2f(D) + D) = O(f(D) + D) $$ (18) 策略3在划分后,还需要随机选择个体进行靠拢操作与贪心选择,所以策略3的时间复杂度为:
$$ \begin{split} & {T_5} = {T_4} + O(D) + O({t_5} + 2f(D) + {t_6}) =\\ & O(f(D) + D) + O(f(D))= O(f(D) + D) \end{split} $$ (19) 故最大迭代次数为itermax时,RSSA的时间复杂度为:
$$ {T_R} = T + {\rm{ite}}{{\rm{r}}_{{\rm{max}}}}({T_1} + {T_2} + {T_3} + {T_5}) = O(f(D) + D) $$ (20) 综上可知,RSSA与SSA时间复杂度相同,即基于低差异序列的初始化与粗糙数据推理理论的引入并不会提高算法的时间复杂度。
-
利用3种不同类型共计11个测试函数进行对比仿真实验,来验证RSSA对于麻雀搜索算法改进的科学性以及相较于灰狼优化(grey wolf optimization, GWO)算法、鹈鹕优化算法(Pelican optimization algorithm, POA)[24]、被囊群算法(tunicate swarm algorithm, TSA)[25]、麻雀搜索算法(sparrow search algorithm, SSA)等智能算法的优越性。各测试函数如表1所示,6个可变维度的单峰函数F1~F6,4个可变维度的多峰函数F7~F10,1个固定维多峰函数F11。为了保证实验的公平性,所有算法的种群个数均为100,迭代次数为500,实验在同一环境下独立运行50次。将各个算法最优值的平均值与标准差作为评价指标,如表4所示。
表 4 实验结果对比表
函数 指标 GWO POA TSA SSA RSSA F1 平均值 9.2157×10−41 9.9805×10−102 4.2666×10−205 0×100 0×100 标准差 1.2198×10−40 6.9374×10−101 0×100 0×100 0×100 F2 平均值 4.0882×10−24 2.4642×10−52 1.8823×10−106 2.9702×10−90 1.6559×10−175 标准差 3.0422×10−24 1.4866×10−51 1.0496×10−105 1.6238×10−89 5.7586×10−174 F3 平均值 1.4339×10−11 1.6184×10−101 3.1309×10−191 1.6822×10−112 0×100 标准差 3.3720×10−11 1.0244×10−100 0×100 9.2138×10−112 0×100 F4 平均值 1.8738×10−10 1.4842×10−51 5.7000×10−96 7.0150×10−100 0×100 标准差 2.2864×10−10 5.4263×10−51 2.1262×10−95 3.8423×10−99 0×100 F5 平均值 2.6549×101 2.7834×101 2.8597×101 4.7076×10−5 4.6906×10−9 标准差 7.4458×10−1 8.7888×10−1 4.2103×10−1 1.2807×10−4 5.7558×10−9 F6 平均值 1.7449×10−1 2.4745×100 5.9513×100 5.9078×10−7 0×100 标准差 1.7603×10−1 5.8354×10−1 7.8780×10−1 9.9105×10−7 0×100 F7 平均值 −6.3093×103 −7.8797×103 −3.6983×103 −8.5347×103 −1.1244×104 标准差 7.6183×102 8.0194×102 4.4204×102 5.5335×102 9.1573×102 F8 平均值 1.6278×100 0×100 1.3051×101 0×100 0×100 标准差 2.9439×100 0×100 4.0340×101 0×100 0×100 F9 平均值 2.6941×10−14 3.8725×10−15 4.4409×10−15 8.8818×10−16 8.8818×10−16 标准差 3.8843×10−15 1.3157×10−15 0×100 0×100 0×100 F10 平均值 3.8038×10−43 6.0396×10−101 1.6041×10−207 2.9457×10−169 0×100 标准差 4.1934×10−43 4.2462×10−100 0×100 0×100 0×100 F11 平均值 −1.0316×100 −1.0316×100 −1.0304×100 −1.0316×100 −1.0316×100 标准差 0×100 3.4603×10−16 6.2593×10−3 0×100 0×100 -
通过表4可以得出,在F1~F6的高维单峰值函数测试中,RSSA均优于其他算法多个数量级,除F2与F5外,RSSA算法平均最优值都能收敛到理论最优解0;标准差是反映数据离散程度的数值,从标准差上可以看出收敛到0的情况非常稳定,即每次实验都可以得到理论最优解。在F7~F10的高维多峰值函数测试中RSSA也强于其他算法,跳出局部最优解的能力有所提升,在大多数情况下收敛到最优解0;对于最优解不在0处的高维多峰值函数F7,RSSA算法也最接近最优解−12 569.487,标准差也属于可接受的范围,相较于其他群体智能算法收敛精度更高也更稳定。
为了证明同时引入低差异序列与粗糙数据推理的必要性,选取对算法收敛速度与跳出局部最优能力要求较高的多峰值函数F7~F10,分别对SSA、引入低差异序列的SSA、引入粗糙数据推理的SSA和RSSA进行对比实验。实验的种群个数与迭代次数分别为100和500,独立运行30次记录找到的最优解结果如表5所示。
表 5 多峰值函数不同策略对比表
函数名 30次实验的最优解 SSA 低差异序列SSA 粗糙推理SSA RSSA F7 −9016.3366 −9936.5046 −10220.3075 −12569.4866 F8 0×100 0×100 0×100 0×100 F9 8.88×10−16 8.88×10−16 8.88×10−16 8.88×10−16 F10 1.35×10−209 5.44×10−245 1.02×10−255 0×100 通过表5可得,对于简单的多峰值函数F8,4种算法都能收敛到最优解,说明每种改进单独存在都是可行的,而对于复杂的多峰值函数,在单独引入低差异序列或粗糙数据推理后,算法的性能都有所提高,但是依然无法收敛到全局最优,在同时引入低差异序列与粗糙数据推理后,RSSA全局寻优能力增强,求解出了理论最优值。这说明同时引入低差异序列与粗糙数据推理是必要的,进一步证明了粗糙数据推理的引入并非简单地增加策略和迭代中的种群多样性,而是利用适应度、高纬欧氏距离与式(12)中内涵的3种等价关系进行策略的推理,通过表2、表3执行概率控制。在算法执行过程中,将推理出的3种策略有机的结合,自适应地选择,最终保证算法能够兼顾收敛速度与搜索范围,增大收敛到全局最优的可能。
综上所述,在融合粗糙数据推理以及使用低差异序列进行初始化后,算法具备了跳出局部最优的能力,全局搜索能力也有提升。
为比较5种算法的收敛性能,本文对5种算法进行仿真对比,结果如图6所示。
收敛曲线图反映了算法每次迭代所获得的最优解,当收敛曲线在某次迭代中消失时即代表已经收敛为0。观察图6可得出结论:RSSA算法的收敛速度与精度都高于其他算法,能够随迭代次数的增加不断地寻优,多数情况下都可以收敛到理论最优值,全局寻优能力有所提高,相较于其他算法有优势。
-
为了提高基本麻雀搜索算法解决高维多峰值问题的能力及群体智能算法改进策略的可解释性,本文将粗糙数据推理与麻雀搜索算法合理融合,提出了一种融合粗糙数据推理的多策略改进麻雀搜索算法(RSSA),并使用3种类型共计11个测试函数对RSSA进行性能测试,与灰狼算法(GWO)、鹈鹕优化算法(POA)、被囊群算法(TSA)等群体智能算法以及传统麻雀搜搜算法(SSA)算法进行对比,得出以下结论:
1) RSSA的优化效果明显,算法性能提升较大,且可有效地跳出局部最优解。2) 11个基准函数的对比实验结果与收敛曲线表明:RSSA算法在收敛速度、收敛精度与跳出局部最优的能力上优于其他算法。后续将把RSSA算法应用在求解具体的工程问题中。
Multi Strategy Improved Sparrow Search Algorithm Based on Rough Data Reasoning
-
摘要: 针对麻雀搜索算法在迭代过程中种群多样性减少、容易陷入局部最优的问题,提出了一种融合粗糙数据推理的多策略改进麻雀搜索算法(RSSA)。该算法先结合低差异序列的思想进行种群初始化,增强算法的全局搜索能力,保障粗糙数据推理论域的完整性;然后引入粗糙数据推理理论,结合适应度与距离建立个体间的联系,提高收敛速度,增强跳出局部最优的能力,改良麻雀搜索算法在多峰值问题中的不足;并且对于迭代中的超界个体,在超界的同时将其赋值为边界附近的值而非边界最大或最小值,保证种群的多样性且提高算法收敛速度。仿真实验结果表明,RSSA与其他4种算法相比,收敛速度更快,精度更高,在面对多峰值问题时效果更好。Abstract: Aiming at the problem that the diversity of sparrow search algorithm is reduced and it is easy to fall into local optimum in the iterative process, a multi strategy improved sparrow search algorithm (RSSA) based on rough data-deduction is proposed. Firstly, the algorithm initializes the population with the idea of low difference sequence to enhance the global search ability of the algorithm and ensure the integrity of rough data reasoning domain. Then, the rough reasoning data theory is introduced, and the relationship between individuals is established by combining fitness and distance, so as to improve the convergence speed and the ability to jump out of the local optimum. Moreover, the over bounded individuals in the iteration are assigned to the value near the boundary instead of the maximum or minimum value of the boundary at the same time, which ensures the diversity of the population and improves the convergence speed of the algorithm. Compared with the other three algorithms and traditional sparrow search algorithm, the simulation results based on 11 test functions show that RSSA has faster convergence speed, higher accuracy and better effect in the face of multi peak problems.
-
表 1 待测试函数
函数类型 测试函数 范围 维度 最优值 单峰值 ${F_{\text{1} } }(x) = \displaystyle\sum\limits_{ { {i = 1} } }^{ {n} } {x_{{i} }^{\text{2} } }$ [−100,100] 30 0 ${F_{\text{2} } }(x) = \displaystyle\sum\limits_{ { {i = 1} } }^{ {n} } {\left| { {x_{{i} } } } \right|} + \displaystyle\prod\nolimits_{ { { {{i} } = 1} } }^{ {n} } {\left| { {x_{{i} } } } \right|}$ [−10,10] 30 0 ${F_{\text{3} } }(x) = {\displaystyle\sum\limits_{ { {i = 1} } }^{ {n} } {(\displaystyle\sum\limits_{ { {j = 1} } }^{ {i} } { {x_{ {j} } } } )^{\text{2} }} }$ [−100,100] 30 0 单峰值 ${F_{\text{4} } }(x) = {\max _{{i} } }\{ \left| { {x_{{i} } } } \right|,{ { - 1} } \leqslant i \leqslant n\}$ [−100,100] 30 0 ${F_{\text{5} } }(x) = \displaystyle\sum\limits_{ {{i = 1} } }^{{n} } {[100{ {({x_{ {{i + 1} } } } - x_{{i} }^{\text{2} })}^{\text{2} } } + { {({x_{{i} } } - {\text{1} })}^{\text{2} } }]}$ [−30,30] 30 0 ${F_{\text{6} } }(x) = \displaystyle\sum\limits_{ {{i = 1} } }^{{n} } { { {([{x_{{i} } } + {\text{0} }{\text{.5} }])}^{\text{2} } } }$ [−100,100] 10 0 多峰值 ${F_{\text{7} } }(x) = \displaystyle\sum\limits_{ {{i = 1} } }^{{n} } { - {x_{{i} } }\sin (\sqrt {\left| { {x_{{i} } } } \right|} )}$ [−500,500] 30 −418.9×d ${F_{\text{8} } }(x) = \displaystyle\sum\limits_{ {{i = 1} } }^{{n} } {[x_{{i} }^{\text{2} } - {\text{10} }\cos ({\text{2π} }x) + {\text{10} }]}$ [−5.12,5.12] 30 0 ${F_{\text{9} } }(x) = - {\text{20} }\exp ( - {\text{0} }{\text{.2} }\sqrt {\dfrac{ {\text{1} } }{ {{n} } }\displaystyle\sum\limits_{ {{i = 1} } }^{{n} } {x_{{i} }^{\text{2} } } } ) - \exp (\dfrac{ {\text{1} } }{ {{n} } }\displaystyle\sum\limits_{ {{i = 1} } }^{{n} } {\cos ({\text{2π} }{x_i})} ) + {{e} } + {\text{20} }$ [−32,32] 30 0 ${F_{ {\text{10} } } }(x) = \dfrac{ {\text{1} } }{ { {\text{4000} } } }\displaystyle\sum\limits_{ { {i = 1} } }^{ {n} } {x_{{i} }^{\text{2} } } - \displaystyle\prod\limits_{ { {i = 1} } }^{ {n} } {\cos (\dfrac{ { {x_{ {i} } } } }{ {\sqrt i } })} + {\text{1} }$ [−600,600] 30 0 固定维
多峰值$ {F_{{\text{11}}}}(x) = {\text{4}}x_{\text{1}}^{\text{2}} - {\text{2}}{\text{.1}}x_{\text{1}}^{\text{4}} + \dfrac{{\text{1}}}{{\text{3}}}x_{\text{1}}^{\text{6}} + {x_{\text{1}}}{x_{\text{2}}} - {\text{4}}x_{\text{2}}^{\text{2}} + {\text{4}}x_{\text{2}}^{\text{4}} $ [−5,5] 2 −1.0316 表 2 F1正交实验结果
组合 前期执行概率 中期执行概率 后期执行概率 平均值 策略1 策略2 策略3 策略1 策略2 策略3 策略1 策略2 策略3 1 0.3 0.4 0.3 0.2 0.7 0.1 0.1 0.2 0.7 167.4 2 0.3 0.4 0.3 0.2 0.7 0.1 0.2 0.2 0.6 214.8 3 0.3 0.4 0.3 0.3 0.6 0.1 0.1 0.2 0.7 206.9 4 0.3 0.4 0.3 0.3 0.6 0.1 0.2 0.2 0.6 275.4 5 0.4 0.3 0.3 0.2 0.7 0.1 0.1 0.2 0.7 212.4 6 0.4 0.3 0.3 0.2 0.7 0.1 0.2 0.2 0.6 251.3 7 0.4 0.3 0.3 0.3 0.6 0.1 0.1 0.2 0.7 283.3 8 0.4 0.3 0.3 0.3 0.6 0.1 0.2 0.2 0.6 234.9 表 3 剩余函数正交实验结果
函数名 组合 最小迭代次数均值 F2 2 370.9 F3 1 203.8 F4 1 313.6 F5 6 490.2 F6 3 498.8 F7 2 469.5 F8 1 15.7 F9 6 26.7 F10 5 196.4 F11 1 11.3 表 4 实验结果对比表
函数 指标 GWO POA TSA SSA RSSA F1 平均值 9.2157×10−41 9.9805×10−102 4.2666×10−205 0×100 0×100 标准差 1.2198×10−40 6.9374×10−101 0×100 0×100 0×100 F2 平均值 4.0882×10−24 2.4642×10−52 1.8823×10−106 2.9702×10−90 1.6559×10−175 标准差 3.0422×10−24 1.4866×10−51 1.0496×10−105 1.6238×10−89 5.7586×10−174 F3 平均值 1.4339×10−11 1.6184×10−101 3.1309×10−191 1.6822×10−112 0×100 标准差 3.3720×10−11 1.0244×10−100 0×100 9.2138×10−112 0×100 F4 平均值 1.8738×10−10 1.4842×10−51 5.7000×10−96 7.0150×10−100 0×100 标准差 2.2864×10−10 5.4263×10−51 2.1262×10−95 3.8423×10−99 0×100 F5 平均值 2.6549×101 2.7834×101 2.8597×101 4.7076×10−5 4.6906×10−9 标准差 7.4458×10−1 8.7888×10−1 4.2103×10−1 1.2807×10−4 5.7558×10−9 F6 平均值 1.7449×10−1 2.4745×100 5.9513×100 5.9078×10−7 0×100 标准差 1.7603×10−1 5.8354×10−1 7.8780×10−1 9.9105×10−7 0×100 F7 平均值 −6.3093×103 −7.8797×103 −3.6983×103 −8.5347×103 −1.1244×104 标准差 7.6183×102 8.0194×102 4.4204×102 5.5335×102 9.1573×102 F8 平均值 1.6278×100 0×100 1.3051×101 0×100 0×100 标准差 2.9439×100 0×100 4.0340×101 0×100 0×100 F9 平均值 2.6941×10−14 3.8725×10−15 4.4409×10−15 8.8818×10−16 8.8818×10−16 标准差 3.8843×10−15 1.3157×10−15 0×100 0×100 0×100 F10 平均值 3.8038×10−43 6.0396×10−101 1.6041×10−207 2.9457×10−169 0×100 标准差 4.1934×10−43 4.2462×10−100 0×100 0×100 0×100 F11 平均值 −1.0316×100 −1.0316×100 −1.0304×100 −1.0316×100 −1.0316×100 标准差 0×100 3.4603×10−16 6.2593×10−3 0×100 0×100 表 5 多峰值函数不同策略对比表
函数名 30次实验的最优解 SSA 低差异序列SSA 粗糙推理SSA RSSA F7 −9016.3366 −9936.5046 −10220.3075 −12569.4866 F8 0×100 0×100 0×100 0×100 F9 8.88×10−16 8.88×10−16 8.88×10−16 8.88×10−16 F10 1.35×10−209 5.44×10−245 1.02×10−255 0×100 -
[1] YANG X S, GANDOMI A H. Bat algorithm: A novel approach for global engineering optimization[J]. Engineering Computations:International Journal for Computer-Aided Engineering and Software, 2012, 29(5): 464-483. [2] PAITHANKAR A, CHATTERJEE S. Open pit mine production schedule optimization using a hybrid of maximum-flow and genetic algorithms[J]. Applied Soft Computing Journal, 2019, [3] DHALIWAL J S, DHILLON J S. Profit based unit commitment using memetic binary differential evolution algorithm[J]. Applied Soft Computing Journal, 2019, [4] COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]//The 1st European Conference on Artificial Life. Paris: [s.n.], 1991: 134-142. [5] COLORNI A, DORIGO M, MANIEZZO V. An investigation of some properties of an ant algorithm[C]//Parallel Problem Solving from Nature Conference. Brussels: [s.n.], 1992: 509-520. [6] COLORNI A, DORIGO M, MANIEZZO V, et al. Ant system for job shop scheduling[J]. Operations Research Statistics and Computer Science, 1994, 34(1): 39-53. [7] SMETS P, KENNES R. The transferable belief model[J]. Artificial Intelligence, 1994, 66(2): 191-234. doi: 10.1016/0004-3702(94)90026-4 [8] YANG X S. A new metaheuristic bat-inspired algorithm[J]. Computer Knowledge& Technology, 2010, 284: 65-74. [9] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007 [10] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008 [11] XUE J, SHEN B. A novel swarm intelligence optimization approach: Sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. [12] 李雅丽, 王淑琴, 陈倩茹, 等. 若干新型群智能优化算法的对比研究[J]. 计算机工程与应用, 2020, 56(22): 1-12. doi: 10.3778/j.issn.1002-8331.2006-0291 LI Y L, WANG S Q, CHEN Q R, et al. Comparative study of several new swarm intelligence optimization algorithms[J]. Computer Engineering and Applications, 2020, 56(22): 1-12. doi: 10.3778/j.issn.1002-8331.2006-0291 [13] DEMO N, TEZZELE M, ROZZA G. A supervised learning approach involving active subspaces for an efficient genetic algorithm in high-dimensional optimization problems[J]. SIAM Journal on Scientific Computing, 2021, 43(3): B831-B853. doi: 10.1137/20M1345219 [14] OLIVEIRA F, OLIVEIRA F R. A Global newton method for the nonsmooth vector fields on riemannian manifolds[J]. Journal of Optimization Theory and Applications, 2021, 190(1): 259-273. doi: 10.1007/s10957-021-01881-4 [15] HEDAR A R, DEABES W, AMIN H H, et al. Global sensing search for nonlinear global optimization[J]. Journal of Global Optimization, 2022, [16] 吕鑫, 慕晓冬, 张钧, 等. 混沌麻雀搜索优化算法[J]. 北京航空航天大学学报, 2021(8): 1712-1720. doi: 10.13700/j.bh.1001-5965.2020.0298 LYU X, MU X D, ZHANG J, et al. Chaos sparrow search optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021(8): 1712-1720. doi: 10.13700/j.bh.1001-5965.2020.0298 [17] 吕鑫, 慕晓冬, 张钧. 基于改进麻雀搜索算法的多阈值图像分割[J]. 系统工程与电子技术, 2021, 43(2): 318-327. doi: 10.12305/j.issn.1001-506X.2021.02.05 LYU X, MU X D, ZHANG J. Multi-threshold image segmentation based on improved sparrow search algorithm[J]. Systems Engineering and Electronics, 2021, 43(2): 318-327. doi: 10.12305/j.issn.1001-506X.2021.02.05 [18] MA J, HAO Z, SUN W. Enhancing sparrow search algorithm via multi-strategies for continuous optimization problems[J]. Information Processing & Management, 2022, 59(2): 102854. [19] MIRJALILI S, GANDOMI A H. Chaotic gravitational constants for the gravitational search algorithm[J]. Applied Soft Computing, 2017, 53: 407-419. doi: 10.1016/j.asoc.2017.01.008 [20] SHUO Y, LIN Y, WU J Z. Rough data-deduction based on the upper approximation[J]. Information Sciences, 2016, 373: 308-320. doi: 10.1016/j.ins.2016.09.011 [21] CV L, BRIZUELA C A, BARÁN B. Clustering-Based multipopulation approaches in MOEA/D for many-objective problems[J]. Computational Optimization and Applications, 2022, 81(3): 789-828. doi: 10.1007/s10589-022-00348-0 [22] 闫硕. 基于上近似的粗糙数据推理研究及应用[D]. 北京: 北京交通大学, 2017. YAN S. Rough data-deduction based on the upper approximation and its applications[D]. Beijing: Beijing Jiaotong University, 2017. [23] 付华, 刘昊. 多策略融合的改进麻雀搜索算法及其应用[J]. 控制与决策, 2022, 37(1): 87-96. doi: 10.13195/j.kzyjc.2021.0582 FU H, LIU H. Improved sparrow search algorithm with multi-strategy integration and its application[J]. Control and Decision, 2022, 37(1): 87-96. doi: 10.13195/j.kzyjc.2021.0582 [24] TROJOVSKÝ P, DEHGHANI M. Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications[J]. Sensors, 2022, 22(3): 855. doi: 10.3390/s22030855 [25] KAUR S, AWASTHI L K, SANGAL A L, et al. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization[J]. Engineering Applications of Artificial Intelligence, 2020, 90: 103541. doi: 10.1016/j.engappai.2020.103541 -


 ISSN
ISSN 




 下载:
下载: