ISSN 
-
在大数据时代[1]，数据分类是数据应用的基础，由于无监督的分类(unsupervised classification)或聚类(clustering)[2]不需要对数据进行训练，因而获得了广泛应用。聚类是采用多元统计方法，依据数据间的相似性或距离测度直接把性质相近的数据归为一类，性质差异较大的样本归属于不同的类。聚类分析中的聚类结构有3种：分区(partitional)聚类、层次(hierarchical)聚类和单个(individual)集群。层次聚类又分为凝聚层次聚类[3]和分裂层次聚类[4]。常用的聚类法有模糊C均值聚类[5]、密度基(density-based)聚类[6]以及K-均值(K-Means)类的聚类[7]等。
在无先验知识情况下对数据分析的关键是找出数据中的固有划分(inherent partitions)，尽管聚类算法可以划分数据，但不同算法或同一种算法采用不同的参数将产生出不同的数据划分或揭示不同的聚类结构(clustering structures)。因此，客观、定量地评价算法的聚类结果就显得十分重要。换句话说，由一种聚类算法得到的聚类结构是否有意义，即聚类验证(cluster validation)非常重要。层次聚类是基于邻近矩阵(proximity matrix)将数据组织到层次结构中，其结果通常用树状图[8]表示。与层次聚类相比，分区聚类将一组数据对象分配到没有任何层次结构的 k 个聚类中[9]，而且这个过程通常伴随着对一个准则函数的不断优化。在分区聚类算法中，应用最广泛的一种准则函数是平方误差和准则(sum-of-squared-error criterion)[2]。使得平方误差和为最小的划分被认为是最优的，一般称其为最小方差(minimum variance)划分[7]。数据的聚类是指：在同一类中数据对象具有很高的相似度(similarity)，而不同聚类之间的数据则具有较高的相异性(dissimilarity)[10]。显然，相似性与相异性(或称距离)可概括为邻近性，它既可以描述数据点之间、数据类之间的远近关系，又可以描述数据点与数据类之间的远近关系。对于聚类分析，常用的距离是欧几里得(欧氏)距离，利用欧氏距离形成的聚类对特征空间中的平移和旋转变换具有不变性[11]。
-
K-均值属于分区聚类的结构，目标是将数据组织成若干类，并且任一数据点只能属于一个类而不能同时属于多个类，这就意味着K-均值算法生成的是特定数量、互不相交、非层次的聚类。K-均值算法通过迭代优化步骤，利用最小化平方误差和准则来寻求数据的最佳划分，属于爬山(hill-climbing)类算法的范畴[7]。本质上，K-均值就是期望最大化(expectation maximization, EM)算法的经典范例。EM算法的第一步是寻找与聚类相关的期望点，第二步是利用第一步的知识改进对聚类的估计，重复这两个步骤直到算法收敛。
K-均值算法中，数据对象之间采用欧氏距离来度量相异性。设数据集有n个样本，它的p维观测为：
$$ {{\boldsymbol{x}}_i} = {({x_{i_1}},{x_{i_2}}, \cdots ,{x_{ip}})^{\text{T}}}\quad i = 1,2, \cdots ,n $$ (1) 任意两个样本点xi, xj (i, j=1, 2, ···, n)之间的欧氏距离表示为dij=d(xi, xj)。如果将n个样本分成k个聚类，则选择全部数据之间距离最远的两个(序号为i1, i2)样本作为初始聚类中心(聚点)：
$$ d({x_{{i_1}}},{x_{{i_2}}}) = {d_{{i_1}{i_2}}} = \max \{ {d_{ij}}\} $$ (2) 然后再确定下一个聚点(序号i3)，使得i3与i1, i2距离最小者等于所有其他点与i1, i2较小距离中的最大者：
$$ \begin{gathered} \;\;\;\;\;\;\;\;\;\; \min \{ d({x_{{i_3}}},{x_{{i_r}}}),\;r = 1,2\} = \\ \max \{ \min [d({x_j},{x_{{i_r}}}),\;r = 1,2],\;j \ne {i_1},{i_2}\} \\ \end{gathered} $$ (3) 不断重复以上过程，即可确定全部k个初始聚点。因此，K-均值算法的基本过程可以归纳如下。
1) 设随机选取的k个初始聚点的集合为：
$$ {S^{(0)}} = \{ {\boldsymbol{x}}_1^{(0)},{\boldsymbol{x}}_2^{(0)}, \cdots ,{\boldsymbol{x}}_k^{(0)}\} $$ (4) 对于任意的数据点x，对它的划分原则为：
$$ \begin{gathered} {\boldsymbol{x}} \in C_i^{(0)}\quad {\text{if }}\;\;d({\boldsymbol{x}},{\boldsymbol{x}}_i^{(0)}) \leqslant d({\boldsymbol{x}},{\boldsymbol{x}}_j^{(0)}) \\ \quad \quad \forall i,j = 1,2, \cdots ,k;\;\;j \ne i \\ \end{gathered} $$ (5) 即将所有样本分成不相交的k个类，得到初始分类：
$$ {C^{(0)}} = \{ C_1^{(0)},C_2^{(0)}, \cdots ,C_k^{(0)}\} $$ (6) 2) 从初始的C(0)开始重新计算新的聚点：
$$ {\boldsymbol{x}}_i^{(1)} = \frac{1}{{{n_i}}}\sum\limits_{{{\boldsymbol{x}}_i} \in C_i^{(0)}} {{{\boldsymbol{x}}_i}} \quad i = 1,2, \cdots ,k $$ (7) 式中，ni是类
$ C_i^{(0)} $ 中样本的数量，于是得到新的聚点：$$ {S^{(1)}} = \{ {\boldsymbol{x}}_1^{(1)},{\boldsymbol{x}}_2^{(1)}, \cdots ,{\boldsymbol{x}}_k^{(1)}\} $$ (8) 从
$S^{(1)} $ 开始再对数据重新进行分类，其原则为：$$ \begin{gathered} {\boldsymbol{x}} \in C_i^{(1)}\quad {\text{if }}\;\;d({\boldsymbol{x}},{\boldsymbol{x}}_i^{(1)}) \leqslant d({\boldsymbol{x}},{\boldsymbol{x}}_j^{(1)}) \\ \quad \quad \forall i,j = 1,2, \cdots ,k;\;\;j \ne i \\ \end{gathered} $$ (9) 得到一个新的分类集合：
$$ {C^{(1)}} = \{ C_1^{(1)},C_2^{(1)}, \cdots ,C_k^{(1)}\} $$ (24) 3) 重复上述步骤m次，得到分类：
$$ {C^{(m)}} = \{ C_1^{(m)},C_2^{(m)}, \cdots ,C_k^{(m)}\} $$ (25) 而对应的
$ {\boldsymbol{x}}_i^{(m)} $ 是类$ C_i^{(m - 1)} $ 的质心，质心不一定就是样本点，可能是样本之间的某个点。显然，当迭代次数m逐渐增大时，聚类结果也逐渐趋于稳定。在K-均值算法中，当m很大时，$ {\boldsymbol{x}}_i^{(m)} $ 可以近似地看作是类$ C_i^{(m)} $ 的质心。这就引出K-均值算法的终止条件：即当$ {\boldsymbol{x}}_i^{(m + 1)} \approx {\boldsymbol{x}}_i^{(m)} $ ，$ C_i^{(m - 1)} \approx C_i^{(m)} $ 时，迭代结束。显然，K-均值聚类算法的基本思想是将数据空间首先随机地划分为事先指定的k个类，然后通过迭代计算不断更新每个类的质心。当相邻两次迭代计算的结果基本相同时，则算法收敛。尽管K-均值算法被证明是收敛的[12]，然而困扰K-均值聚类的第一个问题是它的迭代优化过程不能保证算法收敛到全局最优。由于K-均值算法可以收敛到局部最优[7]，不同的初始划分将导致不同的收敛质心。第二个问题是K-均值算法对数据中的异常值也即野值(outliers)以及噪声(noise)很敏感[2, 7]，在迭代计算聚点的过程中算法却是考虑了所有的样本。即使某个样本点离质心很远，但K-均值算法仍然将该点强行纳入最邻近的类中用于计算其质心，这样就造成了聚类形状的扭曲。另外，K-均值类算法要求用户事先指定聚类数量，这在实际中很难做到。聚类数量是否正确将直接影响聚类效果，确定最优的聚类数量也称为聚类有效性分析(clustering validity analysis)[13]。因此，在聚类分析中，一个必不可少的步骤是验证聚类结果并确保它能正确地反映数据的本质结构。基于统计理论对算法生成的聚类结构进行评估，强调以客观和定量的方式对聚类结果进行评价，这就是聚类趋势分析(clustering tendency analysis)[14]。
分区聚类、层次聚类和单个集群的结构所对应的聚类有效性测试标准分别为外部的(external)、内部的(internal)和相对的标准(relative criteria)[15]，这3种标准的适用范围不同。外部与内部标准都涉及到统计方法和假设检验[16]，这将导致计算开销增加。而相对标准则无须进行统计检验，它致力于比较不同的聚类结果。因此，相对标准可用于比较K-均值类算法一系列不同聚类数量k的聚类效果，以便找出数据划分最适合的k值，这个问题也被称为聚类有效性的基本问题(fundamental problem)[17]。
K-均值类算法包括一系列聚类方法，如K-medoids算法[18]和K-均值算法，它们的适用范围和特点各不相同。K-均值的时间复杂度为O(nkpT)，其中，n为样本数量，k为聚类数量，p为数据维数，T为算法迭代次数，由于k, p, T通常都比n小很多，因此K-均值的时间复杂度为近似的线性关系[2, 7]，因而它以低计算复杂度体现出高效率[18]，但它的聚类结果很大程度上受数据中噪声与异常值的影响。为了解决K-均值算法的这个缺陷，K-medoids算法以中心点(medoids)作为聚类中心，对噪声及异常点处理能力优秀且具有较强的鲁棒性。然而它的缺点是计算复杂度较高，因此学者们致力于改进K-medoids算法，以期在计算效率上追赶K-均值算法[18]。在众多改进的K-medoids方法中，围绕中心点划分(partitioning around medoids, PAM)算法[19]被认为是最有效的K-medoids算法之一。但PAM算法的迭代次数较多，时间效率低[19]。在不考虑迭代次数的情况下，K-medoids和PAM算法的时间复杂度都为O(k(n-k)2)[18]，即为二次函数。对于这3种经典的K-均值类聚类算法，仅从时间开销的角度来看，K-均值算法的计算速度是最快的。另外，这3种算法的共同缺点仍是聚类数量k作为算法的参数必须事先指定。聚类数量k过大或过小的估计都将严重影响最终的聚类质量。过多的聚类数量造成真正的数据聚类结构变得复杂，使得对聚类结果的解释和分析变得困难，而过少的聚类数量将损失信息并造成错误的聚类结果。
本文主要研究经典K-均值聚类算法中最佳聚类数量的确定问题，因此，其基本的思路为：对于具体的数据集，首先在聚类数量的可能范围内，采用不同的聚类数量来运行K-均值算法以获得相应的聚类结果；然后以聚类数量k为自变量构造一种聚类有效性函数(指标)对K-均值的聚类结果进行评估，通过优化聚类有效性函数来确定最优的聚类数量。
-
对于理想的聚类效果，从相似性角度要求类内样本点之间尽可能相似，同时类与类之间的样本点尽可能相异。从距离的角度则要求类内样本点之间距离的代数和应尽量小，而在不同类之间样本点距离的代数和应尽量大。在整个数据空间中，样本点与它所在类的聚点之间的距离，要比它与其他类的聚点间的距离都要小。满足这个条件的聚类就是有效的数据划分。
对于全部的n个数据点，其样本均值(质心)为：
$$ {\boldsymbol{\bar x}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\boldsymbol{x}}_i}} $$ (12) 在所有的数据中，假设第i个聚类Ci中有ni个数据对象，则定义该类的样本质心(中心)为：
$$ {{\boldsymbol{\bar x}}_i} = \frac{1}{{{n_i}}}\sum\limits_{{\boldsymbol{x}} \in {C_i}} {\boldsymbol{x}} $$ (13) 将所研究的数据集合用其聚类的质心表示为：
$$ S = \{ {{\boldsymbol{\bar x}}_1},{{\boldsymbol{\bar x}}_2}, \cdots ,{{\boldsymbol{\bar x}}_k}\} $$ (14) 式中，k为全部数据形成的聚类数量。由S和k构成的聚类空间为I={S，k}。
定义1 类间质心距离之和 在聚类空间I上，由各个聚类中心
$ {{\boldsymbol{\bar x}}_i} $ (i=1, 2, ···, k)到全体数据的质心$ {\boldsymbol{\bar x}} $ 的欧氏距离之和定义为类间质心距离之和：$$ {D_{{\text{betw}}}}(k) = \sqrt {\sum\limits_{i = 1}^k {|{{{\boldsymbol{\bar x}}}_i} - {\boldsymbol{\bar x}}{|^2}} } $$ (15) 从定义1的表达式可看出，当所有样本都属于同一个类(即聚类数量k=1)时，则这个类的中心就是全体数据的质心
$ {\boldsymbol{\bar x}} $ 。在这种情况下，类间质心距离之和Dbetw取值为0，即取Dbetw(k)的极小值。随着聚类数量k的增加，类间质心距离之和函数Dbetw(k)是递增的。定义2 类内距离之和 在聚类空间I上，由每个类中的各样本到该类中心的欧氏距离之和为同一类的内部距离，而所有k个聚类的内部距离之和则定义为类内距离之和：
$$ {D_{{\text{with}}}}(k) = \sqrt {\sum\limits_{i = 1}^k {\sum\limits_{{\boldsymbol{x}} \in {C_i}} {|{\boldsymbol{x}} - {{{\boldsymbol{\bar x}}}_i}{|^2}} } } $$ (16) 从定义2可知，当整个数据集的样本属于同一个类(聚类数量k=1)时，Dwith就是所有数据点与其质心
$ {\boldsymbol{\bar x}} $ 的距离之和，即取Dwith(k)的极大值。随着聚类数量k的增加，类内距离之和函数Dwith(k)是递减的。定义3 聚类有效性评价函数 在聚类空间I上，基于类间质心距离之和Dbetw与类内距离之和Dwith，定义一种综合评价函数(指标)：
$$ f(k) = \left| {\frac{{{D_{{\text{betw}}}}(k)}}{{{D_{{\rm{with}}}}(k)}} - 1} \right| $$ (17) 式中，|⋅|表示取绝对值。当所有数据样本点都属于同一类(聚类数量k=1)时，由于Dbetw(k)=0，则f(k)=1。显然，随着聚类数量k的变化，函数f(k)的值也发生相应变化，即f(k)是以聚类数量k为自变量的函数。对于K-均值算法，最好的聚类效果意味着聚类数量k是最优的，因此将f(k)称为聚类有效性评价函数(指标)。
在统计学中，经验规则(empirical rules)[20]常用来预测最终的结果，它也称为3σ规则或68-95-99.7规则。经验规则表明：对于正态分布，几乎所有的观测数据X都将落在平均值E[X]的3个标准差σ之内。具体地说，68%的数据落在平均值的1个σ之内，95%的数据落在平均值的2个σ之内，99.7%的数据落在平均值的3个σ之内[21]。在某些情况下，获取数据的分布可能很耗时，甚至是不可能的，因此正态概率分布可以作为一种临时启发式(heuristic)方法，如当一家公司正在审查其质量控制措施或评估其风险暴露(risk exposure)时，风险价值(value-at-risk)作为常用的风险工具，假设风险事件的概率服从正态分布，对于服从其他分布的观测数据来说，将经验规则推广为经验贝叶斯规则(empirical Bayes rules)[22-23]，则可实现对具有k类的观测数据总体进行推断。因此，在计算出数据的均值和标准偏差之后，经验规则可用于粗略地估计观测数据总体中所隐含的数据类k的数量范围。
定理 最佳聚类数量准则 在聚类空间I上，根据经验规则，可以估计出聚类数量k可能的最小值kmin和最大值kmax，因而获得k的取值范围[kmin, kmax]。当k在[kmin, kmax]变化时，如果聚类有效性评价函数f(k)获得最小值，则K-均值算法的聚类效果为最优，即对应的最佳聚类数量k为：
$$ k = \mathop {\arg \min }\limits_{k \in [{k_{\min }},\;{k_{\max }}\} } \{ f(k)\} $$ (18) 证明：由定义1可知，类间质心距离之和Dbetw(k)是聚类数量k的单调增函数，由定义2可知，类内距离之和Dwith(k)是k的单调减函数。因此随着k取值的变化，由定义3可知，聚类有效性评价函数f(k)存在极小值，但并不存在有限的极大值。换句话说，函数f(k)可能取值为无穷大，此时对应的聚类数量k是不合理的。
在实际应用中，聚类数量k只能取正整数，而且函数Dbetw(k)和Dwith(k)也都只能取正实数值(非负值)。在k的有限取值范围[kmin, kmax]内，函数f(k)一定存在有全局的极小值，即最小值。显然，聚类有效性评价函数的最小值所对应的k值就是数据集的最优聚类数量。由定义3可知，只有当Dbetw(k)和Dwith(k)的取值相等或二者非常接近时，函数f(k)才能取得最小值。换句话说，通过调整聚类数量k的取值使得Dbetw(k)和Dwith(k)达到最接近的程度，K-均值聚类的效果才是最佳的，此时对应的聚类数量k值就使得数据的分类达到最优。因此，利用聚类有效性评价函数f(k)作为确定最佳聚类数量k的准则，也就是确定f(k)的最小值准则。
为了找到K-均值算法的最佳聚类数量k，从可视化的角度，在k值的可能变化范围[kmin, kmax]内，通过绘制聚类有效性评价函数f(k)随聚类数量k的变化曲线，直观地搜寻函数f(k)的最小值点所对应的聚类数量k，即为最佳的聚类数量。
-
为了验证本文提出的聚类有效性评价函数的性能以及由此获得的最佳聚类数k是否符合数据本身内在的分类结构，利用加州大学欧文分校的机器学习库(UC Irvine machine learning repository)中的多个数据集进行仿真实验。
仿真PC机的CPU为：Intel(R) Celeron(R) 1007U-1.5 GHz，内存4 GB，操作系统为Windows 10，仿真是在MATLAB 9 (R2016a)上运行。
对于数据的分类与聚类问题，最常用的UCI数据集有Iris、Seeds和Wind数据集。这3种数据集的数据样本数量、属性(特征)数量以及数据真实的聚类数量如表1所示。
表 1 3种UCI数据集的有关信息
数据集名称 样本数量 属性数量 真实聚类数量 Iris 150 4 3 Seeds 210 7 3 Wine 178 13 3 仿真的基本过程为：对于每一种数据集，根据经验规则估计数据的可能聚类数量范围[kmin, kmax]。在这个范围内的每个k值，首先分别运行K-均值算法一次，并计算相对应的聚类有效性评价函数f(k)。然后多次运行K-均值算法以观察函数f(k)的变化趋势，从而对聚类有效性评价指标f(k)的平均性能进行测试。
-
鸢尾花Iris数据集记录了3种花setosa、versicolor和virginica的4种属性，即萼片长(sepal length)表示为x1、萼片宽(sepal width)表示为x2、花瓣长(petal length)表示为x3、花瓣宽(petal width)表示为x4。3种花各记录了50组特征(即属性)的数据，按照setosa、versicolor和virginica的顺序存放。
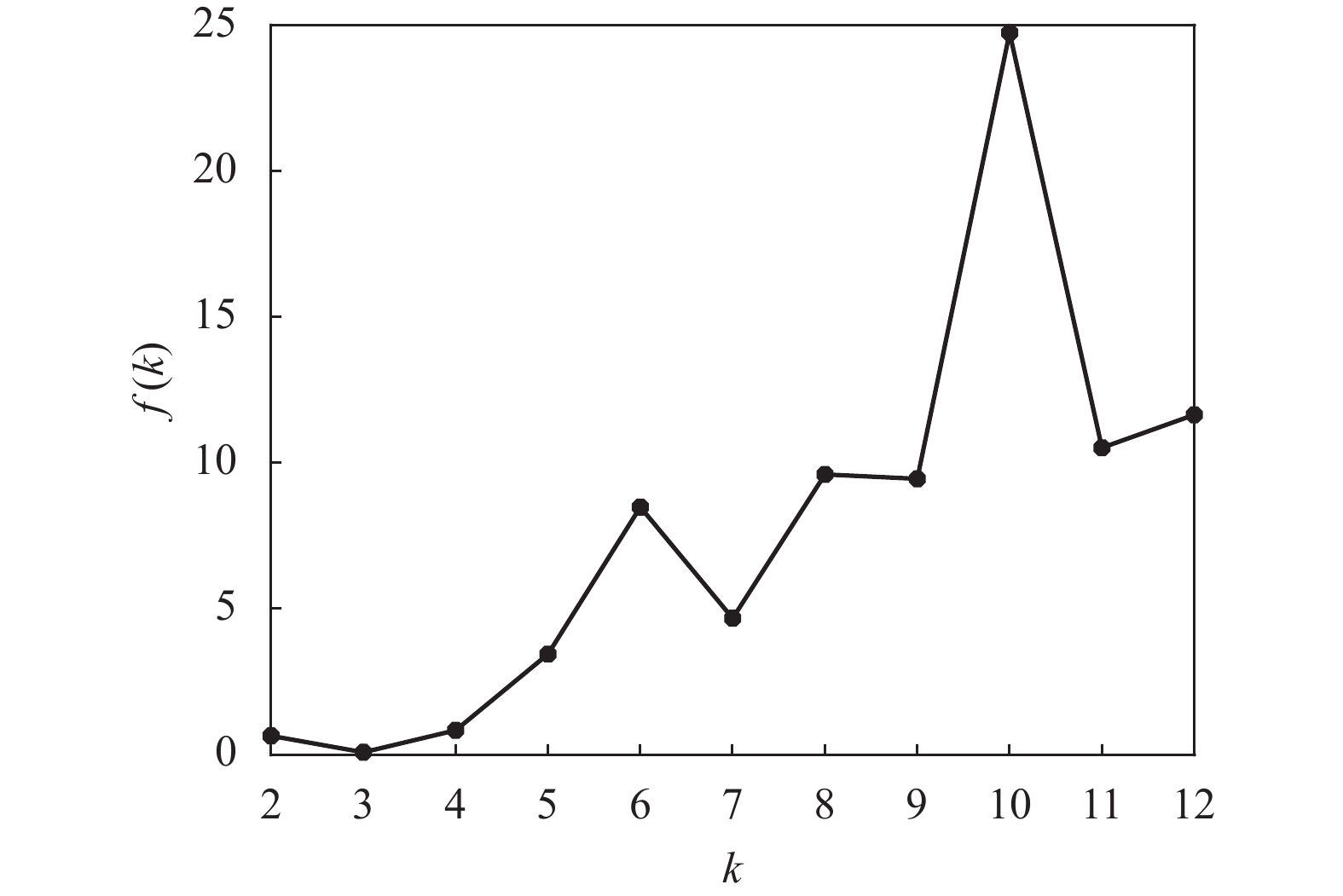
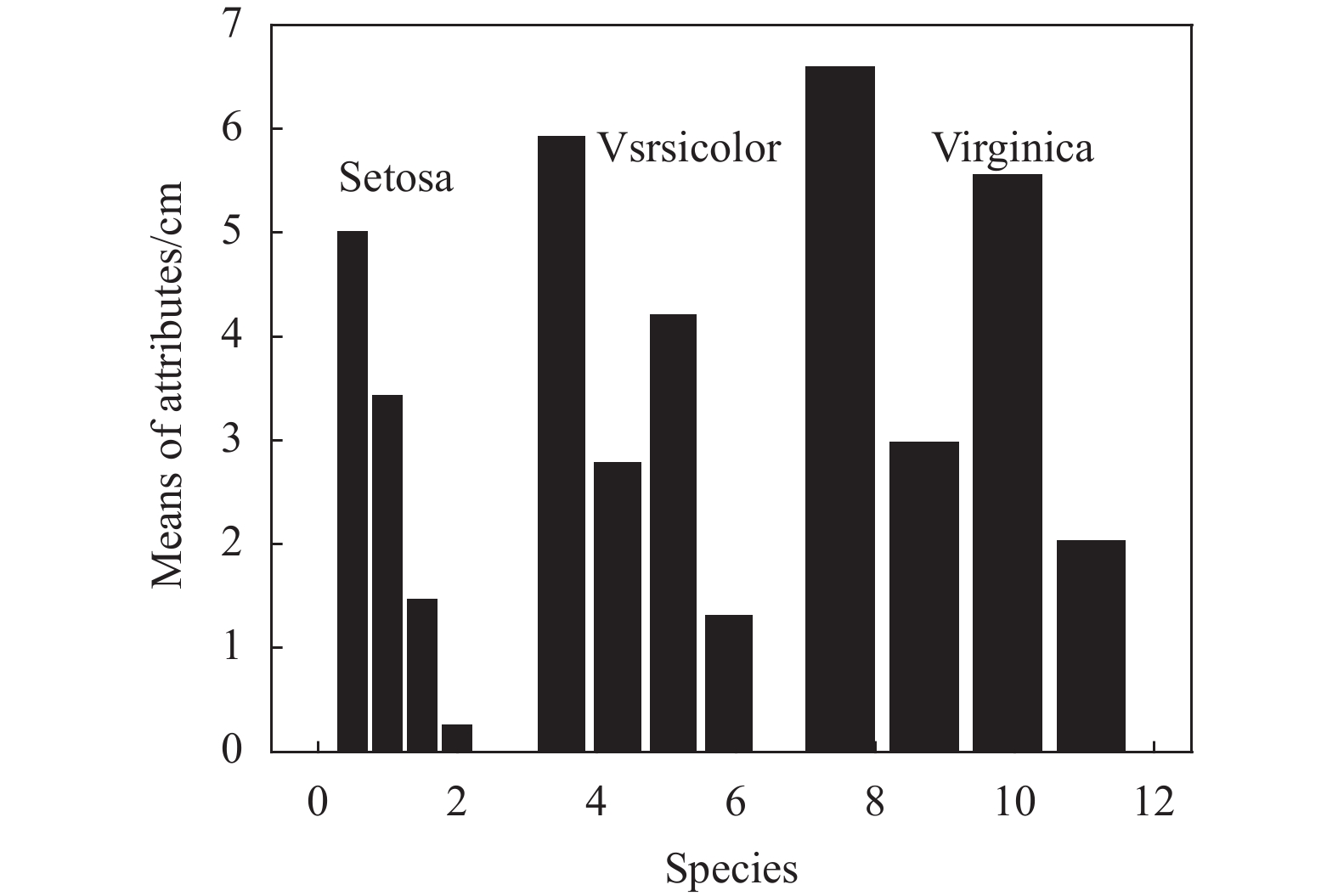
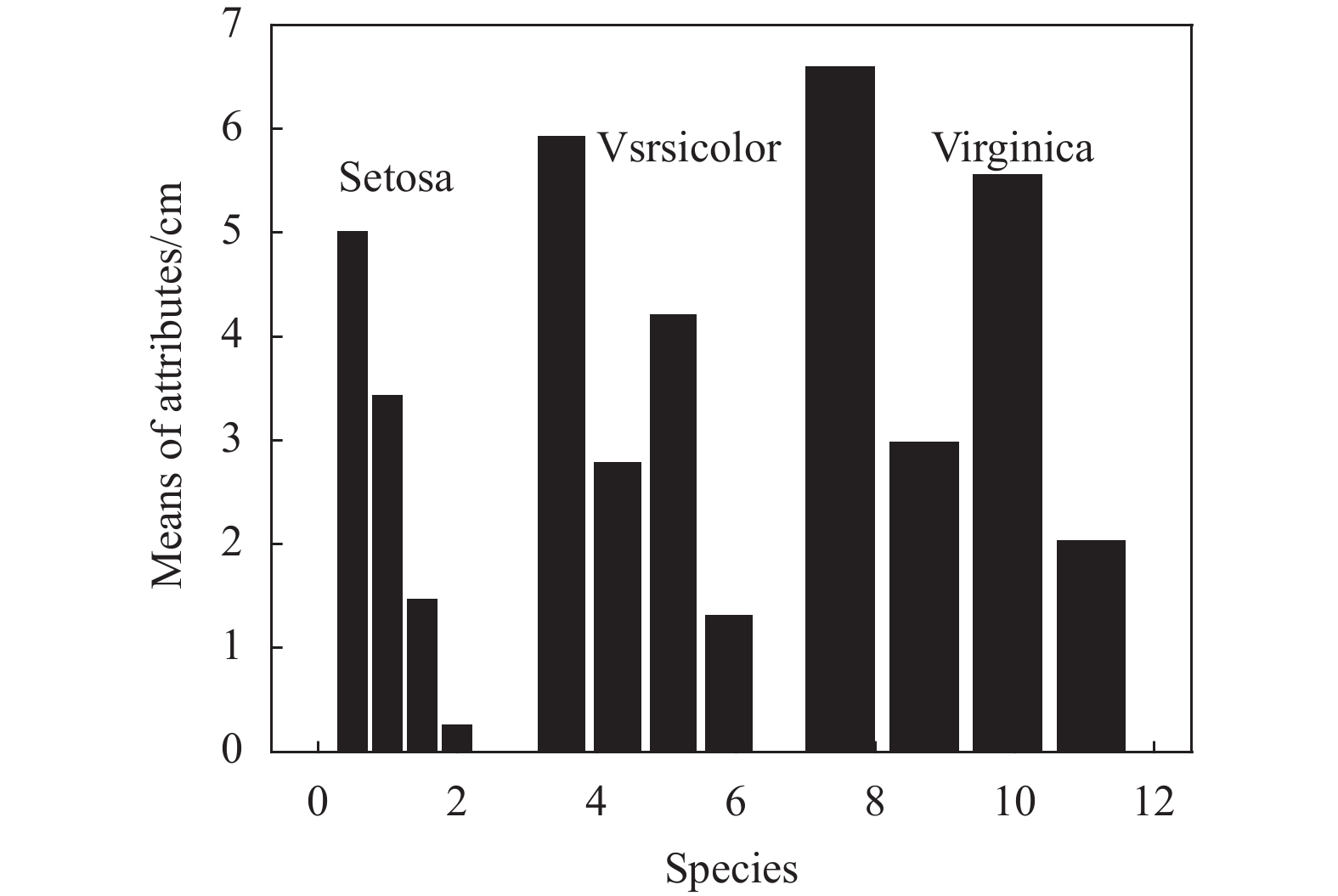
为了观察Iris数据集对应特征的统计中心位置，即不同属性值的分布范围所围绕的大致中心，首先计算出每种鸢尾花的4个属性，即变量x1, x2, x3, x4的均值，如表2和图1所示。
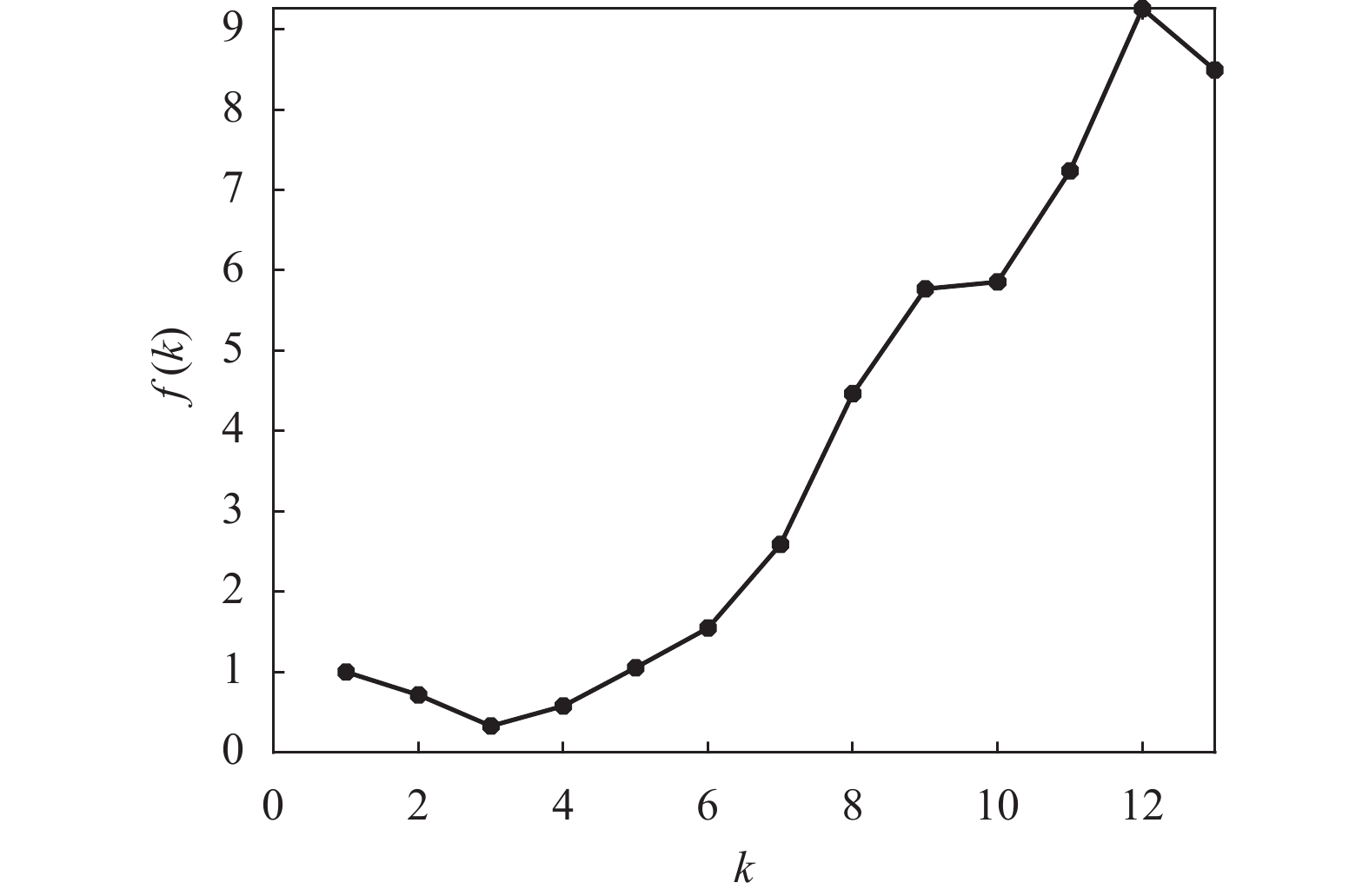
根据数据样本数量以及经验规则，设Iris数据可能的聚类数量范围为[kmin, kmax]，其中kmin=2，kmax=12。对于[kmin, kmax]中的每个k值，运行K-均值算法一次，并计算出相对应的聚类有效性评价函数f(k)的值，其结果如表3和图2所示。
表 2 3种花4个属性的均值
cm 花种类 E[x1] E[x2] E[x3] E[x4] Setosa 5.006 3.428 1.462 0.246 Versicolor 5.936 2.770 4.260 1.326 Virginica 6.588 2.974 5.553 2.026 
图 1 3种鸢尾花特征变量均值的条形图
表 3 Iris数据的f(k)与k的对应表
k f(k) k f(k) k f(k) 2 0.6469 6 8.4878 10 24.7449 3 0.0831 7 4.6767 11 10.5197 4 0.8377 8 9.6060 12 11.6496 5 3.4491 9 9.4557 − − 
图 2 Iris数据的f(k)随聚类数量k的变化曲线
从图2和表3可以看出：1)函数f(k)随着k值做相应变化，这就说明聚类有效性评价函数f(k)用来对聚类数量k的选择进行评价是有效的；2)当k=3时，f(k)取得最小值，即最佳的聚类数量为3。这个结果证明聚类有效性评价函数f(k)能够从Iris数据集中找出最佳的聚类数量，即真实的鸢尾花所包含的种类。
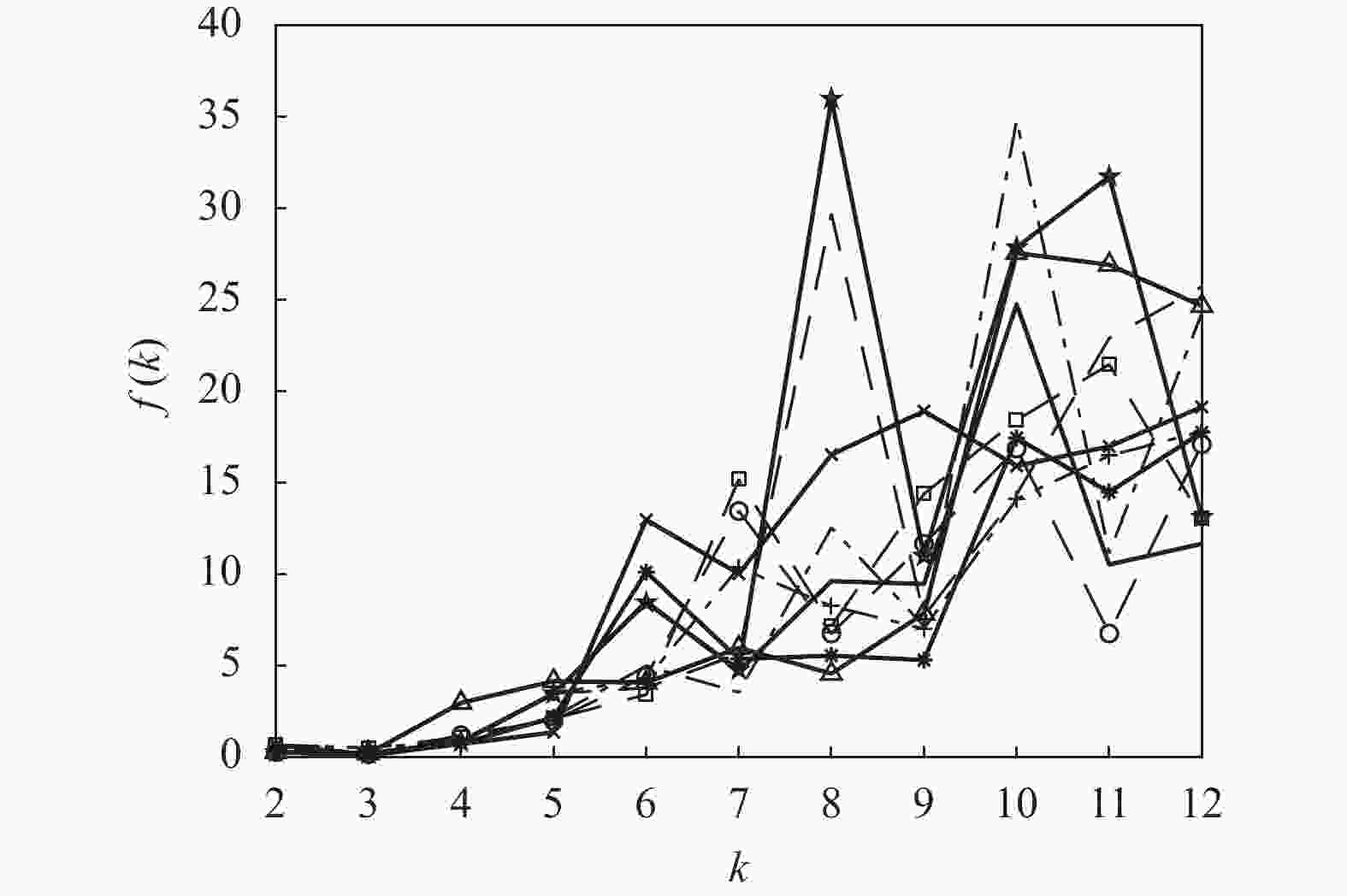
这里需要说明，K-均值算法的另一个缺陷是它可以收敛到局部最优，而且每次运行K-均值算法时，初始的聚类中心是从所有数据中随机选取的。因此算法要求必须有一个合理的初始化，在实际应用中这是不现实的。对于不同的初始划分，将导致K-均值算法收敛到不同的质心位置。一种解决方案是通过重复运行K-均值算法多次，并以多次运行的平均结果来降低随机初始化的影响。为此，将K-均值算法按照上述的仿真条件重复运行10次，每次分别记录下对应的聚类有效性评价函数f(k)的值。为观察方便，这里仅绘制出每次运行中函数f(k)随聚类数量k的变化曲线，其结果如图3所示。
图 3 10次运行中Iris数据的f(k)随k变化的曲线
从图3可以看出，虽然K-均值算法的10次运行结果各不相同，但在每次运行中，聚类有效性评价函数f(k)的最小值都是在k=3时取得的，这是不变的。图3的结果说明f(k)对于确定最佳聚类数量是有效的。
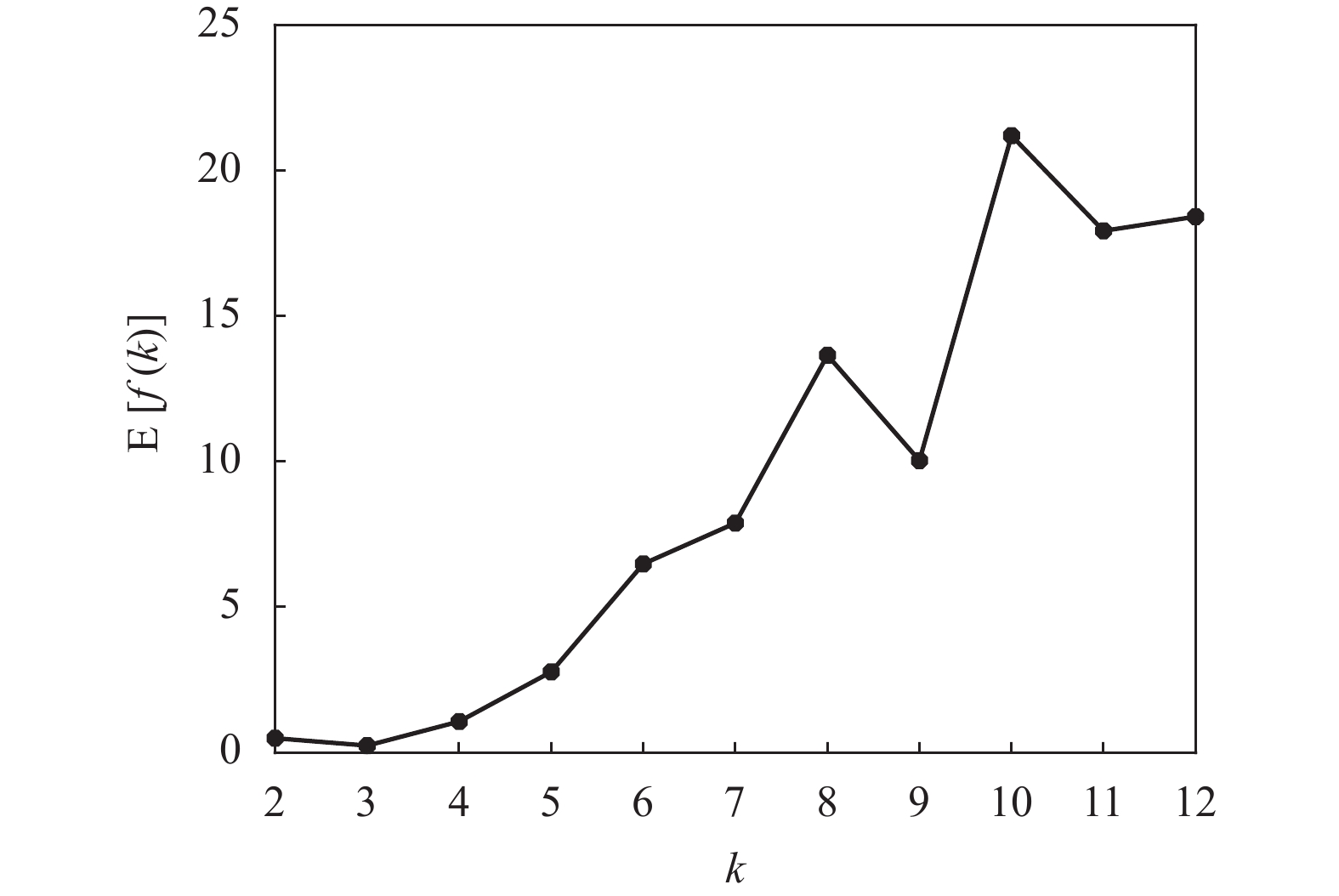
在多次运行K-均值算法的基础上，再考虑聚类有效性评价函数f(k)的平均性能。对于每个可能的k值，将10次运行的f(k)求平均值可得到E[f(k)]，其结果如表4和图4所示。可以看出，聚类有效性评价函数f(k)在K-均值算法10次运行中的平均值E[f(k)]仍然在k=3时取得最小值，这也反映了Iris数据集中真实的鸢尾花品种为k=3。另外，由于K-均值算法对数据采用随机的初始划分，使得每次运行获得的聚类中心位置并不相同，但从多次运行的结果来看，E[f(k)]仍然能够准确地反映Iris数据集的本质结构。即聚类有效性评价函数对K-均值的随机初始化具有鲁棒性(robustness)。
表 4 Iris数据的E[f(k)]值与k的对应表
k E[f(k)] k E[f(k)] k E[f(k)] 2 0.4940 6 6.4861 10 21.2041 3 0.2399 7 7.8881 11 17.9314 4 1.0678 8 13.6567 12 18.4198 5 2.7753 9 10.0362 − − 
图 4 10次运行中Iris数据的E[f(k)]随k变化的曲线
-
种子(Seeds)数据包括3种小麦粒(wheat kernels)的7个几何参数(属性)：面积(area)x1、周长(perimeter)x2、密度(compactness)x3、长度(length)x4、宽度(width)x5、不对称系数(asymmetry coefficient)x6、沟槽长度(length of kernel groove)x7。显然，这些属性的度量单位是不相同的。Seeds数据集对每一类小麦分别记录了70组特征的数据，按照类标签1、2、3的顺序存放。
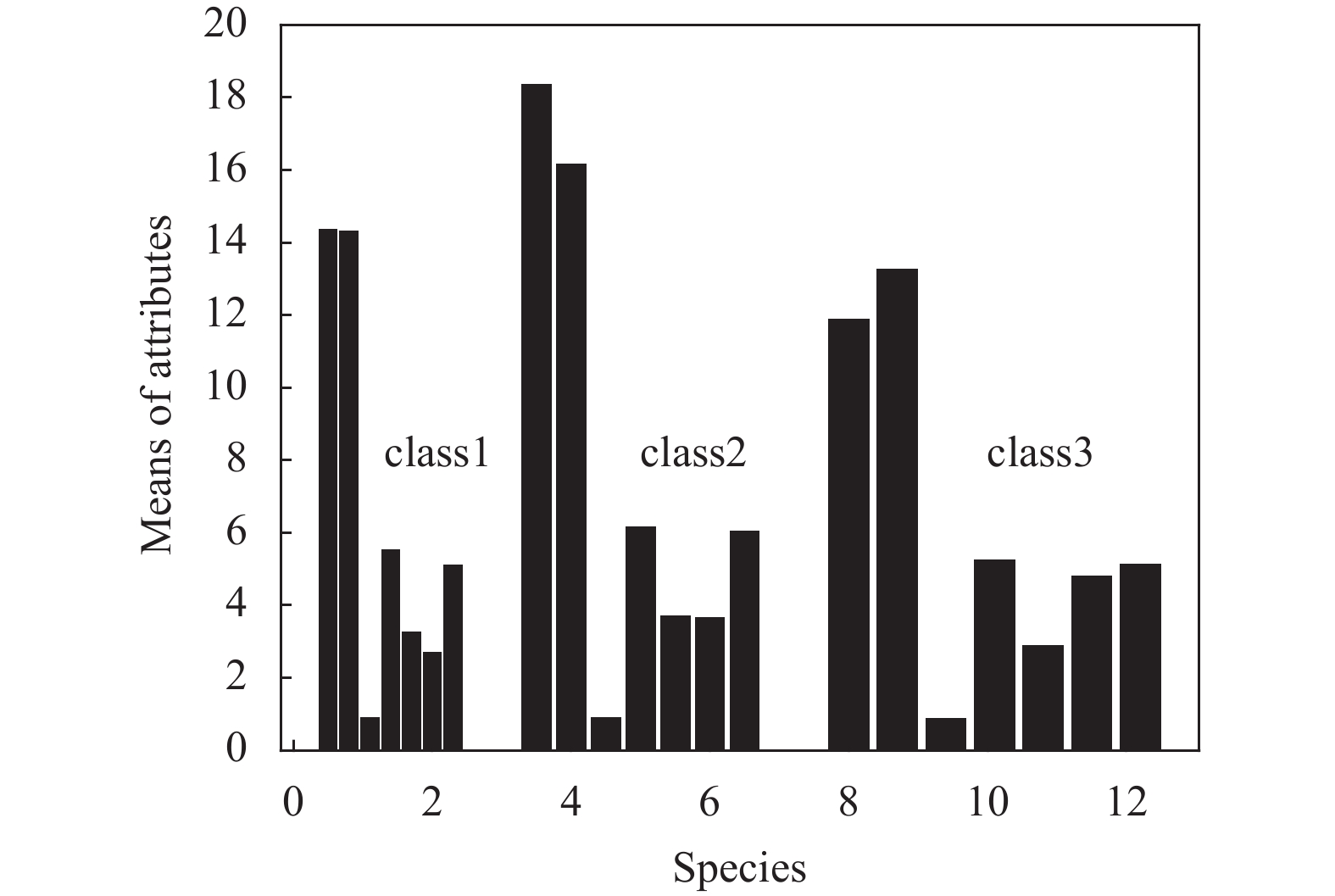
对于Seeds数据，分别计算3类(class 1, 2, 3)小麦7个属性x1, x2, ···, x7的均值，如图5所示。以上均值给出的是3类小麦所有样本几何参数的分布中心。根据数据集的样本数量以及经验规则，设Seeds数据集中可能的聚类数量范围为[kmin, kmax]，其中kmin=2，kmax=13。对于[kmin, kmax]中的每个k值，运行K-均值算法一次，并计算出相对应的聚类有效性评价函数f(k)，其结果如图6所示。
由聚类有效性评价函数(指标)的定义可知，若所有数据都属于同一类(即k=1)，则指标f(k)=1。为了便于观察和比较，在图6中还给出了k=1的波形。可以看出，当k=3时，聚类有效性评价指标f(k)取得一个最小值0.3271，即给出了K-均值算法的最佳聚类数量为3。这一结果与Seeds数据集的实际情况是一致的。
图 5 3种小麦特征变量均值的条形图
图 6 Seeds数据的f(k)随聚类数量k的变化曲线
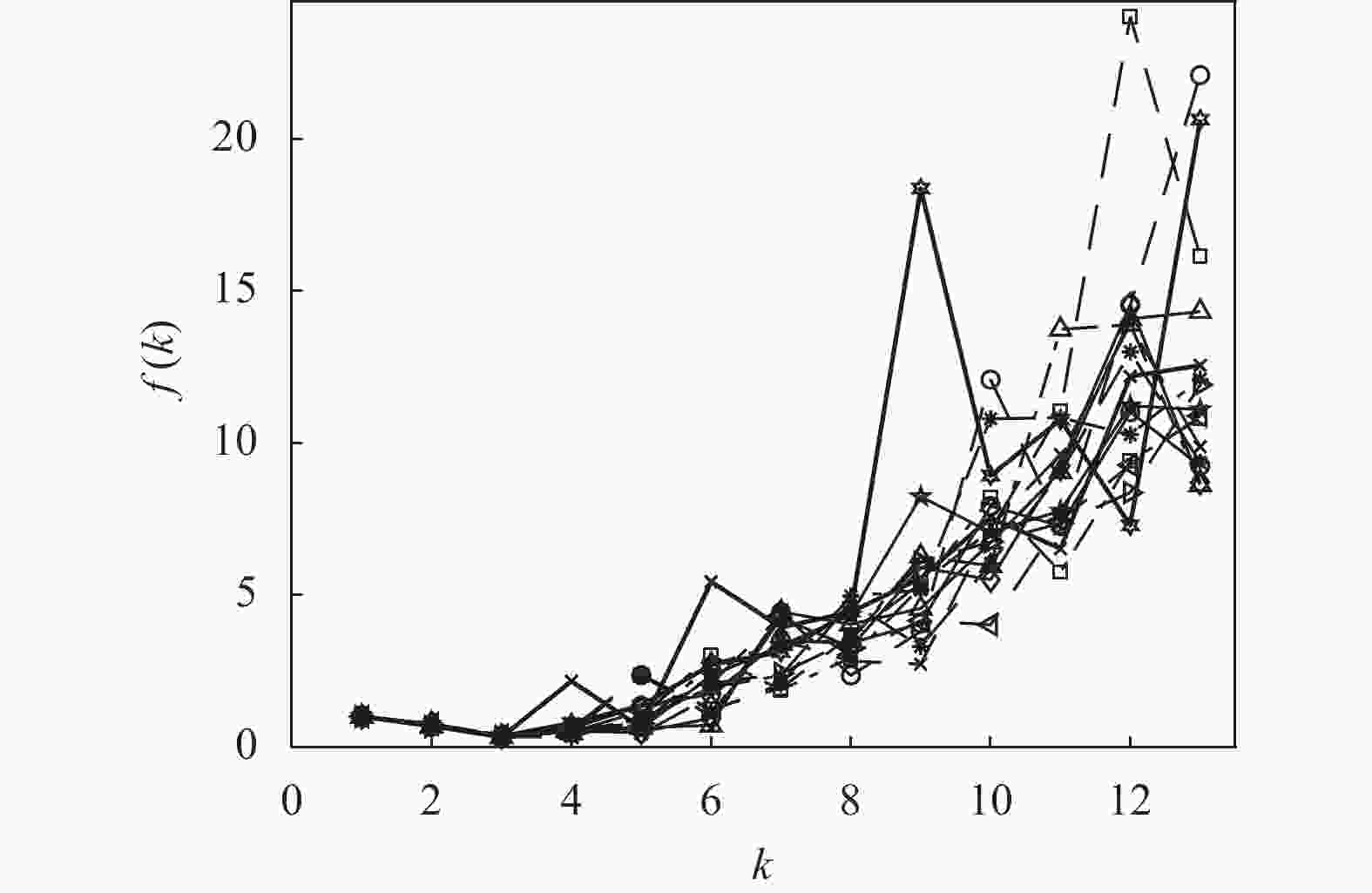
同样地，为了考察K-均值算法在重复多次运行情况下的整体性能。对于Seeds数据集，在k的可能取值范围[kmin, kmax]内重复运行K-均值算法15次，每次运行记录和保存聚类有效性评价函数f(k)的对应值，其结果如图7所示。可以看到，在K-means算法的15次运行中，尽管每次运行f(k)的取值以及取值的分布情况都不相同，但是指标f(k)的最小值毫无例外地在k=3时获得。这表明聚类有效性评价函数f(k)在确定最优聚类数量方面的性能是非常稳定的。
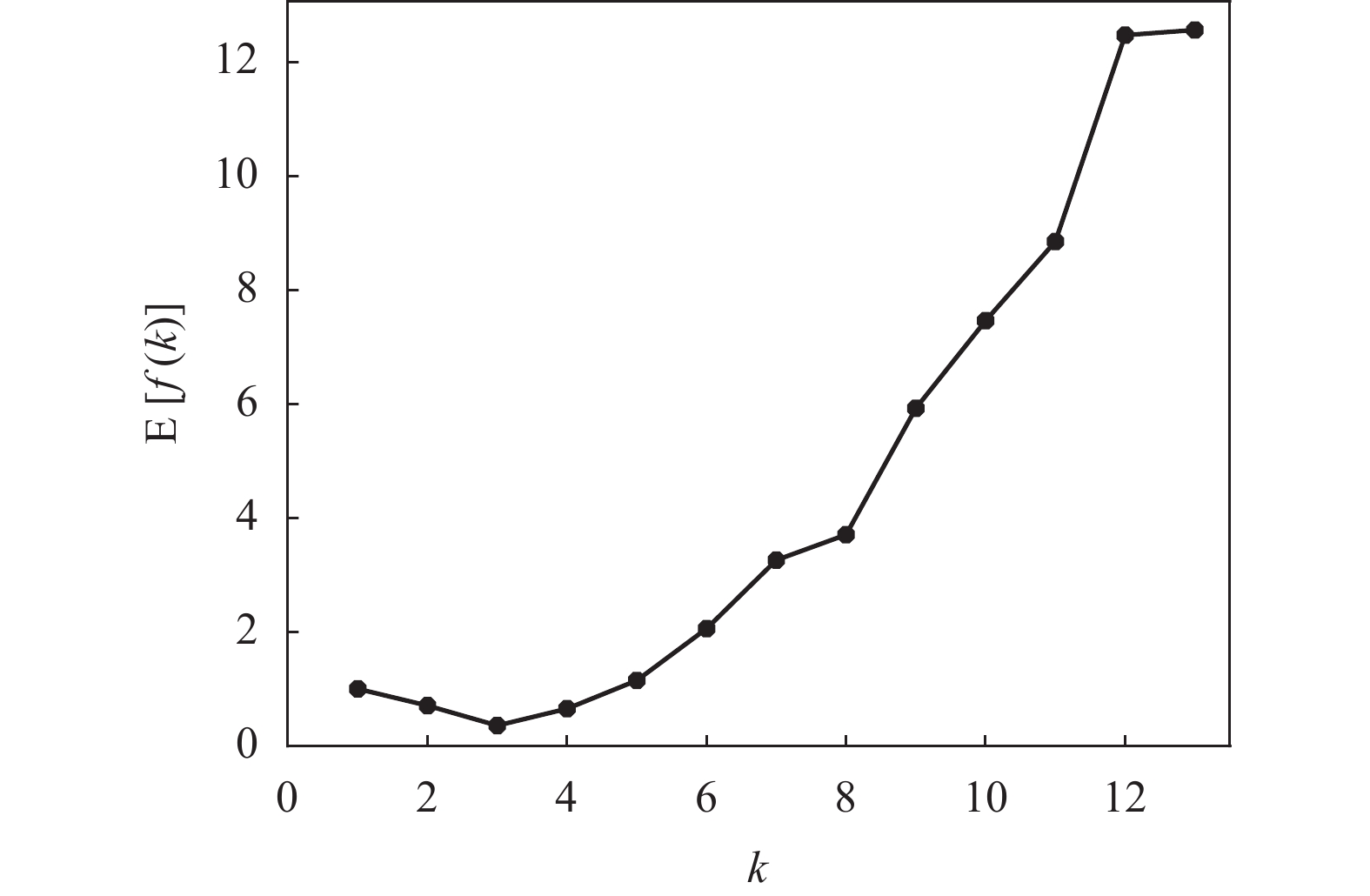
对于每个可能的k值，把上述15次K-均值算法运行所得到的f(k)值取平均得到E[f(k)]，绘制出E[f(k)]随k值变化的曲线如图8所示。
由图8可以看出，从聚类有效性评价函数的平均性能E[f(k)]仍然可以清晰地识别出Seeds数据集的真实聚类结构(k=3)。另外，从图7和图8的结果可知，在最优聚类数量的确定方面，指标f(k)以及其平均值E[f(k)]的性能不会受到K-均值算法随机初始化的影响。
图 7 15次运行中Seeds数据的f(k)随k变化的曲线
图 8 15次运行中Seeds数据的E[f(k)]随k变化的曲线
-
葡萄酒(Wine)数据是对在意大利同一地区种植，但来自3个不同品种的葡萄酒进行化学分析的结果。这种分析确定了3种类型的葡萄酒中所含13种成分(属性、特征)的含量。这些属性分别为酒精(x1)、苹果酸(x2)、灰(x3)、灰分碱度(x4)、镁(x5)、总酚(x6)、黄酮素类化合物(x7)、非黄酮类酚类(x8)、原花青素(x9)、颜色强度(x10)、色调(x11)、稀释葡萄酒的OD280/OD315(x12)和脯氨酸(x13)。这些特征值的度量单位是不相同的。Wine数据集中共记录了178组数据，3种类型葡萄酒的类标签分别为1, 2, 3，它们各自的样本数分别为59, 71, 48。对于Wine数据集，由于不同属性(变量)的取值之间差距太大(相差3720倍)，无法用图形表示变量的均值。这里仅给出全部13个变量的平均值(包括所有葡萄酒的种类)，其结果如表5所示。
表 5 Wine(全部种类)数据各属性的平均值
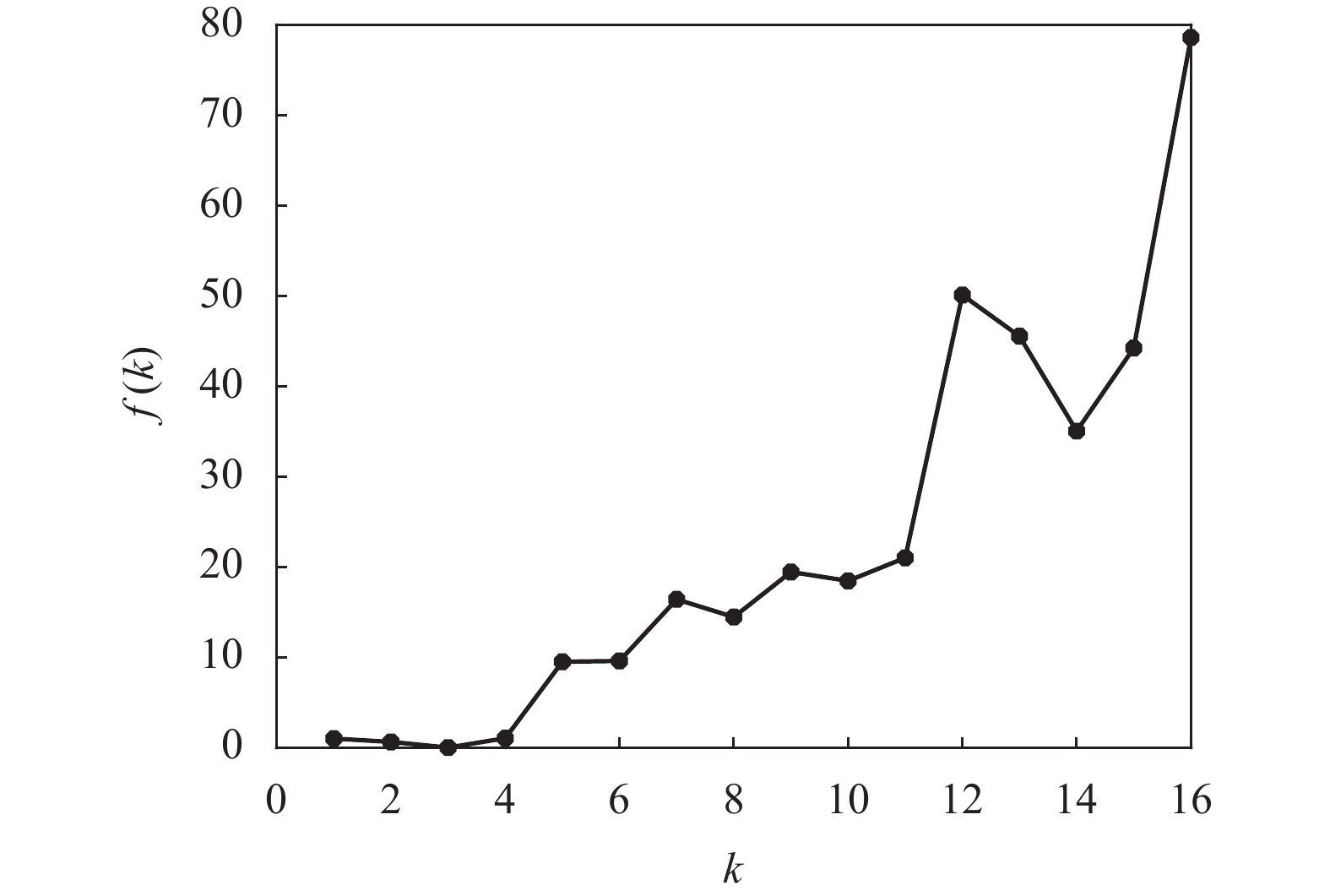
x1 x2 x3 x4 x5 x6 x7 E[x] 13.00 2.34 2.37 19. 50 99.74 2.30 2.03 x8 x9 x10 x11 x12 x13 E[x] 0.36 1.59 5.06 0.96 2.61 746.90 Wine数据的均值给出了各属性值分布的大致统计中心。考虑到Wine数据集的属性较多，根据经验规则将数据可能的聚类数量设置为kmin=2, kmax=16。首先对于区间[kmin, kmax]中的每个k值，运行K-均值算法一次，并计算出相对应的聚类有效性评价函数f(k)的值，其结果如表6和图9所示。
表 6 Wine数据的f(k)与k的对应表
k f(k) k f(k) k f(k) 2 0.6299 7 16.4146 12 50.1047 3 0.0044 8 14.4553 13 45.5446 4 1.0391 9 19.4455 14 35.0423 5 9.5062 10 18.4569 15 44.2383 6 9.5934 11 21.0099 16 78.6142 
图 9 Wine数据的f(k)随聚类数量k的变化曲线
为观察方便，图9也给出了k=1对应的数据。由于f(k)取值的范围较大，最小值附近其差别不易区分，为此把图9中的数据列在表6中。从表6中的数据可知，f(2)是f(3)的143倍，f(4)是f(3)的236倍。显然，k=3是指标f(k)的最小值点，即k=3是最优的聚类数量，这与Wine数据本质结构是一致的。
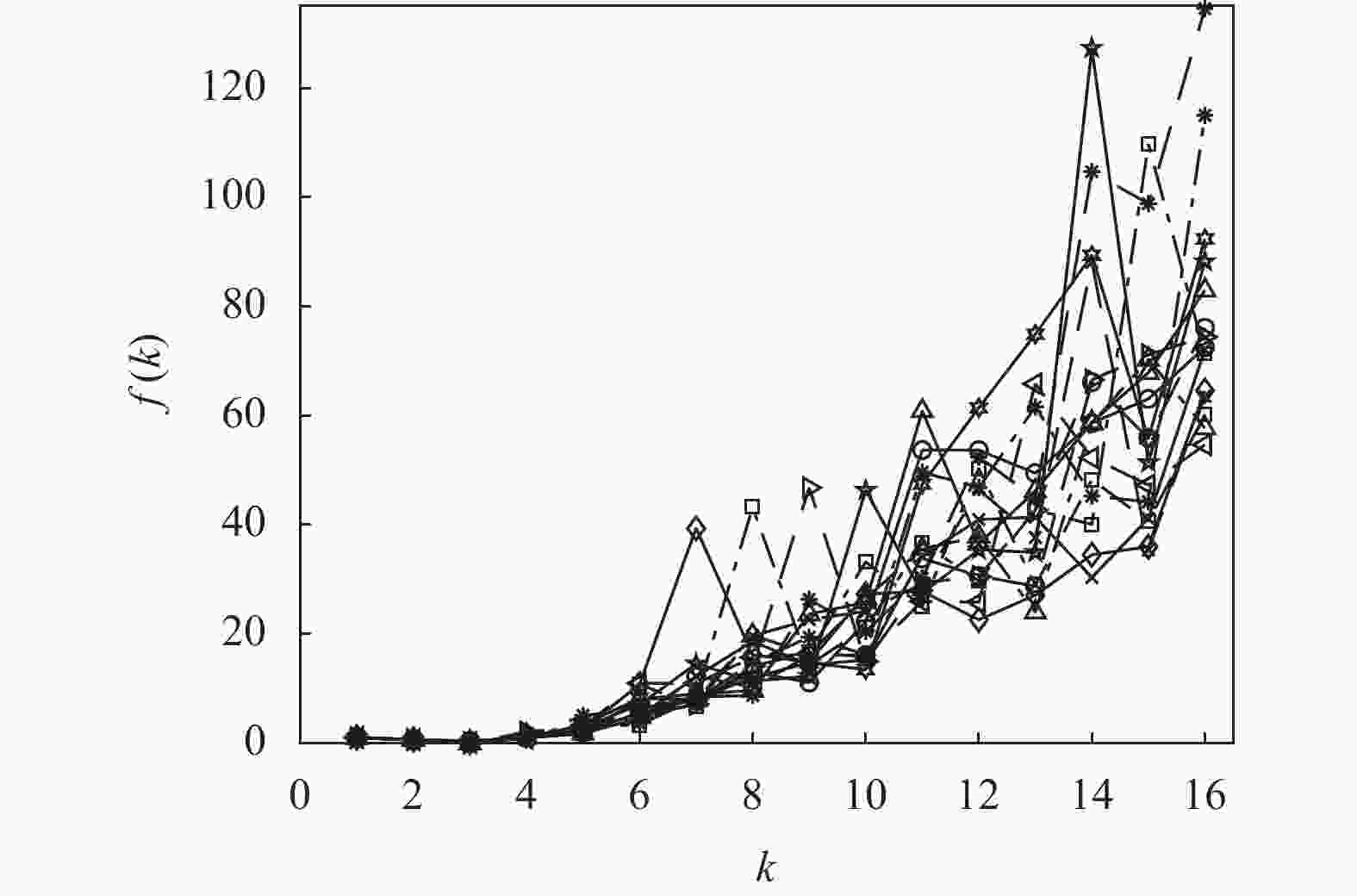
类似地，对于Wine数据集，在可能的聚类数量范围[kmin, kmax]内重复运行K-均值算法15次，计算并记录每次运行中指标f(k)的取值，其结果如图10所示。
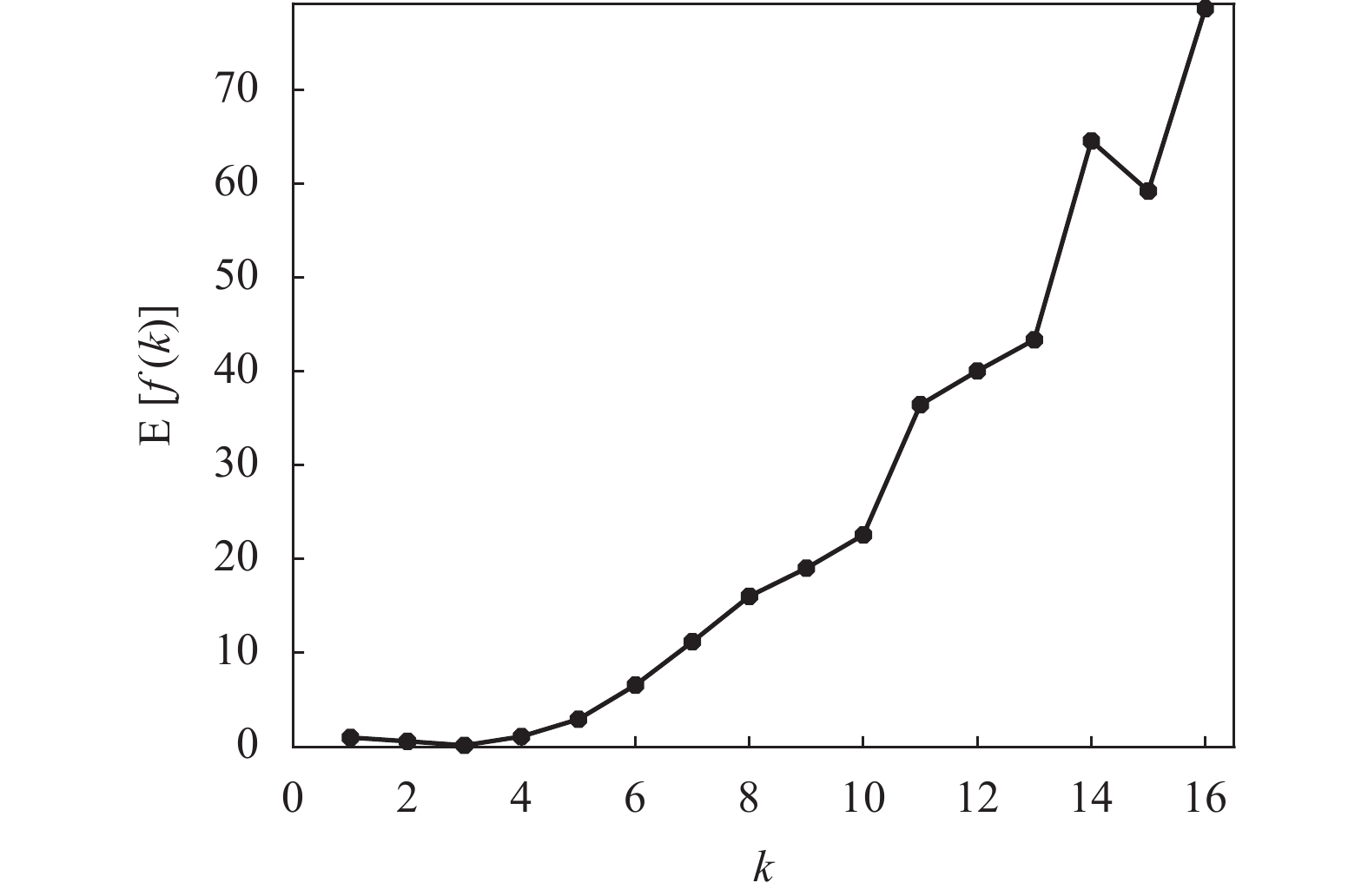
从图10也可看出，在运行K-均值算法的过程中，由于指标f(k)的取值范围较大，在它的最小值点附近的指标f(k)取值也不易区分。为此，考虑15次运行K-均值算法得到的平均性能E[f(k)]，其结果如图11所示。
从图11可以看出，对于Wine数据，随着聚类数量k值的增加，指标的平均值E[f(k)]曲线变化的大致趋势是：当k<3时，E[f(k)]曲线是递减的；当k>3时，E[f(k)]曲线是递增的，因此在k=3时取得E[f(k)]的最小值。为了更清楚地比较在E[f(k)]最小值附近数值上的差别，将图11中的E[f(k)]值列在表7中。可以看出，E[f(2)]大约是E[f(3)]的3.65倍，而E[f(4)]大约是E[f(3)]的6.8倍。
图 10 15次运行中Wine数据的f(k)随k变化的曲线
图 11 15次运行中Wine数据的E[f(k)]随k变化的曲线
表 7 Wine数据的E[f(k)]值与k的对应表
k f(k) k f(k) k f(k) 2 0.5939 7 11.2073 12 40.0710 3 0.1627 8 16.0550 13 43.3987 4 1.1079 9 19.0451 14 64.5943 5 2.9447 10 22.5938 15 59.2443 6 6.5854 11 36.4730 16 78.6860 尽管Wine数据集的平均性能E[f(k)]的取值范围相当大，但从它的全局极小值即最小值来说，仍然能辨别出k=3是Wine数据集最优的聚类数量。
从以上对3个UCI数据集(Iris, Seeds, Wine)的仿真结果可知，利用聚类有效性评价函数f(k)，不仅能够对原始数据集提供最优的聚类数量，而且从多次重复运行K-均值算法的效果来看，函数f(k)还能够对随机初始化提供很强的鲁棒性。
-
为了克服K-均值聚类算法需要用户预先指定聚类数量的缺陷，本文对K-均值算法的基本迭代步骤和聚类有效性进行了分析；然后，基于数据点的欧几里得距离，给出了类间质心距离之和、类内距离之和的定义，用于度量不同聚类间和同一聚类的数据距离；最后，提出了一种由类间质心距离之和与类内距离之和构造而成的聚类有效性评价函数，用以确定数据最优的聚类数量。在数据可能的聚类数量范围内，利用求解聚类有效性评价函数的最小值来确定K-均值算法的最佳聚类数量。通过对UCI中Iris、Seeds和Wine数据集的仿真，证明了所提出的聚类有效性评价函数不仅能够准确地反映原始数据的真实聚类结构，而且还能有效地降低K-均值算法对随机初始化的敏感性。
Determination of the Optimal Number of Clusters in K-Means Algorithm
-
摘要: K-均值(K-means)聚类算法是学术与工业领域的经典算法。然而，它却具有两个明显缺陷：1) 需要预先知道聚类的数量；2) 对算法的随机初始化非常敏感。为了解决这两个问题，首先归纳了K-均值算法的基本步骤，并对聚类有效性进行了分析；然后以数据样本点的欧几里德距离为基础，定义了以聚类数量k为自变量的类间质心距离之和以及类内距离之和，由此构造了聚类有效性评价函数；最后根据经验规则，在聚类数量的可能范围内通过求解聚类有效性评价函数的最小值以确定数据集的最优聚类数量。对UCI的3个数据集Iris、Seeds和Wine的仿真结果说明，提出的聚类有效性评价函数不仅能够准确地反映数据的真实聚类结构，还能有效地抑制算法对随机初始化的敏感性，通过对K-均值算法的多次运行，其结果也验证了聚类有效性评价函数的鲁棒性。Abstract: K-means clustering algorithm is a classic algorithm in academic and industrial fields. However, it has two most obvious defeats: one is that the number of clusters needs to be known in advance; the other is that it is very sensitive to the random initialization of the algorithm. In order to solve these problems, this paper summarizes the basic step of K-means algorithm and analyzes the clustering validity. Then, based on the Euclidean distance of the data points, the sum of centroid distances between classes and the sum of distances within cluster with the number of clusters k as the independent variable are defined, and the cluster validity evaluation function is constructed. Finally, according to the empirical rules, the optimal number of clusters in the data set is determined by solving the minimum value of the cluster validity evaluation function within the possible range of number of clusters. The simulation results of the three UCI datasets Iris, Seeds, and Wine shows that the proposed cluster validity evaluation function can not only accurately reflect the true cluster structure of the data, but also effectively suppress the sensitivity of the algorithm to random initialization. The multiple runs of the K-means algorithm also verify the robustness of the cluster validity evaluation function.
-
表 2 3种花4个属性的均值
cm 花种类 E[x1] E[x2] E[x3] E[x4] Setosa 5.006 3.428 1.462 0.246 Versicolor 5.936 2.770 4.260 1.326 Virginica 6.588 2.974 5.553 2.026 
下载: 导出CSV
表 3 Iris数据的f(k)与k的对应表
k f(k) k f(k) k f(k) 2 0.6469 6 8.4878 10 24.7449 3 0.0831 7 4.6767 11 10.5197 4 0.8377 8 9.6060 12 11.6496 5 3.4491 9 9.4557 − −
下载: 导出CSV
表 4 Iris数据的E[f(k)]值与k的对应表
k E[f(k)] k E[f(k)] k E[f(k)] 2 0.4940 6 6.4861 10 21.2041 3 0.2399 7 7.8881 11 17.9314 4 1.0678 8 13.6567 12 18.4198 5 2.7753 9 10.0362 − −
下载: 导出CSV
表 5 Wine(全部种类)数据各属性的平均值
x1 x2 x3 x4 x5 x6 x7 E[x] 13.00 2.34 2.37 19. 50 99.74 2.30 2.03 x8 x9 x10 x11 x12 x13 E[x] 0.36 1.59 5.06 0.96 2.61 746.90
下载: 导出CSV
表 6 Wine数据的f(k)与k的对应表
k f(k) k f(k) k f(k) 2 0.6299 7 16.4146 12 50.1047 3 0.0044 8 14.4553 13 45.5446 4 1.0391 9 19.4455 14 35.0423 5 9.5062 10 18.4569 15 44.2383 6 9.5934 11 21.0099 16 78.6142
下载: 导出CSV
表 7 Wine数据的E[f(k)]值与k的对应表
k f(k) k f(k) k f(k) 2 0.5939 7 11.2073 12 40.0710 3 0.1627 8 16.0550 13 43.3987 4 1.1079 9 19.0451 14 64.5943 5 2.9447 10 22.5938 15 59.2443 6 6.5854 11 36.4730 16 78.6860
下载: 导出CSV
-
[1] CHEN M, MAO S, LIU Y. Big data: A survey[J]. Mobile Networks & Applications, 2014, 19: 171-209. [2] XU R, WUNSCH II D C. Clustering[J]. IEEE Computational Intelligence Magazine, 2009, 4(3): 92-95. doi: 10.1109/MCI.2009.933101 [3] PASUPATHI S, SHANMUGANATHAN V, MADASAMY K, et al. Trend analysis using agglomerative hierarchical clustering approach for time series big data[J]. The Journal of Supercomputing, 2021, 77: 6505-6524. doi: 10.1007/s11227-020-03580-9 [4] ISHIZAKA A, LOKMAN B, TASIOU M. A stochastic multi-criteria divisive hierarchical clustering algorithm[J]. Omega, 2021, 103: 102370. [5] YANG M S, SINAGA K P. Collaborative feature-weighted multi-view fuzzy c-means clustering[J]. Pattern Recognition, 2021, 119: 108064. doi: 10.1016/j.patcog.2021.108064 [6] ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD-96). Portland: AAAI, 1996: 1-6. [7] STEINLY D. K-means clustering: A half-century synthesis[J]. British Journal of Mathematical and Statistical Psychology, 2006, 59: 1-34. doi: 10.1348/000711005X48266 [8] ROUX M. A Comparative study of divisive and agglomerative hierarchical clustering algorithms[J]. Journal of Classification, 2018, 35: 345-366. doi: 10.1007/s00357-018-9259-9 [9] SMIEJA M, WIERCIOCH M. Constrained clustering with a complex cluster structure[J]. Advances in Data Analysis and Classification, 2017, 11: 493-518. doi: 10.1007/s11634-016-0254-x [10] MORLINI I, ZANI S. Dissimilarity and similarity measures for comparing dendrograms and their applications[J]. Advances in Data Analysis and Classification, 2012, 6: 85-105. doi: 10.1007/s11634-012-0106-2 [11] LEONARDI M, GREGORIO L D, FAUSTO D D. Air traffic security: Aircraft classification using ADS-B message’s phase-pattern[J]. Aerospace, 2017, 4(51): 1-13. [12] SELIM S Z, ISMAIL M A. K-means-type algorithms: A generalized convergence theorem and characterization of local optimality[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(1): 81-87. [13] ZHU E, MA R. An effective partitional clustering algorithm based on new clustering validity index[J]. Applied Soft Computing, 2018, 71: 608-621. doi: 10.1016/j.asoc.2018.07.026 [14] GORDON A D. Cluster validation[C]//Proceedings of the 5th Conference of the International Federation of Classification Societies (IFCS-96). [S. l. ]: Springer, 1998: 22-39. [15] SERGIOS T, KONSTANTINOS K. Pattern recognition[M]. 4th ed. San Diego: Academic Press, 2009. [16] JAIN A K, DUBES R C. Algorithms for clustering data[M]. Englewood Cliffs NJ: Prentice Hall, 1988. [17] CHEN C H. Handbook of pattern recognition and computer vision[M]. 6th ed. Hackensack: World Science Publishing Company, 2020. [18] 余冬华, 郭茂祖, 刘扬, 等. 基于距离不等式的K-medoids聚类算法[J]. 软件学报, 2017, 28(12): 3115-3128. doi: 10.13328/j.cnki.jos.005237 YU D H, GUO M Z, LIU Y, et al. K-medoids clustering algorithm based on distance inequality[J]. Journal of Software, 2017, 28(12): 3115-3128. doi: 10.13328/j.cnki.jos.005237 [19] 周恩波, 毛善君, 李梅, 等. GPU加速的改进PAM聚类算法研究与应用[J]. 地球信息科学学报, 2017, 19(6): 782-791. doi: 10.3969/j.issn.1560-8999.2017.06.007 ZHOU E B, MAO S J, LI M, et al. Research and application of accelerating improved PAM clustering algorithm by GPU[J]. Journal of Geo-Information Science, 2017, 19(6): 782-791. doi: 10.3969/j.issn.1560-8999.2017.06.007 [20] HUANG W T, CHANG Y P. Some empirical Bayes rules for selecting the best population with multiple criteria[J]. Journal of Statistical Planning and Inference, 2006, 136: 2129-2143. doi: 10.1016/j.jspi.2005.08.032 [21] 李霓, 齐琦, 王凯华. 基于改进型经验法则的工艺偏差统计[J]. 海南师范大学学报(自然科学版), 2016, 29(1): 22-25. LI N, QI Q, WANG K H. Deviation analysis of process parameter based on improved empirical rule[J]. Journal of Hainan Normal University (Natural Science), 2016, 29(1): 22-25. [22] BALAKRISHNAN N, MA Y. Empirical Bayes rules for selecting the most and least probable multivariate hypergeometric event[J]. Statistics & Probability Letters, 1996, 27: 181-188. [23] GUPTA S S, HSIAO P. Empirical Bayes rules for selecting good populations[J]. Journal of Statistical Planning and Inference, 1983, 8: 87-101. doi: 10.1016/0378-3758(83)90064-2 -
点击查看大图
图(11) / 表(7)
计量
- 文章访问数: 4395
- HTML全文浏览量: 1089
- PDF下载量: 80
- 被引次数: 0
