The base of logarithmic used in this paper is always 2. We use ${\mathbb{Z}}_{q}$ to represent $ \mathbb{Z}\cap [0,q) $ when $ q $ is a positive integer. $ \lfloor r\rceil $ represents the nearest integer of the real number $ r $. When the value of $ r $ is the middle value of the two nearest integers, it is rounded up. $ \lfloor r\rfloor $ represents round down operation. We use lowercase bold letters to represent column vectors, such as $ \mathbf{a} $. Specifically, 0 represents the zero vector. We use $ \left|r\right| $ to represent the absolute value of the number $ r $. The dot product operation of vectors is represented as $ \left\langle{·,·}\right\rangle $. $x\leftarrow {D}$ means that $ x $ is sampled from the distribution ${D}$. When ${D}$ is a finite set, it means being uniformly sampled from ${D}$. In particular, we use ${{D}}_{{\mathbb{Z}}_{q},\sigma }$ to represent a discrete gaussian distribution with the parameter $ \sigma $ on $ {\mathbb{Z}}_{q} $. We use capital bold letters to denote matrices. $ |{|·||}_{\mathrm{\infty }} $ represents the infinite norm and $ \left|\right|·\left|\right| $ represents the Euclidean norm. The Gram-Schmidt order orthogonalization of matrix ${\boldsymbol{A}}$ is denoted by $\tilde{{\boldsymbol{A}}}$. We use $ {R}_{q} $ to represent $ {\mathbb{Z}}_{q}\left[x\right]/({x}^{n}+1) $.

Given positive integers $ q,m,n\in \mathbb{Z} $, and an arbitrary matrix ${\boldsymbol{A}}\in {\mathbb{Z}}_{q}^{n\times m}$, we can define a lattice described as follows:

For an arbitrary vector ${\boldsymbol{u}}\in {\mathbb{Z}}^{n}$, a coset of lattice ${\varLambda }_{q}^{\perp }\left({\boldsymbol{A}}\right)$ is defined as:

In the rest sections, we will use ${D}_{{\varLambda }_{q}^{\perp }\left({\boldsymbol{A}}\right),s}$ and ${D}_{{\varLambda }_{q}^{\boldsymbol{u}}\left({\boldsymbol{A}}\right),s}$ to represent the discrete gaussian distribution with the parameter $ s $ over ${\varLambda }_{q}^{\perp }\left({\boldsymbol{A}}\right)$ and ${\varLambda }_{q}^{{\boldsymbol{u}}}\left({\boldsymbol{A}}\right)$ respectively.

Definition 1^[13] (short integer solution (SIS))For positive integers $ m,n,q $, a uniformly random matrix ${\boldsymbol{A}}\in {\mathbb{Z}}_{q}^{n\times m}$and a positive real number $ \beta $, the goal of the $ {{\rm{SIS}}}_{n,q,\beta ,m} $ is to find a nonzero vector ${\boldsymbol{x}}\in {\varLambda }_{q}^{\perp }\left({\boldsymbol{A}}\right)$ which satisfies $\left|\right|\boldsymbol{x}\left|\right| < \beta$.

It is obviously that when $ \beta $ is small enough, the vector ${\boldsymbol{x}}$ will be a short vector of ${\varLambda }_{q}^{\perp }\left({\boldsymbol{A}}\right)$. To guarantee that the solution vector exists, the parameters $ m $ and $ \beta $ should satisfy $\beta \geqslant \sqrt{n{\rm{log}}q}$ and $m\geqslant n{\rm{log}}q$. The inhomogeneous SIS problem is to find a nonzero vector ${\boldsymbol{x}}\in {\varLambda }_{q}^{{\boldsymbol{u}}}\left({\boldsymbol{A}}\right)$ that satisfies $\left|\right|{\boldsymbol{x}}\left|\right| < \beta$, where $ \boldsymbol{u} $ is uniformly random and independent with of ${\boldsymbol{A}}$. It has been proved that the hardness of inhomogeneous SIS is the same as SIS.

Definition 2^[14] (ring short integer solution (RSIS)) For positive integers $ m,n,q $, a uniformly random vector ${\boldsymbol{a}}\in {R}_{q}^{m}$ and a positive real number $ \beta $, the goal of the $R-{{\rm{SIS}}}_{n,q,\beta ,m}$ is to find a nonzero vector ${\boldsymbol{x}}\in {R}_{q}^{m}$ which satisfies $\left\langle{{\boldsymbol{a}},{\boldsymbol{x}}}\right\rangle=0\in {{\boldsymbol{R}}}_{q}$ and has norm $\left|\right|{\boldsymbol{x}}\left|\right| < \beta$.

In the RSIS problem, to guarantee that the solution vector exists, $ m $ should be no less than ${\rm{log}}q.$

Definition 3^[3] (LWE) For integers $ n\geqslant 1,q\geqslant 2 $, a real number $ \alpha \in \left(\mathrm{0,1}\right) $ and a uniformly random vector ${\boldsymbol{s}}\in {\mathbb{Z}}_{q}^{n}$, we can define a distribution ${{\rm{LWE}}}_{n,q,\alpha }$ over $ {\mathbb{Z}}_{q}^{n}\times {\mathbb{Z}}_{q} $ as this:

where ${{\boldsymbol{a}}}\leftarrow {\mathbb{Z}}_{q}^{n}$ and $ {e\leftarrow D}_{{\mathbb{Z}}_{q},\alpha q} $.

The decision LWE problem can be described as a challenge game between an adversary $ A $ and a challenger oracle $ O $. First, given ${{\rm{LWE}}}_{n,q,\alpha }$, define two types of challenge oracle $ {O}_{1} $ and $ {O}_{2} $ that output a sample in $ {\mathbb{Z}}_{q}^{n}\times {\mathbb{Z}}_{q} $:

$ {O}_{1} $: The output sample is sampled from ${{\rm{LWE}}}_{n,q,\alpha }$.

$ {O}_{2} $: The output sample is sampled from uniformly random distribution.

The challenger oracle $ O $ in the game is either $ {O}_{1} $ or $ {O}_{2} $. The adversary $ A $ can repeat queries of the oracle $ O $ to get fresh samples. At the end of the game, $ A $ outputs a bit $ b $ to guess the type of $ O $. The advantage of $ A $ is:

It has been proved that the decision LWE problem is as hard as some worst-case hard problems on $ n $-dimensional lattices under a quantum reduction.

Ref. [15] proved that when ${{{\boldsymbol{s}}}\leftarrow {{{{D}}}}}_{{\mathbb{Z}}_{q}^{n},\alpha q}$, the LWE problem is still hard. This form of LWE is called normal form LWE.

Definition 4^[16] (ring learning with errors (RLWE)) For integers $ n\geqslant 1,q\geqslant 2 $, a real number $ \alpha \in \left(\mathrm{0,1}\right) $, a uniformly random element $ s\in {R}_{q} $, we can define a distribution $ {{\rm{RLWE}}}_{n,q,\alpha } $ over $ {R}_{q}\times {R}_{q} $ as this:

where $ a\leftarrow {R}_{q} $ and ${e\leftarrow {{{D}}}}_{{R}_{q},\alpha q}$.

The RLWE problem and its normal form have also been proved as hard as some worst-case hard problems on lattices under a quantum reduction.

The paper introduces some algorithms for lattices which are important for building a encryption scheme.

Lemma 1^[17] For positive integers $ q,n,m $, where $ q > 2 $ and $ m\approx 2n\mathrm{l}\mathrm{o}\mathrm{g}q $, the PPT algorithm TrapGen$ (n,m,q) $ can output a matrix ${{\boldsymbol{A}}}\in {\mathbb{Z}}_{q}^{n\times m}$ and a short basis ${{{\boldsymbol{T}}}}_{{{\boldsymbol{A}}}}\in {\mathbb{Z}}_{q}^{m\times m}$ for lattice ${\varLambda }_{q}^{\perp }\left({{\boldsymbol{A}}}\right)$. The statistical distance between the distribution of the output ${\boldsymbol{{A}}}$ and uniform distribution over $ {\mathbb{Z}}_{q}^{n\times m} $ is negligible. The norm of the Gram-Schmidt ordered orthogonalization of the output basis ${{{\boldsymbol{T}}}}_{{{\boldsymbol{A}}}}$ satisfies $\left|\right|\widetilde{{{{\boldsymbol{T}}}}_{{{\boldsymbol{A}}}}}\left|\right|\leqslant {{3.8}}\sqrt{n{\rm{log}}q}$.

Lemma 2^[2] There exists a PPT algorithm SamplePre$({{\boldsymbol{A}}},{{{\boldsymbol{T}}}}_{{{\boldsymbol{A}}}},{{\boldsymbol{u}}},\sigma )$ that can output a vector ${{\boldsymbol{x}}}\in {\varLambda }_{q}^{{{\boldsymbol{u}}}}\left({{\boldsymbol{A}}}\right)$ which is sampled from a distribution statistically close to ${{D}}_{{\varLambda }_{q}^{\boldsymbol{u}}\left({{\boldsymbol{A}}}\right),\sigma }$. The inputs of SamplePre should satisfy that ${{\boldsymbol{A}}}\in {\mathbb{Z}}_{q}^{n \times m},m > n,q > 2$ and $\sigma \geqslant \left|\right|\widetilde{{{{\boldsymbol{T}}}}_{{{\boldsymbol{A}}}}}\left|\right|·\omega \left(\sqrt{{\rm{log}}m}\right)$. ${{{\boldsymbol{T}}}}_{{{\boldsymbol{A}}}}$ is a short basis of ${\varLambda }_{q}^{\perp }\left({{\boldsymbol{A}}}\right)$.

Lemma 3^[11] For positive integers $ q,n,m,k $ and a real number $ \sigma $, where $ k=⌈{\rm{log}}q⌉,m > k $, $ n $ is a power of two and $ q $ is a prime satisfying $ q\equiv 1\;{\rm{mod}}\;2n $. There exists a PPT algorithm TrapGen$ (n,m,q,\sigma ) $ that outputs a uniformly random vector $ {\boldsymbol{a}}\in {R}_{q}^{m} $ and a trapdoor $ {{\boldsymbol{T}}}_{{\boldsymbol{a}}}\in {R}^{(m-k)\times k} $.

Lemma 4^[18] There exists a PPT algorithm SamplePre$ (\boldsymbol{a},{{\boldsymbol{T}}}_{{\boldsymbol{a}}},u,\sigma ) $ that can output a vector ${\boldsymbol{x}}\in {R}_{q}^{m}$ which satisfies ${{\boldsymbol{a}}}^{\mathrm{T}}{\boldsymbol{x}}=u$ and follows a discrete gaussian distribution of parameter $ \sigma $. $ {{\boldsymbol{T}}}_{{\boldsymbol{A}}} $ is the trapdoor of $ {\boldsymbol{a}} $.

The IBE scheme uses the TrapGen and SamplePre algorithms to generate the master public key, master secret key and users' secret keys, which is similar with other LWE-based IBE schemes. The main difference between our scheme and others is in the encryption. Compared with other LWE-based schemes, the first part of ciphertexts of our scheme can also encrypt messages. While other schemes only encrypt the message in the second part of ciphertexts. This makes our scheme encrypt more bits than other schemes. To encrypt messages, our scheme uses LWE instances to mask the plaintext. As the LWE instances $\left({\boldsymbol{A}},{\boldsymbol{A}}{\boldsymbol{s}}+{\boldsymbol{e}}\right)$ are indistinguishable from uniformly random, ${\boldsymbol{A}}{\boldsymbol{s}}+{\boldsymbol{e}}+{\boldsymbol{\varDelta}} {\boldsymbol{m}}$ and ${\boldsymbol{A}}{\boldsymbol{s}}+{\boldsymbol{e}}+{\boldsymbol{A}}{\boldsymbol{\varDelta}} {\boldsymbol{m}}$ will also be indistinguishable from uniformly random vector, where ${\boldsymbol{\varDelta}}$ is $ ⌊q/2⌉ $.

Our IBE scheme is described as follows:

Setup($ {1}^{\lambda } $): The PKG chooses an odd prime number $ q > 2 $, positive integers $ n,m,l,k $, a real number $ \sigma $ and a hash functions $ H:{\left\{\mathrm{0,1}\right\}}^{k}\to {\mathbb{Z}}_{q}^{n\times n}\times {\mathbb{Z}}_{q}^{n\times l} $, where $ k $ is the length of an identity and $ l $ is the length of the second part of message. The first part of the output of $ H $ is an invertible matrix. Then it runs TrapGen($ n,m,q $) to generate a uniformly random matrix ${\boldsymbol{A}}\in {\mathbb{Z}}_{q}^{n\times m}$and a short basis ${{\boldsymbol{T}}}_{{\boldsymbol{A}}}\in {\mathbb{Z}}_{q}^{m\times m}$ of the lattice ${\varLambda }_{q}^{\perp }\left({\boldsymbol{A}}\right)$. The PKG sets the master public key ${\rm{mp}}k={\boldsymbol{A}}$ and master secret key ${\rm{msk}}={{\boldsymbol{T}}}_{{\boldsymbol{A}}}$. Finally, the PKG publishes the parameters ${\rm{param}}=(n,m,l,q,\sigma ,\boldsymbol{A},H)$.

Extract(${\rm{param,id,msk}}$): For a users' identity ${\rm{id}}$, the PKG first calculates $({\mathbf{U}}_{1{\rm{id}}},{\mathbf{U}}_{2{\rm{id}}})= H\left({\rm{id}}\right)\in {\mathbb{Z}}_{q}^{n\times n}\times {\mathbb{Z}}_{q}^{n\times l}$. Then it runs SamplePre(${\boldsymbol{A}},{{\boldsymbol{T}}}_{{\boldsymbol{A}}},{{\boldsymbol{u}}}_{1i},\sigma$) for $ i=\mathrm{1,2}, \cdots ,n $ to generate a matrix ${{{\boldsymbol{S}}}}_{1{\rm{id}}}$ satisfying ${\boldsymbol{A{S}}}_{1{\rm{id}}}={{\boldsymbol{U}}}_{1{\rm{id}}}$, where ${{\boldsymbol{u}}}_{1i}$ is the $ i $-th column of ${{\boldsymbol{U}}}_{1{\rm{id}}}$. Next, it computes ${{\boldsymbol{U}}}_{{\rm{id}}}={{\boldsymbol{U}}}_{1{\rm{id}}}{{\boldsymbol{U}}}_{2{\rm{id}}}$. Then PKG runs SamplePre(${\boldsymbol{A}},{{\boldsymbol{T}}}_{{\boldsymbol{A}}},{{\boldsymbol{U}}}_{{\rm{id}}},\sigma$) to sample a matrix ${{\boldsymbol{S}}}_{2{\rm{id}}}$ satisfying ${{\boldsymbol{U}}}_{1{\rm{id}}}^{-1}{\boldsymbol{A}}{{\boldsymbol{S}}}_{2{\rm{id}}}={{\boldsymbol{U}}}_{2{\rm{id}}}$. Finally, PKG sends ${{\rm{sk}}}_{{\rm{id}}}=({{\boldsymbol{S}}}_{1{\rm{id}}},{{\boldsymbol{S}}}_{2{\rm{id}}})$ to the user securely.

Enc(${\rm{param,id,}}{\boldsymbol{m}}$): To encrypt a message ${\boldsymbol{m}}\in {\left\{\mathrm{0,1}\right\}}^{n+l}$, the sender first encodes the message as ${{\boldsymbol{m}}}'=\lfloor q/2 \cdot {\boldsymbol{m}} \rceil \in {\mathbb{Z}}_{q}^{n+l}$ and partitions it into two parts ${{{\boldsymbol{m}}}'}_{1}\in {\mathbb{Z}}_{q}^{n},{{{\boldsymbol{m}}}'}_{2}\in {\mathbb{Z}}_{q}^{l}$ satisfying ${{\boldsymbol{m}}}'={[{{{\boldsymbol{m}}}'}_{1}^{\mathrm{T}}|{{{\boldsymbol{m}}}'}_{2}^{\mathrm{T}}]}^{\mathrm{T}}$. The public key of receiver can be calculated as ${{\rm{pk}}}_{{\rm{id}}}=({{\boldsymbol{A}}}_{{\rm{id}}},{{\boldsymbol{U}}}_{2{\rm{id}}})=({{\boldsymbol{}}U}_{1{\rm{id}}}^{-1}{\boldsymbol{A}},{{\boldsymbol{U}}}_{2{\rm{id}}})$. Then he samples are ${{\boldsymbol{e}}}_{1}\leftarrow {{D}}_{{\mathbb{Z}}_{q}^{n},\sigma },{{\boldsymbol{e}}}_{2}\leftarrow {{D}}_{{\mathbb{Z}}_{q}^{m},\sigma },{{\boldsymbol{e}}}_{3}\leftarrow {{D}}_{{\mathbb{Z}}_{q}^{l},\sigma }$ and we can calculate the ciphertext as $\mathbf{c}=({\mathbf{c}}_{0},{\mathbf{c}}_{1})=({{{\boldsymbol{A}}}_{{\rm{id}}}^{\mathrm{T}}{\boldsymbol{m}}'}_{1}+{{\boldsymbol{A}}}_{{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}_{1}+{{\boldsymbol{e}}}_{2}, {{\boldsymbol{U}}}_{2{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}_{1}+{{\boldsymbol{e}}}_{3}+ {{{\boldsymbol{m}}}'}_{2})\in {\mathbb{Z}}_{q}^{m}\times {\mathbb{Z}}_{q}^{l}$.

Dec(${\rm{param}},{{\rm{sk}}}_{{\rm{id}}},{\boldsymbol{c}}$): After receiving a ciphertext ${\boldsymbol{c}}$, the receiver calculates ${{{\boldsymbol{m}}}}_{1}= \lfloor 2/q \cdot {{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{{\boldsymbol{c}}}}_{0} \rceil \in {\left\{\mathrm{0,1}\right\}}^{n}$, ${{\boldsymbol{m}}}_{2}= \lfloor 2/q \cdot {({{{\boldsymbol{c}}}}_{1}-{{\boldsymbol{S}}}}_{2{\rm{id}}}^{\mathrm{T}}({{{\boldsymbol{c}}}}_{0}-{{{\boldsymbol{A}}}}_{{\rm{id}}}^{\mathrm{T}} \lfloor q/2 \cdot {{{\boldsymbol{m}}}}_{1} \rceil )) \rceil$. The message is ${{\boldsymbol{m}}}={[{{{\boldsymbol{m}}}}_{1}^{\mathrm{T}}|{{{\boldsymbol{m}}}}_{2}^{\mathrm{T}}]}^{\mathrm{T}}$.

Theorem 1　The decrypt algorithm can recover the message from ciphertext correctly if the following inequations are hold.

where ${{{{\boldsymbol{e}}}}_{1}}_{i}$ is the $ i $-th component of ${{{\boldsymbol{e}}}}_{1}$, ${{{{\boldsymbol{e}}}}_{3}}_{i}$ is the $ i $-th component of ${{{\boldsymbol{e}}}}_{3}$, ${{\mathbf{s}}_{1{\rm{id}}}}_{i}$ is the $ i $-th column of ${{{\boldsymbol{S}}}}_{1{\rm{id}}}$ and ${{{{\boldsymbol{s}}}}_{2{\rm{id}}}}_{i}$ is the $ i $-th column of ${{{\boldsymbol{S}}}}_{2{\rm{id}}}$.

Proof　We first consider the error term of the first part of the decryption result. According to the scheme, we have ${{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{{\boldsymbol{c}}}}_{0}={{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{{\boldsymbol{A}}}}_{{\rm{i}}d}^{\mathrm{T}}{{{{\boldsymbol{m}}}}'}_{1}+ {{{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{A}}}}_{{\rm{i}}{\rm{d}}}^{\mathrm{T}}{{{\boldsymbol{e}}}}_{1}+ {{{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}}_{2} = {{{\boldsymbol{S}}}}_{1{\rm{{\rm{id}}}}}^{\mathrm{T}}{{{\boldsymbol{A}}}}_{{\rm{id}}}^{\mathrm{T}} \left({{{{\boldsymbol{m}}}}'}_{1} + {{{\boldsymbol{e}}}}_{1}\right) + {{{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}}_{2} = {{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{{\boldsymbol{A}}}}^{\mathrm{T}}{{{{\boldsymbol{U}}}}_{1{\rm{id}}}^{-1}}^{\mathrm{T}}\left({{{{\boldsymbol{m}}}}'}_{1} + {{{\boldsymbol{e}}}}_{1}\right) $+$ {{{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}}_{2} = {{{\boldsymbol{U}}}}_{1{\rm{id}}}^{\mathrm{T}}{{{{\boldsymbol{U}}}}_{1{\rm{id}}}^{-1}}^{\mathrm{T}} \left({{{{\boldsymbol{m}}}}'}_{1} + {{{\boldsymbol{e}}}}_{1}\right) + {{{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}}_{2} = {{{{\boldsymbol{m}}}}'}_{1} + {{{\boldsymbol{e}}}}_{1} + {{{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}}_{2} = \lfloor q/2 $·$ {{{\boldsymbol{m}}}}_{1} \rceil + {{{\boldsymbol{e}}}}_{1}+{{{\boldsymbol{m}}}}_{1} \rceil +{{{\boldsymbol{e}}}}_{1}+{{{{\boldsymbol{S}}}}_{1{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}}_{2}$. The $ i $-th component of the first part of the decryption result and the message will be equal to each other if $|{{{{\boldsymbol{e}}}}_{1}}_{i}+\left\langle{{{{{{\boldsymbol{s}}}}_{1{\rm{id}}}}_{i},{{\boldsymbol{e}}}}_{2}}\right\rangle| < q/4$. If the first part of the decryption result is correct, then for the second part of the decryption result, we have ${{{{\boldsymbol{c}}}}_{1}- {{\boldsymbol{S}}}}_{2{\rm{id}}}^{\mathrm{T}} ({{{\boldsymbol{c}}}}_{0}- {{{\boldsymbol{A}}}}_{{\rm{id}}}^{\mathrm{T}} \lfloor q/2 \cdot {{{\boldsymbol{m}}}}_{1} \rceil )$ = ${{{{\boldsymbol{c}}}}_{1}-{{\boldsymbol{S}}}}_{2{\rm{id}}}^{\mathrm{T}}({{{\boldsymbol{A}}}}_{{\rm{id}}}^{\mathrm{T}}{{{\boldsymbol{e}}}}_{1}+{{{\boldsymbol{e}}}}_{2})={{{\boldsymbol{U}}}}_{2{\rm{id}}}^{\mathrm{T}}{{{\boldsymbol{e}}}}_{1}+{{{\boldsymbol{e}}}}_{3}+ {{{{\boldsymbol{m}}}}'}_{2}- ({{{\boldsymbol{U}}}}_{2{\rm{id}}}^{\mathrm{T}}{{{\boldsymbol{e}}}}_{1}+{{{\boldsymbol{S}}}}_{2{\rm{id}}}^{\mathrm{T}}{{{\boldsymbol{e}}}}_{2})= \lfloor q/2 \cdot {{{\boldsymbol{m}}}}_{2} \rceil + {{{\boldsymbol{e}}}}_{3}-{{{{\boldsymbol{S}}}}_{2{\rm{id}}}^{\mathrm{T}}{{\boldsymbol{e}}}}_{2}$. So the $ i $-th component of the second part of the decryption result is correct if $|{{{{\boldsymbol{e}}}}_{3}}_{i}-\left\langle{{{{{{\boldsymbol{s}}}}_{2{\rm{id}}}}_{i},{{\boldsymbol{e}}}}_{2}}\right\rangle| < \frac{q}{4}$.

We first give the definition of IND-ID-CPA. Then we prove that our scheme can achieve IND-ID-CPA security.

Definition 5　For a IBE scheme P(Setup, Extract, Enc, Dec), a challenger $ C $ and an adversary $ A $, the IND-ID-CPA game is described as follows.

Setup　$C$ runs the Setup algorithm to generate the public parameters ${\rm{param}}$, master public key ${\rm{ mpk}}$ and master secret key ${\rm{msk}}$, then sends ${\rm{param }}$ and ${\rm{mpk }}$ to $ A $.

Phase 1　$ A $ can make secret key extraction queries for any identity ${\rm{id}}$. The challenger $ C $ runs Extract(${\rm{param,id,msk}}$) to generate the secret key ${\rm{sk}}$ and sends it to $ A $.

Challenge　$ A $ selects an identity ${{\rm{id}}}^{*}$ which has not been queried in phase 1 and two different messages ${{{m}}}_{0}$, ${{{m}}}_{1}$ and sends them to $ C $. $ C $ runs $ c $← Enc(${\rm{param}},{{\rm{id}}}^{*},{m}_{b}$) and responses $ c $ to $ A $, where $ b $ is a uniformly random bit.

Phase 2　$A$ can repeat Phase 1. The only restriction is that he can’t query the secret key of ${{\rm{id}}}^{*}$.

Guess　$A $ outputs a bit $b'$.

If there does not exist any polynomial adversary $ A $ that achieves non-negligible ${\rm{Adv}}\left(A\right)=\left|\mathrm{P}\mathrm{r}\right[b'=b]- \mathrm{P}\mathrm{r}[b'\ne b\left]\right|$, we say that P is IND-ID-CPA secure. If the target identity is submitted before the setup, the game is named indistinguishability of ciphertexts against selectively chosen identity and chosen plaintext attack (IND-sID-CPA).

Theorem 2　If there exists a polynomial adversary $ A $ that can break the IND-ID-CPA secure of the scheme described in section 3.1 in the random oracle model, then there exists a polynomial algorithm that can solve the normal form decision-LWE problem.

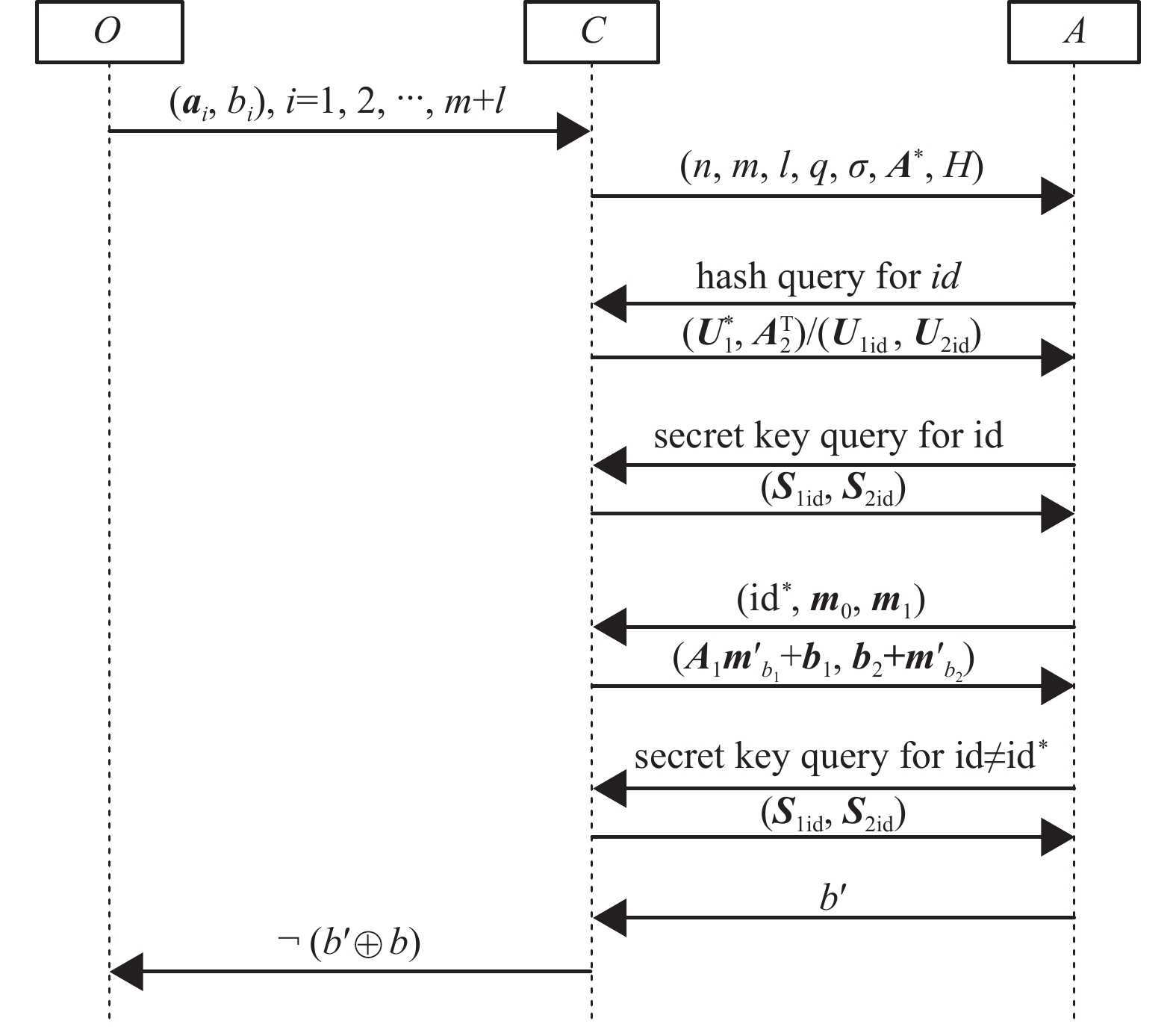
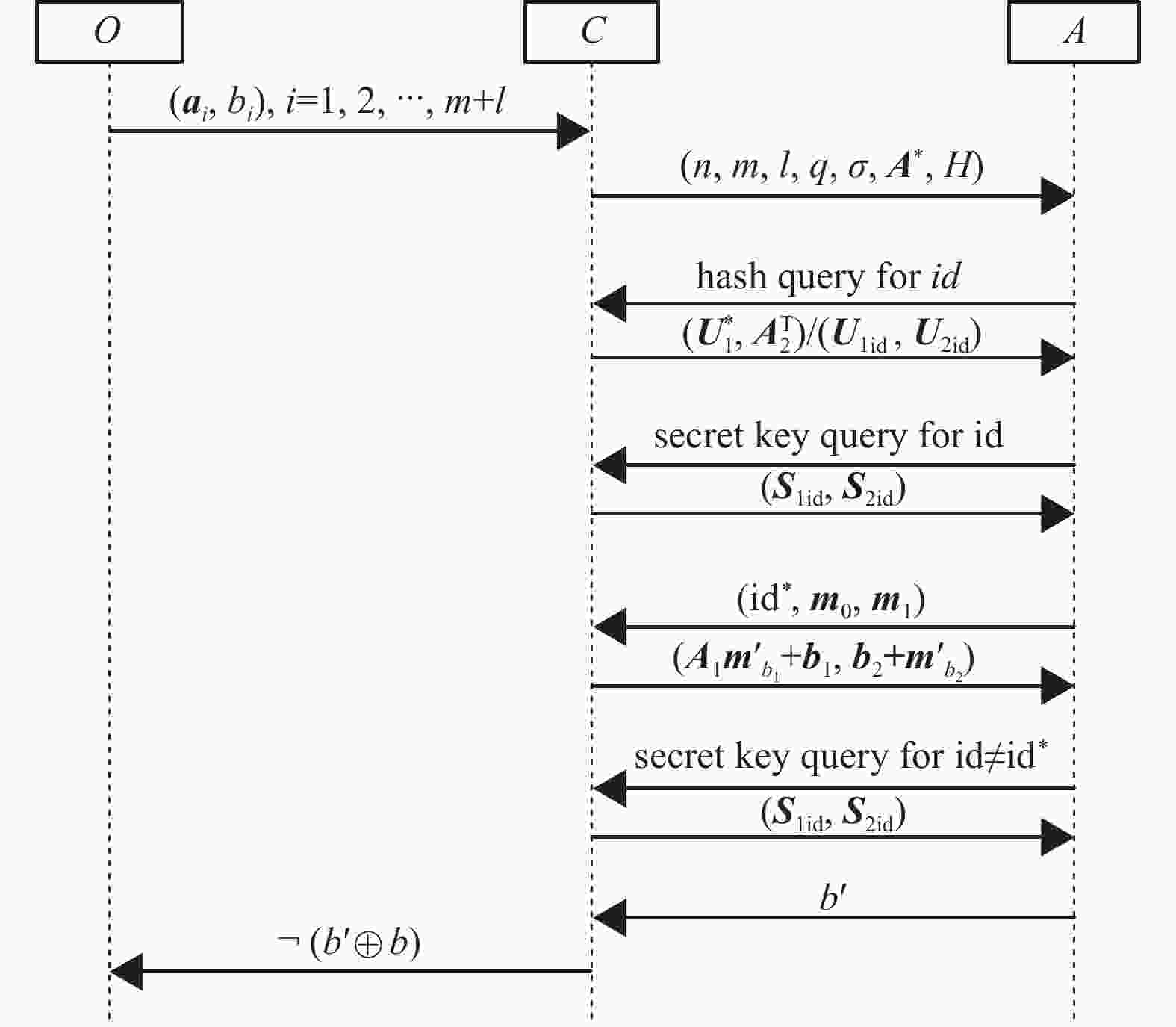
Proof　We show that how to use the adversary $ A $ to construct an algorithm $ C $ that can answer the normal form LWE oracle $ O $. We set $ C $ to be the challenger of the IND-ID-CPA game. First, $ C $ queries the oracle $ O $ and gets $ m+l $ instances $\left({{{\boldsymbol{a}}}}_{i},{b}_{i}\right)\in {\mathbb{Z}}_{q}^{n}\times {\mathbb{Z}}_{q}$. Then $ C $ uses these instances to combine two matrices ${{{\boldsymbol{A}}}}_{{\bf{1}}}\in {\mathbb{Z}}_{q}^{m\times n}$,${{{\boldsymbol{A}}}}_{{\bf{2}}}\in {\mathbb{Z}}_{q}^{l\times n}$ and two vectors ${{{\boldsymbol{b}}}}_{{\bf{1}}}\in {\mathbb{Z}}_{q}^{m}$,${{{\boldsymbol{b}}}}_{{\bf{2}}}\in {\mathbb{Z}}_{q}^{l}$ , where every row of matrices is ${\boldsymbol{a}}_{i}$ and every component of vectors is $ {b}_{i} $. The rank of the matrix ${{{\boldsymbol{A}}}}_{{\bf{1}}}$ must be $ n $. If not, $ C $ can repeat the query until he gets a rank $ n $ matrix. After this, $ C $ performs the game with $ A $ as follows.

Setup　$ C $ generates the public params of the IBE scheme as follows.

1) Let $ {Q}_{H} $ be the number of hash queries made by $ A $. $ C $ selects a random number $ 1\leqslant I\leqslant {Q}_{H} $.

2) $ C $ selects a uniformly random invertible matrix ${{{\boldsymbol{U}}}}_{1}^{*}\in {\mathbb{Z}}_{q}^{n\times n}$, then it calculates ${{{\boldsymbol{A}}}}^{*}$=${{{\boldsymbol{U}}}}_{1}^{*}{{{\boldsymbol{A}}}}_{1}^{\mathrm{T}}$ and returns the ${\rm{param}}=(n,m,l,q,\sigma ,{{{\boldsymbol{A}}}}^{*},H)$ to $ A $, where $ n,q,\sigma $ are the parameters of the normal LWE oracle.

Random-oracle hash queries　For the $ Q $-th query submitted by $ A $, $ C $ answers the query as follows. (We assume that each identity will only be queried once.)

1) If $ Q=I $, $ C $ returns (${{{\boldsymbol{U}}}}_{1}^{*}$,${{{\boldsymbol{A}}}}_{2}^{\mathrm{T}}$) and saves the tuple ($Q,{\rm{id}},{{{\boldsymbol{U}}}}_{1}^{*},{{{\boldsymbol{A}}}}_{2}^{\mathrm{T}},\perp ,\perp$).

2) If $ Q\ne I $, $ C $ samples $ n+l $ vectors $ {\mathbf{e}}_{i}\leftarrow {{{D}}}_{{\mathbb{Z}}_{q}^{m},\sigma } $ and uses these vector to combine two matrices ${{{\boldsymbol{S}}}}_{1{\rm{id}}}\in {\mathbb{Z}}_{q}^{m\times n}$, ${{{\boldsymbol{S}}}}_{2{\rm{id}}}\in {\mathbb{Z}}_{q}^{m\times l}$, which satisfies that ${{{\boldsymbol{A}}}}^{*}{{{\boldsymbol{S}}}}_{1{\rm{id}}}$ is an invertible matrix. Then $ C $ calculates ${{{\boldsymbol{U}}}}_{1{\rm{id}}}={{{\boldsymbol{A}}}}^{*}{{{\boldsymbol{S}}}}_{1{\rm{id}}}\;{\rm{and}} \; {{{\boldsymbol{U}}}}_{2{\rm{id}}}= {{{\boldsymbol{U}}}}_{1{\rm{id}}}^{-1}{{{\boldsymbol{A}}}}^{*}{{{\boldsymbol{S}}}}_{2{\rm{id}}}$. $ C $ saves the tuple ($Q,{\rm{id}},{{{\boldsymbol{U}}}}_{1{\rm{id}}}, {{{\boldsymbol{U}}}}_{2{\rm{id}}},{{{\boldsymbol{S}}}}_{1{\rm{id}}},{{{\boldsymbol{S}}}}_{2{\rm{id}}}$) and returns (${{{\boldsymbol{U}}}}_{1{\rm{id}}},{{{\boldsymbol{U}}}}_{2{\rm{id}}}$) to $ A $.

Secret key queries　When $ A $ queries the secret key for an $ {\rm{id}} $, $ C $ searches the saved tuple ($Q,{\rm{id}}, {{\boldsymbol{U}}}_{1{\rm{id}}},{{{\boldsymbol{U}}}}_{2{\rm{id}}},{{{\boldsymbol{S}}}}_{1{\rm{id}}},{{{\boldsymbol{S}}}}_{2{\rm{id}}}$) from the history of the hash oracle query. (We assume that every $ {\rm{id}} $ has been queried in hash query before secret key query.) If ${{{\boldsymbol{S}}}}_{1{\rm{id}}}=\perp$ and ${{{\boldsymbol{S}}}}_{2{\rm{id}}}=\perp$, $ C $ aborts and outputs a random bit. Else, $ C $ returns (${{{\boldsymbol{S}}}}_{1{\rm{id}}},{{{\boldsymbol{S}}}}_{2{\rm{id}}}$) to $ A $.

Challenge　$ A $ submits the target $ {{\rm{id}}}^{*} $ and two random messages $ {\mathbf{m}}_{0},{\mathbf{m}}_{1} $ to $ C $. If $ {{\rm{id}}}^{*} $ is not the identity that is queried in the $ I $-th hash query, $ C $ aborts and outputs a random bit. Otherwise, $ C $ chooses a random bit $ b $, and computes the challenge ciphertext ${{\boldsymbol{c}}}=({{{\boldsymbol{c}}}}_{0},{{{\boldsymbol{c}}}}_{1})=({{{{\boldsymbol{A}}}}_{{\bf{1}}}{{\boldsymbol{m}}}'}_{{b}_{1}}+{{{\boldsymbol{b}}}}_{{\bf{1}}},{{{\boldsymbol{b}}}}_{{\bf{2}}}+{{{\boldsymbol{m}}}'}_{{b}_{2}})$, where ${{{{\boldsymbol{m}}}}'}_{b}= \lfloor q/2 \cdot {{{\boldsymbol{m}}}}_{b} \rceil ={[{{{{\boldsymbol{m}}}}'}_{{b}_{1}}^{\mathrm{T}}|{{{{\boldsymbol{m}}}}'}_{{b}_{2}}^{\mathrm{T}}]}^{\mathrm{T}}$.

If the instances returned by $ O $ are uniformly random vectors, the challenge ciphertext is uniformly random and completely hides the information of $ b $. If the instances returned by $ O $ are normal LWE instances, then the challenge ciphertext will be a valid encryption of $ {\mathbf{m}}_{b} $ for identity ${{\rm{id}}}^{*}$.

$ A $ can make more secret key queries after the challenge phase with the restriction that it can’t make the secret key query for identity ${{\rm{id}}}^{*}$. After that, $ A $ outputs a bit $b'$ to $ C $. If $b'=b$, $ C $ outputs $ 1 $, else $ C $ outputs $ 0 $.

If $ C $ dose not abort, the interaction between oracle $ O $, algorithm $ C $ and adversary $ A $ will be as shown in Figure 1.

By a standard argument, $ C $ will not abort during the game with the probability $ 1/{Q}_{H} $. If $ C $ does not abort, it means that the target identity submitted by $ A $ is the identity queried by the $ I $-th hash query. In this case, if the challenge ciphertext is uniformly random, the probability $b'=b$ is $ 1/2 $. (Which means that the instances returned by $ O $ are uniformly random.) If the challenge ciphertext is a valid encryption, the probability $b'=b$ is $1/2+{\rm{Adv}}\left(A\right)$. (Which means that the instances returned by $ O $ are LWE instances.) So the advantage that $ C $ can distinguish LWE instances from uniformly random vectors is ${\rm{Adv}}\left(A\right)/{Q}_{H}$. Thus, if $ A $ has an non-negligible advantage to break the IND-ID-CPA security, then $ C $ has a non-negligible advantage to solve decision normal LWE problem.

Figure 1.  The interaction between $ O $,$ C $ and $ A $.

Our ring version IBE scheme is described as follows:

Setup($ {1}^{\lambda } $): The PKG chooses positive integers $ n,m,q,k,l $, two real number $ \sigma ,\theta $ and a hash functions $ H:{\left\{\mathrm{0,1}\right\}}^{l}\to {R}_{q}\times {R}_{q} $, where $ l $ is the length of an identity. The first part of the output of $ H $ is an invertible element of $ {R}_{q} $. Then PKG runs TrapGen$ (n,m,q,\theta ) $ to generate a random vector $ \boldsymbol{a}\in {R}_{q}^{m} $ and a short basis ${{{\boldsymbol{T}}}}_{{{\boldsymbol{a}}}}\in {R}_{q}^{(m-k)\times k}$ of the lattice ${\varLambda }_{q}^{\perp }\left({{\boldsymbol{a}}}\right)$. The PKG sets the master public key ${\rm{mpk}}={{\boldsymbol{a}}}$ and master secret key ${\rm{msk}}={{{\boldsymbol{T}}}}_{{{\boldsymbol{a}}}}$. Finally, the PKG publishes the parameters $ param=(n,m,l,q,k,\sigma ,\theta ,\boldsymbol{a},H) $.

Extract($ {\rm{param}},{\rm{id}},{\rm{msk}} $): For a users' identity $ {\rm{id}} $, the PKG first calculates $({u}_{1{\rm{id}}},{u}_{2{\rm{id}}})=H\left({\rm{id}}\right)\in {R}_{q}\times {R}_{q}$. Then it runs SamplePre(${{\boldsymbol{a}}},{{{\boldsymbol{T}}}}_{{{\boldsymbol{a}}}},{u}_{1{\rm{id}}},\sigma$) to generate a vector $ {\mathbf{x}}_{1{\rm{id}}} $ satisfying ${{{\boldsymbol{a}}}}^{\mathrm{T}}{{{\boldsymbol{x}}}}_{1{\rm{id}}}={u}_{1{\rm{id}}}$. Next, it computes ${u}_{{\rm{id}}}={u}_{1{\rm{id}}}{u}_{2{\rm{id}}}$. Then PKG runs SamplePre$({{\boldsymbol{a}}},{{{\boldsymbol{T}}}}_{{{\boldsymbol{a}}}},{u}_{{\rm{id}}},\sigma )$ to sample a vector ${{{\boldsymbol{x}}}}_{2{\rm{id}}}$ satisfying ${u}_{1{\rm{id}}}^{-1}{{{\boldsymbol{a}}}}^{\mathrm{T}}{{{\boldsymbol{x}}}}_{2{\rm{id}}}={u}_{2{\rm{id}}}$. Finally, PKG sends ${{\rm{sk}}}_{{\rm{id}}}=({{{\boldsymbol{x}}}}_{1{\rm{id}}},{{{\boldsymbol{x}}}}_{2{\rm{id}}})$ to the user securely.

Enc(${\rm{param}},{\rm{id}},{{\boldsymbol{m}}}$): To encrypt a message ${{\boldsymbol{m}}}\in {R}_{2}\times {R}_{2}$, the sender first encodes the message as ${{{\boldsymbol{m}}}}'= \lfloor q/2 \cdot {{\boldsymbol{m}}} \rceil \in {R}_{q}\times {R}_{q}$ and partitions it into two parts $ {{m}'}_{1}\in {R}_{q},{{m}'}_{2}\in {R}_{q} $. The public key of receiver can be calculated as ${{\rm{pk}}}_{{\rm{id}}}=({{{\boldsymbol{a}}}}_{{\rm{id}}},{u}_{2{\rm{id}}})=({u}_{1{\rm{id}}}^{-1}{{\boldsymbol{a}}},{u}_{2{\rm{id}}})$. Then it samples ${e}_{1},{e}_{3}\leftarrow {{{D}}}_{{R}_{q},\sigma },{{{\boldsymbol{e}}}}_{2}\leftarrow {{{D}}}_{{R}_{q}^{m},\sigma }$ and calculates the ciphertext $\boldsymbol{c}=({\mathbf{c}}_{0},{c}_{1})=({m'}_{1}{{{\boldsymbol{a}}}}_{{\rm{id}}}+{e}_{1}{{{\boldsymbol{a}}}}_{{\rm{id}}}+{{{\boldsymbol{e}}}}_{2},{u}_{2{\rm{id}}}{e}_{1}+ {e}_{3}+ {{m}'}_{2})\in {R}_{q}^{m}\times {R}_{q}$.

Dec(${\rm{param}},{{\rm{sk}}}_{{\rm{id}}},{{\boldsymbol{c}}}$): After receiving a ciphertext ${{\boldsymbol{c}}}$, the receiver calculates ${m}_{1}= \lfloor 2/q \cdot {{{\boldsymbol{c}}}}_{0}^{\mathrm{T}}{{{\boldsymbol{x}}}}_{1{\rm{id}}} \rceil \in {R}_{q}$, ${m}_{2}= \lfloor 2/q \cdot \left({{c}_{1}-({\mathbf{c}}_{0}- \lfloor q/2 \cdot {{{\boldsymbol{m}}}}_{1} \rceil {{{\boldsymbol{a}}}}_{{\rm{id}}})}^{\mathrm{T}}{{{\boldsymbol{x}}}}_{2{\rm{id}}}\right) \rceil$. The message is ${{\boldsymbol{m}}}=({m}_{1},{m}_{2})$.

The decrypt algorithm can recover the message from ciphertext correctly if the following inequations hold:

The proof is similar as that in section 3.2, so we omit it.

Assume that the decision-RLWE problem is hard, the ring version IBE is IND-ID-CPA secure. The proof of the security of the ring version IBE is similar as that in section 2.3, so we omit it.

We compare the correctness conditions for our scheme with the conditions for GPV^[2] and ABB^[5]. The security model and the error term in the decryption results of our scheme, GPV^[2] and ABB^[5] are listed in Table 1. (The schemes used for comparison are multi bits encryption version.)

The correctness condition of our scheme is similar with GPV^[2]. The difference between GPV^[2] and our scheme is that our scheme needs to guarantee the second inequation. As we can set the distribution parameters of secret random vector $ {\boldsymbol{e}}_{1} $ to be the same as the distribution parameters of $ {\boldsymbol{e}}_{2} $, the second inequation will always hold as long as the first inequation holds. Thus, the parameter setting of GPV^[2] can be used for our scheme without losing correctness and security. ABB^[5] has more decryption noise because of the standard model. The length of the error term used in ABB's^[5] encryption is $ 2m $. The distribution of the outputs of $ \mathrm{S}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{L}\mathrm{e}\mathrm{f}\mathrm{t} $ is the same as the outputs of $ \mathrm{S}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{P}\mathrm{r}\mathrm{e} $ except the length of outputs. Therefore, the parameter setting that guarantee the correctness of ABB^[5] can also guarantee the correctness of our scheme.

Compared with other lattice-based IBE schemes, our scheme can encrypt more bits in a ciphertext, which means that our scheme can achieve smaller ciphertext size than other lattice-based IBE schemes when the length of the plaintext is fixed. To encrypt more bits, the size of secret key of our IBE scheme is bigger than that of other schemes. However, the ratio of the size of secret key to the size of plaintext is not greater than that of other schemes. The comparison of the ciphertext size, secret key size and plaintext size is shown by Table 2. To encrypt $ kl $ bits, one can just divide it into $ k $ pieces and encrypt each piece to get $ k $ ciphertexts. However, the ratio of the ciphertext size to the plaintext size of each scheme will not be changed, as every ciphertext only corresponds to a piece of plaintext with $ l $ bits.

When the parameters $ n,m,l,q $ of schemes are chosen, our scheme can encrypt $ l+n $ bits in a ciphertext whose size is $ (m+l)\mathrm{l}\mathrm{o}\mathrm{g}q $, while other LWE-based schemes can only encrypt $ l $ bits in a ciphertext with the same ciphertext size. If $ l=n $, the length of message that our scheme can encrypt is twice of other schemes, and the size of the ciphertext is not bigger than that of other schemes.

The disadvantage of our scheme is the computation cost. Our scheme needs to perform one more discrete gaussian sampling and vector addition in encryption than other schemes. In decryption, our scheme needs to perform two more matrix multiplications, and one more vector subtraction. However, as our scheme is able to transmit $ n $ more bits, we think the performance penalty of adding these computations is acceptable.

In this paper, we propose an IBE scheme and its ring version based on LWE/RLWE problem and prove that our schemes is IND-ID-CPA secure under the random oracle model. Compared with previous lattice-based IBE schemes, the computation cost of encryption and decryption of the proposed schemes is more than others, but our schemes can encrypt more message without increasing the size of ciphertext.