-
近年来,量子计算所获得的各领域的关注与日俱增[1-2]。然而,容错(fault-tolerant)量子计算机在近期出现的可能性仍然较低[3]。因此,近期能够真正付诸实际应用的量子计算算法将主要围绕中等规模噪声量子(noisy intermediate-scale quantum, NISQ)计算机展开。大部分NISQ计算机上的算法都是经典−量子混合的,这类算法将待解决问题中经典计算机上计算较为困难而适合量子计算完成的部分交由量子计算机完成,而其他部分仍然由经典计算机完成。这类算法通过经典计算机上的优化方法,不断迭代含参量子线路中的参数以得到优化后的量子线路,进而得到所期望的量子态,因而被称为变分量子算法(variational quantum algorithm, VQA)[4]。
在VQA中,文献[5]提出的量子近似优化算法(quantum approximation optimization algorithm, QAOA)能够高效解决具有特定特征的无向图上最大割(max-cut)问题。这一问题在经典计算机上是NP完备的[6]。文献[7]在其基础上提出了量子交替算子拟设(quantum alternating operator ansatz, QAOA),通过对量子线路上算子结构的不同设计,将文献[5]提出的近似优化算法拓展到有关字符串、排序和流程规划的一系列问题上,因而可以视作前者的拓展。本文将二者及在其之上进一步衍生的这一类算法统称为量子近似优化算法,并在下文以QAOA指代。
目前,除了QAOA之外,还有运用其他类型的量子算法进行投资组合优化的研究。如文献[8]提出了基于HHL的最优化均值−方差模型的方法,这一方法经文献[9]的拓展,可以解决任意数量的整数约束和预算约束下的均值−方差模型下的投资组合优化问题。文献[10]提出了NISQ硬件条件下HHL解决投资组合优化问题的方法。这些基于HHL的投资组合优化方案所考虑的解空间是连续的,而非QAOA所关注的离散化模型。由于HHL的关键要素QRAM的高效实现仍待探索[11],因而基于HHL的投资组合优化算法相较在NISQ时代的实际应用仍有一定的距离。文献[12]提出了基于Grover搜索算法的投资组合优化方案,其考虑的问题与下文中介绍的投资组合优化再平衡模型相同,这一方案的优点在于量子线路的设计清晰简洁,可解释性强。然而,该算法对于均值向量和协方差矩阵中非整数的系数按比例使用整数近似,受限于NISQ时代较少的量子比特数,面对非整数参数的投资组合优化问题存在着精度不足的瓶颈。另一方面,利用量子退火进行投资组合优化也是许多研究关注的重点,如文献[13]对于反向量子退火在投资组合优化中的应用的研究以及文献[14]对于量子退火中的控制对于无约束组合优化问题求解的影响。量子退火由于其对应的硬件发展较为成熟、规模较大,因此在近期有可能展现量子计算相较经典计算的优势,但其所能带来的效率提升如何却仍待探索[15]。此外,亦有利用量子随机游走进行投资组合优化的研究[16],其实际上属于QAOA的一种变体。总而言之,QAOA对于本文所关注的NP难的离散投资组合优化问题有着精度更高、更可能在NISQ时代付诸实际应用的优点。
-
均值−方差模型[17-18]是金融学中最经典的模型之一。假设投资者有
$ n $ 个备选资产,其收益率均为随机变量。这些资产的期望收益率向量为$ {\boldsymbol{\mu}} = {({\mu _1},{\mu _2}, \cdots ,{\mu _n})^{\rm{T}} } \in {\mathbb{R}^n} $ ,收益率的协方差矩阵为$ {\boldsymbol{\varSigma }} = \left( {{\sigma _{ij}}} \right) \in {\mathbb{R}^{n \times n}} $ 。投资者可以对这$ n $ 个资产进行加权组合。记其在第$ i $ 个资产上的投资份额为$ {x_i} $ ,则该投资组合的向量表示为$ {\boldsymbol{x}} = {({x_1},{x_2}, \cdots ,{x_n})^{\rm{T}}} \in {\mathbb{R}^n} $ 。相应地,该投资组合的期望收益为$ {{\boldsymbol{\mu }}^{\rm{T}} }{\boldsymbol{x}} $ ,方差为$ {{\boldsymbol{x}}^{\rm{T}} }{\boldsymbol{\varSigma x}} $ 。投资者希望在给定期望收益$ {\mu _0} \in \mathbb{R} $ 时,最小化投资组合的方差,于是可作如下优化:$$ \begin{split} & \min \quad {{\boldsymbol{x}}^{\rm{T}} }{\boldsymbol{\varSigma x}} \\ & {\text{ s}}{\text{.t}}{\text{. }}{{\boldsymbol{\mu}} ^{\rm{T}} }{\boldsymbol{x}} = {\mu _0} \\ &\quad {{\boldsymbol{1}}^{\rm{T}} }{\boldsymbol{x}} = 1 \end{split} $$ (1) 由于协方差矩阵一定是半正定的,因此,式(1)可在经典计算机上以多项式时间复杂度的算法解决。
式(1)的一个等价形式如下[19]:
$$ \begin{split} & \min \quad \eta {{\boldsymbol{x}}^{\rm{T}} }{\boldsymbol{\varSigma x}} - (1 - \eta ){{\boldsymbol{\mu}} ^{\rm{T}} }{\boldsymbol{x}} \\ & \qquad{\text{ s}}{\text{.t}}{\text{.}}\quad {{\boldsymbol{1}}^{\rm{T}} }{\boldsymbol{x}} = 1 \end{split} $$ (2) 式中,
$ \eta \in [0,1] $ ;$ {\boldsymbol{1}} = {(1,1, \cdots ,1)^{\rm{T}} } $ 。$\eta $ 代表了投资者在风险和收益二者间的权衡情况,称为权衡系数。显然,当$\eta = 0$ 时,投资者只关注收益,倾向于选择最为激进的投资组合;而当$\eta = 1$ 时,投资者只关注方差,倾向于选择最为稳健、方差最小的投资组合。 -
如果增加离散的限制,并进一步假设所有
$ {x_i} $ 的取值都在$ \left[ { - \dfrac{k}{D},\dfrac{k}{D}} \right] \supseteq \left[ { - \dfrac{1}{n},\dfrac{1}{n}} \right]\;(k,D \in {\mathbb{Z}_ + }) $ 内的均匀网格上,即$ \forall i,{x_i} \in \left\{ {\dfrac{j}{D}|j = - k, - k + 1, \cdots ,k} \right\} $ ,此时,对$ {x_i} $ 的取值进行等比例放大,使其落在整数域上,则式(2)的一个等价形式为:$$ \begin{split} & \min \quad \lambda {{\boldsymbol{z}}^{\rm{T}} }{\boldsymbol{\varSigma z}} - (1 - \lambda ){{\boldsymbol{\mu }}^{\rm{T}} }{\boldsymbol{z}} \\ &\qquad {\text{ s}}{\text{.t}}{\text{.}}\quad {{\boldsymbol{1}}^{\rm{T}} }{\boldsymbol{z}} = D \end{split} $$ (3) 式中,
$ {\boldsymbol{z}} = {({z_1},{z_2}, \cdots ,{z_n})^{\rm{T}} } \in {\{ - k, - k + 1, \cdots ,k\} ^n} $ ;$ \lambda = \dfrac{\eta }{{D - (D - 1 )\eta }} $ 。显然,$\lambda \in [0,1]$ 。如前文所述,式(3)在经典计算机上是NP难的。由于任意取值范围为$\{ - {k_0}, - {k_0} + 1, \cdots ,{k_0}\} $ 的变量${z_i}$ 都能由${k_0} \in {\mathbb{Z}_ + }$ 个均值、方差与${z_i}$ 均值、方差相等的,且取值范围为$\{ - 1,0,1\} $ 的变量${z_{i1}}, \cdots ,{z_{i{k_0}}}$ 等价替代,故不失一般性,本文仅考虑$k = 1$ 的情形。 -
投资组合再平衡(Rebalancing)问题[20]是式(3)的拓展。在再平衡问题中,投资者在决策前已经有一定的持仓
$ {\boldsymbol{y}} = {({y_1},{y_2}, \cdots ,{y_n})^{\rm{T}} } $ 。在单笔交易成本$T \ne 0$ 的情况下,式(3)相当于$ {\boldsymbol{y}} = (0, 0, \cdots ,0)^{\rm{T}} $ 的特殊情形,而一般情况下,$\exists i,{y_i} \ne 0$ 。于是,就有了本文剩余部分所关注的模型:$$ \begin{split} &{{\rm{min}} \quad \lambda {{\boldsymbol{z}}^{\rm{T}} }{\boldsymbol{\varSigma}} {\boldsymbol{z}} - (1 - \lambda ){{\boldsymbol{\mu }}^{\rm{T}} }{\boldsymbol{z}} + T\sum\limits_{i = 1}^n | {y_i} - {z_i}|}\\ &\qquad\qquad{{\rm{s}}{\rm{.t}}{\rm{.}} \quad {{\bf{1}}^{\rm{T}} }{\boldsymbol{z}} = D}\\ & \quad \quad\quad\quad {{\boldsymbol{z}} \in {{\{ - 1,0,1\} }^n}} \end{split}$$ (4) 显然,这一问题仍旧是NP难的。
-
QAOA将原问题的可变向量映射为量子比特的张量积,经量子线路变换后,将逆映射作用于测量结果得到特定条件下近似最小(大)化目标函数的可变向量取值。以最小化问题为例,QAOA的基本框架如下。
1)设投资者需要最小化的目标函数为可变向量
${\boldsymbol{z}}$ 的函数$f({\boldsymbol{z}}),{\boldsymbol{z}} \in {\mathbb{R}^n}$ 。则需要构造合适的映射$\phi ( \cdot ),\phi ({\boldsymbol{z}}) = |\varphi \rangle ,\langle \varphi |\varphi \rangle = 1$ ,并确定目标函数对应的哈密顿量${\boldsymbol{C}}$ ,使得$f({\boldsymbol{z}}) = \langle \varphi |{\boldsymbol{C}}|\varphi \rangle $ 。2)构造演化算子(evolution operator)
$ U({\boldsymbol{\gamma}} ,{\boldsymbol{\beta}} )= \displaystyle\prod _{k=1}^{p}U({\boldsymbol{B}},{\beta }_{k})U({\boldsymbol{C}},{\gamma }_{k}) $ [21]。$U({\boldsymbol{C}},{\gamma _k}) = {{\rm{e}}^{ - \imath {\gamma _k}{\boldsymbol{C}}}}$ 称作相位分离(Phase-separation)算子[7],$U({\boldsymbol{B}},{\beta _k}) = {{\rm{e}}^{ - \imath {\beta _k}{\boldsymbol{B}}}}$ 称作混合算子(mixer)[7],${\boldsymbol{B}}$ 是哈密顿量。其中$\imath = \sqrt { - 1} $ ,${\gamma _k} \in [0,2{\text{π}} )$ 。而${\beta _k}$ 的取值范围与${\boldsymbol{B}}$ 的选取有关,一般是区间$[0,{\text{π}} )$ 的子集。参数$p$ 代表了演化算子所包含相位分离算子和混合算子的层数。3)选定合适的初态
$|{\varphi _0}\rangle $ ,初始化演化算子的参数$ {\boldsymbol{\gamma}} ,{\boldsymbol{\beta}} $ ,将演化算子作用于初态得到末态$|\varphi \rangle $ ,$|\varphi \rangle $ 往往并非单态。接下来,要对$|\varphi \rangle $ 进行${m_1} \in {\mathbb{Z}_ + }$ 次测量,记第$j$ 次测量得到的结果为$|{\varphi _j}\rangle $ ,相应地,向量${{\boldsymbol{z}}_j} = {\phi ^{ - 1}}(|{\varphi _j}\rangle ) \in {\mathbb{R}^n}$ 。可用$\dfrac{1}{m}\displaystyle\sum\limits_{j = 1}^m {\langle {\varphi _j}|{\boldsymbol{C}}|{\varphi _j}\rangle } $ 估计$ \mathbb{E}\left( {\langle \varphi |{\boldsymbol{C}}|\varphi \rangle } \right) $ ,即算法得到的目标函数的期望值$ {\mathbb{E}_{{{\boldsymbol{z}}_j}}}(f({{\boldsymbol{z}}_j})) $ 。4)通过经典计算机上的优化算法(如梯度下降法),不断迭代更新参数
$ {\boldsymbol{\gamma}} ,{\boldsymbol{\beta}} $ 。每次迭代计算得到新的$ {\boldsymbol{\gamma}} ,{\boldsymbol{\beta}} $ 值之后,重复步骤3),将新参数下的演化算子作用于初态$|{\varphi _0}\rangle $ ,测量末态并计算出新的函数值,进而利用新的函数值算出下一步迭代的$ {\boldsymbol{\gamma}} ,{\boldsymbol{\beta}} $ ,直至算法收敛为止。此时,算法得到最终的一组参数$ {{\boldsymbol{\gamma}} ^*},{{\boldsymbol{\beta}} ^*} $ 及其对应的演化算子$ U({{\boldsymbol{\gamma}} ^ * },{{\boldsymbol{\beta}} ^ * }) $ 。5)将
$ U({{\boldsymbol{\gamma}} ^ * },{{\boldsymbol{\beta}} ^ * }) $ 作用于$|{\varphi _0}\rangle $ 得到$|{\varphi ^*}\rangle $ 。对$|{\varphi ^*}\rangle $ 进行${m_2} \in {\mathbb{Z}_ + }$ 次测量,将测量结果由${\phi ^{ - 1}}$ 映射得到原优化问题中的可变向量集合$\mathcal{Z} = \{ {{\boldsymbol{z}}_j}\} _{j = 1}^{{m_2}}$ ,并计算得到一组相应的目标函数值$ \left\{ {f({{\boldsymbol{z}}_j})} \right\}_{j = 1}^{{m_2}} $ 。则可以认为$ {{\boldsymbol{z}}^*} = {\text{argmi}}{{\text{n}}_{{{\boldsymbol{z}}_j} \in \mathcal{Z}}}f({{\boldsymbol{z}}_j}) $ 为QAOA得到的最优可变向量,相应的$f({{\boldsymbol{z}}^*})$ 即为算法得到目标函数的近似最小值。 -
为形式统一,可以变换式(4)中的交易成本项,得到:
$$ T\sum _{i=1}^{n}|{y}_{i}-{z}_{i}|=T\sum _{i=1}^{n}\left[(1-{y}_{i}{}^{2}){z}_{i}^{2}-{y}_{i}{z}_{i}+{y}_{i}{}^{2}\right] $$ (5) 记
${\boldsymbol{y}} \odot {\boldsymbol{y}} = {(y_1^2,y_2^2, \cdots ,y_n^2)^{\rm{T}} }$ ,令:$$ \left\{ \begin{array}{l} \tilde {\boldsymbol{\mu}} = (1 - \lambda ){\boldsymbol{\mu}} \; + T{\boldsymbol{y}} \odot {\boldsymbol{y}} \equiv {({{\tilde \mu }_1},{{\tilde \mu }_2}, \cdots ,{{\tilde \mu }_n})^{\rm{T}} } \\ \widetilde {\boldsymbol{\varSigma }} = \lambda {\boldsymbol{\varSigma }} + T{\text{diag}}\{ 1 - {y_1}^2,1 - {y_2}^2, \cdots ,1 - {y_n}^2\} \equiv ( {\widetilde {{\sigma _{ij}}}} ) \end{array} \right. $$ (6) 则最小化式(4)中的
$f({\boldsymbol{z}})$ 等价于最小化:$$ g({\boldsymbol{z}}) = {{\boldsymbol{z}}^{\rm{T}} }{\boldsymbol{\tilde \varSigma z}} - {\tilde {\boldsymbol{\mu}} ^{\rm{T}} }{\boldsymbol{z}} $$ (7) 对于任意
$ {z}_{i},i\in \{1,2,\cdots ,n\} $ ,将其映射到${s_{i1}},{s_{i2}}$ 两个量子比特的张量积$|{s_{i1}}\rangle \otimes |{s_{i2}}\rangle $ 上,即$\phi ({z_i}) = |{s_{i1}}\rangle \otimes |{s_{i2}}\rangle $ 。令:$$ |\varphi \rangle =\phi (z)=\underset{i=1}{\overset{n}{\otimes }}\phi ({z}_{i})=\underset{i=1}{\overset{n}{\otimes }}\left(|{s}_{i1}\rangle \otimes |{s}_{i2}\rangle \right) $$ (8) 具体地,
${z_i}$ 和${s_{i1}},{s_{i2}}$ 的映射关系如表1所示[20]。此外,本文约定
${\phi ^{ - 1}}(|1\rangle \otimes |1\rangle ) = 0$ 。考虑泡利−Z矩阵(Pauli-Z matrix):
$$ {{{\boldsymbol{\sigma }}}_z} = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right) $$ (9) 表 1
${z_i}$ 和${s_{i1}},{s_{i2}}$ 的映射关系${z_i}$取值 ${s_{i1}}$状态 ${s_{i2}}$状态 0 $|0\rangle $ $|0\rangle $ 1 $|0\rangle $ $|1\rangle $ −1 $|1\rangle $ $|0\rangle $ 有关系式
$\langle 0|{{\boldsymbol{\sigma }}_z}|0\rangle = 1$ ,$\langle 1|{{\boldsymbol{\sigma }}_z}|1\rangle = - 1$ 。如果记$ {\boldsymbol{\sigma }}_z^{ij} = {\boldsymbol{I}}_2^{ \otimes (2i - 3 + j)} \otimes {{\boldsymbol{\sigma }}_z} \otimes {\boldsymbol{I}}_2^{ \otimes (2n - 2i + 2 - j)} $ (下类同),并令:$$ {{\boldsymbol{C}}_i} = {\boldsymbol{\sigma }}_z^{i1} - {\boldsymbol{\sigma }}_z^{i2} $$ (10) 那么由于:
$$ {z_i} = \frac{{\langle {s_{i1}}|{{\boldsymbol{\sigma }}_z}|{s_{i1}}\rangle - \langle {s_{i2}}|{{\boldsymbol{\sigma }}_z}|{s_{i2}}\rangle }}{2}\;\;\;\;i \in \{ 1,2, \cdots ,n\} $$ (11) 有关系式
$ {z_i} = \langle \varphi |{{\boldsymbol{C}}_i}|\varphi \rangle $ 。因此,目标函数$g({\boldsymbol{z}})$ 对应的哈密顿量为:$$ {\boldsymbol{C}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {\widetilde {{\sigma _{ij}}}{{\boldsymbol{C}}_i}{{\boldsymbol{C}}_j}} \right)} } - \sum\limits_{i = 1}^n {\widetilde {{\mu _i}}{{\boldsymbol{C}}_i}} $$ (12) 自此,本文构造完成了上一节步骤1)所需的对应关系,得以进行QAOA的后续步骤。
-
文献[5]提出QAOA时所选定的初态为均匀叠加态。这在本文的设定下,即
$ |{\varphi }_{0}\rangle =\underset{i=1}{\overset{2n}{\otimes }}|+\rangle $ ,${{\boldsymbol{B}}_{{X}}} = \displaystyle\sum\limits_{i = 1}^n { \displaystyle\sum \limits_{j = 1}^2 {{\boldsymbol{\sigma }}}_x^{ij}}$ 。X−混合算子[22]$ U({{\boldsymbol{B}}_X},{\beta _k}) $ 并不能保证优化在约束条件${{\boldsymbol{1}}^{\rm{T}} }{\boldsymbol{z}} = D$ 对应的量子态的子空间${\mathcal{H}_D}$ 内进行。如果直接最小化$\langle \varphi |{\boldsymbol{C}}|\varphi \rangle $ ,很有可能在测量时得到非可行解。一种解决方法是在目标函数中引入惩罚项$A{({{\boldsymbol{1}}^{\rm{T}}}{\boldsymbol{z}} - D)^2}$ ,一般$A > {D^2}$ ,使得最小化算法倾向于选择满足约束条件的解,这种约束方法被称作软约束(soft constraint)。本文称软约束下使用均匀叠加态作初态的QAOA是“标准”的。文献[20]的实验结果显示,软约束下的标准近似优化算法解决投资组合优化问题的效果相较经典穷举法(brute-force search)没有明显的优势,因此本文的数值模拟将不涉及该方法。
-
对于最大割等整数优化问题,在经典计算机上,可以采用随机取整(randomized rounding)[ 23-24]的方法,利用放松原问题的整数约束进行优化所得到的结果寻找整数约束下的最优解。相应地,也可以利用放松整数约束的经典优化结果设计QAOA初态,这种方法被称作热启动[25](warm-starting)。对于式(4),记:
$$ {\mathfrak{s}_{ij}} = \frac{{\langle {s_{ij}}|{{\boldsymbol{\sigma }}_z}|{s_{ij}}\rangle + 1}}{2}\;\;\;\;i \in \{ 1,2, \ldots ,n\} ,j \in \{ 1,2\} $$ (13) 令:
$$ {{\boldsymbol{s}}_1} = {({\mathfrak{s}_{11}},{\mathfrak{s}_{21}}, \cdots ,{\mathfrak{s}_{n1}})^{\rm{T}} },\;{{\boldsymbol{s}}_2} = {({\mathfrak{s}_{12}},{\mathfrak{s}_{22}}, \cdots ,{\mathfrak{s}_{n2}})^{\rm{T}} } $$ (14) 则
${{\boldsymbol{s}}_1},{{\boldsymbol{s}}_2} \in {[0,1]^n}$ ,${\boldsymbol{z}} = {{\boldsymbol{s}}_1} - {{\boldsymbol{s}}_2}$ 。求解:$$ \begin{split} &\min \quad \lambda {({{\boldsymbol{s}}_1} - {{\boldsymbol{s}}_2})^{\rm{T}} }{\boldsymbol{\varSigma }}({{\boldsymbol{s}}_1} - {{\boldsymbol{s}}_2}) - (1 - \lambda ){\mu ^{\rm{T}} }({{\boldsymbol{s}}_1} - {{\boldsymbol{s}}_2}) + \\ &\quad \quad\quad\quad \;\; T\sum\limits_{i = 1}^n | {y_i} - {s_{i1}} + {s_{i2}}| \\ &\quad\quad\quad\quad{\text{ s}}{\text{.t}}{\text{.}}\quad {{\boldsymbol{1}}^{\rm{T}} }({{\boldsymbol{s}}_1} - {{\boldsymbol{s}}_2}) = D \\ &\qquad \;\;0 \leqslant {s_{ij}} \leqslant 1,\;i \in \{ 1,2, \cdots ,n\} ,\;j \in \{ 1,2\} \end{split} $$ (15) 得到一组放松整数约束的最优解
${\boldsymbol{s}}_1^*,{\boldsymbol{s}}_2^*$ 。令:$$ {\theta _{ij}} = 2\arcsin \left( {\sqrt {\mathfrak{s}_{ij}^*} } \right) $$ (16) 则软约束下热启动的初态:
$$ |{\varphi }_{0}^{\text{SWS}}\rangle =\underset{i=1}{\overset{n}{\otimes }}\left({{\boldsymbol{R}}}_{Y}({\theta }_{i1})|0\rangle \otimes {{\boldsymbol{R}}}_{Y}({\theta }_{i2})|0\rangle \right) $$ (17) 相应地,算法使用混合算子
$ U({{\boldsymbol{B}}_{{\text{SWS}}}},{\beta _k}) $ ,其中:$$\left\{ \begin{array}{l} {{\boldsymbol{B}}_{{\text{SWS}}}} = \displaystyle\sum\limits_{i = 1}^n \displaystyle\sum \limits_{j = 1}^2 {\boldsymbol{\sigma }}_{{\text{SWS}},ij}^{ij} \\ {{\boldsymbol{\sigma }}_{{\text{SWS}},ij}} = \left( {\begin{array}{*{20}{c}} {2{\mathfrak{s}_{ij}}^* - 1}&{ - 2\sqrt {{\mathfrak{s}_{ij}}^*(1 - {\mathfrak{s}_{ij}}^*)} } \\ { - 2\sqrt {{\mathfrak{s}_{ij}}^*(1 - {\mathfrak{s}_{ij}}^*)} }&{1 - 2{\mathfrak{s}_{ij}}^*} \end{array}} \right) \end{array} \right.$$ (18) 当
${\mathfrak{s}_i} = 1$ 或${\mathfrak{s}_i} = 0$ 时,${{\boldsymbol{B}}_{{\text{WS}}}}$ 仅能在相位的意义上改变相应的量子比特。为了避免出现诸如放松整数约束时的最优解和原问题恰好分别为0和1的情形,令:$$ \widetilde{{\mathfrak{s}}_{ij}}=\mathrm{max}(\epsilon ,\mathrm{min}({\mathfrak{s}}_{ij}{}^{*},1-\epsilon)) $$ (19) 可以使用
$\widetilde {{\mathfrak{s}_{ij}}}$ 代替${\mathfrak{s}_{ij}}^*$ 计算${\theta _{ij}},{{\boldsymbol{\sigma }}_{{\text{SWS}},ij}}$ 。混合算子
$ U({{\boldsymbol{B}}_{{\text{SWS}}}},{\beta _k}) $ 并不能保证优化过程在${\mathcal{H}_D}$ 下进行,因此本节引入3.1节所述的惩罚项$A{({{\boldsymbol{1}}^{\rm{T}} }{\boldsymbol{z}} - D)^2}$ 对优化过程进行约束。因此,本文称本方法为软约束下的热启动QAOA,在下文用SWS-QAOA指代。 -
3.2节中的混合算子
$ U({{\boldsymbol{B}}_{{\text{SWS}}}},{\beta _k}) $ 均由单比特门构成,并没有考虑不同量子比特之间的相关性。因此,一个自然的想法便是在混合算子中引入不同量子比特的相互作用因素。可以构建连接混合算子$U({{\boldsymbol{B}}_{{\text{cop}}}},{\beta _k})$ [26],其中:$$ {{\boldsymbol{B}}}_{\text{cop}}=-\sum _{i=1}^{n}\sum _{j=1}^{2}{{\boldsymbol{R}}}_{{p}_{ij}}^{ij}\left({{\boldsymbol{\sigma }}}_{z}^{ij}+{{\boldsymbol{\sigma}} }_{z}^{(i+2)j}\right){({{\boldsymbol{R}}}_{{p}_{ij}}^{ij})}^{\dagger } $$ (20) 本文约定
$n + 1 \equiv 1,\;n + 2 \equiv 2$ 。$ {\boldsymbol{R}}_{{p_{i,j}}}^{i,j} $ 是有关参数$t \in [ - 1,1]$ 的量子门操作,其中$t$ 代表不同量子比特之间的相关性,同$ {\boldsymbol{\gamma}} ,{\boldsymbol{\beta}} $ 相同,由经典优化算法确定最优值。自此,本文得到了软约束下使用连接混合算子的热启动QAOA,在下文用SX-QAOA指代。 -
另一种解决使用X-混合算子时容易得到非可行解的方法是修改混合算子的设计。XY−混合算子[22]
$U({{\boldsymbol{B}}_{{\text{XY}}}},{\beta _k})$ 能够使得只要初态$|{\varphi _0}\rangle \in {\mathcal{H}_D}$ ,近似优化算法一定在${\mathcal{H}_D}$ 内进行,因而能够显著地减小算法最小化目标函数的搜索范围。在两类主要的XY−混合算子中,全连接(complete-graph)XY−混合算子[22]考虑了所有可互相交换(即交换后,量子态所对应的资产组合不违背约束条件)的两个量子比特,在投资组合优化问题的背景下,即:
$$ {{\boldsymbol{B}}}_{{{\rm{XY}}}}={\displaystyle \sum _{{i}_{1},{i}_{2}\in \{1,2,\cdots ,n\}\text{,}{i}_{1}\equiv {i}_{2}\mathrm{mod}2}\displaystyle \sum _{j=1}^{2}{\boldsymbol{\sigma }}_{x}^{{i}_{1}j}}{\boldsymbol{\sigma }}_{x}^{{i}_{2}j}+\text{}{\boldsymbol{\sigma }}_{y}^{{i}_{1}j}{\boldsymbol{\sigma }}_{y}^{{i}_{2}j} $$ (21) 而环形XY−混合算子(ring mixer)[20, 22]仅考虑了相邻的可互相交换的两个量子比特。尽管前者在实现效率上较后者略低,但由于其优化效果更好[22],因此本文选用完全图XY−混合算子作为硬约束下的混合算子。
此外,还需要确定满足相应约束条件的量子态作为初态。与文献[20]所采用的方法略有不同,本文令备选资产中期望收益最高的
$\left\lfloor {\dfrac{{n + D}}{2}} \right\rfloor $ 个资产每个资产所对应的量子比特对均为$|01\rangle $ ;令备选资产中期望收益最低的$\left\lfloor {\dfrac{{n - D}}{2}} \right\rfloor $ 个资产所对应的量子比特对均为$|10\rangle $ ;对于其余资产,令其对应的量子比特对均为$\dfrac{{|00\rangle + |11\rangle }}{{\sqrt 2 }}$ 。由此构造的初态即符合优化问题的约束条件。本文称硬约束下利用该初态的QAOA是“标准”的,在下文用H-QAOA指代。 -
本文基于股票收益率和协方差数据进行数值模拟,比较不同QAOA方法求解投资组合优化式(4)的效果。模拟所使用数据为由2021年第3季度A股3847支股票(已剔除单日收益率大于20%及含有缺失值的股票)日收盘价计算得到的日均收益率及收益率协方差数据。
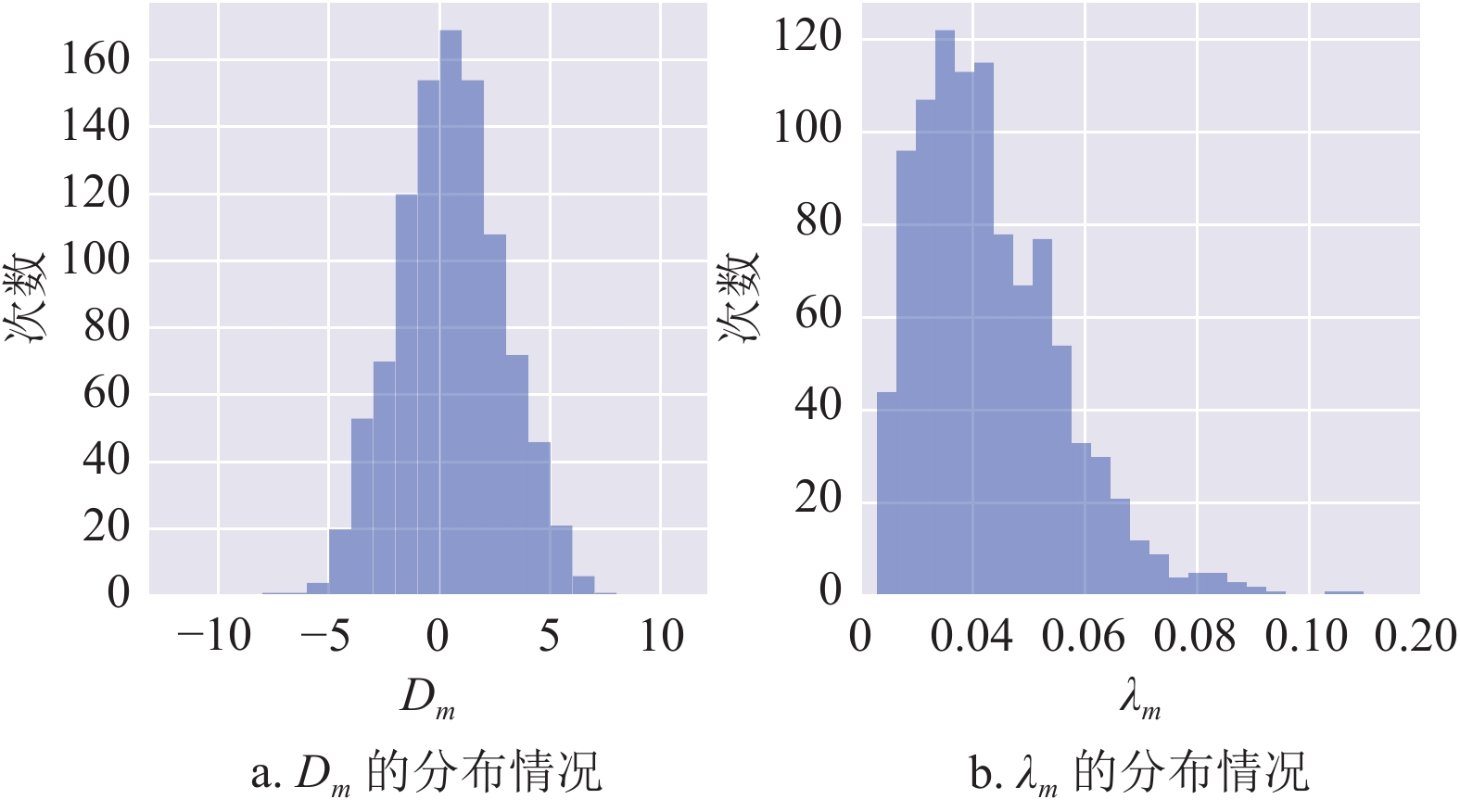
对于
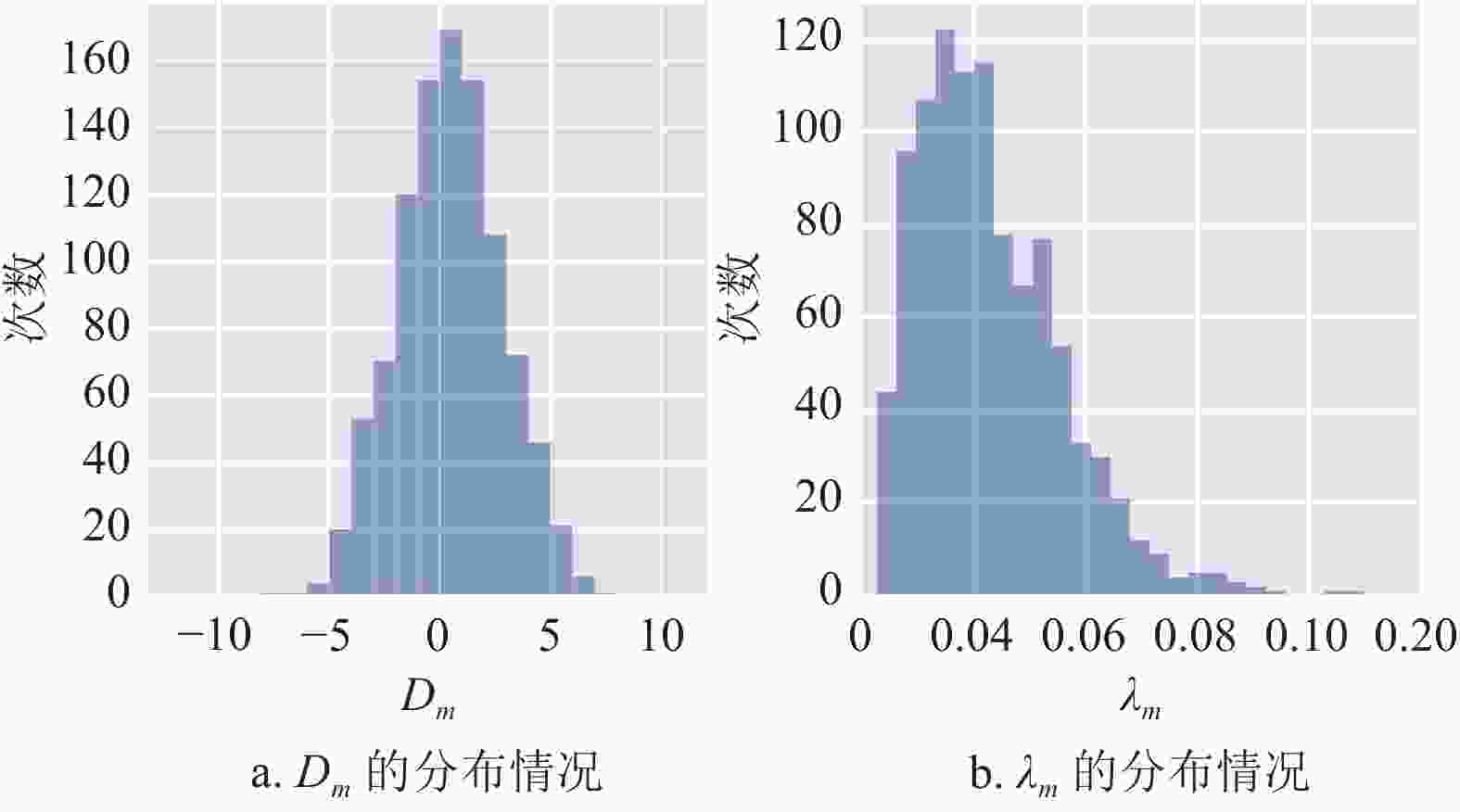
$p = 1,2,3,4$ 的不同情形,本文分别进行1000次数值模拟。每次数值模拟,均从3847支股票中随机抽取12支股票,将其日均收益率及收益率协方差矩阵代入式(4),并分别用经典穷举法、SWS-QAOA、 SX-QAOA及H-QAOA进行求解。如图1所示,在参数设置方面,本文根据一定的分布随机生成参数$ {\boldsymbol{y}},\;\lambda ,D $ 的值。记第$m \in {\mathbb{Z}_ + }$ 次模拟中,参数$ {\boldsymbol{y}},\;\lambda ,D $ 的取值分别为${{\boldsymbol{y}}_m} = {({y_{m1}},{y_{m2}}, \cdots ,{y_{m12}})^{\rm{T}} }$ ,${\lambda _m}, {D_m}$ ,则:$$ \begin{split} & {y_{mi}} \sim {\rm{Binomial}}(2,0.5) - 1\;\;\;i = 1,2, \cdots ,12 \\ &\qquad\qquad\quad {\lambda _m} \sim {\rm{Beta}}(3,60) \\ &\qquad\quad{D_m} \sim \left\lfloor {24{\rm{Beta}}(12,12) - 11.5} \right\rfloor \end{split} $$ (22) 此外,本文令
$ {\boldsymbol{\gamma}} ,{\boldsymbol{\beta}} $ 的初值均为$p$ 维0向量,$t$ 的初值为0.2,并设置$ {m}_{1}={m}_{2}=1000,\;\epsilon =0.25 $ [25],惩罚项$A = 50$ ,交易成本$T = 0.14$ 。 -
本文从近似比(AR)和成功比例(SR)两个角度比较不同QAOA方法的效果。对于第
$m$ 次实验,某QAOA方法的近似比${\text{A}}{{\text{R}}_m}$ 的定义为:$$ {\text{AR}}_{m}=\frac{1}{{m}_{2}}\displaystyle \sum _{j}^{{m}_{2}}\frac{{1}_{{{\boldsymbol{z}}}_{j}\in {\cal{H}}_{D}}\left({\mathrm{max}}_{{\boldsymbol{z}}}{f}_{m}({\boldsymbol{z}})-{f}_{m}({{\boldsymbol{z}}}_{j})\right)}{{\mathrm{max}}_{{\boldsymbol{z}}}{f}_{m}({\boldsymbol{z}})-{\mathrm{min}}_{{\boldsymbol{z}}}{f}_{m}({\boldsymbol{z}})} $$ (23) 其中:
$$ {1_{{{\boldsymbol{z}}_j} \in {\mathcal{H}_D}}} = \left\{ {\begin{array}{*{20}{c}} 1&{{\boldsymbol{z}}_j} \in {\mathcal{H}_D} \\ 0&{{\boldsymbol{z}}_j} \notin {\mathcal{H}_D} \end{array}} \right. $$ (24) 而在1000次实验中,某QAOA方法成功比例
${\text{SR}}$ 的定义为:$$ {\text{SR}} = \frac{{\# \{ {{{{\rm{argmin}}} }_{{{\boldsymbol{z}}_j}}}{f_m}({{\boldsymbol{z}}_j}) = {{{{\rm{argmin}}} }_{\boldsymbol{z}}}{f_m}({\boldsymbol{z}})\} }}{{1000}} $$ (25) 即该QAOA方法成功找到全局最优解的次数比例。
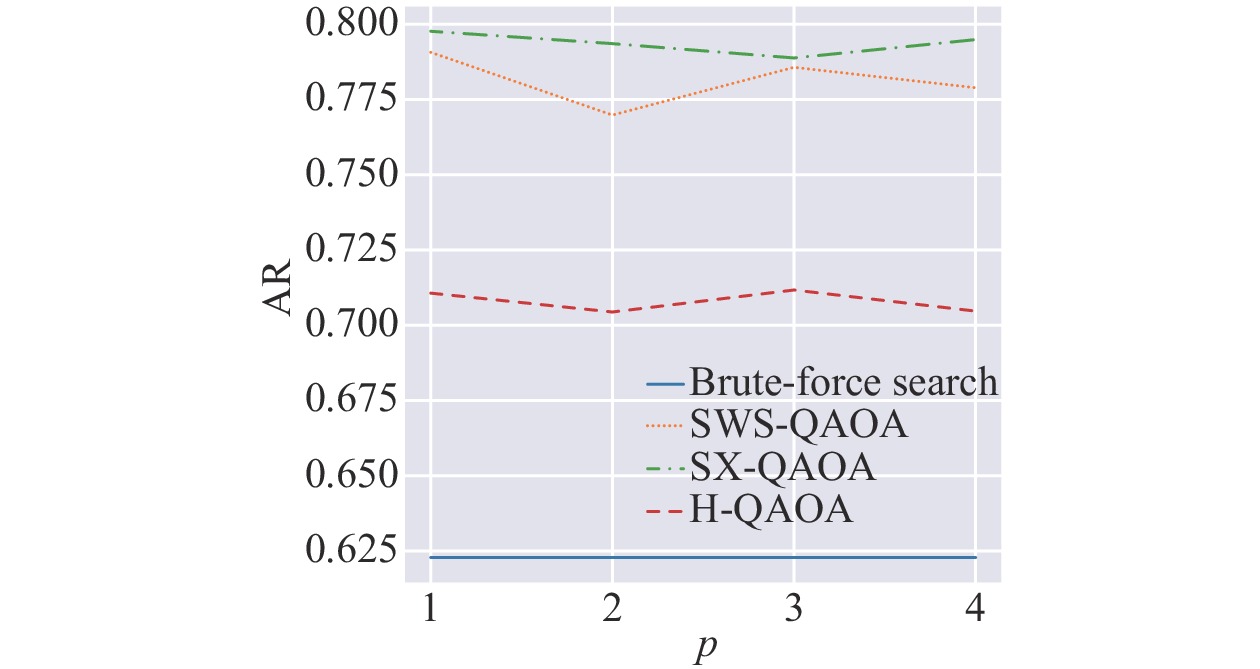
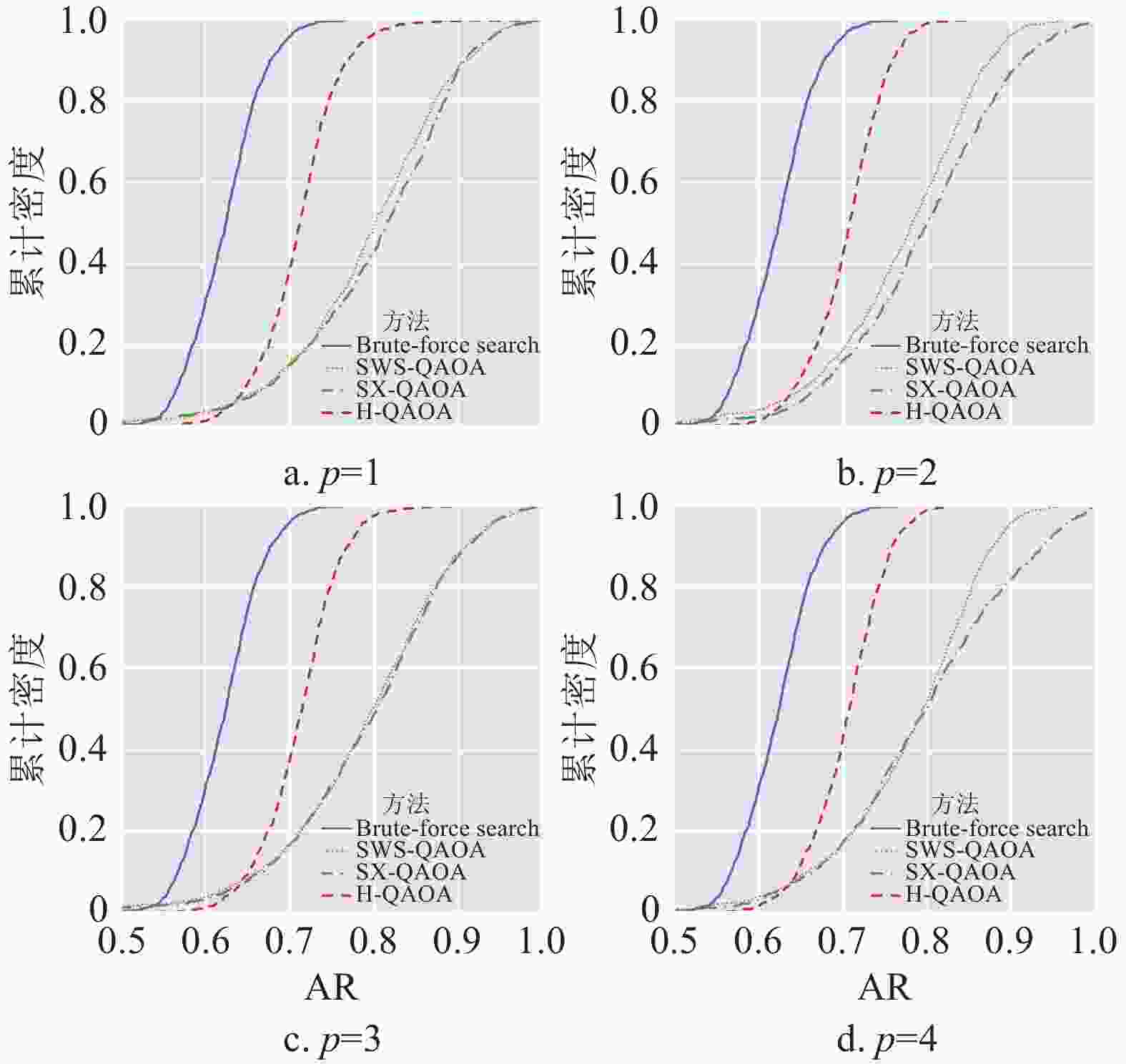
数值模拟的近似比情况如图2所示,不同近似比结果的累计密度如图3所示。
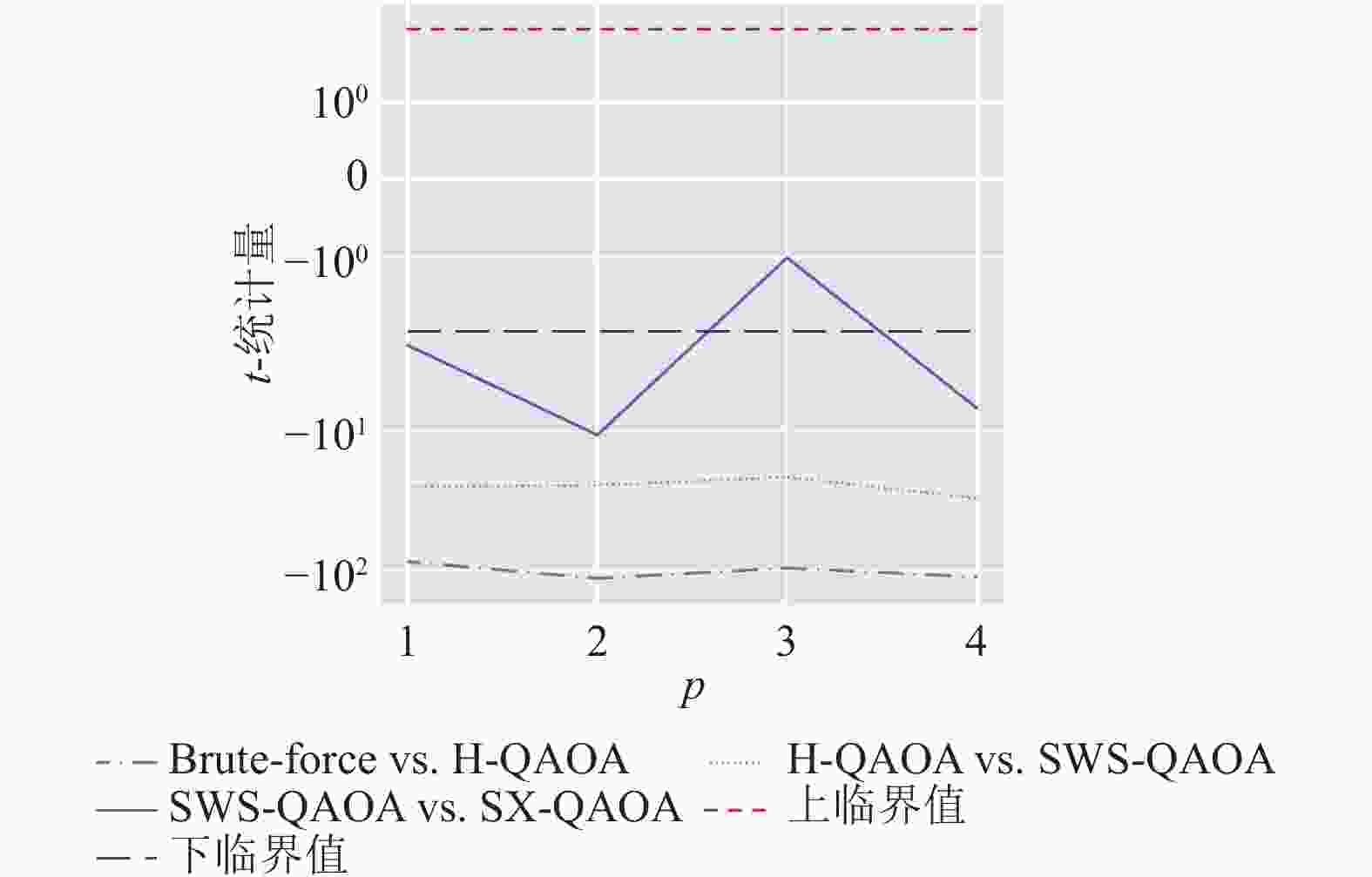
图中所涉及4种方法按近似比从高到低排序分别为SX-QAOA、SWS-QAOA、H-QAQA及穷举法,各量子算法较经典穷举法均有至少7%的提升。为了进一步确定不同方法的效果是否有显著差异,本文基于中心极限定理(central limit theorem)[27],假定4种方法近似比的均值均服从正态分布,对其差异进行双边
$t$ 检验。本文取上、下临界值分别为相应$t$ 分布的97.5%分位数和2.5%分位数。假设检验结果如图4所示,可以认为$t$ 统计量高于上临界值说明该组前一方法的平均近似比显著高于后一方法,若低于临界值说明该组前一方法的平均近似比显著低于后一方法。其他情况意味着该组的两种方法的平均近似比差异不显著。可见,除
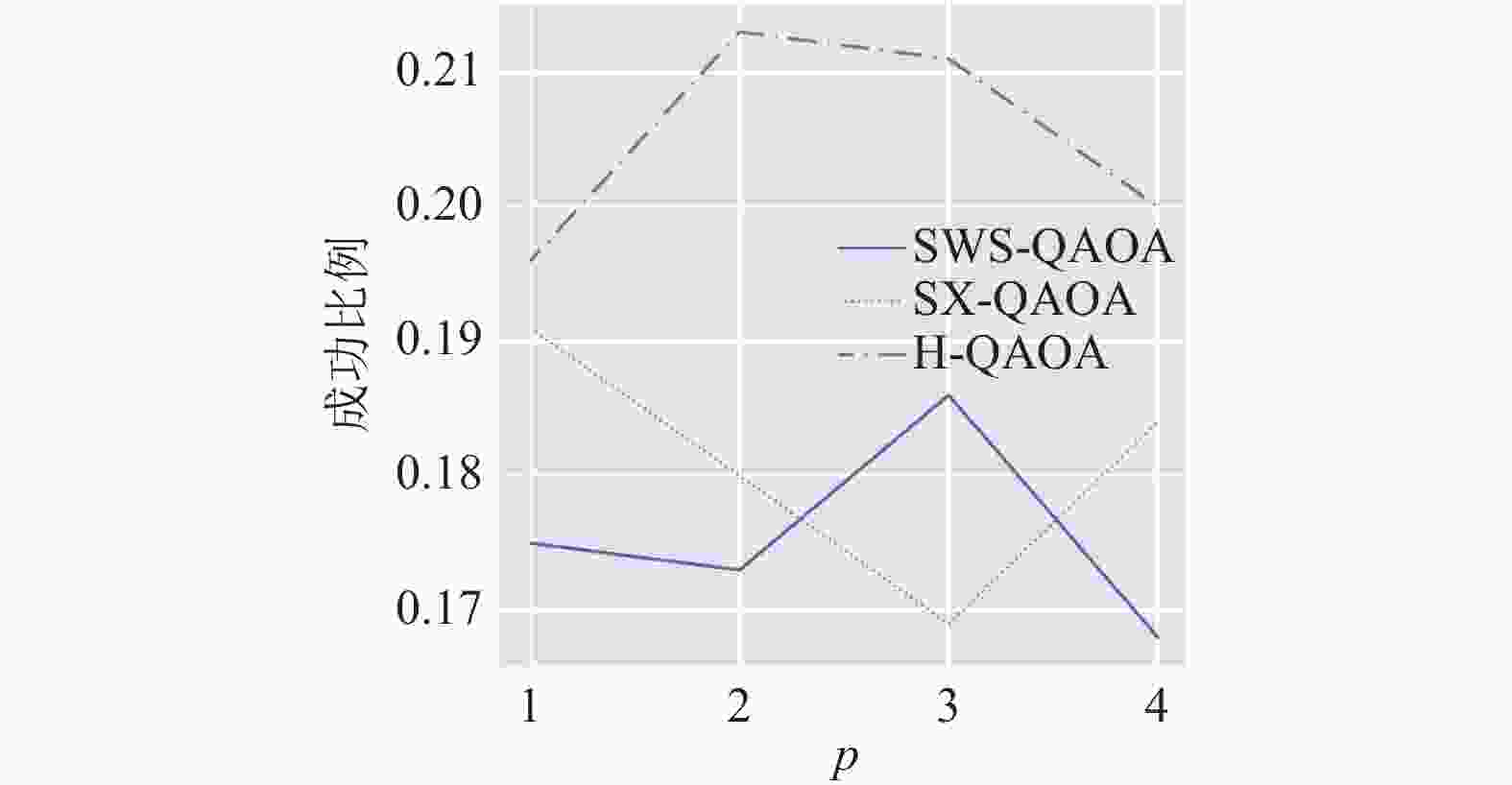
$p = 3$ 时SWS-QAOA和SX-QAOA的平均近似比差异不显著之外,其余11组假设检验结果均显著。本文进一步确定了在近似比的意义上各方法均存在显著差异。量子算法相较经典穷举法在平均近似比上均有着显著的提升,其中SX-QAOA表现最优。3种不同QAOA方法的成功比例情况如图5所示。
直观上看,若将3种QAOA方法按照成功比例从高到低排序,则最高的为H-QAOA,但SWS-QAOA和SX-QAOA较难区分高低。与之前类似,本文进行各方法成功比例差异的双边
$t$ 检验,以判断其是否显著。结果如图6所示。可见,仅在
$p = 2$ 及$p = 4$ 时,H-QAOA的成功比例显著高于SWS-QAOA的成功比例;在$p = 2$ 及$p = 3$ 时,H-QAOA的成功比例显著高于SX-QAOA的成功比例。而其余组假设检验的结果均不显著。因此,本文认为,在成功比例的意义上,H-QAOA略优于SWS-QAOA和SX-QAOA,但后二者之间难分伯仲。 -
本文对于QAOA在投资组合优化中的应用从理论建模、不同方法及数值模拟等多角度进行了详细的讨论。针对未来相关领域的研究,本文有如下两点展望。
1)回顾前面介绍的各种利用QAOA进行投资组合优化的方法,可以注意到,软约束QAOA能够利用放松整数约束的经典优化结果进行热启动,起到类似经典算法中随机取整的效果。然而,软约束QAOA搜索空间是全状态空间,而满足约束条件的子空间
${\mathcal{H}_D}$ 仅仅是其中的一个超平面。随着$n$ 的增大,软约束QAOA所搜索的空间将几乎全是非可行的冗余状态。因此,在测量次数${m_1},{m_2}$ 不变的情况下,随着$n$ 的增大,软约束QAOA很可能将逐渐失效。另一方面,现有的硬约束QAOA尽管将搜索空间缩小至${\mathcal{H}_D}$ 内,但是并未利用经典优化的结果进行初态设计,存在进一步提升的可能。如何将放松约束的经典优化结果与硬约束的QAOA结合起来将成为一项有价值的课题。2)从数值模拟结果来看,各QAOA方法的近似比和成功比例并未随着
$p$ 的增大而单调递增,这表明更加复杂的模型并没有带来更好的表现。此外,各QAOA方法的成功比例均为20%左右,搜索得到全局最优解的概率并不高。导致QAOA表现不及预期的原因很可能是QAOA的经典优化过程中常见的所谓贫瘠高原(barren plateau)问题[4,28]以及QAOA本身存在的可及性缺陷(reachability deficits)问题[29]。前者往往使得经典优化算法提前终止,进而导致QAOA无法找到理论最优值$|{\varphi ^*}\rangle $ ;而后者表明,即便找到了$|{\varphi ^*}\rangle $ ,但可及性缺陷仍然可能较大,这意味着使用某些演化算子的QAOA的效果可能存在着无法逾越的理论上限。如何针对投资组合优化问题设计更加合适的演化算子以解决这些问题亦将是一项富有意义的工作。
The Application of Quantum Approximation Optimization Algorithm in Portfolio Optimization
-
摘要: 讨论了量子近似优化算法(QAOA)在投资组合优化问题上的应用,而后者在离散的约束条件下是NP难的;介绍了QAOA的基本框架以及相应的投资组合优化问题的建模;阐述了数个可用于解决投资组合优化问题的QAOA方法。通过数值模拟及假设检验比较这些方法与经典方法的表现,各量子算法在平均近似比上相较经典方法均有7%以上的提升。Abstract: In this paper, we discuss the application of Quantum Approximation Optimization Algorithm (QAOA) in portfolio optimization problems, which, under discrete constraints, is proved to be NP-hard. We introduce the fundamental framework of QAOA and the corresponding modeling of portfolio optimization problems. We illustrate several variants of QAOA applicable to portfolio optimization problems. Next, we examine their performances and the performance of the classical method with numerical simulation and hypothesis testing. The average approximation ratio of each quantum algorithm is at least 7% higher than that of the classical algorithm.
-
表 1
${z_i}$ 和${s_{i1}},{s_{i2}}$ 的映射关系${z_i}$ 取值${s_{i1}}$ 状态${s_{i2}}$ 状态0 $|0\rangle $ $|0\rangle $ 1 $|0\rangle $ $|1\rangle $ −1 $|1\rangle $ $|0\rangle $ -
[1] 张仕斌, 黄曦, 昌燕, 等. 大数据环境下量子机器学习的研究进展及发展趋势[J]. 电子科技大学学报, 2021, 50(6): 802-819. ZHANG S B, HUANG X, CHANG Y, et al. Research progress and development trends of quantum machine learning in big data environment[J]. Journal of University of Electronic Science and Technology of China, 2021, 50(6): 802-819. [2] 王鹏, 王方. 量子视角下的智能优化算法综述[J]. 电子科技大学学报, 2022, 51(1): 2-15. WANG P, WANG F. A survey of intelligent optimization algorithms from the quantum perspective[J]. Journal of University of Electronic Science and Technology of China, 2022, 51(1): 2-15. [3] SEVILLA J, RIEDEL C J. Forecasting timelines of quantum computing[EB/OL]. [2021-11-02]. http://arxiv.org/abs/2009.05045. [4] BHARTI K, CERVERA-LIERTA A, KYAW T H, et al. Noisy intermediate-scale quantum(NISQ) algorithms[EB/OL]. [2021-10-15]. http://arxiv.org/abs/2101.08448. [5] FARHI E, GOLDSTONE J, GUTMANN S. A quantum approximate optimization algorithm[EB/OL]. [2021-11-02]. http://arxiv.org/abs/1411.4028. [6] KARP R M. Reducibility among combinatorial problems[EB/OL]. [2021-11-07]. http://link.springer.com/10.1007/978-1-4684-2001-2_9. [7] HADFIELD S, WANG Z, O’GORMAN B, et al. From the quantum approximate optimization algorithm to a quantum alternating operator ansatz[J]. Algorithms, 2019, 12(2): 34. doi: 10.3390/a12020034 [8] REBENTROST P, LLOYD S. Quantum computational finance: Quantum algorithm for portfolio optimization[EB/OL]. [2022-03-14]. http://arxiv.org/abs/1811.03975. [9] KERENIDIS I, PRAKASH A, SZILÁGYI D. Quantum algorithms for portfolio optimization[EB/OL]. [2022-03-01]. https://dl.acm.org/doi/10.1145/3318041.3355465. [10] YALOVETZKY R, MINSSEN P, HERMAN D, et al. NISQ-HHL: Portfolio optimization for near-term quantum hardware[EB/OL]. [2022-03-14]. http://arxiv.org/abs/2110.15958. [11] MATTEO O D, GHEORGHIU V, MOSCA M. Fault-tolerant resource estimation of quantum random-access memories[J]. IEEE Transactions on Quantum Engineering, 2020, 1: 1-13. doi: 10.1109/TQE.2020.2965803 [12] GILLIAM A, WOERNER S, GONCIULEA C. Grover adaptive search for constrained polynomial binary optimization[J]. Quantum, 2021, 5: 428. doi: 10.22331/q-2021-04-08-428 [13] VENTURELLI D, KONDRATYEV A. Reverse quantum annealing approach to portfolio optimization problems[J]. Quantum Machine Intelligence, 2019, 1(1-2): 17-30. [14] GRANT E, HUMBLE T S, STUMP B. Benchmarking quantum annealing controls with portfolio optimization[J]. Physical Review Applied, 2021, 15(1): 014012. doi: 10.1103/PhysRevApplied.15.014012 [15] HERMAN D, GOOGIN C, LIU X, et al. A survey of quantum computing for finance[EB/OL]. [2022-03-14]. http://arxiv.org/abs/2201.02773. [16] SLATE N, MATWIEJEW E, MARSH S, et al. Quantum walk-based portfolio optimisation[J]. Quantum, 2021, 5: 513. doi: 10.22331/q-2021-07-28-513 [17] MARKOWITZ H. Portfolio selection[J]. The Journal of Finance, 1952, 7(1): 77-91. doi: 10.2307/2975974 [18] MARKOWITZ H. The optimization of a quadratic function subject to linear constraints[J]. Naval Research Logistics Quarterly, 1956, 3(1-2): 111-133. [19] STEINBACH M C. Markowitz revisited: Mean-Variance models in financial portfolio analysis[J]. SIAM Review, 2001, 43(1): 31-85. doi: 10.1137/S0036144500376650 [20] HODSON M, RUCK B, ONG H, et al. Portfolio rebalancing experiments using the quantum alternating operator ansatz[EB/OL]. [2021-11-02]. http://arxiv.org/abs/1911.05296. [21] MOLL N, BARKOUTSOS P, BISHOP L S, et al. Quantum optimization using variational algorithms on near-term quantum devices[J]. Quantum Science and Technology, 2018, 3(3): 030503. doi: 10.1088/2058-9565/aab822 [22] WANG Z, RUBIN N C, DOMINY J M, et al. XY mixers: Analytical and numerical results for the quantum alternating operator ansatz[J]. Physical Review A, 2020, 101(1): 012320. doi: 10.1103/PhysRevA.101.012320 [23] RAGHAVAN P, TOMPSON C D. Randomized rounding: A technique for provably good algorithms and algorithmic proofs[J]. Combinatorica, 1987, 7(4): 365-374. doi: 10.1007/BF02579324 [24] GOEMANS M X, WILLIAMSON D P. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming[J]. Journal of the ACM, 1995, 42(6): 1115-1145. doi: 10.1145/227683.227684 [25] EGGER D J, MAREČEK J, WOERNER S. Warm-starting quantum optimization[J]. Quantum, 2021, 5: 479. doi: 10.22331/q-2021-06-17-479 [26] VAN DAM W, ELDEFRAWY K, GENISE N, et al. Quantum optimization heuristics with an application to knapsack problems[EB/OL]. [2021-11-02]. http://arxiv.org/abs/2108.08805. [27] CASELLA G, BERGER R L. Statistical inference[M]. 2nd ed. Pacific Grove, CA: Thomson Learning, 2002. [28] WANG S, FONTANA E, CEREZO M, et al. Noise-induced barren plateaus in variational quantum algorithms[EB/OL]. [2021-12-01]. http://arxiv.org/abs/2007.14384. [29] AKSHAY V, PHILATHONG H, MORALES M E S, et al. Reachability deficits in quantum approximate optimization[J]. Physical Review Letters, 2020, 124(9): 090504. doi: 10.1103/PhysRevLett.124.090504 -

 ISSN
ISSN 





 下载:
下载: