-
新轴承的研制需要进行可靠性试验,以验证轴承的可靠性指标是否达到规定的要求,从而为轴承的设计定型提供依据。滚动轴承可靠性的传统评价方法,是从当前批次产品中随机抽样并对样本进行可靠性试验,再依据相关标准对试验数据进行分析,进而确定当前批次轴承产品的可靠性指标。国家相关标准中规定,一般定时截尾试验失效套数不应少于轴承样品容量的2/3(最少应该保证6套)[1]。在样本量充足的情况下,上述方法可以较为精确地对轴承的寿命与可靠性进行评估。然而,航空发动机主轴圆柱滚子轴承具有长寿命、高可靠、高成本等特点,由于研发成本、试验周期和条件等因素的制约,通常不能进行大量试验,导致无法获得足够多的可靠性数据[2]。在小样本情况下,航空发动机主轴圆柱滚子轴承的可靠性分析面临极大的挑战。
针对上述问题,文献[3]研究了在试验性能退化量有缺失的情形下的无失效小样本轴承试验,应用数据模拟方法对样本退化量进行补全,通过自助法对样本进行扩充,实现了基于性能退化轨迹方法的轴承可靠性评估。文献[4]在用自助法和Bayes方法实现小样本滚动轴承寿命分布参数估计的基础上,运用Copula函数实现了滚动轴承在不同失效模式下竞争失效的可靠性建模,并对Copula函数进行了参数估计。文献[5]应用Bayes方法研究滚动轴承的可靠性,在充分利用先验信息的基础上,实现了在小样本少失效数据情形下对滚动轴承寿命的快速评估,通过实例给出了轴承序贯试验方案和判定标准。文献[6]基于无失效试验数据对滚动轴承可靠性进行了研究,在小样本无失效数据的情形下,建立了滚动轴承耐久性寿命的可靠性数学模型,给出了几种不同的可靠性评估方法。文献[7]基于长寿命轴承的性能退化数据,提出了一种小样本情形下的结合退化模型和蒙特卡洛方法的轴承可靠性评估方法,并通过实例验证了方法的有效性。文献[8]通过可靠性试验获得了某零部件的寿命数据,基于威布尔分布拟合其寿命分布类型,并对其进行了可靠性分析。文献[9]对威布尔分布参数估计和零故障数据情况开展研究,开发了一种新的参数估计方法,得到了具有较好的威布尔分布尺度参数的无偏估计量。此外,文献[10-15]还提出了一些轴承的可靠性评估方法,此处不再赘述。
尽管已有很多关于轴承的可靠性分析方法,但当轴承的功能函数未知时,目前的大部分方法都不适用。此时,如何高效地利用轴承的仿真数据进行功能函数拟合并进行可靠性计算,是当前开展轴承可靠性分析面临的严峻挑战。鉴于此,本文对航空发动机主轴圆柱滚子轴承进行有限元仿真分析,并结合Kriging模型对轴承仿真数据进行近似建模,进一步联合主动学习Kriging模型(active learning kriging, ALK)和蒙特卡洛模拟法(Monte Carlo simulation, MCS)进行可靠度计算,形成了求解可靠度的高效高精度ALK-MCS算法。
-
Kriging模型的本质是针对少量样本的函数插值拟合。假定根据拉丁超立方试验设计方法得到输入样本点,并基于相关试验或有限元仿真得到输出样本,具体如下:
$$ {\boldsymbol{S}} = {\left[ {\begin{array}{*{20}{c}} {{x^{\left( 1 \right)}}}&{{x^{\left( 2 \right)}}}& \cdots &{{x^{\left( n \right)}}} \end{array}} \right]^{\text{T}}} \in {R^{n \times m}} $$ (1) $$ \begin{split} &\;\;\;\;\; {{\boldsymbol{Y}}_{_{{{\boldsymbol{S}}}}}} = {\left[ {\begin{array}{*{20}{c}} {{y^{\left( 1 \right)}}}&{{y^{\left( 2 \right)}}}& \cdots &{{y^{\left( n \right)}}} \end{array}} \right]^{\text{T}}} =\\ & {[ {\begin{array}{*{20}{c}} {y( {{x^{\left( 1 \right)}}} )}&{y( {{x^{\left( 2 \right)}}} )}& \cdots &{y( {{x^{\left( n \right)}}} )} \end{array}} ]^{\text{T}}} \in {R^n} \end{split} $$ (2) 根据少量的初始样本点,采用类似于函数拟合插值的方法,获得未知响应与已有功能函数值之间的近似关系:
$$ \hat y\left( x \right) = \sum\limits_{{{i = 1}}}^{{n}} {{\omega ^{\left( i \right)}}y^{\left( i \right)}} $$ (3) 式中,
$ {\omega ^{\left( i \right)}} $ 为权重系数,是模型求解的核心,具体表达为:$$ {\boldsymbol{\omega}} = {\left[ {\begin{array}{*{20}{c}} {{\omega ^{\left( 1 \right)}}}&{{\omega ^{\left( 2 \right)}}}& \cdots &{{\omega ^{\left( n \right)}}} \end{array}} \right]^{\text{T}}} $$ (4) 一旦获得了权重系数
$ {\boldsymbol{\omega}} $ ,则对应的Kriging模型便可以对任何未知点的响应进行求解。Kriging模型基于随机场理论,将未知函数当作随机场的某个具体实现。该随机场具体表述为:
$$ Y\left( x \right) = {\beta _0} + Z\left( x \right) $$ (5) 式中,
$ {\beta _0} $ 是一个常数;$ Z\left( x \right) $ 是一个静态随机过程,其均值为0、方差为$ {\sigma ^2}( {{\sigma ^2}\left( x \right) \equiv {\sigma ^2},\forall x} ) $ ,该随机过程的协方差函数定义为:$$ {\bf{Cov}} = \left[ {Z\left( x \right),Z\left( {x'} \right)} \right] = {\sigma ^2}R\left( {x,x'} \right) $$ (6) 式中,
$ R\left( {x,x'} \right) $ 为相关函数,其大小只与空间距离有关,且与空间距离呈负相关,即变量之间的相关性随着距离增大而减小。Kriging模型的最优加权系数
$ {\boldsymbol{\omega}} $ 能使式(7)所示的均方差达到最小,并满足如式(8)所示的插值条件,即:$$ {\text{MSE}}\left[ {\hat y\left( x \right)} \right] = {\rm{E}}\left[ {{{( {{{\boldsymbol{\omega}} ^{\text{T}}}{{\boldsymbol{Y}}_{_{{{\boldsymbol{S}}}}}} - Y\left( x \right)} )}^2}} \right] $$ (7) $$ {\rm{E}}\left[ {\sum\limits_{{{i = 1}}}^{{n}} {{\omega ^{\left( i \right)}}Y\left( {{x^{\left( i \right)}}} \right)} } \right] = {\rm{E}}\left[ {Y\left( x \right)} \right] $$ (8) 采用拉格朗日乘数法求解
$ \omega $ ,表达如下:$$ \left\{ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{{{j = 1}}}^{{n}} {{\omega ^{\left( j \right)}}R( {{x^{\left( i \right)}},{x^{\left( j \right)}}} )} + \dfrac{\mu }{{2{\sigma ^2}}} = R( {{x^{\left( i \right)}},x} )} \\ {\displaystyle\sum\limits_{{{i = 1}}}^{{n}} {{\omega ^{\left( i \right)}} = 1} } \end{array}} \right. $$ (9) 式中,
$ i = 1,2, \cdots {{,n}} $ ;$ \mu $ 为拉格朗日乘数。式(9)可写成如下所示的矩阵形式:$$ \left[ {\begin{array}{*{20}{c}} {\boldsymbol{R}}&{\boldsymbol{F}} \\ {{{\boldsymbol{F}}^{\text{T}}}}&{\bf{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\boldsymbol{\omega}} \\ {\tilde \mu } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{r}} \\ {\bf{1}} \end{array}} \right] $$ (10) 式中,
$ {\boldsymbol{F}} $ 、$ \tilde \mu $ 、$ {\boldsymbol{R}} $ 和$ {\boldsymbol{r}} $ 的表达式如下:$$\left\{ \begin{array}{c} {\boldsymbol{F}} = {\left[ {\begin{array}{*{20}{c}} 1&1& \cdots &1 \end{array}} \right]^{\text{T}}} \in {{\mathbb{R}}^{{n}}}\\ \tilde \mu = {\mu / {( {2{\sigma ^2}} )}}\\ {\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {R( {{x^{\left( 1 \right)}},{x^{\left( 1 \right)}}} )}& \cdots &{R( {{x^{\left( 1 \right)}},{x^{\left( 1 \right)}}} )} \\ \vdots &{}& \vdots \\ {R( {{x^{\left( 1 \right)}},{x^{\left( 1 \right)}}} )}& \cdots &{R( {{x^{\left( 1 \right)}},{x^{\left( 1 \right)}}} )} \end{array}} \right] \in {{\mathbb{R}}^{n \times n}}\\ {\boldsymbol{r}} = \left[ {\begin{array}{*{20}{c}} {R( {{x^{\left( 1 \right)}},x} )} \\ {R( {{x^{\left( 2 \right)}},x} )} \\ \vdots \\ {R( {{x^{\left( n \right)}},x} )} \end{array}} \right] \in {{\mathbb{R}}^n} \end{array} \right. $$ (11) 式中,
$ {\boldsymbol{R}} $ 为已有样本点间的相关矩阵;$ {\boldsymbol{r}} $ 为未知样本点和已有样本点间的相关向量。Kriging模型的预估值可以表达为:$$ \hat y\left( x \right) = {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{r}}\left( x \right)} \\ {\bf{1}} \end{array}} \right]^{\text{T}}}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{R}}&{\boldsymbol{F}} \\ {{{\boldsymbol{F}}^{\text{T}}}}&{\bf{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{Y}}_{_{{{\boldsymbol{S}}}}}} \\ {\bf{0}} \end{array}} \right] $$ (12) 通过分块矩阵求逆,该模型可写为:
$$ \hat y\left( x \right) = {\beta _0} + {{\boldsymbol{r}}^{\text{T}}}\left( x \right)\underbrace {{{\boldsymbol{R}}^{ - 1}}( {{{\boldsymbol{Y}}_{_{\boldsymbol{S}}}} - {\beta _0}{\boldsymbol{F}}} )}_{ = :{{\boldsymbol{V}}_{{\text{krig}}}}} $$ (13) 式中,
${\beta _0} = {( {{{\boldsymbol{F}}^{\text{T}}}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}}} )^{ - 1}}{{\boldsymbol{F}}^{\text{T}}}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{Y}}_{_{\boldsymbol{S}}}}$ ,列向量$ {{\boldsymbol{V}}_{{\text{krig}}}} $ 只与已知样本点有关。任意$ x $ 处的预测函数值只需要计算$ {\boldsymbol{r}}\left( x \right) $ 与$ {{\boldsymbol{V}}_{{\text{krig}}}} $ 之间的点乘即可。进一步,Kriging模型的预测方差可以表达为:
$$ \begin{gathered} {\text{MSE}}\left[ {\hat y\left( x \right)} \right] = {s^2}\left( x \right) =\\ {\sigma ^2}\left[ {1 - {{\boldsymbol{r}}^{\text{T}}}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{r}} + \frac{{{{\left( {1 - {{\boldsymbol{F}}^{\text{T}}}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{r}}} \right)}^2}}}{{{{\boldsymbol{F}}^{\text{T}}}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}}}}} \right] \\ \end{gathered} $$ (14) -
MCS方法是最简单、最直接的求解失效概率的数值方法,其计算公式为:
$$ {P_{\text{f}}} \approx {\hat P_{\text{f}}} = \frac{1}{{{N_{{\text{MC}}}}}}\sum\limits_{i = 1}^{{N_{{\text{MC}}}}} {{I_{\text{f}}}\left( {G\left( {{x_i}} \right)} \right)} = \frac{{{N_{G \leqslant 0}}}}{{{N_{{\text{MC}}}}}} $$ (15) 式中,
$ {I_{\text{f}}}\left( {G\left( {{x_i}} \right)} \right) $ 为示性函数;$ {\hat P_{\text{f}}} $ 为失效概率的估计值;$ {x_i} $ 为MCS得到的第i个样本点,当$ G\left( {{x_i}} \right) \leqslant 0 $ 时,$ {I_{\text{f}}}\left( {G\left( {{x_i}} \right)} \right) = 1 $ ;当$ G\left( {{x_i}} \right) > 0 $ 时,$ {I_{\text{f}}}\left( {G\left( {{x_i}} \right)} \right) = 0 $ ;$ {N_{G \leqslant 0}} $ 为失效域内的样本数量;$ {N_{{\text{MC}}}} $ 为MCS的总体候选样本数量。因此,MCS方法评估的失效概率变异系数为:
$$ {\delta _{{{\hat P}_{\text{f}}}}} = \sqrt {\frac{{1 - {{\hat P}_{\text{f}}}}}{{\left( {{N_{{\text{MC}}}} - 1} \right){{\hat P}_{\text{f}}}}}} $$ (16) -
从MCS数值模拟的角度求解失效概率的关键在于有效地评估出模拟样本点处响应值的正负符号,而根据Kriging模型可知,在极限状态界面
$ \hat G\left( x \right) = 0 $ 处对应的样本点预测值的符号最容易发生错误。因此,可以对应地将这些样本点加入试验设计中,得到真实响应值,从而进一步来更新Kriging模型,直至达到一定精度水平。此外,Kriging模型的预测值的方差过大,也极有可能导致预测值和真实值的正负符号不一致的情况发生,因此应该保证Kriging模型的预测值的方差尽可能小,从而定义如下学习函数:
$$ U\left( x \right) = \left| {\frac{{\mu \left( x \right)}}{{\sigma \left( x \right)}}} \right| $$ (17) 式中,
$ \mu \left( x \right) $ 为Kriging模型预测值;$ \sigma \left( x \right) $ 为预测值的均方差。$ U\left( x \right) $ 反映了未知点处预测值的正负符号是否正确的程度,即预测值与真实值符号相同的概率:$$ {P_{{\text{right}}}} = \varPhi \left( {U\left( x \right)} \right) = \varPhi \left( {\left| {\frac{{\mu \left( x \right)}}{{\sigma \left( x \right)}}} \right|} \right) $$ (18) 式中,
$\varPhi \left( \cdot \right)$ 为标准正态累积分布函数。 -
当所有候选样本的预测值与真实值符号错误的概率小于给定精度要求时,说明Kriging模型已经达到一定精度要求,因此,停止条件可以表达为:
$$ \min \left( {U\left( x \right)} \right) \geqslant {U_{{\text{limit}}}} $$ (19) 式中,
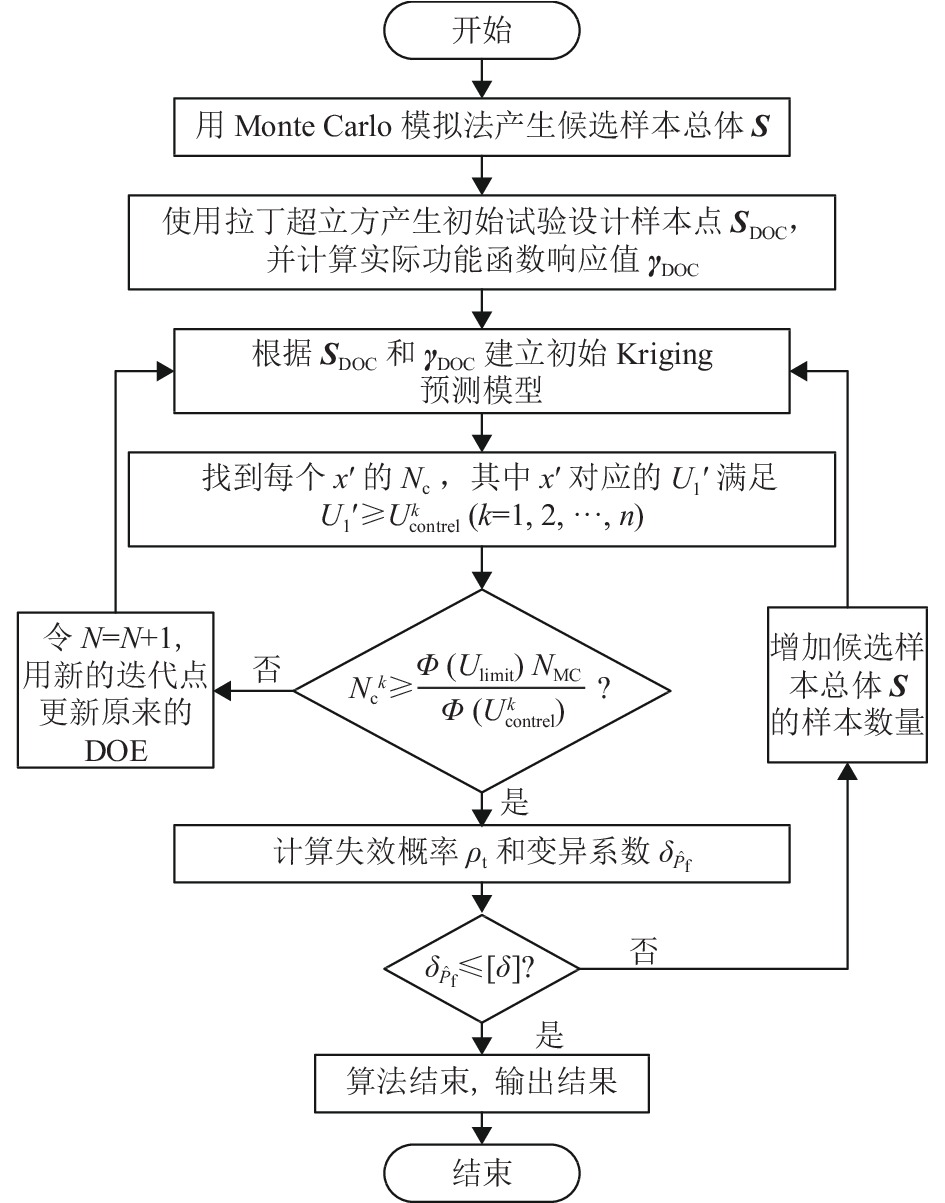
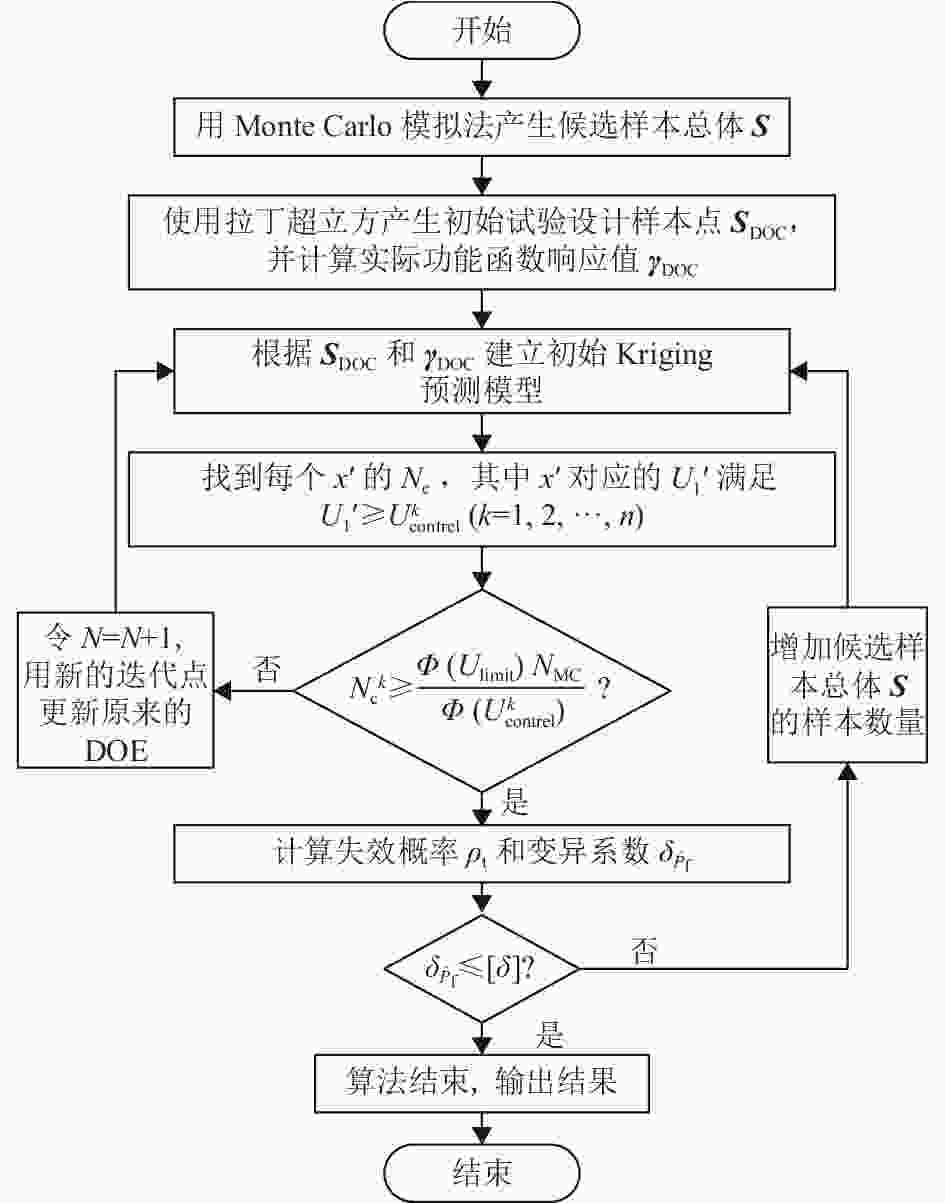
$ {U_{{\text{limit}}}} $ 为给定阈值,例如当$ {U_{{\text{limit}}}} = 2 $ 时,表示Kriging模型预测值和真实值符号正确的概率均大于$\varPhi \left( {{U_{{\text{limit}}}}} \right) = 0.977$ 。本文所述的ALK-MCS算法具体实现流程如图1所示。 -
作为高速旋转部件,滚动轴承通常对内圈、外圈与滚珠的要求较高,应具有良好的冲击韧性与耐磨性,以及较高的强度和硬度。同时,对滚动轴承的保持架要求具备良好的导热性、耐磨性、刚度和弹性。本文以某型号的航空发动机主轴轴承为对象,其内外圈和滚动体的材料采用全淬透型高碳铬轴承钢(GCr15),保持架则通过#J钢板冲压而成,材质为08#低碳钢板;圆柱滚子与滚道为线接触轴承。对于该圆柱滚子轴承,最终构建的三维模型如图2所示。
-
使用ABAQUS软件对轴承进行仿真,具体步骤如下。
1) 通过SOLIDWORKS三维建模软件与ABAQUS有限元分析软件间的配合,实现模型装配的直接传递,将初始三维模型输入ABAQUS中。在ABAQUS软件中,有多种单位制可供选择,如表1所示,本实例选用SI(mm)制单位。在仿真分析模型中,材料参数设置如表2所示。
表 1 仿真软件ABAQUS中SI单位制
标准 单位 长度 mm 力 N 质量 tonne 时间 s 压力 MPa 能量 mJ 密度 tonne/mm3 表 2 有限元分析中的材料参数
名称 材料参数 材料 GCr15 硬度/HBS 800 弹性模量/GPa 207 泊松比 0.27 强度极限/MPa 861.30 屈服极限/MPa 518.42 热处理 渗碳后淬火 2) 装配。装配时轴承的内外圈应保持同轴心,并以计算的游隙为输入,在装配界面通过圆周阵列,将滚动体等间距地装配至轴承内。
3) 网格划分。网格划分在有限元分析模型中极为重要,本实例采用C3D8六面体进行网格划分,图3为网格划分后的有限元分析模型。
4) 设置轴承套圈运动的边界条件。在仿真分析中,仅释放内圈沿X轴径向位移自由度,外圈完全固定。
5) 载荷条件的设定。径向载荷设置为800 N。
6) 接触条件的设定。在实际中,内外圈与滚动体之间有润滑油油膜的作用,使其并未直接接触。润滑油种类不同,其摩擦系数也不一样。选用常用Andok C润滑油,平稳运转、寿命长,摩擦系数约为0.08。故本实例中在初始分析步设置通用接触属性,法向设定为硬接触,切向设定摩擦系数为0.08。
7) 约束条件的设定。本实例通过耦合约束控制轴承内圈内表面与外圈外表面,从而通过控制内圈内表面耦合点与外圈外表面耦合点的运动状态来约束整个轴承的运动状态。
8) 分析步设定。分析步的设定在ABAQUS中十分重要,考虑到轴承中多种因素对应力响应的影响,本实例通过软件中显式动力学分析方法进行求解。设定总分析时长为1 s,最小增量步为0.01 s,稳定最大增量步为0.02 s,最终输出帧数为65帧。
通过以上流程,可以得到圆柱滚子轴承的有限元仿真分析结果整体应力分布图,如图4所示。
-
对航空发动机主轴圆柱滚子轴承进行有限元仿真分析得到轴承内的最大应力。当最大应力小于材料的屈服强度时,说明圆柱滚子轴承安全可靠。然而,在工程实际中,圆柱滚子轴承受到各种不确定性因素的影响,从而造成轴承内的最大应力存在一定的波动性。鉴于此,本文将圆柱滚子轴承材料性能(摩擦系数)、载荷等参数视为随机变量,如表3所示。从而,基于抽取的随机变量样本数据改变有限元分析过程中所施加的边界条件,得到不同随机变量下的最大应力,进而进行圆柱滚子轴承可靠性分析。同时,考虑到轴承单次仿真耗时长,以及直接通过仿真应力求解可靠度时计算量大,本文引入ALK-MCS算法来计算圆柱滚子轴承的可靠度。
表 3 滚子轴承中的随机变量
变量 分布类型 均值 均方差 摩擦系数 正态分布 0.08 0.0012 外部载荷/N 正态分布 800.00 9.6000 采用ALK-MCS算法对航空发动机主轴圆柱滚子轴承进行可靠性分析,具体计算结果如表4所示,图5为提出方法在迭代过程中对应的有限元分析得到的某一迭代点下的最大应力云图。
表 4 基于ALK-MCS算法的计算结果
方法 迭代次数
/次候选样本
/个失效概率 ALK-MCS 43 2000000 0.0002 从表4可知,采用ALK-MCS算法在迭代43次后就能得到轴承的失效概率,说明了该方法对涉及有限元仿真时的可靠性分析是有效的。同时,采用该算法最终得到轴承的失效概率为0.0002,可靠度为0.9998。需要特别指出的是,本文做一次轴承的仿真大概需要25 min,直接采用MCS算法需要仿真2000000次,计算成本无法接受,从而再次说明了本文提出的ALK-MCS算法对涉及有限元仿真时的可靠性计算问题的有效性,同时由于该轴承失效寿命数据有限,通常的基于寿命分布的可靠性评估方法并不适用,本文所得结果可为决策者提供参考。
-
本文对航空发动机主轴圆柱滚子轴承进行了有限元仿真分析,并基于ALK-MCS算法对轴承的可靠性进行了计算。
1)将Kriging代理模型引入航空发动机主轴圆柱滚子轴承的可靠性分析中,提出了一种联合主动学习Kriging和MCS的ALK-MCS可靠性分析方法,有效解决了MCS方法效率低,不适用于可靠性仿真分析的问题。
2)通过SOLIDWORKS三维建模软件建立了某型号航空发动机主轴圆柱滚子轴承的三维模型,并导入有限元仿真软件ABAQUS中,完成相关参数设定、模型网格划分与约束加载,从而求解得到了该轴承内的最大应力,为验证提出的可靠性分析方法提供了仿真数据支撑。
3)基于ALK-MCS算法,对某型号航空发动机主轴圆柱滚子轴承进行了可靠性分析,得出其可靠度为0.9998,验证了ALK-MCS算法是一种高效的结构可靠度计算方法,适用于功能函数为隐函数的情形。
Reliability Analysis for Bearings of Aero-Engine Based on ALK-MCS Algorithm
-
摘要: 作为航空发动机的关键部件,主轴圆柱滚子轴承的可靠性水平直接影响航空发动机性能的稳定性与服役的安全性,因此准确分析主轴圆柱滚子轴承的可靠性至关重要。然而,圆柱滚子轴承的失效行为复杂,其可靠性分析中的功能函数呈现高度非线性且无法给出显式表达,此时使用代理模型近似构建圆柱滚子轴承的功能函数是一种行之有效的方法。将蒙特卡洛模拟法(MCS)和Kriging代理模型相结合,提出了基于主动学习Kriging(ALK)的ALK-MCS算法,并将该算法应用于某型号航空发动机主轴圆柱滚子轴承的可靠性分析。首先,建立圆柱滚子轴承的三维模型,其次对圆柱滚子轴承进行有限元仿真,最后基于ALK-MCS算法对其进行可靠性分析。结果表明ALK-MCS算法计算效率高,显著减少了圆柱滚子轴承的仿真次数,所得到的可靠性分析结果可为实际工程中的决策者提供参考。
-
关键词:
- 航空发动机 /
- ALK-MCS /
- 圆柱滚子轴承 /
- Kriging代理模型 /
- 可靠性分析
Abstract: As one of the key parts of aero-engine, the reliability of cylindrical roller bearings affects the stability of aero-engine to some extent. Therefore, it is very important to study the reliability of cylindrical roller bearings of aero-engine. However, the complex limit state functions often appear in the reliability analysis of cylindrical roller bearings, such as highly nonlinear functions, and even some limit state functions are implicitly given. At this time, it is an effective method to use surrogate model to approximate the limit state function of cylindrical roller bearings. In this paper, by combining with Kriging surrogate model and the active learning (active learning Kriging-Monte Carlo simulation) ALK-MCS algorithm, the reliability of an aero-engine’s cylindrical roller bearings is studied. Firstly, the three-dimensional model of a cylindrical roller bearing is established, then the finite element simulation is performed, and finally the ALK-MCS-based reliability analysis of the cylindrical roller bearing is carried out. The results show that as an active learning reliability method with high efficiency, ALK-MCS algorithm can significantly reduce the iteration. Simultaneously, the reliability result of the cylindrical roller bearing through ALK-MCS algorithm provides some guidance for the decision-maker in actual engineering.-
Key words:
- aero-engine /
- ALK-MCS /
- cylindrical roller bearings /
- Kriging surrogate model /
- reliability analysis
-
表 1 仿真软件ABAQUS中SI单位制
标准 单位 长度 mm 力 N 质量 tonne 时间 s 压力 MPa 能量 mJ 密度 tonne/mm3 表 2 有限元分析中的材料参数
名称 材料参数 材料 GCr15 硬度/HBS 800 弹性模量/GPa 207 泊松比 0.27 强度极限/MPa 861.30 屈服极限/MPa 518.42 热处理 渗碳后淬火 表 3 滚子轴承中的随机变量
变量 分布类型 均值 均方差 摩擦系数 正态分布 0.08 0.0012 外部载荷/N 正态分布 800.00 9.6000 表 4 基于ALK-MCS算法的计算结果
方法 迭代次数
/次候选样本
/个失效概率 ALK-MCS 43 2000000 0.0002 -
[1] 中国机械工业联合会. GB/T 24607-2009 滚动轴承 寿命与可靠性试验及评定[S]//张伟, 杨洁. 北京: 中国标准出版社, 2010. China Machinery Industry Federation. GB/T 24607-2009 rolling bearings-test and assessment for life and reliability[S]//ZHANG W, YANG J. Beijing: Standards Press of China, 2010. [2] 高攀东, 陈晓阳, 沈雪瑾, 等. 小样本下轴承可靠性评估方法对比分析[J]. 轴承, 2014(12): 44-48. doi: 10.3969/j.issn.1000-3762.2014.12.016 GAO P D, CHEN X Y, SHEN X J, et al. Comparative analysis on reliability estimating methods of bearing test with small samples[J]. Bearing, 2014(12): 44-48. doi: 10.3969/j.issn.1000-3762.2014.12.016 [3] 许凌天, 沈雪瑾, 蒋爽, 等. 退化量有缺失的无失效小样本轴承可靠性评估[J]. 航空动力学报, 2020, 35(9): 1977-1987. XU L T, SHEN X J, JIANG S, et al. Reliability assessment of bearings with incomplete performance degradation data under small and non-failure samples[J]. Journal of Aerospace Power, 2020, 35(9): 1977-1987. [4] 秦荦晟, 陈晓阳, 沈雪瑾. 小样本下基于竞争失效的轴承可靠性评估[J]. 振动与冲击, 2017, 36(23): 248-254. QIN L S, CHEN X Y, SHEN X J. Reliability assessment of bearings based on competing failure under small sample data[J]. Journal of Vibration and Shock, 2017, 36(23): 248-254. [5] 徐现昭. 滚动轴承可靠性评价方法研究[D]. 杭州: 中国计量学院, 2012. XU X Z. Study on reliability evaluation method of rolling bearings[D]. Hangzhou: China Jiliang University, 2012. [6] 孙慧洋. 基于无失效数据的轴承可靠性研究[D]. 沈阳: 东北大学, 2014. SUN H Y, Study on reliability of bearing based on zero-failure data[D]. Shenyang: Northeastern University, 2014. [7] QIN L S, SHEN X J, CHEN X Y, et al. Reliability assessment of bearings based on performance degradation values under small samples[J]. Journal of Mechanical Engineering, 2017, 63(4): 248-254. doi: 10.5545/sv-jme.2016.3898 [8] LI H L, ZHENG Z Y. Reliability estimation for zero-failure data based on confidence limit analysis method[J]. Mathematical Problems in Engineering, 2020, 2020: 1-11. [9] ZHANG C W. Weibull parameter estimation and reliability analysis with zero-failure data from high-quality products[J]. Reliability Engineering & System Safety, 2021, 207: 1-15. [10] YANG J W, WANG J H, HUANG Q, et al. Reliability assessment for the solenoid valve of a high speed train braking system under small sample size[J]. Chinese Journal of Mechanical Engineering, 2018, 31(1): 1-11. doi: 10.1186/s10033-018-0219-4 [11] SHAO Y H, LU P M, WANG B H, et al. Fatigue reliability assessment of small sample excavator working devices based on bootstrap method[J]. Fracture and Structural Intregrity, 2019, 13(48): 757-767. [12] FREITAS M A, COLOSIMO E A, SANTOS T R, et al. Reliability assessment using degradation models: Bayesian and classical approaches[J]. Pesquisa Operacional, 2010, 30(1): 194-219. doi: 10.1590/S0101-74382010000100010 [13] LOU H L, LI X L, ZHUO J Z, et al. Reliability evaluation for rolling bearings with small sampling based on Bayes method[C]//The 8th International Conference on Reliability, Maintainability and Safety. Chengdu: [s.n.], 2009: 434-436. [14] XIA X T. Reliability analysis of zero-failure data with poor information[J]. Quality and Reliability Engineering International, 2012, 28(8): 981-990. doi: 10.1002/qre.1279 [15] CAO L L, CAO L, LIU K, et al. Reliability estimation for drive axle of wheel loader under extreme small sample[J]. Advances in Mechanical Engineering, 2019, 11(3): 1-12. -


 ISSN
ISSN 



 下载:
下载: