-
随着全球互联网的全面普及,海量数据随之产生,如何高效地管理和可靠地存储海量数据成为当前的研究热点。海量数据主要采用分布式存储系统,为了维护系统的可用性和可靠性需引入冗余策略,最常见的冗余策略有复制策略和纠删码策略[1],但都存在一定的局限性。随后,文献[2]将网络编码应用到分布式存储系统中,提出了再生码的概念。再生码虽然在一定程度上减小了修复带宽开销,但修复故障节点过程中需连接大量存活节点,增加了系统的磁盘I/O开销。
为了解决上述问题,文献[3]提出了局部修复码(locally repairable codes, LRC),有效降低了故障节点的修复局部性。文献[4]研究了信息位具有局部性和可用性的局部修复码的最小距离限,但关于修复局部性的边界条件没有研究。进一步地,文献[5-6]分别研究了局部修复码的构造并且协作局部修复码,降低了存储开销并降低了修复局部性。文献[7]研究了局部性为2且可用性不等时的局部修复码。
最小距离和码率是衡量局部修复码性能的两个主要性能指标[8],其中最小距离最优的局部修复码一般简称为最优局部修复码。文献[9]利用射影平面和仿射平面理论构造了3种局部性和可用性相等的局部修复码,达到了最优最小距离边界。基于部分几何构造的最优局部修复码[10],通过交换点集和线集的关联结构得到部分几何的对偶,进而构造局部性和可用性不等的局部修复码。基于Gilbert方法的最优二元单校验局部修复码[11],通过结合循环置换矩阵构造了一种新的LDPC码,将其与单位矩阵级联形成校验矩阵,进而构造出满足最小距离界的二元单校验局部修复码。这3种构造出的局部修复码都可达到最优最小距离边界,但是码率较小。
除最小距离和码率之外,在局部修复码中也考虑维度这一参数。有学者基于生成矩阵、校验矩阵和图论相关理论构造局部修复码来提高码率,但都没有分析维度是否达到维度最优的边界条件。文献[12]使用组合设计构造了最优二元局部修复码,运用BIBD和DBBD区组设计构造出的局部修复码在码率上更优,但码长略大。文献[13]使用打包设计构造了最优局部修复码,限制了码长和维度的参数条件,无法灵活地构造不同情况下的局部修复码。文献[14]构造了最优单校验二元局部修复码,但其维度没有达到维度最优的边界条件。利用图论相关理论来构造局部修复码,主要是从二分图的角度出发构造二元局部修复码[15-16],虽然能达到最优最小距离,但是构造算法略复杂。
针对以上问题,本文提出一种基于Hadamard矩阵的最优局部修复码的构造方法。首先基于Hadamard矩阵构造局部修复码的校验矩阵,通过校验矩阵构造局部修复码,构造的局部修复码能达到最优最小距离界,但是维度没有达到最优维度边界条件。为了进一步提高维度,将校验矩阵中的关联矩阵0和1元素互换得到新的关联矩阵,通过和新的关联矩阵级联进行扩展,构造的扩展局部修复码不仅能达到最优最小距离界,且能达到维度最优的边界条件。此外,基于Hadamard矩阵构造的扩展局部修复码的码率也更逼近局部修复码最优码率的边界,参数选择更加灵活。
-
局部修复码作为广义上的纠错码,适用于分布式存储系统。分布式存储系统中存储的文件采用局部修复码进行编码,并将编码后的信息存于存储节点中。当有部分存储节点故障,则可以利用其余存活节点修复故障节点,实现分布式存储系统中数据的可靠存储。本节主要介绍局部修复码的一些相关原理。
-
定义1[8] 在有限域
$ {F_q} $ 上的$ {\left[ {n,k,d} \right]_q} $ 线性分组码中,给定$ \left[ n \right] = \left\{ {1,2, \cdots ,n} \right\} $ ,码字$ c = \left( {{c_1},{c_2}, \cdots ,{c_n}} \right) $ 。如果其中一个编码符号$ {c_i} $ 具有局部性$ r $ 和可用性$ t $ ,需满足下列条件:1) 有
$ t $ 个子集,满足${\varphi _1}(i),{\varphi _2}(i), \cdots ,{\varphi _t}(i) \subset [n]\backslash \left\{ i \right\}$ ,即$ {c_i} $ 能够从$ {\varphi _j}(i)(j \in [t]) $ 中恢复出来;2)
$\left| {{\varphi _j}(i)} \right| \leqslant r,j \in [t]$ ;3)
${\varphi _j}(i) \cap {\varphi _l}(i) = \varnothing$ ,$ j \ne l \in [t] $ 。称
$ {\varphi _j}(i)(j \in [t]) $ 为$ {c_i} $ 的修复集合。如果局部修复码的所有信息位码元都具有$ (r,t) $ 可用性,那么称该码为具有$ (r,t) $ 可用性的局部修复码,记作$ {(n,k,r,t)_i} $ LRC。若每个信息位码元的每个修复集只有一个校验位码元,则这个码称作单校验$ {(n,k,r,t)_i} $ LRC。本文主要研究单校验$ (n,k, r,t)_i $ LRC,该码由关联矩阵和单位矩阵拼接而成,其中关联矩阵的行重为局部性$ r $ ,列重为可用性$ t $ 。 -
$ [n,k,d] $ 线性分组码$ C $ 的最小距离等于非零码字的最小重量,该最小距离是汉明距离,可表示为$ d{\text{ = }}\mathop {\min }\limits_{{C_i} \in [n,k]} w\left( {{C_i}} \right) $ 。码$ C $ 的最小距离越大,可修复的故障节点越多。定理 1[10] 若一个线性分组码
$ C $ 是信息位具有局部性$ r $ 和可用性$ t $ 的局部修复码,最小距离应满足:$$ d \geqslant t + 1 $$ (1) 定理 2[13] 若局部修复码的所有信息位码元的每一个修复集中只含有一个校验位,且该单校验
$ {(n,k,r,t)_i} $ LRC的最小距离满足:$$ d \leqslant n - k - \left\lceil {\frac{{kt}}{r}} \right\rceil + t + 1 $$ (2) 称达到边界(2)的局部修复码是最小距离最优的单校验
$ {(n,k,r,t)_i} $ LRC。 -
一般地,每个码的信息位个数
$ k $ 与码元数$ n $ 之间的比值称作码率,用$ R = {k \mathord{\left/ {\vphantom {k n}} \right. } n} $ 表示。定理3[17] 若
$ (n,k,r,t) $ LRC具有$ (r,t) $ 可用性,且该码码率满足:$$ R \leqslant \frac{1}{{\displaystyle\prod _{i = 1}^t(1 + \dfrac{1}{{ir}})}} $$ (3) 则达到边界(3)的局部修复码的码率最优。
定理 4[18] 特别地,可用性
$ t = 2 $ 的最优码率的$ (n,k,r,t = 2) $ 单校验局部修复码满足的码率边界条件为:$$ R \leqslant \frac{r}{{r + 2}} $$ (4) 定理 5[19] (维度C-M边界限)在有限域
$ {\rm{GF}}(q) $ 中的$ (n,k,r) $ 单校验局部修复码的维度应满足:$$ k \leqslant \min [tr + k_{{\rm{opt}}}^{(q)}(n - t(r + 1),d)] $$ (5) 式中,
$k_{{\rm{opt}}}^{(q)}(n,d)$ 表示$ q $ 元$ (n,k,r) $ LRC的最大可能的维度,且该码满足Singleton限,即$k_{{\rm{opt}}}^{(q)}(n,d) \leqslant n - d + 1, \forall q \in {{\rm Z}_ + }$ 。称满足不等式(5)的$ (n,k,r) $ LRC为维度最优的局部修复码。 -
构造基于Hadamard矩阵的局部修复码,关键在于构造局部修复码的校验矩阵。局部修复码的校验矩阵用
${{{{{\boldsymbol{H}}}}}} = [{{{\boldsymbol{M}}}}|{{{{\boldsymbol{I}}}}}]$ 表示,${{{\boldsymbol{I}}}}$ 是单位矩阵,单位矩阵的列对应局部修复码的校验位符号;${{{\boldsymbol{M}}}}$ 是对应的关联矩阵,关联矩阵的列对应信息位符号。码字和校验矩阵的关系为${{{\boldsymbol{c}}}} \cdot {{{{\boldsymbol{H}}}}^ \bot } = {\mathbf{0}}$ ,通过此关系可知每个信息位码字的修复集,一个基于校验矩阵构造的具有可用性$ (r,t) $ 的局部修复码,它的关联矩阵的行重$ r $ 用来保证局部性,列重$ t $ 用来保证可用性。本节主要基于Hadamard矩阵构造关联矩阵,关联矩阵级联单位矩阵生成校验矩阵,通过校验矩阵来构造局部修复码。
定义2
$ k' $ 阶方阵${{{{\boldsymbol{H}}}}_{k'}}$ ,若其元素为1或−1,且满足:$$ {{{{\boldsymbol{H}}}}_{k'}}{{{{\boldsymbol{H}}}}_{k'}}^{\rm{T}} = k'{{{{\boldsymbol{I}}}}_{k'}} $$ (6) 称
${{{{\boldsymbol{H}}}}_{k'}}$ 为$ k' $ 阶Hadamard矩阵,其中${{{{\boldsymbol{I}}}}_{k'}}$ 是$ k' $ 阶单位阵。若
${{{{\boldsymbol{H}}}}_{k'}}$ 首行首列均为全1向量,则该${{{{\boldsymbol{H}}}}_{k'}}$ 为标准Hadamard矩阵。本文所涉及的Hadamard矩阵均为标准Hadamard矩阵。构造1 基于Hadamard矩阵构造局部修复码的具体步骤如下。
1) 首先将Hadamard矩阵的1元素全部换为0元素,−1元素全部换为1元素,得到一个
$ k' $ 阶方阵,记为${{{{{\boldsymbol{M}}}}}_{k' \times k'}}$ ;2) 根据
$ k' $ 阶方阵${{{{\boldsymbol{M}}}}_{k' \times k'}}$ 构造:$$ {{{{\boldsymbol{M}}}}_{2k' \times 2k'}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{M}}_{k' \times k'}}}&{{{\boldsymbol{M}}_{k' \times k'}}} \\ {{{\boldsymbol{M}}_{k' \times k'}}}&{\overline {{{\boldsymbol{M}}_{k' \times k'}}} } \end{array}} \right] $$ 式中,
$\overline {{{\boldsymbol{M}}_{k' \times k'}}}$ 是对矩阵${{\boldsymbol{M}}_{k' \times k'}}$ 进行0和1元素互换构成的矩阵;3) 将方阵
${{\boldsymbol{M}}_{2k' \times 2k'}}$ 的首行和首列删除,得到$ 2k' - 1 $ 阶方阵${{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}$ ;4) 将
$ 2k' - 1 $ 阶方阵${{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}$ 作为关联矩阵,在其后级联$ 2k' - 1 $ 阶单位矩阵${{\boldsymbol{I}}_{2k' - 1}}$ 得到矩阵${{\boldsymbol{H}}_{(2k' - 1) \times (4k' - 2)}} = \left[ {{{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}|{{{{{\boldsymbol{I}}}}}_{2k' - 1}}} \right]$ ;5) 将矩阵
${{\boldsymbol{H}}_{(2k' - 1) \times (4k' - 2)}}$ 作为局部修复码的校验矩阵,构造得到$ (n = 4k' - 2,{\text{ }}k = 2k' - 1,{\text{ }}r = k', $ $ t = k') $ 局部修复码,其中可用性$ t $ 为2的倍数。推论1 构造1中
$ (n = 4k' - 2,{\text{ }}k = 2k' - 1, r = k', t = $ $ k') $ 局部修复码为最小距离最优的局部修复码,且码的最小距离$ d = t + 1 $ 。证明:将
$ (n = 4k' - 2,{\text{ }}k = 2k' - 1,{\text{ }}r = k',{\text{ }}t = k') $ 局部修复码的参数代入边界条件(2),有:$$ \begin{gathered} d \leqslant n - k - \left\lceil {\frac{{kt}}{r}} \right\rceil + t + 1 = \\(4k' - 2) - (2k' - 1) - (2k' - 1) + k' + 1 = k' + 1 \end{gathered} $$ 因为
$ k' = t $ ,则$ d \leqslant t + 1 $ 。又根据式(1)得$ d \geqslant t + 1 $ ,所以$ d = t + 1 $ ,可得到基于Hadamard矩阵构造的局部修复码的最小距离$ d = t + 1 $ ,满足边界条件(2),则该码是最小距离最优的局部修复码。构造1中的局部修复码的码率
$ R = \dfrac{k}{n} = \dfrac{1}{2} $ ,没有达到式(3)中最优码率的边界条件,故该码不是码率最优的局部修复码。例1 令
$ k' = 4 $ ,得到方阵:$$ {{{{\boldsymbol{M}}}}_{4 \times 4}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&1&0&1 \\ 0&0&1&1 \\ 0&1&1&0 \end{array}} \right] $$ 利用步骤 2) 可得到
${{\boldsymbol{M}}_{8 \times 8}}$ ,将${{\boldsymbol{M}}_{8 \times 8}}$ 的首行和首列全部删除,得到一个7阶的关联矩阵${{\boldsymbol{M}}_{7 \times 7}}$ :$$ {{\boldsymbol{M}}_{7 \times 7}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} 1&0&1&0&1&0&1 \\ 0&1&1&0&0&1&1 \\ 1&1&0&0&1&1&0 \\ 0&0&0&1&1&1&1 \\ 1&0&1&1&0&1&0 \\ 0&1&1&1&1&0&0 \\ 1&1&0&1&0&0&1 \end{array}} \right] $$ 进一步得到局部修复码的校验矩阵:
$$ \begin{split} &\qquad\qquad\qquad{{\boldsymbol{H}}_{7 \times 14}} = [{{\boldsymbol{M}}_{7 \times 7}}|{{\boldsymbol{I}}_7}]{\text{ = }}\\ &\left[ {\begin{array}{*{20}{c}} 1&0&1&0&1&0&1&1&0&0&0&0&0&0 \\ 0&1&1&0&0&1&1&0&1&0&0&0&0&0 \\ 1&1&0&0&1&1&0&0&0&1&0&0&0&0 \\ 0&0&0&1&1&1&1&0&0&0&1&0&0&0 \\ 1&0&1&1&0&1&0&0&0&0&0&1&0&0 \\ 0&1&1&1&1&0&0&0&0&0&0&0&1&0 \\ 1&1&0&1&0&0&1&0&0&0&0&0&0&1 \end{array}} \right] \end{split} $$ 由此可构造出一个单校验
$ (n = 14,{\text{ }}k = 7,{\text{ }}r = 4, t = 4) $ 局部修复码,此码的最小距离$ d = 5 $ 。故障节点的修复方法为:若信息位
$ {c_1} $ 发生故障,由${\boldsymbol{c}} \cdot {{\boldsymbol{H}}^{\rm{T}}} = {\boldsymbol{0}}$ 可知,信息位$ {c_1} $ 可根据${c_1} = {c_8} - {c_3} - $ ${c_5} - {c_7} = $ ${c_{10}} - {c_2} - {c_5} - {c_6} = $ ${c_{12}} - {c_3} - {c_4} - {c_6} $ =${c_{14}} - {c_2} - {c_4} -$ $ {c_7} $ 进行修复,那么信息位$ {c_1} $ 的修复集可表示为$ {\varphi _1} = \left\{ {3,5,7,8} \right\} $ ,$ {\varphi _2} = \left\{ {2,5,6,10} \right\} $ ,$ {\varphi _3} = \left\{ {3,4,6,12} \right\} $ 和${\varphi _4} = \left\{ 2,4, 7,14 \right\}$ ,每个修复集均含有一个校验位符号,同理,其他信息位符号也可用相同的方法进行修复。 -
上述基于Hadamard矩阵构造的局部修复码的局部性和可用性相等,且能够达到最优最小距离界,但是该局部修复码的码率较小,没有达到维度最优的边界条件。为了进一步提高码率和维度,将上述构造中的关联矩阵
${{\boldsymbol{M}}_{(2{k'} - 1) \times (2k' - 1)}}$ 进行扩展,得到码率更高并且维度最优的扩展局部修复码。构造2 基于Hadamard矩阵的扩展局部修复码的具体构造步骤如下。
1) 首先将Hadamard矩阵的1元素全部换为0元素,−1元素全部换为1元素,得到一个
$ k' $ 阶方阵,记为${{{{{\boldsymbol{M}}}}}_{k' \times k'}}$ ;2) 根据
$ k' $ 阶方阵${{\boldsymbol{M}}_{k' \times k'}}$ 构造:$$ {{\boldsymbol{M}}_{2k' \times 2k'}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{M}}_{k' \times k'}}}&{{{\boldsymbol{M}}_{k' \times k'}}} \\ {{{\boldsymbol{M}}_{k' \times k'}}}&{\overline {{{\boldsymbol{M}}_{k' \times k'}}} } \end{array}} \right] $$ 式中,
$\overline {{{\boldsymbol{M}}_{k' \times k'}}}$ 是对矩阵${{\boldsymbol{M}}_{k' \times k'}}$ 进行0和1元素互换构成的矩阵;3) 将方阵
${{\boldsymbol{M}}_{2k' \times 2k'}}$ 的首行和首列删除,得到$ 2k' - 1 $ 阶方阵${{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}$ ,将方阵${{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}$ 中0和1元素互换构成矩阵$\overline {{{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}}$ ;4) 将
${{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}$ 下方级联一个长度为$ 2k' - 1 $ 的全0序列,将$\overline {{{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}}$ 下方级联一个长度为$ 2k' - 1 $ 的全1序列;5) 将步骤 4)的两个矩阵左右级联得到
${{\boldsymbol{M}}_{2k' \times (4k' - 2)}}$ ,具体表示形式为:$$ {{\boldsymbol{M}}_{2k' \times (4k' - 2)}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}}&{\overline {{{\boldsymbol{M}}_{(2k' - 1) \times (2k' - 1)}}} } \\ {\mathbf{0}}&{\mathbf{1}} \end{array}} \right] $$ 6) 将
${{\boldsymbol{M}}_{2k' \times (4k' - 2)}}$ 作为扩展局部修复码的关联矩阵,与单位矩阵${{\boldsymbol{I}}_{2k'}}$ 级联生成校验矩阵${{\boldsymbol{H}}_{2k' \times (6k' - 2)}} = \left[ {{{\boldsymbol{M}}_{2k' \times (4k' - 2)}}|{{\boldsymbol{I}}_{2k'}}} \right]$ ,由此校验矩阵可以构造得到参数条件为$ (n = 6k' - 2,{\text{ }}k = 4k' - 2,{\text{ }}r = 2k' - 1, t = k') $ 的局部修复码,其中可用性$ t $ 为2的倍数。例2 与例1类似,取
$ k' = 4 $ ,将例1中的${{\boldsymbol{M}}_{7 \times 7}}$ 的0和1元素互换组成矩阵$\overline {{{\boldsymbol{M}}_{7 \times 7}}}$ ,具体如下:$$ \overline {{{{{\boldsymbol{M}}}}_{7 \times 7}}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&1&0&1&0 \\ 1&0&0&1&1&0&0 \\ 0&0&1&1&0&0&1 \\ 1&1&1&0&0&0&0 \\ 0&1&0&0&1&0&1 \\ 1&0&0&0&0&1&1 \\ 0&0&1&0&1&1&0 \end{array}} \right] $$ 再在
${{\boldsymbol{M}}_{7 \times 7}}$ 的下方级联一个长度为7的全0序列,在$\overline {{{\boldsymbol{M}}_{7 \times 7}}}$ 的下方级联一个长度为7的全1序列,之后将这两个矩阵左右级联得到关联矩阵:$$ \begin{split} &\qquad\qquad\qquad\qquad{{{{\boldsymbol{M}}}}_{8 \times 14}} =\\ &\left[ {\begin{array}{*{20}{c}} 1&0&1&0&1&0&1&0&1&0&1&0&1&0 \\ 0&1&1&0&0&1&1&1&0&0&1&1&0&0 \\ 1&1&0&0&1&1&0&0&0&1&1&0&0&1 \\ 0&0&0&1&1&1&1&1&1&1&0&0&0&0 \\ 1&0&1&1&0&1&0&0&1&0&0&1&0&1 \\ 0&1&1&1&1&0&0&1&0&0&0&0&1&1 \\ 1&1&0&1&0&0&1&0&0&1&0&1&1&0 \\ 0&0&0&0&0&0&0&1&1&1&1&1&1&1 \end{array}} \right] \end{split} $$ 最后将
${{\boldsymbol{M}}_{8 \times 14}}$ 作为扩展局部修复码的关联矩阵,和单位矩阵${{\boldsymbol{I}}_8}$ 级联生成校验矩阵${{\boldsymbol{H}}_{8 \times 22}} = \left[ {{{\boldsymbol{M}}_{8 \times 14}}\left| {{{\boldsymbol{I}}_8}} \right.} \right]$ ,由此可构造出单校验$ (n = 22,{\text{ }}k = 14, r = 7,{\text{ }}t = 4) $ 局部修复码,此码的最小距离$ d = 5 $ ,码率$ R = {7 \mathord{\left/ {\vphantom {7 {11}}} \right. } {11}} $ ,与构造1相比,有效地提高了局部修复码的码率。故障节点的修复方法为:若信息位
$ {c_1} $ 发生故障,由${\boldsymbol{c}} \cdot {{\boldsymbol{H}}^{\rm{T}}} = {\mathbf{0}}$ 可知,信息位$ {c_1} $ 可根据$ {c_1} = {c_{15}} - {c_3} - {c_5} - {c_7} - {c_9} - {c_{11}} - {c_{13}} = {c_{17}} - {c_2} - {c_5} - {c_6} - {c_{10}} - {c_{11}} - {c_{14}} $ =$ {c_{19}} - {c_3} - {c_4} - {c_6} - {c_9} - {c_{12}} - {c_{14}} = {c_{21}} - {c_2} - {c_4} - {c_7} - {c_{10}} $ −$ {c_{12}} - {c_{13}} $ 进行修复,那么信息位$ {c_1} $ 的修复集可表示为$ {\varphi _1} = \left\{ {3,5,7,9,11,13,15} \right\} $ ,$ {\varphi _2} = \left\{ {2,5,6,10,11,14,17} \right\} $ ,$ {\varphi _3} = \left\{ {3,4,6,9,12,14,19} \right\} $ 和$ {\varphi _4} = \left\{ {2,4,7,10,12,13,21} \right\} $ ,各个修复集都只有一个校验位符号。同理,其他信息位符号也可用相同的方法进行修复。 -
推论2 构造2得到的
$ (n = 6k' - 2, k = 4k' - 2, r = $ $ = 2k' - 1,{\text{ }}t = k') $ 局部修复码是最小距离最优的局部修复码,且码的最小距离$ d = t + 1 $ 。证明:将
$ (n = 6k' - 2,{\text{ }}k = 4k' - 2,{\text{ }}r = 2k' - 1,{\text{ }}t = k') $ 局部修复码的参数代入边界条件(2),可得:$$ \begin{gathered} d \leqslant n - k - \left\lceil {\frac{{kt}}{r}} \right\rceil + t + 1 = \\6k' - 2 - (4k' - 2) - \left\lceil {\frac{{(4k' - 2)k'}}{{2k' - 1}}} \right\rceil + k' + 1 = k' + 1 \\ \end{gathered} $$ 因为
$ k' = t $ ,即$ d \leqslant t + 1 $ 。又根据式(1)得$ d \geqslant t + 1 $ ,所以$ d = t + 1 $ ,可以得到构造2中的局部修复码的最小距离$ d = t + 1 $ 。该局部修复码的最小距离满足边界条件(2),则该码是最小距离最优的局部修复码。推论3 构造2得到的
$ (n = 6k' - 2,{\text{ }}k = 4k' - 2, r = $ $ 2k' - 1,{\text{ }}t = k') $ 局部修复码是维度最优的局部修复码,且码的维度$ k \leqslant 4k' - 2 $ 。证明:当式(1)中最小距离
$ d $ 为最大值时,可以将式(5)简化如下:$$ \begin{gathered} k \leqslant \min [tr + k_{{\rm{opt}}}^{(q)}(n - t(r + 1),d)] =\\ \min [tr + n - t(r + 1) - {d_{\max }} + 1] = \\tr + n - t(r + 1) - (t + 1) + 1 = n - 2t \\ \end{gathered} $$ 将
$ (n = 6k' - 2,{\text{ }}k = 4k' - 2,{\text{ }}r = 2k' - 1,{\text{ }}t = k') $ LRC的参数条件代入简化的公式中,可得$ k \leqslant 4k' - 2 $ ,对于$ \forall k' $ ,基于Hadamard矩阵构造的扩展局部修复码的维度都可达到最优维度边界条件的上界。 -
基于Hadamard矩阵构造的扩展局部修复码的码率为:
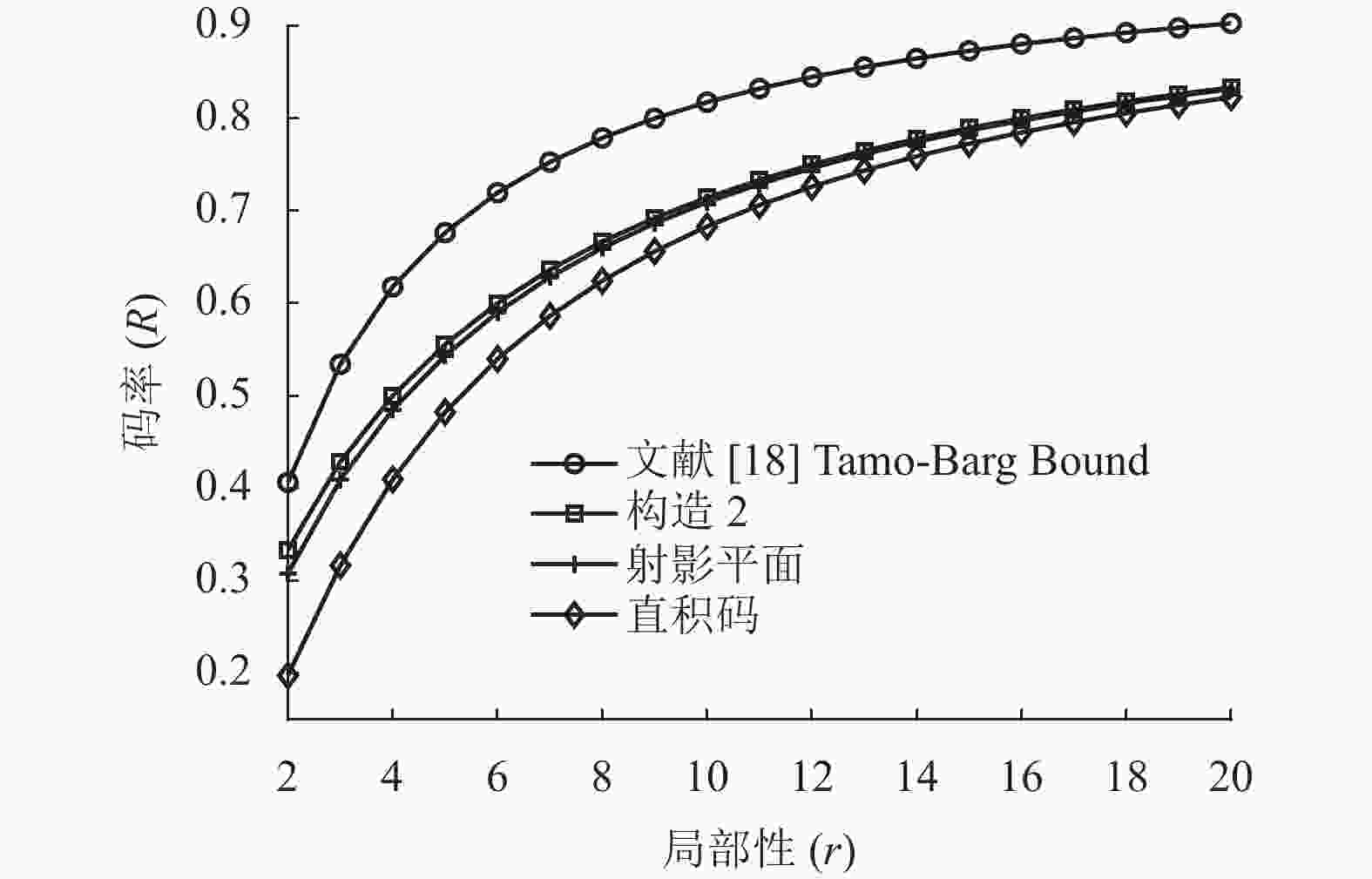
$$ \begin{gathered} R = k/n =\\ \frac{{4k' - 2}}{{6k' - 2}} = \frac{{2k' - 1}}{{2k' - 1 + k'}} = \frac{r}{{r + t}} \\ \end{gathered} $$ 表1是现有的单校验局部修复码和本文构造2中局部修复码的参数对比。与基于射影平面构造的局部修复码[14]相比,尽管构造2中的局部修复码的最小距离小1,但是在码率上有所提升。基于直积码构造的局部修复码是由
$ t $ 个二元单校验$(r + 1,{\text{ }}t)$ 码生成[20],码率为${\left(\dfrac{r}{{r + 1}}\right)^t}$ 。$t > 1$ 时,${\left(1 + \dfrac{1}{r}\right)^t} > 1 + \dfrac{t}{r}$ ,因此可得:$$ {\left(\frac{r}{{r + 1}}\right)^t} = \frac{1}{{{{\left(1 + \dfrac{1}{r}\right)}^t}}} < \frac{1}{{1 + \dfrac{t}{r}}} = \frac{r}{{r + t}} $$ 则本文构造2中局部修复码的码率大于基于直积码构造的局部修复码码率。
表 1 不同局部修复码参数对比
构造方法 $ n $ $ k $ $ d $ $ R = k/n $ 构造2 $ 6k' - 2 $ $ 4k' - 2 $ $ t + 1 $ $ \dfrac{r}{{r + t}} $ DBBD区组设计[12] $ \begin{gathered} k'(k' + 1)/2 \\ + k' + 1 \\ \end{gathered} $ $ k' + 1 $ $ t + 1 $ $ \dfrac{2}{{2 + t}} $ 射影平面[14] $ {r^2} + rt + 1 $ $ {r^2} $ $ t + 2 $ $ \dfrac{{{r^2}}}{{{r^2} + rt + 1}} $ 直积码[20] $ {(r + 1)^t} $ $ {r^t} $ $ t + 1 $ $ {(\dfrac{r}{{r + 1}})^t} $ 图1所示为
$ t = 4 $ 时,不同局部修复码的码率$ R $ 随着局部性$ r $ 的变化曲线,也容易看出构造2的码率是最逼近局部修复码最优码率界限的。根据推论3可以在理论方面证明,构造2在
$ \forall k' $ 的条件下满足维度最优的边界条件。表2是现有局部修复码和构造2的局部修复码关于维度参数的对比。文献[12]的两种局部修复码都是最小距离最优的局部修复码,但是都只有在一定条件下才能达到维度最优。DBBD区组设计构造出的局部修复码需要当$ k' \geqslant 3 $ 时,才能满足定理5的维度最优的边界条件;单位矩阵变换构造出的局部修复码需要当$ r \geqslant 2 $ 时,才能满足定理5的维度最优的边界条件。文献[14]中的局部修复码虽然最小距离比构造2大1,但不是维度最优,将射影平面构造出的局部修复码的参数代入定理5可知,需要满足$ r \geqslant - \dfrac{1}{t} + 2 $ 才能达到维度最优。文献[21]和文献[22]中的局部修复码虽然都是维度最优,但文献[21]最小距离没有达到最优的边界条件,文献[22]只有当$ d = 4 $ 时才是最小距离最优,且参数范围限制较大。二者的可用性$ t =1$ ,限制了修复时可选择的修复集数量。文献[21]中构造的局部修复码的局部性为2或3,限制了其局部性的可选范围。综上,只有本文构造2中的局部修复码在满足最小距离最优的情况下,在任何参数下都能满足维度最优。表 2 不同局部修复码关于维度参数的对比
构造方法 $ k $ $ r $ $ t $ $ d $ 构造2 $ 4k' - 2 $ $ 2k' - 1 $ $ k' $ $ t + 1 $ DBBD区组设计[12] $ k' + 1 $ $ 2 $ $ k' $ $ t + 1 $ 单位矩阵变换[12] $ {r^2} $ $ r $ $ 2 $ $ 3 $ 射影平面[14] $ {r^2} $ $ r $ $ t $ $ t + 2 $ 反码[21] $ m $ $ 2,3 $ $ 1 $ $ \begin{gathered} {2^{m - 1}} - x \\ (x = 2,4,6) \\ \end{gathered} $ 割圆多项式[22] $ \begin{gathered} (u - 1)v \\ - \phi (u) \\ \end{gathered} $ $ u - 1 $ $ 1 $ $ 4 $ -
为了满足在最优最小距离边界条件下,局部修复码的维度也能达到最优,本文首先构造了基于Hadamard矩阵的局部修复码,此局部修复码能达到最优最小距离界,但是维度没有达到维度最优的边界条件。为了提高维度,将校验矩阵中的关联矩阵0和1元素互换得到新的关联矩阵,通过和新的关联矩阵级联进行扩展,构造的扩展局部修复码不仅能达到最优最小距离界,且能达到维度最优的边界条件。将基于Hadamard矩阵构造的扩展局部修复码和现有的局部修复码相比,本文的构造在码率上更逼近局部修复码最优码率的界限。
本文得到长安大学大学生创新创业训练计划项目(G202010710031)资助,在此深表感谢!
Construction of Optimal Locally Repairable Codes Based on Hadamard Matrix
-
摘要: 现有的局部修复码大多能满足最小距离最优的边界条件,但是在满足最小距离最优情况下构造维度最优的局部修复码还比较困难。针对上述问题,提出一种基于Hadamard矩阵的最优局部修复码的构造方法,通过对Hadamard矩阵进行扩展,构造局部修复码的校验矩阵,进而通过此校验矩阵构造最优局部修复码。首先,基于Hadamard矩阵构造局部修复码的校验矩阵,通过校验矩阵构造的局部修复码的最小距离可以达到最优最小距离界,但是其维度没有达到最优维度边界条件;为进一步提高维度,将校验矩阵中的关联矩阵0和1元素互换得到新的关联矩阵,通过和新的关联矩阵级联进行扩展,构造的扩展局部修复码不仅可以达到最小距离最优,且能达到维度最优的边界条件。与现有局部修复码相比,该构造的局部修复码是最小距离和维度最优的局部修复码,且其码率也更逼近局部修复码最优码率的边界。
-
关键词:
- 码率 /
- 维度 /
- Hadamard矩阵 /
- 局部修复码 /
- 最小距离
Abstract: Most of the existing locally repairable codes can meet the boundary condition of minimum distance, but it is difficult to construct the locally repairable codes with optimal dimension under the condition of minimum distance optimization. To solve this problems, this paper proposes a construction method of optimal locally repairable codes based on Hadamard matrix. By expanding Hadamard matrix, the check matrix of the optimal locally repairable code can be obtained. Specifically, the parity matrix of locally repairable codes is constructed using Hadamard matrix, and the minimum distance of the locally repairable codes constructed by the parity matrix can reach the optimal boundary, but its dimension does not reach the optimal dimension boundary condition. In order to improve the dimension, the element 0 and element 1 of the incidence matrix in the check matrix are exchanged to obtain a new incidence matrix. By cascading with the new incidence matrix, the constructed extended locally repairable code can not only achieve the minimum distance optimization, but also achieve the boundary condition of the optimal dimension. Compared with the existing locally repairable codes, the extended locally repairable code based on Hadamard matrix constructed in this paper is the optimal locally repairable code with minimum distance and dimension, and its code rate is closer to the boundary of the optimal code rate of locally repairable codes.-
Key words:
- code rate /
- dimension /
- Hadamard matrix /
- locally repairable codes /
- minimum distance
-
表 1 不同局部修复码参数对比
构造方法 $ n $ $ k $ $ d $ $ R = k/n $ 构造2 $ 6k' - 2 $ $ 4k' - 2 $ $ t + 1 $ $ \dfrac{r}{{r + t}} $ DBBD区组设计[12] $ \begin{gathered} k'(k' + 1)/2 \\ + k' + 1 \\ \end{gathered} $ $ k' + 1 $ $ t + 1 $ $ \dfrac{2}{{2 + t}} $ 射影平面[14] $ {r^2} + rt + 1 $ $ {r^2} $ $ t + 2 $ $ \dfrac{{{r^2}}}{{{r^2} + rt + 1}} $ 直积码[20] $ {(r + 1)^t} $ $ {r^t} $ $ t + 1 $ $ {(\dfrac{r}{{r + 1}})^t} $ 表 2 不同局部修复码关于维度参数的对比
构造方法 $ k $ $ r $ $ t $ $ d $ 构造2 $ 4k' - 2 $ $ 2k' - 1 $ $ k' $ $ t + 1 $ DBBD区组设计[12] $ k' + 1 $ $ 2 $ $ k' $ $ t + 1 $ 单位矩阵变换[12] $ {r^2} $ $ r $ $ 2 $ $ 3 $ 射影平面[14] $ {r^2} $ $ r $ $ t $ $ t + 2 $ 反码[21] $ m $ $ 2,3 $ $ 1 $ $ \begin{gathered} {2^{m - 1}} - x \\ (x = 2,4,6) \\ \end{gathered} $ 割圆多项式[22] $ \begin{gathered} (u - 1)v \\ - \phi (u) \\ \end{gathered} $ $ u - 1 $ $ 1 $ $ 4 $ -
[1] LEE O T, KUMAR S, CHANDRAN P. Erasure coded storage systems for cloud storage—challenges and opportunities[C]//2016 International Conference on Data Science and Engineering (ICDSE). Kochi: Cochin Univ Sci & Technol, 2016: 23-25. [2] DIMAKIS A G, GODFREY P B, WU Y N, et al. Network coding for distributed storage systems[J]. IEEE Transactions on Information Theory, 2010, 56(9): 4539-4551. doi: 10.1109/TIT.2010.2054295 [3] PAPAILIOPOULOS D S, DIMAKIS A G. Locally repairable codes[C]//2012 IEEE International Symposium on Information Theory Proceedings. [S.l.]: IEEE, 2012: 2771-2775. [4] PRAKASH N, KAMATH G M, LALITHA V, et al. Optimal linear codes with a local-error-correction property[C]//2012 IEEE International Symposium on Information Theory Proceedings. Cambridge, MA: IEEE, 2012: 2776-2780. [5] HAO J, XIA S T, KENNETH W, et al. Bounds and constructions of locally repairable codes: Parity-Check matrix approach[J]. IEEE Transactions on Information Theory, 2020, 66(12): 7465-7474. doi: 10.1109/TIT.2020.3021707 [6] WANG J, YAN Z Y, LI K C, et al. Local codes with cooperative repair in distributed storage of cyber-physical-social systems[J]. IEEE Access, 2020, 8: 38622-38632. doi: 10.1109/ACCESS.2020.2975577 [7] LEE K S, PARK H, NO J S, et al. New binary locally repairable codes with locality 2 and uneven availabilities for hot data[J]. Entropy, 2018, 20(9): 636. doi: 10.3390/e20090636 [8] RAWAT A S, PAPAILIOPOULOS D S, DIMAKIS A G, et al. Locality and availability in distributed storage[J]. IEEE Transactions on Information Theory, 2016, 62(8): 4481-4493. doi: 10.1109/TIT.2016.2524510 [9] HAO J, XIA S. Constructions of optimal binary locally repairable codes with multiple repair groups[J]. IEEE Communications Letters, 2016, 20(6): 1060-1063. doi: 10.1109/LCOMM.2016.2539160 [10] TAN P, ZHOU Z, SIDORENKO V, et al. Two classes of optimal LRCs with information (r, t)-locality[J]. Designs, Codes and Cryptography, 2020, 88(9): 1741-1757. [11] 张永. 几个基于校验矩阵构造的最优局部修复码[D]. 上海: 华东师范大学, 2019. ZHANG Y. Several optimal locally repairable codes based on check matrix[D]. Shanghai: East China Normal University, 2019. [12] WANG J, SHEN K Q, LIU X Y, et al. Construction of binary locally repairable codes with optimal distance and code rate[J]. IEEE Communications Letters, 2021, 25(7): 2109-2113. doi: 10.1109/LCOMM.2021.3075520 [13] CAI H, CHENG M, FAN C, et al. Optimal locally repairable systematic codes based on packings[J]. IEEE Transactions on Communications, 2019, 67(1): 39-49. doi: 10.1109/TCOMM.2018.2869800 [14] HAO J, XIA S T, CHEN B. On the single-parity locally repairable codes with availability[C]//Proceedings of International Conference on Communications in China. [S. l. ]: IEEE, 2016: 1-4. [15] KRUGLIK S, NAZIRKHANOVA K, FROLOV A. New bounds and generalizations of locally recoverable codes with availability[J]. IEEE Transactions on Information Theory, 2019, 65(7): 4156-4166. doi: 10.1109/TIT.2019.2897705 [16] SHAHABINEJAD M, KHABBAZIAN M, ARDAKANI M. A class of binary locally repairable codes[J]. IEEE Transactions on Communications, 2016, 64(8): 3182-3193. doi: 10.1109/TCOMM.2016.2581163 [17] TAMO I, BARG A, FROLOV A. Bounds on the parameters of locally recoverable codes[J]. IEEE Transactions on Information Theory, 2016, 62(6): 3070-3083. doi: 10.1109/TIT.2016.2518663 [18] PRAKASH N, LALITHA V, KUMAR P V. Codes with locality for two erasures[C]//Proceedings of International Symposium on Information Theory. [S.l.]: IEEE, 2014: 1962-1966. [19] CADAMBE V R, MAZUMDAR A. Bounds on the size of locally recoverable codes[J]. IEEE Transactions on Information Theory, 2015, 61(11): 5787-5794. doi: 10.1109/TIT.2015.2477406 [20] CHAICHANAVONG P, SIEGEL P H. Relaxation bounds on the minimum pseudo-weight of linear block codes[C]//International Symposium on Information Theory. Adelaide, SA: IEEE, 2005: 805-809. [21] SILBERSTEIN N, ZEH A. Optimal binary locally repairable codes via anticodes[C]//2015 IEEE International Symposium on Information Theory. HongKong, China: IEEE, 2015: 1247-1251. [22] TAN P, ZHOU Z, YAN H, et al. Optimal cyclic locally repairable codes via cyclotomic polynomials[J]. IEEE Communications Letters, 2019, 23(2): 202-205. doi: 10.1109/LCOMM.2018.2882849 -


 ISSN
ISSN 





 下载:
下载:





























































































































































































































































