-
量子密钥分发(quantum key distribution, QKD)[1-5]是一种能够为远距离通信双方(Alice和Bob)提供信息论安全密钥的技术。密钥的安全性由量子力学原理[6-7]来保证。由于实际设备的不完美性,QKD可能面临来自源端和探测端的双重攻击。一方面,理想的QKD协议大多需要完美的单光子源。然而,由于当前技术的限制,实际的QKD系统经常采用相位随机化后的弱相干态(weak coherent state, WCS)光源来代替单光子源。WCS光源发出的脉冲包含的光子数有时不只一个,窃听者Eve就可以利用多光子脉冲来获取密钥而不被Alice和Bob发现,这就是光子数分离(photon number splitting, PNS)[8-14]攻击。该攻击导致了极低的安全成码率和安全传输距离。早期的PNS攻击[8-12]要求Eve具有极强的技术水平,不易实现。后来,改进型PNS[13-14]甚至在现有的条件下就能实现,这直接威胁了现有采用WCS光源QKD协议的安全性。幸运的是,诱骗态方法[15-17]可以很好地抵抗各种类型的PNS攻击,显著提高安全成码率和最大安全传输距离。另一方面,QKD还可能面临来自探测端的攻击,如伪态攻击[18]、时移攻击[19]等。测量设备无关的量子密钥分发(measurement-device-independent quantum key distribution, MDI-QKD)[20]可以先天免疫所有探测端的攻击,但是其安全密钥率不高,不能突破PLOB界[21]。2018年,陆续提出的双场量子密钥分发(twin-field quantum key distribution, TF-QKD)[22-24]成功突破了PLOB界,大大提高了安全密钥率和最大安全传输距离。需要注意的是,无论是MDI-QKD还是TF-QKD,只要采用WCS光源,就会面临PNS攻击的威胁,因此同样需要使用诱骗态方法。总之,对于诱骗态方法的研究仍然很有意义。
在诱骗态QKD中,Alice随机地从不同强度的WCS光源中发出信号态或诱骗态给Bob。同时,Alice和Bob假设Eve不能区分信号态和诱骗态,从而导致信号态和诱骗态拥有相同的
$ i $ 光子透射率,这在诱骗态方法中是一个至关重要的假设。并且,这个假设还被应用到诱骗态QKD的安全性证明中。实际上,由于信号态和诱骗态的强度差异,二者的光子数概率分布是不同的。基于此,Eve可以以一定概率区分信号态和诱骗态。一旦Eve区分出了信号态和诱骗态,就可以分别对其执行不同的PNS攻击策略,使其分别具有不同的$ i $ 光子透射率。进一步地,如果Eve还能够保证攻击前后信号态和诱骗态的测量统计量不变,那么它就可以获得最终密钥而不被Alice和Bob发现。根据以上分析,基于不同强度导致的光子数概率分布差异,本文采用贝叶斯决策来区分信号态和诱骗态,发现同样只能得到信号态和诱骗态具有相同$ i $ 光子透射率的结论,这就验证了诱骗态QKD中信号态和诱骗态不可区分假设的合理性。另外,分别对比单信号态QKD和信号态+单诱骗态QKD两种情况下PNS攻击前后的安全密钥率,结果表明前者攻击成功,后者攻击失败,这就验证了诱骗态方法确实能够抵抗PNS攻击。综合来看,上述两项研究内容验证了诱骗态方法的安全性。 -
在诱骗态QKD中,Alice随机地发送信号态
$ \left(s\right) $ 或者诱骗态$ \left(d\right) $ 。信号态和诱骗态的强度分别为$ \mu $ 和$ \mathrm{\nu } $ 。不失一般性,假设$ 1 > \mu > \nu > 0 $ ,由于使用WCS光源,信号态和诱骗态的光子数均服从泊松分布。具体地,来自信号态和诱骗态的$ i $ 光子态的概率分别为:$$ {P}_{i}^{s}=\frac{{\text{e}}^{-\mu }{\mu }^{i}}{i!}\;\;\;\;{P}_{i}^{d}=\frac{{\text{e}}^{-\nu }{\nu }^{i}}{i!} $$ (1) 信号态和诱骗态的响应率和量子比特错误率(quantum bit error rate, QBER)分别为:
$$ {Q}_{\mathrm{\mu }}=\sum _{i=0}^{\mathrm{\infty }}{P}_{i}^{s}{Y}_{i}^{s}\;\;\;\;{Q}_{\nu }=\sum _{i=0}^{\mathrm{\infty }}{P}_{i}^{d}{Y}_{i}^{d} $$ (2) $$ {Q}_{\mathrm{\mu }}{E}_{\mathrm{\mu }}=\sum _{i=0}^{\mathrm{\infty }}{P}_{i}^{s}{Y}_{i}^{s}{e}_{i}^{s}\;\;\;\;{Q}_{\mathrm{\nu }}{E}_{\mathrm{\nu }}=\sum _{i=0}^{\mathrm{\infty }}{P}_{i}^{d}{Y}_{i}^{d}{e}_{i}^{d}$$ (3) 式中,
${Y}_{i}^{s}({Y}_{i}^{d})$ 和${e}_{i}^{s}({e}_{i}^{d})$ 分别是来自信号态(诱骗态)的$ i $ 光子态的透射率和量子比特错误率。在诱骗态方法中有一个重要假设,即Eve无法区分信号态和诱骗态,并由此有以下重要等式:$$ {Y}_{i}^{s}={Y}_{i}^{d}={Y}_{i}\;\;\;\;{e}_{i}^{s}={e}_{i}^{d}={e}_{i}\left(i\geqslant 0\right)$$ (4) 实际上,由于信号态和诱骗态的强度差异,二者的光子数概率分布是不同的。基于此,Eve是可以以一定概率区分信号态和诱骗态的,并由此导致式(4)可能不再成立。
在诱骗态QKD[25]中,使用WCS光源的安全密钥率下界为:
$$ {R}^{{\rm{decoy}}}=q\left\{-{Q}_{\mu }f({E}_{\mu }){H}_{2}({E}_{\mu })+{Y}_{1}\mu {\text{e}}^{-\mu }\left[1-{H}_{2}\left({e}_{1}\right)\right]\right\}$$ (5) 式中,
$q=1/2$ 表示BB84协议的基矢比对效率(如果使用高效的BB84协议[26],$ q\approx 1 $ );$ f\left(x\right) $ 是双向纠错效率,通常$ f\left(x\right)\geqslant 1 $ , 香农极限时$ f\left(x\right)=1 $ ;$ {H}_{2}\left(x\right)= -x{\mathrm{log}}_{2}\left(x\right)-\left(1-x\right){\mathrm{log}}_{2}\left(1-x\right) $ 是二进制香农熵;$ {Y}_{1} $ 和$ {e}_{1} $ 分别是单光子态的透射率和量子比特错误率,它们可以通过诱骗态方法估计得到。根据诱骗态QKD的后处理方案[25],可以得到
$ {Y}_{1} $ 的下界和$ {e}_{1} $ 的上界:$$ \begin{split} &{Y}_{1}\geqslant \frac{\mu }{\mu \nu -{\nu }^{2}}\left({Q}_{\nu }{\text{e}}^{\nu }-{Q}_{\mu }{\text{e}}^{\mu }\frac{{\nu }^{2}}{{\mu }^{2}}-{E}_{\mu }{Q}_{\mu }{\text{e}}^{\mu }\frac{{\mu }^{2}-{\nu }^{2}}{{e}_{0}{\mu }^{2}}\right) \\ &\qquad\qquad\qquad\qquad{e}_{1}\leqslant \frac{{E}_{\mu }{Q}_{\mu }{\text{e}}^{\mu }}{{Y}_{1}\mu } \end{split} $$ (6) 在正常信道中,信号态和诱骗态的响应率和量子比特错误率分别是:
$$ \begin{split} &\qquad{Q}_{\mu }={Y}_{0}+1-{\text{e}}^{-\eta \mu } \\ &\qquad{Q}_{\nu }={Y}_{0}+1-{\text{e}}^{-\eta \nu } \\ &{E}_{\mu }{Q}_{\mu }={e}_{0}{Y}_{0}+{e}_{d}\left(1-{\text{e}}^{-\eta \mu }\right) \\ &{E}_{\nu }{Q}_{\nu }={e}_{0}{Y}_{0}+{e}_{d}\left(1-{\text{e}}^{-\eta \nu }\right) \end{split} $$ (7) 式中,
$ {Y}_{0} $ 和$ {e}_{0} $ 分别是暗计数率和相应的量子比特错误率;$ {e}_{d} $ 是一个光子触发错误探测器的概率,它刻画了光学系统的稳定性;$ \eta $ 表示Alice和Bob之间的总透射率,记作$\eta ={\eta }_{{\rm{Bob}}}{10}^{-\alpha L \times 10}$ ,其中,$ {\eta }_{{\rm{Bob}}} $ 是Bob端的传输效率,包括光学组件的内部传输效率和探测效率,$ \alpha $ 是衰减系数(dB/km),$ L $ 是信道长度(km)。 -
假设样本只可能来自两个类,并且已知样本的某项特征。在该特征条件下,确定样本来自条件概率较大的类,这就是贝叶斯决策或最大后验概率估计。
不失一般性,假设Alice等概率地发送信号态
$ \left(s\right) $ 或者诱骗态$ \left(d\right) $ 给Bob。Eve拦截该量子态,然后通过量子非破坏性(quantum non-demolition, QND)[27-28]测量得到该量子态的光子数。根据贝叶斯决策理论,给定量子态的光子数,就判断该量子态来自信号态和诱骗态中条件概率较大的态。用随机变量$ M $ 表示截获量子态的来源,$ M\in \left\{s,d\right\} $ ,用随机变量$ N $ 表示截获量子态包含的光子数,$ N\in \left\{0, 1, 2, \cdots \right\} $ 。在光子数为$ i $ 的条件下,截获的量子态来自信号态和诱骗态的概率分别为:$$ \begin{split} &P\left(M=s|N=i\right)=\frac{P\left(M=s,N=i\right)}{P\left(N=i\right)} =\\ & \qquad\quad\frac{P\left(M=s\right)P\left(N=i|M=s\right)}{P\left(N=i\right)} \end{split} $$ (8) $$ \begin{split} &P\left(M=d|N=i\right)=\frac{P\left(M=d,N=i\right)}{P\left(N=i\right)} =\\ &\qquad\quad\frac{P\left(M=d\right)P\left(N=i|M=d\right)}{P\left(N=i\right)} \end{split} $$ (9) 因为信号态和诱骗态是等概率地从Alice发出的,所以有
$ P\left(M=s\right)=P\left(M=d\right)=1/2 $ 。式(8)和式(9)的分母相同,所以如果想比较$ P\left(M=s|N=i\right) $ 和$ P\left(M=d|N=i\right) $ 的大小,只需比较$ P\left(N=i|M=s\right) $ 和$ P\left(N=i|M=d\right) $ 的大小。实际上,$ P\left(N=i|M=s\right) $ 就是$ {P}_{i}^{s} $ 。$ P\left(N=i|M=d\right) $ 就是$ {P}_{i}^{d} $ 。给定光子数$ i $ 、信号态强度$ \mu $ 和诱骗态强度$ \nu ,{P}_{i}^{s} $ 和$ {P}_{i}^{d} $ 很容易通过式(1)得到。因此,Eve只需要知道截获量子态的光子数、信号态和诱骗态的强度,就可以根据贝叶斯决策判断出该量子态来自信号态还是诱骗态。假设
$ 1 > \mu > \nu > 0 $ ,通过式(1)很容易得到${P}_{0}^{s} < {P}_{0}^{d},{P}_{i}^{s} > {P}_{i}^{d},\left(i > 1 \right)$ ,就是说,凡是空脉冲,Eve全都判为来自诱骗态;凡是非空脉冲,Eve全都判为来自信号态。基于此,Eve对信号态和诱骗态分别采用不同的透射率。定义$ {Z}_{i}^{\mu } $ 和$ {Z}_{i}^{\nu } $ 分别是Eve根据贝叶斯决策设置的信号态和诱骗态$ i $ 光子的透射率。具体地:$$ {Y}_{0}^{s}={Y}_{0}^{d}={Z}_{0}^{\nu }\;\;\;\;{Y}_{i}^{s}={Y}_{i}^{d}={Z}_{i}^{\mu }\left(i\geqslant 1\right) $$ (10) 综合来看,
$ {Y}_{i}^{s}={Y}_{i}^{d}={Y}_{i}\left(i\geqslant 0\right) $ ,式(4)仍然成立。也就是说,Eve即使利用信号态和诱骗态的唯一差异——强度不同导致的光子数概率分布差异,结合贝叶斯决策来区分信号态和诱骗态,也无法得到更多关于信号态和诱骗态的有用信息,最后同样也只能得到信号态和诱骗态具有相同$ i $ 光子透射率的结论,从而验证了诱骗态QKD中信号态和诱骗态不可区分这一假设的合理性。这里只分析了窃听者Eve的攻击对$ i $ 光子透射率的影响,因为Eve的攻击可以做到对量子比特错误率的影响忽略不计[29]。 -
在诱骗态方法的后处理过程中,安全密钥只能从单光子成分中得到。在Eve执行PNS攻击之后,真正安全密钥率的上限[30]是:
$$ {R}^{{\rm{Eve}}}={Y}_{1}\mu {\text{e}}^{-\mu } $$ (11) 特别地,在文献[29]中,有一种PNS攻击成功的判别准则,即:
$$ {R}^{{\rm{sec}}} > {R}^{{\rm{Eve}}} $$ (12) 式中,
$ {R}^{{\rm{sec}}} $ 代表的是Alice和Bob认为安全的密钥率,如果这个值大于Eve攻击之后真正安全的密钥率$ {R}^{{\rm{Eve}}} $ ,这就意味着Alice和Bob生成的一部分密钥是不安全的。换言之,Eve已经知道了关于最终密钥的部分信息。因此,可以说Eve的攻击是成功的,反之,攻击是失败的。式(5)和式(11)中
$ {Y}_{1} $ 的值在计算上是不同的。$ {R}^{{\rm{decoy}}} $ 中的$ {Y}_{1} $ 是Alice和Bob通过诱骗态方法的后处理过程估计得到的,即式(6)。$ {R}^{{\rm{Eve}}} $ 中的$ {Y}_{1} $ 是Eve在PNS攻击中优化得到的。当Eve执行PNS攻击时,她可以任意改变$ i $ 光子的透射率。为了不被Alice和Bob发现,Eve需要保持攻击前后的测量统计量不变。假设Eve的攻击对误码率的影响忽略不计,因此只需保证响应率这一个统计量不变。根据文献[31]可知,只需考虑包含6光子及6光子以下脉冲带来的影响即可。即只需要优化$ {Y}_{1},{Y}_{2}, {Y}_{3},{Y}_{4},{Y}_{5},{Y}_{6} $ 以求得真正的安全密钥率$ {R}^{{\rm{Eve}}} $ 的上限。特别地,令优化后的$ {Y}_{0}=0 $ ,这是因为如果Eve收到了一个空脉冲,她转发任何光子给Bob都可能引入误码[29]。 -
首先考虑最原始的BB84-QKD的情况,即只有一种WCS光源发出脉冲——信号态。此时,Alice和Bob认为单光子脉冲和多光子脉冲都能够生成安全密钥,并且认为安全的密钥率为
$ {R}^{{\rm{sec}}}= {R}^{{\rm{full}}} $ :$$ {R}^{{\rm{full}}}=q{Q}_{\mu }\left[1-f({E}_{\mu }){H}_{2}({E}_{\mu })-{H}_{2}({E}_{\mu })\right] $$ (13) 在只有信号态的情况下,根据前面的分析,在Eve执行PNS攻击之后,真正安全的密钥率
$ {R}^{{\rm{Eve}}}={Y}_{1}\mu {\text{e}}^{-\mu } $ 的求解可以归结为:$$ \underset{\left\{{Y}_{1},{Y}_{2},{Y}_{3},{Y}_{4},{Y}_{5},{Y}_{6}\right\}}{\mathrm{min}}{Y}_{1}\mu {\text{e}}^{-\mu } $$ (14) 当满足以下条件:
$$ {Q}_{\mu }={Y}_{0}+1-{\text{e}}^{-\eta \mu }=\sum _{i=1}^{6}{P}_{i}^{s}{Y}_{i} $$ (15) 式中,
$ {Y}_{1},{Y}_{2},{Y}_{3},{Y}_{4},{Y}_{5},{Y}_{6}\in \left[0, 1\right] $ 。通过计算,可以得到$ {R}^{{\rm{Eve}}} $ 。如果这个值小于Alice和Bob认为安全的密钥率$ {R}^{{\rm{sec}}} $ ,表明Eve攻击成功。否则,攻击失败。利用Matlab进行仿真。仿真参数主要来源于文献[32-33],是单信号态QKD典型实验系统的参数,具体如表1所示。
表 1 单信号态QKD仿真参数表
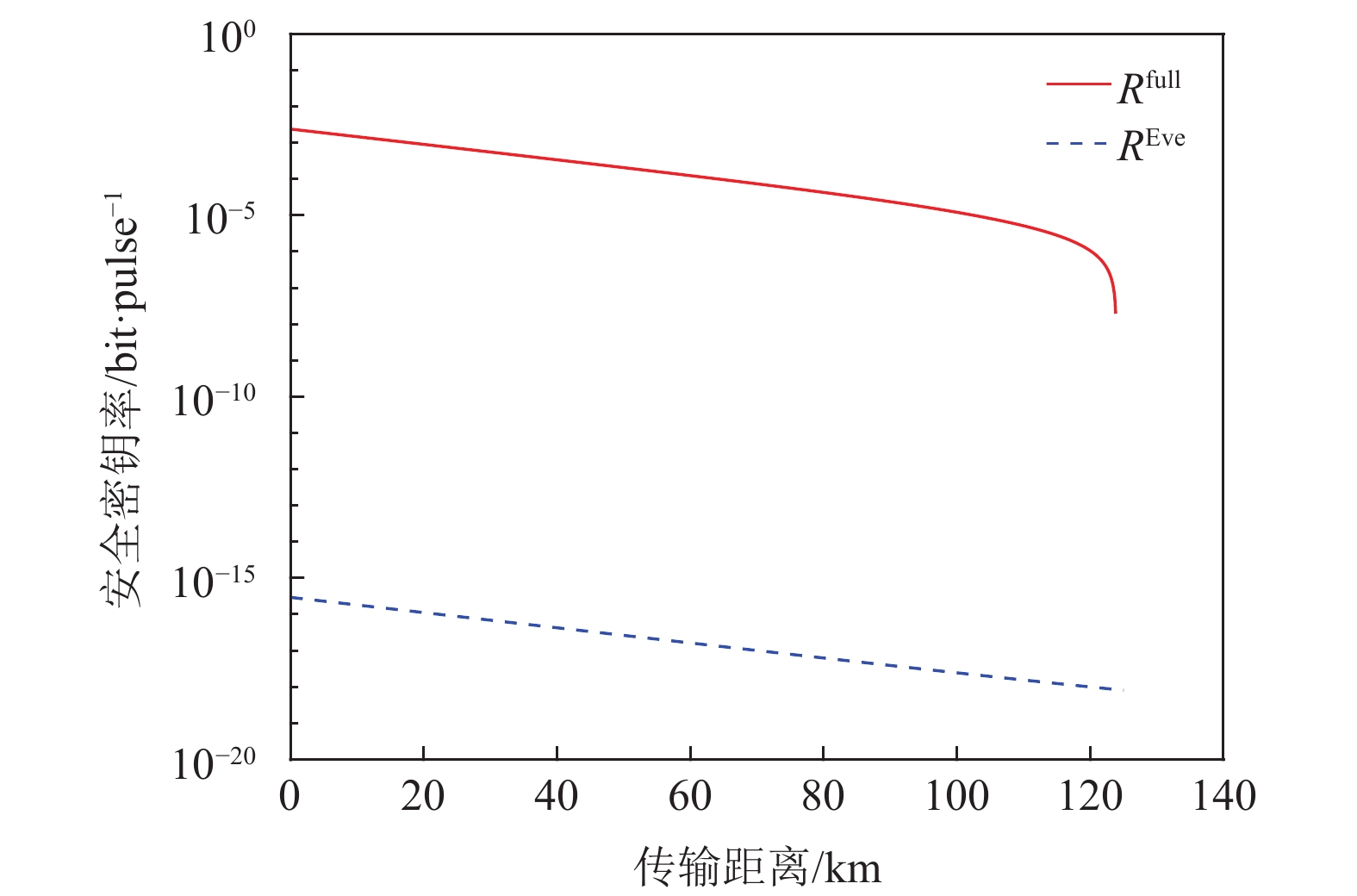
采用文献[32]和[33]中的实验参数,当QKD协议中只有一个WCS光源发出脉冲即信号态,Eve执行PNS攻击并且保证攻击前后信号态响应率
$ {Q}_{\mu } $ 不变时,PNS攻击前后的安全密钥率比较分别如图1和图2所示。由图1和图2可知,Alice和Bob认为安全的密钥率$ {R}^{{\rm{full}}} $ 大于Eve攻击之后真正安全的密钥率$ {R}^{{\rm{Eve}}} $ ,即$ {R}^{{\rm{sec}}}={R}^{{\rm{full}}} > {R}^{{\rm{Eve}}} $ ,Eve攻击成功。即,Alice和Bob认为安全的密钥率并不安全。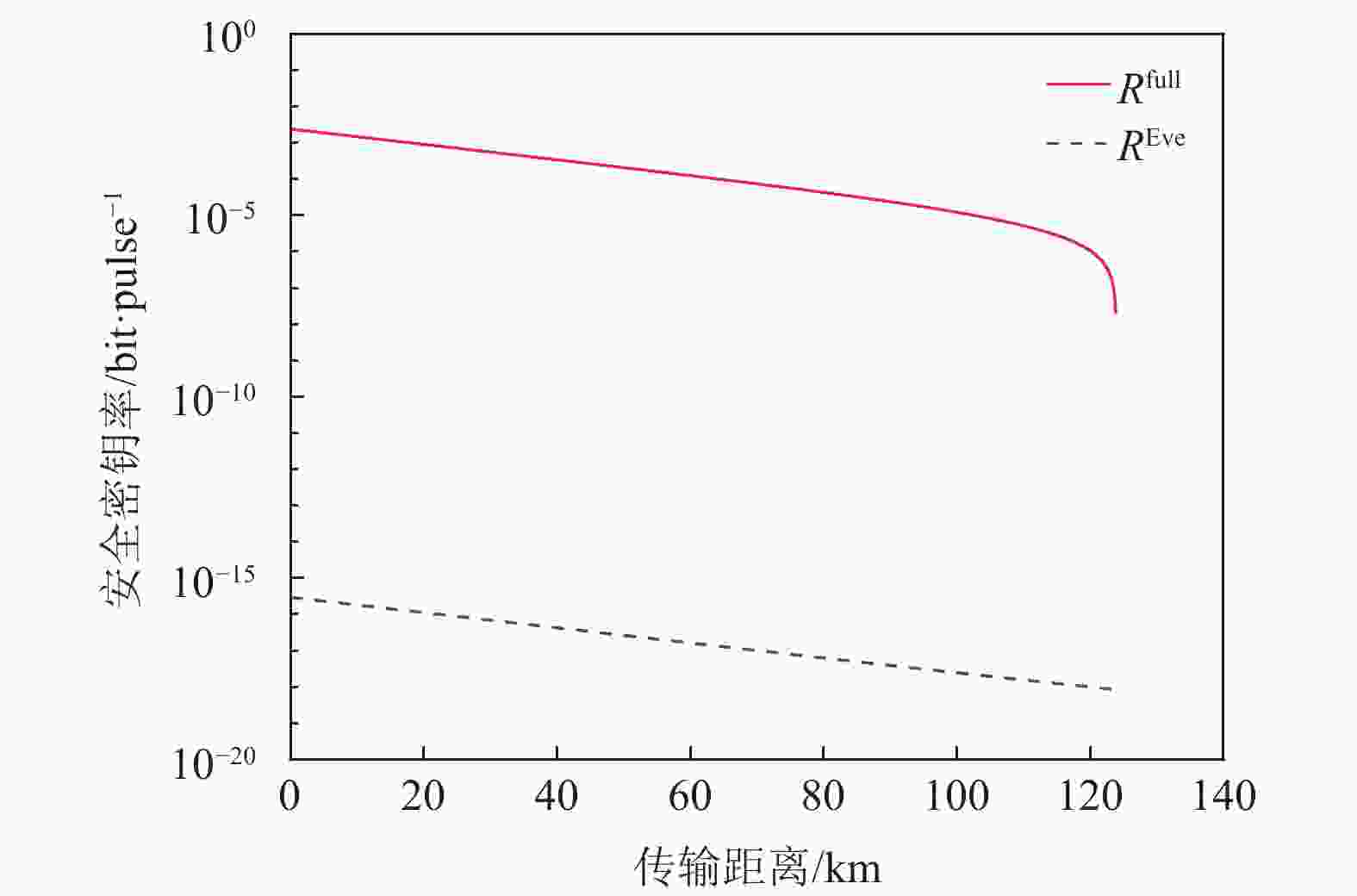
图 1 采用文献[32]的实验参数,只有信号态时,PNS攻击前后的安全密钥率比较
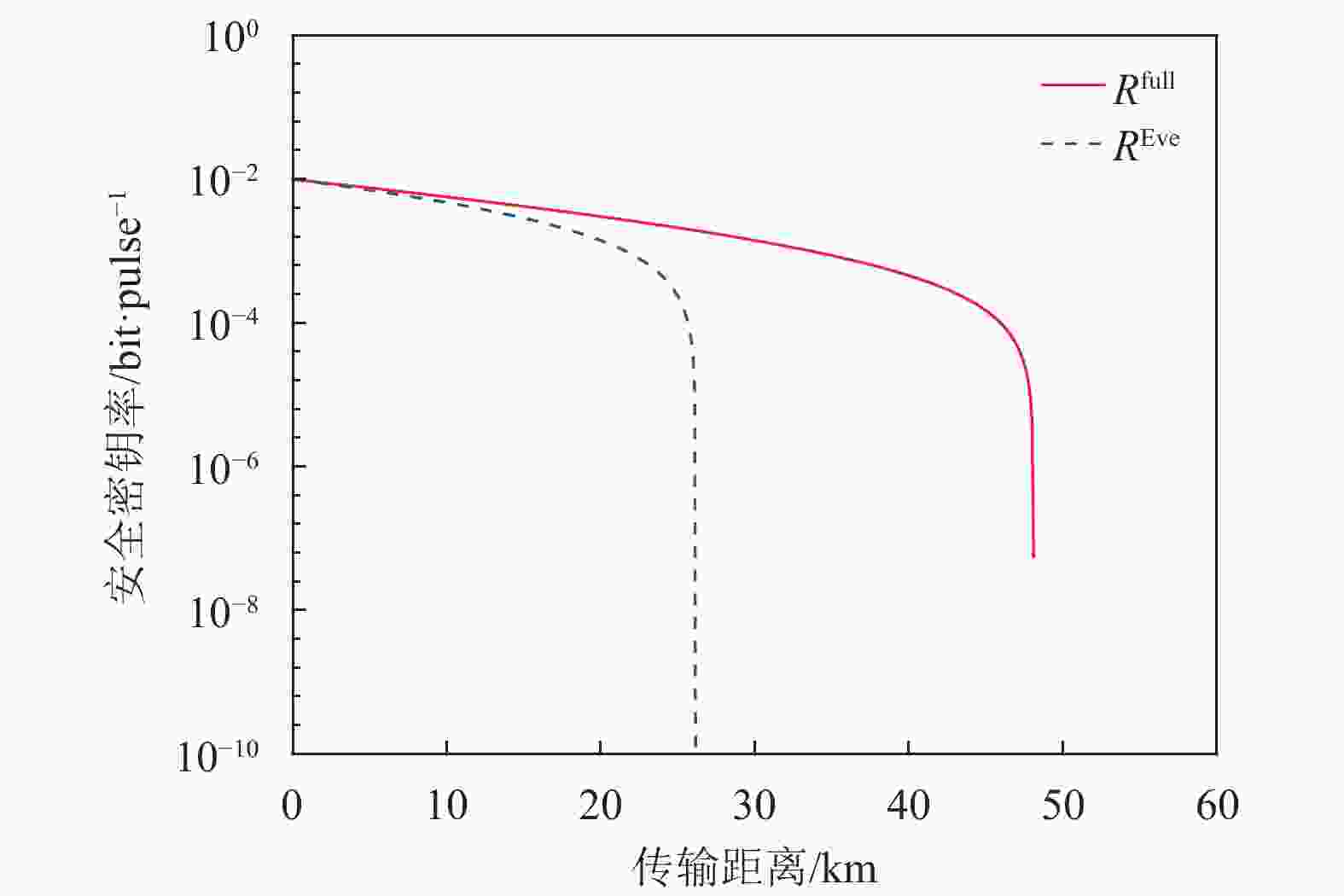
图 2 采用文献[33]的实验参数,只有信号态时,PNS攻击前后的安全密钥率比较
-
考虑信号态+单诱骗态QKD的情况。此时,Alice和Bob认为只有单光子脉冲能够生成安全密钥,并且认为安全的密钥率为
$ {R}^{{\rm{sec}}}={R}^{{\rm{decoy}}} $ ,可以通过式(5)计算得到。在信号态+单诱骗态QKD的情况下,根据前面的分析,在Eve执行PNS攻击之后,真正安全的密钥率
$ {R}^{{\rm{Eve}}}={Y}_{1}\mu {\text{e}}^{-\mu } $ 的求解可以归结为一个优化问题。为了不被Alice和Bob发现,Eve需要保持攻击前后信号态的响应率$ {Q}_{\mu } $ 和诱骗态的响应率$ {Q}_{\nu } $ 均不变。上述优化问题具体描述如下:$$ \underset{\left\{{Y}_{1},{Y}_{2},{Y}_{3},{Y}_{4},{Y}_{5},{Y}_{6}\right\}}{\mathrm{min}}{Y}_{1}\mu {\text{e}}^{-\mu } $$ (16) 当满足以下条件:
$$ {Q}_{\mu }={Y}_{0}+1-{\text{e}}^{-\eta \mu }=\sum _{i=1}^{6}{P}_{i}^{s}{Y}_{i} $$ (17) $$ {Q}_{\nu }={Y}_{0}+1-{\text{e}}^{-\eta \nu }=\sum _{i=1}^{6}{P}_{i}^{d}{Y}_{i} $$ (18) 式中,
$ {Y}_{1},{Y}_{2},{Y}_{3},{Y}_{4},{Y}_{5},{Y}_{6}\in \left[0, 1\right] $ 。通过计算,可以得到$ {R}^{{\rm{Eve}}} $ 。如果这个值小于Alice和Bob认为安全的密钥率$ {R}^{{\rm{sec}}}={R}^{{\rm{decoy}}} $ ,表明Eve攻击成功。否则,攻击失败。利用Matlab进行仿真。仿真参数主要来源于文献[29, 34],是信号态+单诱骗态QKD典型实验系统的参数,具体如表2所示。
采用文献[29]和[34]的实验参数,在信号态+单诱骗态QKD中,Eve执行PNS攻击并且保证攻击前后信号态响应率
$ {Q}_{\mu } $ 和诱骗态响应率$ {Q}_{\nu } $ 均不变,PNS攻击前后的安全密钥率比较分别如图3和图4所示。由图3和图4可知,Alice和Bob认为安全的密钥率$ {R}^{{\rm{decoy}}} $ 小于Eve攻击之后真正安全的密钥率$ {R}^{{\rm{Eve}}} $ ,即$ {R}^{{\rm{sec}}}={R}^{{\rm{decoy}}} < {R}^{{\rm{Eve}}} $ ,Eve攻击失败。换言之,Alice和Bob认为安全的密钥率确实是安全的。特别地,虽然此时用式(13)计算的密钥率$ {R}^{{\rm{full}}} $ 可能仍然大于$ {R}^{{\rm{Eve}}} $ ,但是Alice和Bob已不再将其作为安全密钥率。表 2 信号态+单诱骗态QKD仿真参数表
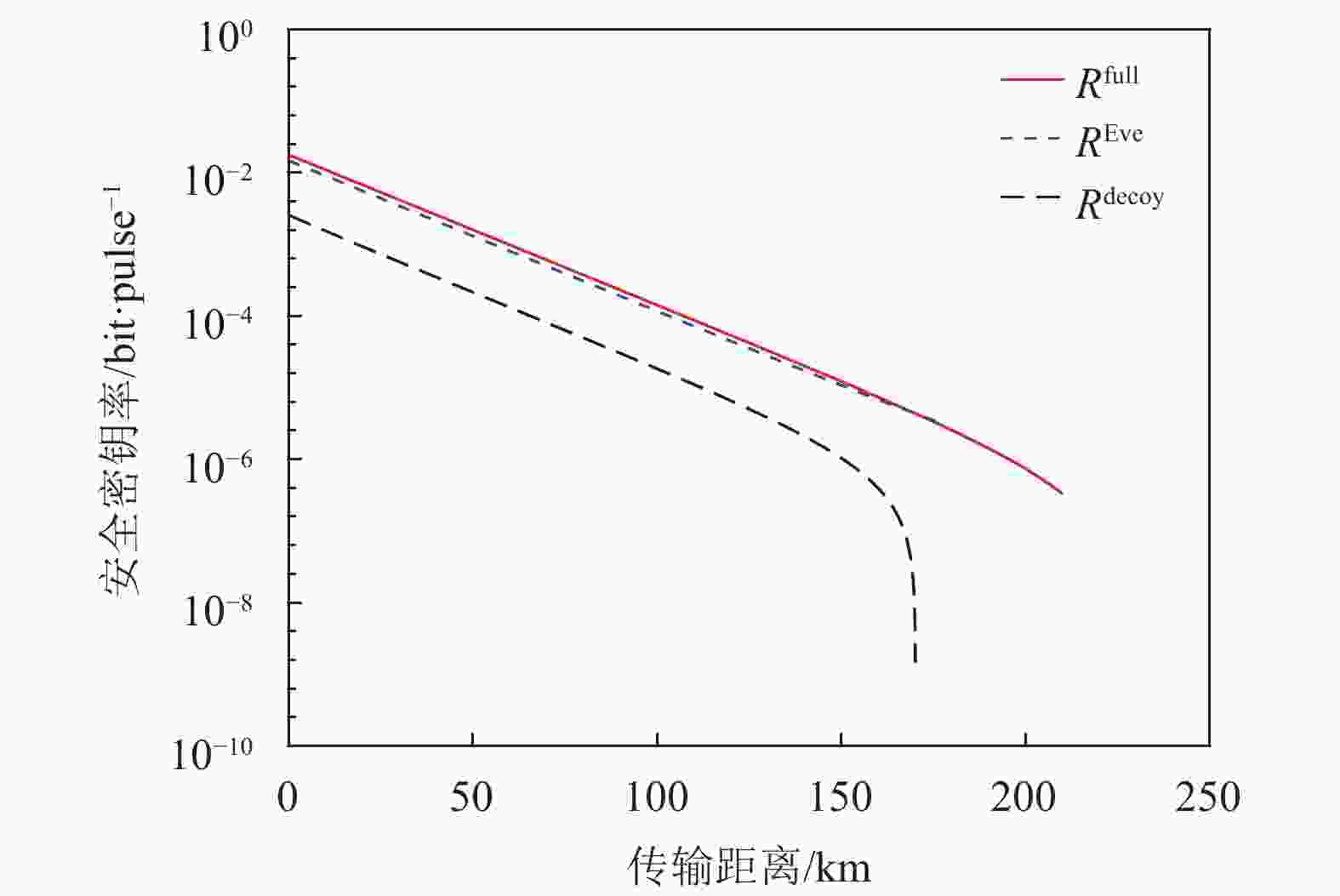
图 3 采用文献[29]的实验参数,信号态+单诱骗态QKD时,PNS攻击前后的安全密钥率比较
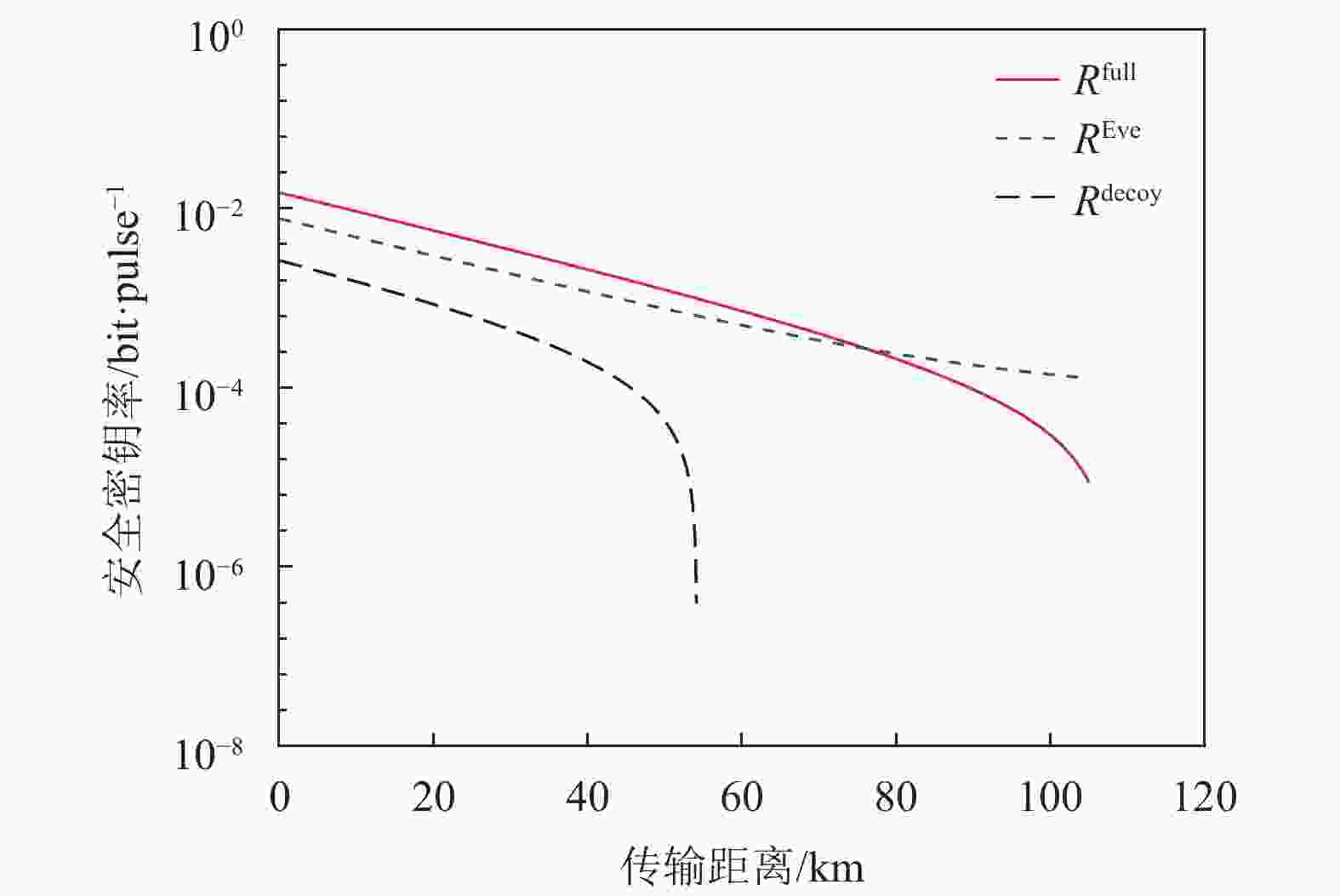
图 4 采用文献[34]的实验参数,信号态+单诱骗态QKD时,PNS攻击前后的安全密钥率比较
结合单信号态QKD的攻击结果,综合来看,没有诱骗态时,Eve的PNS攻击是成功的;有诱骗态时,Eve的PNS攻击是失败的,这说明了诱骗态存在的必要性,验证了诱骗态方法确实能够抵抗PNS攻击。
-
本文首先利用诱骗态方法中信号态和诱骗态的唯一差异,即强度不同导致的光子数概率分布差异,结合贝叶斯决策,验证了诱骗态方法中信号态和诱骗态不可区分这一假设的合理性。另外,本文还通过单信号态QKD和信号态+单诱骗态QKD的两个例子,分别对比分析PNS攻击前后的安全密钥率,仿真结果表明没有诱骗态时,Eve的PNS攻击是成功的;使用诱骗态时,Eve的PNS攻击是失败的,这说明了诱骗态存在的必要性,验证了诱骗态方法确实能够很好地抵抗PNS攻击。综合来看,本文从以上两个方面验证了诱骗态方法本身的安全性。
Rationality and Security Verification of Indistinguishability Assumption in Decoy-State Quantum Key Distribution
-
摘要: 采用贝叶斯决策来区分单诱骗态量子密钥分发中的信号态和诱骗态。分析结果表明,仍然只能得到信号态和诱骗态拥有相同
$ i $ 光子透射率的结论,从而验证了信号态和诱骗态不可区分这一假设的合理性,也验证了诱骗态方法的安全性。此外,分别对比单信号态和信号态+单诱骗态两种情况下光子数分离攻击前后的安全密钥率,发现前者攻击成功,后者攻击失败,这证明了诱骗态存在的必要性,验证了诱骗态方法确实能够抵抗光子数分离攻击,同时也进一步验证了诱骗态方法的安全性。Abstract: In this paper, we use Bayesian decision to distinguish signal state from decoy state in one decoy-state quantum key distribution. The analysis results show that we can still only get the conclusion that the signal state and decoy state have the same$ i $ -photon transmittance, which verifies the rationality of the assumption that signal state and decoy state are indistinguishable, and also verifies the security of decoy-state method. In addition, by comparing the secure key rate of two cases including only signal state and signal state + one decoy state before and after photon number splitting attack, we find the former is successful and the latter is failed. This just proves the necessity of the existence of decoy state, verifies that the decoy-state method can indeed resist photon number splitting attack, and further verifies the security of decoy-state method. -
图 1 采用文献[32]的实验参数,只有信号态时,PNS攻击前后的安全密钥率比较
图 2 采用文献[33]的实验参数,只有信号态时,PNS攻击前后的安全密钥率比较
图 3 采用文献[29]的实验参数,信号态+单诱骗态QKD时,PNS攻击前后的安全密钥率比较
图 4 采用文献[34]的实验参数,信号态+单诱骗态QKD时,PNS攻击前后的安全密钥率比较
表 1 单信号态QKD仿真参数表
-
[1] BENNETT C H, BRASSARD G. Quantum cryptography: Public key distribution and coin tossing[C]//Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing. Bangalore: IEEE, 1984, 175-179. [2] GISIN N, RIBORDY G, TITTEL W, et al. Quantum cryptography[J]. Reviews of Modern Physics, 2002, 74(1): 145-195. doi: 10.1103/RevModPhys.74.145 [3] GISIN N, THEW R. Quantum communication[J]. Nature Photonics, 2007, 1(3): 165-171. doi: 10.1038/nphoton.2007.22 [4] SCARANI V, BECHMANN-PASQUINUCCI H, CERF N J, et al. The security of practical quantum key distribution[J]. Reviews of Modern Physics, 2009, 81(3): 1301-1350. doi: 10.1103/RevModPhys.81.1301 [5] DUSEK M, LUTKENHAUS N, HENDRYCH M. Progress in optics[M]. [S.l.]: Elsevier, 2006. [6] WOOTTERS W K, ZUREK W H. A single quantum cannot be cloned[J]. Nature, 1982, 299(5886): 802-803. doi: 10.1038/299802a0 [7] DEUTSCH D, EKERT A, JOZSA R, et al. Quantum privacy amplification and the security of quantum cryptography over noisy channels[J]. Physical Review Letters, 1996, 77(13): 2818-2821. doi: 10.1103/PhysRevLett.77.2818 [8] BRASSARD G, LUTKENHAUS N, MOR T, et al. Limitations on practical quantum cryptography[J]. Physical Review Letters, 2000, 85(6): 1330-1333. doi: 10.1103/PhysRevLett.85.1330 [9] LUTKENHAUS N. Security against individual attacks for realistic quantum key distribution[J]. Physical Review A, 2000, 61(5): 052304. doi: 10.1103/PhysRevA.61.052304 [10] LUTKENHAUS N, JAHMA M. Quantum key distribution with realistic states: Photon-number statistics in the photon-number splitting attack[J]. New Journal of Physics, 2002, 4: 44.1-44.9. [11] ACIN A, GISIN N, SCARANI V. Coherent-pulse implementations of quantum cryptography protocols resistant to photon-number-splitting attacks[J]. Physical Review A, 2004, 69(1): 012309. doi: 10.1103/PhysRevA.69.012309 [12] SCARANI V, ACIN A, RIBORDY G, et al. Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulse implementations[J]. Physical Review Letters, 2004, 92(5): 057901. doi: 10.1103/PhysRevLett.92.057901 [13] LIU W T, SUN S H, LIANG L M, et al. Proof-of-principle experiment of a modified photon-number-splitting attack against quantum key distribution[J]. Physical Review A, 2011, 86(4): 042326. [14] LIU D, WANG S, YIN Z Q, et al. The security of decoy state protocol in the partial photon number splitting attack[J]. Chinese Science Bulletin, 2013, 58(31): 3859. doi: 10.1007/s11434-013-6037-2 [15] HWANG W Y. Quantum key distribution with high loss: Toward global secure communication[J]. Physical Review Letters, 2003, 91(5): 057901. doi: 10.1103/PhysRevLett.91.057901 [16] WANG X B. Beating the photon-number-splitting attack in practical quantum cryptography[J]. Physical Review Letters, 2005, 94(23): 230503. doi: 10.1103/PhysRevLett.94.230503 [17] LO H K, MA X F, CHEN K. Decoy state quantum key distribution[J]. Physical Review Letters, 2005, 94(23): 230504. doi: 10.1103/PhysRevLett.94.230504 [18] MAKAROV V, ANISIMOV A, SKAAR J. Effects of detector efficiency mismatch on security of quantum cryptosystems[J]. Physical Review A, 2006, 74(2): 022313. doi: 10.1103/PhysRevA.74.022313 [19] ZHAO Y, FUNG C H F, QI B, et al. Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems[J]. Physical Review A, 2008, 78(4): 042333. doi: 10.1103/PhysRevA.78.042333 [20] LO H K, CURTY M, QI B. Measurement-device-independent quantum key distribution[J]. Physical Review Letters, 2012, 108(13): 130503. doi: 10.1103/PhysRevLett.108.130503 [21] PIRANDOLA S, LAURENZA R, OTTAVIANI C, et al. Fundamental limits of repeaterless quantum communications[J]. Nature Communications, 2017, 8: 15043. doi: 10.1038/ncomms15043 [22] LUCAMARINI M, YUAN Z L, DYNES J F, et al. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters[J]. Nature, 2018, 557(7705): 400. doi: 10.1038/s41586-018-0066-6 [23] MA X F, ZENG P, ZHOU H Y. Phase-Matching quantum key distribution[J]. Physical Review X, 2018, 8(3): 031043. doi: 10.1103/PhysRevX.8.031043 [24] WANG X B, YU Z W, HU X L. Twin-field quantum key distribution with large misalignment error[J]. Physical Review A, 2018, 98(6): 062323. doi: 10.1103/PhysRevA.98.062323 [25] MA X F, QI B, ZHAO Y, et al. Practical decoy state for quantum key distribution[J]. Physical Review A, 2005, 72(1): 012326. doi: 10.1103/PhysRevA.72.012326 [26] LO H K, CHAU H F, ARDEHALI M. Efficient quantum key distribution scheme and a proof of its unconditional security[J]. Journal of Cryptology, 2005, 18(2): 133-165. doi: 10.1007/s00145-004-0142-y [27] LECOCQ F, CLARK J B, SIMMONDS R W, et al. Quantum nondemolition measurement of a nonclassical state of a massive object[J]. Physical Review X, 2015, 5(4): 041037. doi: 10.1103/PhysRevX.5.041037 [28] ZHANG G Y, ZHAO K F. Quantum nondemolition measurement by pulsed oscillation[J]. Physical Review A, 2016, 93(3): 033841. doi: 10.1103/PhysRevA.93.033841 [29] TANG Y L, YIN H L, MA X F, at al. Source attack of decoy-state quantum key distribution using phase information[J]. Physical Review A, 2013, 88(2): 022308. doi: 10.1103/PhysRevA.88.022308 [30] MA X F, FUNG C H F, DUPUIS F, et al. Decoy-state quantum key distribution with two-way classical postprocessing[J]. Physical Review A, 2006, 74(3): 032330. doi: 10.1103/PhysRevA.74.032330 [31] MA X F, FUNG C H F, RAZAVI M. Statistical fluctuation analysis for measurement-device-independent quantum key distribution[J]. Physical Review A, 2012, 86(5): 052305. doi: 10.1103/PhysRevA.86.052305 [32] GOBBY C, YUAN Z L, SHIELDS A J. Quantum key distribution over 122 km of standard telecom fiber[J]. Applied Physics Letters, 2004, 84(19): 3762-3764. doi: 10.1063/1.1738173 [33] BOURENNAN M, GIBSON F, KARLSSON A, et al. Experiments on long wavelength (1550nm) “plug and play” quantum cryptography systems[J]. Optics Express, 1999, 4(10): 383-387. doi: 10.1364/OE.4.000383 [34] ZHAO Y, QI B, MA X F, et al. Experimental quantum key distribution with decoy states[J]. Physical Review Letters, 2006, 96(7): 070502. doi: 10.1103/PhysRevLett.96.070502 -


 ISSN
ISSN 





 下载:
下载: