-
量子密钥分发(quantum key distribution, QKD)以量子力学原理为基础,使得远距离合法通信双方(Alice和Bob)能够实现无条件安全密钥共享,是当前量子信息领域最成功的应用之一。在实际环境中,所使用的光源和设备等无法满足QKD理想模型的要求,窃听者可对此发动光子数分离攻击和边信道攻击,严重威胁QKD系统的安全。随着诱骗态协议[1]、测量设备无关(measurement-device-independent, MDI)协议[2]、循环差分相移(round-robin differential phase shift, RRDPS)协议[3]等QKD协议的提出,QKD系统的安全性及实用性都得到了保障和改善。然而这些QKD协议在不使用可信中继情况下,始终难以突破线性密钥生成率边界(pirandola-laurenza-ottaviani-banchi bound, PLOB)的限制[4-5],即密钥生成率
$ R $ 与信道传输效率$ \eta $ 之间的关系为$ R \leqslant {{O}}\left( \eta \right) $ 。这极大制约了QKD协议的实际应用。2018年,文献[6]提出了双场(twin field, TF)协议,TF协议在不使用可信中继情况下,将
$ R $ 与$ \eta $ 的关系由线性相关提升至平方根相关,即$ R \leqslant {{O}}( {\sqrt \eta } ) $ ,突破了PLOB界,具有里程碑式的意义。TF协议提出后,其相关的理论与实验都得到了巨大发展[7],理论上相位匹配(phase matching, PM)[8]、发送或者不发送(sending-or-not-sending, SNS)[9]及无相位后选择(no phase post-selection, NPP)[10]等协议从不同方向对TF协议进行了扩展;实验上通过对相关协议的参数优化设计、利用超低损耗光纤和单光子检测器等方法,多个实验系统已实现距离超过500 km的量子密钥分发[11-12],其中基于NPP协议的实验最远可达833 km。PM协议采用相位编码对TF协议中的密钥生成进行具体化,信源端对相干态光源进行相位调制,测量端采用相位后补偿技术,具有稳定性好、抗干扰能力强、误比特率低等优势,相较其他TF变种协议具有更高的实用性。在PM协议实际应用中,有一个问题急需解决[13-14]:用于提取密钥的数据长度有限,由此带来的统计波动会对系统性能产生较大影响[15-16]。文献[8]仅对无穷诱骗态情况进行了分析,没有考虑有限诱骗态情况,也没有考虑数据有限长带来的统计波动影响;文献[17]基于弱相干态光源提出了三诱骗态PM方案,并用切诺夫界进行了统计波动分析;文献[18]针对信源错误提出了四诱骗态PM方案,并用高斯分析[19]进行了统计波动分析;文献[20-21]基于不同光源,对比了二诱骗态和三诱骗态PM协议性能,并用切诺夫界分别进行了统计波动分析。总的来看,当前对PM协议的研究中,大多关注信源的特性及诱骗态方案的设计,统计波动仅仅作为证明其所提出协议有效性的一环,缺少系统性研究。
本文基于光子数信道模型,利用切诺夫−霍夫丁界和高斯分析[22]对二诱骗态及三诱骗态PM协议进行系统性统计波动分析,结合线性规划对相关参数进行估计,最后得出仿真结果并进行对比分析。
-
本文主要关注有限数据长对PM协议造成的统计波动影响,对PM协议的实际实现方式不作过多讨论。假设Alice和Bob使用弱相干态光源(weak coherent state, WCS),诱骗态PM协议可表述如下。
1) Alice产生随机密钥
$ {\kappa _{\text{a}}} \in \left\{ {0,1} \right\} $ ,随机相位$ {\phi }_{\text{a}}\in \left[0,2{\text{π}} \right) $ ,随机选取光源脉冲强度${\mu _{\text{a}}} \in \left\{ {\mu \mathord{\left/ {\vphantom {\mu 2}} \right. } 2},{{{\mu _1}} \mathord{\left/ {\vphantom {{{\mu _1}} 2}} \right. } 2}, {{{\mu _2}} \mathord{\left/ {\vphantom {{{\mu _2}} 2}} \right. } 2}, \cdot \cdot \cdot \right\}$ ,调制后发送至第三方Eve,相干态脉冲可表示为$ {\left| {\sqrt {{\mu _{\text{a}}}} \exp \left( {i\left( {{\phi _{\text{a}}}{\text{ + }}{\text{π}}{\kappa _{\text{a}}}} \right)} \right)} \right\rangle _{\text{A}}} $ 。Bob产生的相干态脉冲也可类似表示。2) 光脉冲到达不可信第三方Eve,Eve执行相干检测并记录探测器响应的结果,随后将该结果通报给Alice和Bob。Alice和Bob声明脉冲信号强度。
3) Alice和Bob对发送的密钥比特进行筛选。若
$ {\mu _{\text{a}}} \ne {\mu _{\text{b}}} $ ,直接丢弃该比特,否则根据Eve的检测结果再进一步判断;若Eve有且仅有一个探测器响应,则保留该比特,若该响应的探测器为右侧探测器时,Bob还需进行比特翻转操作。4) 重复执行上述步骤若干次后得到原始密钥序列。对每一个比特,Alice声明其随机相位的序号
$ {j_{\text{a}}} $ ,同时随机选取一定长度的比特序列公布其真实值,用以估计量子比特误码率(quantum bit error rate, QBER)。Bob根据Alice的声明对相位进行后补偿,而后筛选出$ \left| {{j_{\text{b}}} - {j_{\text{a}}} + {j_{\text{d}}}} \right|\bmod M $ ($ M $ 为相位分片数)为0或者$ {M \mathord{\left/ {\vphantom {M 2}} \right. } 2} $ 的比特保留($ {j_{\text{d}}} $ 为相位后补偿系数),并在结果为$ {M \mathord{\left/ {\vphantom {M 2}} \right. } 2} $ 时对比特进行翻转。Bob向Alice声明保留的密钥比特,Alice同步保留相应比特。5) Alice和Bob根据信号强度将密钥序列分组,分析不同信号强度时的全局增益
$ {Q_{{\mu _n}}} $ 和量子比特误码率$ E_{{\mu _n}}^{\text{Z}} $ ,同时估计相位错误率$ E_\mu ^{\text{X}} $ 。6) Alice和Bob执行纠错和私密放大后得到最终密钥。
-
若Alice和Bob使用相位随机相干态光源,可用光子数信道模型来描述量子信道[1]。假设信源光子数满足泊松分布,系统全局增益和量子比特误码率可分别表示为:
$$ \begin{split} & \quad {Q_\mu } = \sum\limits_{k = 0}^\infty {\frac{{{\mu ^k}}}{{k!}}} \exp \left( { - \mu } \right){Y_k} \\ & E_\mu ^{\text{Z}}{Q_\mu } = \sum\limits_{k = 0}^\infty {\frac{{{\mu ^k}}}{{k!}}\exp \left( { - \mu } \right)e_k^{\text{Z}}{Y_k}} \end{split} $$ (1) 式中,
$\mu $ 为信源强度;${Y_k}$ 为$k$ 光子态计数率;$e_k^{\text{Z}}$ 为$k$ 光子态计数错误率;$ {Q_\mu } $ 和$E_\mu ^{\text{Z}}$ 分别是全局增益和量子比特误码率,可实际观测得到。 -
为得到系统极限性能,假设无窃听及攻击,数据长度为无穷大,直接引用文献[8]附录中相关结论。全局增益、量子比特误码率如下:
$$ \begin{split} & {Q_\mu } = 1 - \exp \left( { - \eta \mu } \right) + 2{p_{\text{d}}}\exp \left( { - \eta \mu } \right) \\ &\quad E_\mu ^{\text{Z}}{Q_\mu } = \left( {{p_{\text{d}}} + \eta \mu e{}_{\text{δ}}} \right)\exp \left( { - \eta \mu } \right) \end{split} $$ (2) 式中,
$ \eta $ 表示Alice(Bob)到Eve之间信道的传输率(考虑对称信道);$ {p_{\text{d}}} $ 表示检测器的暗计数;$ {e_\delta } $ 表示信号和暗计数同时引起检测器响应的错误概率:$$ {e_{\text{δ}}} = \frac{{\text{π}}}{M} - \frac{{{M^2}}}{{{{\text{π}}^2}}}{\sin ^3}\left( {\frac{{\text{π}}}{M}} \right) $$ (3) 相位错误率如下:
$$ \begin{split} & E_\mu ^{\text{X}} = \sum\limits_{k = 0}^\infty {{q_{2k + 1}}e_{2k + 1}^{\text{Z}}} + \sum\limits_{k = 0}^\infty {{q_{2k}}\left( {1 - e_{2k}^{\text{Z}}} \right)} \leqslant\\ & \quad {q_0}e_0^{\text{Z}} + \left( {{q_1}e_1^{\text{Z}} + {q_3}e_3^{\text{Z}} + {q_5}e_5^{\text{Z}}} \right) + \\ & \qquad\quad \left( {1 - {q_0} - {q_1} - {q_3} - {q_5}} \right) \end{split} $$ (4) 高阶项对最终结果影响很小,因而式(4)中第二步忽略光子数
$ k \geqslant 6 $ 时的影响。上式中$ {q_k} $ 表示$k$ 光子态对有效检测的贡献:$$ {q_k} = {P^\mu }\left( k \right)\frac{{{Y_k}}}{{{Q_\mu }}} = \frac{{{\mu ^k}}}{{k!}}\exp \left( { - \mu } \right)\frac{{{Y_k}}}{{{Q_\mu }}} $$ (5) 此外,为计算系统在理想情况下的密钥生成率,还需要对
$k$ 光子态计数率、$k$ 光子态信号比特误码率进行建模:$$ \begin{split} &\qquad {Y_k} = 1 - \left( {1 - 2{p_{\text{d}}}} \right){\left( {1 - \eta } \right)^k} \\ & e_k^{\text{Z}}{Y_k} = {p_{\text{d}}}{\left( {1 - \eta } \right)^k} + {e_{\text{δ}}}\left[ {1 - {{\left( {1 - \eta } \right)}^k}} \right] \end{split} $$ (6) -
密钥生成率的最终公式如下[8]:
$$ {R_{{\text{PM}}}} = \frac{2}{M}{Q_\mu }\left[ {1 - fH\left( {E_\mu ^{\text{Z}}} \right) - H\left( {E_\mu ^{\text{X}}} \right)} \right] $$ (7) 式中,M是相位分片数;
$f$ 是纠错效率;$ H\left( x \right) = - x{\log _2}\left( x \right) - \left( {1 - x} \right){\log _2}\left( {1 - x} \right) $ ,为香农熵函数。PM协议后处理包括密钥纠错和私钥放大。密钥纠错依赖于观测值
$ E_\mu ^Z $ ,不需要额外处理;私密放大依赖于$E_\mu ^{\text{X}}$ 的估计值,结合式(4)~式(5)可知,需要用诱骗态方法对$e_k^{\text{Z}}$ 和${Y_k}$ 进行估计。求解密钥生成率R的问题可转化为在一定约束条件下求解$E_\mu ^{\text{X}}$ 最大值的问题,可表述为:$$ \mathop {\max }\limits_{{Y_k},e_k^Z} (E_\mu ^{\text{X}}) $$ 约束条件为:
$$ {Q_{{\mu _m}}} = \sum\limits_{k = 0}^\infty {\frac{{\mu _m^k}}{{k!}}} \exp \left( { - {\mu _m}} \right){Y_k} $$ (8) $$ E_{{\mu _m}}^{\text{Z}}{Q_{{\mu _m}}} = \sum\limits_{k = 0}^\infty {\frac{{\mu _m^k}}{{k!}}\exp \left( { - {\mu _m}} \right)e_k^{\text{Z}}{Y_k}} $$ (9) 式中,
$m = 0,1,\cdots,n - 1$ ,线性约束方程总数为2n。为了得到
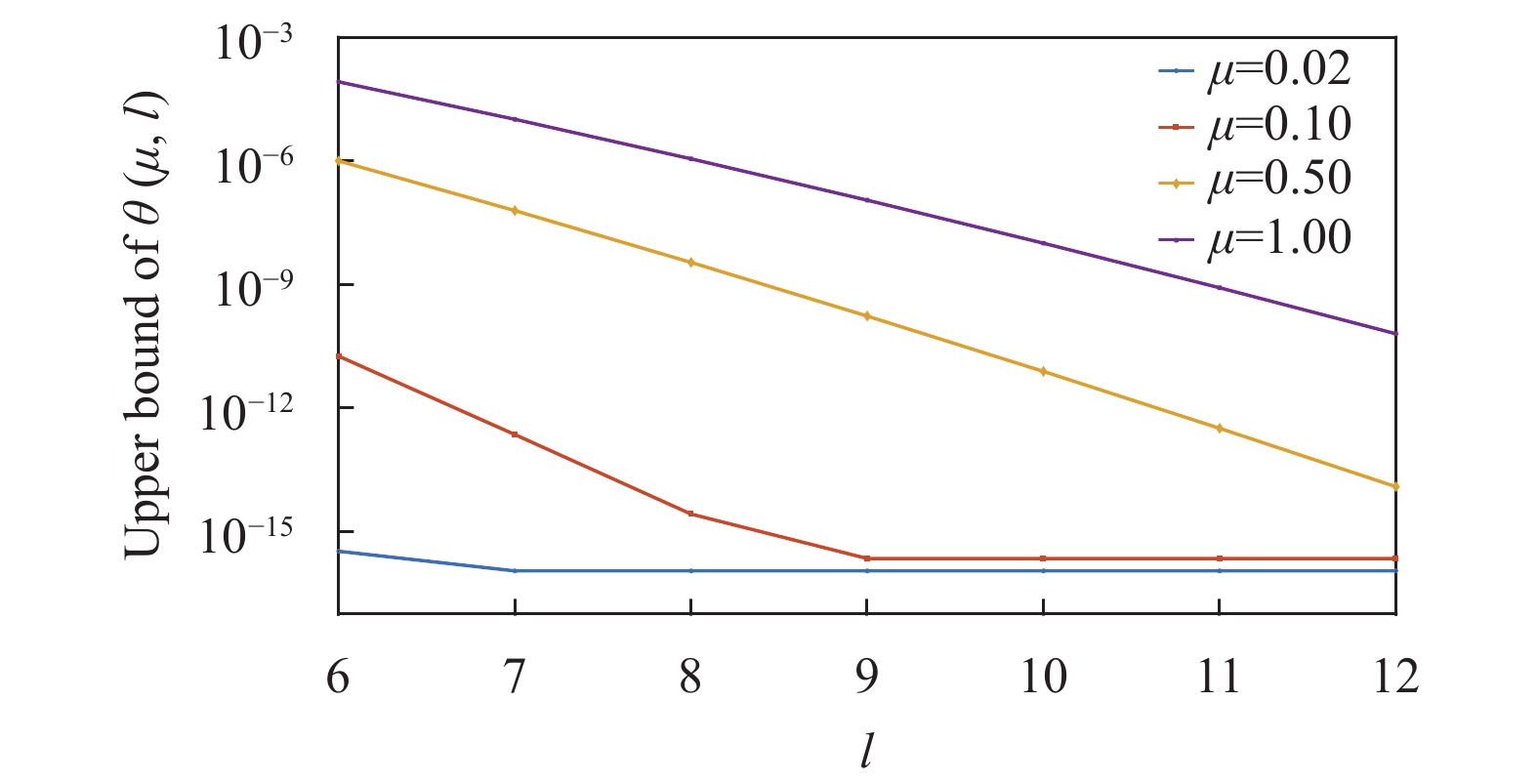
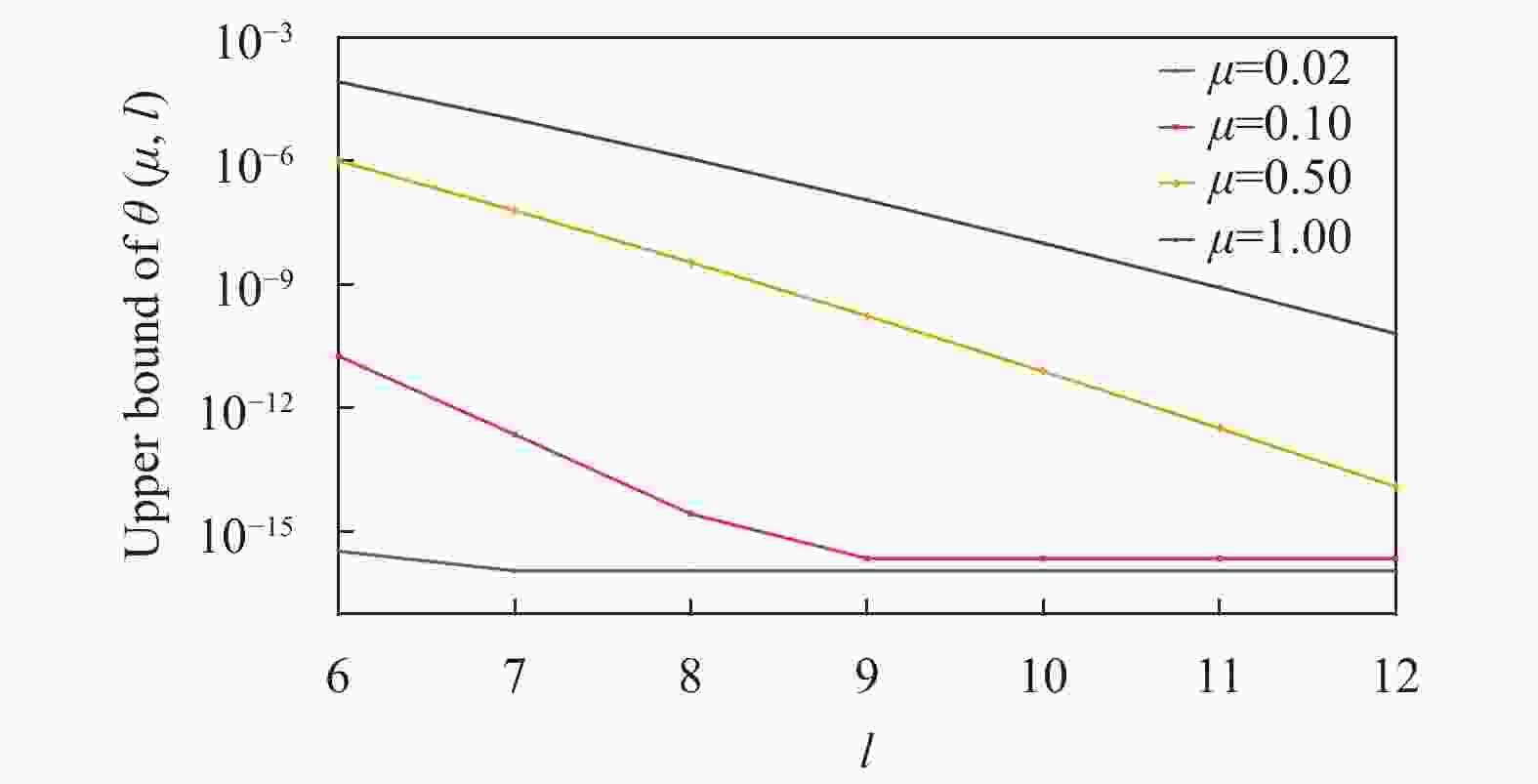
$E_\mu ^{\text{X}}$ 的最大值,可以分别估计${Y_k}$ 的最小值和$e_k^{\text{Z}}$ 的最大值。而这两个问题都可以用线性规划来求解。式(8)~式(9)中右侧均有无穷多项,需进一步简化。因为泊松分布中,随着$k$ 的增大,高阶项系数呈指数下降,可直接忽略高阶项而不会对最终分析结果产生明显影响。以式(8)为例,其右侧$k \geqslant l$ 所有项的和可表示为:$$ \theta \left( {\mu ,l} \right) = 1 - \sum\limits_{k = 0}^{l - 1} {\frac{{{\mu ^k}}}{{k!}}} \exp \left( { - \mu } \right){Y_k} $$ (10) 令
${Y_k} = 1$ ,可得$\theta \left( {\mu ,l} \right)$ 的上边界${\theta ^{\text{U}}}\left( {\mu ,l} \right)$ 。根据经验取常用信号强度值,$\mu \in \left\{ {0.02,0.1,0.5,1} \right\}$ ,在$l = 6,\cdots,12$ 时,${\theta ^{\text{U}}}\left( {\mu ,l} \right)$ 仿真结果如图1所示。当信号强度为1和0.5时,9阶以上的高阶项的和分别接近
${10^{-7}}$ 和${10^{{{ - 10}}}}$ ,影响很小,可以忽略。因此本文对式(8)取前9项进行仿真计算,即$l = 9$ 。同理,式(9)有类似结论。统计波动会对参数的估计带来影响,分别用文献[19]中的高斯分析和文献[23]中的切诺夫−霍夫丁界来进行统计波动分析。高斯分析需假设信道统计波动满足正态分布,实际中这一条件难以满足,因此在面对相干攻击等特定威胁时,难以达到无条件安全要求,一般仅作为理论分析工具;切诺夫−霍夫丁界在实际应用中相对具有更高的安全性[22-24]。
1) 高斯分析
根据文献[19]结论,约束条件式(8)、式(9)变为不等式组:
$$ \begin{split} &\qquad {{\hat Q}_{{\mu _m}}}( {1 - {\beta _{\text{q}}}} ) \leqslant \sum\limits_{k = 0}^8 {\frac{{\mu _m^k}}{{k!}}} \exp \left( { - {\mu _m}} \right){Y_k} \leqslant\\ & \qquad\qquad {{\hat Q}_{{\mu _m}}}( {1 + {\beta _{\text{q}}}} ) \\ & \hat E_{{\mu _m}}^{\text{Z}}{{\hat Q}_{{\mu _m}}}( {1 - {\beta _{{\text{eq}}}}} ) \leqslant \sum\limits_{k = 0}^8 {\frac{{\mu _m^k}}{{k!}}\exp \left( { - {\mu _m}} \right)e_k^{\text{Z}}{Y_k}} \leqslant \\ &\qquad\qquad \hat E_{{\mu _m}}^{\text{Z}}{{\hat Q}_{{\mu _m}}}( {1 + {\beta _{{\text{eq}}}}} ) \end{split} $$ (11) 式中,
${\hat Q_{{\mu _m}}}$ 和$\hat E_{{\mu _m}}^{\text{Z}}$ 是测量值;${\beta _{\text{q}}}$ 和${\beta _{{\text{eq}}}}$ 可由下式计算:$$ {\beta }_{\text{q}}=\frac{{n}_{\text{α}}}{\sqrt{{N}_{{\mu }_{m}}{\hat{Q}}_{{\mu }_{m}}}}\text{;}{\beta }_{\text{eq}}=\frac{{n}_{\text{α}}}{\sqrt{{N}_{{\mu }_{m}}{\hat{E}}_{{\mu }_{m}}{\hat{Q}}_{{\mu }_{m}}}} $$ (12) 式中,
${N_{{\mu _m}}}$ 是光源强度为${\mu _m}$ 时脉冲总数;${n_{\text{α }}}$ 是高斯分析的标准差倍数,与置信度直接相关。2) 切诺夫−霍夫丁界
根据文献[22]附录D中的结论,约束条件式(8)~式(9)变为不等式组:
$$ \begin{split} & \qquad {{\hat Q}_{{\mu _m}}}\left( {1 - \delta _{\text{q}}^{\text{L}}} \right) \leqslant \sum\limits_{k = 0}^8 {\frac{{\mu _m^k}}{{k!}}} \exp \left( { - {\mu _m}} \right){Y_k} \leqslant\\ &\qquad\qquad {{\hat Q}_{{\mu _m}}}\left( {1 + \delta _{\text{q}}^{\text{U}}} \right) \\ & \hat E_{{\mu _m}}^{\text{Z}}{{\hat Q}_{{\mu _m}}}\left( {1 - \delta _{{\text{eq}}}^{\text{L}}} \right) \leqslant \sum\limits_{k = 0}^8 {\frac{{\mu _m^k}}{{k!}}\exp \left( { - {\mu _m}} \right)e_k^{\text{Z}}{Y_k}} \leqslant \\ & \qquad\qquad \hat E_{{\mu _m}}^{\text{Z}}{{\hat Q}_{{\mu _m}}}\left( {1 + \delta _{{\text{eq}}}^{\text{U}}} \right) \end{split} $$ (13) 其中:
$$ \begin{split} & {\delta }_{\text{q}}^{\text{L}}=\sqrt{\frac{-3\mathrm{ln}\left(\dfrac{\varepsilon }{2}\right)}{{N}_{{\mu }_{m}}{\hat{Q}}_{{\mu }_{m}}}}\text{;}{\delta }_{\text{q}}^{\text{U}}=2\sqrt{\frac{-2\mathrm{ln}\left(\dfrac{\varepsilon }{2}\right)+2\mathrm{ln}2}{{N}_{{\mu }_{m}}{\hat{Q}}_{{\mu }_{m}}}}\\ & {\delta }_{\text{eq}}^{\text{L}}=\sqrt{\frac{-3\mathrm{ln}\left(\dfrac{\varepsilon }{2}\right)}{{N}_{{\mu }_{m}}{\hat{E}}_{{\mu }_{m}}{\hat{Q}}_{{\mu }_{m}}}}\text{;}{\delta }_{\text{eq}}^{\text{U}}=2\sqrt{\frac{-2\mathrm{ln}\left(\dfrac{\varepsilon }{2}\right)+2\mathrm{ln}2}{{N}_{{\mu }_{m}}{\hat{E}}_{{\mu }_{m}}{\hat{Q}}_{{\mu }_{m}}}} \end{split} $$ (14) -
假设Alice和Bob发送的脉冲数相同,实验中相关参数主要来源于文献[25],如表1所示。
${e_{\text{d}}}$ 是检测错误概率,主要影响信道传输效率,$\alpha $ 为信道损耗,当${n_{\text{α }}} = 5$ 时,可直接计算得失败的概率为$\varepsilon = 5.73 \times {10^{ - 7}}$ ,置信度为$1 - \varepsilon $ 。表 1 仿真中用到的实验参数
${e_{\text{d}}}$/% ${p_{\text{d}}}$ $f$ ${\eta _{\text{d}}}$/% M ${n_{\text{α}}}$ $\alpha $ 1.5 $ 8 \times 10^{-8} $ 1.15 14.5 16 5 0.2 需要说明的是,仿真中所用参数是较为典型的参数,当前实验室中信道损耗、检测效率、暗计数率等均可以做到更优,如最近实现的833 km量子密钥分发实验[11]中,
$\alpha = 0.158$ ,${p_{\text{d}}} = 1.5 \times {10^{ - 11}}$ ,${\eta _{\text{d}}} = 83\% $ ,但在实际应用中成本过高。仿真中PM协议采用最简单的参数设定,主要比较不同统计波动分析方法性能。将理想情况下计算所得的全局增益和QBER作为测量值。
-
在二诱骗态PM协议下,Alice和Bob选择相同的信源强度,一组典型值为
$\left\{ {0,0.05,0.2} \right\}$ ,其中信号态强度为0.2。每种信源强度发送的脉冲数均为$N = 2 \times {10^{13}}$ 。Alice和Bob相距50 km时,分别利用高斯分析和切诺夫−霍夫丁界对二诱骗态PM协议进行统计波动分析,通过线性规划方法估计所得的
${e_k}$ 的最大值和${Y_k}$ 的最小值列于表2中。从表2可以看出,高斯分析对
${Y_k}$ 和${e_k}$ 的估计更加紧致;由式(4)可知,${e_k}{\text{ = }}1$ 的项不会对$E_\mu ^X$ 的结果产生影响,因而两种方法对${Y_3}$ 和${e_3}$ 的估计值没有意义。用上述方法计算$k > 3$ 的项均无法得到有效的估计值。这主要是因为诱骗态数量有限,对系统参数估计的能力有限,无法准确估计高阶参数。结合式(4)及式(7),将表2中的数据代入计算可得,高斯分析与切诺夫−霍夫丁界对应的密钥生成率分别为$3.059 \times {10^{ - 4}}$ bits/脉冲和$3.058 \times {10^{ - 4}}$ bits/脉冲。按照类似的方法计算不同数据长度情况下,不同距离时系统的密钥生成率,可得图2。表 2 二诱骗态PM协议部分计数率下界及错误率上界的仿真估计值
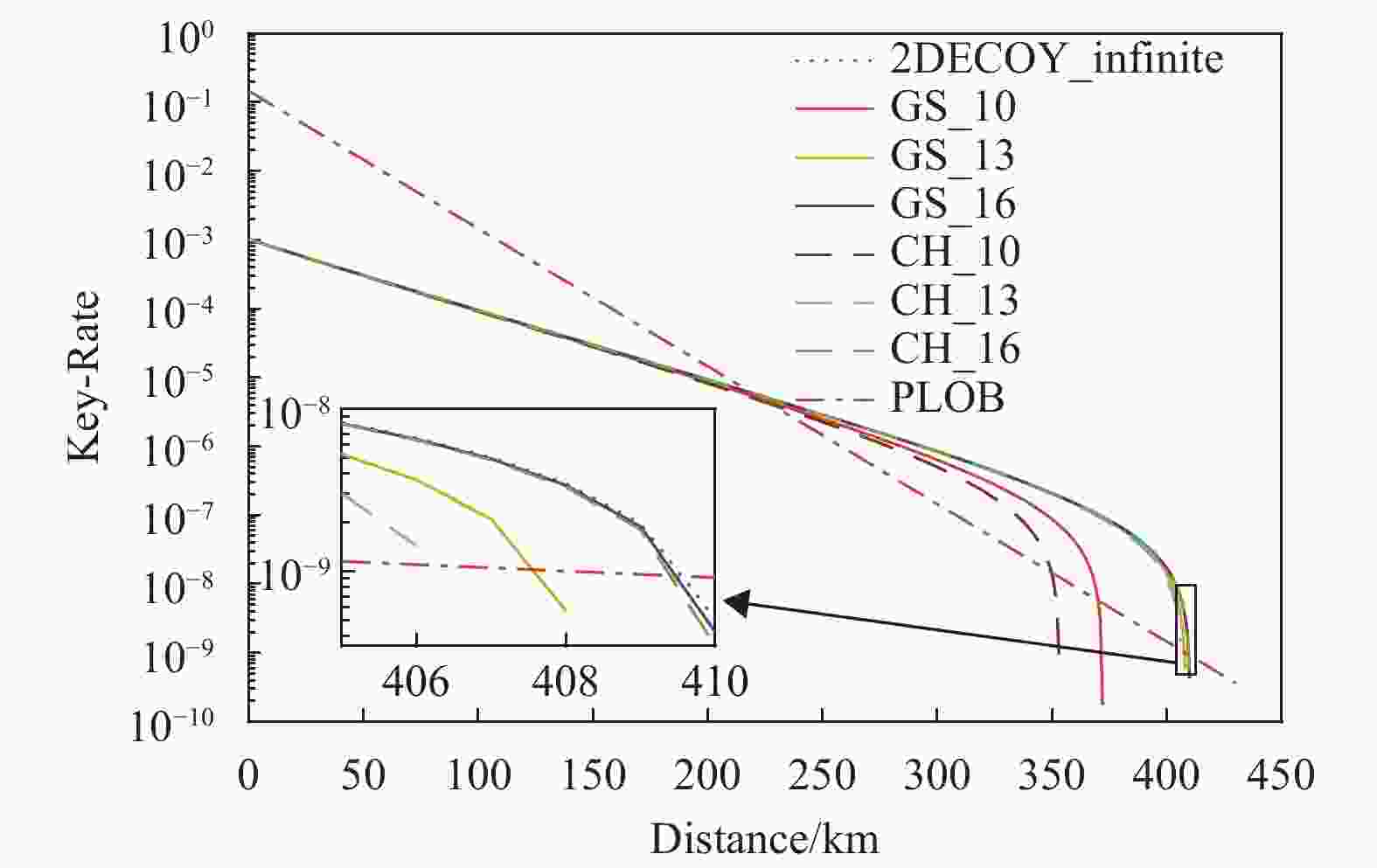
统计波动分析方法 ${Y_0}$ ${Y_1}$ ${Y_3}$ ${e_0}$ ${e_1}$ ${e_3}$ 理想值 $1.600\;0 \times {10^{ - 7}}$ 0.045853 0.13135 0.50000 0.0037551 0.0013109 高斯分析 $1.595\;5 \times {10^{ - 7}}$ 0.045614 $3.571\;7 \times {10^{ - 33}}$ 0.50338 0.0039549 1 切诺夫−霍夫丁界 $1.594\;0 \times {10^{ - 7}}$ 0.045613 $3.914\;8 \times {10^{ - 15}}$ 0.50632 0.0039570 1 图2中,2DECOY_infinite表示不考虑统计波动的二诱骗态情况,GS_10、GS_13、GS_16分别表示
$ N\in \left\{2\times {10}^{10},\;2\times {10}^{13},\;2\times {10}^{16}\right\} $ 时采用高斯分析的二诱骗态情况,类似的CH_10、CH_13、CH_16,分别表示$ N\in \left\{2\times {10}^{10},\;2\times {10}^{13},\;2\times {10}^{16}\right\} $ 时采用切诺夫−霍夫丁界的二诱骗态情况。结果表明,考虑统计波动,即便在数据较少的情况下,PM协议仍可突破PLOB界;高斯分析在数据较少的情况下具有明显的性能优势,而数据较少时较难满足正态分布的要求,因而高斯分析的实用性不高;但随着数据量的增加,高斯分析与切诺夫−霍夫丁界分析的结果都趋于无穷数据长度的情况,高斯分析的性能优势不再明显。 -
在三诱骗态PM协议下,Alice和Bob选择一组典型的信源强度,分别为
$\left\{ {0,\;0.01,\;0.05,\;0.2} \right\}$ ,其中信号态强度为0.2。每种信源强度发送的脉冲数为$N = 2 \times {10^{13}}$ 。与二诱骗态PM协议类似,表3列举了三诱骗态情况下
${e_k}$ 最大和${Y_k}$ 最小估计值。从表3中数据可以看出,相比
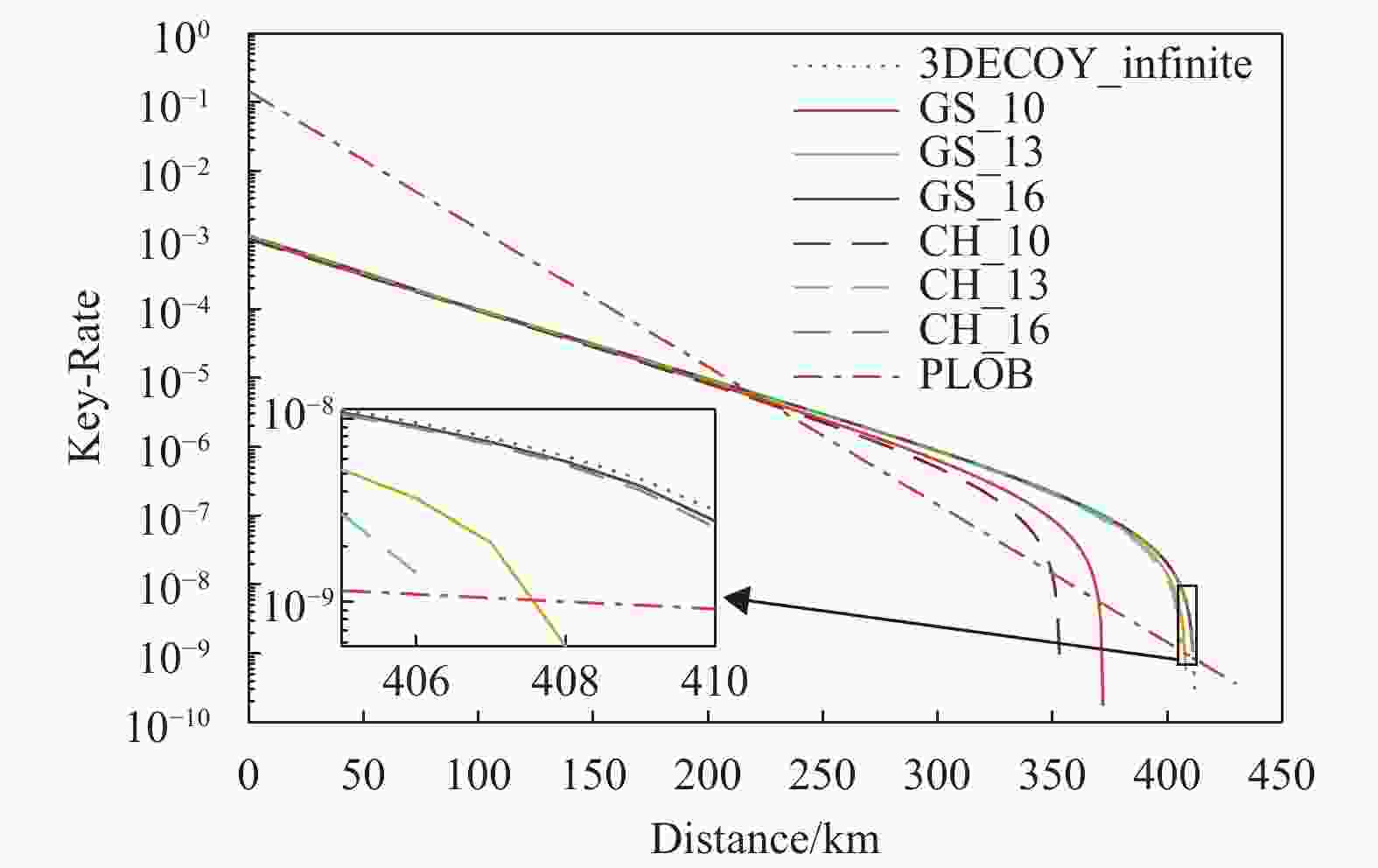
${Y_1}$ 、${e_1}$ 的估计值,${Y_3}$ 、${e_3}$ 的估计与理论值之间的误差更大,但与二诱骗态PM协议不同的是,其估计值对密钥生成率仍具有积极的贡献。结合式(4)及式(7),将表3中的数据代入计算可得,高斯分析与切诺夫−霍夫丁界对应的三诱骗态PM协议的密钥生成率分别为$3.38 \times {10^{ - 4}}$ 比特/脉冲和$3.37 \times {10^{ - 4}}$ 比特/脉冲,比二诱骗态PM协议的密钥生成率高,但差异仅有${10^{ - 5}}$ 量级。按照类似的方法计算不同数据长度情况下,不同距离时系统的密钥生成率,可得图3。图3中,3DECOY_infinite表示不考虑统计波动的三诱骗态情况,GS_10、GS_13、GS_16分别表示
$ N\in \left\{2\times {10}^{10},\;2\times {10}^{13},\;2\times {10}^{16}\right\} $ 时采用高斯分析的三诱骗态情况,类似的CH_10、CH_13、CH_16,分别表示$ N\in \left\{2\times {10}^{10},\;2\times {10}^{13},\;2\times {10}^{16}\right\} $ 时采用切诺夫−霍夫丁界的三诱骗态情况。该仿真结果与二诱骗态PM协议仿真结果具有相同的趋势,进一步证明了两种统计波动分析方法的通用性。表 3 三诱骗态部分计数率下界及错误率上界的仿真估计值
统计波动分析方法 ${Y_0}$ ${Y_1}$ ${Y_3}$ ${e_0}$ ${e_1}$ ${e_3}$ 理想值 $1.600\;0 \times {10^{ - 7}}$ 0.045853 0.131350 0.50000 0.0037551 0.0013109 高斯分析 $1.595\;5 \times {10^{ - 7}}$ 0.045846 0.072025 0.50338 0.0037615 0.0100970 切诺夫−霍夫丁界 $1.594\;0 \times {10^{ - 7}}$ 0.045844 0.069886 0.50634 0.0037676 0.0131220 -
对比表2与表3数据可知,在统计波动分析方法相同的条件下,对
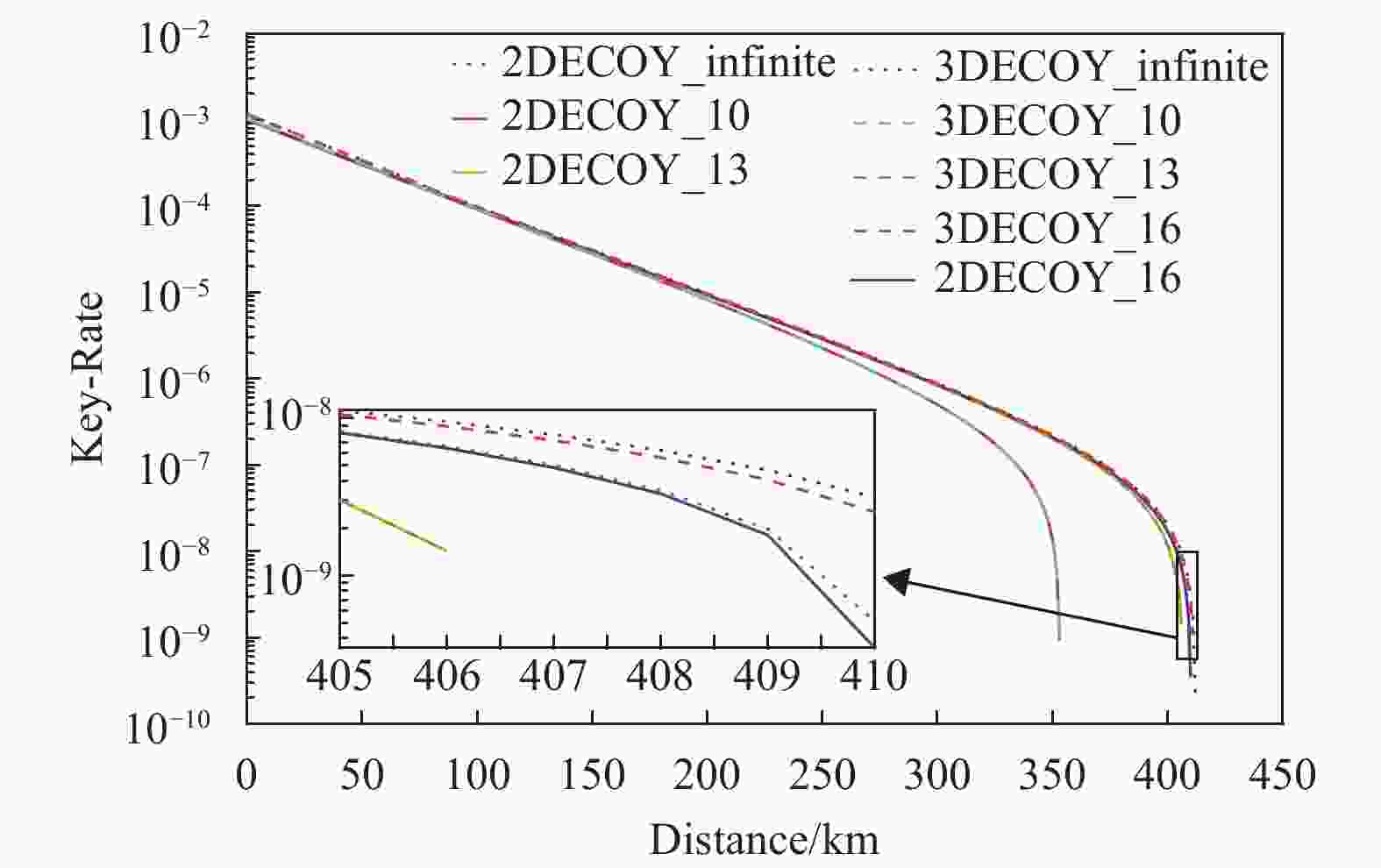
${Y_0},{Y_1},{e_0},{e_1}$ 的估计,三诱骗态PM协议略优于二诱骗态PM协议,但两种协议相差很小;对${Y_3},{e_3}$ 的估计,三诱骗态PM协议提升明显。能对更多参数进行有效估计是三诱骗态相对二诱骗态性能更好的原因之一。基于切诺夫−霍夫丁界更高的实用价值,进一步对比三诱骗态和二诱骗态PM协议利用该方法进行统计波动分析时的性能,如图4所示。
图 4中,2DECOY_infinite、2DECOY_10、2DECOY_13、2DECOY_16分别表示
$N \in \left\{\infty ,\;2\times {10}^{10}, 2\times {10}^{13},\;2\times {10}^{16}\right\}$ 时采用切诺夫−霍夫丁界的二诱骗态情况,类似地,3DECOY_infinite、3DECOY_10、3DECOY_13、3DECOY_16表示相应数据长度下三诱骗态情况。图中结果显示,在数据长度较短($N$ 取$2 \times {10^{10}},2 \times {10^{13}}$ )时,二诱骗态与三诱骗态PM协议密钥生成率曲线基本重合,性能差异极小;当$N$ 取$2 \times {10^{16}}$ 时,二诱骗态与三诱骗态PM协议性能分别趋近于对应的无限数据长时性能,性能差异在实际应用中仍可忽略。三诱骗态PM协议通过增加诱骗态数量,为参数估计提供更多的约束条件,以此提升参数估计的精确度,对比表2与表3中的数据,可以看出这种提升,但图4也反应出这种提升无法在密钥生成率及最大安全传输距离上体现出来。综合来看,三诱骗态PM协议利用了更多的数据,其所消耗的时间及存储空间较二诱骗态PM协议多33%,但是并不能得到较好的性能提升,因而二诱骗态PM协议具有更高的实用价值。 -
考虑统计波动后,PM协议仍能突破PLOB界实现无条件安全密钥分发。在信道损失较小(距离小于200 km)且数据长度大于
${10^{10}}$ 时,二诱骗态和三诱骗态PM协议性能都接近无穷数据长情况;反之,当信道损失较大时,数据长度对PM协议性能影响较大,随着数据长度增大,PM协议性能增强,当数据长度大于${10^{13}}$ 时,系统性能提升不再明显。采用切诺夫−霍夫丁界进行统计波动分析,可以保证PM协议的安全性,但是在数据量较小时,其性能与利用高斯分析进行统计波动分析的PM协议有一定差距,数据量增大可以逐渐缩小这种差距。
增加诱骗态无法显著提高考虑统计波动的PM协议性能,特别是在数据量较小时,增加诱骗态只能增大系统开销,系统性能提升可以忽略。
综合来看,采用二诱骗态PM协议、切诺夫−霍夫丁界统计波动分析方法,取数据长度为
${10^{13}}$ 量级,是一种较实用的量子密钥分发方案。
StatisticaL Fluctuation Analysis for Phase Matching Quantum Key Distribution
-
摘要: 相位匹配协议是双场量子密钥分发协议的一种,能突破密钥容量限制且安全性得到了理论和实践的证明。针对实际应用中数据有限长效应产生的不良影响,系统地分析了相位匹配协议统计波动性能;利用高斯分析和切诺夫−霍夫丁界等统计波动分析方法,结合线性规划对相关参数进行估计,分别对不同数据长度情况下三诱骗态及二诱骗态相位匹配协议的性能进行了仿真分析。仿真结果表明:考虑统计波动的相位匹配协议仍能突破线性密钥容量的限制,在数据长度达到1016量级时,密钥生成率和最大安全传输距离均接近理想值;在数据长度小于等于1013时,增加诱骗态并不能显著提升相位匹配协议性能;随着数据长度的增加,采用切诺夫−霍夫丁界系统性能逐渐趋近采用高斯分析法的系统性能。Abstract: The phase matching protocol, which can break through the limitation of key capacity and has been proved by theory and practice, is a kind of twin-field quantum key distribution protocol. Aiming at the adverse effects of the finite data length effect in practical applications, the statistical fluctuation performance of the phase matching protocol is systematically analyzed. Using Gaussian analysis, Chernoff-Hoeffding bounds, and other statistical fluctuation analysis methods, the performances of the three-decoy and two-decoy phase matching protocols under different data lengths were simulated and analyzed combined with linear programming to estimate the relevant parameters. The simulation results show that the phase matching protocol considering statistical fluctuation can still break through the limitation of linear key capacity. When the data length reaches the order of 1016, the key generation rate and the maximum secure transmission distance are both close to ideal values. When the data length is less than or equal to 1013, adding decoy states cannot significantly improve the performance of the phase-matching protocol. As the data length increases, the performance of the system using the Chernoff-Hoeffding bound gradually approaches the performance of the system using the Gaussian analysis method.
-
表 1 仿真中用到的实验参数
${e_{\text{d}}}$ /%${p_{\text{d}}}$ $f$ ${\eta _{\text{d}}}$ /%M ${n_{\text{α}}}$ $\alpha $ 1.5 $ 8 \times 10^{-8} $ 1.15 14.5 16 5 0.2 表 2 二诱骗态PM协议部分计数率下界及错误率上界的仿真估计值
统计波动分析方法 ${Y_0}$ ${Y_1}$ ${Y_3}$ ${e_0}$ ${e_1}$ ${e_3}$ 理想值 $1.600\;0 \times {10^{ - 7}}$ 0.045853 0.13135 0.50000 0.0037551 0.0013109 高斯分析 $1.595\;5 \times {10^{ - 7}}$ 0.045614 $3.571\;7 \times {10^{ - 33}}$ 0.50338 0.0039549 1 切诺夫−霍夫丁界 $1.594\;0 \times {10^{ - 7}}$ 0.045613 $3.914\;8 \times {10^{ - 15}}$ 0.50632 0.0039570 1 表 3 三诱骗态部分计数率下界及错误率上界的仿真估计值
统计波动分析方法 ${Y_0}$ ${Y_1}$ ${Y_3}$ ${e_0}$ ${e_1}$ ${e_3}$ 理想值 $1.600\;0 \times {10^{ - 7}}$ 0.045853 0.131350 0.50000 0.0037551 0.0013109 高斯分析 $1.595\;5 \times {10^{ - 7}}$ 0.045846 0.072025 0.50338 0.0037615 0.0100970 切诺夫−霍夫丁界 $1.594\;0 \times {10^{ - 7}}$ 0.045844 0.069886 0.50634 0.0037676 0.0131220 -
[1] LO H K, MA X F, CHEN K. Decoy state quantum key distribution[J]. Physical Review Letters, 2005, 94: 230504. doi: 10.1103/PhysRevLett.94.230504 [2] LO H K, CURTY M, QI B. Measurement-Device-Independent quantum key distribution[J]. Physical Review Letters, 2012, 108: 130503. doi: 10.1103/PhysRevLett.108.130503 [3] ZHANG Y Y, BAO W S, ZHOU C, et al. Round-Robin differential phase shift with heralded single-photon source[J]. Chinese Physics Letters, 2017, 34(4): 040301. doi: 10.1088/0256-307X/34/4/040301 [4] TAKEOKA M, GUHA S, WILDE M M. Fundamental rate-loss tradeoff for optical quantum key distribution[J]. Nature Communications, 2014, 5: 5235. doi: 10.1038/ncomms6235 [5] PIRANDOLA S, LAURENZA R, OTTAVIANI C, et al. Fundamental limits of repeaterless quantum communications[J]. Nature Communications, 2017, 8: 15043. doi: 10.1038/ncomms15043 [6] LUCAMARINI M, YUAN Z L, DYNES J F, et al. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters[J]. Nature, 2018, 557: 400-403. doi: 10.1038/s41586-018-0066-6 [7] GRASSELLI F, CURTY M. Practical decoy-state method for twin-field quantum key distribution[J]. New Journal of Physics, 2019, 21: 073001. doi: 10.1088/1367-2630/ab2b00 [8] MA X F, ZENG P, ZHOU H Y. Phase-Matching quantum key distribution[J]. Physical Review X, 2018, 8: 031043. [9] WANG X B, YU Z W, HU X L. Twin-Field quantum key distribution with large misalignment error[J]. Physical Review A, 2018, 98(6): 1-12. [10] CUI C H, YIN Z Q, WANG R, et al. Twin-Field quantum key distribution without phase postselection[J]. Physical Review Applied, 2019, 11(3): 1. [11] WANG S, YIN Z Q, HE D Y, et al. Twin-Field quantum key distribution over 830 km fibre[J]. Nature Photonics, 2022, 16(2): 154-161. doi: 10.1038/s41566-021-00928-2 [12] CHEN J P, ZHANG C, LIU Y, et al. Twin-Field quantum key distribution over a 511 km optical fibre linking two distant metropolitan areas[J]. Nature Photonics, 2021, 15(8): 570-575. doi: 10.1038/s41566-021-00828-5 [13] CHEN G, WANG L, LI W, et al. Multiple-Pulse phase-matching quantum key distribution[J]. Quantum Information Processing, 2020, 19: 416. doi: 10.1007/s11128-020-02920-1 [14] LI W, WANG L, ZHAO S M. Phase matching quantum key distribution based on single-photon entanglement[J]. Scientific Reports, 2019, 9: 15466. doi: 10.1038/s41598-019-51848-9 [15] BUNANDAR D, GOVIA L C G, KROVI H, et al. Numerical finite-key analysis of quantum key distribution[J]. NPJ Quantum Information, 2020, 6: 104. doi: 10.1038/s41534-020-00322-w [16] CURRÁS-LORENZO G, NAVARRETE Á, AZUMA K, et al. Tight finite-key security for twin-field quantum key distribution[J]. NPJ Quantum Information, 2021, 7: 22. doi: 10.1038/s41534-020-00345-3 [17] 虞味, 周媛媛, 周学军. 基于弱相干态光源的相位匹配诱骗态量子密钥分配方案[J]. 量子电子学报, 2021, 38(1): 37-44. YU W, ZHOU Y Y, ZHOU X J. Phase-Matching decoystate quantum key distribution scheme with weak coherent source[J]. Chinese Journal of Quantum Electronics, 2021, 38(1): 37-44. [18] YU Y, WANG L, ZHAO S M, et al. Decoy-State phase-matching quantum key distribution with source errors[J]. Optics Express, 2021, 29(2): 2227. doi: 10.1364/OE.404567 [19] MA X F, QI B, ZHAO Y, et al. Practical decoy state for quantum key distribution[J]. Physical Review A: Atomic, Molecular, and Optical Physics, 2005, 72: 012326. doi: 10.1103/PhysRevA.72.012326 [20] 周江平, 周媛媛, 周学军, 等. 二诱骗态相位匹配量子密钥分发方案[J]. 电子科技大学学报, 2021, 50(5): 650-655. doi: 10.12178/1001-0548.2021171 ZHOU J P, ZHOU Y Y, ZHOU X J, et al. Two-Decoystate phase matching quantum key distribution method[J]. Journal of University of Electronic Science and Technology of China, 2021, 50(5): 650-655. doi: 10.12178/1001-0548.2021171 [21] ZHOU J P, ZHOU Y Y, GU R W, et al. Passive decoy state phase matching quantum key distribution[J]. International Journal of Quantum Information, 2022, 20(4): 2250005. doi: 10.1142/S0219749922500058 [22] ZHANG Z, ZHAO Q, RAZAVI M, et al. Improved key-rate bounds for practical decoy-state quantum-key-distribution systems[J]. Physical Review A, 2017, 95: 012333. doi: 10.1103/PhysRevA.95.012333 [23] CURTY M, XU F H, CUI W, et al. Finite-Key analysis for measurement-device-independent quantum key distribution[J]. Nature Communications, 2014, 5: 3732. doi: 10.1038/ncomms4732 [24] DING H J, MAO C C, ZHANG C M, et al. Improved statistical fluctuation analysis for measurement-device-independent quantum key distribution[J]. Quantum Information Processing, 2018, 17: 332. doi: 10.1007/s11128-018-2026-3 [25] MA X F, FUNG C H F, RAZAVI M. Statistical fluctuation analysis for measurement-device-independent quantum key distribution[J]. Physical Review A: Atomic, Molecular, and Optical Physics, 2012, 86: 052305. doi: 10.1103/PhysRevA.86.052305 -


 ISSN
ISSN 



 下载:
下载: