-
随着量子计算的发展,其在解决特定问题时的量子优越性正在体现出来。在理论方面,Shor算法[1]在解决大素数分解问题时可以实现指数加速,这给现代密码行业造成了冲击。Grover算法[2]可以二次加速数据库中的搜索问题。在实验方面,谷歌悬铃木超导量子计算机首次实现量子计算优越性。而中国科学技术大学的“祖冲之号”[3]和“九章号”[4]分别在超导和光量子计算机上进一步提升了性能。“祖冲之号”进行1.2小时的取样任务需要超算花费8年[3],而“九章号”的取样速度比经典计算机快
$ {10^{24}} $ 倍[4]。现代金融学在解决一些特定任务时,需要极大的算力。这些算力主要被用于对历史数据的分析、高频交易、金融衍生品定价、投资组合优化以及风险管理等领域[5-7]。由于数据集的庞大,算法时间复杂度的略微提升,都会对运算时间造成严重影响。除此之外,金融学中的算法对时间异常敏感,耗费几小时或几天生成的算法可能不再实用。因此,这种特性也激发出金融学与量子计算的结合[8-10]。
本文提出了一种基于量子判别分析法(quantum linear discriminant analysis, QLDA)的投资组合优化方案,求得无目标利润下马科维茨均值方差模型[11-12]的最优解。该解在所有满足条件的投资方案中达到夏普率[13]最大。对比经典方法,可实现准指数加速。
-
投资组合优化可以描述为如下问题:投资者将一笔资金进行投资,在初期用来购买一些证券,然后在末期卖出。投资者需要在众多证券中选择哪些证券进行购买,并决定分配在这些证券上资金的份额。投资者有两个决策目标:收益率最高;风险最低。马科维茨均值方差模型[11–12]针对投资组合优化问题的建模表示为:
$$ \begin{split} &{{\min }}\;{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{\varSigma w}}\\ &\text{s}\text{.}\text{t}\text{.}\left\{\begin{array}{c}{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)={\boldsymbol{\mu}} \\ \displaystyle{\sum} {w}_{i}=1\end{array}\right. \end{split} $$ (1) 式中,
$ {\boldsymbol{w}} = {\left({{w_1}},\, {{w_2}},\,\cdots \,{{w_N}} \right)^{\rm{T}}} $ ,N表示可投资资产数量;${w_i}$ 表示投资第$ i $ 个资产的资金占总资金的份额,其解空间是连续的,因此这种模型被称为连续马科维茨均值方差模型;$ {\boldsymbol{\varSigma}} $ 代表收益率的协方差矩阵,大小为$ N \times N $ 维;${\boldsymbol{E}}\left( {\boldsymbol{r}} \right)$ 为每个资产收益率的期望;$ {\boldsymbol{\mu}} $ 为预先决定的收益目标。马科维茨均值方差模型的目的在于在给定收益目标后,求得一种资产配置方案使得投资风险最小。对于不设置收益目标,只追求最大利润风险比的投资者,该模型可以转化为:
$$ \begin{split} &\max \dfrac{{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}}^{{\rm{T}}}\boldsymbol{\varSigma w}}}\\ &\text{s}\text{.}\text{t}\text{.}\displaystyle{\sum} {w}_{i}=1 \end{split} $$ (2) 也可以转化为:
$$ \begin{split} &\max {(1-\lambda ){\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)-\lambda {{\boldsymbol{w}}}^{{\rm{T}}}\displaystyle{\sum} {\boldsymbol{w}}\\ &\qquad\qquad\text{s}\text{.}\text{t}\text{.}\displaystyle{\sum} {w}_{i}=1 \end{split} $$ (3) 如果利率
$ {\boldsymbol{r}} $ 代表资产利率减去无风险利率的净值,式(2)的目标函数$\dfrac{{{{\boldsymbol{w}}^{\rm{T}}}{\boldsymbol{E}}\left( {\boldsymbol{r}} \right)}}{{\sqrt {{{\boldsymbol{w}}^{\rm{T}}}{\boldsymbol{\varSigma w}}} }}$ 被称为夏普率[13],其代表投资人每多承担一分风险,就可以多拿到几分超额报酬。夏普率是衡量一个投资方案优劣的重要指标之一。式(3)的线性形式更加普遍运用于各个优化模型中[14-16],其中$\lambda \in \left[ {0,} \right.\left. 1 \right]$ 表示风险偏好,其值越大,投资策略更加偏向于考虑风险。马科维茨均值方差模型在不同的市场或假设下也会有细微的差别。如在一个只允许做多,不允许做空的市场下,
${w_i}$ 被约束在[0, 1]间。而在允许做空的市场下就没有这个假设。在小额投资中,${w_i}$ 不认为是第$ i $ 个资产的资金占总资金的份额,而是购买第$ i $ 个资产的手数。在这种情况下,${w_i}$ 是离散的,这种模型称为离散马科维茨均值方差模型。其约束条件将会调整为$\displaystyle{\sum} {{w_i} = D} $ 。在允许做空市场中$ {w_i} \in \{ { - 1,}\;{0,}\;1 \} $ ,而在不允许做空的市场中$ {w_i} \in \{ {0,}\;1\} $ 。$D$ 为所有资产的总手数。连续型的马科维茨均值方差模型被广泛应用于实际场景,投资机构根据其结果精度,配置与精度相对应的资金规模。离散型的马科维茨均值方差模型更贴近真实情况,因为在股票市场中,投资者必须以“手”为最小单位,进行购买。离散模型可以通过增加可能离散解的个数来逼近连续模型,但算法的时间复杂度会大大提升。求解连续马科维茨均值方差模型的经典算法包含拉格朗日乘子法[14]、混合灰色关联度法[15]、遗传算法[16] 。这些算法的前提需要计算收益率的协方差矩阵,时间复杂度为
$ O\left( {{N^2}M} \right) $ ,其中$ M $ 为历史时间节点数。在求解拉格朗日乘子法时,需要计算矩阵乘积和求逆,其时间复杂度为$ O\left( {{N^3}} \right) $ 。因此这些算法的时间复杂至少是多项式级别的。而求解离散马科维茨均值方差模型的确定性经典算法是Brute-Force算法,其时间复杂度为$ O\left( {{2^N}} \right) $ 。除此之外,GW优化[17]算法被认为有解决离散马科维茨均值方差模型的潜力,GW算法可以以多项式时间解决相似的最大割问题,其近似比可以达到最优解的80%[18]。即使对于马科维兹模型的延伸模型[19],求解离散问题也是一个NP完全问题[20-21]。解决马科维茨均值方差模型的最著名的两个量子算法是量子退火(quantum annealing, QA)[22-23]与量子近似优化算法(quantum approximation optimization algorithm, QAOA)[24-25]。这两个算法都通过解决组合优化问题来解决离散马科维茨模型。QA利用量子的隧穿效应,进而加速优化时间[26-28]。D-Wave量子退火机可以实现伊辛模型的优化。伊辛模型哈密顿函数表示为:
$$ {\boldsymbol{H}}=\displaystyle\sum _{i,j=1}^{N}{J}_{ij}{{\boldsymbol{\sigma}}}_{i}^{Z}{{\boldsymbol{\sigma}} }_{j}^{Z}+\sum _{i=1}^{N}{h}_{i}{{\boldsymbol{\sigma }}}_{i}^{Z} $$ (4) 而将组合优化问题式(3)写为二次型形式后,可以发现该模型恰好就是伊辛模型。QAOA将可行解编码为量子态后放入量子参数线路(quantum parameterized circuit, QPC)[29],然后利用变分量子特征值求解算法,运用经典的非线性优化器求得最优参数,最后对量子态进行测量。除这两个算法外,文献[30]基于HHL算法,设计出复杂度为
${\text{poly(log(}}NM{\text{))}}$ 的组合优化算法[31],而文献[32]将马科维兹模型规约为二阶锥优化,然后用量子优化算法求解,其时间复杂度是$O{\text{(}}{N^{1.5}}{\text{)}}$ 。 -
线性判别分析(linear discriminant analysis, LDA)是一种监督学习下的降维方法[33]。假设数据集是
${\boldsymbol{F}}:M \times N$ ,数据表示为$ \{ {{\boldsymbol{x}}_i} \in {\mathbb{R}^N}:{\text{ }}1 \leqslant i \leqslant M\} $ 。这$ M $ 个数据被分在$ k $ 个类中。记第$c $ 个类数据的均值为$ {{\boldsymbol{\mu }}_c} $ ,记所有数据的均值为$ \bar {\boldsymbol{x}}$ 。则有类内散度矩阵${\boldsymbol{S}}_{{\rm{W}}} $ 和类间散度矩阵$ {{\boldsymbol{S}}_{{\rm{B}}}} $ 分别为:$$ {{\boldsymbol{S}}}_{{\rm{W}}}=\displaystyle\sum _{c=1}^{k}\displaystyle\sum _{x\in c}\left({\boldsymbol{x}}-{{\boldsymbol{\mu }}}_{c}\right){\left({\boldsymbol{x}}-{{\boldsymbol{\mu}} }_{c}\right)}^{{\rm{T}}} $$ (5) $$ {{\boldsymbol{S}}_{{\rm{B}}}} = \displaystyle\sum\limits_{c = 1}^k {\left( {{{\boldsymbol{\mu }}_c} - \bar {\boldsymbol{x}}} \right){{\left( {{{\boldsymbol{\mu }}_c} - \bar {\boldsymbol{x}}} \right)}^{\rm{T}}}} $$ (6) LDA的目的是寻找一个
$ N \times K $ 特征矩阵$ {\boldsymbol{V}} $ ,使得降维后的$ M \times K $ 数据$ {\boldsymbol{FV}} $ 类内散度矩阵足够小,类间散度矩阵足够大。因此LDA问题变成求解优化问题:$$ \max \;J\left({\boldsymbol{w}}\right)=\dfrac{{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{S}}}_{{\rm{B}}}{\boldsymbol{w}}}{{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{S}}}_{{\rm{W}}}{\boldsymbol{w}}} $$ (7) 在此将特征矩阵
$ {\boldsymbol{V}} $ 转化为特征向量$ {\boldsymbol{w}} $ 分析这个问题。上述问题的对偶问题可以变为:$$ \begin{split} &\underset{{\boldsymbol{w}}}{\min }\;-{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{S}}}_{{\rm{B}}}{\boldsymbol{w}}\\ &\text{s}\text{.}\text{t}\text{.}\;{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{S}}}_{{\rm{W}}}{\boldsymbol{w}}=1 \end{split}$$ (8) 这是因为式(7)中
$ {\boldsymbol{w}} $ 可以随意缩放,对于任意常数$ k $ 满足$ J({\boldsymbol{w}}) = J(k{\boldsymbol{w}}) $ 。因此增加条件$ {{\boldsymbol{w}}^{\rm{T}}}{{\boldsymbol{S}}_{{\rm{W}}}}{\boldsymbol{w}} = 1 $ 后,依旧与原问题等价。该问题使用拉格朗日乘子法求解:$$ {\mathcal{L}}_{P}=-{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{S}}}_{{\rm{B}}}{\boldsymbol{w}}+\lambda \left({{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{S}}}_{{\rm{W}}}{\boldsymbol{w}}-1\right) $$ (9) 将上式对
$ {\boldsymbol{w}} $ 求偏导后,得到KKT条件:$$ {{\boldsymbol{S}}}_{{\rm{W}}}^{-1}{{\boldsymbol{S}}}_{{\rm{B}}}{\boldsymbol{w}}=\lambda {\boldsymbol{w}} $$ (10) 对比式(7),上式等价于:
$$ J\left({\boldsymbol{w}}\right)=\lambda $$ (11) 根据式(7)、式(10)和式(11)得到
$ {\boldsymbol{w}} $ 就是${\boldsymbol{S}}_{{\rm{W}}}^{ - 1}{{\boldsymbol{S}}_{\rm{B}}}$ 最大特征值所对应的特征向量。然后进行进一步转化:$$ {{\boldsymbol{S}}}_{{\rm{W}}}^{-1}{{\boldsymbol{S}}}_{{\rm{B}}}{\boldsymbol{w}}=\lambda {\boldsymbol{w}}\stackrel{{\boldsymbol{w}}={{\boldsymbol{S}}}_{{\rm{B}}}^{-1/2}{\boldsymbol{v}}}{\to}{{\boldsymbol{S}}}_{{\rm{B}}}^{1/2}{{\boldsymbol{S}}}_{{\rm{W}}}^{-1}{{\boldsymbol{S}}}_{{\rm{B}}}^{1/2}{\boldsymbol{v}}=\lambda {\boldsymbol{v}} $$ (12) 问题转变为求解厄米特矩阵最大特征值所对应的特征向量:
$$ {{\boldsymbol{S}}}_{{\rm{B}}}^{1/2}{{\boldsymbol{S}}}_{{\rm{W}}}^{-1}{{\boldsymbol{S}}}_{{\rm{B}}}^{1/2}=\left[{{\boldsymbol{S}}}_{{\rm{B}}}^{1/2}{{\boldsymbol{S}}}_{{\rm{W}}}^{-1/2}\right]{\left[{{\boldsymbol{S}}}_{{\rm{B}}}^{1/2}{{\boldsymbol{S}}}_{{\rm{W}}}^{-1/2}\right]}^{\dagger } $$ (13) 因此,如果想求解特征矩阵
$ {\boldsymbol{V}} $ ,就需要求解式(13)最大的$ K $ 个特征值对应的特征向量$ {\boldsymbol{v}} $ ,然后将其转化为向量$ {\boldsymbol{w}} $ 后,拼接为$ {\boldsymbol{V}} $ 。 -
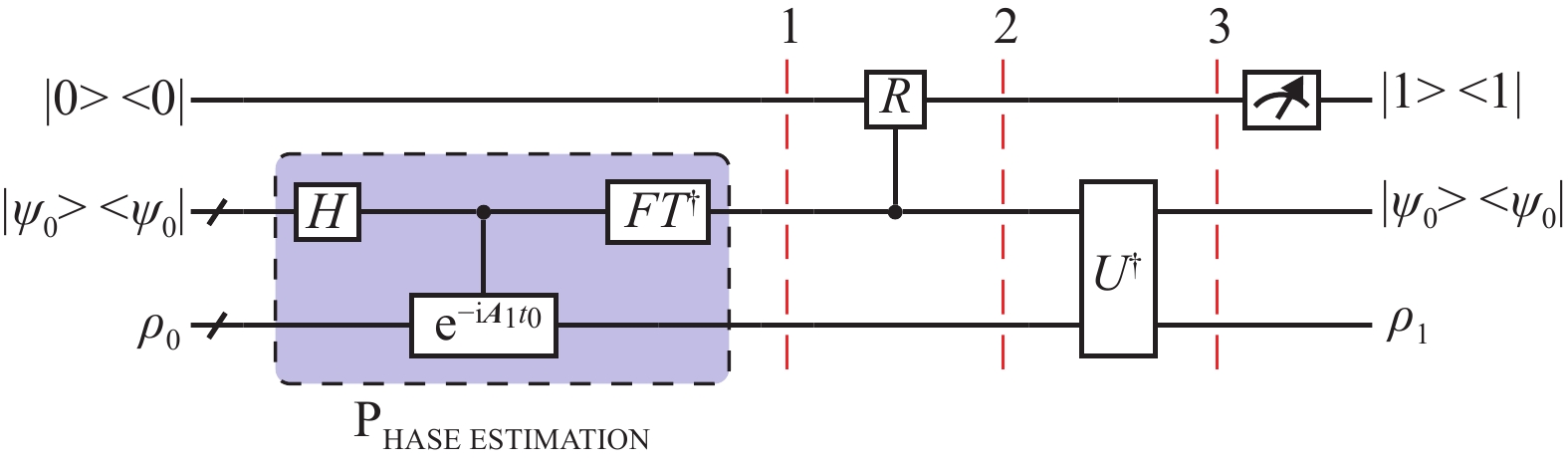
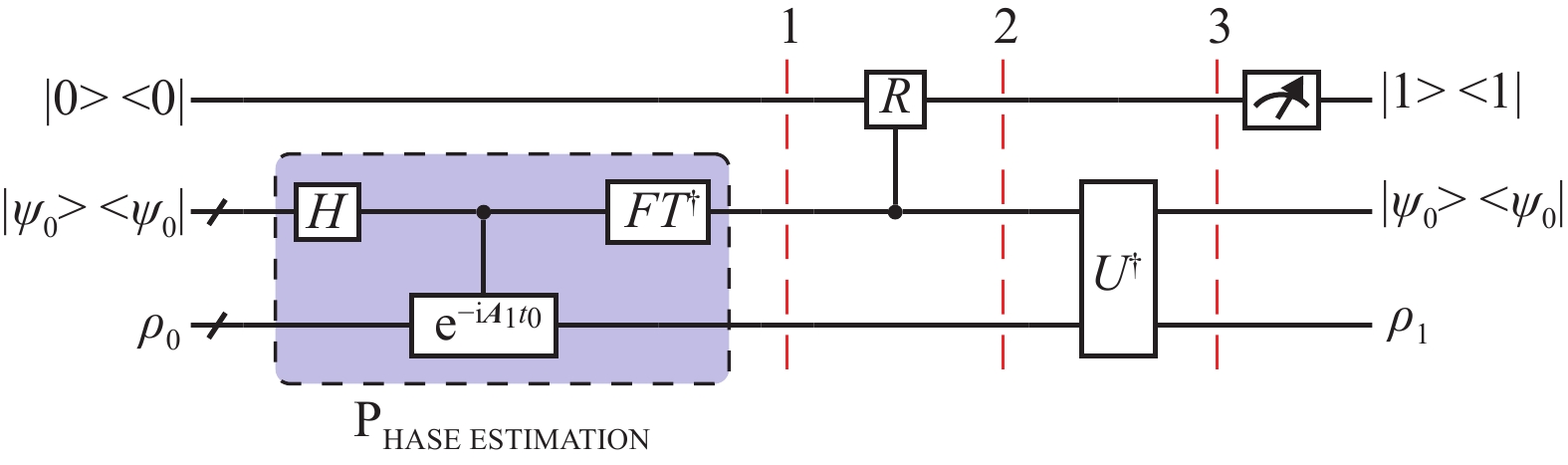
文献[34]提出了一种方案来求解厄米特矩阵的特征向量,这种方案称为厄米特链积(hermitian chain product, HCP)。HCP的线路如图1所示,与HHL算法十分相似,其目的是将
$ {f_1}\left( {{{\boldsymbol{A}}_1}} \right){\boldsymbol{I}}{\left( {{f_1}\left( {{{\boldsymbol{A}}_1}} \right)} \right)^\dagger } $ 编码于量子密度算子内。量子线路的初态被储存在3个寄存器中,第1个储存器储存单量子比特
$ \left| 0 \right\rangle $ ;第2个寄存器可以设计任意态为初态,在理论计算上没有区别;第3个寄存器储存可变的密度算子$ {\rho _0} $ ,$ {\rho _0} $ 在第一轮中为:$$ {\rho }_{0}=\dfrac{1}{\sqrt{N}}\displaystyle\sum _{i=1}^{N}\left| {i} \right\rangle \left\langle {i} \right| $$ (14) 量子线路被分为3部分,第一部分是相位估计门[35-36],其哈密顿模拟的哈密顿量就是厄米特矩阵
$ {{\boldsymbol{A}}_1} $ 。相位估计门可以将矩阵$ {{\boldsymbol{A}}_1} $ 的特征向量与其特征值进行纠缠。第二部分是一个控制旋转门,其旋转角度与函数$ {f_1} $ 有关,第三部分为第一部分的逆操作。最后测量第一个量子比特,如果结果为1,那么第三寄存器的密度算子则为$ {\rho _1} = {f_1}\left( {{{\boldsymbol{A}}_1}} \right){\boldsymbol{I}}{\left( {{f_1}\left( {{{\boldsymbol{A}}_1}} \right)} \right)^\dagger } $ 。如果以
$ {\rho _1} $ 作为第三寄存器的输入,以$ {{\boldsymbol{A}}_2} $ 和$ {f_2} $ 作为参数构造HCP线路,那么第三寄存器的量子态表示为$ {\rho _2} = {f_2}\left( {{{\boldsymbol{A}}_2}} \right){f_1}\left( {{{\boldsymbol{A}}_1}} \right)I{\left( {{f_2}\left( {{{\boldsymbol{A}}_2}} \right){f_1}\left( {{{\boldsymbol{A}}_1}} \right)} \right)^\dagger } $ 。这与式(13)的形式一致。整个算法的时间复杂度是
$O\left(\mathrm{l}\mathrm{o}\mathrm{g}\left(MN\right){\kappa }_{\text{eff}}^{3.5}/{\epsilon }^{3}\right) $ ,其中$ {\kappa }_{\text{eff}} $ 是一个预定义的条件数(一个矩阵的最大值与最小特征值之比),限制了相位估计所考虑的特征值的范围,而ϵ代表误差。由于$ {{\boldsymbol{A}}_1} $ 和$ {{\boldsymbol{A}}_2} $ 要作为哈密顿量进行哈密顿模拟,因此$ {{\boldsymbol{A}}_1} $ 和$ {{\boldsymbol{A}}_2} $ 必须为半正定厄米特矩阵。在LDA中,两个散度矩阵${{\boldsymbol{S}}_{\rm{W}}}$ 和${{\boldsymbol{S}}_{{\rm{B}}}}$ 都满足此条件。 -
在量子判别分析[34]中,散度矩阵
${{\boldsymbol{S}}_{\rm{W}}}$ 和${{\boldsymbol{S}}_{{\rm{B}}}}$ 通过量子随机存储器(QRAM[37-38])编码为密度算子:$$ {{\boldsymbol{S}}}_{{\rm{W}}}=\dfrac{1}{B}\displaystyle\sum _{c=1}^{k}\displaystyle\sum _{{x_i} \in c}{\|{{\boldsymbol{x}}}_{i}-{{\boldsymbol{\mu }}}_{c}\|}^{2}\left| {{{\boldsymbol{x}}}_{i}-{{\boldsymbol{\mu }}}_{c}} \right\rangle \left\langle {{{\boldsymbol{x}}}_{i}-{{\boldsymbol{\mu }}}_{c}} \right| $$ (16) $$ {{\boldsymbol{S}}}_{{\rm{B}}}=\dfrac{1}{A}\displaystyle\sum _{c=1}^{k}{\|{{\boldsymbol{\mu}} }_{c}-\bar{{\boldsymbol{x}}}\|}^{2}\left| {{{\boldsymbol{\mu}} }_{c}-\bar{{\boldsymbol{x}}}} \right\rangle \left\langle {{{\boldsymbol{\mu }}}_{c}-\bar{{\boldsymbol{x}}}} \right| $$ (17) 式中,
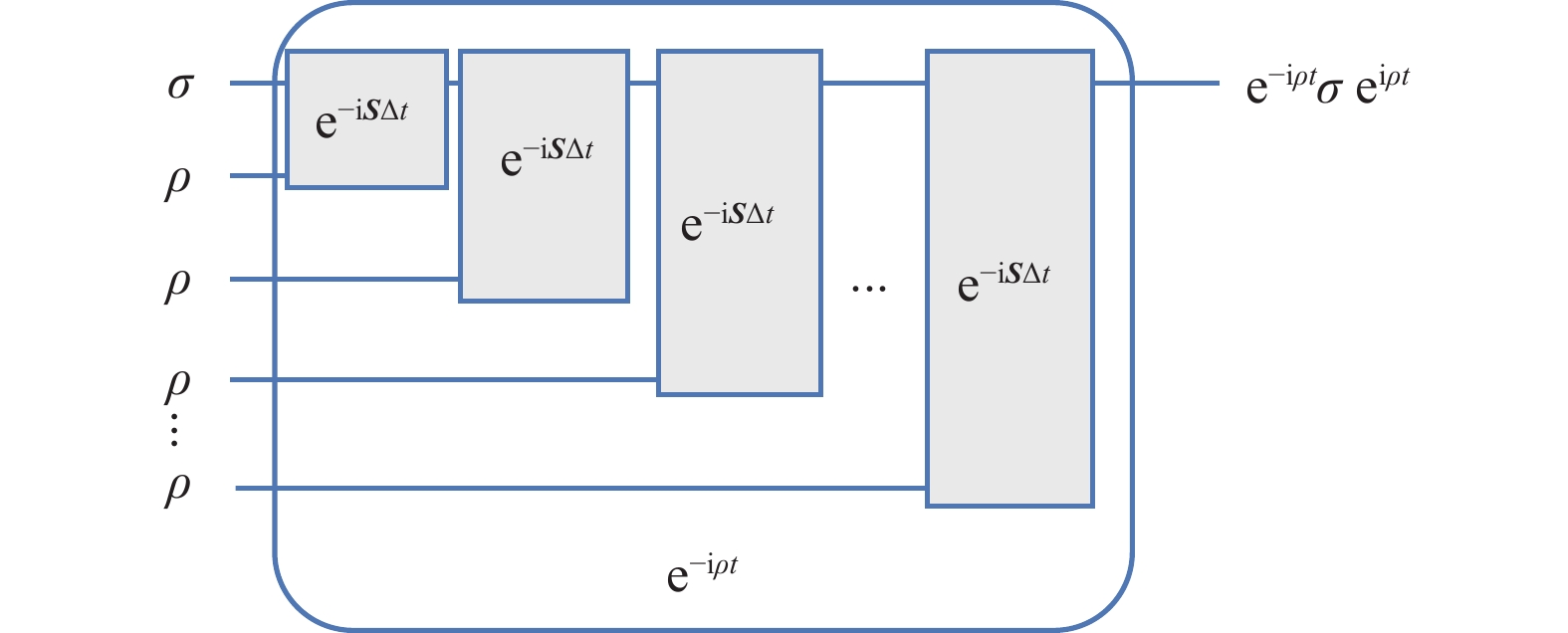
$ A $ 和$ B $ 是配平常数。而在厄米特链积中,${{\boldsymbol{S}}_{\rm{W}}}$ 和${{\boldsymbol{S}}_{{\rm{B}}}}$ 需要作为哈密顿算子${{\rm{e}}^{ - {\rm{i}}{{\boldsymbol{S}}_{\rm{W}}}t}}$ 和${{\rm{e}}^{ - {\rm{i}}{{\boldsymbol{S}}_{{\rm{B}}}}t}}$ 而非密度算子输入给相位估计门。因此,需要使用量子主成分分析(quantum principal component analysis, QPCA)[39]算法中的密度矩阵指数化算法(density matrix exponentration, DME)将密度算子转化为哈密顿量。DME算法的线路如图2所示,其输入态包含
$ n $ 个辅助态$ \rho $ (被指数化的态)和一个目标态$ \sigma $ (被作用于哈密顿模拟$ {{\rm{e}}^{ - {\rm{i}}\rho t}} $ 的态)。$ n $ 越大模拟精度越高。其时间复杂度为$ O\left({t}^{2}{\epsilon }^{-1}\right) $ ,$\epsilon $ 代表误差。整个电路由
$ n $ 个以交换门为哈密顿量的模拟组成,模拟时间为$ \Delta t = t/n $ 。$ {\boldsymbol{S}} $ 表示量子交换门。该算法基于公式:$$ {\mathrm{t}\mathrm{r}}_{P}\;\;{\mathrm{e}}^{-{\rm{i}}{\boldsymbol{S}}\mathrm{\Delta }t}\rho \otimes \sigma {\mathrm{e}}^{{\rm{i}}{\boldsymbol{S}}\mathrm{\Delta }t}=\sigma -{\rm{i}}\mathrm{\Delta }t[\rho ,\sigma ]+O\left(\mathrm{\Delta }{t}^{2}\right) $$ (18) 接着利用Hadamard引理可以得到:
$$ {{\rm{e}}}^{-{\rm{i}}\rho \mathrm{\Delta }t}\sigma {{\rm{e}}}^{{\rm{i}}\rho \mathrm{\Delta }t}=\sigma -{\rm{i}}\mathrm{\Delta }t[\rho ,\sigma ]+O\left(\mathrm{\Delta }{t}^{2}\right) $$ (19) 因此利用交换门的哈密顿模拟可以实现密度算子的指数化。最后根据Trotter公式[40]将上述算法递归
$ n $ 次后,对第一个量子比特取偏迹后为$ {{\rm{e}}^{ - {\rm{i}}\rho t}}\sigma {{\rm{e}}^{{\rm{i}}\rho t}} $ 。因此通过复制多个密度算子,可以将其指数化。相位估计算法使用控制下的哈密顿模拟,DME算法也证明出,将交换门
$ {\boldsymbol{S}} $ 变为控制交换门就可以实现控制哈密顿模拟的操作[39]。HCP将矩阵
${\boldsymbol{S}}_{{\rm{B}}}^{1/2}{\boldsymbol{S}}_{\rm{W}}^{ - 1}{\boldsymbol{S}}_{{\rm{B}}}^{1/2}$ 编码为密度算子,因此${\boldsymbol{S}}_{{\rm{B}}}^{1/2}{\boldsymbol{S}}_{\rm{W}}^{ - 1}{\boldsymbol{S}}_{{\rm{B}}}^{1/2}$ 是半正定厄米特矩阵,为了求其最大特征值对应的特征向量,需要将其通过DME算法指数化放入相位估计门中。 -
首先将式(7)按照式(2)中的均值方差构造,其模型变为:
$$ \begin{split} &\max \frac{{{\boldsymbol{w}}}^{{\rm{T}}}\left({\boldsymbol{E}}\left({\boldsymbol{r}}\right){\boldsymbol{E}}({\boldsymbol{r}}{)}^{{\rm{T}}}\right){\boldsymbol{w}}}{{{\boldsymbol{w}}}^{{\rm{T}}}\boldsymbol{\varSigma }{\boldsymbol{w}}}\\ &\qquad \text{s}\text{.}\text{t}\text{.}\displaystyle\sum _{i}\left||{w}_{i}\right|{|}^{2}=1 \end{split} $$ (20) 因为该模型将解
$ {\boldsymbol{w}} $ 编码为量子态的概率幅,受量子计算限制,其模平方和为1。为方便书写,记$ {\boldsymbol{R}} = {\boldsymbol{E}}({\boldsymbol{r}}){\boldsymbol{E}}{({\boldsymbol{r}})^{\rm{T}}} $ 。这里$ {\boldsymbol{E}}\left( {\boldsymbol{r}} \right) $ 表示净利率。然后将$ {\boldsymbol{R}} $ ,$ {\boldsymbol{\varSigma}} $ 和$ {{\boldsymbol{R}}^{1/2}}{{\boldsymbol{\varSigma }}^{ - 1}}{{\boldsymbol{R}}^{1/2}} $ 谱分解得到:$$ \begin{split} &\qquad\qquad\qquad{\boldsymbol{R}}=\left| {{\boldsymbol{E}}({\boldsymbol{r}})} \right\rangle \left\langle {{\boldsymbol{E}}({\boldsymbol{r}})} \right|\\ & {\boldsymbol{\varSigma}} =C\displaystyle\sum _{i=1}^{M}\frac{\parallel {{\boldsymbol{x}}}_{i}-{\boldsymbol{E}}\left({\boldsymbol{r}}\right){\parallel }^{2}}{N-1}\left|{{\boldsymbol{x}}}_{i}-{\boldsymbol{E}}({\boldsymbol{r}})\right\rangle \left\langle {{\boldsymbol{x}}}_{i}-{\boldsymbol{E}}({\boldsymbol{r}})\right|\\ &\qquad{{\boldsymbol{R}}}^{1/2}{{{\boldsymbol{\varSigma}} }}^{-1}{{\boldsymbol{R}}}^{1/2}=\displaystyle\sum _{i}\frac{N-1}{\parallel {{\boldsymbol{x}}}_{i}-{\boldsymbol{E}}\left({\boldsymbol{r}}\right){\parallel }^{2}}\times\\ & \qquad\parallel \left\langle {{\boldsymbol{E}}\left({\boldsymbol{r}}\right)|{{\boldsymbol{x}}}_{i}-{\boldsymbol{E}}({\boldsymbol{r}})} \right\rangle {\parallel }^{2}\left| {{\boldsymbol{E}}\left({\boldsymbol{r}}\right)} \right\rangle \left\langle {{\boldsymbol{E}}\left({\boldsymbol{r}}\right)} \right| \end{split} $$ (21) 式中,
$ {{\boldsymbol{x}}_i} $ 是时间节点$ i $ 时$ N $ 个股票的利润向量。根据谱分解,不难看出这3个矩阵是半正定的厄米特矩阵。使用QLDA方法可以求解式(19)。接着将式(19)规约为式(2),并证明以下定理。定理 如果已知式(19)的解,那么在多项式时间内可以求得式(2)的解。
在证明之前首先引入模型:
$$\begin{split} &\max \dfrac{{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{\varSigma }}}{\boldsymbol{w}}}}\\ &\text{s}\text{.}\text{t}\text{.}\displaystyle\sum _{i}\|{w}_{i}\|^{2}=1 \end{split} $$ (22) 进而有如下引理。
引理1 如果有解
$ {\boldsymbol{w}} $ 满足式(19),那么$ {\boldsymbol{w}} $ 或$ -{\boldsymbol{w}} $ 其中之一满足式(21)。证明:使用反证法进行证明,如果
$ {\boldsymbol{w}} $ 或$ - {\boldsymbol{w}} $ 都不满足式(21),那么存在${\boldsymbol{w}}' $ 满足$ {\displaystyle\sum\limits_i {\| {{{w'_i}}} \|} ^2} = 1 $ ,使得下列两式之一成立:$$ \dfrac{{{\boldsymbol{w}}'}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}'}^{{\rm{T}}}{{\boldsymbol{\varSigma }}}{{\boldsymbol{w}}'}}} > \dfrac{{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{\varSigma }}}{\boldsymbol{w}}}}\ge 0 $$ (23) $$ \dfrac{{{\boldsymbol{w}}'}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}'}^{{\rm{T}}}{{\boldsymbol{\varSigma }}}{{\boldsymbol{w}}'}}} > \dfrac{-{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{\varSigma }}}{\boldsymbol{w}}}}\ge 0 $$ (24) 将不等式左右取平方,有:
$$ \dfrac{{{\boldsymbol{w}}'}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right){\boldsymbol{E}}({\boldsymbol{r}}{)}^{{\rm{T}}}{{\boldsymbol{w}}'}}{{{\boldsymbol{w}}'}^{{\rm{T}}}{{\boldsymbol{\varSigma }}}{{\boldsymbol{w}}'}} > \dfrac{{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right){\boldsymbol{E}}({\boldsymbol{r}}{)}^{{\rm{T}}}{\boldsymbol{w}}}{{{\boldsymbol{w}}}^{{\rm{T}}}{{\boldsymbol{\varSigma }}}{\boldsymbol{w}}} $$ (25) 则
$ {\boldsymbol{w}} $ 不满足式(19)条件的最大值,与原假设矛盾。引理2 如果有解
$ {\boldsymbol{w}} $ 满足式(21),那么有解${\boldsymbol{u}} = \dfrac{{\boldsymbol{w}}}{{\left| {\displaystyle\sum\limits_i {{w_i}} } \right|}}$ 满足式(2)。证明:使用反证法进行证明,首先
$ \displaystyle\sum\limits_i {{u_i}} = 1 $ 满足式(2)条件,如果$ {\boldsymbol{u}} $ 不满足式(2),那么存在$ {u'_i} $ 使得$ \displaystyle\sum\limits_i {{{u'_i}}} = 1 $ 满足:$$ \dfrac{{{\boldsymbol{u}}'}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{u}}'}^{{\rm{T}}}\boldsymbol{\varSigma }{{\boldsymbol{u}}'}}} > \dfrac{{{\boldsymbol{u}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{u}}}^{{\rm{T}}}\boldsymbol{\varSigma }{\boldsymbol{u}}}} $$ (26) 由于目标函数的缩放性质,解乘以一个正常数时,取值不变。因此:
$$ \dfrac{{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}}^{{\rm{T}}}\boldsymbol{\varSigma }{\boldsymbol{w}}}}=\dfrac{{{\boldsymbol{u}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{u}}}^{{\rm{T}}}\boldsymbol{\varSigma }{\boldsymbol{u}}}} $$ (27) 之后,记:
$$ {{\boldsymbol{w}}'}=\dfrac{{{\boldsymbol{u}}'}}{\sqrt{\displaystyle\sum _{i} \parallel {u}_{i}{\parallel }^{2}}} $$ (28) 因为
$ {\displaystyle\sum\limits_i {\| {{{w'_i}}} \|} ^2} = 1 $ ,故:$$ \dfrac{{{\boldsymbol{w}}'}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}'}^{{\rm{T}}}\boldsymbol{\varSigma }{{\boldsymbol{w}}'}}}=\dfrac{{{\boldsymbol{u}}'}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{u}}'}^{{\rm{T}}}\boldsymbol{\varSigma }{{\boldsymbol{u}}'}}} $$ (29) 根据式(25)和式(26),式(28)满足:
$$ \dfrac{{{\boldsymbol{w}}'}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}'}^{{\rm{T}}}\boldsymbol{\varSigma }{{\boldsymbol{w}}'}}} > \dfrac{{{\boldsymbol{w}}}^{{\rm{T}}}{\boldsymbol{E}}\left({\boldsymbol{r}}\right)}{\sqrt{{{\boldsymbol{w}}}^{{\rm{T}}}\boldsymbol{\varSigma }{\boldsymbol{w}}}} $$ (30) 所以
$ {\boldsymbol{w}} $ 不满足式(21)条件的最大值,与原假设矛盾。综上,根据引理1和引理2,如果使用QLDA可以求得式(19)的解
$ {\boldsymbol{w}} $ ,首先计算$ {{\boldsymbol{w}}^{\rm{T}}}{\boldsymbol{E}}({\boldsymbol{r}}) \geqslant 0 $ 是否成立,若是,$ {\boldsymbol{u}} = \dfrac{{\boldsymbol{w}}}{{\left| {\displaystyle\sum\limits_i {{w_i}} } \right|}} $ 则为夏普率最大的投资组合,否则$ {\boldsymbol{u}} = \dfrac{{ - {\boldsymbol{w}}}}{{\left| {\displaystyle\sum\limits_i {{w_i}} } \right|}} $ 则为夏普率最大的投资组合,其计算复杂度为$ O(N) $ 。 -
结合第2部分内容,使用QLDA计算投资组合问题。
1)使用QRAM按照式(20)将矩阵
$ {\boldsymbol{R}} $ 与$ {\boldsymbol{\varSigma}} $ 编码为密度算子。其构造方法由文献[30]给出。2)使用DME算法将密度算子转化为关于
$ {\boldsymbol{R}} $ 与$ {\boldsymbol{\varSigma}} $ 的控制哈密顿算子,以此构造HCP线路。3)使用HCP算法,其链长为2,参数为
$ {f_1}(x) = {x^{ - 1/2}} $ ,$ {{\boldsymbol{A}}_1} = {\boldsymbol{\varSigma}} $ ,$ {f_2}(x) = {x^{1/2}} $ ,$ {{\boldsymbol{A}}_2} = {\boldsymbol{R}} $ 。结果得到形式为$ {{\boldsymbol{R}}^{1/2}}{{\boldsymbol{\varSigma}} ^{ - 1}}{{\boldsymbol{R}}^{1/2}} $ 的密度算子。4)使用DME算法将
$ {{\boldsymbol{R}}^{1/2}}{{\boldsymbol{\varSigma }}^{ - 1}}{{\boldsymbol{R}}^{1/2}} $ 密度算子转化为控制哈密顿算子,并以此构造相位估计算法,并且以$ {{\boldsymbol{R}}^{1/2}}{{\boldsymbol{\varSigma}} ^{ - 1}}{{\boldsymbol{R}}^{1/2}} $ 作为密度算子输入。测量占比最多的量子态则对应最大特征值的特征向量$ {\boldsymbol{v}} $ 。5)使用DME算法将
$ {\boldsymbol{R}} $ 转化为控制哈密顿算子,并构造HHL线路,输入的函数为$ {f_1}(x) = {x^{ - 1/2}} $ ,输入的量子态为$ {\boldsymbol{v}} $ 。输出的量子态$ {\boldsymbol{w}} $ 满足$ {{\boldsymbol{R}}^{1/2}}{\boldsymbol{w}} = {\boldsymbol{v}} $ 。6)使用Swap-Test方法[41]或经典方法计算
$ {{\boldsymbol{v}}^{\rm{T}}}{\boldsymbol{E}}(r) \geqslant 0 $ ,然后用经典方法计算$ {\boldsymbol{u}} = \dfrac{{\boldsymbol{v}}}{{\left| {\displaystyle\sum\limits_i {{v_i}} } \right|}} $ 或$ {\boldsymbol{u}} = \dfrac{{ - {\boldsymbol{v}}}}{{\left| {\displaystyle\sum\limits_i {{v_i}} } \right|}} $ 最优配置。资产配置的信息在这个过程中被提取在概率幅中,如何将其概率幅提取为经典信息是量子计算的解决难题。一种直观的方法是对量子态进行
$ M $ 次测量,然后统计每个基态的次数$ {M_i} $ 。那么有$ \left| {{v_i}} \right| = \sqrt {\dfrac{{{M_i}}}{M}} $ 。文献[30]给出一种判断$ {v_i} $ 的符号的方法,利用$ {\boldsymbol{E}}({r_i}) $ 的符号来判断$ {v_i} $ 的符号,它的意义是对于正利润股票进行做多,对负利润股票进行做空。这在大多数情况是正确的,但是对于相关性比较强的股票组合,会存在误差。配置态$ \left| {\boldsymbol{v}} \right\rangle $ 的其他作用包括计算风险$ \left\langle {\left. {\boldsymbol{v}} \right|{\boldsymbol{\varSigma }}\left| {\boldsymbol{v}} \right.} \right\rangle $ 或者计算$ \left\langle {\left. {\boldsymbol{v}} \right|{\boldsymbol{v}}'} \right\rangle $ 来衡量其他投资策略的优劣。这两个算法无须测量都可以使用Swap-Test方法[41]来计算。在投资组合模型中,
$ {\boldsymbol{R}} $ 只有一个非0特征值,而$ {\boldsymbol{\varSigma}} $ 也不一定满秩,也可能存在多个0特征值。为了避免这些0特征值带来的干扰,本算法在控制旋转门中规定一个下限$ \kappa $ ,小于$ \kappa $ 的特征值将不会引起目标比特的翻转,进而在最终测量结果为1时,不会出现小于$ \kappa $ 特征值的基矢。特别地,在这种情况下,一个带有0特征值矩阵$ {\boldsymbol{A}} $ 的逆表示为:$$ {{\boldsymbol{A}}^{ - 1}} = \displaystyle\sum\limits_{{\lambda _{{i}}} \geqslant \kappa } {\lambda _i^{ - 1}\left| {{{\boldsymbol{e}}_i}} \right\rangle } \left\langle {{{\boldsymbol{e}}_i}} \right| $$ (31) 式中,
$ {\lambda _i} $ 为$ {\boldsymbol{A}} $ 的特征值;$ {{\boldsymbol{e}}_i} $ 为$ {\lambda _i} $ 的特征向量。 -
基于QLDA算法可以实现准指数加速。考虑误差项,其总时间复杂度与QLDA一致,为
$ O\text{(poly}(\mathrm{log}(MN))/{\epsilon }^{3}) $ 。其中将数据存储到QRAM的时间复杂度是$ O(\log (NM)) $ ;HCP算法不计入误差项其时间复杂度也是$ O(\log (NM)) $ ;DME算法的时间复杂度是$ O(n) $ ,因为与$ N $ 无关,被认为是常数项;相位估计算法的时间复杂度是$ O{\text{(poly}}(\log (MN))) $ ;HHL算法的时间复杂度是$ O(\log (NM)) $ ;Swap-Test算法的时间复杂度是$ O(\log (N)) $ 。因此所有的量子算法可以实现指数加速。但在最后一步,还需要将$ {v_i} $ 求和,这一步的复杂度是$ O(N) $ 。考虑到目前应用投资组合资产种类小于100,即使将这个值扩大到$ {10^6} $ ,普通的经典计算机也可以瞬间完成,因此,这部分时间可以忽略不计。在QRAM中,算法需要提前将数据存储在经典RAM中,然后使用Oracle查询获取感兴趣的数值,这一部分的准备时间是
$ O(NM) $ 且是一次性的,对比其他算法也可以实现二次加速。表1描述了不同投资组合优化问题算法的时间复杂度。由于部分算法分析时间复杂度没有考虑误差项,因此在比较时认为误差项为常数项。
表 1 不同投资组合优化算法的对比
算法名称 运行复杂度 准备复杂度 算法类型 拉格朗日乘子[14] $ O({N^3}) $ $ O({N^2}M) $ 经典连续 QLDA 约$ O{\text{(poly}}(\log (MN))) $ $ O(NM) $ 量子连续 HHL[31] 约$ O{\text{(poly}}(\log (MN))) $ $ O(NM) $ 量子连续 二阶锥优化[32] $ O({N^{1.5}}) $ $ O(NM) $ 量子连续 Brute-Force $ O\left( {{2^N}} \right) $ $ O({N^2}M) $ 经典离散 QAOA[29] $ O(pt) $ $ O({N^2}M) $ 量子离散 QA[26] $ O(t) $ $ O({N^2}M) $ 量子离散 表1中QAOA与QA的运行复杂度与资产数量无关,与实验重复次数
$ t $ 有关,$ p $ 为QAOA的参数,即迭代线路的深度。从表中可见QLDA算法与HHL算法维持在同一水平。HHL方法虽然没在文中特别说明,但也需要对向量上的每个元素进行求和,以满足约束条件。此表没有对消耗量子比特数目进行对比,这是因为QLDA和HHL需要使用Oracle利用辅助比特构造QRAM,而二阶锥优化、QAOA、QA需要重复算法,其消耗的量子比特难以估算。在制备QRAM过程中,QLDA与HHL算法消耗的量子比特是一致的。在算法过程中,HHL需要求解
$ 3N $ 个线性方程组,其HHL线路需要的量子比特大致是HCP的3倍。因此QLDA算法相比HHL更加经济。 -
本文基于QLDA的HCP算法与QPCA的DME算法设计了无预先获利目标下的量子投资组合优化算法,算法可以求得满足最大夏普率的投资组合方案解,并且其算法的时间复杂度约为
${\text{poly(log(}}NM{\text{))}}$ ,相比于经典解决方案可以达到准指数加速。这在投资组合优化场景中,可以使投资组合优化算法所考虑的股票数量大大提高。然而,本算法和诸多基于DME的算法在实施时有着局限性。DME算法需要
$ n > 100 $ 时,才有逼近指数化算子的效果。最后需要重复$ n $ 次HCP实验来获得$ n $ 个$ {{\boldsymbol{R}}^{1/2}}{{\boldsymbol{\varSigma}} ^{ - 1}}{{\boldsymbol{R}}^{1/2}} $ 算子才可以实施相位估计算法。那么一开始在QRAM中准备$ {\boldsymbol{R}} $ ,$ {\boldsymbol{\varSigma}} $ 的数量时将达到$ O( {{n^2}} ) $ 。尽管在理论分析中因为$ n $ 与资产数量$N$ 无关,所以被认为是常数项,但在试验中这个常数值将达到${10^4}$ ,是不可忽视的。如何在真实量子计算机上完成DME算法也是挑战之一。
Financial Portfolio Optimization Method Based on the Quantum Linear Discriminant Analysis
-
摘要: 利用马科维茨投资组合优化问题和量子线性判别分析(quantum linear discriminant analysis, QLDA)的相似性,将马科维茨投资组合优化问题规约为量子线性判别分析的优化问题,并通过解决QLDA的技术厄米特链积(hermitian chain product, HCP)以及密度矩阵指数化算法(density matrix exponentiation, DME)来求得马科维茨均值方差模型中夏普率最大的最优解。量子连续投资组合优化方案相比于经典方案可以实现准指数加速。Abstract: This paper reduces the Markowitz’s model to the Quantum Linear Discriminant Analysis (QLDA) model. Hermitian Chain Product (HCP) and Density Matrix Exponentiation (DME) are used to solve the optimal solution with the largest Sharpe rate in the Markowitz mean-variance model. The quantum continuous portfolio optimization scheme can achieve quasi-exponential acceleration compared to the classical scheme.
-
表 1 不同投资组合优化算法的对比
算法名称 运行复杂度 准备复杂度 算法类型 拉格朗日乘子[14] $ O({N^3}) $ $ O({N^2}M) $ 经典连续 QLDA 约 $ O{\text{(poly}}(\log (MN))) $ $ O(NM) $ 量子连续 HHL[31] 约 $ O{\text{(poly}}(\log (MN))) $ $ O(NM) $ 量子连续 二阶锥优化[32] $ O({N^{1.5}}) $ $ O(NM) $ 量子连续 Brute-Force $ O\left( {{2^N}} \right) $ $ O({N^2}M) $ 经典离散 QAOA[29] $ O(pt) $ $ O({N^2}M) $ 量子离散 QA[26] $ O(t) $ $ O({N^2}M) $ 量子离散 -
[1] SHOR P W. Algorithms for quantum computation: Discrete logarithms and factoring[EB/OL]. [2022-03-27]. http://ieeexplore.ieee.org/document/365700/. [2] GROVER L K. Quantum computers can search arbitrarily large databases by a single query[J]. Physical Review Letters, 1997, 79(23): 4709-4712. doi: 10.1103/PhysRevLett.79.4709 [3] WU Y, BAO W S, CAO S, et al. Strong quantum computational advantage using a superconducting quantum processor[J]. Physical Review Letters, 2021, 127(18): 180501. doi: 10.1103/PhysRevLett.127.180501 [4] ZHONG H S, DENG Y H, QIN J, et al. Phase-programmable gaussian boson sampling using stimulated squeezed light[J]. Physical Review Letters, 2021, 127(18): 180502. doi: 10.1103/PhysRevLett.127.180502 [5] HULL J. Options, futures, and other derivatives[M]. 9th ed. Boston: Pearson, 2015. [6] FÖLLMER H, SCHIED A. Stochastic finance: An introduction in discrete time[M]. Berlin: Walter de Gruyter, 2004. [7] GLASSERMAN P. Monte Carlo methods in financial engineering[M]. New York: Springer, 2010. [8] LEE R S T. Quantum finance: Intelligent forecast and trading systems[M]. [S.l.]: Springer, 2020. [9] REBENTROST P, GUPT B, BROMLEY T R. Quantum computational finance: Monte Carlo pricing of financial derivatives[J]. Physical Review A, 2018, 98(2): 022321. doi: 10.1103/PhysRevA.98.022321 [10] WOERNER S, EGGER D J. Quantum risk analysis[J]. NPJ Quantum Information, 2019, 5(1): 15. doi: 10.1038/s41534-019-0130-6 [11] MARKOWITZ H M. Portfolio selection: Efficient diversification of investments[EB/OL]. [2022-03-11]. https://www.degruyter.com/document/doi/10.12987/9780300191677/html. [12] FABOZZI F J, MARKOWITZ H M, KOLM P N, et al. Mean-variance model for portfolio selection[EB/OL]. [2022-03-11]. https://onlinelibrary.wiley.com/doi/10.1002/9781118182635.efm0003. [13] SHARPE W F. Mutual fund performance[J]. The Journal of Business, 1966, 39(S1): 119. doi: 10.1086/294846 [14] SHAW D X, LIU S, KOPMAN L. Lagrangian relaxation procedure for cardinality-constrained portfolio optimization[J]. Optimization Methods and Software, 2008, 23(3): 411-420. doi: 10.1080/10556780701722542 [15] HUANG K, JANE C, CHANG T. An enhanced approach to optimizing the stock portfolio selection based on modified markowitz MV method[J]. Journal of Convergence Information Technology, 2011, 6(2): 226-239. doi: 10.4156/jcit.vol6.issue2.24 [16] SOLEIMANI H, GOLMAKANI H R, SALIMI M H. Markowitz-based portfolio selection with minimum transaction lots, cardinality constraints and regarding sector capitalization using genetic algorithm[J]. Expert Systems with Applications, 2009, 36(3): 5058-5063. doi: 10.1016/j.eswa.2008.06.007 [17] WILLIAMSON D P, GOEMANS M X, MIHAIL M, et al. A primal-dual approximation algorithm for generalized steiner network problems[J]. Combinatorica, 1995, 15(3): 435-454. doi: 10.1007/BF01299747 [18] GOEMANS M X, WILLIAMSON D P. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming[J]. Journal of the ACM, 1995, 42(6): 1115-1145. doi: 10.1145/227683.227684 [19] KONNO H, YAMAZAKI H. Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market[J]. Management Science, 1991, 37(5): 519-531. doi: 10.1287/mnsc.37.5.519 [20] KELLERER H, MANSINI R, SPERANZA M G. Selecting portfolios with fixed costs and minimum transaction lots[J]. Annals of Operations Research, 2000, 99(1): 287-304. doi: 10.1023/A:1019279918596 [21] MANSINI R, SPERANZA M G. Heuristic algorithms for the portfolio selection problem with minimum transaction lots[J]. European Journal of Operational Research, 1999, 114(2): 219-233. doi: 10.1016/S0377-2217(98)00252-5 [22] FINNILA A B, GOMEZ M A, SEBENIK C, et al. Quantum annealing: A new method for minimizing multidimensional functions[J]. Chemical Physics Letters, 1994, 219(5-6): 343-348. doi: 10.1016/0009-2614(94)00117-0 [23] 王宝楠, 水恒华, 王苏敏, 等. 量子退火理论及其应用综述[J]. 中国科学: 物理学 力学 天文学, 2021, 51(8): 5-17. WANG B N, SHUI H H, WANG S M, et al. Summary of quantum annealing theory and its applications[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2021, 51(8): 5-17. [24] FARHI E, GOLDSTONE J, GUTMANN S. A quantum approximate optimization algorithm[EB/OL]. [2021-03-13]. http://arxiv.org/abs/1411.4028. [25] HADFIELD S, WANG Z, O’GORMAN B, et al. From the quantum approximate optimization algorithm to a quantum alternating operator ansatz[J]. Algorithms, 2019, 12(2): 34. doi: 10.3390/a12020034 [26] APOLLONI B, CARVALHO C, DE FALCO D. Quantum stochastic optimization[J]. Stochastic Processes and their Applications, 1989, 33(2): 233-244. doi: 10.1016/0304-4149(89)90040-9 [27] VENTURELLI D, KONDRATYEV A. Reverse quantum annealing approach to portfolio optimization problems[J]. Quantum Machine Intelligence, 2019, 1(1-2): 17-30. doi: 10.1007/s42484-019-00001-w [28] ROSENBERG G, HAGHNEGAHDAR P, GODDARD P, et al. Solving the optimal trading trajectory problem using a quantum annealer[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(6): 1053-1060. doi: 10.1109/JSTSP.2016.2574703 [29] HODSON M, RUCK B, ONG H, et al. Portfolio rebalancing experiments using the quantum alternating operator ansatz[EB/OL]. [2021-10-11]. http://arxiv.org/abs/1911.05296. [30] HARROW A W, HASSIDIM A, LLOYD S. Quantum algorithm for linear systems of equations[J]. Physical Review Letters, 2009, 103(15): 150502. doi: 10.1103/PhysRevLett.103.150502 [31] REBENTROST P, LLOYD S. Quantum computational finance: Quantum algorithm for portfolio optimization[EB/OL]. [2022-03-11]. https://arxiv.org/abs/1811.03975v1. [32] KERENIDIS I, PRAKASH A, SZILÁGYI D. Quantum algorithms for portfolio optimization[EB/OL]. [2021-10-10]. https://doi.org/10.1145/3318041.3355465. [33] IZENMAN A J. Linear discriminant analysis[EB/OL]. [2022-03-14]. http://link.springer.com/10.1007/978-0-387-78189-1_8. [34] CONG I, DUAN L. Quantum discriminant analysis for dimensionality reduction and classification[J]. New Journal of Physics, 2016, 18(7): 073011. doi: 10.1088/1367-2630/18/7/073011 [35] MOSCA M. Quantum computer algorithms[D]. Oxford: University of Oxford, 1999. [36] CLEVE R, EKERT A, MACCHIAVELLO C, et al. Quantum algorithms revisited[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1969): 339-354. doi: 10.1098/rspa.1998.0164 [37] SOKLAKOV A N, SCHACK R. Efficient state preparation for a register of quantum bits[J]. Physical Review A, 2006, 73(1): 012307. doi: 10.1103/PhysRevA.73.012307 [38] GROVER L, RUDOLPH T. Creating superpositions that correspond to efficiently integrable probability distributions[EB/OL]. [2022-03-14]. http://arxiv.org/abs/quant-ph/0208112. [39] LLOYD S, MOHSENI M, REBENTROST P. Quantum principal component analysis[J]. Nature Physics, 2014, 10(9): 631-633. doi: 10.1038/nphys3029 [40] TROTTER H F. On the product of semi-groups of operators[J]. Proceedings of the American Mathematical Society, 1959, 10(4): 545-551. doi: 10.1090/S0002-9939-1959-0108732-6 [41] BUHRMAN H, CLEVE R, WATROUS J, et al. Quantum fingerprinting[J]. Physical Review Letters, 2001, 87(16): 167902. doi: 10.1103/PhysRevLett.87.167902 -

 ISSN
ISSN 



 下载:
下载: