给定一个无向图$ G = \left( {V,E} \right) $，其中集合$ V $为N个节点的顶点集，$ E $为M条边的边集。每一条边$ e \in E $都对应于一个非负实数$ w $，称为边权值。有一条指定的目标路径$ {p^*} $，攻击者希望该路径是源节点s到目标节点t之间的最短路径，因此可以通过扰动边的权值，以最小的成本来实现这一目标。在扰动过程中，扰动成本定义为边权重的增加量，在不同应用场景中，扰动成本意味着对改变边多少所需的代价。如交通网络中的危险品运输管控，作为交通管制的阻断者可以通过增加部分路段的通行时间成本来改变承运商的运输路线选择，如调控红绿灯时长，设置检测卡点等，改变得越大所需扰动成本越大。当然，为了满足扰动的隐秘性，要求路径$ {p^*} $上的边不能被扰动，因此，要想以最小成本来扰动网络，只能通过对非目标路径上的边进行加权处理。总而言之，强制路径问题是基于两个关键的约束条件：首先，任何不大于$ {p^*} $的路径p必须被扰动，使之超过$ {p^*} $；其次，路径扰动不得干扰目标路径$ {p^*} $。则强制路径问题的线性规划公式^[18]如下：

式中，$ {\boldsymbol{\varDelta }} $是边权重的扰动向量；$ {\boldsymbol{w}} $是原始图G中边权重向量。对于G中从s到t的任意路径p，设$ {{\boldsymbol{x}}_p} \in {\left\{ {0,1} \right\}^M} $为路径p的边指示向量，$ {{\boldsymbol{w}}^{\rm T}}{{\boldsymbol{x}}_p} $为原图中p的长度，${\left( {{\boldsymbol{w}} + {\boldsymbol{\varDelta }}} \right)^{\rm T}}{{\boldsymbol{x}}_p}$为在扰动后图中p的长度；$ \ell $是$ {p^*} $的长度，$ \delta $是确保$ {p^*} $是唯一最短路径的“缓冲”：$ {p^*} $的长度与第二短路径的长度之差；$ {P_{\ell + \delta }} $是从s到t其长度小于$ \ell + \delta $的路径集合。

关于问题(1)的求解，由于约束条件中需要寻找所有G中从s到t中不大于$ {p^*} $长度的路径，这是一个操作困难且时间复杂度很高的问题，所以文献[18]设计了一种迭代算法，通过每一步只寻找一条最短路径加入集合$ {P_{\ell + \delta }} $中，求解最优化式(1)，更新权重后，再寻找一条最短路径，加入集合$ {P_{\ell + \delta }} $中，求解最优化式(1)。重复操作，直到寻找的最短路径长度为$ {p^*} $为止。该算法可以在多项式时间内得到任意指定精度的解，算法1提供了强制路径算法的伪代码。

算法1　强制路径算法：$ {\boldsymbol{\varDelta}} $=Alg1 (G, w, p^*, δ)

输入：图G，边权重向量w，目标路径p^*，参数δ

输出：边权重扰动向量$ {\boldsymbol{\varDelta }}$

1) s ← first node in p^*

2) t ← last node in p^*

3) l ← length of p^*

4) P_l+δ ← ∅

5) w' ← w

6) while 1 do

7) 　 p ← shortest path from s to t with w'

8) 　 if p == p^* then

9) 　　 p ← scecond shortest path from s to t

10)　end if

11) 　 if length(p) ≥ length(p^*) + δ then

12) 　　 p ← $\phi $

13) 　 end if

14) 　 if p == $\phi $ then

15) 　　 break(跳出循环)

16) 　 end if

17) 　 P_l+δ ← P_l+δ∪{p}

18) 　 $ \Delta $ ← solution to (1)

19) 　 w' ← w +$ {\boldsymbol{\varDelta }}$

20) end while

强制路径问题考虑到了如何通过扰动非目标路径的边来实现最低成本的扰动和提高扰动的隐秘性。但是忽略了扰动路径时，扰动边数的增加和单边扰动无界限所带来的成本增加和扰动攻击曝光的风险。如在网络安全中，扰动更多的目标，或对某一目标进行无限扰动，不仅会增加隐私泄露和行动暴露的风险，从某种意义上也会增加扰动成本(扰动次数增加)。因此，每条边存在一定的扰动界限，对其进行有限的扰动更符合现实情况。

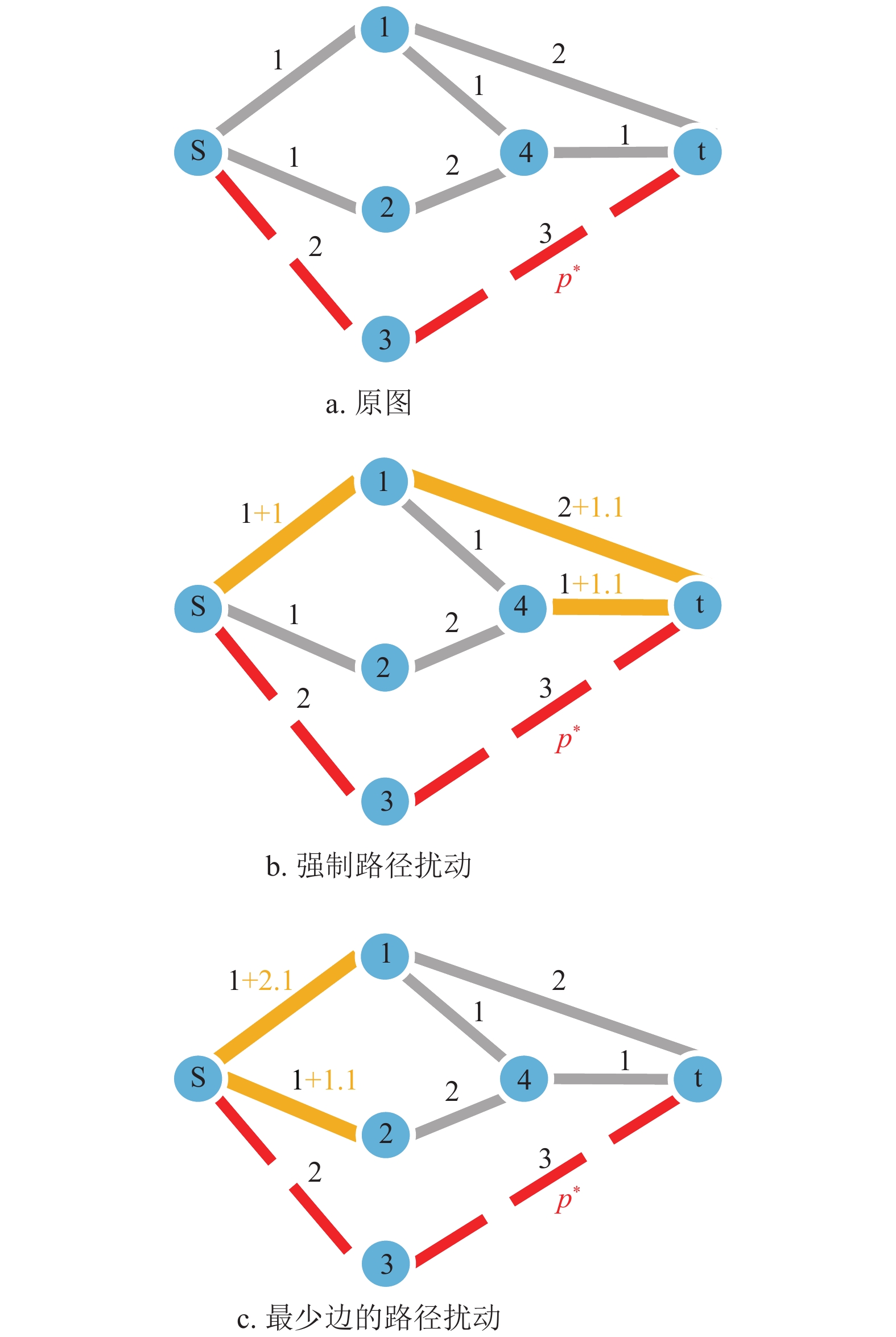
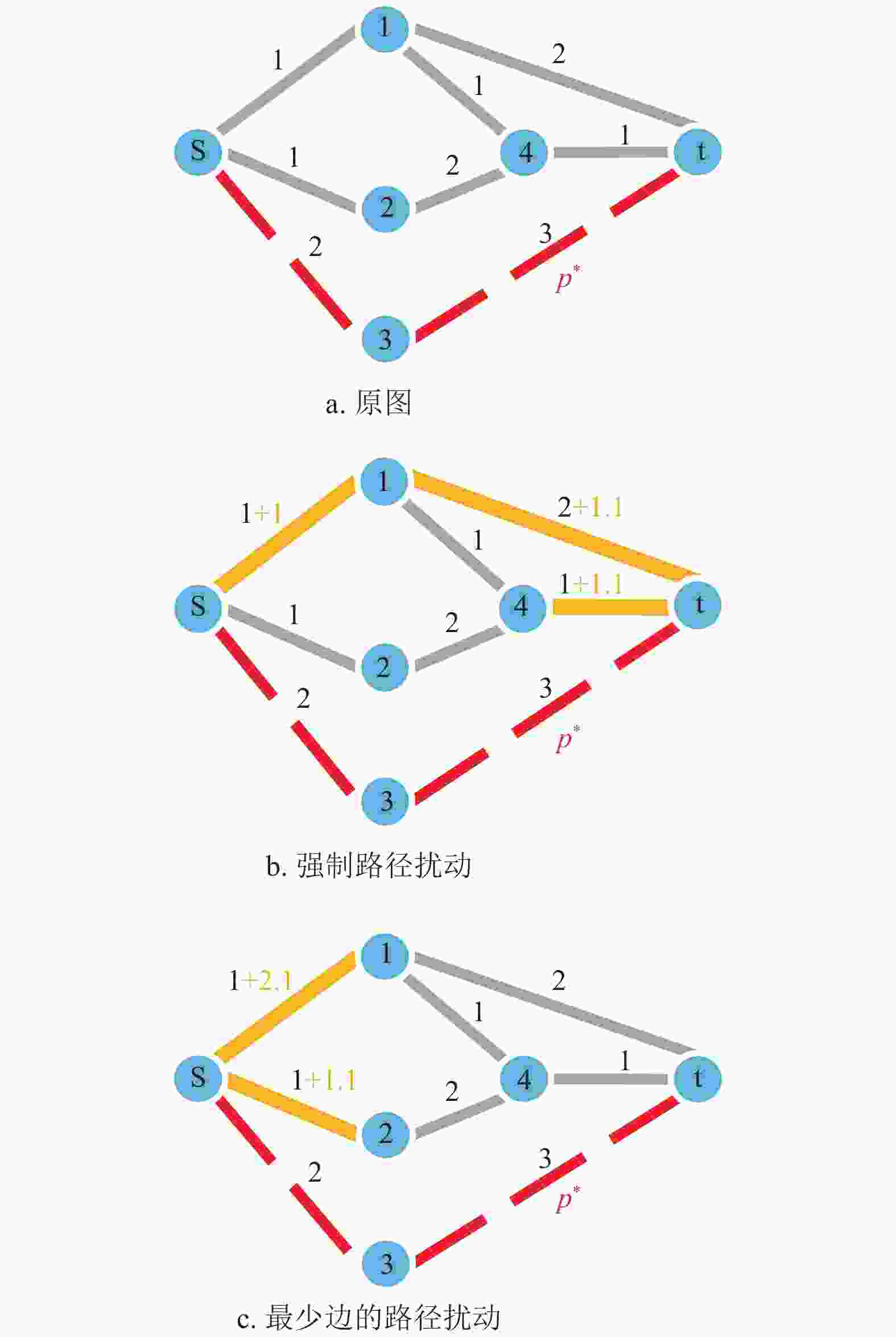
本文考虑的是基于最少边的路径扰动问题，其包含了对单边扰动限制的需求，同时降低扰动所需边数使得路径扰动问题更具隐蔽性和可操作性。如图1显示了两种不同扰动方式的结果图，其中通过基于最少边的路径扰动能够带来更优的扰动效果。图1a显示了最短路径扰动问题的一个图例，其中s、t分别表示源节点和目标节点，$ {p^*} $表示目标路径，设置扰动后的路径至少比$ {p^*} $大0.1(即$ \delta {\text{ = }}0.1 $)。图1b显示了强制路径问题中边扰动后的结果，扰动边数为3；图1c显示了基于最少边的路径扰动后的结果，扰动边数为2，总扰动成本为3.2，并且总扰动成本与图1b中最少的扰动成本相等。很显然：1) 图1c比图1b的扰动更隐秘；2) 在某些场合下，图1c比图1b的扰动更节约成本。如每条边的扰动都需要某台机器或某个人去操作，虽然总操作成本一样，但是图1c比图1b更少地利用物力或人力资源。接下来，将给出最少边扰动模型。

图  1  强制路径扰动和最少边的路径扰动的结果图

最少边的路径扰动问题类似于强制路径问题，不同之处在于扰动的结果和约束条件：不仅希望扰动成本的总和最小，且要求扰动所需的总边数最少，同时考虑每条边的扰动范围都有一个界限$ {h_i} $。这种差异对于实际问题的应用有着深刻的影响，在实际问题中，每条边的权重都有上下界限，不能被无限扰动，设定单条边扰动的界限，更具有合理性和可行性，同时随着扰动所需的边数减少，对扰动攻击而言更具隐蔽性，更节约实施成本。

该问题的目标是在确保扰动最少的边和使用最小的成本条件下，对图中路径上的边在可控范围内进行的加权处理，使得目标路径$ {p^*} $成为唯一的最短路径。基于最少边的路径扰动的结果是，从$ s $到$ t $除$ {p^*} $以外的所有路径都必须严格大于$ {p^*} $。所以主要有3个约束条件：1)所有路径上的边扰动后都不得超过界限$ {h_i} $的上界值；2)所有路径长度中小于或等于$ {p^*} $的路径都要被扰动；3)目标路径$ {p^*} $上的边不能被扰动。因此最少边的路径扰动问题公式化如下：

式中，$ {{\mathbf{1}}^{\rm T}}{\boldsymbol{\varDelta }} $和$ \parallel {\boldsymbol{\varDelta }}{\parallel _0} $分别表示扰动成本和扰动边数；$ \alpha $表示为调节参数；$ {h_i} $表示第i条边的边权重上界，所以约束条件1表示每条边不能无限地被扰动；约束条件2表示每条非目标路径的长度都要大于等于$ \ell + \delta $；约束条件3表示目标路径不能被扰动。

虽然式(2)相比式(1)，最主要的变化是多了一个零范数约束，但是该约束的增加使得原本问题变得极其复杂，因此需要寻求一种简单的方法进行求解。

在理论上，式(2)最小成本约束等价一范数约束，即$ {{\mathbf{1}}^{\rm T}}{\boldsymbol{\varDelta }} = \parallel {\boldsymbol{\varDelta }}{\parallel _1} $，最少边约束为零范数约束($ \parallel {\boldsymbol{\varDelta }}{\parallel _0} $)，在实际求解中，由于零范数的非凸性，往往应用一范数近似代替零范数^[19]($ \parallel {\boldsymbol{\varDelta }}{\parallel _1} \approx \parallel {\boldsymbol{\varDelta }}{\parallel _0} $)。因此在理论近似情况下，最小成本约束的优先级与最少边约束一致。实际应用中，在存在扰动上界的情况下，扰动最少边本身就可以带来扰动成本的降低，正如前面所分析最少边约束不仅可以带来扰动的隐秘性，还因操作个体的减少带来了成本的降低。

综上所述，式(2)中目标函数的最小成本约束的优先级要低于最少边约束。因此，式(2)的求解可以近似看作：在最少边扰动的情况下，实现扰动成本最小。即式(2)可以分为两个步骤：1) 基于最少边进行路径扰动；2) 已知扰动边的基础上，使得扰动成本最低。本文把式(2)求解近似转化成了两步走的形式。这个近似求解的过程，一方面消除了$ \alpha $这个参数对其的影响；另一方面，随着边数的增加，同时扰动更多边会带来更高的难度，也就是说目标函数关于扰动边数应该是非线性的，但是只要扰动边数越小目标函数也越小，本文两步走的近似过程就可以消除式(2)线性组合带来的不合理性。

最少扰动边生成的目标是扰动最少的边使得目标路径成为s到t之间所有路径中最短的。即：

因为，在此过程中只关注哪些边(最少的边)被扰动，并不关注扰动边所需扰动多少，而且每条边扰动具有上限。所以上述问题，等价为如何选取最少的边进行扰动(这个扰动量为每条边的最大扰动量)，使得目标路径最短。

设边的指示向量$ {\boldsymbol{S}} \in {\left\{ {0,1} \right\}^M} $表示为：$ E $中被扰动的边对应值为1，没有被扰动的边对应值为0；$ {\boldsymbol{h}} = {\left[ {{h_1},{h_2}, \cdots ,{h_M}} \right]^{\text{T}}} $表示每条边的扰动上界，则所有边被扰动的增量上界向量为：

则式(3)变成下面简单0-1规划问题：

式中，$ {\text{diag}}(*) $表示把向量变成矩阵，对角线元素为该向量对应元素。该问题的求解可以类似算法1进行求解。首先初始化路径集合$ {P_{\ell + \delta }} $，将从$ s $到$ t $的路径长度不大于$ {p^*} $的最短路径加入到集合$ {P_{\ell + \delta }} $中，通过0-1规划求解找到集合$ {P_{\ell + \delta }} $中每条路径上必须被扰动的边，即每条路径都至少有一条边增加权值；然后通过最短路径搜索找到被扰动后的网络中符合约束的最短路径，在迭代过程中不断将所有选中的路径加入到集合$ {P_{\ell + \delta }} $；最后集合中的全部路径被扰动后长度都足够大，输出边扰动向量${\boldsymbol{S}}$和满足约束路径集合$ P_{\ell + \delta }^{} $。算法2提供了最少扰动边算法的伪代码。

算法2　最少扰动边算法：S, P_l+δ =Alg2 (G,w,h,p^*,δ)

输入：图G = (V, E)，边权重向量w，边权界限向量h，目标路径p^*，参数δ

输出：扰动边指示向量S，扰动边集合P_l+δ

1) s, t, l ← first and last node, length in p^*

2) P_l+δ ← $\phi $

3) ${\boldsymbol{\varDelta } _{{\text{max}}}}$ ← h – w

4) w' ← w

5) while 1 do

6) 　 p ← shortest path from s to t with w'

7) 　 if p == p^* then

8) 　　 p ← scecond shortest path from s to t

9) 　 end if

10)　if length(p) ≥ length(p^* ) + δ then

11) 　　 p ← $\phi $

12)　end if

13)　if p == $\phi $ then

14) 　　 break (跳出循环)

15) 　 end if

16) 　 P_l+δ ← P_l+δ∪{p}

17) 　 S ← solution to 5)

18) 　 w' ← w + diag(S)∗${\boldsymbol{\varDelta } _{{\text{max}}}}$

19) end while

当选中哪些边进行扰动后，需要考虑具体扰动多少成本，即最小扰动成本约束。

在算法2中求解得到最少边扰动的边指示向量$ {\boldsymbol{S}} $时，假设每条边的扰动都是按照最大扰动上界计算的。实际上不需要这么大的成本，因此需要在已经确定的被扰动边基础上最小化所需的扰动成本。即：

其中$ {\varDelta _i}\left( {1 - {S_i}} \right) = 0 $约束，保证式(5)中没有被选中的边不进行扰动。

该算法的求解类似算法1，为了加快算法效率，可以不用搜索一条条最短路径加入到$ P_{\ell + \delta }^{} $中，初始加入路径可以为算法2中的集合$ P_{\ell + \delta }^{} $。首先迭代算法2求解得到$ {\boldsymbol{S}} $和$ P_{\ell + \delta }^{} $，通过线性规划得到满足集合$ P_{\ell + \delta }^{} $中所有路径所需的最小扰动成本；然后通过最短路径搜索寻找被扰动后的网络中是否还存在满足约束的最短路径，若存在将所选中的路径加入到集合$ {P_{\ell + \delta }} $中再进行迭代求解；最后使得被扰动后的结果图中，满足目标路径$ {p^*} $是唯一的最短路径。算法3提供了最小扰动成本算法的伪代码。

算法3　最小扰动成本算法：$\boldsymbol{\varDelta }$=Alg3 (G, w, h, p^*,δ)

输入：图G = (V, E)，边权重向量w，边权界限向量h，目标路径p^*，参数δ

输出：边权重扰动向量$\boldsymbol{\varDelta }$

1) s, t, l ← first and last node, length in p^*

2) S, P_l+δ = Alg2 (G, w, h, p^*, δ)

3) while 1 do

4) 　 $\boldsymbol{\varDelta }$ ← solution to 6)

5) 　 w' ← w +$\boldsymbol{\varDelta }$

6) 　 p ← shortest path from s to t with w'

7) 　 if p == p^* then

8) 　　 p ← scecond shortest path from s to t

9) 　 end if

10)　if length(p) ≥ length(p^* ) + δ then

11) 　　 p ← $\phi $

12)　end if

13)　if p == $\phi $ then

14) 　　 break (跳出循环)

15)　end if

16) 　 P_l+δ ← P_l+δ∪{p}

17) end while

最少扰动边算法和最小扰动成本算法共同组成了最少边扰动算法，用于求解最少边扰动模型和解决基于最少边的最短路径扰动问题。

本文在合成网络和真实网络上运行了最少边扰动算法和强制路径算法，所有选择的网络都是无向的，共使用了13个不同的网络模型，并对最终扰动所需的成本和边数进行了对比。

对于合成网络，使用5种不同的随机图模型： 随机网络^[20](Erdös-Rényi, ER)、小世界网络^[21](Watts-Strogatz, WS)、无标度网络^[22](Barabasi-Albert, BA)、二维网格网络^[17](Lattice, LAT)和完全图网络^[17](complete, COMP)。对于真实网络，选取了共8个加权和非加权网络。未加权网络包括电子邮件网络^[23](email)、电力网络^[24](power)、路由网络^[24](router)和自治系统网络^[25](autonomous system, AS)；加权网络包括科学家合作网络^[24](NetScience, NS)、爵士音乐人合作网络^[24](jazz)、美国航空网络^[24] (USAir)和美国城市道路网^[24](USAroadtNY)。

针对未加权网络进行人工加权设置，其中合成网络和未加权的真实网络，设置了3种不同的边加权方式：等权值、泊松权值和均匀权值。对于等权值，所有边的权重值都设为1；对于泊松权值，每条边e都有一个独立的随机权值，从速率参数为20的泊松分布中绘制一个值并加1得到该边的权重值；对于均匀权值，每条边e从整数1到41的均匀分布中选取一个值作为该边的权重值。

表1表示13个网络的基本信息，其中N为节点数，M为边数，$\left\langle k \right\rangle $为平均度，$\left\langle w \right\rangle $为所有边的平均权值，3种平均权值对应：等权值/泊松权值/均匀权值，w_min为边的最小权值，w_max为边的最大权值。

对于每个网络，针对目标路径$ {p^*} $的选择，在所有节点中随机选择源节点s和目标节点t，选择单条边扰动界限h的上界为该网络中最大边权值w_max的2倍，设置$ \delta $为0.001，其中USAir的最小边权值w_min为0.000 9，则设$ \delta $为0.000 1。

每次将最少边扰动算法和强制路径算法结果中的最小值作为基线值，并将另外一个算法的结果除以该基线值求解得到比例，作为两种算法性能的对比参照量。

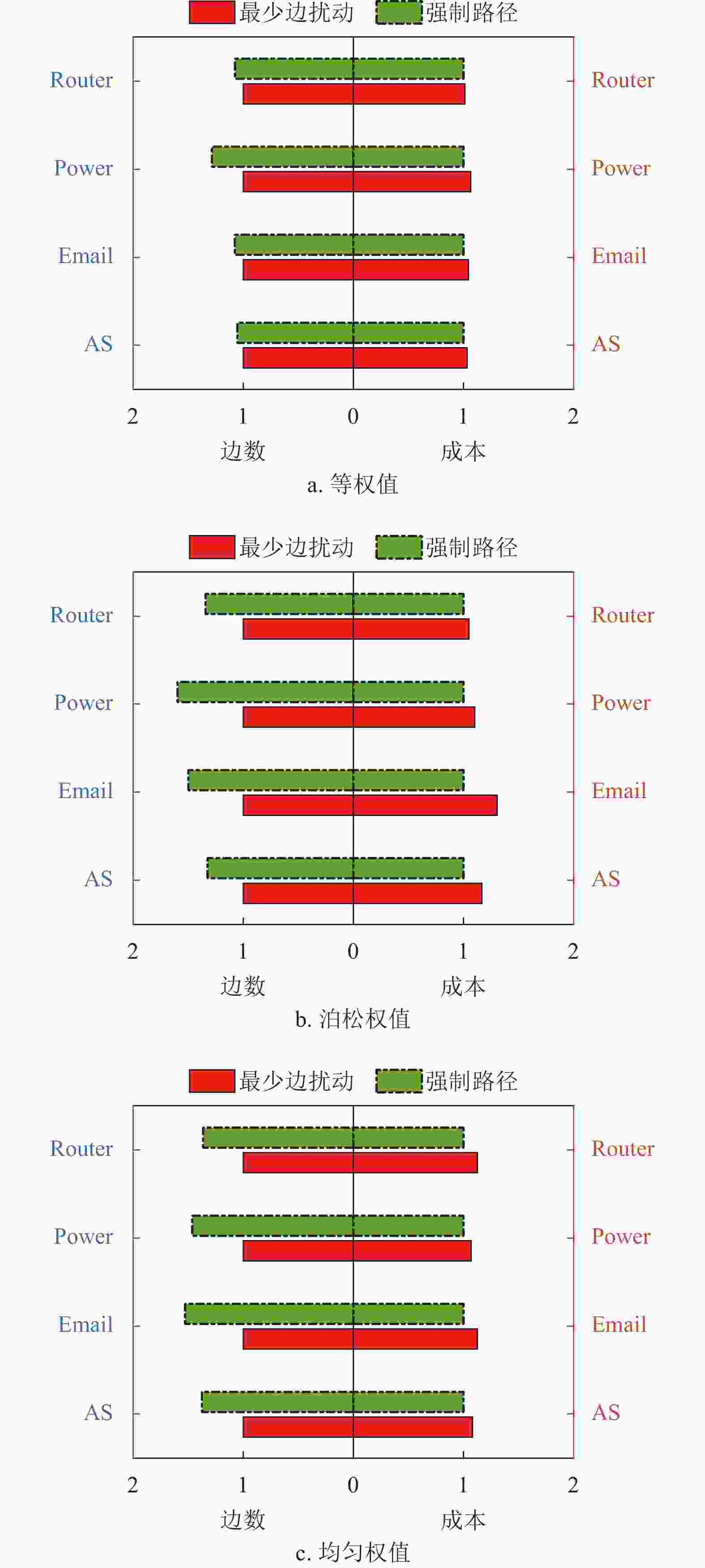
通过多次重复实验，最少边扰动算法的结果在扰动所需边数上的表现相对较好，扰动所需边数更少但成本有所增加，其中成本增长比例远小于边数减少比例。图2显示了在合成网络中扰动的成本和边数对比的结果；图3显示了在真实未加权网络中扰动的成本和边数对比的结果；图4显示了真实加权网络中扰动的成本和边数对比的结果，左边部分为所需边数对比，右边部分为所需成本对比，其中比例值为1表示该算法求得的边数或成本最少。

图  2  本文算法与强制路径算法在合成网络中对比

图  3  本文算法与强制路径算法在真实网络中对比

图  4  本文算法与强制路径算法在真实权值网络中对比

在所有实验中，通过使用最少边扰动算法，总体扰动边数的减少量有了实质性的提升。总体上，最少边扰动算法比强制路径算法所需边数平均减少了27.44%，强制路径算法比最少边扰动算法所需成本平均减少了7.24%，因为最少边扰动算法是以减少扰动边数为代价，会增加一定量的扰动成本。

对于合成网络，如图2所示，通过3种不同的边加权方式可以看出，本文中的最少边扰动算法有显著效果。特殊情况是当所有边的权值为相等时，在COMP网络上的扰动效果没有明显变化，此时的完全图就像一个极端的网络，每两个节点之间都有一条等长的边连接，所以每条边的重要性相同，无法通过集中选择重要性大的边来降低扰动的边数。当权值服从泊松分布和均匀随机分布时，随着边权重差异性的增加，最少边扰动算法明显降低了扰动边数，除COMP网络外，其中路径扰动算法所需的扰动边数是该算法的1.5倍以上。在选择扰动边时，最少边扰动算法最大限度地寻找能够通过扰动一条边使得多条路径成功被扰动的边，进而减少总体上的扰动边数。

对于真实网络，如图3所示，在Power网络中，因为节点之间存在更多的重叠邻居，所以最少边扰动算法在扰动时尽可能选择不同路径中的相同边来减少扰动的边数，相对于强制路径算法边数上平均减少了30.44%。总体上在4种网络中，增加少量扰动成本的同时扰动边数的减少量相对更加明显。

对于真实加权网络，如图4所示，相对于NS和Jazz合作网络，最少边扰动算法明显降低了USAir网络和USAroadtNY网络上扰动边数的总量。在USAroadtNY网络中，在扰动成本增量为1%的情况下，最少边扰动算法降低了39%的扰动边数。在道路网络中，网络分布更类似于LAT网络，聚集性的城市道路分布类似于网络，其中某些主要的路段被扰动后，对应的多条路径能够同时被扰动，在最少边扰动算法中，能够优先寻找道路网络中的关键边(起始目的地之间通行次数较多的路段)来减少总体扰动边数。如图5所示，通过在USAroadtNY道路网络上选取一条路径作为目标路径，用虚线标记，其中s、t分别为起点和终点，对两个地点之间进行危险品运输管控，引导承运商走指定目标路径对应的运输路线更有利于实施布控，黑色数字表示某路段的通行时间，分别用两种算法对s-t地点之间的路段进行扰动，右下图为最少边扰动算法的结果图，其结果在与强制路径算法扰动成本相等的同时，扰动边数减少了2条，在实际操作过程中，阻塞更少的路段意味着减少了更多的布控资源的投入。在USAir网络上扰动边数的减少量最为明显，可能受到中心枢纽的影响，在实际应用中，通过扰动大型机场之间的航空数据，能有效扰动更多条航行路线，以此来减少需要扰动边的次数，虽然增加了相应的扰动成本，但整体上提高了扰动的隐蔽性。

综上所述，在以扰动最少边为主要目标时，算法能够通过有效地扰动最少量的边来实现最短路径扰动的目的，在所有网络模型中，算法在成本上增加一小部分代价的同时，扰动边数上实现了较多的改善，所需扰动边数平均减少了27.44%，同时平均增加了8.13%的成本为代价。但在以扰动相对较少边为条件下，可以通过减少扰动次数来控制扰动成本，进而实现较少扰动成本下的最短路径扰动。同时可以根据实际问题中的需求，来控制最终路径扰动问题中的优化目标。

图  5  两种算法在 USAroadtNY 道路网络中对比

本文描述了复杂网络中最短路径的强制路径问题，提出了一个新的路径扰动问题——基于最少边的路径扰动，它对传统的路径问题进行了重要的补充，并为现实中的许多实际应用带来了实质性的好处。在最少边的路径扰动中，单条边的扰动范围有上下界，并且要保证以最少的边以及最小的成本来实现最短路径的扰动问题，因此，解决含有单边扰动界限的最少边路径扰动问题更难。为了解决这个问题，本文提出了一种最少边扰动算法，通过最少化扰动边和最小化扰动成本相结合来解决对应的路径扰动问题。在实验分析中，使用13个数据集，最少边扰动算法在扰动所需边数上的性能有明显提升。

在未来的研究中，对于路径扰动的多目标问题中，可以通过与其他优化算法进行结合，使得结果更接近最优解。近年来，随着网络阻断问题的发展，图攻击可以允许对边、节点属性或同时进行操作，所以在最短路径扰动的问题上，可以考虑对节点或边进行攻击，从而满足实际问题中的需求，这也是个重要的研究方向。

本文研究工作还得到农业生态大数据分析与应用技术国家地方联合工程研究中心开放项目(AE202006)的资助，在此表示感谢。