-
随着各应用领域的数据量呈爆炸式增长,物理世界、人类社会和网络空间中的数据不断连接和融合,催生了大数据时代的到来[1]。大数据时代给人们的生活和工作带来了无限的发展机遇,也引发了前所未有的挑战。一方面,通过对大数据的挖掘与分析,可以发现其中隐含的有价值的数据和信息;另一方面,大数据类型、结构、模式以及关系的复杂性是大数据区别于传统数据的根本所在,必将会带来不可预测的不确定性问题[2-3]。不确定性因素给处理大数据算法的准确性、高效性、安全性、鲁棒性带来了巨大挑战[4]。高效、安全、准确处理大数据所具有的复杂性和不确定性问题已经成为大数据知识发现的前提和关键。
现有的计算策略(如采样[5]、降维[6]、分治、特征提取[7]、分布式计算等)在处理具有复杂结构、超高维的大数据问题上需要消耗大量的计算资源。近年来兴起的增量学习[8] (Incremental Learning)通过处理连续传入的信息流实现新旧知识的整合、优化,进一步节约计算资源;粒计算[9] (Granular Computing) 通过将大数据中的信息粒化,将合适的粒度颗粒作为处理对象从而缩减数据规模,提高了解决大数据问题的质量和效率。然而,数据本身的不确定性和处理数据过程中的不确定性,不可避免地会导致这些计算策略的性能大大降低。值得注意的是,模糊集理论已经成为表示数据本身和处理数据过程中的各种不确定性的重要工具[10-11]:一方面,通过建立模糊规则减少原始数据中的不确定性[12];另一方面,直觉模糊集 (Intuitionistic Fuzzy Set, IFS) [13-14]引入犹豫度表示现实世界中的犹豫边界,能够更好地将存在于海量数据和各种类型数据转换中的不确定性以及模型学习计算中的不确定性定量、准确地描述。
量子计算是一种结合量子力学处理信息的方式,利用量子比特的存储能力和并行计算能力来提高处理大数据的计算效率,在处理大数据所具有的复杂性和不确定问题上有更大优势[15-16]。然而量子系统容易受到噪声干扰,这些噪声会影响量子比特和量子线路从而降低量子机器学习算法的性能[17]。在达到理想的纠错效果之前,参数化量子线路 (Parameterized-Quantum Circuit, PQC) 是一种实现量子算法和展示量子优势的具体方法,通过使用量子−经典混合系统找到问题的近似解[18-19]。
本文将“不确定性问题 + 直觉模糊集理论 + 量子计算”交叉融合,利用直觉模糊集理论易于刻画具有不确定性问题的优势,将大数据所具有的不确定性问题模糊化;引入量子计算理论,将模糊信息(即不确定性问题模糊化后的信息)量子化;以量子态作为信息处理单元,构建基于直觉模糊集理论的量子模糊信息管理数学模型(简称量子模糊信息管理数学模型),并给出了与此模型相关基础问题的定义。
-
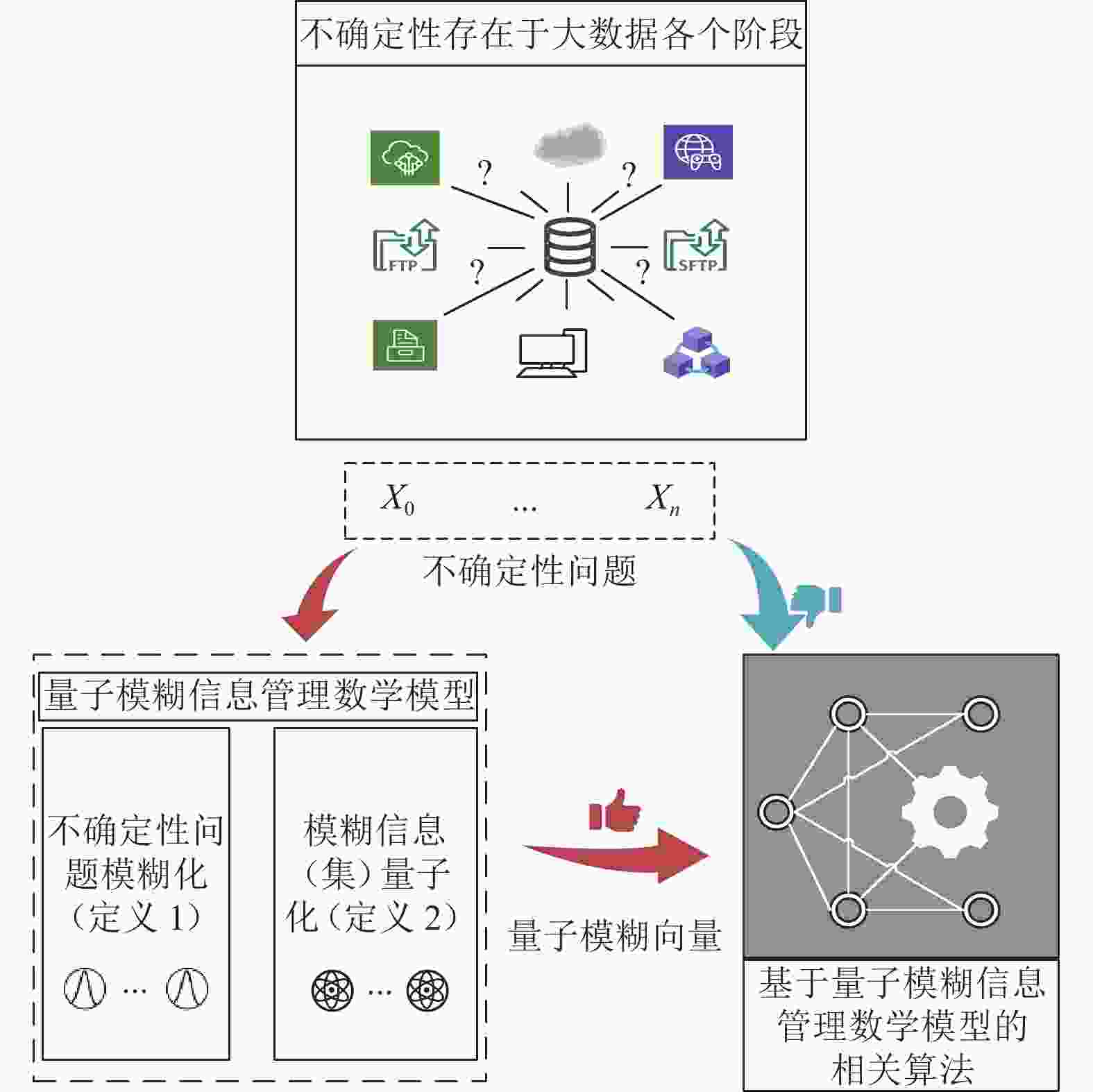
不确定性存在于大数据处理的各个阶段,简单的将数据作为量子机器学习算法的输入,不利于挖掘、分析出大数据所蕴含的信息。
为了高效处理大数据所具有的复杂性和不确定性问题,本文提出构建基于直觉模糊集理论的量子模糊信息管理数学模型,如图1所示,其具体思路:首先,通过直觉模糊集描述系统中的不确定元素,利用直觉模糊集中的隶属度、非隶属度和犹豫度来描述数据的不确定性,生成直觉模糊样本(即不确定性问题模糊化);然后,将直觉模糊样本编码为量子态得到量子模糊向量(即模糊信息量子化);最后,将量子模糊向量作为基于量子模糊信息管理数学模型的相关算法的输入。
-
设
$X$ 为量子模糊信息管理数学模型所研究的问题域,${x_i}(i = 1,2,\cdots, n)$ 表示所研究问题域中的不确定性元素。定义 1 不确定性问题模糊化:设
$X$ 为非空集合,$X$ 上的一个直觉模糊集定义为[21]:$$ A = \{ < {x_i},{\mu _A}({x_i}),{\nu _A}({x_i}) > \left| {{x_i} \in X} \right.\} $$ (1) 式中,
${\mu _A}({x_i}):X \to [0,1]$ ;${\nu _A}({x_i}):X \to [0,1]$ ,对$\forall {x_i} \in X$ ,有$0 \leqslant {\mu _A}({x_i}) + {\nu _A}({x_i}) \leqslant 1$ ,${\mu _A}({x_i})$ 为${x_i}$ 对直觉模糊集$A$ 的隶属度,${\nu _A}({x_i})$ 为${x_i}$ 对直觉模糊集$A$ 的非隶属度。由于专家在对不确定元素分配隶属函数时会犹豫,直觉模糊集$A$ 中用犹豫度表示这种犹豫程度:${\pi _A}({x_i}) = 1 - {\mu _A}({x_i}) - {\nu _A}({x_i})$ ,${\pi _A}({x_i})$ 为${x_i}$ 对直觉模糊集$A$ 的犹豫度,也称为直觉模糊指数。 -
定义 2 模糊信息(集)量子化(隶属度函数量子化):设
${x_i}$ 为问题域中的第$i$ 个元素,描述${x_i}$ 与直觉模糊集$A$ 的关系(即隶属于$A$ ,非隶属于$A$ ,犹豫于$A$ ),可以用量子态(称为量子模糊信息)表示为:$$ |{a_k}{\rangle _{{x_k}}} = \sum\limits_{k = 1}^3 {{\chi _k}} |k\rangle $$ (2) 式中,
$ {\chi _1} = \sqrt {{\mu _A}({x_i})} $ ,${\chi _2} = \sqrt {{\nu _A}({x_i})} $ ,$ {\chi _3} = $ $ \sqrt {{\pi _A}({x_i})} $ ,$ {\chi _1}^2 + {\chi _2}^2 + {\chi _3}^2 = 1 $ ,$|k\rangle $ 是第$k$ 个计算基态。若把
$X$ 中的所有不确定性元素$ {x_i}(i = 1,2,\cdots, n) \in X$ 量子化,则整个问题域$X$ 量子化后的量子态可以表示为:$$ |a{\rangle _x} = |{a_1}{\rangle _{{x_1}}} \otimes |{a_2}{\rangle _{{x_2}}} \otimes \cdots \otimes |{a_n}{\rangle _{{x_n}}} = \sum\limits_{j = 1}^{{3^n}} {{\beta _j}} |j\rangle $$ (3) 式中,不失一般性,将
$ |j\rangle $ 中的基态表示为$ |0\rangle $ ,$ |1\rangle $ ,$ |2\rangle $ ,则${\beta _j} = \displaystyle\prod\limits_{i = 1}^n {h({j_i})} $ ,$h({j_i}) = \left\{ {\begin{array}{*{20}{c}} {\sqrt {{\mu _A}({x_i})} ,{j_i} = 0} \\ {\sqrt {{\nu _A}({x_i})} ,{j_i} = 1} \\ {\sqrt {{\pi _A}({x_i})} ,{j_i} = 2} \end{array}} \right.$ 。则式(3)可以表示为:$$\begin{split} & |a{\rangle _x} = \sum\limits_{j = 1}^{{3^n}} {{\beta _j}} |j\rangle = {\beta _1}|000 \cdots 00\rangle + {\beta _2}|000 \cdots 01\rangle + \\ &\qquad\quad {\beta _3}|000 \cdots 02\rangle + \cdots + {\beta _{{3^n}}}| 222 \cdots 22\rangle \end{split} $$ (4) 式中,
$ {({\beta _j})^2} = {\left( {\displaystyle\prod\limits_{i = 1}^n {h({j_i})} } \right)^2} = {h^2}({j_1}) {h^2}({j_2}) $ $ \cdots {h^2}({j_n})$ 。问题域$X$ 与直觉模糊集$A$ 中的不确定性元素分为3种情况。1)当
$j = 1$ 时,即$|j\rangle $ 中所有态为$|0\rangle $ ,${({\beta _1})^2} = \displaystyle\prod\limits_{i = 1}^n {{\mu _A}({x_n})} $ ,${({\beta _1})^2}$ 是问题域$X$ 中所有元素都隶属于直觉模糊集$A$ 的程度,${({\beta _1})^2}$ 越大,问题域$X$ 隶属于直觉模糊集$A$ 的程度越大。2)当
$j = \dfrac{{{3^n} - 1}}{2} + 1$ 时,即$|j\rangle $ 中所有态为$|1\rangle $ ,${\Big( {{\beta _{\tfrac{{{3^n} - 1}}{2} + 1}}} \Big)^2} = \displaystyle\prod\limits_{i = 1}^n {{\nu _A}({x_i})}$ ,${\Big( {{\beta _{\tfrac{{{3^n} - 1}}{2} + 1}}} \Big)^2}$ 是问题域$X$ 中所有元素都不隶属于直觉模糊集$A$ 的程度,${\Big( {{\beta _{\tfrac{{{3^n} - 1}}{2} + 1}}} \Big)^2}$ 越大,问题域不隶属于直觉模糊集$A$ 的程度越大。3)当
$j = {3^n}$ 时,即$|j\rangle $ 中所有态为$|2\rangle $ ,$ {\left( {{\beta _{{3^n}}}} \right)^2} = \displaystyle\prod\limits_{i = 1}^n {{\pi _A}({x_i})} $ ,$ {\left( {{\beta _{{3^n}}}} \right)^2} $ 是问题域$X$ 中所有元素都犹豫于直觉模糊集$A$ 的程度,$ {\left( {{\beta _{{3^n}}}} \right)^2} $ 越大,问题域犹豫于直觉模糊集$A$ 的程度越大。因此,对于量子态
$|\alpha {\rangle _X} = \displaystyle\sum\limits_{j = 1}^{{3^n}} {{\beta _j}} |j\rangle $ ,如果$ j \to 1 $ ,可以判定问题域$X$ 隶属于直觉模糊集$A$ ;如果$ j \to \dfrac{{{3^n} - 1}}{2}{\text{ + }}1 $ ,可以判定问题域$X$ 不隶属于直觉模糊集$A$ ;如果$ j \to {3^n} $ ,可以判定问题域$X$ 犹豫于直觉模糊集$A$ 。由定义1和定义2可知,借助于直觉模糊集理论,把
$X$ 中具有不确定性问题的元素$ {x_i}(i = 1,2,\cdots $ $ ,n) $ 用模糊直觉理论的隶属度、非隶属度和犹豫度来描述(不确定性问题模糊化),比较客观地反映了不确定性元素的实际情况;同时结合量子计算处理复杂性和不确定性问题的高效率优势,将不确定性问题模糊化后的信息量子化,从而建立量子模糊信息管理数学模型。 -
定义 3 量子模糊向量:假定问题域
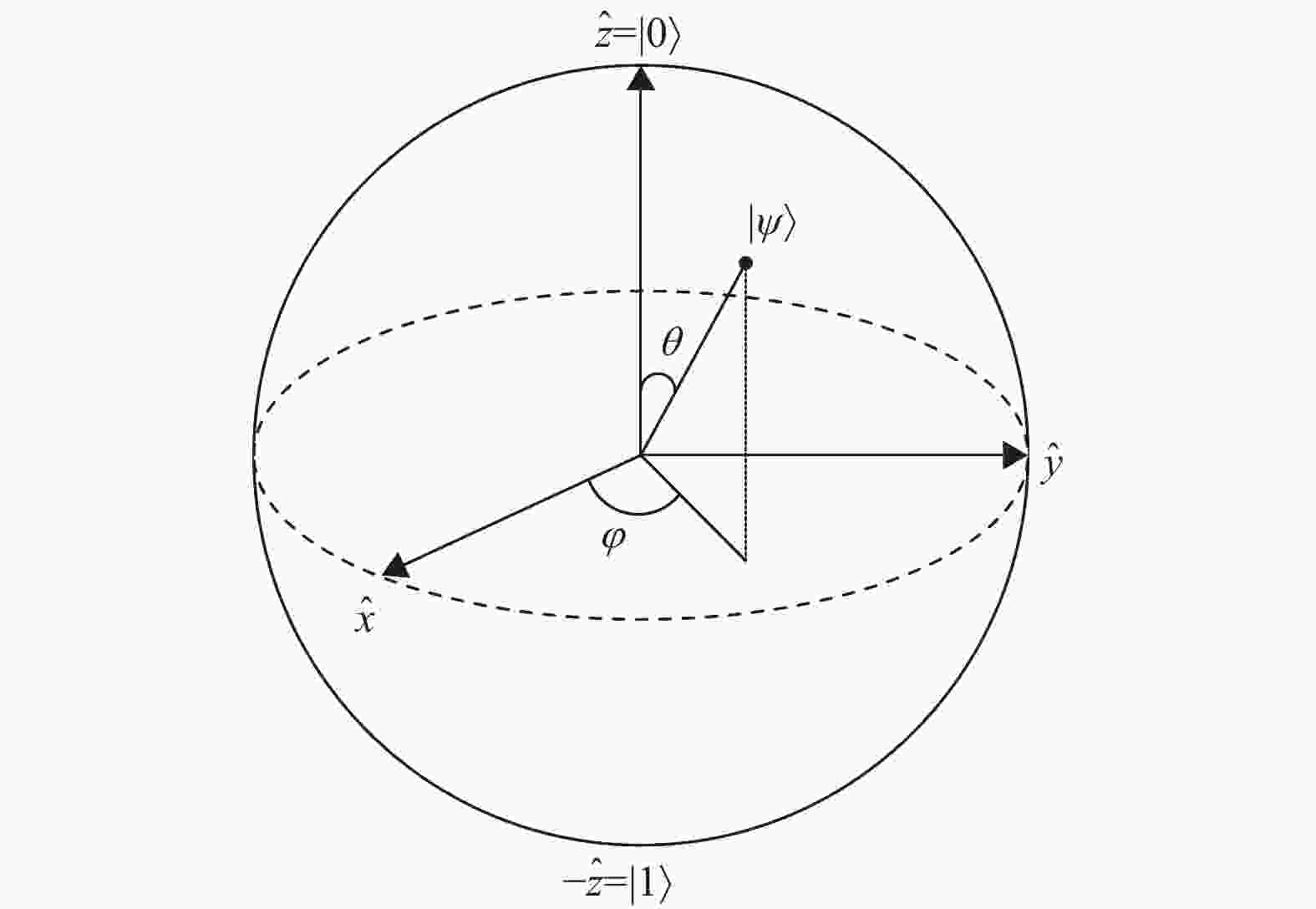
$X$ 中的第$j$ 个不确定元素为${x_j}$ ,且${\mu _A}({x_j})$ 为${x_j}$ 对直觉模糊集$A$ 的隶属度,${\nu _A}({x_j})$ 为${x_j}$ 对直觉模糊集$A$ 的非隶属度,${\pi _A}({x_j})$ 为${x_j}$ 对直觉模糊集$A$ 的犹豫度。则不确定元素${x_j}$ 量子化后的量子态用向量表示为:$ ( \sqrt {{\mu _A}({x_j})} ,\sqrt {{\nu _A}({x_j})} , \sqrt {{\pi _A}({x_j})} ) = (\cos {\phi _j} \sin {\theta _j}, $ $ \sin {\phi _j} \sin {\theta _j},\cos {\theta _j}) = ({x_j},{y_j},{z_j}) $ ,且$ {\mu _A}({x_j}) + $ $ {\nu _A}({x_j}) + {\pi _A}({x_j}) = {x_j}^2 + {y_j}^2 + {z_j}^2 = 1 $ 。实际上,量子模糊向量是三维球面上的任意一点。为了更有效地描述量子化后的模糊信息,利用密度矩阵来表示不确定元素
${x_j}$ 的量子模糊信息,则使用密度矩阵表示${x_j}$ 的量子模糊信息为:$$\begin{split} &\quad {{{\boldsymbol{\rho }}_j}}{ = \frac{{I + {{\boldsymbol{\sigma }}_x} {x_j} + {{\boldsymbol{\sigma }}_y} {y_j} + {{\boldsymbol{\sigma }}_z} {z_j}}}{2}} =\\ &\qquad { \left[ {\begin{array}{*{20}{l}} {\dfrac{{1 + {z_j}}}{2}}&{\dfrac{{x - i{y_j}}}{2}} \\ {\dfrac{{{x_j} + i{y_j}}}{2}}&{\dfrac{{1 - {z_j}}}{2}} \end{array}} \right]} =\\ &\qquad { \left[ {\begin{array}{*{20}{l}} {\dfrac{{1 + \cos {\theta _j}}}{2}}&{\dfrac{{{\psi _A} \sin {\theta _j}}}{2}} \\ {\dfrac{{{\psi _B} \sin {\theta _j}}}{2}}&{\dfrac{{1 - \cos {\theta _j}}}{2}} \end{array}} \right]} =\\ & \qquad \left( {\cos \frac{{{\theta _j}}}{2}|0\rangle + {{\rm{e}}^{{\rm{i}}\phi }} \sin \frac{{{\theta _j}}}{2}|1\rangle } \right) \times \\ & \left( {\cos \frac{{{\theta _j}}}{2}|0\rangle + {{\rm{e}}^{ - {\rm{i}}\phi }} \sin \frac{{{\theta _j}}}{2}|1\rangle } \right) = |{\psi _j}\rangle \langle \psi _j^\dagger | \end{split} $$ (5) 式中,
$ {\psi _A} = (\cos {\phi _j} - {\rm{i}}\sin {\phi _j}) \sin {\theta _j} $ ;$ {\psi _B} = (\cos {\phi _j} $ $ + i\sin {\phi _j}) \times \sin {\theta _j} $ ;${\sigma _x}$ ,${\sigma _y}$ ,${\sigma _z}$ 分别表示PauliX,PauliY和PauliZ矩阵。此时,量子模糊信息可以表示为:$$ \begin{split} &\quad |{\psi _j}\rangle = \cos \frac{{{\theta _j}}}{2}|0\rangle + {{\rm{e}}^{{\rm{i}}{\phi _j}}} \sin \frac{{{\theta _j}}}{2}|1\rangle = \\ & \cos \frac{{{\theta _j}}}{2}|0\rangle + (\cos {\phi _j} + i \sin {\phi _j}) \sin \frac{{{\theta _j}}}{2}|1\rangle \end{split} $$ (6) 式中,
$0 \leqslant {\theta _j} \leqslant {\text π} $ ,$0 \leqslant {\phi _j} \leqslant 2 {\text π}$ 。对应量子态的Bloch球,如图2所示。若
$X$ 中所有不确定元素转换成量子模糊信息后,可通过计算$ \cos \dfrac{{{\theta _j}}}{2} $ 和$ {{\rm{e}}^{i{\phi _j}}} \sin \dfrac{{{\theta _j}}}{2} $ 得到量子模糊信息的隶属函数如下:$$ \left\{ {\begin{array}{*{20}{l}} {\sqrt {{\mu _A}({x_j})} = \cos {\phi _j}\sin {\theta _j} = \cos {\phi _j} \times 2 \sin \dfrac{{{\theta _j}}}{2} \cos \dfrac{{{\theta _j}}}{2}} \\ {\sqrt {\nu {}_A({x_j})} = \sin {\phi _j}\sin {\theta _j} = \sin {\phi _j} \times 2 \sin \dfrac{{{\theta _j}}}{2} \cos \dfrac{{{\theta _j}}}{2}} \\ {\sqrt {{\pi _A}({x_j})} = \cos {\theta _j} = 2{{\cos }^2}\dfrac{{{\theta _j}}}{2} + 1} \end{array}} \right. $$ (7) 特别地,当犹豫度
${\pi _A}({x_j}) = {(\cos {\theta _j})^2} = 0$ ,即${\theta _j} = \dfrac{{\text π}}{2}$ 时,直觉模糊集就退化成Zadeh模糊集,则有:$$\begin{split} &\qquad\qquad |{\psi _j}\rangle = \cos \frac{{{\theta _j}}}{2}|0\rangle + {{\rm{e}}^{i{\phi _j}}} \sin \frac{{{\theta _j}}}{2}|1\rangle =\\ &\qquad\qquad {{\rm{e}}^{i\tfrac{{{\phi _j}}}{2}}} ({{\rm{e}}^{ - i\tfrac{{{\phi _j}}}{2}}}\frac{{\sqrt 2 }}{2}|0\rangle + {{\rm{e}}^{i\tfrac{{{\phi _j}}}{2}}}\frac{{\sqrt 2 }}{2}|1\rangle ) =\\ & {{\rm{e}}^{i\tfrac{{{\phi _j}}}{2}}} ((\cos \frac{{{\phi _j}}}{2} - i\sin \frac{{{\phi _j}}}{2}) |0\rangle + (\cos \frac{{{\phi _j}}}{2}{\text{ + }}i\sin \frac{{{\phi _j}}}{2}) |1\rangle ) =\\ &\qquad\qquad {{\rm{e}}^{i\tfrac{{{\phi _j}}}{2}}} (\cos \frac{{{\phi _j}}}{2}| + \rangle + i\sin \frac{{{\phi _j}}}{2}| - \rangle ) \end{split}$$ (8) 式中,
$ | + \rangle = \dfrac{{\sqrt 2 }}{2} (|0\rangle + |1\rangle ) $ ,$ | - \rangle = \dfrac{{\sqrt 2 }}{2} (|0\rangle - |1\rangle ) $ 。此时,可以通过计算角度$ {\phi _j} $ ,求得隶属度$ {\mu _A}({x_j}) = ( $ $ \cos {\phi _j}\sin {\theta _j}{)^2} $ 和非隶属度$ \nu {}_A({x_j}) = (\sin {\phi _j}\sin {\theta _j} $ $ {)^2} $ 。 -
定义 4 量子模糊信息熵:根据定义2,假设问题域
$X$ 中不确定元素${x_j}(j = 1,2,\cdots,n)$ 转换成量子模糊信息后可表示为$ {\rho _j} = |{\psi _j}\rangle \langle {\psi _j}| $ ,$ |{\psi _j}\rangle = \cos \dfrac{{{\theta _j}}}{2} $ $ |0\rangle + {{\rm{e}}^{i{\phi _j}}} \sin \dfrac{{{\theta _j}}}{2}|1\rangle $ ,则不确定性元素${x_j}$ 的量子模糊信息熵表示为:$$ S({{\boldsymbol{\rho }}_j}) = S(|{\psi _j}\rangle \langle {\psi _j}|) = - {\rm{tr}}({{\boldsymbol{\rho }}_j}\log {{\boldsymbol{\rho }}_j}) $$ (9) 式中,若
$ {\lambda _{j,x}} $ 是$ {{\boldsymbol{\rho }}_j} $ 的特征值,则量子模糊信息熵的定义重新描述为:$$ S({{\boldsymbol{\rho }}_j}) = S(|{\psi _j}\rangle \langle {\psi _j}|) = - \sum\limits_{j,x} {{\lambda _{j,x}}\log {\lambda _{j,x}}} $$ (10) 定义5 量子模糊信息熵:设
$ {\rho _i} $ 和$ {\rho _j} $ 是量子模糊信息中的密度算子,$ {\rho _i} $ 相对于$ {\rho _j} $ 的量子模糊信息相对熵定义为:$$ S(\left. {{\rho _i}} \right\|{\rho _j}) = {\rm{tr}}({\rho _i}\log {\rho _i}) - {\rm{tr}}({\rho _j}\log {\rho _j}) $$ (11) 量子相对熵是区分两个量子状态之间的度量,量子模糊信息相对熵将量子相对熵扩展到量子模糊信息领域。
-
定义 6 量子模糊集之间的迹距离:设
$B$ 和$C$ 是给定问题域$X$ 上的直觉模糊子集,将$B$ 和$C$ 中所有不确定元素量子化后得到量子态$ {\rho _B} $ 和$ {\rho _C} $ ,则量子模糊集之间的迹距离定义为:$$ d({\rho _B},{\rho _C}) = \frac{1}{2}{\rm{tr}}\left| {{\rho _B} - {\rho _C}} \right| $$ (12) 衡量两个量子状态有多接近,除了用迹距离作为距离度量,还可以采用保真度作为度量方法。
定义 7 量子模糊集之间的保真度:设
$B$ 和$C$ 是给定问题域$X$ 上的直觉模糊子集,将$B$ 和$C$ 中所有不确定元素量子化后得到量子态$ {\rho _B} $ 和$ {\rho _C} $ ,则量子模糊集之间的保真度定义为:$$ F({\rho _{_B}},{\rho _{_C}}) = {\rm{tr}}\sqrt {{\rho _{_B}}^{\tfrac{1}{2}}{\rho _{_C}}{\rho _{_B}}^{\tfrac{1}{2}}} $$ (13) 在式(12)和式(13)中,
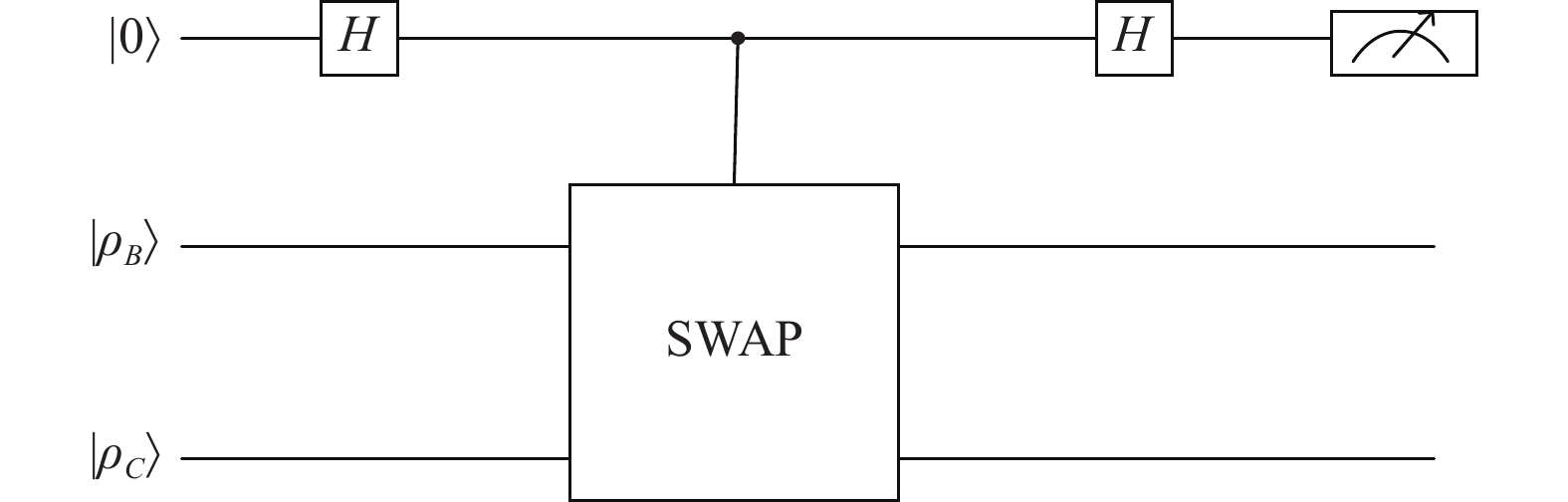
$ {\rho _{_B}} = |\alpha {\rangle _B}\langle \alpha {|_B} $ ,$ {\rho _{_C}} = |\alpha {\rangle _C}\langle \alpha {|_C} $ 。其中,$ |\alpha {\rangle _B} = \displaystyle\sum\limits_{j = 1}^{{3^{(B,n)}}} {{\beta _j}} |j\rangle $ ,$ |\alpha {\rangle _C} = \displaystyle\sum\limits_{j = 1}^{{3^{(C,n)}}} {{\beta _j}} |j\rangle $ ,$ (B,n) $ 与$ (C,n) $ 表示$B$ 和$C$ 中的不确定元素的个数。除了使用迹距离与保真度度量量子模糊集之间的距离,还可以使用Swap-test量子电路衡量量子态
$ {\rho _{_B}} $ 和$ {\rho _{_C}} $ 之间的相似程度[20],如图3所示。 -
为了验证量子模糊信息管理数学模型的可行性、合理性和有效性,使用Iris数据集[21]在Pennylane[22]量子计算框架下进行实验。具体来说,基于量子模糊信息管理数学模型构建混合量子−经典模糊神经网络,通过模糊层将数据进行模糊化处理,减少数据中的不确定性;同时将数据编码为量子态(量子模糊向量)作为量子神经网络的输入。实验表明,基于量子模糊信息管理数学模型的量子模糊神经网络面对不确定性数据时的性能优于量子神经网络。
-
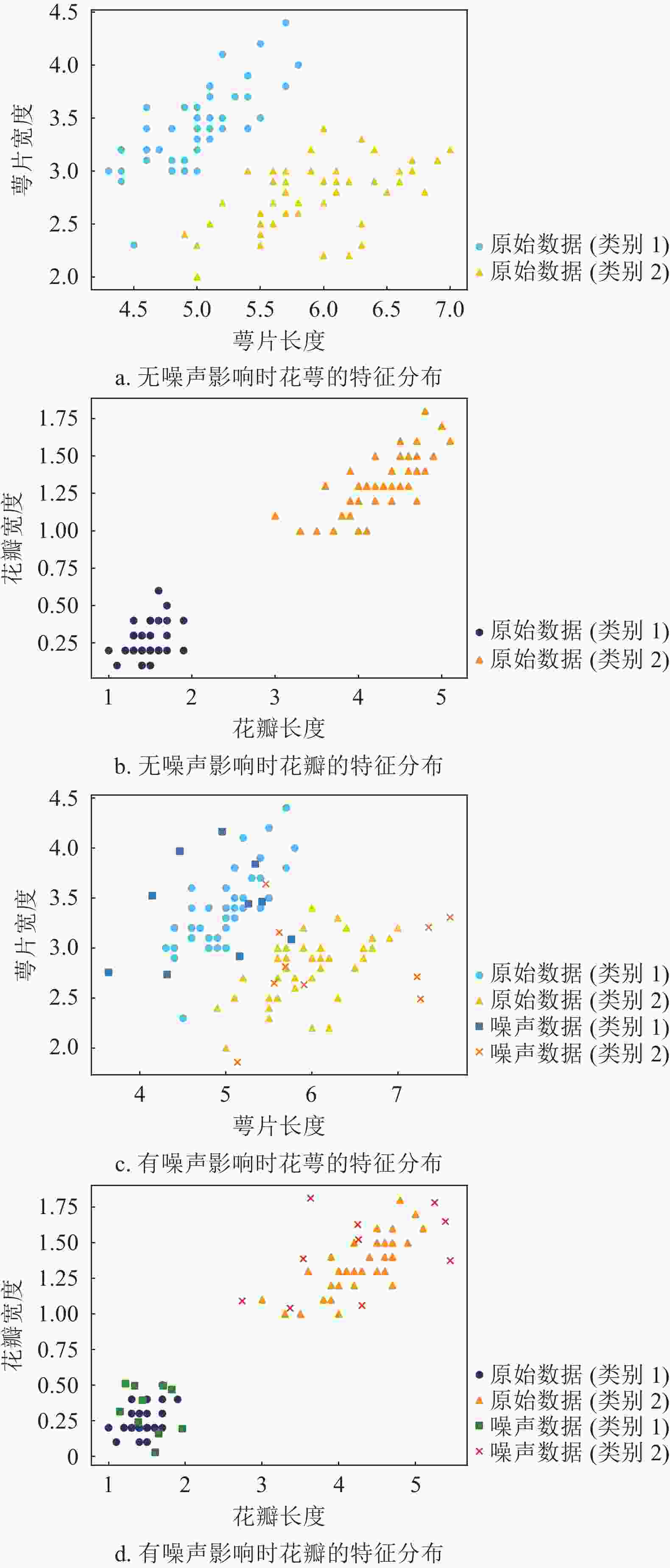
由于量子计算模拟环境使用的资源较多,在本实验中选取数据集中的前100个样本(即山鸢尾与杂色鸢尾)打乱后进行实验,选择30%的样本作为测试集,验证算法的准确性。对于数据的不确定性模拟,随机选取Iris数据集中的部分样本添加一定大小的噪声扰动。噪声样本中每个特征值都会根据扰动大小发生改变。本文选择噪声样本数量为
${\text{\{ }}10,15,20,25,30,35,40,45{\text{\} }}$ 、扰动大小为$ \{ 0.1, 0.2, 0.3,0.4,0.5\} $ 进行实验。图4展示了随机选择30个噪声样本,噪声扰动大小为0.2时,噪声对数据的影响。 -
正如前文所述,对于不确定性的数据,模型首先需要通过隶属度、非隶属度和犹豫度来描述数据的不确定性。根据文献[4,23],本实验使用高斯函数作为隶属度函数,将输入变量进行直觉模糊化处理,结合实际情况将模型中的直觉指数(即犹豫度)设置为0.1。模糊化操作的最后一步是将所有特征的隶属度进行AND模糊逻辑运算。之后,模型需要将模糊化后的数据转化为量子态。根据定义2,本文采用振幅编码[24-25]将模糊样本编码成量子态(量子模糊向量)作为量子神经网络的输入。
采用文献[24]提出的量子神经网络电路模型作为比较基准,量子神经网络中用于训练的线路称为ansatz。采用StronglyEntanglingLayers[24]作为ansatz线路,层数设置为5层,在数值模拟中通过parameter-shift rule[26-27]获得量子线路中的梯度值,量子线路中的参数更新借助Pennylane Tensorflow 插件,将量子电路转换为Kears层并添加到经典层中。对于整个混合量子−经典模糊神经网络,迭代轮次为30,批量大小设置为5,采用交叉熵作为损失函数,利用Adam自适应优化器[28]进行优化,学习率为0.01。为公平比较量子模糊信息管理数学模型的有效性,将未进行模糊化操作的数据直接作为量子神经网络[24]的输入,量子神经网络的结构以及参数设置与混合量子−经典模糊神经网络相同。
-
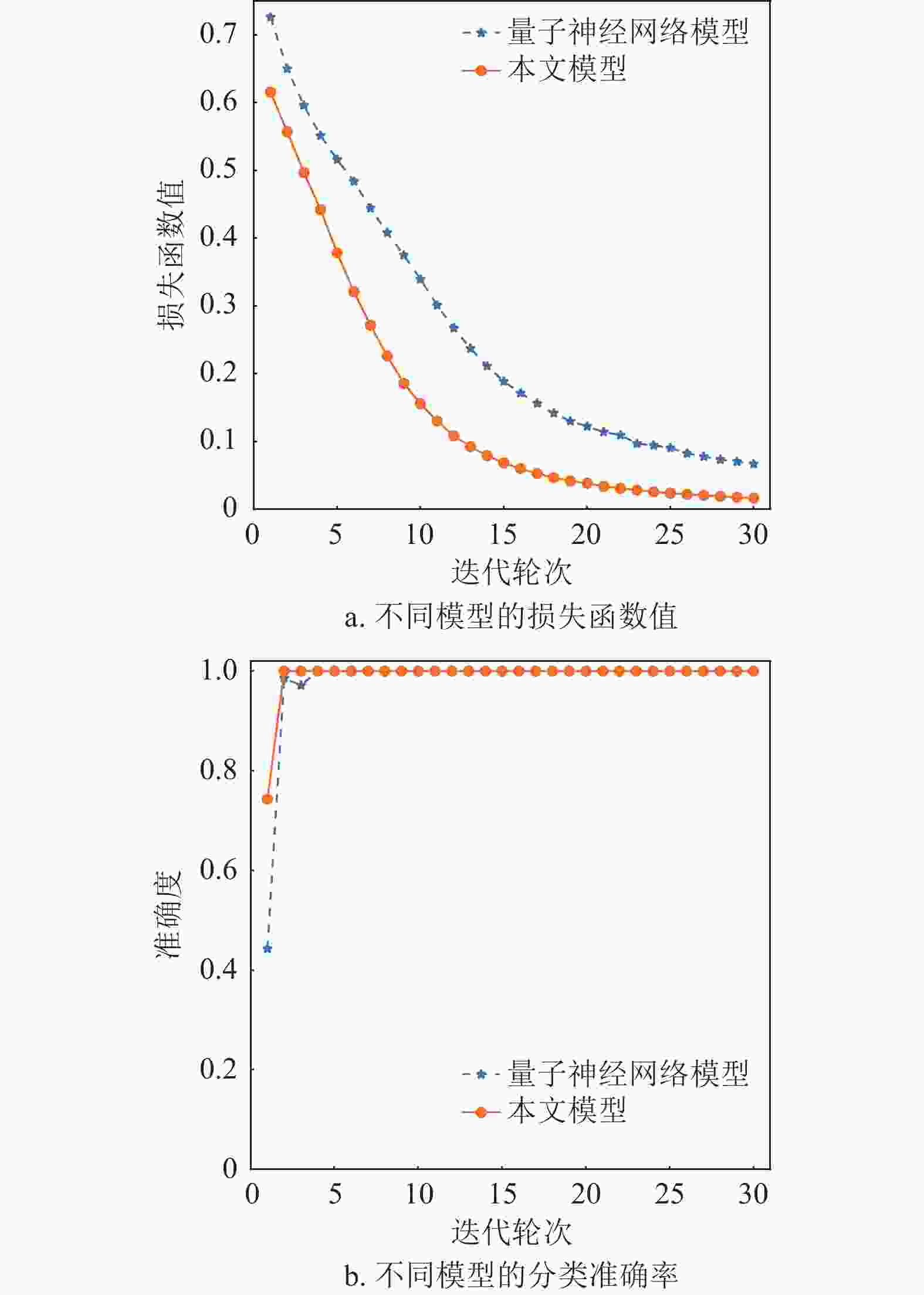
采用量子模糊信息管理数学模型建模后的量子模糊神经网络模型与纯量子神经网络模型在未受噪声干扰影响下的训练结果如图5所示。
在未添加噪声样本时,两种模型在Iris分类任务中表现出色,准确率达到100%。但随着噪声样本数量以及噪声扰动的增加,未经过量子模糊信息管理数学模型建模的量子神经网络准确率不断降低,而本文模型几乎不受噪声干扰,面对数据中的不确定性因素有更好的性能表现。
表 1 面对不同噪声样本数量以及噪声扰动大小时量子神经网络模型的准确度
% 噪声样本
数量噪声扰动大小 0.1 0.2 0.3 0.4 0.5 10 98.34±1.66 98.34±1.66 94.50±2.17 94.50±2.17 92.92±1.24 15 91.66±2.41 92.67±1.83 90.56±1.10 91.67±1.66 92.46±0.79 20 91.25±0.41 94.16±2.17 94.50±2.17 94.50±2.17 91.67±1.66 25 94.50±2.17 94.50±2.17 93.09±1.41 89.17±2..67 88.33±1.66 30 90.83±0.83 91.25±1.66 91.08±1.01 90.41±1.26 88.75±0.42 35 86.67±3.33 85.00±1.67 86.67±3.33 86.25±0.42 86.67±2.08 40 91.67±1.66 91.67±1.66 91.67±1.66 91.67±1.66 91.67±1.66 45 88.75±2.92 89.17±2.50 88.87±0.27 87.91±0.42 85.54±2.37 表 2 面对不同噪声样本数量以及噪声扰动大小时量子模糊神经网络的准确度
% 噪声样本
数量噪声扰动大小 0.1 0.2 0.3 0.4 0.5 10 100 100 100 100 100 15 100 100 100 100 100 20 100 100 100 100 100 25 100 100 100 99.90±0.03 99.87±0.20 30 100 100 100 99.93±0.02 100 35 100 100 100 99.83±0.12 99.50±0.33 40 100 100 100 99.80±0.05 99.34±0.83 45 100 100 98.34±1.66 98.34±1.66 99.17±0.83 -
针对如何高效、准确处理大数据所具有的复杂性、不确定性问题,本文提出了基于直觉模糊集理论的量子模糊信息管理数学模型。一方面,借助直觉模糊集理论直观、定量、准确地反映大数据中不确定元素的实际情况;另一方面,结合量子计算在处理复杂性和不确定性问题上具有高效率的优势,建立起了实际可行的量子模糊信息管理数学模型。在此基础上,对相关基础问题进行了研究与分析。最后,仿真实验表明,面对不确定性环境,利用量子模糊信息管理数学模型建模后有更好的性能表现。在一定程度上说明将“不确定性问题 + 直觉模糊集理论 + 量子计算”进行交叉融合研究是可行的,为研究量子模糊人工智能算法奠定了理论和实践基础。
Research on Mathematical Model of Quantum Fuzzy Information Management
-
摘要: 为了高效处理大数据所具有的复杂性和不确定问题,将“不确定性问题 + 直觉模糊集理论 + 量子计算”交叉融合,构建基于直觉模糊集理论的量子模糊信息管理数学模型。为了验证该模型的可行性、合理性和有效性,设计了不确定性环境下基于参数化量子线路的量子模糊神经网络仿真实验。实验结果表明,基于该模型的量子模糊神经网络模型能更客观、准确、全面地反映不确定性问题中各对象所蕴含的知识信息,从而提高算法处理大数据的准确性。Abstract: In order to efficiently deal with the complexity and uncertainty of big data, this paper integrates “uncertainty problem + intuitionistic fuzzy set theory + quantum computing”, to build a quantum fuzzy information management mathematical model based on intuitionistic fuzzy set theory. To verify the feasibility, rationality and validity of this model, a simulation experiment of quantum fuzzy neural network based on parameterized quantum circuit is designed under uncertainty environment. The experimental results show that the quantum fuzzy neural network based on this model can more objectively, accurately and comprehensively reflect the knowledge information contained in each object in the uncertainty problem, and improve the accuracy of the algorithm processing big data.
-
表 1 面对不同噪声样本数量以及噪声扰动大小时量子神经网络模型的准确度
% 噪声样本
数量噪声扰动大小 0.1 0.2 0.3 0.4 0.5 10 98.34±1.66 98.34±1.66 94.50±2.17 94.50±2.17 92.92±1.24 15 91.66±2.41 92.67±1.83 90.56±1.10 91.67±1.66 92.46±0.79 20 91.25±0.41 94.16±2.17 94.50±2.17 94.50±2.17 91.67±1.66 25 94.50±2.17 94.50±2.17 93.09±1.41 89.17±2..67 88.33±1.66 30 90.83±0.83 91.25±1.66 91.08±1.01 90.41±1.26 88.75±0.42 35 86.67±3.33 85.00±1.67 86.67±3.33 86.25±0.42 86.67±2.08 40 91.67±1.66 91.67±1.66 91.67±1.66 91.67±1.66 91.67±1.66 45 88.75±2.92 89.17±2.50 88.87±0.27 87.91±0.42 85.54±2.37 表 2 面对不同噪声样本数量以及噪声扰动大小时量子模糊神经网络的准确度
% 噪声样本
数量噪声扰动大小 0.1 0.2 0.3 0.4 0.5 10 100 100 100 100 100 15 100 100 100 100 100 20 100 100 100 100 100 25 100 100 100 99.90±0.03 99.87±0.20 30 100 100 100 99.93±0.02 100 35 100 100 100 99.83±0.12 99.50±0.33 40 100 100 100 99.80±0.05 99.34±0.83 45 100 100 98.34±1.66 98.34±1.66 99.17±0.83 -
[1] JIN X L, WAH B W, CHENG X Q, et al. Significance and challenges of big data research[J]. Big Data Research, 2015(2): 59-64. [2] 张仕斌, 黄曦, 昌燕, 等. 大数据环境下量子机器学习的研究进展及发展趋势[J]. 电子科技大学学报, 2021, 50(6): 802-819. doi: 10.12178/1001-0548.2021332 ZHANG S B, HUANG X, CHANG Y, et al. Research progress and perspectives of quantum machine learning in big data environment[J]. Journal of University of Electronic Science and Technology of China, 2021, 50(6): 802-819. doi: 10.12178/1001-0548.2021332 [3] TSAI C W, LAI C F, CHAO H C, et al. Big data analytics: A survey[J]. Journal of Big Data, 2015, 2(1): 1-32. doi: 10.1186/s40537-014-0007-7 [4] DENG Y, REN Z, KONG Y, et al. A hierarchical fused fuzzy deep neural network for data classification[J]. IEEE Transactions on Fuzzy Systems, 2016, 25(4): 1006-1012. [5] ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[EB/OL]. [2022-06-15]. https://www.cs.upc.edu/~bejar/URL/material_art/DM%20clustring%20DBSCAN%20kdd-96.pdf. [6] DING C, HE X. K-means clustering via principal component analysis[C]//International Conference on Machine Learning. [S.l.]: ACM, 2004: 225-232. [7] LI J, LIU H. Challenges of feature selection for big data analytics[J]. IEEE Intelligent Systems, 2017, 32(2): 9-15. doi: 10.1109/MIS.2017.38 [8] GEPPERTH A, HAMMER B. Incremental learning algorithms and applications[EB/OL]. [2022-05-15]. https://hal.science/hal-01418129/file/article.pdf. [9] BARGIELA A, PEDRYCZ W. Granular computing[M]//Handbook on Computational Intelligence: Volume 1: Fuzzy Logic, Systems, Artificial Neural Networks, and Learning Systems. [S.l.]: IEEE, 2016: 43-66. [10] ZADEH L A. Fuzzy sets[M]//Fuzzy sets, fuzzy logic, and fuzzy systems. [S.l.]: ACM, 1996: 449-463. [11] KLIR G J, FOLGER T A. Fuzzy sets, uncertainty, and information[M]. [S.l.]: Prentice-Hall, Inc., 1987. [12] HÜLLERMEIER E. Fuzzy sets in machine learning and data mining[J]. Applied Soft Computing, 2011, 11(2): 1493-1505. doi: 10.1016/j.asoc.2008.01.004 [13] ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets & Systems, 1986, 20(1): 87-96. [14] ATANASSOV K. Review and new results on intuitionistic fuzzy sets[J]. International Journal Bioautomotion, 2016, 20(1): S17-S26. [15] 黄一鸣, 雷航, 李晓瑜. 量子机器学习算法综述[J]. 计算机学报, 2018, 41(1): 145-163. doi: 10.11897/SP.J.1016.2018.00145 HUANG Y M, LEI H, LI X Y, et al. A survey on quantum machine learning[J]. Chinese Journal of Computers, 2018, 41(1): 145-163. doi: 10.11897/SP.J.1016.2018.00145 [16] BIAMONTE J, WITTEK P, PANCOTTI N, et al. Quantum machine learning[J]. Nature, 2017, 549(7671): 195-202. doi: 10.1038/nature23474 [17] PRESKILL J. Quantum computing in the NISQ era and beyond[J]. Quantum, 2018, 2: 79. doi: 10.22331/q-2018-08-06-79 [18] BENEDETTI M, LLOYD E, SACK S, et al. Parameterized quantum circuits as machine learning models[J]. Quantum Science and Technology, 2019, 4(4): 043001. doi: 10.1088/2058-9565/ab4eb5 [19] CEREZO M, ARRASMITH A, BABBUSH R, et al. Variational quantum algorithms[J]. Nature Reviews Physics, 2021, 3(9): 625-644. doi: 10.1038/s42254-021-00348-9 [20] BUHRMAN H, CLEVE R, WATROUS J, et al. Quantum fingerprinting[J]. Physical Review Letters, 2001, 87(16): 167902. doi: 10.1103/PhysRevLett.87.167902 [21] FISHER R A. The use of multiple measurements in taxonomic problems[J]. Annals of eugenics, 1936, 7(2): 179-188. doi: 10.1111/j.1469-1809.1936.tb02137.x [22] BERGHOLM V, IZAAC J, SCHULD M, et al. Pennylane: Automatic differentiation of hybrid quantum-classical computations[EB/OL]. [2022-07-20]. https://arxiv.org/pdf/1811.04968.pdf. [23] LIN F J, LIN C H, SHEN P H. Self-constructing fuzzy neural network speed controller for permanent-magnet synchronous motor drive[J]. IEEE Transactions on Fuzzy Systems, 2001, 9(5): 751-759. doi: 10.1109/91.963761 [24] SCHULD M, BOCHAROV A, SVORE K M, et al. Circuit-centric quantum classifiers[J]. Physical Review A, 2020, 101(3): 032308. doi: 10.1103/PhysRevA.101.032308 [25] LLOYD S, MOHSENI M, REBENTROST P. Quantum algorithms for supervised and unsupervised machine learning[EB/OL]. [2022-07-25]. http://www.arxiv.org/pdf/1307.0411.pdf. [26] MITARAI K, NEGORO M, KITAGAWA M, et al. Quantum circuit learning[J]. Physical Review A, 2018, 98(3): 032309. doi: 10.1103/PhysRevA.98.032309 [27] SCHULD M, BERGHOLM V, GOGOLIN C, et al. Evaluating analytic gradients on quantum hardware[J]. Physical Review A, 2019, 99(3): 032331. doi: 10.1103/PhysRevA.99.032331 [28] KINGMA D P, BA J. Adam: A method for stochastic optimization[EB/OL]. [2022-08-25]. http://www.arxiv.org/pdf/1412.6980.pdf. -


 ISSN
ISSN 



 下载:
下载: