复合种群^[20]用来刻画农田里害虫繁衍的种群动力学问题。相对于单种群来说，复合种群在结构上包含若干个子种群，每个子种群内部有一定数量代表某种个体的粒子，在动力学方面强调了子种群之间由于个体的迁移造成的耦合相互作用。这一模型将空间因素纳入考虑的范畴，因而广泛应用于探索空间效应对于传播动力学的影响。

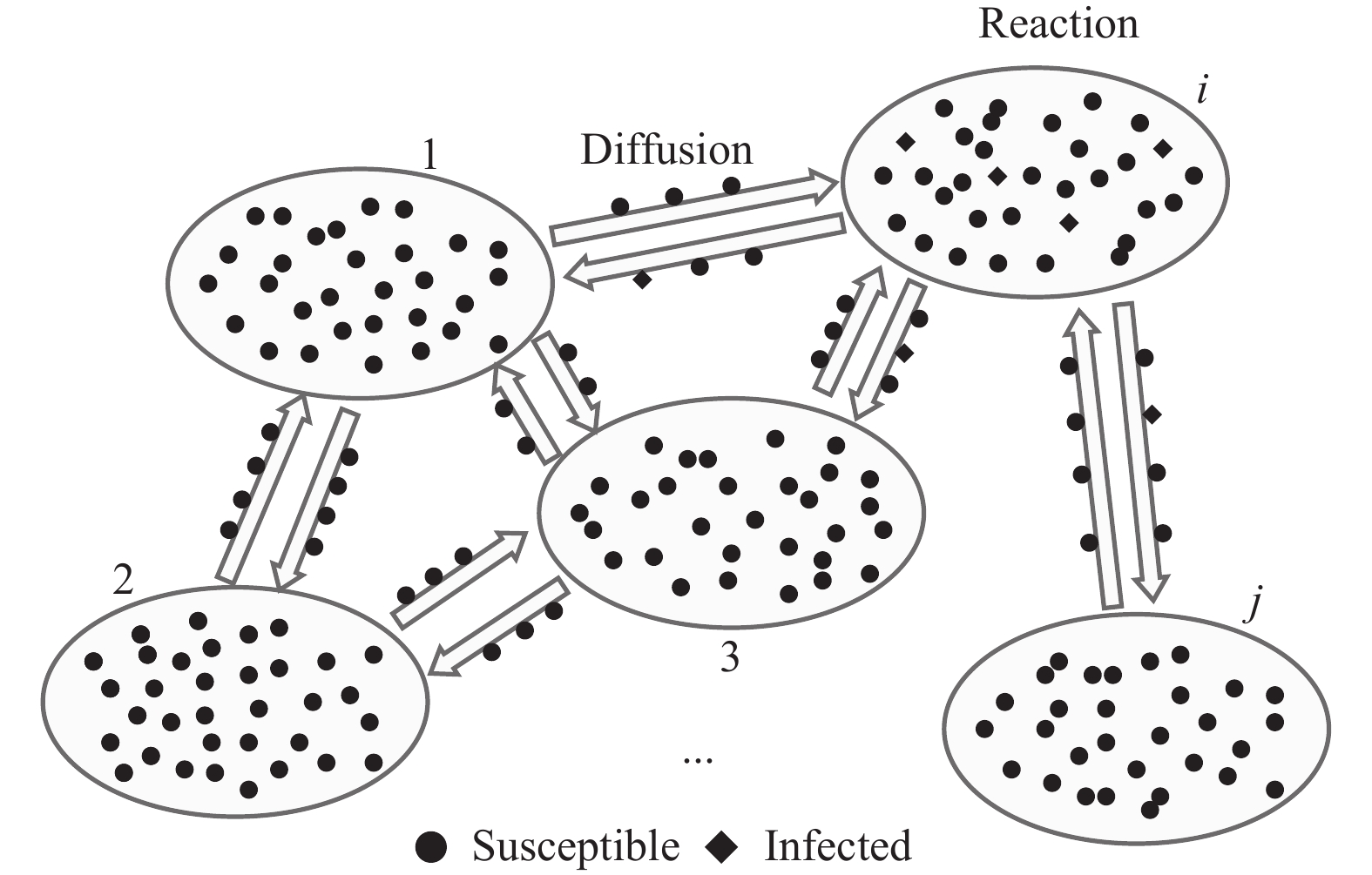
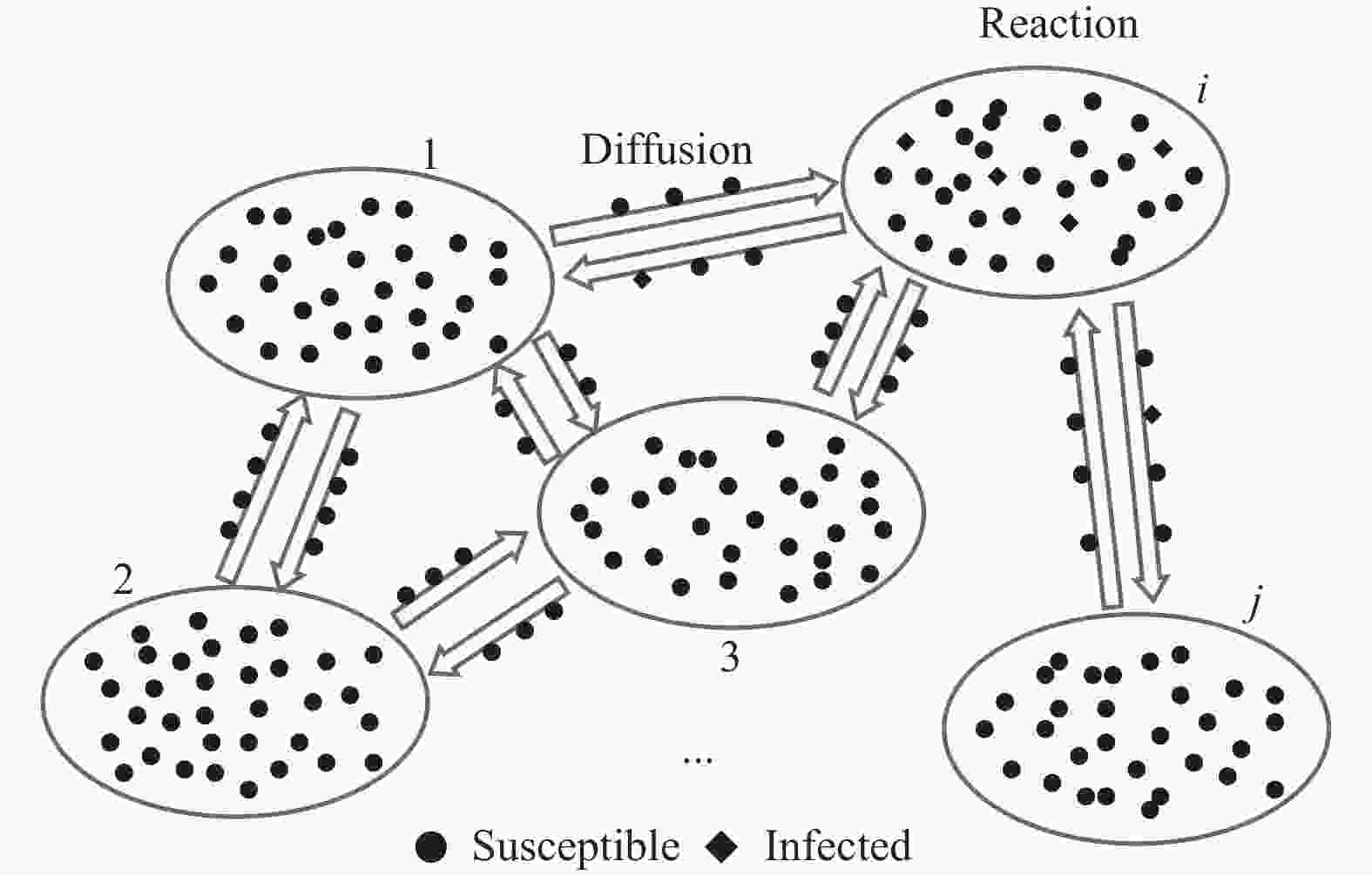
如图1所示，复合种群网络中每个节点代表一个子种群，内部包含一定数量同种属性的粒子，一般假设子种群内部个体均匀混合，子种群之间的连边反映了个体（在子种群间）的迁移途径^[21]，个体在子种群之间的移动由反应散射^[22]机制来刻画。这种建模方式抓住了影响流行病在大尺度空间范围传播的关键因素，与现实情况存在很强的对应：考虑城市间起联系纽带作用的公共交通网络（如航空运输网络），其中每个子种群代表一个城市，子种群内的粒子代表个体，粒子在子种群之间的迁移则反映人群在城市间的旅行现象。

本文采用复合种群网络作为流行病传播的载体，其中流行病在子种群内部的反应过程用传统的易感−感染(SI)模型描述：

式中，$i = 1,2,\cdots,n$，${N_i}$是子种群$i$的人口规模，$n$是子种群数量；${I_i}$和${S_i} = {N_i} - {I_i}$分别表示感染者和易感者的人数；参数$\beta $是平均传染率。除了局部动态之外，个体根据迁移率方程在子种群之间扩散：

式中，${U_i}$是${S_i},{I_i}$的占位符；${w_{i,j}}$代表从子种群$i$到子种群$j$的迁移率。于是：

反映了感染个体在子种群内部的反应过程和子种群之间的扩散过程。

图  1  复合种群网络

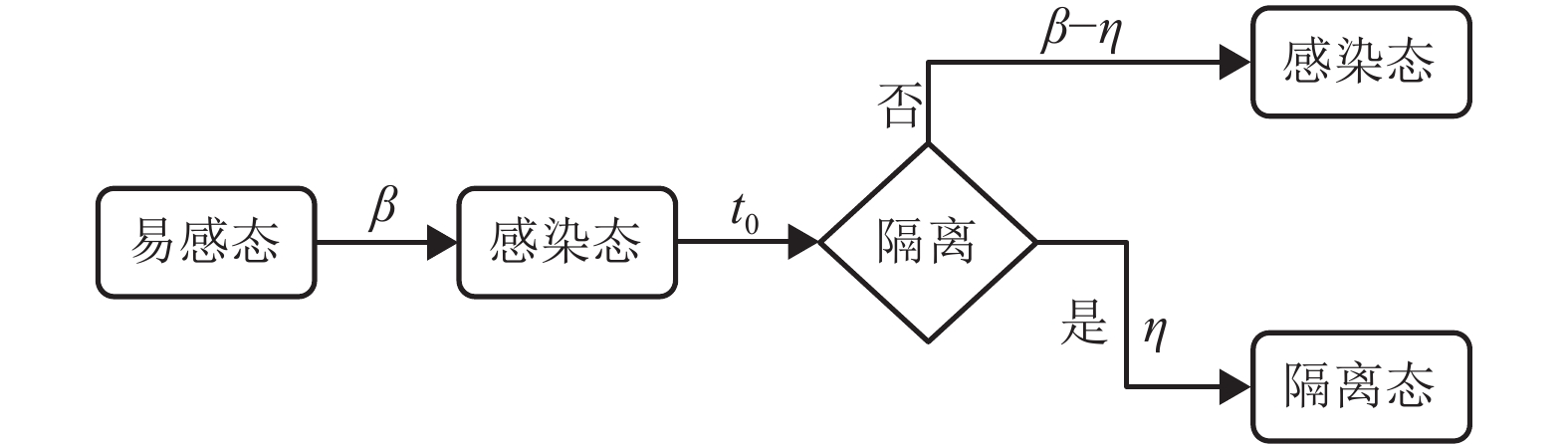
本文主要讨论了病患隔离和航空管制这两类典型的控制策略。病患隔离控制策略通过限制感染者的活动，抑制流行病在子种群内部的传染过程。由于受社会经济等现实因素的影响，病患隔离或航空管制控制策略的推行大多存在一定的延迟。因此，引入响应延时参量^[23]${t_0}$来刻画从流行病爆发初期到实施控制策略的时间间隔。令$\eta $为病患隔离控制策略的强度，即${t_0}$时刻以后的每个时间步，平均意义上百分比为$\eta $的感染者会被隔离。需要说明的是，在社区防控中降低$\beta $、缩短${t_0}$、增加$\eta $在遏制流行病的传播上是互为助益的，但通过接触控制（contact control）降低$\beta $比增加$\eta $更为重要，尤其是在流行病传播早期。本文仅从$\eta $的角度出发，考虑社区防控对流行病传播的影响。在SI模型中引入隔离过程，即令单位时间内每个感染者以概率$\eta $被隔离，处于隔离态的个体不再参与传染和扩散过程。图2表示引入病患隔离控制策略的SI模型过程^[24]。

航空管制控制策略主要限制个体在各个子种群之间迁移，令$\alpha $反映航空管制控制策略的强度，表示采取航空管制控制策略后子种群每天扩散的平均人数下降的比例。在本文所讨论的复合种群网络模型中，${t_0}$时刻之后个体迁移率从$w$减少到$(1 - \alpha )w$。直观起见，式(4)给出了在采取航空管制控制策略后，子种群间个体迁移率的变化：

图  2  引入病患隔离控制策略的易感-感染(SI)模型过程

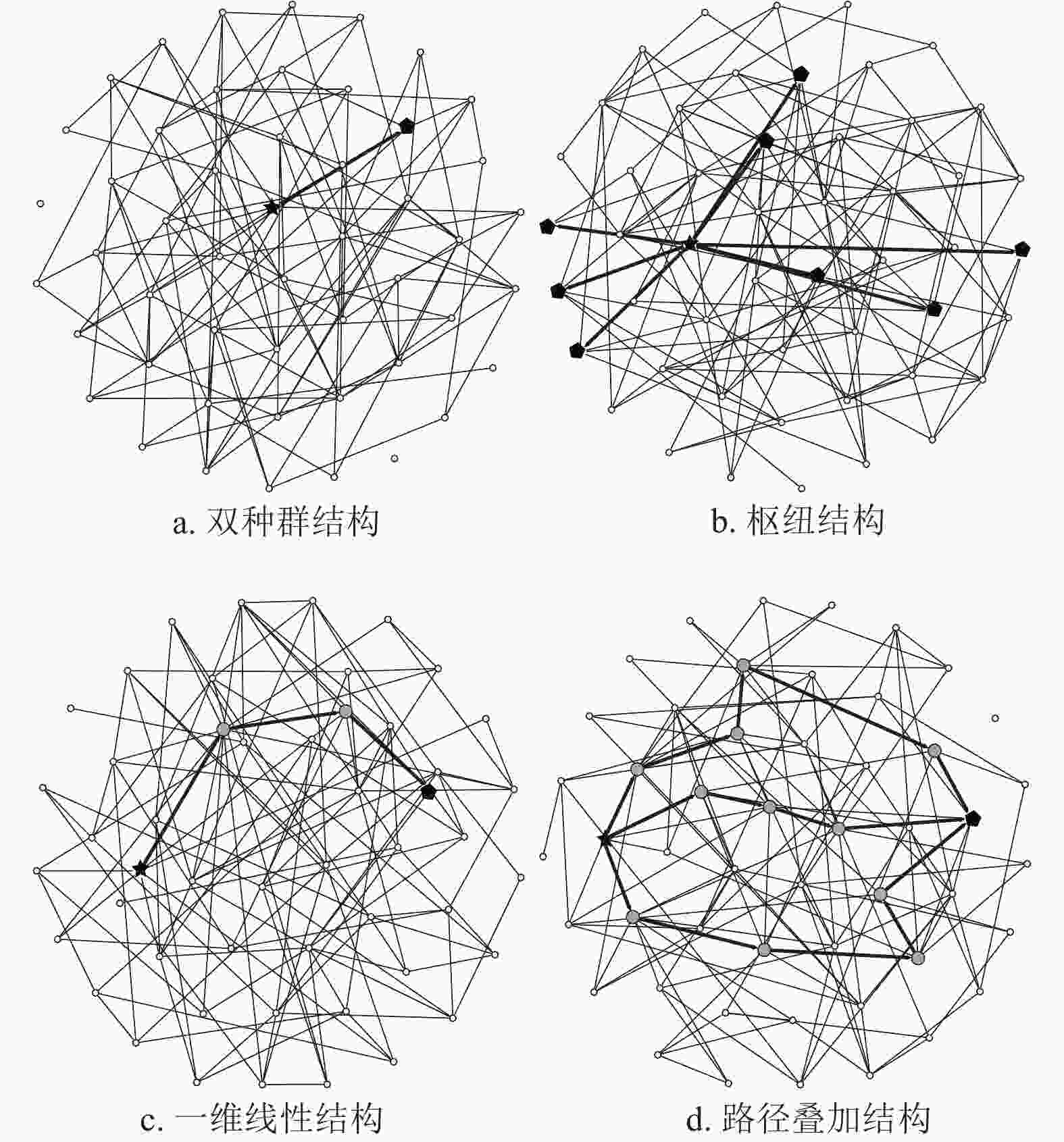
流行病在复合种群网络中的传播，有4种基本的传播结构：双种群结构、枢纽（Hub）结构、一维线性结构和路径叠加结构，如图3所示。双种群结构指的是感染子种群与目标子种群之间直接相连的情形；枢纽结构指的是感染子种群与多个子种群直接相连的情形；一维线性结构指的是感染子种群与目标子种群之间并没有直接相连，而是通过一个或多个中间子种群实现连接；路径叠加结构指的是感染子种群与目标子种群之间存在着多条传播路径的结构。为了简化模型，假设各子种群$1,2,\cdots,n$的总人口数${N_1},{N_2},\cdots,{N_n}$相等且记为$N$；不同子种群内部反应过程的传染率${\beta _1},{\beta _2},\cdots,{\beta _n}$相等且记为$\beta $；不同子种群之间的迁移率${w_{i,j}}$相等且记为$w$。值得指出的是，这样的简化不会对实验结果造成影响。

图  3  4种基本的传播结构模型

双种群结构如图3a所示，假设子种群$i$（五角形）为疫源中心，种群$j$（五边形）为目标子种群。在初始时刻$t = 0$，有${I_i}(0) = I_i^*$和${I_j}(0) = 0$，且子种群$i$和$j$中感染个体的传染率为$\beta $。流行病爆发的初始阶段，子种群$i$中感染个体的数量只有其人口总数的一小部分，${I_i}(t) \ll N$。通过平均场近似方程^[25]，得到：

假定从$t = 0$时刻开始到$t = {t_{i,j}}$时，流行病首次从子种群$i$传播到子种群$j$，有：

式中，${t_{i,j}}$表示流行病首次从感染子种群$i$传播到子种群$j$所花费的时间，则${t_{i,j}}$代表子种群$j$零号病人的首达时间，记为${T_j}$。根据近似条件$\displaystyle\sum\limits_0^{{t_{i,j}}} I_i^*\exp (\beta t)w \approx \displaystyle\int_0^{{t_{i,j}}} {I_i^*\exp (\beta t)w{\rm{d}}t}$，可以计算出不采取任何控制策略时，有：

当子种群$i$的初始感染个体数$I_i^* = 1$时，式(7)近似Gumbel分布^[26]的平均值$T_j^G = \dfrac{1}{\beta }\ln \left(\dfrac{\beta }{w} - \gamma \right)$。其中，$\gamma $是Euler常数。

采取航空管制策略后，若感染个体首达时间${T_j}$小于延时响应${t_0}$，首达时间仍然可以用式(7)表示。当首达时间大于${t_0}$，有：

此时$j$种群零号病人的首达时间记为$ T_j^\alpha = {t_{i,j}} $，通过数值求解便可得到：

求解得到采取航空管制控制策略推迟零号病人首达时间的长度$\Delta {T_j}(\alpha )$。其中，$T_j^\alpha $和${T_j}$分别代表采取航空管制控制策略和未采取航空管制控制策略时子种群$j$零号病人的首达时间。当响应延时${t_0}$很小时，可近似为0，则有：

采取病患隔离策略时，重点关注感染个体首达时间大于响应延时${t_0}$的情况。当$t \leqslant {t_0}$，${I_i}(t) \approx I_i^*\exp (\beta t)$；当$t > {t_0}$时，马尔萨斯增长率降低为$\beta - \eta $，即采取病患隔离控制策略后流行病的传染率，记为${\beta _\eta }$。因此，当${t_0} < {t_{i,j}}$时，有：

如果响应延时小到可以被忽略（$ {{t_0} \approx 0} $），式(11)可进一步简化为：

此时，采取病患隔离控制策略后，零号病人的首达时间为：

当${t_0} > 0$时，根据式(11)，通过数值求解得到采取病患隔离控制策略后零号病人的首达时间。由：

计算得到采取病患隔离控制策略对于延缓零号病人入侵子种群$j$的延时$\Delta {T_j}(\eta )$。

考虑一个简单的枢纽结构，如图3b所示。假设疫源子种群$i$具有$k(1,2,\cdots,j,\cdots,k)$个直接相连的子种群，且子种群$i$的传染率和与相邻子种群$j$的迁移率分别表示为$\beta $和${w_{i,j}}$。在无控制策略的双种群模型中，马尔萨斯增长率为$\beta $。当疫源中心种群是枢纽结构时，将疫源中心子种群$ i $到子种群$j$的马尔萨斯增长率调整为$\beta - \displaystyle\sum\limits_{l = 1\parallel l \ne j}^k {{w_{i,j}}} $，记为${\beta ^H}$。由式(4)可得，枢纽结构下疫源子种群$i$到子种群$j$的零号病人首达时间$T_j^H$为：

则在枢纽结构中引入病患隔离控制策略和航空管制控制策略后子种群$ j $的零号病人首达时间$T_j^\eta $和$T_j^\alpha $可分别表示为：

式中，$ \beta _\eta ^H = {\beta ^H} - \eta $，表示枢纽结构中病患隔离控制强度$\eta $下的传染率调整结果。

假设一维线性结构中存在$k$个子种群，如图3c所示。给定初始情况下疫源子种群$i$中存在$I_i^*$名感染者，用${w_{j,j + 1}}$表示子种群$j$到子种群$j + 1$的迁移率，用$\beta $表示各个子种群的传染率。同时，用${t_{j,j + 1}}$表示子种群$j$出现感染到子种群$j + 1$感染时所经过的时间，则子种群$j$零号病人首达时间记为${T_j} = {t_{i,l}} + {t_{l,m}} + \cdots + {t_{j - 1,j}}$。

路径$\varPsi :i \to j \to l$表示流行病从子种群$i$传播到子种群$j$再传播到子种群$l$的传播过程，其中${t_{i,j}}$可由式(7)得出，${t_{j,l}}$则可由下式得到：

通过数值求解得到子种群$j$出现零号病人到子种群$l$出现零号病人所经历的时间${t_{j,l}}$。

同时考虑路径$\varPsi :i \to j \to l \to m$，由式(7)和式(18)分别求得${t_{i,j}}$和${t_{j,l}}$。采用路径缩减的思路，假设子种群$i$和子种群$l$间存在一条直接连边，其迁移率表示为${w_{i,j}}$。令式(7)中的${T_l} = {t_{i,j}} + {t_{j,l}}$，即可得：

由：

可得从子种群$l$出现感染者到子种群$m$出现零号病人的时间间隔${t_{l,m}}$。

在一维线性结构中加入航空管制策略时，相应的理论计算变为：

同样的，当采取病患隔离控制策略时，理论计算变为：

在复合种群网络中，疫源子种群$i$到子种群$j$之间通常具有多条传播路径，如图3d所示。已经证明首达时间不仅仅只受到最短路径的影响，多条路径的存在也会减小目标城市零号病人的首达时间^[27]。假设从子种群$i$到子种群$j$存在$P$条最短路径，用路径缩减思路，将这些路径缩减为$P$条与子种群$j$直接相连的路径，调整后的迁移率分别记为$w_{i,j}^1, w_{i,j}^2,\cdots,w_{i,j}^P$。子种群$i$到子种群$j$的首达时间$ {T_j} $则有：

即：

分别考虑航空管制策略和病患隔离策略，子种群$i$到子种群$j$的首达时间${T_j}$分别有：

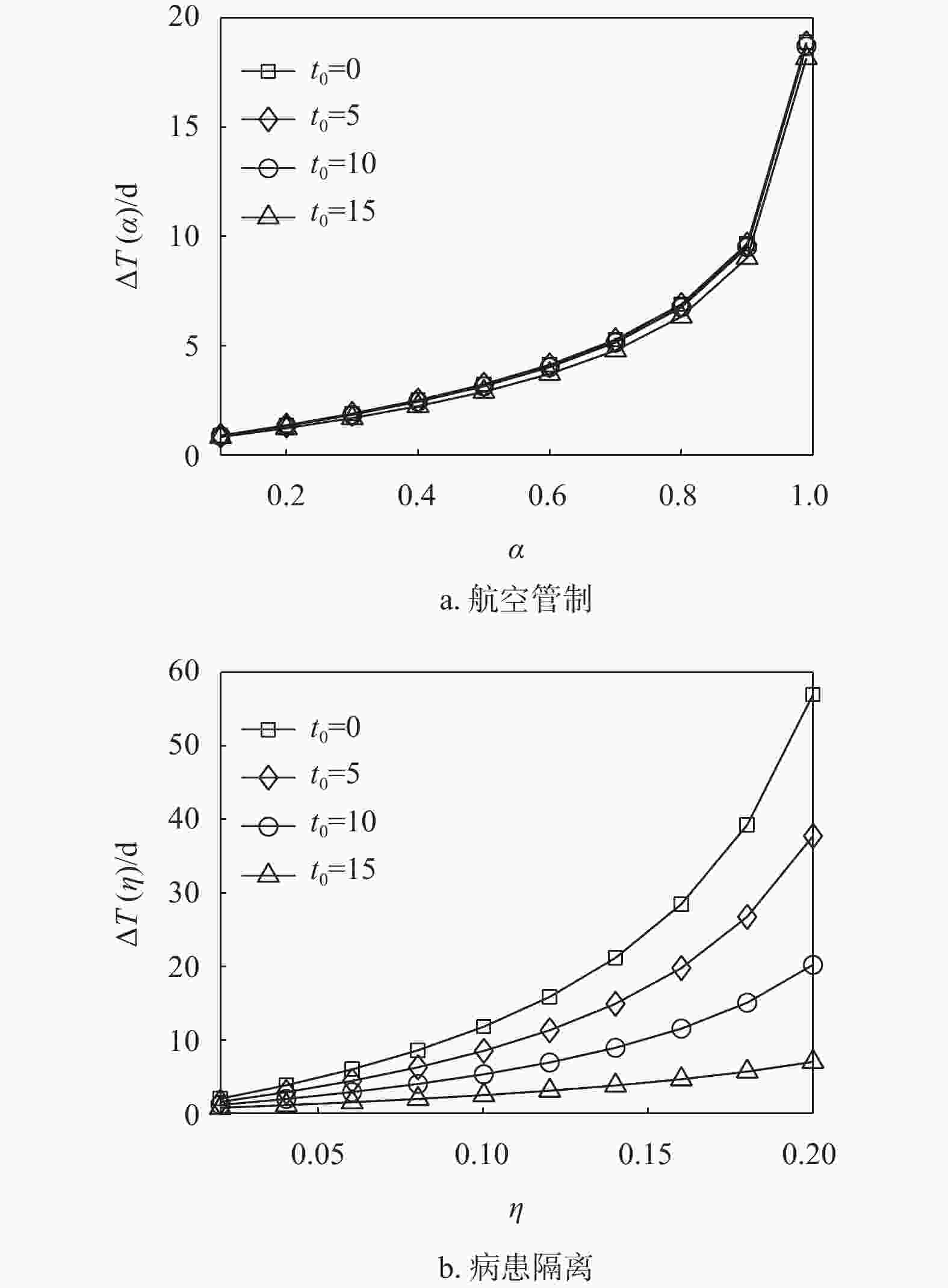
在现实生活中，每天离开一个城市的人数要比这个城市的总人数小若干个数量级，即每天只有相对少量个体从其所在的城市迁出。全美国内航空运输实际统计数据显示，每天沿着各条航线个体迁出扩散率的数量级大体保持在0.0001甚至更小。在这里将每个城市视为一个子种群，因此设定子种群间的迁移率和各个子种群的人口数分别为$w = 1.0 \times {10^{ - 4}}$和$N = 1.0 \times {10^6}$。在实验中，假设该种流行病的传染率$\beta = 0.25$与流感一致。通过仿真500次得到子种群$j$的平均流行病首达时间为$T_j^E = 21.81\;{\text{d}}$，由式(7)得到的首达时间${T_j} = 22.10\;{\text{d}}$，通过Gumbel分布得到的首达时间$T_j^G = 19.78\;{\text{d}}$。可见，本文方法对首达时间估计更为准确，后面便将其作为首达时间的近似估计。

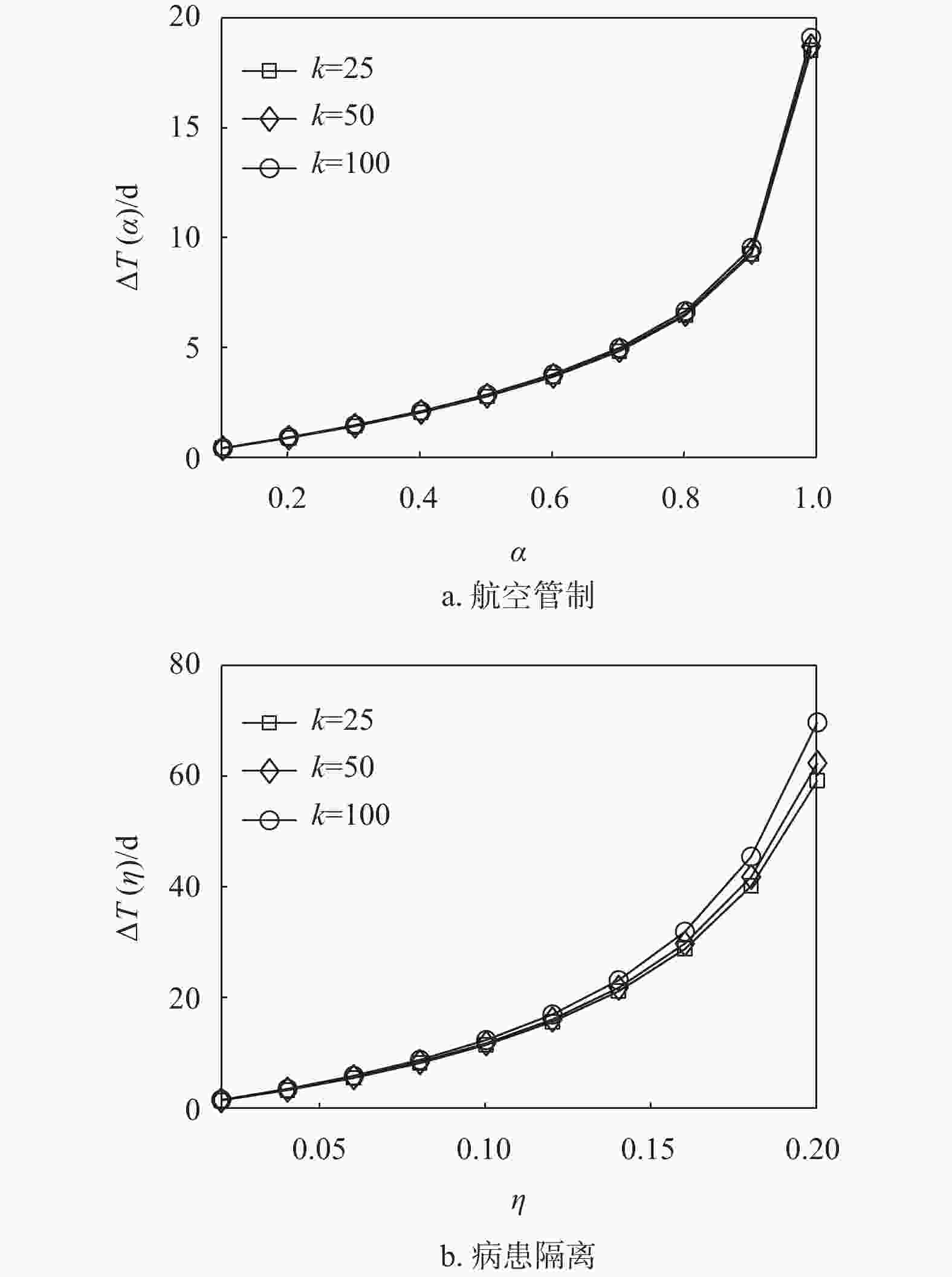
由图4可知，当${t_0} = 0$，$\beta = 0.25$时，中等强度$\eta = 0.14$的病患隔离控制策略就可以使得零号病人入侵子种群$j$的时间延缓$23\;{\text{d}}$以上。因此，如果在流行病爆发早期就能启动病患隔离控制策略（即${t_0} = 0$），会取得显著优于航空管制控制策略对延缓流行病入侵的效果，这里得到的结果与文献[28]相似。因为即使采取了航空管制策略，也不能抑制在流行病爆发早期感染人数以指数形式增长。然而，延时响应${t_0}$的增大对病患隔离控制策略的效果影响很大。当${t_0}$从0增大到15 d时，病患隔离控制策略的首达时间延迟逐渐缩短。当延时${t_0} \geqslant 10\;{\text{d}}$时，病患隔离控制策略取得的效果就与航空管制控制策略的效果相近甚至更差。

分析式(16)和式(17)可知，相较于双种群结构情形，枢纽结构实质上只影响了流行病的传染率，而传染率的变化取决于枢纽子种群与邻居子种群之间的迁移率。因为子种群之间的迁移率往往较小，即使子种群的枢纽性很强，对流行病传染率的影响仍然可以忽略。图5显示了不同枢纽强度下，航空管制和病患隔离控制策略对流行病入侵的延缓效果。由图可知，枢纽结构几乎不影响航空管制控制策略的延缓入侵效果，而在一定程度上能够增强病患隔离控制策略的延缓入侵效果。

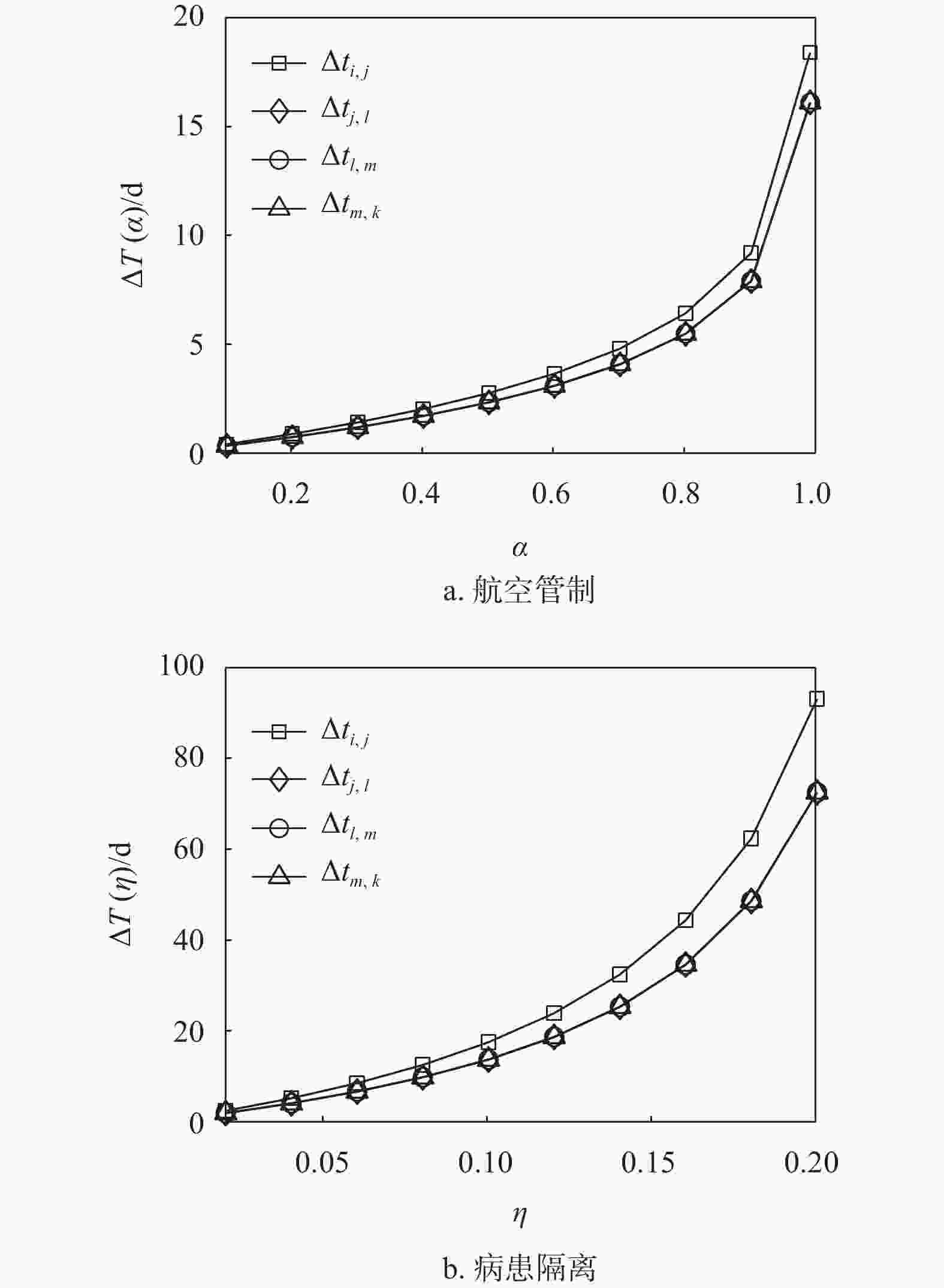
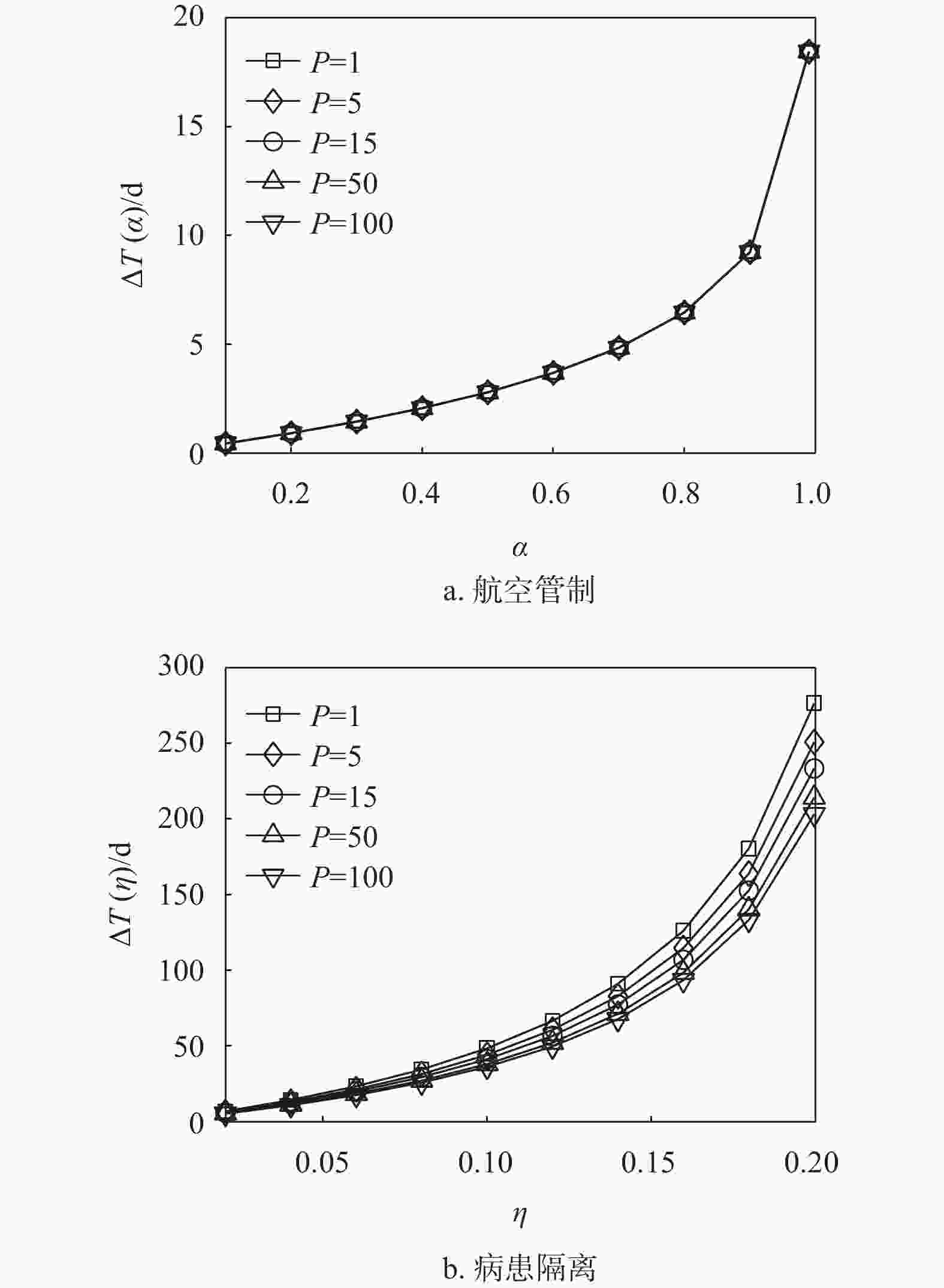
图6分别计算了一维线性结构中相邻两个子种群在不同控制策略下的首达时间延迟。图中显示，病患隔离控制策略对零号病人首达时间的延迟效果仍然好于航空管制控制策略。在同一种控制策略下，子种群$j$到子种群$l$、子种群$l$到子种群$m$、子种群$m$到子种群$k$的首达时间延迟基本相同。因为在流行病的线性传播中，子种群$k$相对于种群$k - 1$的首达时间间隔${t_{k - 1,k}}$主要受到上游$k - 1,k - 2$两个子种群的连续播种影响，其他上游子种群对${t_{k - 1,k}}$的影响基本可以忽略。于是，子种群$i$到子种群$k$的入侵时间延迟$\Delta T = \Delta {t_{i,j}} + \Delta {t_{j,l}} + \cdots + \Delta {t_{k - 1,k}}$。由此可知，入侵时间的延迟很大程度上取决于子种群$i$到子种群$k$的传播路径跳数。

图  4  双种群结构中两种控制策略对比

图7绘制了在1 条、5 条、15条、50条、100条最短路径叠加下两种控制策略延缓入侵所产生的延迟与控制强度之间的关系。可以发现随着路径叠加数量的增加，两种控制策略延缓入侵时间的效果越来越弱，尤其是病患隔离控制策略对路径叠加数量的变化更为敏感。这主要是因为路径叠加结构的存在，加速了流行病的传播，在相同强度的控制策略下，首达时间的延迟则会减小。同时，图6b显示15条路径叠加就能使入侵时间的延迟低于14天。

通过以上实验可以发现，双种群结构中，病患隔离控制策略对于延缓流行性入侵的效果远好于航空管制控制策略。枢纽结构和路径叠加结构的存在都会影响两种控制策略对零号病人入侵首达时间的延迟，且枢纽性越强、路径叠加数量越少，控制措施延缓流行病的入侵效果越好。而线性结构主要是通过结构的长度来延缓流行病的入侵，不论是航空管制控制策略或是病患隔离控制策略，对流行病入侵时间的延缓效果都随着线性结构长度的增加而增强。

图  5  枢纽结构中两种控制策略对比

图  6  一维线性结构中两种控制策略对比

图  7  路径叠加结构中两种控制策略对比

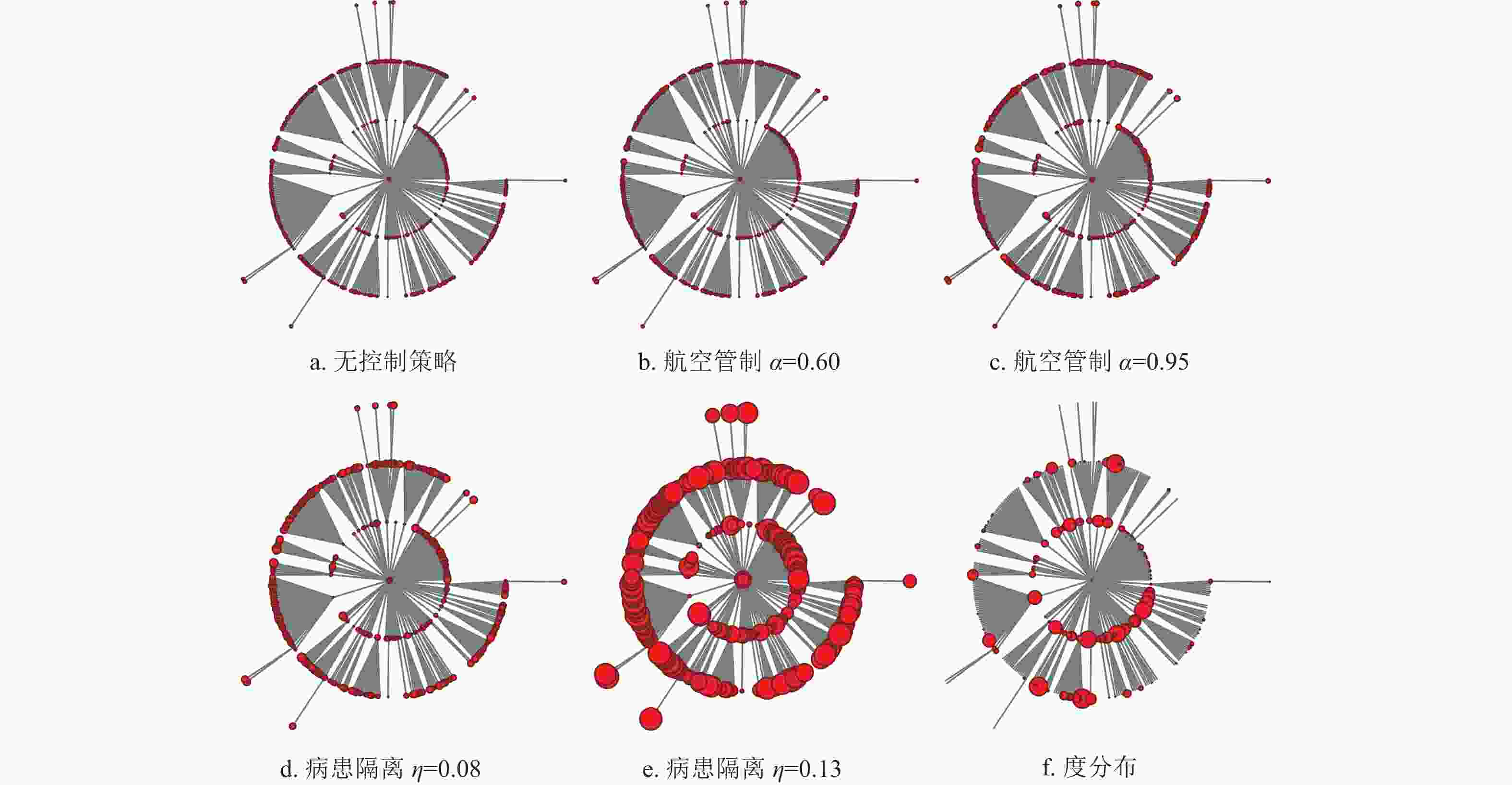
本文用来构建美国航空网的高质量城市人口数据和城市间航空客运数据来源与文献[29]一致，仿真采用的传染率$\beta $取值0.15。模拟仿真过程采用离散时间步，每个时间步内所有个体的状态同步更新。在不采取任何控制策略时，每个时间步内，每个子种群内个体的传染过程和个体扩散到另一子种群的仿真模拟如下。1）反应过程。假设每个子种群中的个体均匀混合，在$t$时刻，子种群$i$、$j$中每个易感个体被感染的概率分别为$\beta {I_i}(t)/{N_i}$、$\beta {I_j}(t)/{N_j}$。因此，在$t$时刻子种群$i$、$j$中新增感染个体数量的概率为$\beta {I_i}(t)/{N_i}$、$\beta {I_j}(t)/{N_j}$，实验次数为${S_i}(t)$、${S_j}(t)$的二项分布生成。2）扩散过程。在每个时间步，两个子种群中的所有个体在传染过程结束后开始扩散。单位时间里，从每个子种群迁出的易感个体的数量由概率为${w_{i,a}},{w_{i,b}}, \cdots ,{w_{i,m}}$，实验次数为${S_i}(t)$的多项分布生成。其中$a,b, \cdots ,m$表示子种群$i$的邻居，${w_{i,a}}$表示子种群$ i $到子种群$a$的迁移率。同样的，感染个体的扩散数量也由相应的多项分布生成。在采取航空管制控制策略时，只需要将任意两个子种群$i$到子种群$j$之间的迁移率调整为${w_{i,j}}(1 - \alpha )$，参数$\alpha $反映了所采取航空管制策略的强度。在采取病患隔离控制策略时，保持迁移率不变，将传染率$\beta $用控制强度$\eta $修正为$\beta - \eta $。为了排除随机性对统计结果的干扰，实验中每个子种群的首达时间都是500次蒙特卡洛独立仿真实验中感染个体成功入侵到目标种群的平均首达时间。其中，每次蒙特卡洛独立仿真实验运行700个时间步。

使用入侵树^[30]来观察流行病在不同子种群之间蔓延的先后层次关系。固定疫源中心子种群不变时，从所有可能的传播路径中挖掘出有向加权的最小生成树（Minimun Spanning Tree），由此得到流行病扩散过程的入侵树。对此，通过仿真统计出每对子种群$i$、$j$之间从子种群$i$中迁出的感染个体造成子种群$j$爆发此次流行病的概率${Q_{i,j}}$。令子种群$i$、$j$之间的距离${d_{i,j}} = \sqrt {1 - {Q_{i,j}}} $，进而利用Chu-Liu-Edmunds算法^[31]计算得到最小生成树，即得到最可能反映此次流行病空间入侵过程的入侵树。图8所示的入侵树中，节点代表子种群，中心节点是此次流行病的疫源子种群。每条入侵路径上与中心节点拓扑距离相等的节点安置在同一层，节点大小按照首达时间或节点度值进行编码。

图  8  流行病首达时间及度值分布示意图

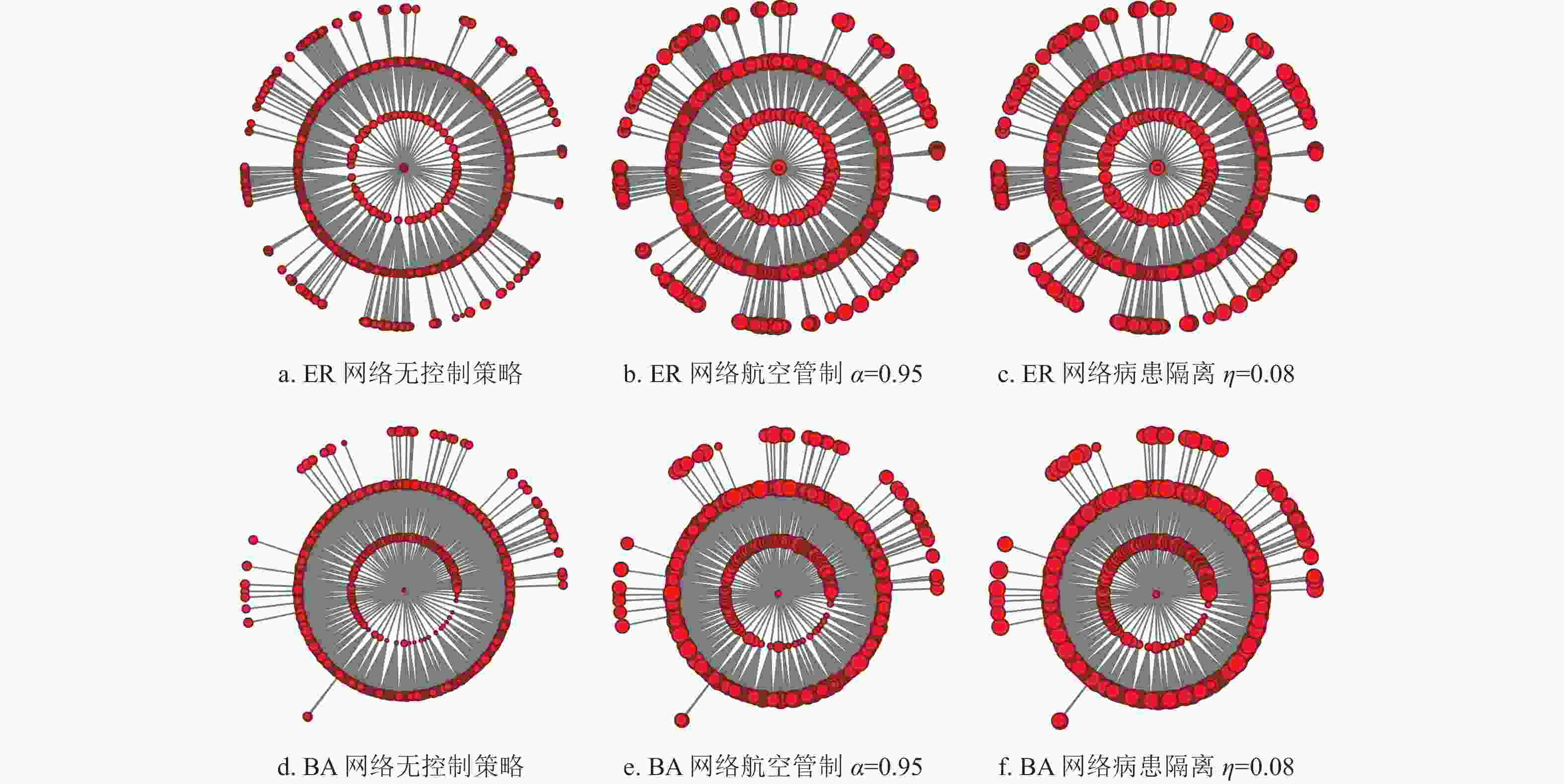
图8a表示无控制策略时，每个节点的流行病首达时间仿真结果，其中节点越大，代表首达时间越大。图8b和图8c分别表示采取航空管制控制策略强度为0.60和0.95时的仿真结果，可以发现，相对于图8a每个节点的大小都有一定程度的增加，但不明显。这说明航空管制控制策略在一定程度上能够延缓目标城市零号病人的入侵时间，但效果有限。对比图8a与图8d，当病患隔离控制策略强度$\eta = 0.08$，即中等控制强度下，各目标子种群的首达时间均显著增大，且控制效果略微好于控制强度为0.95的航空管制控制策略。这说明在流行病爆发早期，病患隔离控制策略优于航空管制控制策略，同时图8e进一步证明了此观点。图8f显示入侵树中节点的度值分布，节点大的城市对应美国航空网中的枢纽城市。可以发现，枢纽城市的流行病爆发时间不一定比非枢纽城市流行病爆发时间提前，也不一定更易将流行病扩散到更广阔的区域。实际上扩散的容易程度和零号病人到达目标子种群的首达时间最终取决于相对于目标子种群的迁移率和路径缩减、路径叠加后的迁移率。

另一方面，为了研究航空管制和病患隔离对流行病首达时间的控制效果是否会受到网络拓扑性质的影响，生成了含有1000个节点，节点的平均人口数为$6 \times {10^5}$的ER复合种群网络和BA复合种群网络^[32]。其中ER复合种群网络中节点间的连接概率为0.03，BA复合种群网络中的平均度值为15。在ER复合种群网络和BA复合种群网络中的仿真实验结果如图9所示。可以发现，不论是在ER复合种群网络还是BA复合种群网络中，高强度的航空管制所产生的流行病首达时间延迟效果有限，而中等控制强度下的病患隔离策略便可以达到相同或略好于高强度下的航空管制策略的控制效果。

图  9  ER复合种群网络和BA复合种群网络中首达时间模拟结果

本文从复合种群网络出发，考虑存在的双种群结构、枢纽结构、一维线性结构以及路径叠加结构，考查不同强度下的航空管制策略、病患隔离策略对目标子种群零号病人首达时间的延缓效果，并通过绘制入侵树直观反应流行病传播的路径、目标子种群的度值和实验仿真的首达时间。实验结果表明，在传播早期，控制策略响应延时的大小几乎不改变航空管制控制策略对流行病首达时间的影响，但一定程度上会改变病患隔离控制策略对首达时间的影响。随着响应延时长的增加，病患隔离控制策略延缓流行病首达时间的效果越来越弱。枢纽结构的存在几乎不会影响航空管制控制策略的延缓效果，但随着枢纽节点邻居的增加，病患隔离控制策略的效果略微变好。在一维线性结构中，航空管制控制策略和病患隔离控制策略对入侵时间延迟效果均随着感染子种群到目标子种群之间跳数的增加而增加。另外也通过实验证明：一维线性结构中，相邻子种群之间首达时间的变化主要由上游两个子种群决定。路径叠加模型中，多条路径的存在实际上是增加感染子种群到目标子种群的迁移率，随着疫源子种群与目标子种群之间路径数量的增加，航空管制控制策略延缓流行病的入侵效果基本不会受到影响，而病患隔离控制策略延缓流行病的入侵效果越来越差。总的来看，病患隔离控制策略比航空管制控制策略在延缓流行病首达时间上具有更好的效果。

在实际的流行病防控中，流行病传播早期，及时采取病患隔离控制策略将取得比航空管制控制策略更好的控制效果；通过研究复合种群网络拓扑结构，对关键节点或关键连边施行控制策略，从而实现增加疫源子种群到目标子种群的跳数，减少子种群之间的传播路径数量，将极大提升延迟流行病入侵的效果；同时不是所有度值较大的子种群都有可能成为关键节点，至少入侵树外层的子种群应当优先排除，这也可作为寻找关键节点的出发点；识别复合种群网络中迁移率较大的连边并控制或阻断相关子种群之间的迁移，能够实现与控制路径叠加数量相同的效果。另一方面，本文仅从病患隔离的角度思考了社区防控对流行病传播的影响，而在流行病早期接触控制更为重要，进一步从接触控制如何影响传染率以及实施成本的角度出发展开讨论具有重要意义。同时，如果能将本实验与单种群层面的免疫策略以及网络拓扑识别^[33]有机结合起来，或许能够构成从个体到种群层面、网络拓扑层面的复合控制方案，无论是延缓流行病入侵或是抑制流行病扩散，都值得系统思考。