-
随着网络科学的发展与进步,复杂系统已深入人类社会的各个领域,复杂网络作为刻画复杂系统的工具,在生态、社会、经济、交通等诸多系统中有着重要影响[1-2]。关键节点影响着网络的结构和信息传递功能,评估关键节点是复杂网络的研究热点[3-4]。一方面,快速准确地识别出关键节点并提供保护机制可提升网络的抗毁性[5]。另一方面,基于关键节点也可以提出更高效的攻击策略[6-7]。因此,设计高效的关键节点评估算法具有重要的理论和实践意义。
近年来,研究人员关于识别关键节点已有许多研究成果,经典的评估算法有基于节点邻近信息的度中心性[8]、基于最短路径数目的介数中心性[9]、基于平均距离的接近中心性[10]以及基于网络位置的K-壳分解法[11]等。其中度中心性虽然简单直接,但对邻居节点的重要性区分度较低,并且考虑的邻近信息有限,因此评估的精确性不高。介数和接近中心性仅考虑信息在最短路径上传播,而实际上传播可能基于其他可达路径,此外基于路径的算法时间复杂度较高,不适用于大型网络。而具有较低时间复杂度的K-壳分解法认为节点重要性取决于所处网络的位置,内核层节点的重要性高于边缘的节点,但对同一壳层的节点却无法进一步区分其重要性差异,并且节点在剥离时会对网络的整体结构信息造成破坏[12]。为弥补经典算法评估的局限性,文献[13]考虑节点与其相邻节点之间的相关性,提出了映射熵来评估网络中节点的重要性。文献[14]通过衡量节点的局部拓扑重合度来刻画节点间的相似性,提出了邻域相似度算法用于评估节点的重要性。文献[15]结合节点的K-壳以及信息熵,根据其分层大小依次进行迭代,可区分内层壳与外层壳中的节点重要性。文献[16]受引力公式启发,将节点的度值作为质量,并将最短路径长度作为距离,考虑了节点的近邻以及路径信息,提出了引力模型算法。文献[17]考虑节点在网络中所处的位置,提出了一种基于K-壳分解法的改进引力模型算法。
熵[18]可用于定量描述信息量的大小,当使用熵理论刻画复杂网络时,信息熵可表征节点的局部重要性,因此,可考虑用子网络的熵来表征网络整体结构的特性。如文献[19]提出了信息熵来评估复杂系统的结构特征,取得了较好的成效。文献[20]改进了K-壳值对信息熵的计算,提出了一种结合节点信息熵与迭代因子的算法。文献[21]基于非广延统计力学,提出了一种局部结构熵来量化复杂网络中的关键节点。文献[22]结合网格约束系数以及节点的K-壳中心性,基于Tsallis熵提出了一种节点重要性识别方法。
受上述研究启发,本文提出了一种基于交叉熵的节点重要性识别算法CE+(cross entropy),该方法充分考虑了节点自身以及其周围节点信息的整体重要性,CE+的值反映了节点与其近邻节点之间的差异性,并且该算法时间复杂度仅为
$ O(n) $ ,适用于大型网络。通过在8个不同领域的真实网络上进行蓄意攻击实验,并选用7种不同的节点重要性排序算法作为对比,采用单调性指标[23]、极大连通系数[24]、网络效率[25-26]以及SIR模型[27]等指标验证了本文所提出CE+算法的有效性和适用性。 -
假设无向未加权的网络
$ G = (V,E) $ ,其中$ V $ 是网络$ G $ 的节点集合,$ \left| V \right| = n $ ,$ E $ 是网络的边集合,$ \left| E \right| = m $ 。$ {\boldsymbol{A}} = {({a_{ij}})_{n \times n}} $ 通常表示网络的邻接矩阵,若节点$ i $ 与节点$ j $ 相连,则$ {a_{ij}} = 1 $ ,否则$ {a_{ij}} = 0 $ 。 -
度中心性[9]是度量重要节点性能最基础的指标,节点的邻居节点数越多,则自身的影响力越大,其定义为:
$$ {\rm{D}}{{\rm{C}}_i} = \frac{{{k_i}}}{{n - 1}} $$ (1) 式中,
$ {k_i} = \displaystyle\sum\limits_{j = 1}^n {{a_{ij}}} $ ;$ n $ 表示网络的节点数。 -
当网络中某一节点
$ i $ 存在于其他节点之间的最短路径上并且次数越多时,则说明节点$ i $ 的关键程度越高,其定义为:$$ {\rm{B}}{{\rm{C}}_i} = \sum\limits_{i \ne s \ne t} {\frac{{g_{st}^i}}{{{g_{st}}}}} $$ (2) 式中,
$ g_{st}^i $ 表示节点$ i $ 存在于节点$ s $ 到节点$ t $ 之间的最短路径中的次数;$ {g_{st}} $ 表示节点$ s $ 到节点$ t $ 之间的全部路径条数。 -
文献[13]考虑节点中所有邻域相关的局部信息,提出了映射熵来评估复杂网络中的节点中心性,定义为:
$$ {\rm{M}}{{\rm{E}}_i} = - {\rm{D}}{{\rm{C}}_i}\sum\limits_{j = 1}^M {\log {\rm{D}}{{\rm{C}}_j}} $$ (3) 式中,
$M$ 是节点$i$ 的邻居集;${\rm{D}}{{\rm{C}}_j}$ 是其相邻节点之一的度中心性。 -
文献[14]综合考虑了节点的度值和邻居节点的拓扑重合度,提出了一种基于邻域相似度的评估算法,定义为:
$$ {\rm{LL}}{{\rm{S}}_i} = \sum\limits_{b,c \in n(i)} {(1 - {\rm{sim}}(b,c))} $$ (4) 式中,
$ n(i) $ 为节点$ i $ 的邻居节点;若节点$ b $ 与$ c $ 无连边,则$ {\rm{sim}}(b,c) = \left| {n(b) \cap n(c)} \right|/\left| {n(b) \cup n(c)} \right| $ ;若节点$ b $ 与$ c $ 有连边,则$ {\rm{sim}}(b,c) = 1 $ 。 -
文献[15]结合K-壳分解法以及节点的信息熵,根据K-壳的分层大小依次进行迭代,每层中选择节点信息熵最高的节点,直到所有节点均被选中为止,定义为:
$$ {e_i} = - \sum\limits_{j \in \tau (i)}^{} {{I_j}\ln {I_j}} $$ (5) 式中,
$\tau (i)$ 表示节点$i$ 的邻居集;$ {I_i} = {k_i}/\displaystyle\sum\limits_{j = 1}^n {{k_j}} $ 。 -
文献[16]综合考虑了节点的邻居信息和节点间的路径信息,分别将节点的度值和最短路径长度类比为物体的质量和距离,提出了引力模型算法,计算公式如下:
$$ {\rm{G}}{{\rm{M}}_i} = \sum\limits_{{d_{ij < R,j \ne i}}} {\frac{{{k_i}{k_j}}}{{{d_{ij}}^2}}} $$ (6) 式中,
$ R $ 表示截断半径,通常为平均最短距离的一半。由于仅考虑了截断半径内的引力,该算法也被称为局部引力模型。 -
文献[17]认为节点在网络中所处的位置是一个重要属性,因此,在K-壳分解法的基础上对引力模型进行了改进,提出了KSGC算法用于评估节点的影响力,计算公式如下:
$$ {\rm{KSG}}{{\rm{C}}_i} = \sum\limits_{{d_{ij < R,j \ne i}}} {{C_{ij}}\frac{{{k_i}{k_j}}}{{{d_{ij}}^2}}} $$ (7) 式中,
$ {C_{ij}} = {{\rm{e}}^{\tfrac{{{\rm{K}}{{\rm{S}}_i} - {k_i}}}{{{\rm{K}}{{\rm{S}}_{\max }} - {\rm{K}}{{\rm{S}}_{\min }}}}}} $ ;$ {\rm{K}}{{\rm{S}}_{\max }} $ 为节点K-壳的最大值;$ {\rm{K}}{{\rm{S}}_{\min }} $ 为节点K-壳的最小值。 -
交叉熵[28]广泛应用于逻辑回归模型分析中,其定义为随机分布
$ p $ 和$ q $ 之间的自信息差异,可用来量化两个变量之间的相似度,通常交叉熵值越大,则两个变量之间的差异性越大,其计算公式如下:$$ H(p,q) = {E_p}[ - \ln q(x)] = - \sum\limits_x {p(x)\ln q(x)} $$ (8) 式中,
$ x $ 表示事件包含的信息量。对式(8)同时增减$ \displaystyle\sum\nolimits_x {p(x)\ln p(x)} $ ,可得:$$ \begin{split} & H(p,q) = - \sum\limits_x {p(x)\ln q(x)} + \sum\limits_x {p(x)\ln p(x)} - \\ &\qquad\qquad\qquad \sum\limits_x {p(x)\ln p(x)} \end{split} $$ (9) 将式(9)中的前两项对数函数合并可得:
$$ H(p,q){\text{ = }} - \sum\limits_x {p(x)\ln p(x)} + \sum\limits_x {p(x)\ln \frac{{p(x)}}{{q(x)}}} $$ (10) 则式(10)可被定义为:
$$ H(p,q)=H(p)+{D}_{{\rm{KL}}}(p\Vert q) $$ (11) 式中,
$ H(p) $ 为信息熵,表示随机分布$ p $ 的平均信息量;$ {D}_{{\rm{KL}}}(p\Vert q) $ 为相对熵,同样反映随机分布$ p $ 和$ q $ 之间的差异程度。因此,交叉熵作为信息熵与相对熵之和,对于随机变量的信息量及其差异性刻画更加直观。 -
交叉熵可衡量随机变量所包含信息量的差异,类似地,复杂网络中不同节点之间的拓扑信息也存在差异,因此考虑引入交叉熵衡量复杂网络中节点的统计特征。
基于交叉熵的节点重要性排序算法的原理是综合考察节点自身以及其周围节点信息的整体重要性,结合这两种拓扑信息,可利用交叉熵值来量化节点分布之间的差异,若交叉熵值越大,则节点之间分布差异性越大,说明该节点代表性越高,重要性更显著。因此本文提出了基于交叉熵的算法CE+,其定义如下:
$$ {\rm{C}}{{\rm{E}}_{i + }} = - \sum\limits_{j \in \varGamma (i)} {{I_i} \ln {I_j}} $$ (12) 式中,
$ j \in \varGamma (i) $ 表示节点$ j $ 是节点$ i $ 的邻居节点;$ {I_i} $ 表示节点$ i $ 的异构性。考虑到度中心性可在时间复杂度较低的同时较好地反映节点及其近邻节点所构成子网络的拓扑结构,因此将$ {I_i} $ 定义为:$$ {I_i} = \frac{{{\rm{D}}{{\rm{C}}_i}}}{{\displaystyle\sum\limits_{j = 1}^n {{\rm{D}}{{\rm{C}}_j}} }} $$ (13) 由此,节点之间的异构性可得以良好的表征。在基于交叉熵的节点重要性计算方法中,通过融合中心节点与其局部节点的信息结构并相互交叉考虑,使得节点影响力的差异刻画更为准确。该算法的伪代码如下。
1)输入:网络 G = (V, E)
2)输出:节点
$ i $ 的重要性评估值$ {\rm{C}}{{\rm{E}}_{i + }} $ ①遍历节点
$ i $ 的邻居节点$ j $ ②计算节点
$ i $ 的度中心性${\rm{D}}{{\rm{C}}_i}$ ③计算邻居节点
$ j $ 的度中心性之和$ \displaystyle\sum\limits_{j = 1}^n {{\rm{D}}{{\rm{C}}_j}} $ ④计算节点
$ i $ 的异构性$ {I_i} $ ⑤计算节点
$ i $ 的交叉熵值$ {\rm{C}}{{\rm{E}}_{i + }} $ 表1列出了8种不同评估算法的时间复杂度,分别包括局部、全局以及混合3个类型的网络信息。其中CE+算法的时间复杂度与DC、LLS、ME以及IKS算法同为最低。
表 1 不同评估算法的时间复杂度
算法 类型 时间复杂度 DC Local O(n) BC Global O(n3) or O(nm) LLS Local O(n) KSGC Hybrid O(n2) GM Global O(n2) ME Local O(n) IKS Hybrid O(n) CE+ Local O(n) -
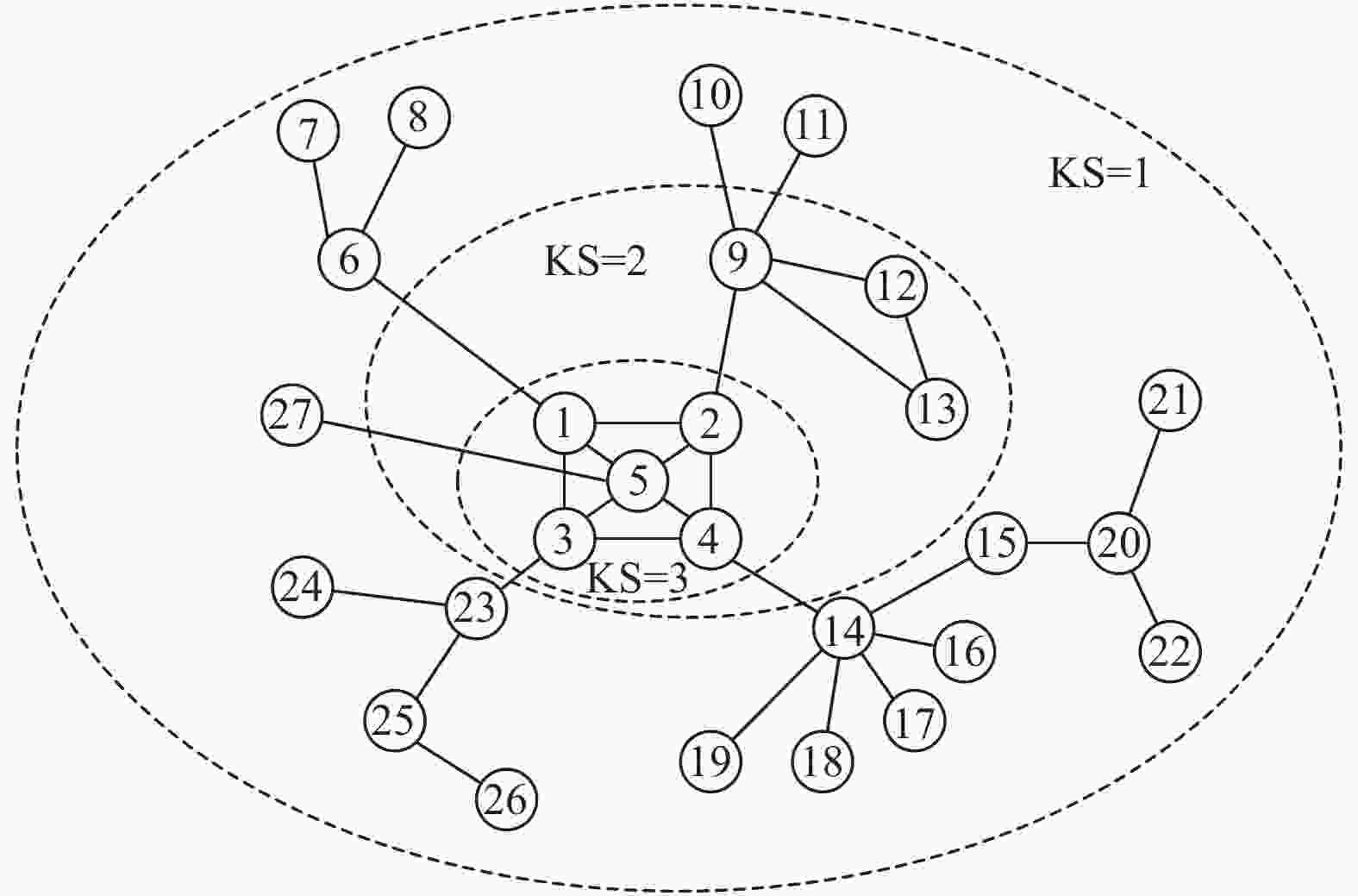
为初步验证CE+算法的量化分辨率与精确性,构建示例网络如图1所示。
在示例网络中,以节点24为例,其交叉熵计算过程如下:
$$ \begin{split} &{\rm{C}}{{\rm{E}}_{24 + }} = - \sum\limits_{j \in \varGamma (i)} {{I_i} \ln {I_j}} = \\ & - (\frac{1}{3}\ln \frac{3}{{4 + 2 + 1}}) = 0.2824 \end{split} $$ (14) 节点24的度值为1,其邻居节点23的度值为3,而节点23的其余邻居节点3、25的度值分别为4、2,故计算节点24的交叉熵值为0.2824。同理,可以计算示例网络中其他节点的交叉熵值,其计算结果如表2所示。
表3记录了不同评估算法对示例网络中节点进行排序的结果,可以看出,KSGC和GM算法与本文所提出的CE+算法具有相同的排名广度,但其对首要节点的排序结果略有不同,分别移除节点4、5和14,得出非连通子图的数量分别为2、2和6,显然移除节点14对网络破坏性更大。此外其余算法对网络外围节点的量化区分度较低,过于粗粒化。因此CE+算法对重要节点排序的精确性得到了初步验证。
表 2 各节点的交叉熵值
节点 CE+值 节点 CE+值 节点 CE+值 1 1.2018 10 0.1386 19 0.0851 2 1.0803 11 0.1386 20 2.7760 3 1.2539 12 0.5560 21 0.0959 4 0.9737 13 0.5560 22 0.0959 5 2.1895 14 6.1376 23 1.3620 6 1.7918 15 0.1774 24 0.2824 7 0.2310 16 0.0851 25 0.7702 8 0.2310 17 0.0851 26 0.3466 9 3.6142 18 0.0851 27 0.2448 表 3 不同评估算法排序结果
排名 DC BC LLS KSGC GM ME IKS CE+值 1 14 14 14 4 5 5 1 14 2 5,9 4 9 2 4 4 4 9 3 1~4 2 5 3 2 2 7 20 4 6,20,23 3 4 1 14 1,3 10,12 5 5 12,13,15,25 9 2 5 3 9 3 6 6 others 1 1,3 9 1 14 2 23 7 23 23 12,13 9 23 6 3 8 15 6 23 23 15 9 1 9 6,20 20 15 6 12,13 5,8 2 10 5 15 14 15 6 11 4 11 25 25 6 12,13 25 13 25 12 others others 27 20 20 14~17 12,13 13 16~19 25 16~19 18 26 14 20 27 10,11,27 19~21 24 15 25 16~19 7,8 22~26 27 16 10,11 10,11 21,22 27 7,8 17 24 24 24 15 18 7,8 7,8 26 10,11 19 21,22 21,22 21,22 20 26 26 16~19 -
实验选用了8个不同领域的真实网络数据集,分别是:维基语录编辑网络Wikiquote[29]、金融网络Economic[30]、约束优化模型网络BP[31]、犯罪案件人物关系网络Crime[32]、大学生电子邮件网络Email[33]、空中交通管制网络Traffic[34]、智人细胞中的蛋白质网络Proteins[35]以及青少年朋友关系网络Adolescent[36]。表4列出了各网络的拓扑统计参数,其中
$ N $ 和$ E $ 分别为网络的节点总数和连边总数,$ D $ 表示网络的密度,kmax表示网络节点的最大度值,<k>和<d>分别为网络节点的平均度值与平均最短路径距离,βth和β分别为SIR模型传播阈值以及实际传播率。表 4 8个真实网络的拓扑统计特征及传播率
网络 N E D kmax <k> <d> βth β Wikiquote 25 37 0.1233 5 1.4800 1.6092 0.1689 0.17 Economic 260 2942 0.0827 110 21.6970 2.5320 0.0441 0.05 BP 822 3276 0.0097 266 7.6233 3.3549 0.1254 0.13 Crime 829 1476 0.0043 25 2.1391 5.0400 0.0928 0.09 Email 1133 5451 0.0085 71 9.6222 3.6060 0.0535 0.05 Traffic 1226 2615 0.0034 37 4.2659 5.9290 0.2344 0.23 Proteins 2239 6452 0.0025 314 5.7632 3.9786 0.1735 0.17 Adolescent 2539 12969 0.0040 36 10.2158 4.5164 0.0978 0.10 -
为验证CE+算法的性能,本文基于网络节点的单调关系、鲁棒性以及SIR传播动力学模型对节点重要性进行研究。首先采用单调性指标定量分析不同算法的分辨率,其次选取极大连通系数以及网络效率指标来评估攻击节点前后网络结构和功能的变化,最后在SIR模型上再进行传播仿真实验分析。
单调性指标[23]是通过计算节点重要性排序中具有相同排名索引的节点比例来度量节点的评估效果,定义为:
$$ M(R)={\left[1-\frac{{\displaystyle \sum _{r\in R}{n}_{r}({n}_{r-1})}}{n(n-1)}\right]}^{2} $$ (15) 式中,
$ R $ 为经由节点重要性排序算法所得到的排名索引;nr表示具有相同排名索引的节点数量;$ M(R) \in [0,1] $ ,若$ M(R) = 1 $ ,则该算法完全单调,所有节点都具有不同的排名索引值。若$ M(R) = 0 $ ,则该算法无法区分,每个节点的排名索引值相同。极大连通系数[24]常用于评价移除网络中的节点后对极大连通子集的影响,表示为:
$$ C = \frac{{{N_i}^R}}{N} $$ (16) 式中,
$ {N_i}^R $ 为移除节点$ i $ 后网络巨片的规模。网络巨片中包含的节点数若随攻击节点数的增多而急剧减少,则说明该评估算法更准确。网络效率[25-26]常用于度量网络连通性的强弱,计算公式为:
$$ E = \frac{1}{{N(N - 1)}}\sum\limits_{1 \leqslant i < j \leqslant N}^{} {\frac{1}{{{d_{ij}} }}} $$ (17) 攻击网络中一定比例的节点,若网络效率下降趋势越明显,则该算法的排序准确性越高。
SIR模型[27]常用于验证节点传播信息与病毒的能力,在SIR模型中,网络中的所有节点具有3种状态,分别是易感状态S、感染状态I以及免疫状态R。病毒传播初始时,除少数节点处于感染状态外,其他节点均处于易感状态。每个时间步长里,感染节点以β的概率尝试感染易感的邻居节点,此外,感染节点还以μ 的概率尝试恢复为免疫节点,为不失一般性,本文设定恢复率μ =1。需要注意的是,免疫节点不会被再次感染,同样也不具有感染能力。当网络达到稳定时,传播过程结束,此时免疫节点的数量可用于量化初始感染节点的传播能力。
-
本文选取了度中心性(DC)、介数中心性(BC)等经典算法作为对比方法,还选取了邻域相似度(LLS)、引力模型(GM)、改进的引力模型(KSGC)、映射熵(ME)以及改进的K-壳分解法(IKS)等近期提出的性能显著的排序算法进行比较,记录8种排序算法在8个真实网络数据上各评估指标的实验结果。
-
表5记录了本文所提出的CE+算法与其他评估算法的单调性指标,加粗数值为最优值,可以看出,CE+算法在大部分网络中均表现出较好的分辨率,并在一些网络(如BP、Adolescent)中达到了1,这说明CE+算法是完全单调的,网络中的每个节点都具有不同的排名索引值。此外,KSGC和GM算法也表现出良好的区分度。
表 5 不同评估算法的单调性指标
网络 DC BC LLS KSGC GM ME IKS CE+值 Wikiquote 0.4807 0.5136 0.4139 0.8040 0.8040 0.7685 0.7685 0.8040 Economic 0.8300 0.9774 0.9759 0.9990 0.9989 0.9946 0.9948 0.9994 BP 0.8518 1 0.9992 1 1 0.9995 0.9997 1 Crime 0.6990 0.8669 0.8651 0.9994 0.9993 0.9837 0.9846 0.9988 Email 0.8874 0.9400 0.9400 0.9999 0.9999 0.9989 0.9990 0.9999 Traffic 0.5922 0.9770 0.9624 0.9997 0.9998 0.9884 0.9916 0.9993 Proteins 0.5928 0.6233 0.6201 0.9937 0.9938 0.9912 0.9913 0.9942 Adolescent 0.8677 0.9975 0.9974 1 1 0.9997 0.9998 1 -
图2呈现了不同评估算法模拟蓄意攻击网络所造成极大连通系数变化的趋势,其中横坐标为各评估算法排序下依次移除节点占节点总数的比例,纵坐标为极大连通系数,可以看出在8个真实网络中,本文提出的CE+算法均表现出更好的攻击效果。在BP和Adolescent网络中,各算法的前期破坏效果出现了高度重合,这是因为网络的连边总数远高于节点总数,导致节点间紧密连接,而当攻击节点数达到一定比例时,CE+算法表现出了较其他算法更为明显的攻击效果。因此,CE+算法度量节点重要性的准确性得到了验证。
-
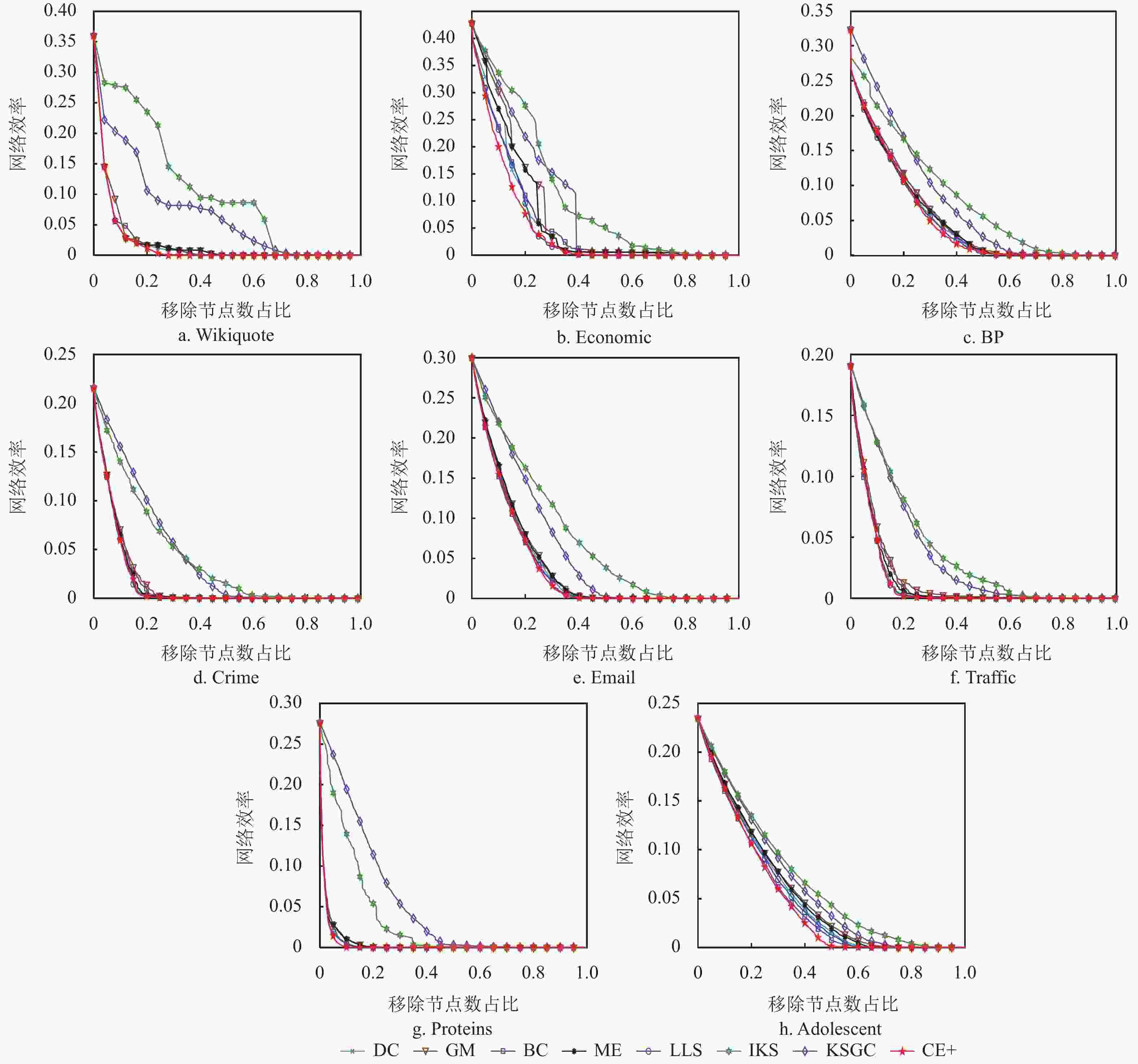
图3展现了利用不同的评估算法排序依次移除节点后,对网络效率所造成的变化趋势。可以看出,在Wikiquote网络、Economic网络和Adolescent网络中,CE+算法相较于其他算法对网络的蓄意攻击效果更为明显,而在Crime网络与Traffic网络中,KSGC和IKS算法的攻击效果基本一致,ME和DC算法分别在移除节点比例达到16%以及18%时,破坏效果最明显。此外,当攻击节点比例相同时,CE+算法的破坏曲线整体下降最快,这说明此时的网络连通性最差。因此,CE+算法度量节点重要性的准确性得到了进一步验证。
-
为从不同角度评价CE+算法的有效性和适用性,在SIR模型中再进行传播实验分析,利用各种评估算法排序前10%的节点作为初始感染节点,传播率阈值设定为βth=<k>/<k2>。其中<k>为平均度,<k2>为二阶平均度。实际传播率基于阈值四舍五入并精确到百分位,具体取值如表5所示。为减小迭代过程随机的影响,本文选择对于
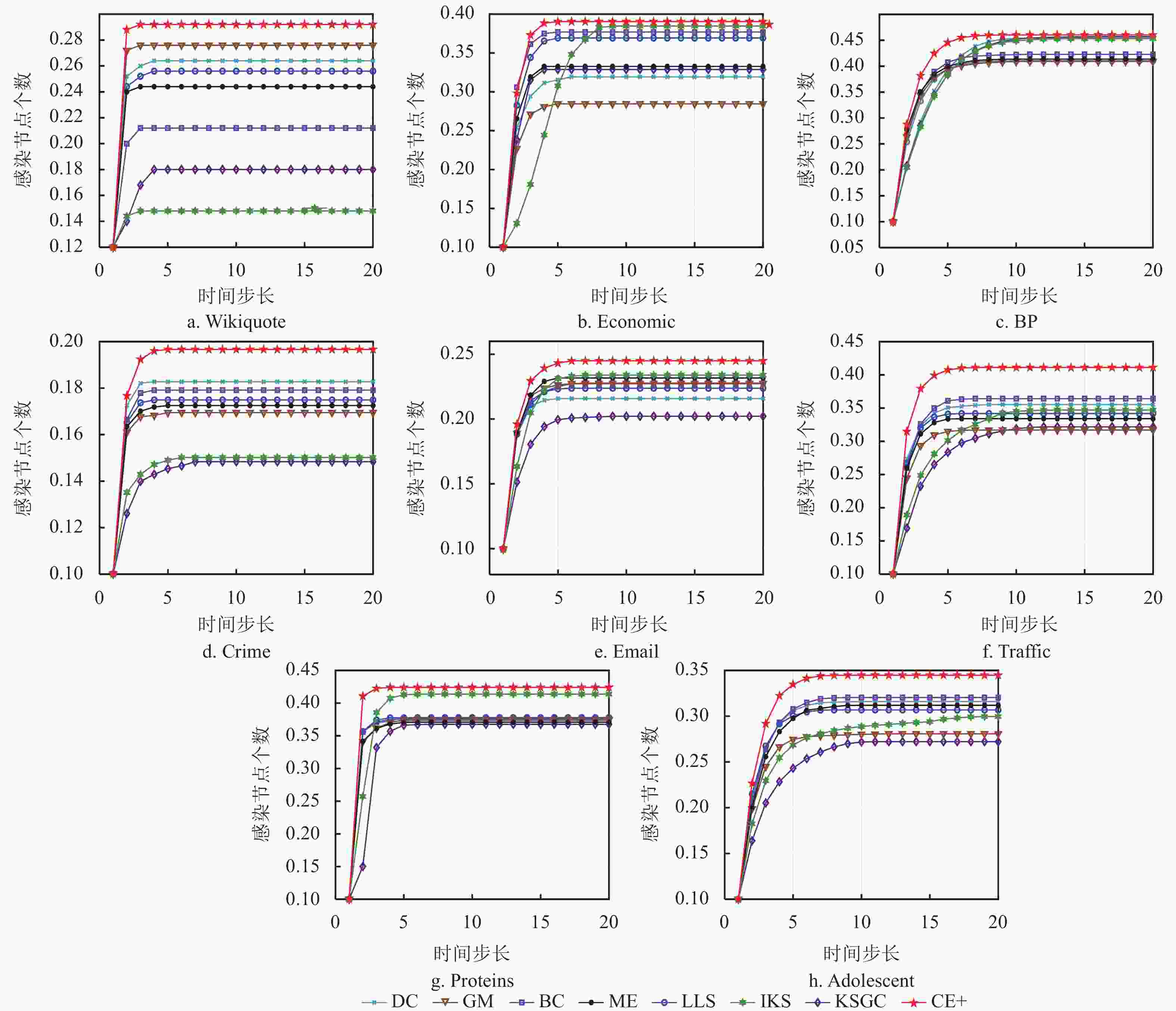
$ N $ <1000的网络模拟迭代1000次,对于$ N $ >1000的网络模拟迭代100次。图4反映了各评估算法中重要性排名前10%的节点作为感染节点
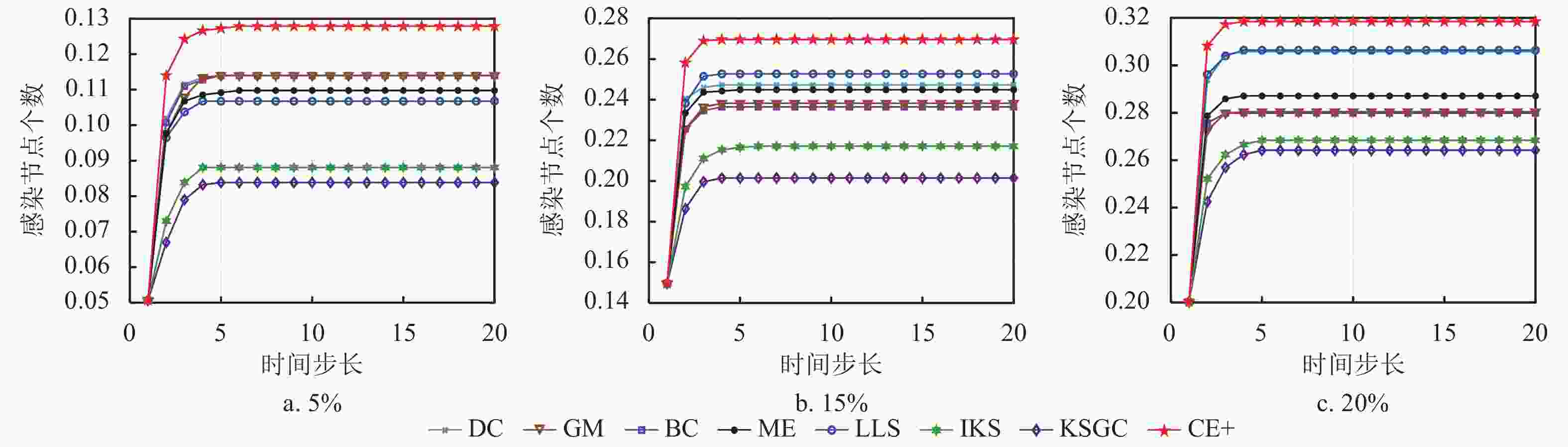
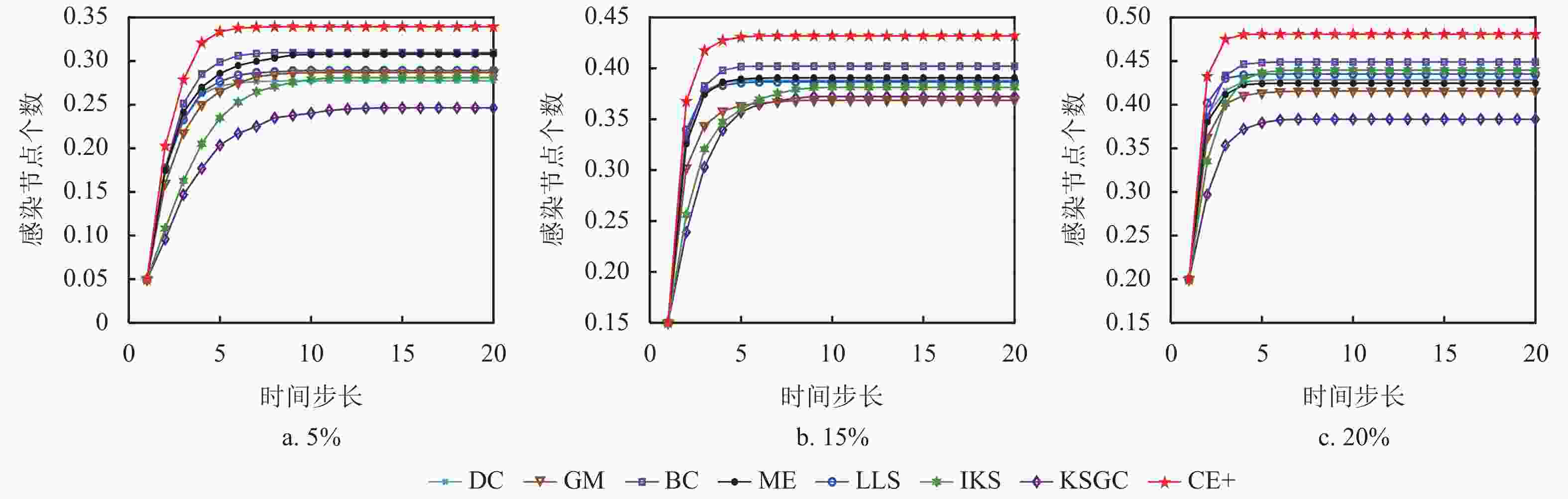
$ N $ 随时间步长t的变化趋势,可以看出当时间步长达到15时,大部分网络趋于稳定,其中CE+算法的传播曲线具有处于稳定状态时的最高高度以及最大斜率,这说明本文所提出的算法具有最广泛的传播范围以及最快传播速率。而在BP网络中,CE+算法的传播效果与其他算法的差异较小,是因为该网络的节点间分布密集,关联程度较高,信息具有易传播、易扩散的特点。整体来看,CE+算法相较于其他算法更能准确快速地挖掘出网络中影响能力较强的节点。为比较不同比例的初始节点在传播达到稳态时的规模,本文分别选取模拟迭代1000次的Crime网络以及模拟迭代次数100次的Traffic网络,并分别选取各种算法排名前5%、15%以及20%的节点作为感染节点进行传播验证实验,实验结果分别如图5和图6所示。结合图5中Crime和Traffic网络图可知,BC算法曲线趋于稳态的高度仅在初始感染节点为5%时较高,IKS算法曲线也仅在初始感染节点比例为20%时具有较大的斜率,而CE+算法在各种比例初始感染节点下均具有显著的传播范围以及感染速率,可知CE+算法在这两方面优于其他算法,由此验证了CE+算法的有效性以及适用性。
-
在网络科学研究中,识别复杂网络中的核心关键节点有助于提高网络的鲁棒性和抗毁性。本文基于交叉熵提出了一种新的节点性能评价排序算法,算法只需获取中心节点与其近邻节点的信息就可反映节点之间的差异性,并且时间复杂度仅为
$ O(n) $ ,适用于刻画大规模复杂网络中节点的重要性。通过在8个不同领域的真实网络上进行单调关系、极大连通系数、网络效率以及SIR模型传播实验,结果表明,本文所提的CE+算法对比DC、BC、LLS、KSGC、GM、ME和IKS算法具有更高效的性能。
Node Importance Ranking Algorithm Based on Cross Entropy
-
摘要: 如何高效地度量节点的重要性一直是复杂网络研究的热点问题。在节点重要性研究中,目前已有许多算法被提出用于判断关键节点,然而多数算法局限于时间复杂度过高或评估角度单一。考虑到熵可用于定量描述信息量的大小,因此,提出了一种基于交叉熵的节点重要性排序算法,该算法兼顾了中心节点与其近邻节点之间的整体影响力,并将节点的邻域拓扑信息有机地融合,使用交叉熵值来量化节点之间的信息差异性。为验证该算法的性能,首先采用单调关系、极大连通系数、网络效率以及SIR模型作为评价指标,其次在8个不同领域的真实网络上与其他7种算法进行比较实验。实验结果表明,该算法具有有效性和适用性,此外时间复杂度仅为
$ O(n) $ ,适用于大型网络。Abstract: How to efficiently measure the importance of nodes has been a hot issue in the research of complex networks. In the research of node importance, many algorithms have been proposed to judge key nodes, but most of them are limited to high time complexity or single evaluation angle. Considering that entropy can be used to quantitatively describe the amount of information, this paper proposes a node importance ranking algorithm based on cross entropy. This algorithm takes into account the overall influence among the central node and its neighbor nodes, organically fuses the neighborhood topology information of nodes, and uses cross entropy to quantify the information differences between nodes. In order to verify the performance of the algorithm, this paper first uses monotone relation, maximum connectivity coefficient, network efficiency and SIR model as evaluation indicators, and then compares with other seven algorithms on eight real networks in different fields. The experimental results show that the algorithm proposed in this paper is effective and applicable, and the time complexity is only$ O(n) $ , which is suitable for large networks.-
Key words:
- attack strategy /
- cross entropy /
- complex network /
- node importance
-
表 1 不同评估算法的时间复杂度
算法 类型 时间复杂度 DC Local O(n) BC Global O(n3) or O(nm) LLS Local O(n) KSGC Hybrid O(n2) GM Global O(n2) ME Local O(n) IKS Hybrid O(n) CE+ Local O(n) 表 2 各节点的交叉熵值
节点 CE+值 节点 CE+值 节点 CE+值 1 1.2018 10 0.1386 19 0.0851 2 1.0803 11 0.1386 20 2.7760 3 1.2539 12 0.5560 21 0.0959 4 0.9737 13 0.5560 22 0.0959 5 2.1895 14 6.1376 23 1.3620 6 1.7918 15 0.1774 24 0.2824 7 0.2310 16 0.0851 25 0.7702 8 0.2310 17 0.0851 26 0.3466 9 3.6142 18 0.0851 27 0.2448 表 3 不同评估算法排序结果
排名 DC BC LLS KSGC GM ME IKS CE+值 1 14 14 14 4 5 5 1 14 2 5,9 4 9 2 4 4 4 9 3 1~4 2 5 3 2 2 7 20 4 6,20,23 3 4 1 14 1,3 10,12 5 5 12,13,15,25 9 2 5 3 9 3 6 6 others 1 1,3 9 1 14 2 23 7 23 23 12,13 9 23 6 3 8 15 6 23 23 15 9 1 9 6,20 20 15 6 12,13 5,8 2 10 5 15 14 15 6 11 4 11 25 25 6 12,13 25 13 25 12 others others 27 20 20 14~17 12,13 13 16~19 25 16~19 18 26 14 20 27 10,11,27 19~21 24 15 25 16~19 7,8 22~26 27 16 10,11 10,11 21,22 27 7,8 17 24 24 24 15 18 7,8 7,8 26 10,11 19 21,22 21,22 21,22 20 26 26 16~19 表 4 8个真实网络的拓扑统计特征及传播率
网络 N E D kmax <k> <d> βth β Wikiquote 25 37 0.1233 5 1.4800 1.6092 0.1689 0.17 Economic 260 2942 0.0827 110 21.6970 2.5320 0.0441 0.05 BP 822 3276 0.0097 266 7.6233 3.3549 0.1254 0.13 Crime 829 1476 0.0043 25 2.1391 5.0400 0.0928 0.09 Email 1133 5451 0.0085 71 9.6222 3.6060 0.0535 0.05 Traffic 1226 2615 0.0034 37 4.2659 5.9290 0.2344 0.23 Proteins 2239 6452 0.0025 314 5.7632 3.9786 0.1735 0.17 Adolescent 2539 12969 0.0040 36 10.2158 4.5164 0.0978 0.10 表 5 不同评估算法的单调性指标
网络 DC BC LLS KSGC GM ME IKS CE+值 Wikiquote 0.4807 0.5136 0.4139 0.8040 0.8040 0.7685 0.7685 0.8040 Economic 0.8300 0.9774 0.9759 0.9990 0.9989 0.9946 0.9948 0.9994 BP 0.8518 1 0.9992 1 1 0.9995 0.9997 1 Crime 0.6990 0.8669 0.8651 0.9994 0.9993 0.9837 0.9846 0.9988 Email 0.8874 0.9400 0.9400 0.9999 0.9999 0.9989 0.9990 0.9999 Traffic 0.5922 0.9770 0.9624 0.9997 0.9998 0.9884 0.9916 0.9993 Proteins 0.5928 0.6233 0.6201 0.9937 0.9938 0.9912 0.9913 0.9942 Adolescent 0.8677 0.9975 0.9974 1 1 0.9997 0.9998 1 -
[1] WATTS D J, STROGATZ S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393(6684): 440-442. doi: 10.1038/30918 [2] BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. doi: 10.1126/science.286.5439.509 [3] 任晓龙, 吕琳媛. 网络重要节点排序方法综述[J]. 科学通报, 2014, 59(13): 1175-1197. REN X L, LYU L Y. Review of ranking nodes in complex networks[J]. Science Bulletin, 2014, 59(13): 1175-1197. [4] 朱军芳, 陈端兵, 周涛, 等. 网络科学中相对重要节点挖掘方法综述[J]. 电子科技大学学报, 2019, 48(4): 595-603. doi: 10.3969/j.issn.1001-0548.2019.04.018 ZHU J F, CHEN D B, ZHOU T, et al. A survey on mining relatively important nodes in network science[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(4): 595-603. doi: 10.3969/j.issn.1001-0548.2019.04.018 [5] GUO Y, GUO C, YANG J. A tri-level optimization model for power systems defense considering cyber-physical interdependence[J]. IET Generation, Transmission and Distribution, 2023, 17(7): 1477-1490. [6] VIDAL M, CUSICK M E, BARABASI A L. Interactome networks and human disease[J]. Cell, 2011, 144(6): 986-998. doi: 10.1016/j.cell.2011.02.016 [7] ROGERS T. Assessing node risk and vulnerability in epidemics on networks[J]. Europhysics Letters, 2015, 109(2): 28005. doi: 10.1209/0295-5075/109/28005 [8] FREEMAN L C. Segregation in social networks[J]. Social network, 1978, 6(4): 411-429. [9] FREEMAN L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1): 35-41. [10] SABIDUSSI G. The centrality index of a graph[J]. Psychometrika, 1966, 31(4): 581-603. doi: 10.1007/BF02289527 [11] KITSAK M, GALLOS L K, HAVLIN S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2010, 6(11): 888-893. doi: 10.1038/nphys1746 [12] BASARAS P, KATSAROS D, TASSIULAS L. Detecting influential spreaders in complex, dynamic networks[J]. Computer, 2013, 46(4): 24-29. doi: 10.1109/MC.2013.75 [13] NIE T, GUO Z, ZHAO K, et al. Using mapping entropy to identify node centrality in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 453: 290-297. doi: 10.1016/j.physa.2016.02.009 [14] 阮逸润, 老松杨, 王竣德, 等. 基于领域相似度的复杂网络节点重要度评估算法[J]. 物理学报, 2017, 66(3): 371-379. YUAN Y R, LAO S Y, WANG J D, et al. Node importance measurement based on neighborhood similarity in complex network[J]. Acta Physica Sinica, 2017, 66(3): 371-379. [15] WANG M, LI W, GUO Y, et al. Identifying influential spreaders in complex networks based on improved k-shell method[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 554: 124229. doi: 10.1016/j.physa.2020.124229 [16] LI Z, HUANG X Y. Identifying influential spreaders in complex networks by an improved gravity model[J]. Scientific Reports, 2021, 11(1): 1-10. doi: 10.1038/s41598-020-79139-8 [17] YANG X, XIAO F. An improved gravity model to identify influential nodes in complex networks based on k-shell method[J]. Knowledge-Based Systems, 2021, 227: 107198. doi: 10.1016/j.knosys.2021.107198 [18] SHANNON C E. Communication in the presence of noise[J]. Proceedings of the IRE, 1949, 37(1): 10-21. [19] FEI L, DENG Y. A new method to identify influential nodes based on relative entropy[J]. Chaos, Solitons and Fractals, 2017, 104: 257-267. [20] 汪亭亭, 梁宗文, 张若曦. 基于信息熵与迭代因子的复杂网络节点重要性评价方法[J]. 物理学报, 2023, 72(4): 1-25. WANG T T, LIANG Z W, ZHANG R X. Identifying influential nodes in complex networks using iteration factor and information entropy[J]. Acta Physica Sinica, 2023, 72(4): 1-25. [21] ZHANG Q, LI M Z, DENG Y. A new structure entropy of complex networks based on nonextensive statistical mechanics[J]. International Journal of Modern Physics C, 2016, 27(10): 440-452. [22] 杨松青, 蒋沅, 童天驰, 等. 基于Tsallis熵的复杂网络节点重要性评估方法[J]. 物理学报, 2021, 70(21): 273-284. YANG S Q, JIANG Y, TONG T C, et al. A method of evaluating importance of nodes in complex network based on Tsallis entropy[J]. Acta Physica Sinica, 2021, 70(21): 273-284. [23] BAE J, KIM S. Identifying and ranking influential spreaders in complex networks by neighborhood coreness[J]. Physica A: Statistical Mechanics and Its Applications, 2014, 395: 549-559. doi: 10.1016/j.physa.2013.10.047 [24] DEREICH S, MORTERS P. Random networks with sublinear preferential attachment: The giant component[J]. The Annals of Probability, 2013, 41(1): 329-384. [25] VRAGOVIC I, LOUIS E, DIAZ-GUILERA A. Efficiency of informational transfer in regular and complex networks[J]. Physical Review E, 2005, 71(3): 036122. doi: 10.1103/PhysRevE.71.036122 [26] LATORA V, MARCHIORI M. A measure of centrality based on network efficiency[J]. New Journal of Physics, 2007, 9(6): 188. doi: 10.1088/1367-2630/9/6/188 [27] CASTELLANO C, PASTOR-SATORRAS R. Thresholds for epidemic spreading in networks[J]. Physical Review Letters, 2010, 105(21): 218701. doi: 10.1103/PhysRevLett.105.218701 [28] JAMIN A, HUMEAU-HEURTIER A. (Multiscale) cross-entropy methods: A review[J]. Entropy, 2019, 22(1): 45. doi: 10.3390/e22010045 [29] CHANDRA A, GARG H, MAITI A. A general growth model for online emerging user-object bipartite networks[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 517: 370-384. doi: 10.1016/j.physa.2018.10.051 [30] SARKAR D, ANDRIS C, CHAPMAN C A, et al. Metrics for characterizing network structure and node importance in spatial social networks[J]. International Journal of Geographical Information Science, 2019, 33(5): 1017-1039. doi: 10.1080/13658816.2019.1567736 [31] ZHANG L, WANG F, SUN T, et al. A constrained optimization method based on BP neural network[J]. Neural Computing and Applications, 2018, 29: 413-421. [32] TRONCOSO F, WEBER R. A novel approach to detect associations in criminal networks[J]. Decision Support Systems, 2020, 128: 113159. doi: 10.1016/j.dss.2019.113159 [33] GUIMERA R, DANON L, DIAZ-GUILERA A, et al. Self-similar community structure in a network of human interactions[J]. Physical Review E, 2003, 68(6): 065103. doi: 10.1103/PhysRevE.68.065103 [34] PIEN K C, HAN K, SHANG W, et al. Robustness analysis of the European air traffic network[J]. Transportmetrica A: Transport Science, 2015, 11(9): 772-792. doi: 10.1080/23249935.2015.1087233 [35] GURSOY A, KESKIN O, NUSSINOV R. Topological properties of protein interaction networks from a structural perspective[J]. Biochemical Society Transactions, 2008, 36(6): 1398-1403. doi: 10.1042/BST0361398 [36] HUNTER D R, GOODREAU S M, HANDCOCK M S. Goodness of fit of social network models[J]. Journal of the American Statistical Association, 2008, 103(481): 248-258. doi: 10.1198/016214507000000446 -


 ISSN
ISSN 





 下载:
下载: