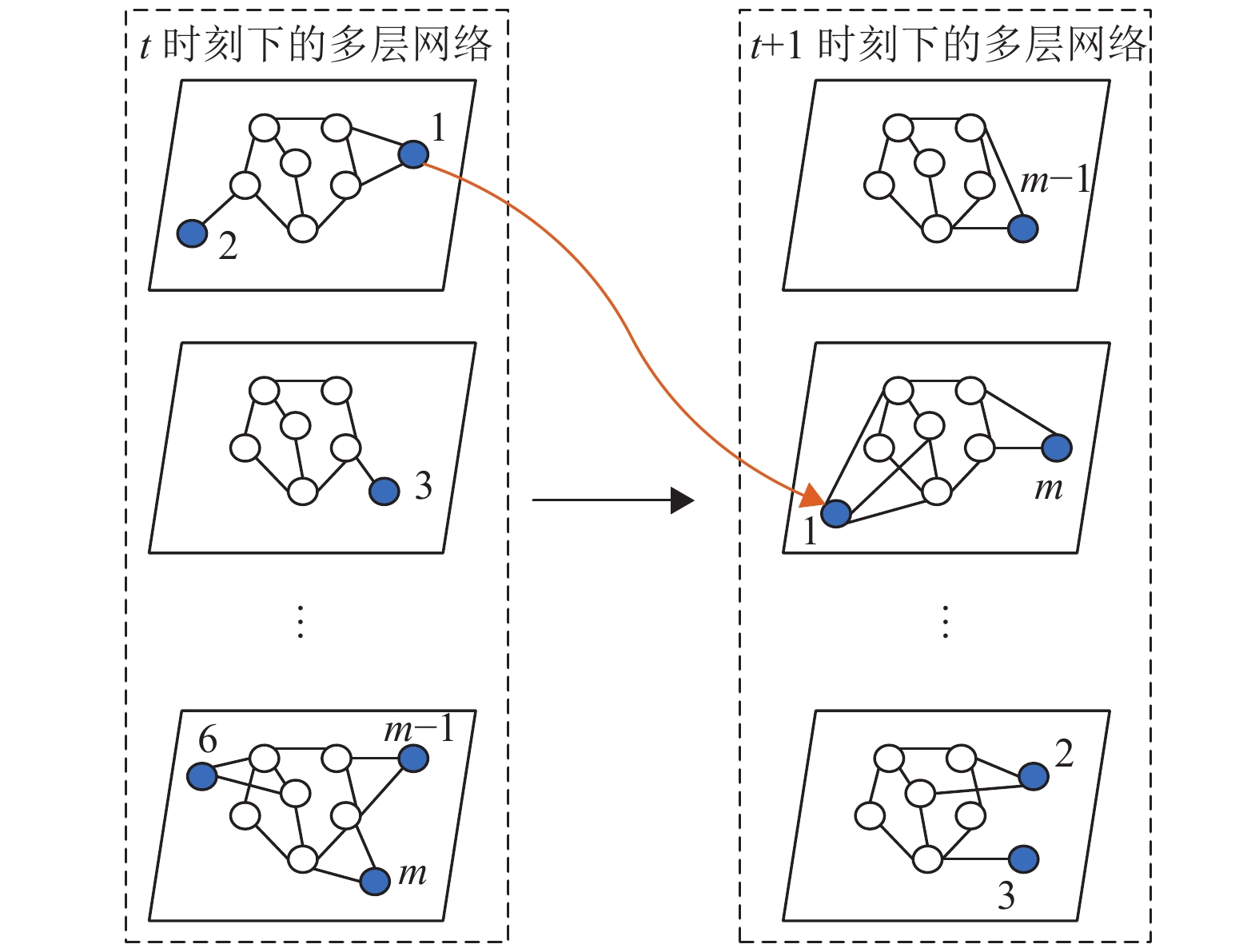
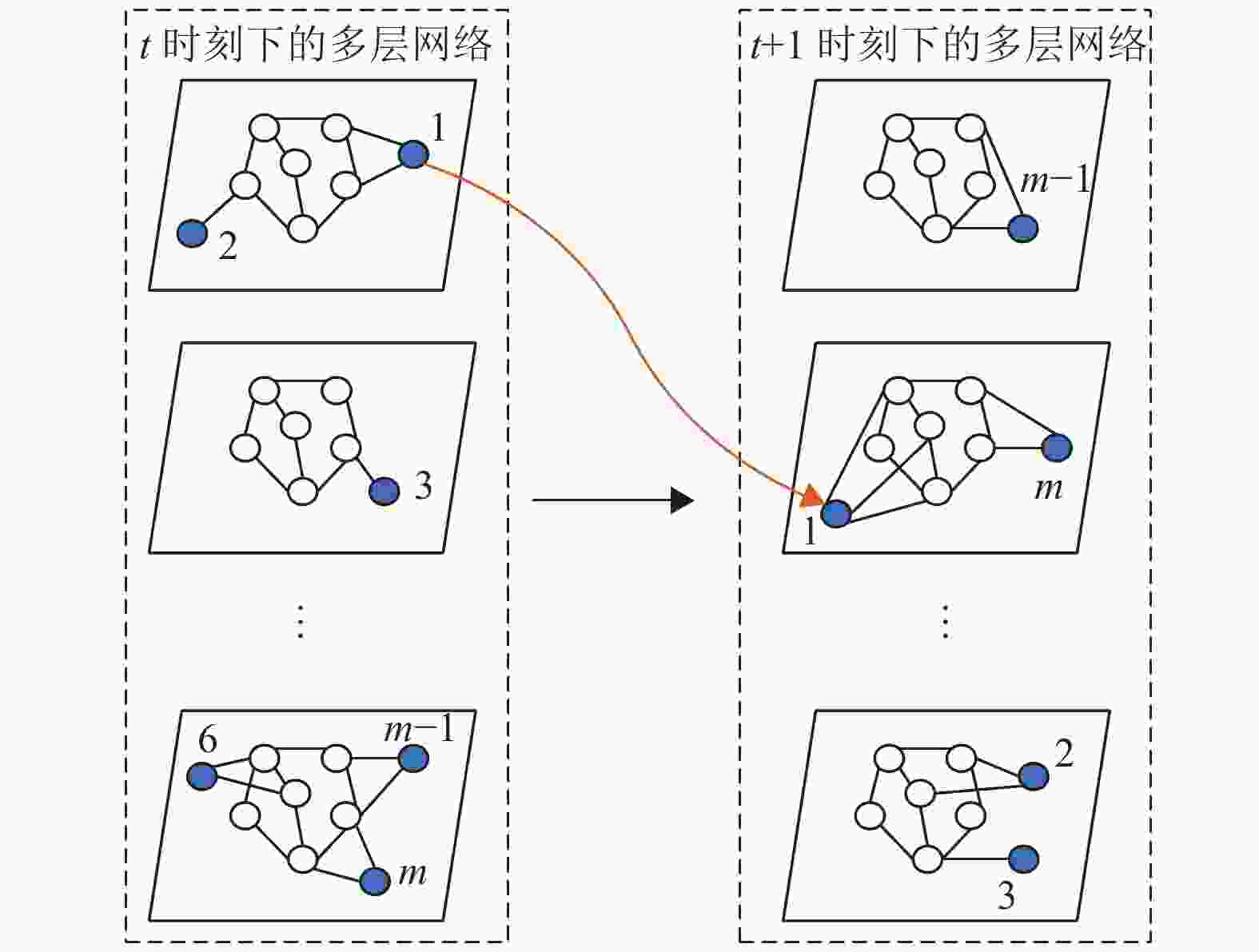
整个系统由多层静态网络与活跃节点共同组成，静态网络中的节点（以下称为静态节点）连边关系不会随着时间的推移而变化，并且每层静态网络相互独立，即属于不同层的静态节点之间不存在连边，而活跃节点随着时间的变化随机在各个静态网络层之间迁移，并随机与所到达层的静态节点连边。活跃节点与当前所属网络层的静态节点断开连边，进入到新的网络层，与新网络层的静态节点建立连边，这一过程称为活跃节点的“跃迁”。活跃节点的这一特性使得整个系统具有时变性^[19]，用该多层网络可以较好地模拟不同城市间的人员流动情况，不同的网络层代表不同的城市，层中的静态节点表示长时间不会进行跨城市活动的人群，而活跃节点则模拟需要时常往返不同城市的人群。如图1所示，白色节点表示静态节点，深色节点表示活跃节点。整个多层网络中共有$m$个活跃节点，如活跃节点1在$t$时刻下处于第一层网络中，并与其中两个静态节点有连边，而在$t + 1$时刻下，跃迁到了第二层网络，并重新与当前网络中的静态节点连边，其他活跃节点的跃迁过程与之类似。

图  1  活跃节点的“跃迁”说明图

设整个多层网络一共有$D$层，每层网络含有$n$个静态节点，整个多层网络有$m$个活跃节点（一般情况下城市间流动人口占每个城市常住人口的比例很小，即$m \ll n$），每层网络可以用一个无权无向连通图表示，对于第$d$层（$ 1 \leqslant d \leqslant D,d \in {N^ + } $）网络对应的图记为${G^d} = ({V^d},{E^d})$，其中${V^d}$代表第$d$层网络的节点集，${E^d}$代表第$d$层网络的连边集。对于整个多层网络模型，则有$\mathcal{G} = (\mathcal{V},\mathcal{E})，\mathcal{V} = \bigcup\nolimits_{d = 1}^D {{V^d}} ，\mathcal{E} = \bigcup\nolimits_{d = 1}^D {{E^d}} $。$\mathcal{G}$表示整个多层网络；$\mathcal{V}$表示整个多层网络的节点集；$\mathcal{E}$表示整个多层网络的连边集。整个多层网络的邻接矩阵记作$ \mathcal{A} = ({{\boldsymbol{A}}_1},{{\boldsymbol{A}}_2}, \cdots ,{{\boldsymbol{A}}_d}, \cdots ,{{\boldsymbol{A}}_D}) $，其中${{\boldsymbol{A}}_d}(1 \leqslant d \leqslant D,d \in {N^ + })$表示第$d$层网络的邻接矩阵，由于每层网络含有$n$个静态节点，以及整个多层网络一共有$m$个活跃节点，每一层网络中最多含有$(n + m)$个节点，为了数学上描述方便，故设$ {A}_{d} $的维度为$(n + m) \times (n + m)$，其中$m$代表全部活跃节点数，如果某时刻活跃节点在$d$层，则可以和该层静态节点产生连边，如果不在该层，则该节点处于未被激活的状态，是孤立节点。在这种规定下，对任意层的邻接矩阵${A_d}$可表示为下式：

式中，${{\boldsymbol{B}}_d}$表示第$d$层网络的静态网络结构，其维度为$n \times n$；${{\boldsymbol{C}}_d}$描述第$d$层网络中活跃节点与该层静态节点的连边关系，其维度为$n \times m$。这些矩阵中的矩阵元为1说明存在连边。而活跃节点与活跃节点之间默认不存在连边，这是因为在模型中活跃节点所占比例较小，而活跃节点联系紧密的情况比较少，如旅游团，这种情况可以把一个团体当成一个活跃节点。因此，为了简化模型，忽略活跃节点内部的连边。

如果不施加干预和控制，新型冠状病毒的传播从短期来看是一个SEIR模型，从中长期来看是一个SEIRS模型，其中S、E、I、R分别表示易感（Susceptible）态节点、潜伏（Exposed）态节点、感染（Infective）态节点和恢复（Removed）态节点^[20]。结合新型冠状病毒的传播特性与现实因素，建立一个时滞SEQS模型来模拟其传播行为。其中Q（Quarantine）态是为了模拟现实中的隔离态，Q态的来源有两种情况：一是E态经过一定时间凸显病症后自动转变为I态后被隔离；二是E态还未发病但是通过检测被确诊为I态后被隔离。

在该时滞SEQS模型中做了一个理想化假设，从E态到I态的转变是个突变，在一个时间步内完成，有明确的界线，但现实中有些疾病E态与I态很难明确划分，如无症状感染者。因此在本模型中引入一种理想的隔离机制，即一旦发现I态节点就及时隔离，因此本模型中的E态实际包含了现实中未能及时隔离的感染个体（包含未能及时发现和故意隐瞒的感染个体），故本模型中E态的传染能力是真正的E态与未被及时隔离的I态的平均。而及时被隔离的I态就转变为Q态，无法传染S态。值得注意的是，Q态与传统的R态的区别在于，R态的移除是由于死亡或者是获得免疫，而Q态的移除是由于隔离，但是Q态与R态在传播过程中起到的动力学作用其实是等效的。

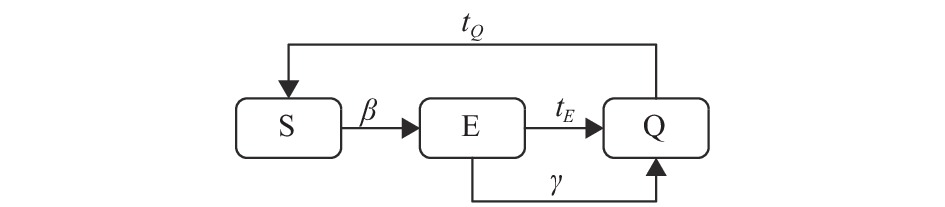
时滞SEQS模型的节点状态转移关系如图2所示。当S态节点的邻接节点中存在E节点时，该S态节点将以概率$ \beta $被感染，如果被成功感染该节点将从S态转为E态；而E态节点则有两种途径转变为Q态节点：1）E态节点的感染时间达到${t_E}$（潜伏期）后，将自动转变为Q态节点，这一过程模拟现实被感染的潜伏个体经过潜伏期后由于病症凸显而被确诊为感染个体；2）E态节点的感染时间并未达到潜伏期${t_E}$，但由于该节点被检测，并且被检测成功，该E态节点则被动转变为Q态节点，检测成功概率为$\gamma $。Q态节点在其感染时间达到${t_Q}$（恢复期或者隔离期）后，将恢复成S态节点继续参与传播。

图  2  节点状态转移图

检测机制将在多层网络中出现Q态节点时被激活，以Q态节点为中心，与该中心节点的距离小于检测半径$r$的节点会被检测，如果被检测的节点处于E态，将有概率$\gamma $被检测成功，而检测成功的E态节点将会转为Q态节点。传染机制、隔离机制与检测机制的具体实现过程在1.3小节中将进行详细说明。

在平均场近似下，模型对应的微分方程组为：

式中，$ \gamma e(t)\left\langle k \right\rangle q(t) $为每次检测成功的部分，而检测未成功的部分，在其转为潜伏态的天数达到潜伏期${t_E}$后自然转变为感染态，即这部分节点每一次检测都未能成功，因此用$ {(1 - \gamma )^{{t_E}}}e(t - {t_E}) $表示。从该动力学方程组可以得到系统的演化信息。

多层网络的层数设定为$D = 5$，既能模拟现实多城市人员流动情况，又不会带来过重的计算负担，每层网络中静态节点数量为$n = 10\;000$，活跃节点个数为$m = 10$，选择BA无标度网络作为各层网络中的静态网络结构，以模拟现实的社交网络，参考新型冠状病毒特性，潜伏期设定为${t_E} = 5$。本文进行了多组实验，以对比在不同的恢复期${t_Q}$、检测半径$r$下，传染概率$\beta $与检测成功率$\gamma $对疾病传播过程的影响。每次模拟实验所迭代的时间步为500，每组参数下重复实验20次，最终的结果为这20次重复实验结果的平均。具体的实验步骤如下。

1）设置矩阵$ \mathcal{A} = \left( {{{\boldsymbol{A}}_1},{{\boldsymbol{A}}_2}, \cdots ,{{\boldsymbol{A}}_d}, \cdots ,{{\boldsymbol{A}}_D}} \right) $储存整个多层网络的结构，其中${{\boldsymbol{A}}_d}\left( {1 \leqslant d \leqslant D,d \in {N^ + }} \right)$为第$d$层网络的邻接矩阵，其维度为$\left( {n + m} \right) \times \left( {n + m} \right)$，如式(1)。设置状态矩阵${\boldsymbol{S}}$、维度为$(D + 1) \times n$，记录多层网络中所有节点的状态，当$i \leqslant D\left( {i \in {N^ + }} \right)$时，状态矩阵${\boldsymbol{S}}$的对应元${s_{ij}}\left( {1 \leqslant j \leqslant n,j \in {N^ + }} \right)$表示第$ i $层网络中第$j$个静态节点所处的状态，${s_{ij}} = 0$表示易感态，${s_{ij}} = 1$表示潜伏态，${s_{ij}} = 2$表示感染态；而当$i = D + 1$时，${s_{ij}}\left( {1 \leqslant j \leqslant m,j \in {N^ + }} \right)$表示第$j$个活跃节点所处的状态（与静态节点相同），由于活跃节点数量$m$远小于一层网络中静态节点的数量$n$，因此当$m < j \leqslant n,j \in {N^ + }$时，${s_{ij}}$没有意义，其值设为0。设置时间矩阵$T$、维度为$(D + 1) \times n$，记录多层网络中所有节点所处状态的时间，活跃节点与静态节点的区分与状态矩阵${\boldsymbol{S}}$相同，S态节点其在时间矩阵${{T}}$的对应元一直为0，当节点由S态转为E态时，其在时间矩阵${{T}}$的对应元初始值设置为1，该节点处于潜伏态的时间加1，其在时间矩阵${{{\boldsymbol{T}}}}$的对应元也加1；当节点由潜伏态转为感染态时，其在时间矩阵${{T}}$的对应元初始值设置为−1，该节点处于感染态的时间加1，其在时间矩阵${\boldsymbol{T}}$的对应元减1。

2）在多层网络中随机选取一个静态节点设置为初始感染节点，设该初始感染节点所处位置为第$i$层网络的第$j$个静态节点，将状态矩阵${\boldsymbol{S}}$中对应元${s_{ij}}$和时间矩阵${\boldsymbol{T}}$中对应元${t_{ij}} $设置为1。

3）将$m$个活跃节点随机分配到各层网络并与所属网络层中的静态节点随机连边。

4）遍历多层网络中所有E态节点的S态邻居节点，以概率$\beta $对其进行传染，若传染成功，分别将状态矩阵${\boldsymbol{S}}$与时间矩阵${{T}}$中对应元设置为1。

5）遍历多层网络中所有E态节点，若其时间矩阵$T$中对应元等于潜伏期${t_E}$，则将其转为Q态，即将状态矩阵${\boldsymbol{S}}$中对应元设置为2，将时间矩阵中对应元设置为−1；若并未达到潜伏期${t_E}$，则将时间矩阵中对应元加1。

6）遍历多层网络中所有Q态节点，若其时间矩阵$T$中对应元绝对值等于恢复期${t_Q}$，则将其转为S态，即将状态矩阵${\boldsymbol{S}}$与时间矩阵$T$中对应元都置0；若并未达到恢复期${t_Q}$，则将时间矩阵中对应元减1。

7）判断是否启动检测机制，若存在Q态节点，则遍历搜索与Q态节点距离小于检测半径$r$的节点，对其进行检测，检测成功率为$\gamma $，若检测成功，将该检测成功的节点转为Q态节点，其状态矩阵$S$中对应元设置为2，时间矩阵$T$中对应元设置为−1；若不存在Q态节点，则跳过这一步。

8）重复执行步骤3）～步骤7），直至迭代结束。

上述步骤中，步骤3）为活跃节点的跃迁，步骤4）～步骤6）为疾病传播阶段，步骤7）对应检测机制，需要注意的是这里的检测机制理想地认为不存在误判的情况，即将S态节点错误地判断为E态节点。每次迭代结束后，记录当前时刻的患病节点比例$\theta $，即E态节点与Q态节点比例之和，500次迭代结束后，获得患病节点比例$\theta $随着时间步$t$的演化曲线，而在每组参数下进行20次重复实验，将这20次重复实验获得的演化曲线进行平均，便得到最终的传播曲线。

根据实验所获得的一系列传播曲线，本文将从两个方向分析所得的结果。

1）总结传播模式，分析恢复期${t_Q}$的改变对传播模式的影响。

2）检测机制的引入将对疾病的传播起到抑制作用，分析检测半径$ r $的取值对抑制效果的影响。

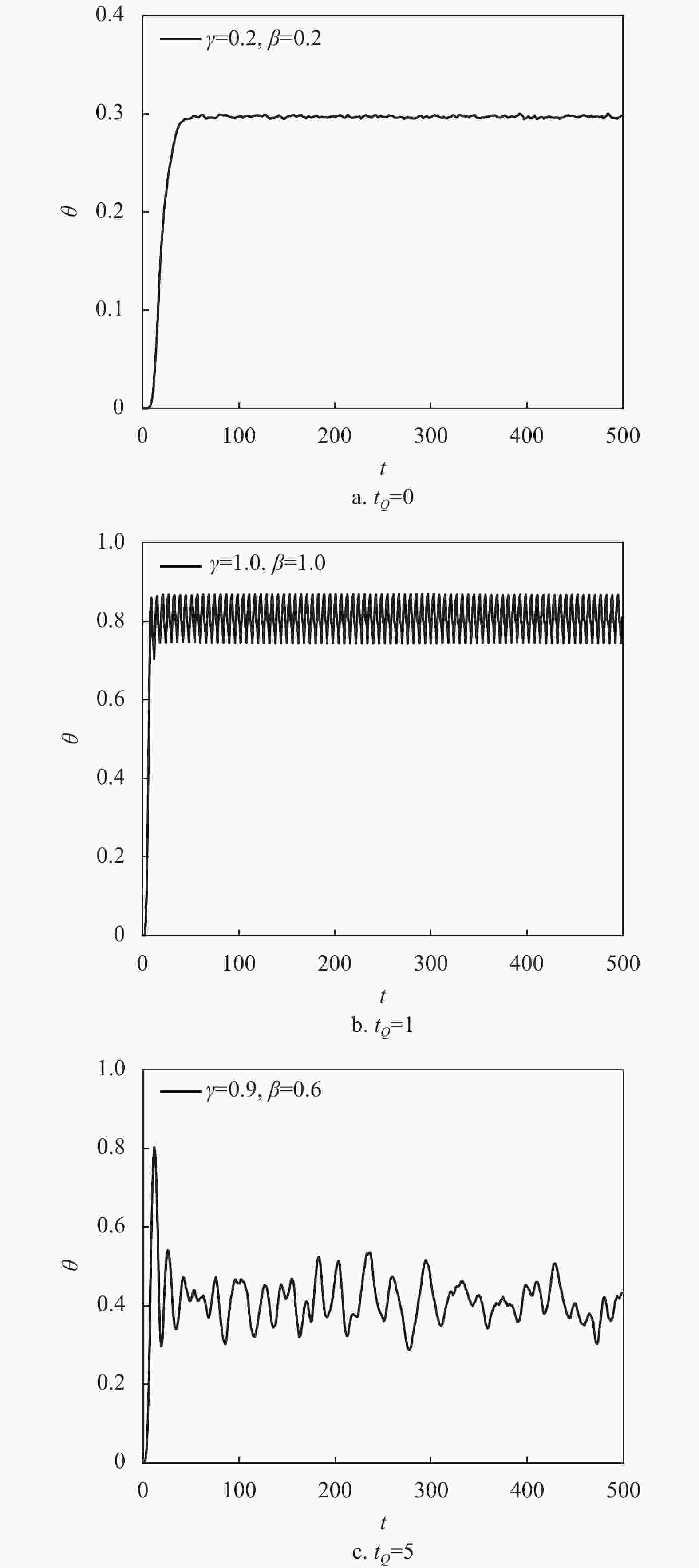
根据最终演化状态的不同，可以将传播模式分为3类。

1）患病节点比例$ \theta $随着时间步$t$的演化曲线达到稳态，如图3a所示。

2）患病节点比例$\theta $随着时间步$t$的增加出现周期性振荡，如图3b所示。

3）患病节点比例$\theta $随着时间步$t$的增加出现无周期性振荡，如图3c所示。

实验发现这3种传播模式的主要影响因素为恢复期${t_Q}$，当恢复期${t_Q} = 0$时，传播曲线可以达到稳态，而随着恢复期${t_Q}$的增大，开始出现稳态消失的传播曲线，当恢复期${t_Q} = 1$时，振荡呈现明显的周期性，而随着恢复期${t_Q}$增大到5时，振荡周期性消失，为了排除这种现象的偶发因素，图3c为50次重复实验的平均结果。

实验表明，恢复期的长短对系统最终状态模式有着重要的影响。其原因可能在于，模型中Q态节点并不参与传播过程（即处于隔离恢复期），所以恢复期的长短会直接影响参与传播过程的节点数，当这部分患病节点同时康复时，导致Q态节点数量发生突变，这就是系统最终状态存在振荡的主要原因。

图  3  3种最终演化状态的传播曲线

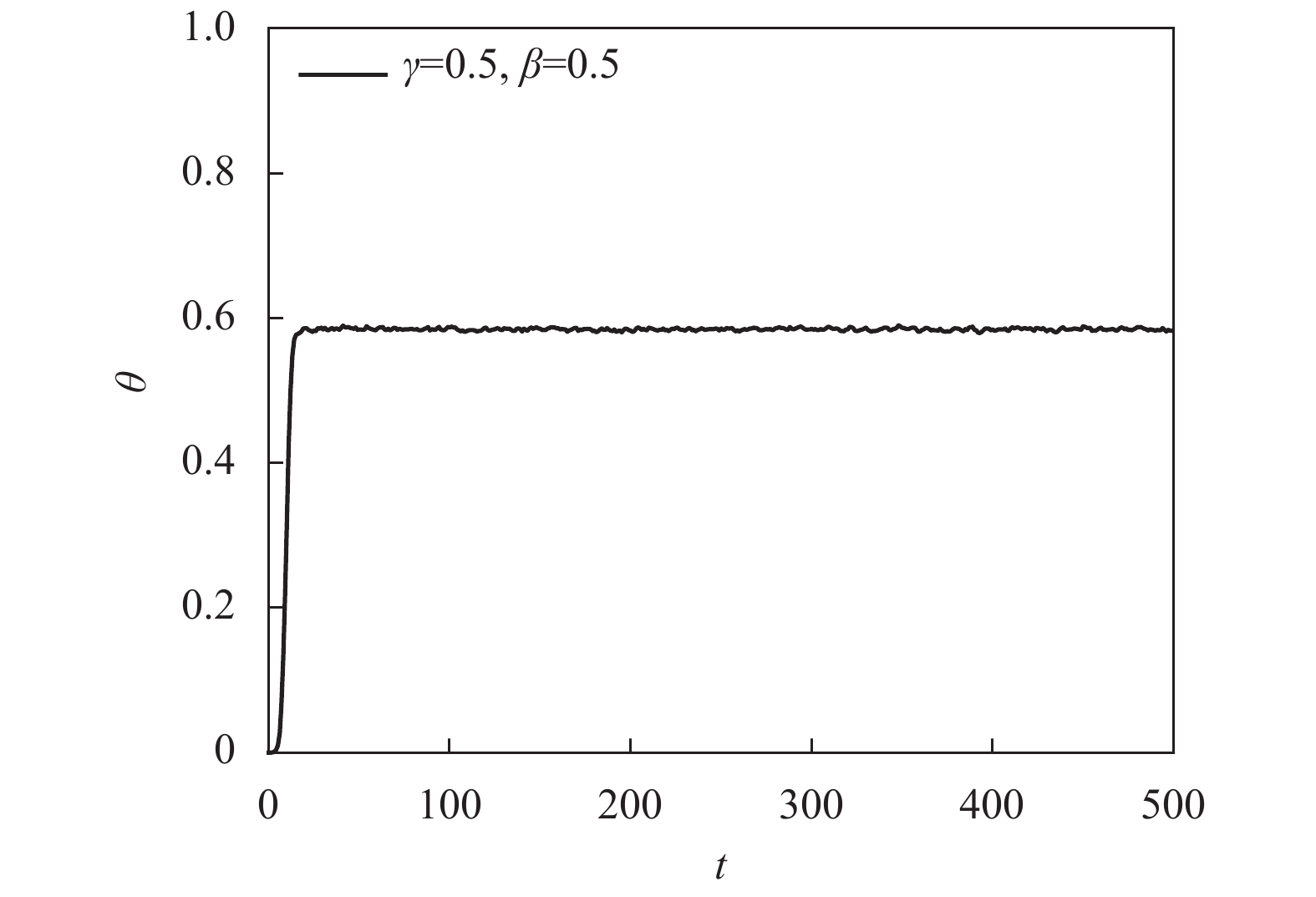
除了恢复期${t_Q}$对传播曲线的最终演化状态有主要影响外，传染概率$\beta $与检测成功率$\gamma $也影响着最终演化状态的模式。当${t_Q} = 1$时，只有在$\beta $和$\gamma $都极大时，才会出现周期性振荡如图3a所示，其余情况下最终演化状态仍然能够达到稳态，如图4所示。其原因是，在$\beta $与$\gamma $都极大时，同样会导致在短时间内Q态节点数量大大增加，由于这部分节点受到控制，间接降低了系统中S态节点的染病风险，这同样导致系统最终状态出现振荡。

图  4  $ {t}_{Q}=1 $时，在$ \gamma =0.5、\beta =0.5 $的传播曲线

在系统能够达到稳态的情况下（如${t_Q} = 0$），本文进一步研究系统疾病传播的中间演化过程存在哪些不同的模式。根据中间演化过程的不同，可以将传播模式分为2类。

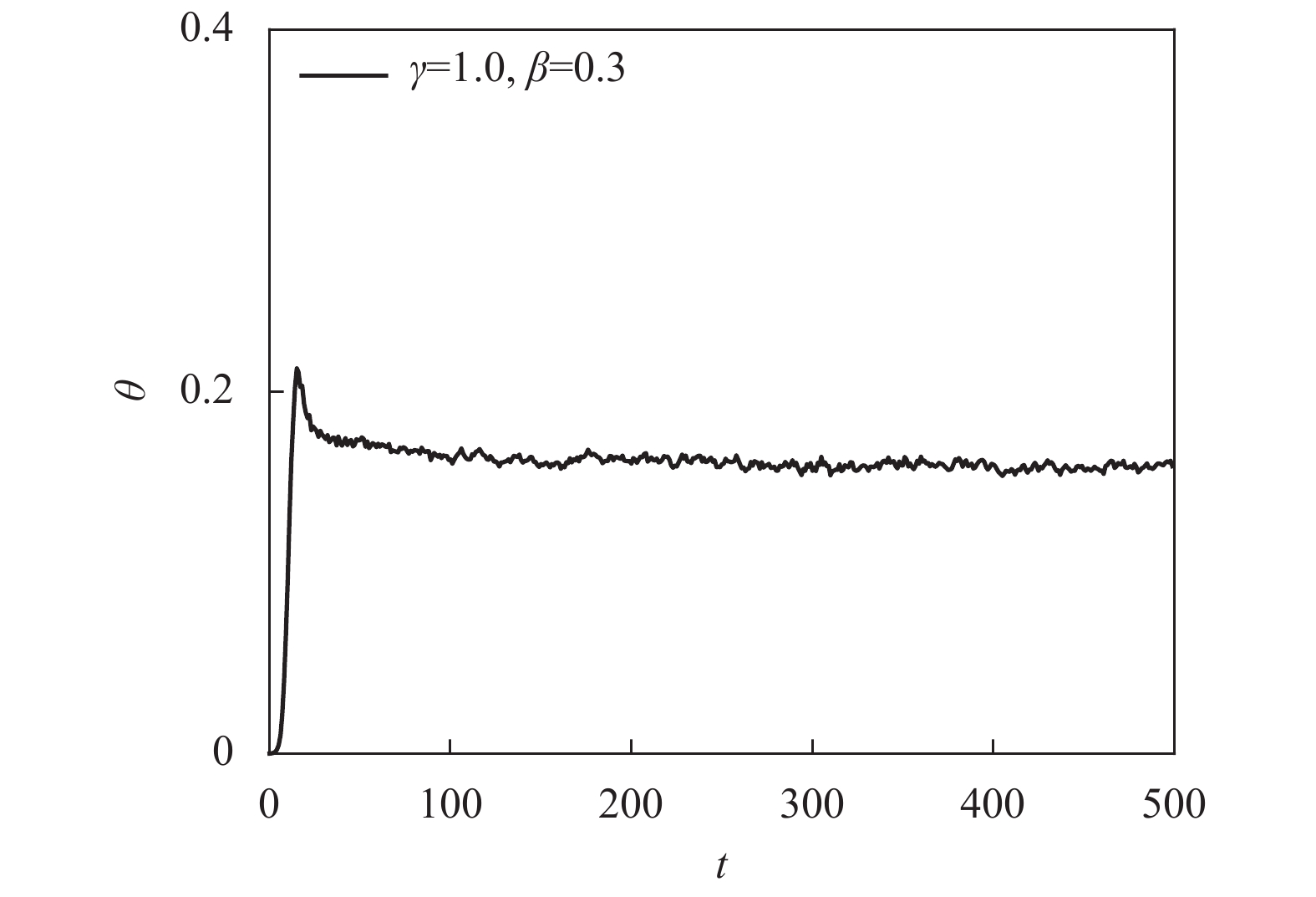
1）患病节点比例$\theta $随着时间步$t$的增加而增加直至达到稳态，如图3a所示。

2）$\theta $随着时间步$t$的增加先增加后下降直至达到稳态，如图5所示。

图  5  $ {t}_{Q}=0 $时，在$ \gamma =1.0、\beta =0.3 $的传播曲线

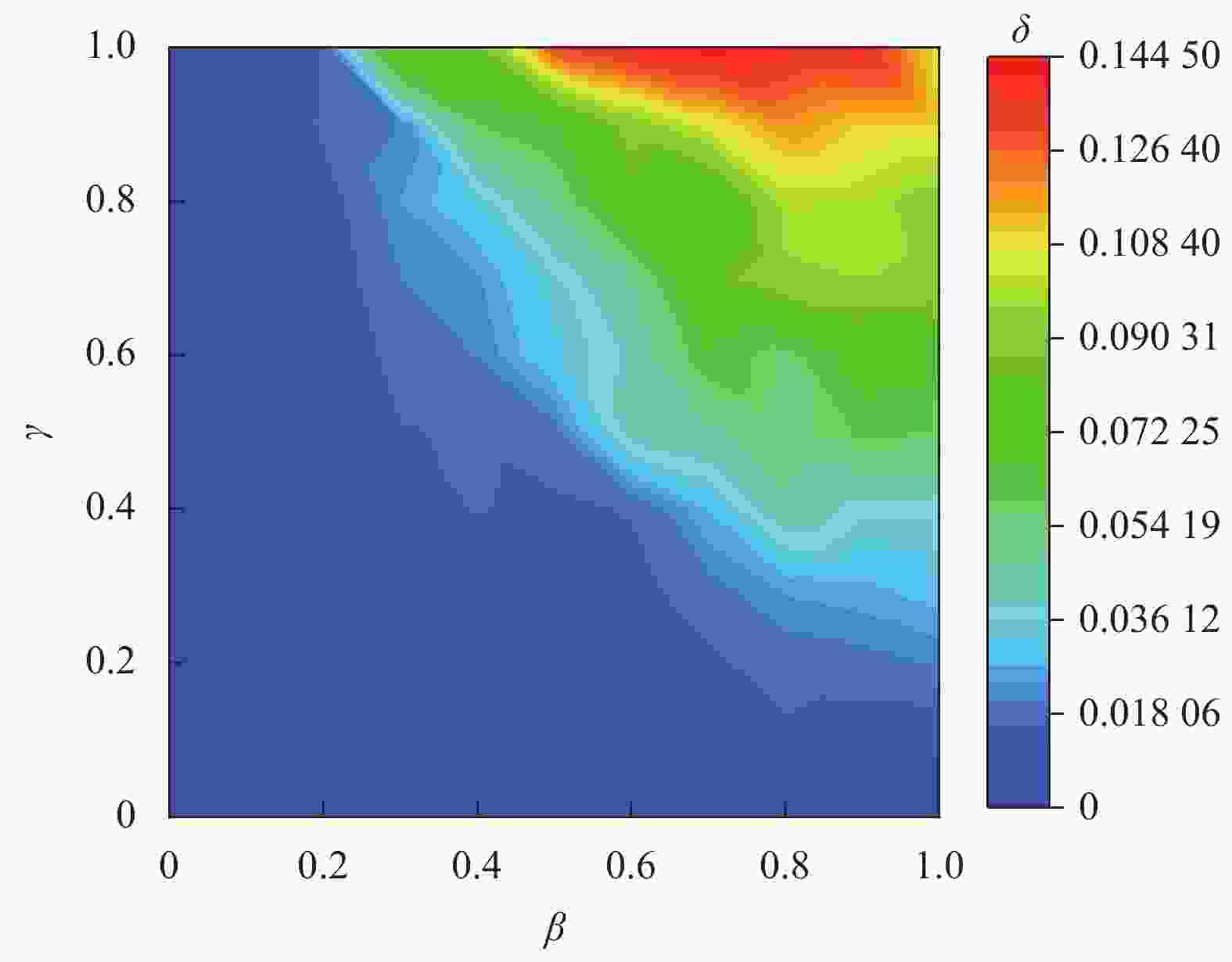
而图5在到达稳态前出现峰的原因也能从演化方程，即式(2)得出。当$\beta $较大时，会导致迭代最初阶段E态节点数迅速增加，这个阶段由于潜伏期的存在，系统启动检测机制的概率较小，从而系统中累积了大量E态节点，如果$\gamma $也较大，这些E态节点中的大部分会在短时内集中转变为Q态节点，这导致在这段时间系统检测范围大大增加，从而迅速降低了S态节点被感染的概率，导致后续系统中患病节点数量的快速下降。快速下降达到稳态的原因是，传染概率对患病节点的增加与检测成功率对患病节点的控制达到了动态平衡。

为了进一步探究这两种模式的影响因素，记传播曲线的峰值为$p = {\max _t}\theta (t)$，令传播曲线的最后100个时间步的患病节点比例$\theta $的平均值为传播曲线的最终演化状态，记为$ s = {{\displaystyle\sum\limits_{t = 401}^{500} {\theta \left( t \right)} } / {100}} $，令传播曲线峰值$p$与最终演化状态$ s $的差值为$\delta = p - s$，作$\delta $与传染概率$\beta $、检测成功率$\gamma $的关系图。图6为当恢复期${t_Q} = 0$时，$\delta - (\beta ,\gamma )$的二维相图，这印证了上文对出现两种不同中间演化过程的分析，恢复期${t_Q} = 1,5$时，$\delta - (\beta ,\gamma )$的变化规律与之类似。

图  6  $ \delta -(\beta ,\gamma ) $的二维相图

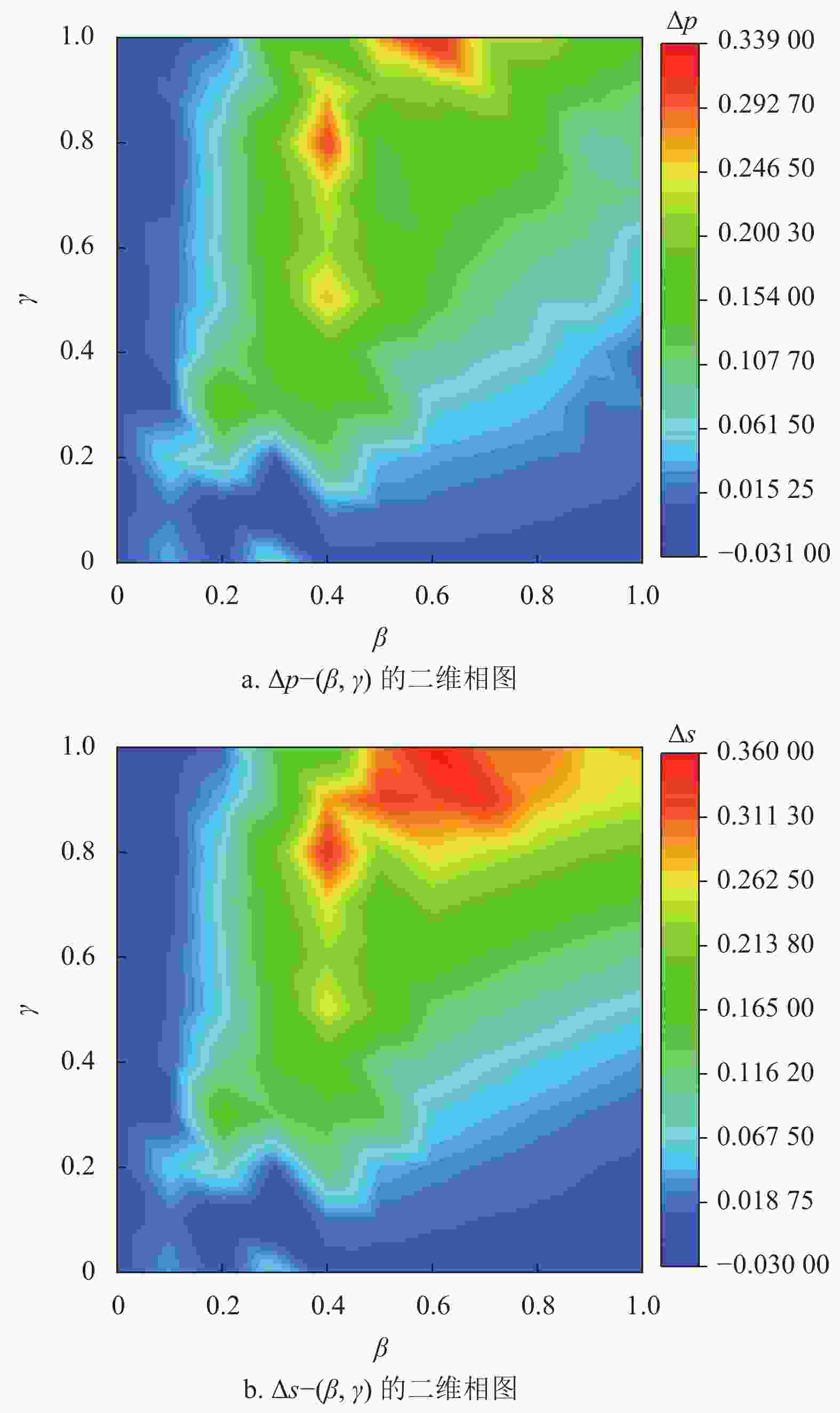
检测机制的引入无疑对疾病的传播过程起到了抑制作用，显然检测机制的强弱由检测成功率$\gamma $与检测半径$r$共同决定，而在现实生活中，检测成功率往往取决于当前医疗科技发展水平，并不会轻易发生改变，但检测半径$r$是人为制定的，因此在这里讨论检测半径$r$对疾病的抑制效果的作用。在检测半径$r$分别为1和2时，对传染概率$\beta $与检测成功率$\gamma $进行遍历，对所获得的传播曲线分别从中间演化过程与最终演化状态两方面进行对比。记检测半径$r = 1$时，传播曲线峰值和最终演化状态分别为${p_1}$与${s_1}$；检测半径$r = 2$时，传播曲线峰值和最终演化状态分别为${p_2}$与${s_2}$；两者的峰值之差记为$\Delta p = {p_1} - {p_2}$，最终演化状态之差记为$\Delta s = {s_1} - {s_2}$。$\Delta p - (\beta ,\gamma )$的二维相图和$\Delta s - (\beta ,\gamma )$的二维相图分别如图7a和图7b所示。

可以看出并不是所有情况下增大检测半径就能够有效抑制疾病的传播，如图7所示，当传染概率$\beta $小于某一值（约为0.2）时，无论检测成功率$\gamma $取值如何，检测半径$r = 1,2$的中间演化过程与最终演化状态都相差不大。这可能是因为在传染概率比较小时，E态节点较少，因此增大检测半径对筛选E态节点的效果提升不大。这一结果也说明，如果能通过接种疫苗、戴口罩等方式显著降低疾病传染率就能在一定范围精准检测的基础上有效控制疾病的大规模流行。

图  7  二维相图

本文研究了一个在具有活跃节点的多层网络作用下的时滞SEQS模型。活跃节点的跃迁给多层网络赋予时变性，用以模拟不同城市间的流动人口，而具有潜伏期和恢复期的时滞SEQS模型用以模拟现实生活中具有潜伏期且恢复后还能被继续感染的疾病。对该模型传播模式的分析有利于预测不同变异毒株带来的感染高峰期，对于个人而言，可以调整自我防疫策略以避开感染高峰期。而改变活跃节点比例以及增加活跃节点之间连边对整个系统的影响将在后续工作中进行探究。