-
精确的节点定位是物联网位置服务应用的关键。获得了节点的准确位置信息,与位置服务应用的有关数据才有价值。因此,研究精确定位对物联网的位置服务应用至关重要[1-2]。根据测量距离建立的定位方程组多数情况下是非线性方程组,对该方程组的求解方法整体上可分为两大类:一类是非线性处理方法,将定位问题看作优化问题进行求解,如遗传算法[3]等;另一类是线性处理方法,通常利用Taylor级数展开法或其他方法[4]将非线性定位方程组变换成线性方程组后求解。与非线性处理方法相比,基于Taylor级数展开的线性方法具有求解精度高、收敛速度快等优点,成为近年来的一个热点研究。文献[5]提出了基于Taylor级数展开和到达时间的定位算法;文献[6]采用Taylor级数展开和最速下降法实现混合定位;文献[7]利用Taylor级数展开法将二次方程组线性化,实现了基于接收信号强度指示的定位等。这些工作通过不同算法与Taylor级数展开法[8-10]相结合的方式,对精确定位进行了一些有益的探索,但是并没有对传统Taylor级数展开的定位模型进行改进。该模型只考虑未知节点和锚节点的距离,没有考虑未知节点之间的距离,定位信息不够全面,从而导致定位精度不高。因此本文考虑未知节点之间的距离,建立一种新的多元变量Taylor级数展开的定位模型。在此模型的基础上,提出了一种新的定位算法。该算法充分发挥粒子群算法的群体搜索性和多元变量Taylor级数展开法的局部细致搜索性,克服了粒子群算法后期搜索效率低下和多元变量Taylor级数展开法对初始值敏感的缺陷。由于增加了未知节点之间的距离信息,该方法能有效地提高定位精度。为了评价该算法的性能,对定位结果的Cramer-Rao下界进行了推导,并通过仿真验证算法的有效性。
-
考虑I个未知节点和K个锚节点随机均匀部署在二维空间中。物联网获得到达时间的测量值[11-12],经过计算得到第i个未知节点(xi, yi)(i=1, 2, …,I)与所有锚节点之间的测量距离:
$$ \left\{ {\begin{array}{*{20}{c}} {{{d'}_{i, 1}} = \sqrt {{{({x_i}-{u_1})}^2} + {{({y_i}-{v_1})}^2}} + {{e'}_{i, 1}}}\\ {{{d'}_{i, 2}} = \sqrt {{{({x_i}-{u_2})}^2} + {{({y_i} - {v_2})}^2}} + {{e'}_{i, 2}}}\\ \vdots \\ {{{d'}_{i{\rm{, }}K}} = \sqrt {{{({x_i} - {u_K})}^2} + {{({y_i} - {v_K})}^2}} + {{e'}_{i{\rm{, }}K}}} \end{array}} \right. $$ (1) 式中,$ ({u_k}, {v_k}) $为$ k\; \in (1, 2, \cdots, K) $个锚节点的坐标;$ {d'_{i, k}} $和$ \sqrt {{{({x_i}-{u_k})}^2} + {{({y_i}-{v_k})}^2}} $分别表示未知节点与锚节点之间的测量距离和实际距离;$ {e'_{i, k}} $表示距离测量误差,假设该误差服从均值为0、方差为$ \sigma _{{{l}_{1}},k}^{'2}$ 的高斯分布[13-14]。在未知节点的初始值$ ({\hat x_i}, {\hat y_i})$上,对式(1)中的$ \sqrt {{{({x_i}-{u_k})}^2} + {{({y_i}-{v_k})}^2}} $进行基于(xi, yi)的Taylor级数展开并忽略二阶以上分量,有:
$$ \left\{ {\begin{array}{*{20}{c}} {{{d'}_{i, 1}} = {{\hat d'}_{i, 1}} + \Delta {x_i}\frac{{{{\hat x}_i}-{u_1}}}{{{{\hat d'}_{i, 1}}}} + \Delta {y_i}\frac{{{{\hat y}_i}-{v_1}}}{{{{\hat d'}_{i, 1}}}} + {{e'}_{i, 1}}}\\ {{{d'}_{i, 2}} = {{\hat d'}_{i, 2}} + \Delta {x_i}\frac{{{{\hat x}_i}-{u_2}}}{{{{\hat d'}_{i, 2}}}} + \Delta {y_i}\frac{{{{\hat y}_i} - {v_2}}}{{{{\hat d'}_{i, 2}}}} + {{e'}_{i, 2}}}\\ \vdots \\ {{{d'}_{i, K}} = {{\hat d'}_{i, K}} + \Delta {x_i}\frac{{{{\hat x}_i} - {u_K}}}{{{{\hat d'}_{i, K}}}} + \Delta {y_i}\frac{{{{\hat y}_i} - {v_K}}}{{{{\hat d'}_{i, K}}}} + {{e'}_{i, K}}} \end{array}} \right. $$ (2) 式中,$ {\hat d'_{i, k}} = \sqrt {{{({{\hat x}_i} - {u_k})}^2} + {{({{\hat y}_i} - {v_k})}^2}} $ 为未知节点与锚节点之间的估计距离;$ \Delta {x_i} = {x_i}-{{\hat x}_i};\Delta {y_i} = {y_i}-{{\hat y}_i} $;将式(2)移项后得到矩阵形式:
$$ \left[\begin{array}{c} {{d'}_{i, 1}}-{{\hat d'}_{i, 1}}\\ \vdots \\ {{d'}_{i, K}}-{{\hat d'}_{i, K}} \end{array} \right] = \left[\begin{array}{c} \begin{array}{*{20}{c}} {\frac{{{{\hat x}_i}-{u_1}}}{{{{\hat d'}_{i, 1}}}}}&{\frac{{{{\hat y}_i}-{v_1}}}{{{{\hat d'}_{i, 1}}}}} \end{array}\\ \vdots {\rm{ }} \vdots \\ \begin{array}{*{20}{c}} {\frac{{{{\hat x}_i}-{u_K}}}{{{{\hat d'}_{i, K}}}}}&{\frac{{{{\hat y}_i} - {v_K}}}{{{{\hat d'}_{i, K}}}}} \end{array} \end{array} \right]\left[{\begin{array}{*{20}{c}} {\Delta {x_i}}\\ {\Delta {y_i}} \end{array}} \right] + \left[\begin{array}{c} {{e'}_{i, 1}}\\ \vdots \\ {{e'}_{i, K}} \end{array} \right] $$ (3) 由式(3)可得到定位模型:
$$ \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{Q}}\mathit{\Delta } + \mathit{\boldsymbol{E}} $$ (4) 利用该模型可以求出第i个未知节点的位置估计值。传统Taylor定位模型只能实现单个未知节点的定位,若要对所有未知节点进行定位,需要循环计算。
-
通过TOA测量法可得到所有节点间的测量距离:
$$ \left\{ \begin{array}{l} {d_{i, j}} = \sqrt {{{({x_i}-{x_j})}^2} + {{({y_i}-{y_j})}^2}} + {e_{i, j}}, {\rm{ }}i < j\\ {{d'}_{i, k}} = \sqrt {{{({x_i}-{u_k})}^2} + {{({y_i} - {v_k})}^2}} + {{e'}_{i, k}}, {\rm{ }}1 < k < K \end{array} \right. $$ (5) 式中,di, j和$\sqrt {{{({x_i}-{x_j})}^2} + {{({y_i}-{y_j})}^2}} $分别表示未知节点(xi, yi)与未知节点(xi, yi)(i=1, 2, …,I)的测量距离和实际距离;ei, j表示距离测量误差,假设该误差服从均值为0、方差为$ \sigma _{i, j}^2$ 的高斯分布。在未知节点的初始值$ ({\hat x_1}, {\hat y_1}, {\hat x_2}, {\hat y_2}, \cdots, {\hat x_I}, {\hat y_I}) $上,对式(5)中的实际距离进行基于多元变量$ ({x_1}, {y_1}, {x_2}, {y_2}, \cdots, {x_I}, {y_I}) $的Taylor级数展开并忽略二阶以上分量,有:
$$ \left\{ \begin{array}{l} {d_{i, j}} = {{\hat d}_{i, j}} + \Delta {x_i}\frac{{{{\hat x}_i}-{{\hat x}_j}}}{{{{\hat d}_{i, j}}}} + \Delta {y_i}\frac{{{{\hat y}_i}-{{\hat y}_j}}}{{{{\hat d}_{i, j}}}}-\Delta {x_j}\frac{{{{\hat x}_i} - {{\hat x}_j}}}{{{{\hat d}_{i, j}}}} - \\ \Delta {y_j}\frac{{{{\hat y}_i} - {{\hat y}_j}}}{{{{\hat d}_{i, j}}}} + {e_{i, j}}\\ {{d'}_{i, k}} = {{\hat d'}_{i, k}} + \Delta {x_i}\frac{{{{\hat x}_i} - {u_k}}}{{{{\hat d'}_{i, k}}}} + \Delta {y_i}\frac{{{{\hat y}_i} - {v_k}}}{{{{\hat d'}_{i, k}}}} + {{e'}_{i, k}} \end{array} \right. $$ (6) 式中,$ {\hat d_{i, j}} = \sqrt {{{({{\hat x}_i} - {{\hat x}_j})}^2} + {{({{\hat y}_i} - {{\hat y}_j})}^2}} $ 为未知节点之间的估计距离;$ \Delta {x_i} = {x_i}-{\hat x_i} $;$ \Delta {y_i} = {y_i}-{\hat y_i} $;$ \Delta {x_j} = {x_j}-{\hat x_j} $;$ \Delta {y_j} = {y_j}-{\hat y_j} $。将式(6)移项后得到矩阵形式:
$$ \left[\begin{array}{c} {d_{1, 2}}-{{\hat d}_{1, 2}}\\ \vdots \\ {d_{(I-1), I}}-{{\hat d}_{(I - 1), I}}\\ {{d'}_{1, 1}} - {{\hat d'}_{1, 1}}\\ \vdots \\ {{d'}_{I, K}} - {{\hat d'}_{I, K}} \end{array} \right] = {Q_1}\left[\begin{array}{c} \Delta {x_1}\\ \Delta {y_1}\\ \vdots \\ \Delta {x_I}\\ \Delta {y_I} \end{array} \right] + \left[\begin{array}{c} {e_{1, 2}}\\ \vdots \\ {e_{(I-1), I}}\\ {{e'}_{1, 1}}\\ \vdots \\ {{e'}_{I, K}} \end{array} \right] $$ (7) 由式(7)可得到新的定位模型:
$$ {\mathit{\boldsymbol{D}}_1} = {\mathit{\boldsymbol{Q}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_1} + {\mathit{\boldsymbol{E}}_1} $$ (8) 式中,E1为距离测量误差矩阵;$ {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_1} $为节点位置偏差矩阵;测量距离和估计距离之差矩阵D1是一个$ (C_I^{\rm{2}} + C_I^1C_K^1) \times 1$矩阵;Q1为$ (C_I^{\rm{2}} + C_I^1C_K^1) \times 2I $矩阵,若D1中第q个元素为$ {d_{i, j}}-{\hat d_{i, j}} $,则Q1中第q行第2i-1、2i、2j-1和2j个元素分别为$ \frac{{{{\hat x}_i}-{{\hat x}_j}}}{{{{\hat d}_{i, j}}}} $、$ \frac{{{{\hat y}_i}-{{\hat y}_j}}}{{{{\hat d}_{i, j}}}} $、$ -{\rm{ }}\frac{{{{\hat x}_i}-{{\hat x}_j}}}{{{{\hat d}_{i, j}}}} $、$ -{\rm{ }}\frac{{{{\hat y}_i}-{{\hat y}_j}}}{{{{\hat d}_{i, j}}}} $,该行其余元素为0;若D1中第q个元素为$ {d'_{i, k}}-{\hat d'_{i, k}}{\rm{ }} $,则Q1中第q行第2i-1、2i个元素分别为$ \frac{{{{\hat x}_i}-{u_k}}}{{{{\hat d'}_{i, k}}}}$、$ \frac{{{{\hat y}_i}-{v_k}}}{{{{\hat d'}_{i, k}}}} $,该行其余元素为0。
-
基于多元变量Taylor级数展开模型的定位算法先用粒子群算法[15-16]计算未知节点的初始值,再根据加权最小二乘法求出其位置的估计值。具体步骤如下:
1) 首先计算第i(i=1)个未知节点的初始值。
2) 假设有N个粒子组成的种群,其中第n个粒子的位置和速度分别表示为$ {\mathit{\boldsymbol{X}}_n} = {({x_n}, {y_n})^T} $和$ {\mathit{\boldsymbol{V}}_n} = {({v_{n, x}}, {v_{n, y}})^{\rm{T}}} $。计算每个粒子的适应度值$ \sum\limits_{k = 1}^K {\left| {\sqrt {{{(x_n^{}-{u_k})}^2} + {{(y_n^{}-{v_k})}^2}}-{{d'}_{i, k}}} \right|} $。
3) 对每个粒子,如果其当前的适应度值小于历史最优位置$ {\mathit{\boldsymbol{P}}_n} = {({p_{n, x}}, {p_{n, y}})^{\rm{T}}} $对应的适应度值,则用粒子当前位置更新粒子最优位置,否则保持不变。
4) 对每个粒子,如果当前的适应度值小于群体历史最优位置$ {\mathit{\boldsymbol{P}}_g} = {({p_{g, x}}, {p_{g, y}})^{\rm{T}}} $对应的适应度值,则将粒子当前位置作为群体最优位置;否则保持不变。
$$ \left\{ \begin{array}{l} v_{n, x}^{(l + 1)} = wv_{n, x}^{(l + 1)} + {c_1}{r_1}(p_{n, x}^{(l + 1)}-x_n^{(l)}) + {c_2}{r_2}(p_{g, x}^{(l)}-x_n^{(l)})\\ v_{n, y}^{(l + 1)} = wv_{n, y}^{(l)} + {c_1}{r_1}(p_{n, y}^{(l)}-y_n^{(l)}) + {c_2}{r_2}(p_{g, y}^{(l)} - y_n^{(l)})\\ x_n^{(l + 1)} = x_n^{(l)} + v_{n, x}^{(l + 1)}, y_n^{(l + 1)} = y_n^{(l)} + v_{n, y}^{(l + 1)} \end{array} \right. $$ (9) 根据式(9)更新粒子的速度和位置,式中,$n \in \left\{ {1, 2, \cdots, N} \right\}$;l为迭代次数;w为惯性因子;c1和c2为正的加速因子;r1和r2为分布于[0, 1]之间的随机数。如果达到最大迭代次数,转向步骤5),否则转向步骤2)。
5) 若所有未知节点都计算完毕,转向步骤6)。否则转向步骤2),继续下一个未知节点(i=i+1)初始位置的计算。
6) 根据粒子群算法得到所有未知节点的初始值$ ({\hat x_1}, {\hat y_1}, {\hat x_2}, {\hat y_2}, \cdots, {\hat x_I}, {\hat y_I}) $,利用式(8)建立新的定位模型$ {\mathit{\boldsymbol{D}}_1} = {\mathit{\boldsymbol{Q}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_1} + {\mathit{\boldsymbol{E}}_1} $。
7) 利用加权最小二乘法[17]可求解出:
$$ \begin{array}{c} {\left[{\begin{array}{*{20}{c}} {\Delta {x_1}}&{\Delta {y_1}}& \cdots &{\Delta {x_{\rm{I}}}}&{\Delta {y_{\rm{I}}}} \end{array}} \right]^{\rm{T}}} = \\ {({Q^{\rm{T}}}{\mathit{\boldsymbol{T}}^{ -1}}Q)^{ -1}}{Q^{\rm{T}}}{\mathit{\boldsymbol{T}}^{ -1}}\mathit{\boldsymbol{D}} \end{array} $$ (10) 式中,T为测量误差的协方差矩阵。初始递归时,令$ x_1^{(0)} = {\hat x_1} $,$ y_1^{(0)} = {\hat y_1} $,在下一次递归中令:$ x_1^{(l1 + 1)} = x_1^{(l1)} + \Delta {x_1} $,$ y_1^{(l1 + 1)} = y_1^{(l1)} + \Delta {y_1} $,其中L1为迭代次数。重复以上过程,直到$ \sum\limits_{i = 1}^I {(\left| {\Delta {x_i}} \right| + \left| {\Delta {y_i}} \right|)} $小于一个预定的门限ε。
-
设未知节点的真实坐标矢量$ \mathit{\boldsymbol{\theta }} = [{x_1}, {y_1}, {x_2}, {y_2}, \cdots, {x_I}, {y_I}] $,$ d = {[{d_{1, 2}}{\rm{ }} \cdots {\rm{ }}{d_{(I-1), I}}{\rm{ }}{d'_{1, 1}}{\rm{ }} \cdots {\rm{ }}{d'_{I, K}}]^{\rm{T}}} $。$ {e_{i, j}} \sim N(0, \sigma _{i, j}^2) $,$ {{e'}_{i, k}} \sim N(0, \sigma _{{{l}_{1}},k}^{'2}) $,构造似然函数:
$$ \begin{array}{c} L(d, \theta ) = \prod\limits_{i < j} {\frac{1}{{\sqrt {2\pi \sigma _{i, j}^2} }}} \times \\ \exp \left\{ {- \frac{{{{[{d_{i, j}}-\sqrt {{{({x_i}-{x_j})}^2} + {{({y_i}-{y_j})}^2}}]}^2}}}{{2\sigma _{i, j}^2}}} \right\} \times \\ \prod {\frac{1}{{\sqrt {2\pi \sigma _{{{l}_{1}},k}^{'2}} }}} \exp \left\{ { - \frac{{{{[{{d'}_{i, k}}-\sqrt {{{({x_i}-{u_k})}^2} + {{({y_i}-{v_k})}^2}}]}^2}}}{{2\sigma _{{{l}_{1}},k}^{'2}}}} \right\} \end{array} $$ (11) 对式(11)两边取对数得:
$$ $\begin{array}{c} \ln L(d, \theta ) = {\rm{C}} - \sum\limits_{i < j} {\frac{{{{[{d_{i, j}}-\sqrt {{{({x_i}-{x_j})}^2} + {{({y_i}-{y_j})}^2}}]}^2}}}{{2\sigma _{i, j}^2}}} - \\ \sum {\frac{{{{[{{d'}_{i, k}}-\sqrt {{{({x_i}-{u_k})}^2} + {{({y_i}-{v_k})}^2}}]}^2}}}{{2\sigma _{{{l}_{1}},k}^{'2}}}} {\rm{ }} \end{array}$ $$ (12) 式中,C为一常数。对式(12)求二阶偏导数,构造Fisher信息矩阵:
$$ \mathit{\boldsymbol{F}} = \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{xx}}}&{{\mathit{\boldsymbol{F}}_{xy}}}\\ {\mathit{\boldsymbol{F}}_{xy}^{\rm{T}}}&{{\mathit{\boldsymbol{F}}_{yy}}} \end{array}} \right] $$ (13) $$ {{\left[{{\mathit{\boldsymbol{F}}}_{xx}} \right]}_{{{l}_{1}}{{l}_{2}}}}=\left\{ \begin{align} & \sum\limits_{\begin{smallmatrix} j=1 \\ j\ne {{l}_{1}} \end{smallmatrix}}^{I}{\frac{{{({{x}_{{{l}_{1}}}}-{{x}_{j}})}^{2}}}{\sigma _{{{l}_{1}}, j}^{2}\left[{{({{x}_{{{l}_{1}}}}-{{x}_{j}})}^{2}}+{{({{y}_{{{l}_{1}}}}-{{y}_{j}})}^{2}} \right]}+} \\ & \sum\limits_{k=1}^{K}{\frac{{{({{x}_{{{l}_{1}}}}-{{u}_{k}})}^{2}}}{\sigma _{{{l}_{1}}, k}^{'2}\left[{{({{x}_{{{l}_{1}}}}-{{u}_{k}})}^{2}}+{{({{y}_{{{l}_{1}}}}-{{v}_{k}})}^{2}} \right]}, \rm{ }{{l}_{1}}={{l}_{2}}} \\ & -\rm{ }\frac{{{({{x}_{{{l}_{1}}}}-{{x}_{{{l}_{2}}}})}^{2}}}{\sigma _{{{l}_{1}}, {{l}_{2}}}^{2}\left[{{({{x}_{{{l}_{1}}}}-{{x}_{{{l}_{2}}}})}^{2}}+{{({{y}_{{{l}_{1}}}}-{{y}_{{{l}_{2}}}})}^{2}} \right]}, \rm{ }{{l}_{1}}\ne {{l}_{2}} \\ \end{align} \right.\quad $$ $$ {{[{{\mathit{\boldsymbol{F}}}_{xy}}]}_{{{l}_{1}}{{l}_{2}}}}=\left\{ \begin{matrix} \sum\limits_{\begin{smallmatrix} j=1 \\ j\ne {{l}_{1}} \end{smallmatrix}}^{I}{\frac{({{x}_{{{l}_{1}}}}-{{x}_{j}})({{y}_{{{l}_{1}}}}-{{y}_{j}})}{\sigma _{{{l}_{1}}, j}^{2}\left[{{({{x}_{{{l}_{1}}}}-{{x}_{j}})}^{2}}+{{({{y}_{{{l}_{1}}}}-{{y}_{j}})}^{2}} \right]}}, \rm{ }{{l}_{1}}={{l}_{2}} \\ -\rm{ }\frac{({{x}_{{{l}_{1}}}}-{{x}_{{{l}_{2}}}})({{y}_{{{l}_{1}}}}-{{y}_{{{l}_{2}}}})}{\sigma _{{{l}_{1}}, {{l}_{2}}}^{2}\left[{{({{x}_{{{l}_{1}}}}-{{x}_{{{l}_{2}}}})}^{2}}+{{({{x}_{{{l}_{1}}}}-{{x}_{{{l}_{2}}}})}^{2}} \right]}, \rm{ }{{l}_{1}}\ne {{l}_{2}} \\ \end{matrix} \right.\quad $$ $$ {{[{{\mathit{\boldsymbol{F}}}_{yy}}]}_{~{{l}_{1}}{{l}_{2}}}}=\left\{ \begin{matrix} \begin{align} & \sum\limits_{\begin{smallmatrix} j=1 \\ j\ne {{l}_{1}} \end{smallmatrix}}^{I}{\frac{{{({{y}_{{{l}_{1}}}}-{{y}_{j}})}^{2}}}{\sigma _{{{l}_{1}}, j}^{2}\left[{{({{x}_{{{l}_{1}}}}-{{x}_{j}})}^{2}}+{{({{y}_{{{l}_{1}}}}-{{y}_{j}})}^{2}} \right]}}+ \\ & \sum\limits_{k=1}^{K}{\frac{{{({{y}_{{{l}_{1}}}}-{{v}_{k}})}^{2}}}{\sigma _{{{l}_{1}}, k}^{'2}\left[{{({{x}_{{{l}_{1}}}}-{{u}_{k}})}^{2}}+{{({{y}_{{{l}_{1}}}}-{{v}_{k}})}^{2}} \right]}}, \rm{ }{{l}_{1}}={{l}_{2}} \\ \end{align} \\ -\rm{ }\frac{{{({{y}_{{{l}_{1}}}}-{{y}_{{{l}_{2}}}})}^{2}}}{\sigma _{{{l}_{1}}, {{l}_{2}}}^{2}\left[{{({{x}_{{{l}_{1}}}}-{{x}_{{{l}_{2}}}})}^{2}}+{{({{y}_{{{l}_{1}}}}-{{y}_{{{l}_{2}}}})}^{2}} \right]}, \rm{ }{{l}_{1}}\ne {{l}_{2}} \\ \end{matrix} \right.\quad $$ $ {{l}_{1}}, {{l}_{2}}\ \in (1, 2, \cdots, I) $。对该Fisher矩阵F求逆,得到CRLB表达式:
$$ E({{(\hat{\theta }-\theta )}^{\text{T}}}(\hat{\theta }-\theta ))\ge \text{tr}({{F}^{-1}}) $$ (14) 式中,tr (·)表示矩阵的迹;F-1表示Fisher矩阵的逆。
-
为了验证基于多元变量Taylor级数展开模型的定位算法的有效性,采用Matlab对该算法进行仿真,并与粒子群算法、粒子群和传统Taylor级数展开结合的算法进行对比分析。在120 m × 100 m的矩形仿真区域,随机均匀分布4个锚节点和20个未知节点,仿真次数为1 000次。假设距离测量误差服从均值为0、方差σ2的高斯分布。粒子群参数设定为加速因子c1=c2=1.5,惯性权重w=0.7,粒子群的种群大小N=30,迭代次数l=200。为检验新算法,定位误差定义为$ \frac{\sum\limits_{i=\text{1}}^{I}{\sqrt{{{({{{\hat{x}}}_{i}}-{{x}_{i}})}^{2}}+{{({{{\hat{y}}}_{i}}-{{y}_{i}})}^{2}}}}}{I} $,其中$ ({{\hat{x}}_{i}}, {{\hat{y}}_{i}}) $表示未知节点的估计位置。
-
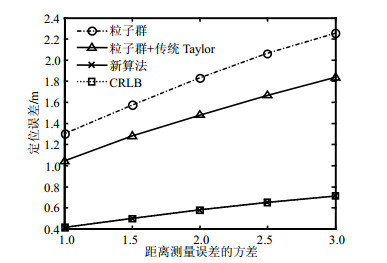
图 1给出了3种算法的定位误差随距离测量误差的方差变化的曲线及CRLB曲线。可以看出,3种算法的定位误差都随测量误差方差的增加而增加,但新算法的定位误差明显小于其他两个算法,且非常接近CRLB曲线。这是因为多元变量Taylor级数展开模型比传统Taylor级数展开模型多考虑了未知节点之间的距离信息,使定位精度得到进一步提高。此外,随着测量误差的变化,新算法的定位误差斜率小于其他两种算法,说明该算法能有效减小测量误差对定位误差的影响。
-
图 2给出了锚节点数目对3种算法定位误差的影响。未知节点数不变时,锚节点数目的变化对定位误差有很大的影响。锚节点数越多,节点的定位误差越小。与此同时,在锚节点数目相同的情况下,新算法的定位精度在原有算法的基础上有了明显的提高。
-
图 3给出了3种算法定位误差的累积分布函数曲线图。可以看出,在90%的累积分布点,粒子群算法、粒子群和传统Taylor级数展开结合的算法、新算法的定位误差分别在14.5、12.2和0.68 m以内,新算法具有较高的定位精度。
-
针对物联网定位精度不高,难以适应复杂信道环境等方面存在的不足,提出了一种新的基于多元变量Taylor级数展开模型的定位方法。该方法结合粒子群算法和多元变量Taylor级数展开法的特点,充分发挥各算法的优点,扬长避短,实现整体定位性能的最优化。通过仿真验证,新算法能有效地减少测量误差对定位精度的影响,提高定位精度。但该算法只考虑了所有距离测量信息已知的情况,部分距离测量信息未知的情况还有待进一步研究。
Localization Algorithm Based on Multivariable Taylor Series Expansion Model
-
摘要: 传统Taylor级数展开模型只考虑未知节点和锚节点之间的距离,没有考虑未知节点之间的距离,定位信息不够全面,从而导致定位精度不高。为了进一步提高定位精度,该文提出了一种新的基于多元变量Taylor级数展开模型的定位算法。首先考虑未知节点之间的距离信息,建立新的基于多元变量Taylor级数展开的定位模型。然后,在对新的定位模型求解过程中,采用粒子群算法对未知节点进行定位,获得其位置的初始值。再根据加权最小二乘法求出新模型的解,作为未知节点的估计位置。最后,为评价该算法的性能,对定位结果的克拉美罗界(CRLB)进行推导。仿真结果表明基于多元变量Taylor级数展开模型的定位精度更高,定位误差接近CRLB。
-
关键词:
- 物联网 /
- 多元变量泰勒级数展开 /
- 粒子群算法 /
- 定位模型
Abstract: Conventional Taylor series expansion model only considers the distances between unknown nodes and anchor nodes, without considering the distances between unknown nodes. As a result, the location information is not comprehensive enough to result in lower positioning accuracy. Thus, a novel localization algorithm based on multivariable Taylor series expansion model is proposed to further enhance positioning accuracy. Firstly, the new positioning model which considers the distances between unknown nodes in multivariable Taylor series expansion is established. In the process of model solution, the particle swarm algorithm is used to obtain the estimated position values of the unknown nodes. Then, the optimal position values are obtained by the weighted least squares method. Finally, the Cramer-Rao lower bound (CRLB) of the positioning result is derived to evaluate the performance of the proposed algorithm. Simulation results demonstrate that the proposed algorithm obtains a higher positioning accuracy, and its positioning error is very close to the CRLB. -
[1] 肖竹, 王东, 李仁发, 等.物联网定位与位置感知研究[J].中国科学:信息科学, 2013, 43(10):1265-1287. http://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201310005.htm XIAO Zhu, WANG Dong, LI Ren-fa, et al. Localization and nodes location-aware in internet of things[J].Scientia Sinica:Sinica Informationis, 2013, 43(10):1265-1287. http://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201310005.htm [2] 钱志鸿, 王义君.面向物联网的无线传感器网络综述[J].电子与信息学报, 2013, 35(1):215-227. http://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201301033.htm QIAN Zhi-hong, WANG Yi-jun. Internet of things-oriented wireless sensor networks review[J]. Journal of Electronics & Information Technology, 2013, 35(1):215-227. http://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201301033.htm [3] ASSIS A F, VIEIRA L F M, RODRIGUS M T R, et al. A genetic algorithm for the minimum cost localization problem in wireless sensor networks[C]//2013 IEEE Congress on Evolutionary Computation. Washington:IEEE, 2013, 797-804. [4] 朱国辉, 冯大政, 向平叶, 等.传感器误差情况下的线性校正TOA定位算法[J].系统工程与电子技术, 2015, 37(3):498-502. http://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201503005.htm ZHU Guo-hui, FENG Da-zheng, XIANG Ping-ye, et al. Linear correction TOA localization algorithm with sensor location error[J]. Journal of Systems Engineering and Electronics, 2015, 37(3):498-502. http://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201503005.htm [5] ZHENG Xiao-neng, HUA Jing-yu, ZHENG Zhi-long, et al. Wireless localization based on the time sum of arrival and Taylor expansion[C]//Proceedings of 2013 IEEE International Conference on Networks. Washington:IEEE, 2013. [6] LIU Li-chuan, MAVIDI G. A hybrid senor localization algorithm for wireless sensor networks[C]//Proceedings of 2013 IEEE International Conference on Systems, Man, and Cybernetics. Washington:IEEE, 2013:1087-1092. [7] LIU Feng, ZHU Hao, GU Zong-hai, et al. A linear localization algorithm for wireless sensor network based on RSSI[J]. Communications in Computer and Information Science, 2011, 176(2):384-389. https://www.researchgate.net/publication/241040312_A_Linear_Localization_Algorithm_for_Wireless_Sensor_Network_Based_on_RSSI [8] 熊瑾煜, 王巍, 朱中梁.基于泰勒级数展开的蜂窝TDOA定位算法[J].通信学报, 2004, 25(4):144-150. http://www.cnki.com.cn/Article/CJFDTOTAL-TXXB200706001.htm XIONG Jin-yu, WANG Wei, ZHU Zhong-liang. A new TDOA algorithm based on Taylor series expansion in cellular networks[J]. Journal on Communications, 2004, 25(4):144-150. http://www.cnki.com.cn/Article/CJFDTOTAL-TXXB200706001.htm [9] 张令文, 谈振辉.基于泰勒级数展开的蜂窝TDOA定位新算法[J].通信学报, 2007, 28(6):7-11. http://www.cnki.com.cn/Article/CJFDTOTAL-TXXB200706001.htm ZHANG Ling-wen, TAN Zhen-hui. New TDOA algorithm based on Taylor series expansion in cellular networks[J]. Journal on Communications, 2007, 28(6):7-11. http://www.cnki.com.cn/Article/CJFDTOTAL-TXXB200706001.htm [10] FOY W H. Position-location solutions by Taylor series estimation[J]. IEEE Transactions on Aerospace Electronic Systems, 1976, AES-12(3):187-194. [11] ZHANG Yan-long, CHEN Wei-dong. Nonparametric TOA estimators for low-resolution IR-UWB digital receiver[J]. Journal of Systems Engineering and Electronics, 2015, 26(1):26-31. doi: 10.1109/JSEE.2015.00004 [12] LI Y, QIAN Z, ZHAO S, et al. A research of TOA wireless sensor network localization algorithm[J]. Advanced Materials Research, 2013, 79(1):1601-1604. [13] PATWARI N, ASH J N, KYPEROUNTAS S, et al. Locating the nodes:Cooperative localization in wireless sensor networks[J]. IEEE Signal Process Mag, 2005, 22(4):54-69. doi: 10.1109/MSP.2005.1458287 [14] ALAVI B, PAHLAVAN K. Modeling of the ToA based distance measurement error using UWB indoor radio measurements[J]. IEEE communications letters, 2006, 10(4):275-277. doi: 10.1109/LCOMM.2006.1613745 [15] REN Xiu-li, GAO Chuan-gen, XI Yuan-hao. A node localization algorithm based on simple particle swarm optimization in wireless sensor networks[J]. Journal of Computational Information Systems, 2013, 9(22):9203-9210. https://www.researchgate.net/publication/289588286_A_node_localization_algorithm_based_on_simple_particle_swarm_optimization_in_wireless_sensor_networks [16] WEI Nuo, GUO Qiang, SHU Ming-lei, et al. Three-dimensional localization algorithm of wireless sensor networks base on particle swarm optimization[J]. Journal of China Universities of Posts and Telecommunications, 2012, 19(2):7-12. https://www.researchgate.net/publication/257446732_Three-dimensional_localization_algorithm_of_wireless_sensor_networks_base_on_particle_swarm_optimization [17] KAY S M. Fundamentals of statistical signal processing[M]//Volume I:Estimation Theory (v.1). Upper Saddle River:Prentice Hall, 1993. -


 ISSN
ISSN 




 下载:
下载: