-
一个系统,如果内部有许多子系统,且这些子系统间可以产生各种各样的复杂相互作用,那么这样的系统可称其为“复杂系统”[1-2]。复杂系统广泛存在于各个领域,无论是从工程科学[3]到物理学[4],还是从生物学[5]到社会科学[6],都可以找到它的身影。本文研究了一个复杂系统中很普遍但也很重要的特征——流量的波动特征。该特征是指复杂系统中的研究对象,如网络中各节点的流量F的均值与其波动大小 (用标准差刻画) 往往呈现出一种幂函数关系,复杂网络领域一般习惯称其为“波动标度”[7]。
在1938年,研究农作物产量时,文献[8]首先发现了这个流量波动的现象,但当时并未引起太多关注。后来,生物学家Taylor在1961年发表了一篇关于自然人口的论文[9]。这篇文章影响十分广泛,因此,人们便把这篇论文中描述的规律称为泰勒定律。这个定律描述了这样一种关系:自然界中,任何给定物种的种群数量的波动大小都可以近似表示成一个常数乘上该种群数量均值的α次方:波动大小≈常数×均值α。生物学家对这种现象十分感兴趣,从内部驱动与外部驱动的角度出发,建立了多种模型[10-14]尝试解释泰勒定律的本源。
尽管泰勒定律在生物学界影响深远,但由于早期不同学科之间的交流有限,所以这个理论长久以来并没有在复杂系统等领域得到广泛关注。直到2004年,文献[15]首先研究了网络中各节点流量与流量波动大小的关系,发现各节点的平均流量〈Fi〉与流量标准差σi满足关系σi~〈Fi〉α,并且认为α只能取到两个离散的值,分别对应于α=0.5的系统与α=1的系统。前者主要包括不同物种的种群数量[16],统计物理中的平方根型波动[17],单位时间股票市场的交易数[7],因特网中传播数据包的数目[18],微芯片[19]等。后者主要包括酵母每小时的基因表达数[20-22]、宇宙辐射[23-24]、森林中各树种的种子年产量[25]、万维网中URLs链接的数目[26]、高速公路网络及天然的河流网络[27-29]等。为理解两种系统的本质差异,他们采用随机游走与有向流动两种动力学机制来模拟流量波动现象,通过改变游走者规模或流动节点对数量,可以分别生成α=0.5和α=1的标度指数。
波动标度的研究为科学家们难以深刻理解现实世界中复杂系统的困境带来了希望。文献[15]发现复杂网络中的流量波动律并提出相应的解释模型之后,研究者们纷纷进入这个领域大展拳脚,为这个领域带来一派繁荣[30]。在过去的十几年中,研究者们从不同的角度提出了若干动力学或非动力学的模型[15, 31-38]来对这一现象进行解释,对于复杂系统流量波动标度律的形成机制已经有了越来越全面和深入的认识。流量波动律研究已逐渐成为复杂网络动力学的一个重要研究方向。本文将对这一方向的主要研究进展进行回顾,并重点介绍提出的一种能够覆盖现有多数经典流量波动规律的新数学模型。
-
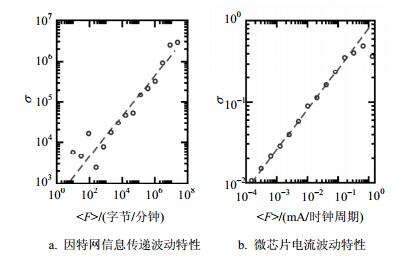
文献[15]在尝试同时刻画复杂系统中成千上万个节点的动力学特性时,发现在复杂网络中单个节点的平均流量〈Fi〉与流量标准差σi之间存在一种特征耦合:σi~〈Fi〉α。经过更深入的研究后,认为纷繁复杂的真实系统可以分成两大类动力学系统或者说两个离散的集合:1) α=1/2的系统 (图 1),如因特网[18]、微芯片[19];2)α=1的系统 (图 2),如万维网[26]、高速公路网络、天然的河流网络[27-29]等。

图 1 流量标准差与均值满足${\sigma _{\text{i}}}{\text{~}}{\left\langle {{F_i}} \right\rangle ^{\frac{1}{2}}} $的系统[15]

图 2 流量标准差与均值满足σi~〈Fi〉的系统[15]
为了更深入地理解这两种系统的本质差异,文献[15]分别用随机游走模型与有向流动模型来模拟真实系统,发现两个模型模拟的结果均为α=1/2。这一定程度上暗示了α=1/2不是某个系统所独有的属性,甚至可能是由系统内部某些因素所决定的特性。文献[15]利用随机游走模型的极限情况来帮助理解α=1/2的本源:使用一种“表层糙化”的模型[39-40],规定每个游走者只随机走一步就会消失,这样每个 节点的流量〈Fi〉就会随时间t线性增加,即:〈Fi〉~t,而波动大小满足σi~t1/2,这样便得到了σi~〈Fi〉1/2。文献[37]的研究者对时间t进行更细致的划分后,发现尽管在规则晶格中,随着t的增加,σi与〈Fi〉的标度关系存在一个拐点,但在复杂网络中,对于任意的t,σi~〈Fi〉1/2恒成立。这个结果也与文献[15]的模型相吻合。
为了理解α=1这种系统的本源,文献[15]认为在真实的系统中,一个给定节点的流量波动不仅被系统内部的动力学机制影响,还会因外部环境的改变而有所变化。为了在模型中体现外部因素的影响,研究人员对模型进行了改进,随机游走模型中 (有向流动模型改进后,结果类似,在此不再赘述),游走者的数量W由常数变成了一个基于时间步t在[W−ΔW, W+ΔW]范围内变化的变量W(t)。当ΔW=0时,节点的流量波动只有系统内部因素的影响,然而,当ΔW≠0时,流量波动同时受内外两个激励源的影响。如果内外激励产生的波动分别用${\sigma _i}^{\operatorname{int} } $与${\sigma _i}^{{\text{ext}}} $表示,那么一个给定节点i的总流量波动就可以表示为${\sigma _i}^2 = {({\sigma _i}^{\operatorname{int} })^2} + {({\sigma _i}^{{\text{ext}}})^2} $。经过分析,可以得到${\sigma _i}^{\operatorname{int} } = {a_i}{\left\langle {{F_i}} \right\rangle ^{1/2}} $(ai是经验得到的比例常数) 与${{\sigma }_{i}}^{\text{ext}}=({{{\sigma }^{\text{dr}}}}/{\left\langle W(t) \right\rangle }\;)\left\langle {{F}_{i}} \right\rangle $。由此可以得到如下方程:
$$ {\sigma _i}^2 = {a_i}^2\left\langle {{F_i}} \right\rangle + {\left[{\frac{{{\sigma ^{{\text{dr}}}}}}{{\left\langle {W(t)} \right\rangle }}\left\langle {{F_i}} \right\rangle } \right]^2} $$ (1) 方程的两项分别表示内部因素的影响与外部环境变化的激励。当ΔW=0时,${\sigma ^{{\text{dr}}}} = 0 $,方程第2项就会消失,此时${\sigma _{\text{i}}}{\text{~}}{\left\langle {{F_i}} \right\rangle ^{\frac{1}{2}}} $,但是当ΔW≠0时,第2项就会对结果产生影响,当ΔW足够大的时候,$\left( {{\sigma }^{\text{dr}}}/\left\langle W\left( t \right) \right\rangle \right)\left\langle {{F}_{i}} \right\rangle \sim \sigma _{i}^{\operatorname{int}}$,那么每个节点的波动仅仅被外部驱动的变化决定,此时σi~〈Fi〉。
-
文献[15]的模型只能生成α=0.5与α=1这两个离散的波动标度指数,而各种各样的研究结果[41-46]表明在真实的复杂系统中波动指标指数取值可能在0.5~1之间,甚至更大的范围。因此,很多理论都一直在试图突破这种分类模式,生成连续的标度指数。文献[32]以随机游走模型为基础,除了考虑单个节点访问量Ni以外,还考虑了访问个体对节点流量的影响Vi是有差异的,最后解析地推出α=$ \frac{\text{1}}{\text{2}}\left( \text{1+}\frac{{\mu }/{\nu }\;}{{\mu }/{\nu }\;\text{+}1} \right)$,其中${{V}_{i}}\propto k_{i}^{\mu },\left\langle {{N}_{i}} \right\rangle \propto k_{i}^{v}$$,ki为第i个节点的度,变量μ、ν分别从节点i的访问代价与访问数量两方面反映出节点的强度。在不同条件下μ/ν的差异就会导致α值偏离0.5或1。文献[35]认为节点的流量波动与网络拓扑结构中的偏好行为有关,而边上的流量波动与动力学机制的偏好行为有关,偏好行为的程度也可能会导致α值偏离0.5或1。
在探索连续标度指数动力学模型的过程中,文献[31]的工作最具有代表性,认为文献[15]的模型忽视了交通网络动力机制中最重要的一个因素——每个节点同时处理数据包的数量是有限的。这个因素导致了数据包与数据包之间的相互作用,最终也使系统有了更大的波动行为,甚至是网络的拥塞[47-49]。为了在模型中考虑这个至关重要的因素,文献[31]基于排队论[50],用数据到达过程与服务过程两个随机过程来确定单个节点的行为。其模型以一个包含N个节点的网络为基础,每个节点被视为一个M/M/1型排队模型中的伺服器。这个排队模型假设每个节点上会形成一个数据包组成的队列,这个队列的长度无限制,可以到达队列的数据包个数也没有限制。队列中,数据包的到达过程被一个参数为λ的泊松分布控制[51],而数据包的发送过程 (服务时间) 被参数为μ的指数分布所决定[52]。然后,用随机游走来模拟数据包在网络上的流动:每个数据包通过一个随机选择的节点进入网络,一旦数据包到达被选定的节点就会进入上述模式的队列,数据包在每个随机步中仅能进入一个节点,并且经过S个随机步后就会消失。另外,在这个模型中,数据包在点间投递的时间被忽略不计。只要每个节点数据包的到达率小于等于它的发送率,系统就会进入一个静止的状态,否则系统就会出现拥塞。节点i的到达率依赖于网络的拓扑结构,并且其所遵循分布的均值为${{\lambda }_{\text{i}}}^{\text{ef}} $。网络中拥有最大${{\lambda }_{\text{i}}}^{\text{ef}} $的节点决定了网络拥塞的开始,记为${{\lambda }_{*}}^{\text{ef}} $。当时间窗的长度$P\tilde{\ }1/{{\lambda }_{*}}^{\text{ef}} $时,无论其他参数是多少,都会得到${{\sigma }_{\text{i}}}\text{ }\!\!\tilde{\ }\!\!\text{ }{{\left\langle {{F}_{i}} \right\rangle }^{\frac{1}{2}}} $。进而可以得到:
$$ {{\sigma }_{i}}={{\left[\left\langle {{F}_{i}} \right\rangle (1-\left\langle {{F}_{i}} \right\rangle ) \right]}^{\frac{1}{2}}} $$ (2) 当〈Fi〉~1时,显然可以得到α=1/2的结果。当$P\tilde{\ }1/{{\lambda }_{*}}^{\text{ef}} $时,整个系统单位时间的数据包数量仅仅被泊松分布的均值决定。通过计算机模拟改变P, λ, S和μ,可以得到不同的属于[0.5, 1]的α值,如图 3所示。并且通过一些实际网络的分析,文献[31]发现在真实网络的α确实可以在0.5~1之间取值 (图 4)。

图 3 指数α随P, λ, S和m变化的关系曲线[31]

图 4 不同时间窗下,阿比林骨干网络的流量波动[31]
-
在突破复杂系统波动标度离散化的限制后,学者们又尝试用统计物理理论研究波动的标度特征[33],但是始终也没有找到通用的波动标度规律,甚至有的学者[36]声称描述每一个节点流量波动行为的通用幂律标度是不存在的。直到2013年,文献[38]提出了一个流量波动定律。该定律的推导不依赖于具体的网络结构、路由等,只取决于一个因素:外部驱动。他们考虑在每个长度为T的时间窗内,外部驱动为RT。当RT是常数且Fi服从泊松分布时,显然〈Fi〉=RT。当RT随时间变化时,可由全概率公式推导出〈Fi〉=RT,$\left\langle {{F}_{i}}^{2} \right\rangle \text{= }\left\langle {{R}_{T}} \right\rangle \text{+}\left\langle {{R}_{T}}^{2} \right\rangle $。再由${{\sigma }_{i}}^{2}=\left\langle {{F}_{i}}^{2} \right\rangle-{{\left\langle {{F}_{i}} \right\rangle }^{2}} $可以解析地得到流量波动与平均流量的普遍的关系式:${{\sigma }_{\text{i}}}=\sqrt{\left\langle {{F}_{i}} \right\rangle +{{\left\langle {{F}_{i}} \right\rangle }^{2}}({\sigma _{{{R}_{T}}}^{2}}/{{{\left\langle {{R}_{T}} \right\rangle }^{2}}}\;)}$,其中${{\sigma }_{{{R}_{T}}}} $表示RT的标准差。该公式能够描述一般化的外界驱动下流量涨落与流量的关系。
文献[38]通过计算机模拟 (图 5) 得到了各种分布的外界驱动形式 (矩形波、均匀分布、泊松分布、高斯分布等)、不同的网络结构 (规则晶格、随机图和无标度网络等) 以及不同的路由策略 (随机行走、最短路径、有效路径等策略等) 的流量涨落特征,实线为上述解析结果,与计算机模拟结果 (图 5a,图 5b) 和实际数据统计结果 (图 5c) 符合得很好。这很好地验证了上一段解析推得的关系式的正确性。此外,对城市交通流量的实际数据的统计分析不仅验证了这个普遍关系式的正确性,还进一步验证了该关系中的标度行为在不同平均流量区间的变化现象,这一现象此前一直没有被实际数据验证过。

图 5 节点流量涨落与流量均值的依赖关系[38]。
之前得到的流量波动定律中波动大小会随着流量的增长而单调增加,原则上这个规律是没有问题的,但是它的合理性仅仅适用于大规模的同质复杂系统。对于有限外部驱动的小规模复杂系统,这个定律就很可能被打破。比如一个小规模复杂系统中存在一个超级节点,系统中绝大多数的流量都会流过这个节点,也就说这个节点有着很大的流量但是流量的波动却很小。一个来自真实数据的证据就是图 6a和图 6b中微芯片的流量波动关系图。虽然在双对数坐标下 (图 6a),真实数据 (空心菱形) 的流量波动行为几乎与式 (1) 的预测 (短线虚线) 吻合,但如果在线性坐标下 (图 6b) 观察,真实数据与式 (1) 的预测却存在一个显著的偏差。

图 6 微芯片与两个模拟系统的流量波动特性[34]
为解决这一问题,文献[34]的研究人员对文献[38]解析推导进行了修正。他们将系统外部驱动与内部波动对流量波动行为的影响区分对待。外部驱动代表外部世界对系统施加的负载,比如人类日常行为的影响[53],这些来自外部的驱动决定了任意给定时间周期的系统总流量。在小规模系统或者异质结构的系统,系统内在的波动也必须被适当地引入,这将为式 (1) 带来一个非平凡的修正。
研究者们基于一个有E条边的网络进行研究,在静态规则下,每一个给定的数据包到达有ki条边的节点i的概率是pi= ki/2E,并且$\sum{i{{p}_{i}}}=1 $[36]。如果这个系统有一个恒定不变的外部驱动M,那么节点i的平均流量$\left\langle {{F}_{i}} \right\rangle =M{{p}_{i}} $。如果M随时间变化,遵循着某种分布,研究人员假设节点i得到n个数据包的概率遵循二项分布。经过数学推导可以得到:
$$ {{\sigma }_{i}}^{2}=\left\langle {{F}_{i}} \right\rangle-\frac{1}{\left\langle M \right\rangle }{{\left\langle {{F}_{i}} \right\rangle }^{2}}+{{\left( \frac{{{\sigma }^{dr}}}{\left\langle M \right\rangle } \right)}^{2}}{{\left\langle {{F}_{i}} \right\rangle }^{2}} $$ (3) 从图 6a和图 6b中可以看出,式 (3) 的预测 (圆点虚线) 更加吻合实际数据。而式 (3) 对异质性网络的有效性可以通过计算机仿真来验证,研究人员模拟了一个异质性网络,它在双对数坐标与线性坐标下的流量波动特性分别在图 6c和图 6e中展示,拓扑结构在图 6g中表示。类比前文的分析,容易看出数据与式 (1) 的预测存在一个显著的偏差,但与式 (3) 完美吻合。如果考虑一个极端情况,为该异质性网络增加一个流量几乎为M的超级枢纽节点,式 (3) 仍然有效 (图 6d、图 6f和图 6h)。经过大量的仿真验证,文献[34]的研究人员得出结论:过去的理论只是式 (3) 的一个特例,而式 (3) 提供了对流量波动律的更一般的描述,适用于不同规模的系统和不同异质性的系统。
-
本文尝试用一套初等的数学模型去统一之前的多种主流物理模型,希望能够为研究人员提供一个从数学角度思考复杂系统的方法。
假设一个系统有N个节点,设随机变量Fi为第i个节点的流量,随机变量M为整个系统的外部驱动,并且Fi与M均为离散型随机变量。已知:
1) M服从某种分布,即已知外部驱动为m时的概率,记为${{P}_{\text{ext}}}\left\{ M=m \right\} $,m=0, 1, 2, 3, …
2) 当M=m时,Fi服从某种分布,即已知外部驱动给定为m时,第i个节点流量为n的概率,换句话说,就是第i个节点从m个外部驱动包中获取n个包的概率,记为$P\left\{ {{F}_{i}}=n|M=m \right\} $,m, n∈N。
则由全概率公式可导出节点流量的标准差σi与均值〈Fi〉的关系:
$$ \begin{matrix} P\{{{F}_{i}}=n\}=\sum\limits_{m=0}^{\infty }{P\{{{F}_{i}}=n|M=m\}P\{M=m\}} \\ \left\langle {{F}_{i}} \right\rangle =\sum\limits_{n=0}^{\infty }{n}P\{{{F}_{i}}=n\}= \\ \sum\limits_{n=0}^{\infty }{n}\sum\limits_{m=0}^{\infty }{P\{{{F}_{i}}=n|M=m\}P\{M=m\}}= \\ \sum\limits_{m=0}^{\infty }{\left[\sum\limits_{n=0}^{\infty }{n}P\{{{F}_{i}}=n|M=m\} \right]P\{M=m\}}= \\ \text{E}\left[\sum\limits_{n=0}^{\infty }{n}P\{{{F}_{i}}=n|M=m\} \right]= \\ \text{E}\left[\text{E}\left[{{F}_{i}}|M \right] \right] \\ \end{matrix} $$ 同理:$\left\langle {{F}_{i}}^{2} \right\rangle =\text{E}\left[\text{E}\left[{{F}_{i}}^{2}|M \right] \right] $,即可得:${{\sigma }_{i}}^{2}=\left\langle {{F}_{i}}^{2} \right\rangle-{{\left\langle {{F}_{i}} \right\rangle }^{2}} $。
下面分情况讨论M和Fi取不同分布时,系统流量波动律的变化:
1) 若M服从单点分布,即M是常数,也就是说M=〈M〉,由于M不变化,也就没有外部环境变化引起的${{\sigma }_{i}}^{\text{ext}} $项。
①当M=〈M〉时,${{F}_{i}}\tilde{\ }P({{\lambda }_{i}}) $,有:
$$ \begin{align} &\left\langle {{F}_{i}} \right\rangle =\text{E}\left[\text{E}\left[{{F}_{i}}|M=\left\langle M \right\rangle \right] \right]=\text{E}[{{\lambda }_{i}}]={{\lambda }_{i}} \\ &{{\sigma }_{i}}^{2}={{({{\sigma }_{i}}^{\operatorname{int}})}^{2}}={{\lambda }_{i}}\Rightarrow \\ &{{\sigma }_{i}}={{\left\langle {{F}_{i}} \right\rangle }^{\frac{1}{2}}}\left( \alpha =\frac{1}{2} \right) \\ \end{align} $$ (4) ②当M=〈M〉时,Fi服从离散型指数分布,即$P\{{{F}_{i}}=n\}=\int_{\text{ }n}^{\text{ }n+1}{\lambda {{\text{e}}^{-\lambda x}}\text{d}x}, n\in N $,有:
$$ \begin{align} &\left\langle {{F}_{i}} \right\rangle =\text{E}\left[\text{E}\left[{{F}_{i}}|M=\left\langle M \right\rangle \right] \right]=\text{E}\left[{{\lambda }_{i}}^{-1} \right]={{\lambda }_{i}}^{-1} \\ &{{\sigma }_{i}}^{2}={{({{\sigma }_{i}}^{\operatorname{int}})}^{2}}={{\lambda }_{i}}^{-2}\Rightarrow \\ &{{\sigma }_{i}}=\left\langle {{F}_{i}} \right\rangle (\alpha =1) \\ \end{align} $$ (5) ③当M=〈M〉时,${{F}_{i}}\tilde{\ }B(\left\langle M \right\rangle, {{P}_{i}}) $,有:
$$ \begin{align} &\left\langle {{F}_{i}} \right\rangle =\text{E}\left[\text{E}\left[{{F}_{i}}|M=\left\langle M \right\rangle \right] \right]=\text{E}\left[\left\langle M \right\rangle {{P}_{i}} \right]=\left\langle M \right\rangle {{P}_{i}} \\ &{{\sigma }_{i}}^{2}={{({{\sigma }_{i}}^{\operatorname{int}})}^{2}}=\left\langle M \right\rangle {{P}_{i}}(1-{{P}_{i}})\Rightarrow \\ &{{\sigma }_{i}}={{\left[\left\langle {{F}_{i}} \right\rangle \left( 1-\frac{1}{\left\langle \text{M} \right\rangle }\left\langle {{F}_{i}} \right\rangle \right) \right]}^{\frac{1}{2}}} \\ \end{align} $$ (6) 若取M≡〈M〉≡1,即在每个时间步,只有1个数据包,则:
$$ {{\sigma }_{i}}={{\left[\left\langle {{F}_{i}} \right\rangle (1-\left\langle {{F}_{i}} \right\rangle ) \right]}^{\frac{1}{2}}} $$ (7) 2) 若M不是常数,将其分解为M=〈M〉+ΔM(ΔM不恒为0) 可以理解〈M〉为内部驱动因素,ΔM为外部环境变化驱动因素。由文献[[15]知:${{\sigma }_{i}}^{\text{ext}}=\left( \frac{{{\sigma }^{\text{dr}}}}{\left\langle M \right\rangle } \right)\left\langle {{F}_{i}} \right\rangle $,其中$ \alpha \text{=}\frac{{{\sigma }^{\text{dr}}}}{\left\langle M \right\rangle }$。
由${{\sigma }_{i}}^{2}={{({{\sigma }_{i}}^{\operatorname{int}})}^{2}}+{{({{\sigma }_{i}}^{\text{ext}})}^{2}} $,在式 (1) 讨论基础上为每个方程加上$ {{({{\sigma }_{i}}^{\text{ext}})}^{2}}$的修正项,则可得:
①Fi服从泊松分布:
$$ {{\sigma }_{i}}^{2}=\left\langle {{F}_{i}} \right\rangle +{{\left( \frac{{{\sigma }^{\text{dr}}}}{\left\langle M \right\rangle } \right)}^{2}}{{\left\langle {{F}_{i}} \right\rangle }^{2}} $$ (8) ②Fi服从指数分布:
$$ {{\sigma }_{i}}^{2}={{\left\langle {{F}_{i}} \right\rangle }^{2}}+{{\left( \frac{{{\sigma }^{\text{dr}}}}{\left\langle M \right\rangle } \right)}^{2}}{{\left\langle {{F}_{i}} \right\rangle }^{2}} $$ (9) ③Fi服从二项分布:
$$ {{\sigma }_{i}}^{2}=\left\langle {{F}_{i}} \right\rangle-\frac{1}{\left\langle M \right\rangle }{{\left\langle {{F}_{i}} \right\rangle }^{2}}+{{\left( \frac{{{\sigma }^{\text{dr}}}}{\left\langle M \right\rangle } \right)}^{2}}{{\left\langle {{F}_{i}} \right\rangle }^{2}} $$ (10) 上述结果可以覆盖绝大多数之前的物理模型:当M是常数时,Fi服从泊松分布得到的式 (4) 与Fi服从指数分布得到的式 (5) 分别反映的是文献[15]中α=0.5与α=1的系统,而静态模型的基础上,加上外部驱动变化因素得到的式 (8),这与文献[15]得到的最终结果相吻合。如果仍然让M是常数,并且Fi服从两点分布,式 (7) 就可以很自然的得到,显然与文献[31]得到的式 (2) 相吻合。如果在Fi服从二项分布的基础上,增加外部环境变化因素的影响,可以推导出与文献[34]结果式 (3) 完全一致的式 (10)。另外,式 (9) 为${{\sigma }_{i}}={{\left[1+{{({{{\sigma }^{\text{dr}}}}/{\left\langle M \right\rangle }\;)}^{2}} \right]}^{{1}/{2}\;}}\left\langle {{F}_{i}} \right\rangle $,其波动标度大于1,可以尝试用这个公式去解释一些特殊系统,如网络空间与物理空间的人类活动[54]
本文工作仍然存在一些不足:
1) 以上的分析均是通过数学假设得到的结果,并未考虑物理过程可行性所需的条件;
2) 本文的模型是在各节点流量同分布前提下考虑的,没有考虑各个节点流量有不同分布的情况;
3) 当节点流量服从某种期望值或方差不收敛的分布时,结果将会有所不同。
尽管如此,本文的数学模型尝试着去统一框架解释现有主流流量涨落物理模型,或许能为其他研究者更深入地理解复杂系统流量波动规律带来启发。
-
探索和揭示隐藏在各种复杂现象背后的简洁规律是复杂系统研究的永恒主题。流量波动标度律恰恰是这样一种典型的规律,且由于它对理解复杂系统动力学特征的重要性,使其成为复杂系统研究领域持续关注的一个重要问题。
文献[15]的研究为揭示各类复杂系统中流量波动律形成的低层机制迈出了开创性的一步。但正如他们在人类动力学研究中发现“普适”标度律的情形[55-56]类似,后续的大量理论和实证研究都表明,α=0.5与α=1两个离散标度指数远不能覆盖各类复杂系统中的流量波动标度关系,且随机游走与有向流动两种简化的动力学过程也不能很好解释实际复杂系统中各种内、外部因素作用对流量波动的影响。
为解决这些问题,国内外学者十几年来陆续提出了考虑个体异质性及不同网络结构的随机游走模型[32, 37]、考虑数据包拥塞的排队模型[31]、考虑内外部驱动影响的流量涨落模型[34, 38]等多种物理模型试图解释复杂系统流量波动律的可能成因,这些工作使人们对复杂系统流量波动标度律的形成机制有了越来越全面和深入的认识。但随之而来的问题是,这些模型的假设往往只针对一类或几类特定的系统,缺乏普适性。似乎已经背离了揭示复杂现象背后一致规律的初衷。
正所谓“天下大势,分久必合,合久必分”,理论研究也同样是如此这般分分合合、螺旋上升。本文认为,未来对于复杂系统流量波动律的研究,一定会回归探索各类复杂系统背后一致规律的本质。而本文提出的简单数学模型,可以看作是一种初步尝试。这一模型虽然缺乏对特定系统物理意义的描述,但却能够用一个统一的数学框架覆盖之前大多数经典的流量波动律模型。希望本文的工作能为其他研究者更深入理解各类复杂系统中流量波动律的共性和个性带来启发,共同推进这一研究领域的深入发展。
Flux-Fluctuation Law in Complex Systems: a Survey
-
摘要: 流量波动律是指复杂系统中的研究对象,如网络中各节点上流量的均值与标准差之间呈现出幂律关系。这一规律普遍存在于多种复杂系统中,探索流量波动律的形成机制对于理解和刻画这些复杂系统的动力学特征具有重要意义。该文对近些年来国内外学者关于复杂系统中流量波动的研究进行回顾,总结了该方向不同时期的主要研究成果以及一些典型的动力学模型。提出了一套简单的数学模型,可将之前的主流动力学模型都纳入一个统一的数学框架之中。最后对未来流量波动律的研究做出了展望。Abstract: Flux-fluctuation law means the scaling relationship between the mean and the stand errors of traffic in networks. This law has been observed in a wide range of complex systems. Understanding the origin of flux-fluctuation law is fundamental and significant to the dynamics of complex systems. This review article summarizes the state-of-the-art progresses of flux-fluctuation law in complex systems, and give a detailed description of typical models and major results in this area. Moreover, we propose an easy mathematical model, with which we use the mathematic language to provide a universal framework for previous major models. Furthermore, this article reviews the advanced and insufficient points of related works, and points out some unsolved challenges in both theoretical and practical aspects.
-
Key words:
- complex systems /
- flux-fluctuation law /
- scaling laws /
- Taylor's law
-
图 1 流量标准差与均值满足${\sigma _{\text{i}}}{\text{~}}{\left\langle {{F_i}} \right\rangle ^{\frac{1}{2}}} $的系统[15]
图 2 流量标准差与均值满足σi~〈Fi〉的系统[15]
图 3 指数α随P, λ, S和m变化的关系曲线[31]
图 4 不同时间窗下,阿比林骨干网络的流量波动[31]
图 5 节点流量涨落与流量均值的依赖关系[38]。
图 6 微芯片与两个模拟系统的流量波动特性[34]
-
[1] AUYANG S Y. Foundations of complex-system theories:in economics, evolutionary biology, and statistical physics[M]. Cambridge, England:Cambridge University Press, 1999. [2] BAR-YAM Y. Dynamics of complex systems[M]. Boston:Addison-Wesley, 1997. [3] LI J, KWAUK M. Exploring complex systems in chemical engineering-the multi-scale methodology[J]. Chemical Engineering Science, 2003, 58(3):521-535. [4] BARABÁSI A-L. The physics of the Web[J]. Physics World, 2001, 14(7):33-38. doi: 10.1088/2058-7058/14/7/32 [5] BULLMORE E, SPORNS O. Complex brain networks:Graph theoretical analysis of structural and functional systems[J]. Nature Reviews Neuroscience, 2009, 10(3):186-198. doi: 10.1038/nrn2575 [6] BUCKLEY W. Society as a complex adaptive system[J]. Emergence:Complexity and Organization, 2008, 10(3):86. https://www.questia.com/library/journal/1P3-1605196631/society-as-a-complex-adaptive-system [7] EISLER Z, KERTESZ J. Scaling theory of temporal correlations and size-dependent fluctuations in the traded value of stocks[J]. Physical Review E, 2006, 73(4):046109. doi: 10.1103/PhysRevE.73.046109 [8] SMITH H F. An empirical law describing heterogeneity in the yields of agricultural crops[J]. The Journal of Agricultural Science, 1938, 28(1):1-23. doi: 10.1017/S0021859600050516 [9] TAYLOR L. Aggregation, variance and the mean[J]. Nature, 1961, 189(4766):732-735. doi: 10.1038/189732a0 [10] BJØRNSTAD O N, GRENFELL B T. Noisy clockwork:Time series analysis of population fluctuations in animals[J]. Science, 2001, 293(5530):638-643. doi: 10.1126/science.1062226 [11] ENGEN S, BAKKE Ø, ISLAM A. Demographic and enviromental stochasticity-concepts and definitians[J]. Biometrics, 1998, 54:840-846. doi: 10.2307/2533838 [12] GRENFELL B, WILSON K, FINKENST DT B, et al. Noise and determinism in synchronized sheep dynamics[J]. Nature, 1998, 394(6694):674-677. doi: 10.1038/29291 [13] PAULSSON J. Summing up the noise in gene networks[J]. Nature, 2004, 427(6973):415-418. doi: 10.1038/nature02257 [14] SÆTHER B-E, TUFTO J, ENGEN S, et al. Population dynamical consequences of climate change for a small temperate songbird[J]. Science, 2000, 287(5454):854-856. doi: 10.1126/science.287.5454.854 [15] DE MENEZES M A, BARABÁSI A-L. Fluctuations in network dynamics[J]. Physical Review Letters, 2004, 92(2):028701. doi: 10.1103/PhysRevLett.92.028701 [16] TAYLOR L, WOIWOD I. Comparative synoptic dynamics. I. Relationships between inter-and intra-specific spatial and temporal variance/mean population parameters[J]. The Journal of Animal Ecology, 1982, 51:879-906. doi: 10.2307/4012 [17] LANDAU L D, LIFSHITZ E M. Course of theoretical physics[M]. Oxford:Pergamon Press, 1980. [18] VÁZQUEZ A, PASTOR-SATORRAS R, VESPIGNANI A. Large-scale topological and dynamical properties of the Internet[J]. Physical Review E, 2002, 65(6):066130 doi: 10.1103/PhysRevE.65.066130 [19] CANCHO R F, JANSSEN C, SOLÉ R V. Topology of technology graphs:Small world patterns in electronic circuits[J]. Physical Review E, 2001, 64(4):046119. doi: 10.1103/PhysRevE.64.046119 [20] CHO R J, CAMPBELL M J, WINZELER E A, et al. A genome-wide transcriptional analysis of the mitotic cell cycle[J]. Molecular Cell, 1998, 2(1):65-73. doi: 10.1016/S1097-2765(00)80114-8 [21] NACHER J, OCHIAI T, AKUTSU T. On the relation between fluctuation and scaling-law in gene expression time series from yeast to human[J]. Modern Physics Letters B, 2005, 19(23):1169-1177. doi: 10.1142/S0217984905009249 [22] ŽIVKOVIĆ J, TADIĆ B, WICK N, et al. Statistical indicators of collective behavior and functional clusters in gene networks of yeast[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2006, 50(1-2):255-258. doi: 10.1140/epjb/e2006-00103-4 [23] UTTLEY P, MCHARDY I M. The flux-dependent amplitude of broadband noise variability in X-ray binaries and active galaxies[J]. Monthly Notices of the Royal Astronomical Society, 2001, 323(2):L26-L30. doi: 10.1046/j.1365-8711.2001.04496.x [24] VAUGHAN S, UTTLEY P. Studying accreting black holes and neutron stars with time series:Beyond the power spectrum[C]//Fourth International Symposium on Fluctuations and Noise. Bellingham:SPIE, 2007:660314-660314-13. [25] SATAKE A, IWASA Y. Pollen coupling of forest trees:Forming synchronized and periodic reproduction out of chaos[J]. Journal of Theoretical Biology, 2000, 203(2):63-84. doi: 10.1006/jtbi.1999.1066 [26] LAWRENCE S, GILES C L. Searching the world wide web[J]. Science, 1998, 280(5360):98-100. doi: 10.1126/science.280.5360.98 [27] BANAVAR J R, MARITAN A, RINALDO A. Size and form in efficient transportation networks[J]. Nature, 1999, 399(6732):130-132. doi: 10.1038/20144 [28] CALDARELLI G. Cellular models for river networks[J]. Physical Review E, 2001, 63(2):021118. doi: 10.1103/PhysRevE.63.021118 [29] CIEPLAK M, GIACOMETTI A, MARITAN A, et al. Models of fractal river basins[J]. Journal of Statistical Physics, 1998, 91(1-2):1-15. https://www.researchgate.net/publication/1946554_Models_of_Fractal_River_Basins [30] EISLER Z, BARTOS I, KERTESZ J. Fluctuation scaling in complex systems:Taylor's law and beyond[J]. Advances in Physics, 2008, 57(1):89-142. doi: 10.1080/00018730801893043 [31] DUCH J, ARENAS A. Scaling of fluctuations in traffic on complex networks[J]. Physical Review Letters, 2006, 96(21):218702. doi: 10.1103/PhysRevLett.96.218702 [32] EISLER Z, KERT S Z J. Random walks on complex networks with inhomogeneous impact[J]. Physical Review E, 2005, 71(5):057104. doi: 10.1103/PhysRevE.71.057104 [33] FRONCZAK A, FRONCZAK P. Origins of Taylor's power law for fluctuation scaling in complex systems[J]. Physical Review E, 2010, 81(6):066112. doi: 10.1103/PhysRevE.81.066112 [34] HUANG Z G, DONG J Q, HUANG L, et al. Universal flux-fluctuation law in small systems[J]. Scientific Reports, 2014, 4:6787. doi: 10.1038/srep06787 [35] KUJAWSKI B, TADIĆ B, RODGERS G J. Preferential behaviour and scaling in diffusive dynamics on networks[J]. New Journal of Physics, 2007, 9(5):154. doi: 10.1088/1367-2630/9/5/154 [36] MELONI S, GÓMEZ-GARDENES J, LATORA V, et al. Scaling breakdown in flow fluctuations on complex networks[J]. Physical Review Letters, 2008, 100(20):208701. doi: 10.1103/PhysRevLett.100.208701 [37] YOON S, YOOK S-H, KIM Y. Scaling property of flux fluctuations from random walks[J]. Physical Review E, 2007, 76(5):056104. doi: 10.1103/PhysRevE.76.056104 [38] ZHOU Z, HUANG Z G, HUANG L, et al. Universality of flux-fluctuation law in complex dynamical systems[J]. Physical Review E, 2013, 87(1):012808. doi: 10.1103/PhysRevE.87.012808 [39] BARABÁSI A-L, STANLEY H E. Fractal concepts in surface growth[M]. Cambridge, England:Cambridge University Press, 1995. [40] FAMILY F, VICSEK T. Dynamics of fractal surfaces[M]. Singapore:World Scientific, 1991. [41] BALLANTYNE I, J KERKHOFF A. The observed range for temporal mean variance scaling exponents can be explained by reproductive correlation[J]. Oikos, 2007, 116(1):174-180. doi: 10.1111/oik.2007.116.issue-1 [42] KEITT T H, AMARAL L A, BULDYREV S V, et al. Scaling in the growth of geographically subdivided populations:Invariant patterns from a continent-wide biological survey[J]. Philosophical Transactions of the Royal Society B:Biological Sciences, 2002, 357(1421):627-633. doi: 10.1098/rstb.2001.1013 [43] KENDAL W S. A stochastic model for the self-similar heterogeneity of regional organ blood flow[J]. Proceedings of the National Academy of Sciences, 2001, 98(3):837-841. doi: 10.1073/pnas.98.3.837 [44] KENDAL W S. Taylor's ecological power law as a consequence of scale invariant exponential dispersion models[J]. Ecological Complexity, 2004, 1(3):193-209. doi: 10.1016/j.ecocom.2004.05.001 [45] REED D H, HOBBS G R. The relationship between population size and temporal variability in population size[J]. Animal Conservation, 2004, 7(1):1-8. doi: 10.1017/S1367943004003476 [46] WEST B J. Comments on the renormalization group, scaling and measures of complexity[J]. Chaos, Solitons & Fractals, 2004, 20(1):33-44. https://www.researchgate.net/publication/223872962_Comments_on_the_renormalization_group_scaling_and_measures_of_complexity [47] GUIMERÀ R, DIAZ-GUILERA A, VEGA-REDONDO F, et al. Optimal network topologies for local search with congestion[J]. Physical Review Letters, 2002, 89(24):248701. doi: 10.1103/PhysRevLett.89.248701 [48] TADIĆ B, THURNER S, RODGERS G. Traffic on complex networks:Towards understanding global statistical properties from microscopic density fluctuations[J]. Physical Review E, 2004, 69(3):036102. doi: 10.1103/PhysRevE.69.036102 [49] YAN G, ZHOU T, HU B, et al. Efficient routing on complex networks[J]. Physical Review E, 2006, 73(4):046108. doi: 10.1103/PhysRevE.73.046108 [50] ALLEN AO P. Probability, statistics and queuing theory with computer science applications[M]. Cambridge, Massachusetts:Academic Press, 1990. [51] KARAGIANNIS T, MOLLE M, FALOUTSOS M, et al. A nonstationary Poisson view of Internet traffic[C]//INFOCOM 2004 Twenty-third AnnualJoint Conference of the IEEE Computer and Communications Societies. Piscataway:IEEE, 2004:1558-1569. [52] JACKSON J R. Networks of waiting lines[J]. Operations Research, 1957, 5(4):518-521. doi: 10.1287/opre.5.4.518 [53] ZHOU Z, HUANG Z G, YANG L, et al. The effect of human rhythm on packet delivery[J]. Journal of Statistical Mechanics:Theory and Experiment, 2010(8):P08001. doi: 10.1088/1742-5468/2010/08/P08001 [54] ZHAO Z D, HUANG Z G, HUANG L, et al. Scaling and correlation of human movements in cyberspace and physical space[J]. Physical Review E, 2014, 90(5):050802. doi: 10.1103/PhysRevE.90.050802 [55] BARABÁSI A L. The origin of bursts and heavy tails in human dynamics[J]. Nature, 2005, 435(7039):207-211. doi: 10.1038/nature03459 [56] 周涛, 韩筱璞, 闫小勇, 等.人类行为时空特性的统计力学[J].电子科技大学学报, 2013, 42(4):481-540. http://www.xb.uestc.edu.cn/nature/index.php?p=item&item_id=1319 ZHOU Tao, HAN Xiao-pu, YAN Xiao-yong, et al. Statistical mechanics on temporal and spatial activities of human[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(4):481-540. http://www.xb.uestc.edu.cn/nature/index.php?p=item&item_id=1319 -


 ISSN
ISSN 



 下载:
下载: