假设脉冲多普勒(PD)雷达发射的第$ m $个线性调频脉冲信号的基带形式如下：

式中，；$ \hat t $为发射脉冲的时间变量，为快时间；$ m $为发射脉冲序列索引；$ {t_m} $为慢时间；$ {T_p} $为发射脉冲宽度；$ \gamma $为调频斜率。

高速多目标的雷达回波信号基带形式为：

式中，$ {A_i} $为第$ i $个目标的回波幅度；慢时间$ {t_m} $时刻目标与雷达的径向距离为$ {R_i}({t_m}) = {R_{0i}} + {v_{0i}}{t_m} + $ $ \frac{1}{2}{a_i}t_m^2 $，$ {R_{0i}} $，$ {v_{0i}} $以及$ {a_i} $分别为目标的径向初始距离，径向初始速度以及径向加速度；$ {f_c} $为雷达载频；$ n(\hat t, {t_m}) $为加性高斯白噪声。

式(2) 对应的频域表示形式为：

利用$ X(f, {t_m}) = {\mathop{\rm rect}\nolimits} \left( {\frac{f}{{\gamma {T_p}}}} \right)\exp \left( { - {\rm{j\pi }}\frac{{{f^2}}}{\gamma }} \right) $匹配滤波器对式(3) 信号进行脉冲压缩处理：

式中，第一个指数项表示目标初始时刻位置；第二个指数项表示目标由于速度和加速度产生的距离徙动；第四个指数项表示目标的多普勒频移，第五个指数项表示目标的多普勒扩散。

循环平稳理论在信号处理领域的一个重要应用方向是目标检测以及信号参数和波形的估计，其信号与干扰分离效果好，计算复杂度低，然而容易受到多普勒模糊的影响^[7-8]。对式(4) 信号进行慢时间维的自相关处理：

式中，

式中，$ {U_{ii}}(u, f, {t_m}) $为目标信号自相关项，存在目标加速度所造成的距离徙动；$ {U_{ij}}(u, f, {t_m}) $为目标信号的互相关项，存在目标速度和加速度造成的距离徙动及目标加速度产生的多普勒扩散；$ u $代表循环延迟，根据文献[7-8]：延迟$ u = \frac{T}{{\rm{2}}} $时估计性能最优，其中$ T $为信号积累总时间；$ {U_n}(u, f, {t_m}) $为信号自相关后的噪声项，能量集中在零循环频率处^[7-8]。对比$ {U_{ii}}(u, f, {t_m}) $与$ {U_{ij}}(u, f, {t_m}) $可以得出：即使$ {U_{ii}}(u, f, {t_m}) $中第$ i $个目标的距离徙动得到补偿，$ {U_{ij}}(u, f, {t_m}) $中每一个互相关项对应的距离徙动及多普勒扩散仍旧存在，且徙动与扩散严重，因此可以认为$ {U_{ij}}(u, f, {t_m}) $对于$ {U_{ii}}(u, f, {t_m}) $相当于干扰。基于上述分析，后续信号处理将针对信号自相关项$ {U_{ii}}(u, f, {t_m}) $距离徙动的补偿。

将$ {U_{ii}}(u, f, {t_m}) $中第$ i $个目标对应的多普勒频率$ {f_{di}} = \frac{{2{a_i}u}}{\lambda } = {f_{di0}} + {n_{ki}}{\rm{prf}} $代入式(6)，可得：

式中，$ \lambda $为波长；$ {f_{di0}} $为$ {R_{ii}}(u, f, {t_m}) $对应的第$ i $个目标折叠以后的多普勒频率；$ {n_{ki}} $为$ {U_{ii}}(u, f, {t_m}) $对应的第$ i $个目标的多普勒模糊数；$ {\rm{prf}} $为脉冲重复频率。式(8) 信号存在距离徙动及多普勒模糊，为完成目标参数化检测，需要进行距离徙动补偿及解多普勒模糊。

Keystone变换不需要目标的先验信息，即可完成距离徙动补偿，在雷达信号处理中得到了广泛的应用，然而Keystone变换本身受限于多普勒模糊，如果目标发生模糊，则需要进行解模糊处理^[6]。

因为$ {f_c} > > f $，则$ \frac{{{f_c}}}{{{f_c} + f}} \approx 1 $，那么进行Keystone变换消除$ {U'_{ii}}(u, f, {t_m}) $的距离徙动，令$ {t_m} = \frac{{{f_c}}}{{f + {f_c}}}{\tau _m} $，可得：

根据式(9) 信号形式，定义解模糊操作函数：

对式(9) 信号进行解模糊处理，并转换到时域：

式中，$ {n'_k} $为模糊数范围中的取值，若$ {n_{ki}} - {n'_k} = 0 $，则目标不再存在距离徙动，反之目标存在距离徙动。

根据设定的模糊数范围，通过代价函数式(12) 可以计算出目标的运动参数：

式中，$ {t'_i} = \frac{{2{v_{0i}}u + {a_i}{u^2}}}{c} $为第$ i $个目标峰值的快时间时刻；$ {f'_{di0}} $和$ {n'_{ki}} $分别为第$ i $个目标的多普勒频移及模糊数；$ {\hat n_k} $为模糊数取值范围。$ {\rm{FFT}} $作用于信号慢时间维，则第$ i $个目标的加速度$ {a'_i} $及初始速度$ {v'_{0i}} $分别为：

根据文献[7-8]的参数所示，设雷达载频为10 $ {\rm{GHz}} $，带宽为10 $ {\rm{MHz}} $，重频为500 $ {\rm{Hz}} $，积累脉冲数为300，在不进行插值处理的情况下，文献[7-8]和式(13) 中的加速度估计精度为$ \frac{1}{6}{\rm{m/}}{{\rm{s}}^2} $，式(13) 中的速度估计精度为50$ {\rm{m/s}} $，文献[7-8]中的速度估计与加速度估计相关，则其速度估计精度更低。由PD雷达的设计原则可知：相参积累时间内目标距离徙动不能超过半个距离单元，多普勒扩散不能超过一个多普勒单元。根据所设定的雷达参数，积累时间内目标距离徙动不超过半个距离单元的最大目标速度$ v $和多普勒扩散不超过一个多普勒单元的最大目标加速度$ a $分别为：12.5 m/s和$ \frac{1}{{24}}{\rm{ m/}}{{\rm{s}}^2} $，可见文献[7-8]和式(13) 的参数估计精度不能满足相参积累的条件。针对此问题，同时考虑到实际工程需求，本文提出联合频域距离徙动补偿与FRFT方法。利用式(13) 得到的运动参数对式(4) 信号进行补偿：

根据式(14) 信号形式定义频域距离徙动补偿处理公式：

式中，$ \hat v $是为补偿距离徙动而假定的值。利用式(15) 对式(14) 信号进行距离徙动补偿，并转换到时域：

式中，$ {\mathop{\rm sinc}\nolimits} (a) = \sin ({\rm{\pi }}a)/{\rm{\pi }}a $。$ {a_i} - {a'_i} $造成的距离徙动可忽略，可见，只要$ {v_{\mathit{0i}}} - {v'_{0i}} - \hat v = 0 $目标距离徙动便可被补偿。

利用FRFT能够对线性调频信号进行能量聚集以及FRFT是线性的优势P^[9-10]，对距离徙动补偿后$ {b_{rm}}(\hat t, \hat a, \hat v, {t_m}) $的每个距离单元进行阶次变换的分数阶傅里叶变换并取模。本方法采用的FRFT的变换核^[8]：

式中，$ \alpha = \frac{{p\pi }}{2} $；$ p $为分数阶傅里叶变换的阶数。

根据$ {a'_i} $, $ v_{0i}^{'} $, $ a $及$ v $可以设定参数搜索范围及搜索范围中的参数取值，通过代价函数式(18) 可以计算出目标的运动参数：

式中，$ (\hat a, \hat v) $为$ (\hat a', \hat v') $搜索范围中的参数取值；$ ({a''_i}, {v''_{0i}}) $是估计得到的目标运动参数。

为验证所提出方法的有效性，假设雷达仿真参数：Ka波段载频30 GHz雷达，带宽为10 $ {\rm{MHz}} $，脉宽为500 $ {\rm{\mu s}} $，采样频率为10 $ {\rm{MHz}} $，重复频率为200 $ {\rm{Hz}} $，积累脉冲数为200。

目标仿真参数的设定如表 1所示。

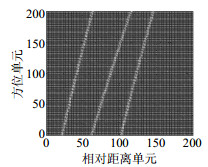
在雷达回波信号信噪比-12 dB条件下，噪声为加性高斯白噪声，距离维脉冲压缩的结果如图 1所示。可以看出目标存在距离徙动，并且由于目标的加速度较高，目标距离维脉冲压缩之后产生距离弯曲。对图 1脉冲压缩后信号的方位单元作傅里叶变换进行能量积累，结果如图 2所示。由图 2结果可以得出：由于距离徙动及多普勒扩散的存在，常规检测方法(目标回波做脉压后数据做纵向FFT进行信号能量积累)不适用于高速目标的检测及运动参数估计。

图  1  距离维脉冲压缩结果

图  2  慢时间维FFT结果

利用文献[2-8]以及本文算法分别对图 1距离维脉冲压缩后对应的目标进行检测。文献[2]的改进Hough变换算法的检测结果如图 3a所示，文献[3-4]的Radon-Fourier变换算法的检测结果如图 3b所示，文献[5]的Keystone变换结合解线频调算法的检测结果如图 3c所示，文献[6]的模糊数搜索算法的检测结果如图 3d所示，文献[7-8]的基于循环平稳理论的迭代算法的检测结果如图 3e所示，本文算法的检测结果如图 3f所示，其中，图 3c~图 3f的检测结果由3次并行处理结果直接相加而成。

图  3  各文献算法检测结果

文献[2]改进Hough变换算法为基于非相参积累方式的线积分算法，由检测结果图 3a可以看出在低信噪比和目标包络呈现弯曲的情况下，检测结果中出现虚假峰值。文献[3-4]中Radon-Fourier变换算法为基于相参积累方式的线积分算法，然而由于包络弯曲及多普勒扩散的原因，如图 3b所示，其信号能量不能够得到有效的积累。实际战场环境中，多普勒模糊数是未知的，由检测结果图 3c可以看出文献[5]中Keystone变换结合解线频调算法的信号积累效果不理想。文献[6]的算法未考虑多普勒扩散的影响，导致能量发生扩散。文献[7-8]中基于循环平稳理论的迭代算法参数估计精度低，而且在实际中对加速度的取值范围没有任何先验信息，为保证不出现相位模糊，第一步迭代中延时值选择最小的非零延时值，即$ u = {\rm{0}}{\rm{.002 s}} $，但是由于信噪比低，首次迭代的结果易出现模糊的结果，导致后续迭代不能收敛，参数估计错误，由检测结果图 3e可以看出信号积累能量发生扩散。比较图 3f与图 3a~图 3e可以看出，本文算法得到了比较理想的检测效果，原因在于低信噪比下目标距离徙动得到了校正，多普勒扩散得到了补偿。

利用本文提出的算法，在信噪比为-15 dB的情况下进行100次Monte Carlo实验估计目标的运动参数。目标A估计得到的平均初始速度和平均加速度分别为：562.85 $ {\rm{m/s}} $，81 $ {\rm{m/}}{{\rm{s}}^2} $；目标B估计得到的平均初始速度和平均加速度分别为：990.85 $ {\rm{m/s}} $，61 $ {\rm{m/}}{{\rm{s}}^2} $；目标C估计得到的平均初始速度和平均加速度分别为：759.85 $ {\rm{m/s}} $，101 $ {\rm{m/}}{{\rm{s}}^2} $。由估计得到的目标运动参数的精确性可以看出，本文算法在低信噪比下估计出满足相参积累的高速多目标的运动参数。

将本文提出的算法利用某型雷达的实测数据进行验证，雷达积累脉冲数为5 120。对目标进行常规检测，其检测结果如图 4a所示。可得到结论：通过常规检测方法，由于距离徙动及多普勒扩散的存在，目标能量发生明显扩散。通过本文检测算法，其检测结果如图 4b所示。由于本文所提出的算法中，目标的距离徙动及多普勒扩散得到一定的补偿，可以在低信噪比条件下估计出满足相参积累条件的目标的运动参数，从而保证目标能量得到有效的积累。

图  4  实测数据检测结果

本文提出了基于循环平稳的联合Keystone变换与模糊数搜索联合方法，估计出满足相参积累的高速多目标的运动参数，解决了循环平稳的多普勒模糊问题，利用联合频域距离徙动补偿处理与分数阶傅里叶变换方法完成参数化检测，克服了已有算法估计精度低和低信噪比下不能收敛的缺陷。计算机仿真和实测数据验证了算法的有效性。