-
随着阵列天线广泛应用于军事领域,阵列信号处理技术得到了迅速地发展,波达方向(direction of arrival, DOA)估计作为阵列信号处理的一个重要组成部分,得到了众多学者的广泛关注。经过几十年的不断研究,先后提出了如多重信号分类(multiple signal classification, MUSIC)算法这类子空间类算法以及其他算法[1-3]。但随着阵列规模的不断增加,整个信号处理过程处理的数据量不断增加,使得算法的实时性变差,因此,人们在探测少量目标时常常会关闭部分阵元进行阵元降采样以降低运算复杂度,但是会降低角度估计精度。同时,随着阵列规模的扩大,提高了阵元损坏的概率,一旦阵元出现损坏,将会影响系统的角度估计精度。这两种情况可认为是相应位置上的阵元出现缺损,阵元接收数据未知,传统估计未知采样数据的方法如内插和学习[4-5]方法过于依赖先验知识,限制了在实际中的应用,如何解决这类问题成为了目前的研究热点。
文献[6-7]提出的矩阵填充(matrix completion, MC)理论利用矩阵少量的已知元素,通过对矩阵低秩性的约束可精确重构出原始矩阵。MC理论广泛应用于雷达成像[8]、多输入多输出(multiple input multiple output, MIMO)体制雷达[9]以及波达方向估计中[10-11],并取得了大量富有成效的成果。但在实际处理过程中,对阵元的降采样或可能出现的阵元损坏会导致接收数据矩阵的某一行上缺失全部数据,而传统的MC方法要求采样矩阵的每一行或每一列至少有一个非零元素,以保证准确恢复出原始的接收数据矩阵。因此,文献[11]将单次快拍下接收到的列向量数据变换为等效低秩矩阵,通过MC理论有效地恢复了原始数据,但由于仅利用单次观测数据,估计精度较低,而且系统自由度受到阵元数量的限制,限制了其在实际中的应用。
本文对均匀线阵阵元缺损位置的接收数据做置零处理,使接收数据矩阵出现全零行,将接收数据矩阵每一列变换成一个Hankel矩阵,并将所有生成的Hankel矩阵构成一个二重块Hankel矩阵,获得一个全新的数据矩阵。通过对变换后的矩阵进行填充恢复,再通过反变换获得完整的接收数据矩阵,因此,实现了在阵列接收存在阵元缺损的情况下,获得了高精度的角度估计值。
-
设空间中存在有K($K \ll L$)个远场窄带目标,接收天线为阵元数为L的均匀线阵,阵元间隔为d,信号发射频率为${f_0}$,波长为$\lambda $,目标反射信号$\tilde s(t) = s(t){{\rm{e}}^{{\rm{j}}2{\rm{\pi }}ft}}$,t时刻有一目标反射信号从$\theta $方向入射到阵列上,不考虑噪声时阵列接收到的数据为:
$$ \boldsymbol{y}(t)=\boldsymbol{a}\tilde{s}(t) $$ (1) 由式(1) 可知,在理想情况下当同时接收K个信源目标的信号时有:
$$ \begin{matrix} \boldsymbol{y}(t)=\sum\limits_{k=1}^{K}{{{\boldsymbol{y}}_{k}}(t)=} \\ [\boldsymbol{a}({{\theta }_{1}}), \boldsymbol{a}({{\theta }_{2}}), \cdots, \boldsymbol{a}({{\theta }_{K}})]{{[{{{\tilde{s}}}_{1}}(t), {{{\tilde{s}}}_{2}}(t), \cdots, {{{\tilde{s}}}_{K}}(t)]}^{\text{T}}} \\ \end{matrix} $$ (2) 可简写式(2) 为:
$$ \boldsymbol{y}=\boldsymbol{As} $$ (3) 式中,称${\boldsymbol{A}} = [{\boldsymbol{a}}({\theta _1}), {\boldsymbol{a}}({\theta _2}), \cdots, {\boldsymbol{a}}({\theta _K})]$为阵列流形矩阵;${\boldsymbol{s}} = {[{\tilde s_1}(t), {\tilde s_2}(t), \cdots, {\tilde s_K}(t)]^\text{T}}$。
由于K个远场窄带目标相互独立,可知:
$$ \operatorname{rank}(\boldsymbol{A})=K $$ (4) $$ \operatorname{rank}(\boldsymbol{s})=K $$ (5) 由${\mathop{\rm rank}\nolimits} ({\boldsymbol{AB}}) \le \min ({\mathop{\rm rank}\nolimits} ({\boldsymbol{A}}), {\mathop{\rm rank}\nolimits} ({\boldsymbol{B}}))$可知:
$$ \operatorname{rank}(\boldsymbol{y})\le \min (\operatorname{rank}(\boldsymbol{A}), \operatorname{rank}(\boldsymbol{s}))=K\ll L $$ (6) 对于多次快拍的情况,则有:
$$ \boldsymbol{Y}=\boldsymbol{AS} $$ (7) 式中,${\boldsymbol{Y}} = [{{\boldsymbol{y}}_1}, {{\boldsymbol{y}}_2}, \cdots, {{\boldsymbol{y}}_M}]$,M为快拍数;${\boldsymbol{S}} = [{{\boldsymbol{s}}_1}, {{\boldsymbol{s}}_2}, \cdots, {{\boldsymbol{s}}_M}]$。
由式(6) 可知:
$$ \operatorname{rank}(\boldsymbol{Y})\le K $$ (8) 因此,本文认为阵列天线接收到的数据矩阵是低秩的;一般情况下,在接收信号时会有一定的噪声进入,一般表示为:
$$ \boldsymbol{Y}=\boldsymbol{AS}+\boldsymbol{N} $$ (9) 式中,${\boldsymbol{N}}$表示空时加性高斯白噪声。
当存在噪声时,一般认为数据矩阵满足近似低秩性,仍然适用MC理论[12]。
-
由于数据矩阵的低秩性,当满足强不相干性[12](strong incoherence property, SIP)条件时,可通过最小秩约束利用已知元素求解出唯一存在的原始矩阵,这个约束优化问题可表示为:
$$ \begin{array}{*{20}{c}} {{\mathop{\rm minmize}\nolimits} \;\;\;\;\;\;\;{\mathop{\rm rank}\nolimits} ({\boldsymbol{M}})}\\ {{\mathop{\rm s}\nolimits} . \text{t}. \;\;\; {\mathit{\Theta _\Omega} }({\boldsymbol{M}}) = {\mathit{\Theta _\Omega} }({\boldsymbol{Y}})} \end{array} $$ (10) 式中,$ \boldsymbol{M}\in {{\mathbb{R}}^{L\times M}} $为决策变量矩阵;$ \mathit{\Omega} $为矩阵Y有效元素位置的集合,对于任意$(i, j)\in \mathit{\Omega} $,均有${{\boldsymbol{Y}}_{ij}}$为矩阵Y的有效元素。类似于压缩感知中的求解零范数问题,矩阵秩的求解是NP-hard问题[13],因此,通常将式(10) 转换为求解:
$$ \begin{array}{*{20}{c}} {{\mathop{\rm minmize}\nolimits} \;\;\;\;{{\left\| {\boldsymbol{M}} \right\|}_ * }}\\ {{\mathop{\rm s}\nolimits} . {\rm t}. \;\;\;\;\;\;\;\;\;\;{\mathit{\Theta _\Omega} }({\boldsymbol{M}}) = {\mathit{\Theta _\Omega} }({\boldsymbol{Y}})} \end{array} $$ (11) 或
$$ \operatorname{minmize} \frac{1}{2}\left\| {\mathit{{\Theta }_{\Omega }}}(\boldsymbol{M}-\boldsymbol{Y}) \right\|_{F}^{2}+\mu {{\left\| \boldsymbol{M} \right\|}_{*}} $$ (12) 式中,${{\left\| \centerdot \right\|}_{*}}$表示求取矩阵的核范数;$\mu $为参数。
不定增广拉格朗日乘子法[14](inexact augmented Lagrange multiplier, IALM)相对于经典的奇异值阈值(singular value thresholding, SVT)算法[7]稳定性更好、运算量更小,因此,本文选择使用IALM算法对数据矩阵进行重构恢复。算法的具体步骤和参数选择见文献[15]。
-
对阵元缺损位置的接收数据做置零处理,所得的数据矩阵$\boldsymbol{Y}$将出现全零行,此时$\boldsymbol{Y}$不满足SIP条件,无法直接通过MC理论恢复数据,因此需要对矩阵$\boldsymbol{Y}$进行变换以确保矩阵满足SIP条件,适用MC理论。根据文献[16]可知,需首先对矩阵$\boldsymbol{Y}$做转置处理:
$$ \boldsymbol{\hat{Y}}={{\boldsymbol{Y}}^{\text{T}}} $$ (13) 定义一个二重块Hankel矩阵结构,如:
$$ {{\boldsymbol{Y}}_{\text{e}}}=\left[\begin{matrix} {{{\boldsymbol{\hat{Y}}}}_{1}}&{{{\boldsymbol{\hat{Y}}}}_{2}}&\cdots &{{{\boldsymbol{\hat{Y}}}}_{M-{{k}_{1}}+1}} \\ {{{\boldsymbol{\hat{Y}}}}_{2}}&{{{\boldsymbol{\hat{Y}}}}_{3}}&\cdots &{{{\boldsymbol{\hat{Y}}}}_{M-{{k}_{1}}+2}} \\ \vdots &\vdots &\ddots &\vdots \\ {{{\boldsymbol{\hat{Y}}}}_{{{k}_{1}}}}&{{{\boldsymbol{\hat{Y}}}}_{{{k}_{1}}+1}}&\cdots &{{{\boldsymbol{\hat{Y}}}}_{M}} \\ \end{matrix} \right] $$ (14) 式中,${{k}_{1}}$($1\le {{k}_{1}}\le M$)为矩阵$ {{\boldsymbol{Y}}_{\text{e}}} $的结构参数。$ {{\boldsymbol{Y}}_{\text{e}}} $中的每一个块矩阵都是一个${{k}_{2}}\times (L-{{k}_{2}}+1)$大小的Hankel矩阵,且具有如下形式:
$$ {{\boldsymbol{\hat Y}}_l} = \left[{\begin{array}{*{20}{c}} {{{\hat Y}_{l, 1}}}&{{{\hat Y}_{l, 2}}}& \cdots &{{{\hat Y}_{l, L-{k_2} + 1}}}\\ {{{\hat Y}_{l, 2}}}&{{{\hat Y}_{l, 3}}}& \cdots &{{{\hat Y}_{l, L-{k_2} + 2}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{{\hat Y}_{l, {k_2}}}}&{{{\hat Y}_{l, {k_2} + 1}}}& \cdots &{{{\hat Y}_{l, L}}} \end{array}} \right] $$ (15) 式中,$l$满足$1\le l\le M$;$ {{\boldsymbol{\hat{Y}}}_{l}} $为$ \boldsymbol{\hat{Y}} $的第l行构成的Hankel矩阵;$1\le {{k}_{2}}\le L$为矩阵的另外一个结构参数。
由文献[16]证明可知$ \operatorname{rank}({{\boldsymbol{Y}}_{\text{e}}})\le K $,且$ {{\boldsymbol{Y}}_{e}} $满足SIP条件。因此,可通过对矩阵$ {{\boldsymbol{Y}}_{\text{e}}} $直接进行MC处理后再经过反变换可恢复出完整的接收数据矩阵,因此,可进行精确的DOA估计。
综上,本文提出的算法可总结如下:
1) 对接收到的数据矩阵在阵元缺损位置做置零处理,获得数据矩阵$\boldsymbol{Y}$,并将$\boldsymbol{Y}$变换成具有式(14) 形式的二重块Hankel矩阵$ {{\boldsymbol{Y}}_{\text{e}}} $;
2) 利用ILAM算法对$ {{\boldsymbol{Y}}_{\text{e}}} $进行精确重构;
3) 通过反变换获取完整的接收数据矩阵;
4) 利用MUSIC算法估计出信源目标角度。
-
定义参数$\chi $为:
$$ \chi = \max \left\{ {\frac{{ML}}{{{k_1}{k_2}}}, \frac{{ML}}{{(M - {k_1} + 2)(L - {k_2} + 1)}}} \right\} $$ (16) 定理 1[16]:矩阵X为具有形式(14) 的$ {{n}_{1}}\times {{n}_{2}} $维矩阵,$ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $为一个大小为m的随机位置矩阵,假设参数$\tau $为小于0.1的正常数,则存在一个只与$\tau $相关的正常数$c$,当:
$$ m > c{\mu ^2}{\chi ^2}{r^2}{\log ^3}({n_1}{n_2}) $$ (17) 使得满足SIP条件的矩阵X以不低于$1-{{({{n}_{1}}{{n}_{2}})}^{-2}}$的概率恢复出数据矩阵M。其中$\mu $为判定矩阵X是否满足SIP条件的参数;r为矩阵的秩。
由定理1不难得出:随着参数$\chi $的增大,对矩阵$ {{\boldsymbol{Y}}_{\text{e}}} $内元素个数m的要求随之增大,使得算法的整体运算复杂度上升。同时由当参数$\chi $最小时,${{k}_{1}}{{k}_{2}}(M-{{k}_{1}}+2)(L-{{k}_{2}}+1)$将取得最大值,此时恢复原始矩阵的概率最大,因此通常将矩阵$ {{\boldsymbol{Y}}_{\text{e}}} $构成一个方阵,方便计算求解。
当阵元出现缺损时,只要构造出的矩阵$ {{\boldsymbol{Y}}_{\text{e}}} $满足定理1,无论缺损位置如何,都可以恢复出精确的原始数据矩阵,仿真实验中通过采用随机缺损阵元的形式给出了验证。
对于阵元缺损程度不同的情况而言,由矩阵$ {{\boldsymbol{Y}}_{\text{e}}} $的子块矩阵$ {{\boldsymbol{\hat{Y}}}_{l}} $不难看出,阵元缺损程度越低,矩阵$ {{\boldsymbol{\hat{Y}}}_{l}} $中未知元素的位置就越少,换言之,矩阵$ {{\boldsymbol{\hat{Y}}}_{l}} $的有效元素越多,也即是矩阵$ {{\boldsymbol{Y}}_{e}} $中的有效元素越多,因此更易满足定理1,所以缺损程度越低,矩阵填充恢复的效果越好。
-
为简化仿真,将对阵元的随机降采样等效为阵元出现的随机缺损。仿真条件设置为:均匀线阵的阵元数$L=25$,阵元间距为半波长,采样快拍数$M=39$,设蒙特卡罗实验次数为100次。
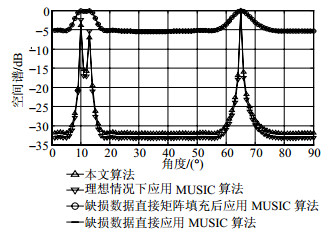
仿真 1 为直观比较验证本文算法的有效性,设阵列分别接收来自10°、13°和65° 3个不相干的远场窄带目标信号,功率经单位化后分别为1.5、1和2,信噪比为20 dB,随机关闭阵列中的8个阵元。仿真结果如图 1所示。
由图 1可知:直接对阵元降采样数据进行矩阵填充处理后再做DOA估计与直接用阵元降采样数据进行DOA估计效果类似,说明此时MC理论失效;而本文算法通过对降采样数据进行变换后再进行MC处理,得到的DOA估计结果近似于利用完整的阵列接收数据直接DOA估计的结果,获得的空间谱峰值明显高于直接利用阵元降采样数据进行DOA估计的情况,角度的分辨率更高,明显提高了阵元降采样时DOA估计的精度,而且对于多目标信源功率变化时仍能有效估计出多个目标信源的角度信息。
仿真 2 为考虑信噪比的变化对估计性能的影响,设阵列天线接收来自45°的远场窄带信号,信噪比以3 dB为间隔、在区间[-7 dB,21 dB]内变化,其余条件设置同仿真1。由于对缺损数据直接进行矩阵填充处理是失效的,因此在仿真2中不考虑这一情况,利用角度估计的均方根误差来反映角度估计性能的变化[17],仿真结果如图 2所示。
由图 2不难发现:随着信噪比的不断增大,3种情况下算法的估计精度均越来越高;本文算法和完整的接收数据直接进行DOA估计性能相近,均优于直接利用阵元降采样数据进行DOA估计的性能,进一步说明了本文算法的有效性。
仿真 3 为考虑可用阵元数对阵列角度估计性能的影响,在仿真中设阵元缺损数量从0~16以2为间隔依次增加,信噪比设定为-5 dB,信号入射方向为45°,以同等阵元数的均匀线阵的性能为对比,利用角度估计的均方根误差来反映角度估计性能的变化。仿真结果如图 3所示。
由图 3可以看出:随着可用阵元数目的降低(阵列缺损阵元数不断增加),系统角度估计性能不断下降。阵列存在阵元缺损时导致可用阵元数减少,但经本文算法处理后仍能获得等效的完整阵列,阵列孔径明显优于相同可用阵元数的均匀线阵,因此,存在阵元缺损的阵列通过本文算法获得的角度估计性能明显高于相同可用阵元数的均匀线阵。因此,在实际使用中,可以采用阵元降采样的方式估计目标角度,在保证获取足够精度的同时,提高系统的利用效率。
-
本文提出了一种阵元缺损情况下精确DOA估计的新方法,通过对阵元缺损位置接收数据的置零处理,利用Hankel矩阵变换的性质,将不满足SIP条件的接收数据矩阵变换为满足SIP条件的新矩阵,再通过MC理论精确重构出了完整的接收数据矩阵,最终获得了阵元缺损情况下的精确DOA估计。本文所提方法适用于多种信号模型,如何解决算法在二维角度估计、相干源目标以及非均匀线阵情况下的应用是下一步需要解决的问题。
A Novel DOA Estimation Algorithm in Conditions of Array Elements Deficiency
-
摘要: 为解决在均匀线阵中阵元降采样或其他因素引起的阵元损坏导致角度估计精度下降的问题,该文对缺损的采样数据矩阵进行Hankel矩阵变换,利用Hankel矩阵变换的性质以及矩阵填充理论,将不满足矩阵填充理论的接收数据矩阵变换为适用于矩阵填充理论的数据矩阵,通过不定增广拉格朗日乘子法精确重构出完整的接收数据矩阵,实现了精确的波达方向估计。仿真实验验证了该方法在均匀线阵阵元出现损毁的情况下,仍能实现对角度的精确估计,同时给出了算法随阵元缺损程度变化的性能变化趋势。
-
关键词:
- 矩阵填充 /
- Hankel矩阵 /
- 不定增广拉格朗日乘子法 /
- 波达方向估计
Abstract: In order to solve the accuracy decrease in angle estimation caused by the undersampling or the damage of the array elements in the uniform linear array, the matrix completion theory and Hankel matrix characteristic are exploited to transform the undersampling data matrix into a two-fold Hankel matrix. The completed data matrix is reconstructed by inexact augmented Lagrange multiplier method and the accurate angle estimation is achieved. Simulation results demonstrate that the proposed method is still effective with damaged and missing elements and show the tendency of the proposed method versus the different elements damage of the uniform linear array. -
[1] 丁姗姗, 张永顺, 牛超, 等. 一种基于Khatri-Rao子空间的非均匀稀疏阵列[J]. 空军工程大学学报(自然科学版). 2015, 16(5):78-82. http://www.cnki.com.cn/Article/CJFDTOTAL-KJGC201505019.htm DING Shan-shan, ZHANG Yong-shun, NIU Chao, et al. A novel sparse linear array geometry via Khatri-Rao subspace[J]. Journal of Air Force Engineering University (Natural Science Edition). 2015, 16(5):78-82. http://www.cnki.com.cn/Article/CJFDTOTAL-KJGC201505019.htm [2] YAN F, JIN M, LIU S, et al. Real-valued music for efficient direction estimation with arbitrary array geometries[J]. IEEE Trans on Signal Processing, 2014, 62(6):1548-1560. doi: 10.1109/TSP.2014.2298384 [3] 梁浩, 崔琛, 代林, 等. 基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2015, 37(8):1828-1935. http://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201508008.htm LIANG Hao, CUI Chen, DAI Lin, et al. Reduceddimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L-shaped array[J]. Journal of Electronics & Information Technology, 2015, 37(8):1828-1935. http://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201508008.htm [4] LARSSON E G, STOICA P. High-resolution direction finding:the missing data case[J]. IEEE Trans on Signal Processing, 2001, 49(5):950-958. doi: 10.1109/78.917799 [5] VIGNESHWARAN S, SUNDARARAJAN N, SARATCHANDRAN P. Direction of arrival estimation under array sensor failures using a minimal resource allocation neural network[J]. IEEE Trans on Antennas and Propagation, 2007, 55(2):334-343. doi: 10.1109/TAP.2006.889794 [6] CANDÀS E J, RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2008, 9(6):717-772. http://dl.acm.org/citation.cfm?doid=2184319.2184343 [7] CANDÀS E J, SING-LONG C A, TRZASKO J D. Unbiased risk estimates for singular value thresholding and spectral estimators[J]. IEEE Trans on Signal Processing, 2013, 61(19):4643-4657. doi: 10.1109/TSP.2013.2270464 [8] YANG D, LIAO G, ZHU S, et al. SAR imaging with undersampled data via matrix completion[J]. IEEE Geoscience & Remote Sensing Letters, 2014, 11(9):1539-1543. http://ieeexplore.ieee.org/document/6729030/ [9] SUN S, BAJWA W U, PETROPULU A P. MIMO-MC radar: a MIMO radar approach based on matrix completion[J]. IEEE Trans on Aerospace & Electronic Systems, 2014, 51(1): 1-13. http://ieeexplore.ieee.org/document/7272834/ [10] WANG M, WANG W. DOA estimation of array radar via random interval sub-Nyquist-sampling[C]//IEEE International Conference on Signal Processing, Communication and Computing. Kunming:IEEE, 2013:1-4. [11] 杨东, 廖桂生, 朱圣棋, 等. 阵列信号降采样低秩矩阵的恢复方法[J]. 西安电子科技大学学报, 2014, 41(5):30-35. http://www.cnki.com.cn/Article/CJFDTOTAL-XDKD201405006.htm YANG Dong, LIAO Gui-sheng, ZHU Sheng-qi, et al. Improved low-rank recovery method for sparsely sampling data in array signal processing[J]. Journal of Xidian University, 2014, 41(5):30-35. http://www.cnki.com.cn/Article/CJFDTOTAL-XDKD201405006.htm [12] CANDÀS E J, PLAN Y. Matrix completion with noise[J]. Proc of the IEEE, 2010, 98(6):925-936. doi: 10.1109/JPROC.2009.2035722 [13] CHEN Y, XU H, CARAMANIS S, et al. Matrix completion with column manipulation:near-optimal sample-robustness-rank tradeoffs[J]. IEEE Trans on Information Theory, 2016, 62(1):503-526. doi: 10.1109/TIT.2015.2499247 [14] EITANTAWY A, SHEHATA, MOHAMED S. Moving object detection from moving platforms using Lagrange multiplier[C]//IEEE International Conference on Image Processing. Québec, Canada:IEEE, 2015:2586-2590. [15] 马晓慧. 矩阵填充理论方法分析[D]. 杭州:浙江大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013146940.htm MA Xiao-hui. Method analysis of matrix completion theory[D]. Hangzhou:Zhejiang University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013146940.htm [16] CHEN Y, CHI Y. Robust spectral compressed sensing via structured matrix completion[J]. IEEE Trans on Information Theory, 2014, 60(10):6576-6601. doi: 10.1109/TIT.2014.2343623 [17] 葛启超, 张永顺, 丁姗姗. 用于二维角度估计的新型阵列结构及性能分析[J]. 空军工程大学学报(自然科学版), 2016, 17(1):60-65. http://www.cnki.com.cn/Article/CJFDTOTAL-KJGC201601012.htm GE Qi-chao, ZHANG Yong-shun, DING Shan-shan. Novel array structure and performance analysis for 2-D angle estimation[J]. Journal of Air Force Engineering University (Natural Science Edition), 2016, 17(1):60-65. http://www.cnki.com.cn/Article/CJFDTOTAL-KJGC201601012.htm -


 ISSN
ISSN 




 下载:
下载: