-
电大导体目标的电磁散射分析在隐身设计和雷达目标识别等领域具有重要应用。表面积分方程(SIE)方法具有精度高、离散未知量数目少的优点,通常作为此类问题的常用数值分析方法。作为积分方程的快速方法,虽然多层快速多极子方法(MLFMA)[1]的计算复杂度和存储复杂度仅为O(NlogN),但对电大目标散射问题的求解依然会消耗大量的计算时间和存储资源。为了提高当前计算平台的求解能力,可以将原问题分解为有限个子问题,并对子问题逐个进行求解。为此,文献[2]提出一种前后向迭代法,求解了三维开放导体平板的散射问题。在此基础上,人们提出了重叠型区域分解方法,分别求解了闭合导体目标[3]、涂覆目标[4]以及均匀介质目标[5]的电磁散射问题,取得了良好的效果。以上工作都引入了一定电尺寸长度的缓冲区来抑制由人工边界产生的伪边缘效应。其中,前者在目标表面直接划分缓冲区,后者则通过种子节点来查找缓冲区。这两种缓冲区的构造方式相对繁琐。文献[6]提出的非重叠型区域分解方法虽然可以通过定常迭代法进行求解[7],但此方法引入的人工端面会带来较多的额外未知量。文献[8]采用定常迭代法成功求解了既不包含人工端面也不包含缓冲区的区域分解问题。但是,该方法利用显示边界条件对两个相邻的半RWG基函数[9]的系数进行约束,生成超定的线性方程组。超定系统的迭代求解多依赖于法方程方法,而法方程方法的困难在于矩阵的条件数变成了原矩阵的平方[10]。这可能导致迭代法的收敛速度变慢。同时,一次迭代需要完成两次矩矢相乘运算,增加了求解时间。这些缺憾不利于该方法在电大问题中的应用。
针对电大导体目标的电磁散射问题,本文将相位提取基函数方法与区域分解方法相结合,在减少待求未知量数目的同时,进一步降低峰值存储需求,以提高单机的求解能力。此外,利用大贴片基函数的优势,本文仅采用一层三角形单元来构造缓冲区,简化了缓冲区的构造过程,并实现了对伪边缘效应的有效抑制。
-
考虑理想导体目标在自由空间中的散射问题。利用导体表面的切向边界条件,可以建立如下的电场积分方程(EFIE)和磁场积分方程(MFIE):
$$ - i{k_0}{\eta _0}\int_{{\rm{ }}s'} {\left( {\mathit{\boldsymbol{J}}(\mathit{\boldsymbol{r'}}) + \frac{1}{{k_0^2}}\nabla ' \cdot \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{r'}})\nabla } \right)} \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{r'}}){\rm{d}}\mathit{\boldsymbol{r'}}{\kern 1pt} {\kern 1pt} = {\mathit{\boldsymbol{E}}^{{\rm{inc}}}}(\mathit{\boldsymbol{r}}) $$ (1) $$ \frac{1}{2}\mathit{\boldsymbol{J}}(\mathit{\boldsymbol{r}}) - \mathit{\boldsymbol{\hat n}} \times P.V.\int_{{\rm{ }}s'} {\nabla G} (\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{r'}}) \times \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{r'}}){\rm{d}}\mathit{\boldsymbol{r'}} = \mathit{\boldsymbol{\hat n}} \times {\mathit{\boldsymbol{H}}^{{\rm{inc}}}}(\mathit{\boldsymbol{r}}) $$ (2) 式中,$ \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{{r}'}})={{{\rm{e}}^{ik\left| \mathit{\boldsymbol{r}}-\mathit{\boldsymbol{{r}'}} \right|}}}/{4\rm{ }\!\!\pi\!\!\rm{ }\left| \mathit{\boldsymbol{r}}-\mathit{\boldsymbol{{r}'}} \right|}\; $为自由空间格林函数;$ {\eta _0} $为波阻抗;$ {k_0} $为波数;$ \mathit{\boldsymbol{\hat n}} $为目标表面的单位外法向量;$ P.V. $表示柯西主值积分。在实际应用中,经常将EFIE和MFIE进行线性组合,得到混合场积分方程(CFIE),用来改善阻抗矩阵的条件数并避免内谐振问题:
$$ {\rm{CFIE}} = \alpha {\rm{EFIE}} + (1 - \alpha ){\eta _0} \times {\rm{MFIE}}, \;{\rm{ }}\alpha \in (0, 1) $$ (3) 式中,$ \alpha $为比例因子,通常取0.5。
-
对于均匀平面波入射下的导体目标,相位提取(PE)基函数[11]描述了目标表面的感应电流随频率和位移快速变化的相位信息。而缓慢变化的幅度信息则作为待求量,通过求解矩阵方程获得。利用该基函数对表面电流进行展开,有:
$$ \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{r}}) = \sum\limits_{n = 1}^N {{a_n}{\mathit{\boldsymbol{f}}_n}(\mathit{\boldsymbol{r}})} {{\rm{e}}^{i{\mathit{\boldsymbol{k}}^i} \cdot \mathit{\boldsymbol{r}}}} $$ (4) 式中,$ N $为未知量数目;$ {a_n} $为展开系数;$ \mathit{\boldsymbol{f}}(\mathit{\boldsymbol{r}}) $为曲面RWG基函数;$ {{\rm{e}}^{{\rm{i}}{\mathit{\boldsymbol{k}}^i} \cdot \mathit{\boldsymbol{r}}}} $为一致相位因子。由于待求系数$ {a_n} $仅需表征缓慢变化的幅度信息,无需表征快速变化的相位信息,因此网格剖分密度可以适当地降低。这将减少待求未知量数目,从而节约计算时间和计算内存。
根据Galerkin测试过程,采用与基函数相同的测试函数对方程两端进行内积,可以得到如下形式的矩阵方程:
$$ \mathit{\boldsymbol{Z}}\, \mathit{\boldsymbol{I}} = \mathit{\boldsymbol{V}} $$ (5) 式中,$ \mathit{\boldsymbol{Z}} $为$ N \times N $维阻抗矩阵;$ \mathit{\boldsymbol{V}} $为$ N $维激励向量;$ \mathit{\boldsymbol{I}} $为待求系数向量。阻抗矩阵和激励向量中的元素分别为:
$$ {\mathit{\boldsymbol{Z}}_{mn}} = \alpha \mathit{\boldsymbol{Z}}_{mn}^E + (1 - \alpha ){\eta _0}\mathit{\boldsymbol{Z}}_{mn}^M $$ (6) $$ \begin{array}{c} \mathit{\boldsymbol{Z}}_{mn}^E = - i{k_0}{\eta _0}\int_s {\int_{s'} {G{{\rm{e}}^{i{\mathit{\boldsymbol{k}}^i} \cdot (\mathit{\boldsymbol{r}}' - \mathit{\boldsymbol{r}})}}\left[{{\mathit{\boldsymbol{f}}_m} \cdot {\mathit{\boldsymbol{f}}_n}} \right.} }-{{\mathit{\boldsymbol{\hat k}}}^i} \cdot {\mathit{\boldsymbol{f}}_m}{{\mathit{\boldsymbol{\hat k}}}^i} \cdot {\mathit{\boldsymbol{f}}_n}-\\ {\kern 1pt} {\kern 1pt} ik_0^{-1}(\nabla \cdot {\mathit{\boldsymbol{f}}_m}{{\mathit{\boldsymbol{\hat k}}}^i} \cdot {\mathit{\boldsymbol{f}}_n} - {{\mathit{\boldsymbol{\hat k}}}^i} \cdot {\mathit{\boldsymbol{f}}_m}\nabla ' \cdot {\mathit{\boldsymbol{f}}_n}){\kern 1pt} - \\ \left. {{\kern 1pt} k_0^{ - 2}\nabla \cdot {\mathit{\boldsymbol{f}}_m}\nabla ' \cdot {\mathit{\boldsymbol{f}}_n}} \right]{\rm{d}}\mathit{\boldsymbol{r'}}{\rm{d}}\mathit{\boldsymbol{r}} \end{array} $$ (7) $$ \begin{array}{c} \mathit{\boldsymbol{Z}}_{mn}^M = \frac{1}{2}\int_{{\rm{ }}s} {{\mathit{\boldsymbol{f}}_m} \cdot {\mathit{\boldsymbol{f}}_n}{\rm{d}}\mathit{\boldsymbol{r}}} - \\ {\kern 1pt} {\kern 1pt} \int_{{\rm{ }}s} {{\mathit{\boldsymbol{f}}_m} \cdot \mathit{\boldsymbol{\hat n}} \times P.V.\int_{{\rm{ }}s'} {\nabla G \times {\mathit{\boldsymbol{f}}_n}} {{\rm{e}}^{i{\mathit{\boldsymbol{k}}^i} \cdot (\mathit{\boldsymbol{r'}} - \mathit{\boldsymbol{r}})}}{\rm{d}}\mathit{\boldsymbol{r'}}{\rm{d}}\mathit{\boldsymbol{r}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} \end{array} $$ (8) $$ {V_m} = \int_{{\rm{ }}s} {{{\rm{e}}^{ - i{\mathit{\boldsymbol{k}}^i} \cdot \mathit{\boldsymbol{r}}}}{\mathit{\boldsymbol{f}}_m}} \cdot \left[{\alpha {\mathit{\boldsymbol{E}}^{{\rm{inc}}}} + (1-\alpha ){\eta _0}\mathit{\boldsymbol{\hat n}} \times {\mathit{\boldsymbol{H}}^{{\rm{inc}}}}} \right]{\rm{d}}\mathit{\boldsymbol{r}} $$ (9) 多层快速多极子方法通过逐层向上聚合,又逐层转移和向下配置的方式,高效地完成远区互耦分析中的矩矢相乘运算。本文采用该方法对式(5) 中的矩矢相乘运算进行加速。
-
重叠型区域分解方法(ODDM)通过逐个求解子域问题的方式来降低原问题求解所需的峰值内存,其实质为高斯-赛德尔迭代。缓冲区的引入有效地抑制了由人工边界引起的伪边缘效应,使外层迭代能够快速收敛。假设原目标被分为$ M $个区域。在第$ k $次外层迭代中,含缓冲区的子域m上的未知电流可以通过求解如下的矩阵方程获得:
$$ \begin{array}{c} {{\mathit{\boldsymbol{\tilde Z}}}_{mm}}\, \mathit{\boldsymbol{\tilde I}}_m^k = {{\mathit{\boldsymbol{\tilde V}}}_m} - \sum\limits_{n = 1}^{m - 1} {{{\mathit{\boldsymbol{\tilde Z}}}_{mn}}\, \mathit{\boldsymbol{\tilde I}}_n^k} - \sum\limits_{n = m + 1}^M {{{\mathit{\boldsymbol{\tilde Z}}}_{mn}}\, \mathit{\boldsymbol{\tilde I}}_n^{k - 1}} \\ {\kern 1pt} {\kern 1pt} n = 1, 2, \cdots, M \end{array} $$ (10) 式中,$ {\mathit{\boldsymbol{\tilde Z}}_{mm}} $表示子域m上基函数所对应的阻抗矩阵;$ {\mathit{\boldsymbol{\tilde Z}}_{mm}} $表示子域n和子域m上基函数间的耦合矩阵;$ \mathit{\boldsymbol{\tilde I}}_m^k $表示待求系数向量;$ \mathit{\boldsymbol{\tilde I}}_n^{k-1} $和$ \mathit{\boldsymbol{\tilde I}}_n^k $为已知系数向量。
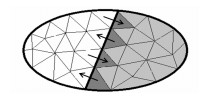
文献[2-3]分别采用了不同的方式来构造具有一定电尺寸长度的缓冲区,取得了良好的收敛效果。但是这些缓冲区的构造过程相对繁琐,同时会引入较多的待求未知量。对于每个待求子域,本文仅选取人工边界外侧的一层三角形单元作为缓冲区,如图 1所示。该缓冲区可由跨边界基函数的定义域确定,易于构造。同时,待求的额外未知量数目仅随人工边界增长,与文献[8]类似。由于PE基函数可以定义在边长为$ 0.5\lambda $~$ 2.0\lambda $的三角形贴片上[12],虽然上述缓冲区的构造方式简单,但仍能够获得足够的电尺寸面积,从而实现对伪边缘效应的有效抑制。
为了考察实际的抑制效果,本文定义了一种对边缘电流的变化更为敏感的相对残差计算方式:
$$ {\varepsilon _1} = \frac{{||\mathit{\boldsymbol{I}}_{{\rm{line}}2{\kern 1pt} {\kern 1pt} }^k - \mathit{\boldsymbol{I}}_{{\rm{line}}1{\kern 1pt} {\kern 1pt} }^k|{|_2}}}{{||\mathit{\boldsymbol{I}}_{{\rm{line}}{\kern 1pt} {\kern 1pt} 2}^k|{|_2}}} $$ (11) 式中,$ \mathit{\boldsymbol{I}}_{{\rm{line}}1}^k $和$ \mathit{\boldsymbol{I}}_{{\rm{line}}2}^k $表示在第$ k $次外层迭代中,先后两次计算得到的跨边界电流的解向量。当伪边缘效应得到有效抑制的时候,随着外层迭代的进行,子域上的感应电流逐渐趋于真实解,此时$ {\varepsilon _1} $应趋于零。此外,用于判断全局电流收敛情况的相对残差定义为:
$$ {\varepsilon _2} = \frac{{||\mathit{\boldsymbol{I}}_{{\kern 1pt} {\kern 1pt} }^k - \mathit{\boldsymbol{I}}_{{\kern 1pt} {\kern 1pt} }^{k - 1}|{|_2}}}{{||\mathit{\boldsymbol{I}}_{}^k|{|_2}}} $$ (12) -
本文的数值算例均在Dell T7500工作站上完成。矩阵方程的求解采用广义最小残差算法(GMRES),并使用稀疏近似逆(SAI)预条件进行预处理。PE基函数的贴片边长取$ 0.5\lambda $,RWG基函数的贴片边长取$ 0.125\lambda $。为了更好地节省CPU时间,在首次外迭代中,内迭代误差门限设为0.01;在后面的外迭代中,内迭代误差门设为0.001。将本文方法表示为ODDM-PE,将采用如图 1所示缓冲区和RWG基函数的方法表示为ODDM-RWG1,将文献[3]方法,即构造更大面积缓冲区并采用RWG基函数的方法表示为ODDM-RWG2。
例1 考虑一个半径为$ 25\lambda $的金属球。该目标被均匀地分为4个区域,如图 2所示。均匀平面波沿-z轴入射,扫描平面为xoz面,HH极化。表 1记录了ODDM-RWG1, ODDM-RWG2和ODDM-PE 3种方法中$ {\varepsilon _1} $和$ {\varepsilon _2} $的变化情况。可以看到,随着外层迭代的进行,3种方法中$ {\varepsilon _1} $和$ {\varepsilon _2} $均呈单调递减趋势。进一步观察可以发现,在ODDM-RWG2和ODDM-PE中,$ {\varepsilon _1} $和$ {\varepsilon _2} $收敛到0.01仅需3次外层迭代,均具有较快的收敛速度。这说明本文方法设置的缓冲区能够有效地抑制伪边缘效应,且与传统方法构造的缓冲区的抑制效果相近。而ODDM-RWG1由于缓冲区面积过小,$ {\varepsilon _1} $和$ {\varepsilon _2} $的收敛速度相对较慢。图 3比较了3种方法与解析方法计算得到的双站RCS曲线。可以看到,3种方法所得结果均与解析结果吻合良好。相比于解析结果,ODDM-RWG1,ODDM-RWG2和ODDM-PE的均方根误差(RMSE)分别为0.33 dB,0.33 dB和0.27 dB。
表 1 例1中3种方法的相对残差变化情况
外迭代次数 ODDM-RWG1 ODDM-RWG2 ODDM-PE $ {\varepsilon _1} $ $ {\varepsilon _2} $ $ {\varepsilon _1} $ $ {\varepsilon _2} $ $ {\varepsilon _1} $ $ {\varepsilon _2} $ 1 7.28×10-1 1.0 2.54×10-1 1.0 6.53×10-1 1.0 2 2.05×10-1 2.35×10-1 2.30×10-2 2.22×10-1 9.00×10-2 2.29×10-1 3 7.82×10-2 1.65×10-2 3.94×10-3 8.08×10-3 8.55×10-3 5.94×10-3 4 4.12×10-2 5.69×10-3 3.74×10-3 1.40×10-3 2.97×10-3 4.97×10-4 5 9.96×10-3 2.30×10-3 3.65×10-3 3.19×10-4 1.76×10-3 2.17×10-4 例2 一个长37.16 m,翼展33.85 m的金属飞机模型被分为6个区域。如图 4所示。平面波沿-x轴入射,频率为2 GHz,扫描平面为xoy面, HH极化。图 5给出了ODDM-RWG1,ODDM-RWG2和ODDM-PE中相对残差$ {\varepsilon _1} $和$ {\varepsilon _2} $随外层迭代的变化情况。可以看到,在ODDM-RWG2和ODDM-PE中,随着迭代的进行,$ {\varepsilon _1} $和$ {\varepsilon _2} $均呈单调递减趋势,且收敛到0.01仅需3次外层迭代,这说明人工边界引起的伪边缘效应得到了有效抑制。而ODDM-RWG1中$ {\varepsilon _1} $并未收敛到0.01,且随着迭代的进行,$ {\varepsilon _1} $和$ {\varepsilon _2} $均呈发散趋势,这说明伪边缘效应并未得到有效抑制,原因在于该方法中缓冲区面积过小。图 6给出了上述方法与传统MLFMA方法计算的双站RCS曲线。可以看到,本文方法和文献[3]方法均与整体计算的结果吻合较好。其中,ODDM-PE(相较于MLFMA-PE)的均方根误差为0.10 dB;ODDM-RWG2(相较于MLFMA-RWG)的均方根误差为0.13 dB。可见,在有效抑制伪边缘效应的基础上,采用区域分解方法带来的误差很小。由于ODDM-RWG1中相对残差$ {\varepsilon _1} $并未收敛到指定精度,迭代发散,其均方根误差为16.77 dB。另外,与MLFMA-RWG相比,ODDM-PE的均方根误差为1.11 dB。表 2统计了不同方法的计算信息。可以看到,采用PE基函数能够有效地降低未知量数目,减少计算时间并降低内存需求。在此基础上结合区域分解算法,虽然未知量数目和计算时间略有增加,但内存需求可以进一步降低。
表 2 算例2中不同方法的计算信息统计
方法 未知量 内存/GB 时间/min MLFMA-RWG 6 348 651 40.31 220.95 MLFMA-PE 586 911 10.43 85.35 ODDM-RWG2 6 432 908 12.11 251.63 ODDM-PE 587 697 4.10 87.02 -
将相位提取基函数与区域分解方法相结合,并采用多层快速多极子算法加速矩矢相乘运算,大大降低了原问题所需的计算时间和存储资源,为电大导体目标的电磁散射分析提供了可行的途径。同时利用大贴片基函数的优势,简化缓冲区的构造过程,并最大限度地降低额外未知量数目。数值实验发现,边长约为$ 0.5\lambda $的单层三角形贴片所构成的缓冲区能够有效地抑制伪边缘效应,并使外层迭代快速收敛。值得注意的是,本文方法中缓冲区对伪边缘效应的抑制效果受剖分贴片尺寸影响。当贴片尺寸小于$ 0.5\lambda $时,缓冲区面积变小,伪边缘效应可能无法得到有效抑制。后续工作将引入电流连续性条件来抑制伪边缘效应[13],以消除对贴片边长的依赖,实现更为自由的剖分密度选择。
An Efficient Domain Decomposition Method Using Phase Extracted Basis Functions
-
摘要: 为了进一步提高电大导体目标电磁散射问题的计算能力,给出了一种高效的区域分解方法。该方法采用定义在曲面三角形单元上的相位提取基函数来展开目标表面的感应电流,大幅减少了待求未知量的数目;同时结合区域分解方法,将原问题分解为若干个重叠的子问题并逐个进行求解,进一步降低了峰值内存需求。此外,为了简化缓冲区的构造过程,采用了仅一层锯齿状的边长约为0.5个波长的三角形单元作为缓冲区,取得了良好的收敛效果。多层快速多极子方法被用于加速矩矢相乘运算。数值算例说明了该方法的高效性和稳健性。Abstract: To further improve the ability of analyzing electromagnetic scattering from electrically large perfect electric conducting objects, an efficient domain decomposition method is presented. In this method, the approximated current density is expanded with the phase-extracted basis functions defined over curvilinear triangular patches, and the number of unknowns to be solved is significantly reduced. Meanwhile, to further reduce the memory requirement, the original problem domain is divided into a number of small overlapped sub-domains and the sub-domain problems are solved one by one. In addition, the buffer regions introduced in this method are limited to only a single layer of jagged triangular mesh cells whose edges are about half a wavelength long, leading to a simplified construction process of buffer zones as well as a smaller number of additional variables to be solved. A good convergence behavior is observed. The multilevel fast multipole algorithm is applied to accelerate the matrix-vector products. Numerical examples are given to show the efficiency and robustness of the proposed approach.
-
表 1 例1中3种方法的相对残差变化情况
外迭代次数 ODDM-RWG1 ODDM-RWG2 ODDM-PE $ {\varepsilon _1} $ $ {\varepsilon _2} $ $ {\varepsilon _1} $ $ {\varepsilon _2} $ $ {\varepsilon _1} $ $ {\varepsilon _2} $ 1 7.28×10-1 1.0 2.54×10-1 1.0 6.53×10-1 1.0 2 2.05×10-1 2.35×10-1 2.30×10-2 2.22×10-1 9.00×10-2 2.29×10-1 3 7.82×10-2 1.65×10-2 3.94×10-3 8.08×10-3 8.55×10-3 5.94×10-3 4 4.12×10-2 5.69×10-3 3.74×10-3 1.40×10-3 2.97×10-3 4.97×10-4 5 9.96×10-3 2.30×10-3 3.65×10-3 3.19×10-4 1.76×10-3 2.17×10-4 表 2 算例2中不同方法的计算信息统计
方法 未知量 内存/GB 时间/min MLFMA-RWG 6 348 651 40.31 220.95 MLFMA-PE 586 911 10.43 85.35 ODDM-RWG2 6 432 908 12.11 251.63 ODDM-PE 587 697 4.10 87.02 -
[1] SONG J M, LU C C, CHEW W C. Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects[J]. IEEE Trans Antennas Propag, 1997, 45(10):1488-1493. doi: 10.1109/8.633855 [2] BRENNAN C, CULLEN P, CONDON M. A novel iterative solution of the three dimensional electrical field integral equation[J], IEEE Trans Antennas Propag, 2004, 52(10):2781-2784. doi: 10.1109/TAP.2004.834405 [3] LI Wei-dong, HONG Wei, ZHOU Hou-xing. Integral equation-based overlapped domain decomposition method for the analysis of electromagnetic scattering of 3D conducting objects[J]. Microwave Opt Technol Lett, 2007, 49(2):265-274. doi: 10.1002/(ISSN)1098-2760 [4] LI Wei-dong, ZHOU Hou-xing, HU Jun, et al. An ODDM-based solution to CFIE with impedance boundary condition[J]. IEEE Antennas Wire Propag Lett, 2011, 10:1197-1200. doi: 10.1109/LAWP.2011.2172969 [5] LI Wei-dong, ZHOU Hou-xing, WEILAND T. An overlapped domain decomposition method for modified NMüller formulation[J]. IEEE Antennas Wire Propag Lett, 2007, 7:710-713. https://www.researchgate.net/publication/224332426_An_Overlapped_Domain_Decomposition_Method_for_Modified_N-Mller_Formulation [6] PENG Z, WANG X C, LEE J F. Integral equation based domain decomposition method for solving electromagnetic wave scattering from non-penetrable objects[J]. IEEE Trans Antennas Propag, 2011, 59(9):3328-3338. doi: 10.1109/TAP.2011.2161542 [7] JIANG Ming, HU Jun, ZHAO Ran, et al. Hybrid IE-DDMMLFMA with Gauss-Seidel iterative technique for scattering from conducting body of translation[J]. Applied Computational Electromagnetics Society Journal, 2015, 30(2):148-156. https://www.researchgate.net/publication/261125086_Hybrid_IE-DDM-MLFMA_with_forward-backward_method_for_conducting_body_of_translation [8] ZHENG Kai-lai, ZHOU Hou-xing, HONG Wei. Integral equation-based non-overlapping DDM using the explicit boundary condition[J]. IEEE Trans Antennas Propag, 2015, 63(6):2739-2745. doi: 10.1109/TAP.2015.2412145 [9] RAO S M, WILTON D R, GLISSON A W. Electromagnetic scattering by surface of arbitrary shape[J]. IEEE Trans Antennas Propag, 1982, 30(3):409-418. doi: 10.1109/TAP.1982.1142818 [10] GOLUB G H, VAN LOAN C F. Matrix computation[M]. 3rd ed. Baltimore:The Johns Hopkins University Press, 1996, 10:545-546. [11] AN Su, REN Si, NIE Zai-ping, et al. Efficient analysis of electromagnetic scattering from electrically large complex objects by using phase-extracted basis functions[J]. IEEE Antennas Propag Mag, 2012, 54(5):88-108. doi: 10.1109/MAP.2012.6348121 [12] 何十全. 非均匀复杂结构目标电磁散射理论建模与高效算法研究[D]. 成都: 电子科技大学, 2011. http://cdmd.cnki.com.cn/article/cdmd-10614-1011191823.htm HE Shi-quan. Theoretical modeling and efficient algorithm research on electromagnetic scattering from inhomogeneous and complex structures[D]. Chengdu:University of Electronic Science and Technology of China, 2011. http://cdmd.cnki.com.cn/article/cdmd-10614-1011191823.htm [13] HAN Kui, NIE Zai-ping, WANG Yi-ling. A simply constructed overlapped domain decomposition method for solving large scattering problems[J]. Electromagnetics, 2016, 36(7):470-484. doi: 10.1080/02726343.2016.1220908 -


 ISSN
ISSN 




 下载:
下载: