-
认知无线电(cognitive radio, CR)系统中,主用户和次用户通过共享频谱资源,极大地提高了频谱资源利用率[1]。MIMO技术提供多个并行正交子信道,能在不增加带宽的前提下成倍提高系统传输速率[2]。将两者技术进行结合,可以在次用户与主用户共享频谱的条件下最大化频谱利用率同时提高系统传输速率。然而,认知MIMO系统中,由于频谱共享,主次用户之间会产生干扰,次用户之间也会存在干扰,这些干扰严重影响系统的传输速率。
干扰对齐是解决该问题的有效方法。文献[3]提出盲干扰对齐算法,可以抑制来自主用户和其他次用户的干扰,但在接收端需要获取全局信道状态信息。文献[4]研究了MIMO干扰信道下,迭代干扰对齐技术在认知无线电系统中的应用,不需要知道全局信道状态信息,但忽略了次用户对主用户的干扰。文献[5]针对一个主用户、多个次用户的系统,设计了主用户和次用户的预编码矩阵和干扰消除矩阵。文献[6]研究了多个主用户和多个次用户的干扰情况,提出了次用户预编码方案,但文献[5-6]没有考虑主用户对次用户的干扰。文献[7]研究了多个次用户与主用户共享频谱,提出一种干扰消除矩阵的设计方案,在主用户接收端消除次级用户的干扰,然而次用户之间的干扰并没有消除。文献[8-10]描述次用户与主用户共享频谱,提出最大化信噪比的干扰对齐方法,提高了传输速率。文献[11]提出有一个主基站和多个微基站时,主用户和多个次用户共存的情况,选择对主用户造成干扰较大的次用户进行干扰对齐。以上文献都是从最大化单个用户的速率出发,未考虑次用户整体性能和相互影响。文献[12]考虑了次用户系统整体的性能,提出新的干扰对齐方法。但是没有考虑次用户功率分配。文献[13]通过优化主次用户的功率分配和干扰对齐的方法,达到消除次用户对主用户干扰和最大化系统传输速率的目的。该功率分配方法并不能充分利用系统功率资源。
针对以上问题,本文考虑应急通信的情况,提出了基于博弈论的迭代干扰对齐和功率分配算法。该算法不需要知道全局信道状态信息,首先通过次用户预编码的设计消除次用户和主用户之间的干扰。然后将次用户多条干扰链路组成博弈群体,实现次用户之间的干扰对齐消除干扰。最后,使用布谷鸟搜索算法优化次用户功率分配,提高次用户的传输速率。
-
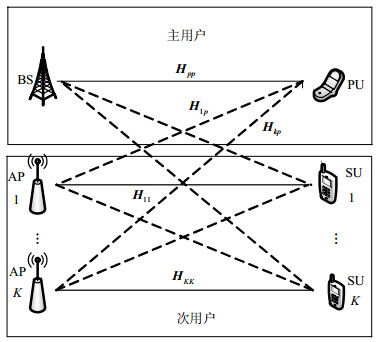
认知MIMO中干扰对齐系统模型[14]如图 1所示,假设次用户和主用户共用同一段频谱,BS为主网络基站,PU为主用户,AP为次级网络的接入点,SU为次用户。假设该系统中有一个主用户,K个次用户。M表示发送端的的天线数,N表示接收端的天线数,假设第i个发送端发送di个独立的数据流。
假设主用户接收信号为:
$$ {y_p} = {\mathit{\boldsymbol{H}}_{pp}}{\mathit{\boldsymbol{x}}_p} + \sum\limits_{i = 1}^K {{\mathit{\boldsymbol{H}}_{ip}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{x}}_i}} + {\mathit{\boldsymbol{n}}_p} $$ (1) 式中,Hpp是主基站和主用户之间的信道;$ {\mathit{\boldsymbol{x}}_p} = {\left[{{x_1}, {x_2}, \cdots, {x_M}} \right]^{\rm{H}}} $是主基站发送的信号,其协方差$ {R_{xx}} = E\{ {\mathit{\boldsymbol{x}}_p}\mathit{\boldsymbol{x}}_p^{\rm{H}}\} $,xp是M×1的矢量,假设$ E\left\{ {{\mathit{\boldsymbol{x}}_p}\mathit{\boldsymbol{x}}_p^{\rm{H}}} \right\} = 1 $;Hip是第i个接入点和主用户之间的信道,$ {\mathit{\boldsymbol{H}}_{ip}} = [{h_{1, }}{h_2} \cdots {h_k}] $,k=1, 2, …, K;Vi是第i个次用户的预编码矩阵;$ {\mathit{\boldsymbol{x}}_i} = {\left[{{x_{i1}}, {x_{i2}} \cdots, {x_{i{d_i}}}} \right]^{\rm{H}}} $表示第i个次用户发送端发送的信号;np遵从循环对称高斯分布,并且不与发射信号相关,其均值为0,方差为σ2。噪声的协方差为:
$$ {R_{nn}} = E\left[{{\mathit{\boldsymbol{n}}_p}{\mathit{\boldsymbol{n}}_p}^{\rm{H}}} \right] = {\sigma ^2}I $$ (2) -
为了使得主用户传输速率最大,本文采用经典的注水法分配功率,提高主用户的信道容量。根据信道质量分配功率,让主用户在信道质量好的子信道进行传输,其他未分配功率的信道则用于次用户的传输。
由式(1) 可以看出,两端同时乘以干扰消除矩阵UpH消除来自次用户的干扰,有:
$$ \mathit{\boldsymbol{U}}_p^{\rm{H}}{y_p} = \mathit{\boldsymbol{U}}_p^{\rm{H}}{\mathit{\boldsymbol{H}}_{pp}}{\mathit{\boldsymbol{x}}_p} + \sum\limits_{i = 1}^K {\mathit{\boldsymbol{U}}_p^{\rm{H}}{\mathit{\boldsymbol{H}}_{ip}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{x}}_i}} + \mathit{\boldsymbol{U}}_p^{\rm{H}}{\mathit{\boldsymbol{n}}_p} $$ (3) 假设主用户的信道状态已知,将Hpp进行奇异值分解,使其对角化,即:
$$ {\mathit{\boldsymbol{H}}_{pp}}{\rm{ = }}{\mathit{\boldsymbol{\bar U}}_p}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_p}\mathit{\boldsymbol{\bar V}}_p^{\rm{H}} $$ (4) 式中,$ {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_p} $是N×M的对角矩阵,对角元素是Hpp的奇异值;预编码矩阵Vp和干扰抑制矩阵Up对应非零功率的信道,功率分配既要使得主用户传输速率最大,又要满足功率限制条件。因此,主用户的功率分配问题可以转化为以下优化问题[15]:
$$ \mathop {{\rm{max}}}\limits_{{\mathit{\boldsymbol{P}}_p}} {\rm{log}_2}\left| {{\mathit{\boldsymbol{I}}_{{N_p}}} + \frac{1}{{{\sigma ^2}}}{\mathit{\boldsymbol{H}}_{pp}}{{\mathit{\boldsymbol{\bar V}}}_p}{\mathit{\boldsymbol{P}}_p}\mathit{\boldsymbol{\bar V}}_p^{\rm{H}}\mathit{\boldsymbol{H}}_{pp}^{\rm{H}}} \right| $$ (5) $$ {\rm{s}}{\rm{.t}}{\rm{. tr}}\left\{ {{\mathit{\boldsymbol{P}}_p}} \right\} \le {p_{\max }}, {\mathit{\boldsymbol{P}}_p} \ge 0 $$ (6) 根据注水功率分配方法理论可得,最优的功率分配矩阵中的对角元素为[15]:
$$ {\mathit{\boldsymbol{P}}_{pi}} = \left( {{\beta _p} - \frac{{{\sigma ^2}}}{{\lambda _{pi}^2}}} \right), {\rm{ }}i = 1, 2, \cdots, M $$ (7) 式中,βp是满足功率限制的拉格朗日系数;Ppi表示主用户第i条子信道的功率。
主用户的干扰消除矩阵满足下面条件时,可消除主用户对次用户的干扰[6]:
$$ \mathit{\boldsymbol{U}}_p^{\rm{H}}{\mathit{\boldsymbol{H}}_{pj}}{\mathit{\boldsymbol{V}}_j} = {\mathit{\boldsymbol{0}}_{{d_0} \times {d_j}}}, {\rm{ }}j \in 1, 2, \cdots, K $$ (8) $$ \mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ip}}{\mathit{\boldsymbol{V}}_p} = {\mathit{\boldsymbol{0}}_{{d_i} \times {d_0}}}, {\rm{ }}j \in 1, 2, \cdots, K $$ (9) 文献[6]已经证明式(8) 和式(9) 的可行性。
-
次级网络中各个次用户之间的干扰通过干扰对齐的方法消除,次用户的预编码矩阵和干扰抑制矩阵必须满足以下两式才可以实现干扰对齐[6]:
$$ \mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ij}}{\mathit{\boldsymbol{V}}_j} = {\mathit{\boldsymbol{0}}_{di \times dj}}, {\rm{ }}\forall j \ne i $$ (10) $$ {\rm{rank}}(\mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{V}}_i}) = {d_i}, {\rm{ }}\forall i = 1, 2, \cdots, K $$ (11) 第i个次用户接收到的信号为:
$$ {y_i} = {\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{x}}_i} + \sum\limits_{l = 1, l \ne i}^K {{\mathit{\boldsymbol{H}}_{li}}{\mathit{\boldsymbol{V}}_l}{\mathit{\boldsymbol{x}}_l}} + {\mathit{\boldsymbol{n}}_p} $$ (12) 式中,Hli表示第l个次用户发送端到第i个次用户接收端的信道,为:
$$ {\mathit{\boldsymbol{H}}_{li}} = \left[{\begin{array}{*{20}{c}} {{h_{11}}}&{{h_{12}}}& \cdots &{{h_{1M}}}\\ {{h_{21}}}&{{h_2}}& \cdots &{{h_{2M}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{h_{N1}}}&{{h_{N2}}}& \cdots &{{h_{NM}}} \end{array}} \right] $$ (13) 式中,hbv表示第b(b=1, 2, …, M)根发射天线到第v(v=1, 2, …, N)根接收天线之间的信道衰落系数。
由文献[11],定义$ {\mathit{\boldsymbol{\bar V}}_j} $为(M-d0)×dj的矩阵,$ j \in 1, 2, \cdots, K $,$ {\mathit{\boldsymbol{\bar U}}_i} $为(N-d0)×di的矩阵,$ i \in 1, 2, \cdots, K $,假设:
$$ {\mathit{\boldsymbol{V}}_j} = {\mathit{\boldsymbol{G}}_j}{\mathit{\boldsymbol{\bar V}}_j} $$ (14) $$ {\mathit{\boldsymbol{U}}_i} = {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{\bar U}}_i} $$ (15) 式中,Gj和Bi分别在$ \mathit{\boldsymbol{U}}_p^{\rm{H}}{\mathit{\boldsymbol{H}}_{pj}} $和$ {\mathit{\boldsymbol{H}}_{ip}}{\mathit{\boldsymbol{V}}_p} $的零空间内。
主用户采用注水法进行功率分配后,由于发送功率的限制,某些子信道上并未分配功率。次用户可以通过已有的感知算法感知主用户的空闲子信道,合理设计次用户预编码矩阵,使得次用户对主用户的干扰信号落入主用户未用的子信道上,消除次用户对主用户的干扰。即矩阵Gj和Bi使次用户信道落入与主用户的期望信号空间正交的子空间内,则Gj和Bi应满足以下条件:
$$ \mathit{\boldsymbol{B}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ij}}{\mathit{\boldsymbol{G}}_j} = 0, {\rm{ }}\forall j \ne i $$ (16) 即取:
$$ {\mathit{\boldsymbol{G}}_j} \in {\rm{null}}(\mathit{\boldsymbol{B}}_1^{\rm{H}}{\mathit{\boldsymbol{H}}_{1, j}}) \cap {\rm{null}}(\mathit{\boldsymbol{B}}_2^{\rm{H}}{\mathit{\boldsymbol{H}}_{2, j}}) \cap \cdots \cap {\rm{null}}(\mathit{\boldsymbol{B}}_M^{\rm{H}}{\mathit{\boldsymbol{H}}_{M, j}}) $$ (17) 由文献[16],上式可以写为:
$$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{G}}_j} \in {\rm{null}}({\mathit{\boldsymbol{H}}_j})\\ {\mathit{\boldsymbol{H}}_j} = \left[{{{(\mathit{\boldsymbol{B}}_1^{\rm{H}}{\mathit{\boldsymbol{H}}_{1, j}})}^{\rm{H}}}, {{(\mathit{\boldsymbol{B}}_2^{\rm{H}}{\mathit{\boldsymbol{H}}_{2, j}})}^{\rm{H}}}, \cdots, {{(\mathit{\boldsymbol{B}}_M^{\rm{H}}{\mathit{\boldsymbol{H}}_{M, j}})}^{\rm{H}}}} \right] \end{array} \right. $$ (18) 式中,Hj是$ \left( {\sum\limits_{i = 1}^M {{d_i}} } \right) \times N $阶矩阵;Gj是$ N \times \left( {N - \sum\limits_{i = 1}^M {{d_i}} } \right) $阶矩阵。则次用户牺牲$ \sum\limits_{i = 1}^M {{d_i}} $根天线可以不对主用户产生干扰,说明可以对次用户信号进行处理使其对主用户无干扰。
矩阵$ {\mathit{\boldsymbol{\bar V}}_i} $和$ {\mathit{\boldsymbol{\bar U}}_i} $用于实现次用户之间的干扰对齐。把式(14) 带入式(10),式(15) 带入式(11),可得:
$$ \mathit{\boldsymbol{\bar U}}_i^{\rm{H}}\mathit{\boldsymbol{B}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ij}}{\mathit{\boldsymbol{G}}_j}{\mathit{\boldsymbol{\bar V}}_j} = {0_{di \times dj}}, {\rm{ }}\forall j \ne i $$ (19) $$ {\rm{rank}}(\mathit{\boldsymbol{\bar U}}_i^{\rm{H}}\mathit{\boldsymbol{B}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{G}}_i}{\mathit{\boldsymbol{\bar V}}_i}) = {d_i} $$ (20) 次级用户的预编码矩阵$ {\mathit{\boldsymbol{\bar V}}_i} $和干扰抑制矩阵$ {\mathit{\boldsymbol{\bar U}}_i} $由下一节得到。
-
在基于博弈论的迭代干扰对齐算法中,把次用户设为局中人,即N={1, 2, …K}, 干扰消除矩阵和预编码矩阵的调整既会影响用户自己的传输速率,同时也会影响其他用户的传输速率。次级用户干扰消除矩阵的获得不仅与其他次用户有关,而且与自身有关。定义用户i的策略集合为:
$$ {S_i} = \left\{ {{{\mathit{\boldsymbol{\bar U}}}_i} \in \mathit{\boldsymbol{C}}, {{\mathit{\boldsymbol{\bar U}}}_i}\mathit{\boldsymbol{\bar U}}_i^{\rm{H}} = \mathit{\boldsymbol{I}}} \right\} $$ (21) 则用户i的收益为:
$$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\pi ({\mathit{\boldsymbol{V}}_i}) = u - c = \\ {\mathit{\boldsymbol{E}}_i} - \sum\limits_{j = 1, j \ne i}^k {{\gamma _{ij}}{\mathit{\boldsymbol{A}}_{ij}}} - \sum\limits_{j = 1, j \ne i}^k {{\lambda _{ji}}{\mathit{\boldsymbol{A}}_{ji}}} \end{array} $$ (22) 式中,u是期望信号值;c是得到期望值需要付出的代价;Ei是用户i的期望信号功率Aij用户对用户i的干扰信号功率;Aji是用户i对用户j的干扰信号功率;γij是用户受到干扰所付出代价的代价因子;λji是用户对其他用户产生干扰所付出代价的代价因子;$ \mathit{\boldsymbol{\bar V}} = \left\{ {{{\mathit{\boldsymbol{\bar V}}}_i}, i \in N} \right\} $为次级用户的预编码矩阵集合,$ {\mathit{\boldsymbol{\bar V}}_{ - i}} = \left\{ {{{\mathit{\boldsymbol{\bar V}}}_j}, j \in N{\rm{且}}j \ne i} \right\} $为除用户i以外其他用户的预编码矩阵的集合。
由于用户i对用户j和用户j对用户i的干扰因子相同,且i与j不相等,则博弈可以看成一种势博弈。
定理 1 定义势函数为[17]:
$$ P(\mathit{\boldsymbol{\bar V}}) = \sum\limits_{i = 1}^K {\left\{ {{\mathit{\boldsymbol{E}}_i} - \alpha \sum\limits_{j = 1, j \ne i}^k {{\gamma _{ij}}{\mathit{\boldsymbol{A}}_{ij}}} - \beta \sum\limits_{j = 1, j \ne i}^k {{\lambda _{ji}}{\mathit{\boldsymbol{A}}_{ji}}} } \right\}} $$ (23) $$ \begin{array}{l} \;\;\;\;\;P({{\mathit{\boldsymbol{\bar V}}}_i}, {{\mathit{\boldsymbol{\bar V}}}_{ - i}}){\rm{ = }}{\mathit{\boldsymbol{E}}_i} - \sum\limits_{j = 1}^k {\left( {\alpha {\gamma _{ij}} + \beta {\lambda _{ij}}} \right){\mathit{\boldsymbol{A}}_{ij}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^k {\left( {\alpha {\gamma _{ji}} + \beta {\lambda _{ji}}} \right){\mathit{\boldsymbol{A}}_{ji}}} = \\ \sum\limits_{j = 1, j \ne i}^K {\left( {{\mathit{\boldsymbol{E}}_j} - \alpha \sum\limits_{k = 1, k \ne i, k \ne j}^k {{\gamma _{ij}}{\mathit{\boldsymbol{A}}_{ij}}} - \beta \sum\limits_{k = 1, k \ne i, k \ne j}^k {{\lambda _{ji}}{\mathit{\boldsymbol{A}}_{ji}}} } \right)} \end{array} $$ (24) 式中,取α=0,β=1;令$ {\gamma _{ij}} = {\lambda _{ij}} = \xi $。
由文献[17],当满足下面条件时,则博弈为势博弈。
$$ \begin{array}{l} P({{\mathit{\boldsymbol{\bar V'}}}_i}, {{\mathit{\boldsymbol{\bar V}}}_{ - i}}) - P({{\mathit{\boldsymbol{\bar V}}}_i}, {{\mathit{\boldsymbol{\bar V}}}_{ - i}}) = \\ \;\;\pi ({{\mathit{\boldsymbol{\bar V'}}}_i}, {{\mathit{\boldsymbol{\bar V}}}_{ - i}}) - \pi ({{\mathit{\boldsymbol{\bar V}}}_i}, {{\mathit{\boldsymbol{\bar V}}}_{ - i}}) \end{array} $$ (25) 文献[18]已证明。
由文献[17]得势函数可以写为:
$$ P(\mathit{\boldsymbol{\bar V}}) = \sum\limits_{i = 1}^K {\left\{ {{\mathit{\boldsymbol{E}}_i} - \sum\limits_{j = 1, j \ne i}^k {\xi {\mathit{\boldsymbol{A}}_{ji}}} } \right\}} $$ (26) 定理 2 文献[18]可知第k次迭代得到的结果为$ ({\mathit{\boldsymbol{\bar V}}_i}, {\mathit{\boldsymbol{\bar U}}_i}) $,其效用函数结果为$ \pi ({\mathit{\boldsymbol{\bar V}}_i}, {\mathit{\boldsymbol{\bar U}}_i}) $。第k+1次迭代后得到的结果为$ ({\mathit{\boldsymbol{V'}}_i}, {\mathit{\boldsymbol{U'}}_i}) $ ,其效用函数结果为$ \pi ({\mathit{\boldsymbol{V'}}_\mathit{\boldsymbol{i}}}, {\mathit{\boldsymbol{U'}}_\mathit{\boldsymbol{i}}}) $。第k+1次迭代得到$ {\mathit{\boldsymbol{V'}}_\mathit{\boldsymbol{i}}} $后有:
$$ \pi ({\mathit{\boldsymbol{V'}}_i}, {\mathit{\boldsymbol{\bar U}}_i}) \ge \pi ({\mathit{\boldsymbol{\bar V}}_i}, {\mathit{\boldsymbol{\bar U}}_i}) $$ (27) 得到Ui'后:
$$ \mathit{\pi }({\mathit{\boldsymbol{V'}}_i}, {\mathit{\boldsymbol{U'}}_i}) \ge \pi ({\mathit{\boldsymbol{\bar V}}_i}, {\mathit{\boldsymbol{\bar U}}_i}) $$ (28) 因此:
$$ \pi ({\mathit{\boldsymbol{V'}}_i}, {\mathit{\boldsymbol{U'}}_i}) \ge \pi ({\mathit{\boldsymbol{\bar V}}_i}, {\mathit{\boldsymbol{\bar U}}_i}) $$ (29) 该博弈具有有限改进特性。
定理 3 若函数有界,且具有有限改进性,则具有纳什均衡点。
证明[18]:
$$ \begin{array}{l} \;\;\;\;\;\;{\mathit{\boldsymbol{A}}_{ji}} = {P_i}/d\left\| {\mathit{\boldsymbol{\bar U}}_i^{\rm{H}}\mathit{\boldsymbol{B}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ji}}{\mathit{\boldsymbol{G}}_j}{{\mathit{\boldsymbol{\bar V}}}_j}} \right\|_F^2 \ge 0\\ P(\mathit{\boldsymbol{V}}) \le \sum\limits_{i = 1}^K {{\mathit{\boldsymbol{E}}_i} \le \left\| {\mathit{\boldsymbol{G}}_i^{\rm{H}}\mathit{\boldsymbol{H}}_{ii}^{\rm{H}}{\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{B}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{G}}_i}} \right\|_F^2} \end{array} $$ (30) 因此,P函数为有界函数,由文献[18]中引理可知,该博弈存在纳什均衡点。
所以,本文算法存在纳什均衡点,可以在有限次迭代内收敛。
博弈论算法中,最主要的目的是使效用函数最大化,信号功率可用信号矩阵的迹表示,由式(22) 可得:
$$ \begin{array}{l} \;\;\;\pi ({{\mathit{\boldsymbol{\bar V}}}_i}) = {\rm{tr}}\left( {\mathit{\boldsymbol{\bar V}}_i^{\rm{H}}{\mathit{\boldsymbol{Q}}_{p1}}{{\mathit{\boldsymbol{\bar V}}}_i}} \right) - \\ \sum\limits_{i = 1, j \ne i}^3 {\xi \left\| {\mathit{\boldsymbol{\bar U}}_i^{\rm{H}}\mathit{\boldsymbol{B}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ji}}{\mathit{\boldsymbol{G}}_j}{{\mathit{\boldsymbol{\bar V}}}_j}} \right\|_F^2} \end{array} $$ (31) 式中,
$$ \begin{array}{l} {\mathit{\boldsymbol{Q}}_{p1}} = \mathit{\boldsymbol{H}}_{ii}^{\rm{H}}{\mathit{\boldsymbol{B}}_i}{{\mathit{\boldsymbol{\bar U}}}_i}\mathit{\boldsymbol{\bar U}}_i^{\rm{H}}\mathit{\boldsymbol{B}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}} - \\ \xi \sum\limits_{j = 1, j \ne i}^K {\mathit{\boldsymbol{H}}_{ij}^{\rm{H}}{\mathit{\boldsymbol{B}}_i}{{\mathit{\boldsymbol{\bar U}}}_j}\mathit{\boldsymbol{\bar U}}_j^{\rm{H}}\mathit{\boldsymbol{B}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ij}}} \end{array} $$ (32) 式(31) 的第二项与$ {\mathit{\boldsymbol{\bar V}}_i} $无关,因此要使得效用函数最大,需使得式(31) 的第一项最大,问题就转化为:
$$ \left[{{{\mathit{\boldsymbol{\bar V}}}_i}} \right] = \arg \mathop {\max }\limits_{{V_i}} \pi ({\mathit{\boldsymbol{\bar V}}_i}) $$ (33) $$ {\mathit{\boldsymbol{\bar V}}_i} = {\upsilon _d}({\mathit{\boldsymbol{Q}}_{p1}}) $$ (34) 同理:
$$ {\mathit{\boldsymbol{\bar U}}_i} = {\upsilon _d}({\mathit{\boldsymbol{Q}}_{p2}}) $$ (35) 其中[18]
$$ \begin{array}{l} {\mathit{\boldsymbol{Q}}_{p2}} = \mathit{\boldsymbol{H}}_{ii}^{\rm{H}}{\mathit{\boldsymbol{G}}_\mathit{\boldsymbol{i}}}{{\mathit{\boldsymbol{\bar V}}}_i}\mathit{\boldsymbol{\bar V}}_i^{\rm{H}}\mathit{\boldsymbol{G}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}} - \\ \xi \sum\limits_{j = 1, j \ne i}^K {\mathit{\boldsymbol{H}}_{ji}^{\rm{H}}{\mathit{\boldsymbol{G}}_j}{{\mathit{\boldsymbol{\bar V}}}_j}\mathit{\boldsymbol{\bar V}}_j^{\rm{H}}\mathit{\boldsymbol{G}}_j^{\rm{H}}{\mathit{\boldsymbol{H}}_{ji}}} \end{array} $$ (36) -
对于次用户而言,次用户的接收信号可以表示为:
$$ \begin{array}{l} {y_i} = \mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{x}}_i} + \mathit{\boldsymbol{U}}_i^{\rm{H}}\sum\limits_{l = 1, l \ne i}^N {{\mathit{\boldsymbol{H}}_{li}}{\mathit{\boldsymbol{V}}_l}{\mathit{\boldsymbol{P}}_l}{\mathit{\boldsymbol{x}}_l}} + \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ip}}{\mathit{\boldsymbol{V}}_p}{\mathit{\boldsymbol{P}}_p}{\mathit{\boldsymbol{x}}_p} + \mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{n}}_p} \end{array} $$ (37) 式中,第二项是来自其他次级用户的干扰;第三项是主用户对次级用的干扰项。由于次用户使用主用户未使用的子信道进行传输,所以主次用户之间的干扰可以忽略。则式(35) 就可以写为:
$$ {y_i} = \mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{x}}_i} + \mathit{\boldsymbol{U}}_i^{\rm{H}}\sum\limits_{l = 1, l \ne i}^N {{\mathit{\boldsymbol{H}}_{li}}{\mathit{\boldsymbol{V}}_l}{\mathit{\boldsymbol{P}}_l}{\mathit{\boldsymbol{x}}_l}} + \mathit{\boldsymbol{U}}_i^{\rm{H}}\mathit{\boldsymbol{n}} $$ (38) 第i个次用户的信干噪比为:
$$ {\rm{SIN}}{{\rm{R}}_i} = \frac{{\left\| {\mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{P}}_i}} \right\|}}{{\left\| {\mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{P}}_i} + \mathit{\boldsymbol{U}}_i^{\rm{H}}\sum\limits_{l = 1, l \ne i}^N {{\mathit{\boldsymbol{H}}_{li}}{\mathit{\boldsymbol{V}}_l}{\mathit{\boldsymbol{P}}_l}} } \right\| + {\sigma ^2}}} $$ (39) 则第i个次用户的功率分配问题可以描述为:
$$ \begin{array}{l} \mathop {\max }\limits_{{\mathit{\boldsymbol{P}}_i}} {\log _2}\left( {1 + \frac{{\left\| {\mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{P}}_i}} \right\|}}{{\left\| {\mathit{\boldsymbol{U}}_i^{\rm{H}}{\mathit{\boldsymbol{H}}_{ii}}{\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{P}}_i} + \mathit{\boldsymbol{U}}_i^{\rm{H}}\sum\limits_{l = 1, l \ne i}^N {{\mathit{\boldsymbol{H}}_{li}}{\mathit{\boldsymbol{V}}_l}{\mathit{\boldsymbol{P}}_l}} } \right\| + {\sigma ^2}}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{. }}\sum\limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{P}}_i}} \right\|} \le p \end{array} $$ (40) 式中,Pi表示第i个次用户的功率矩阵;p表示其最大发送功率。
则次用户的功率优化问题可转化为传输速率最大化问题。
$$ \begin{array}{c} C = {\rm{max}}\sum\limits_{i = 1}^K {{{\log }_2}(1 + {\rm{SIN}}{{\rm{R}}_i})} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\sum\limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{P}}_i}} \right\|} \le p \end{array} $$ (41) 式(36) 中的功率分配问题是一个凸优化问题,求解非常困难。本文采用智能算法求解该问题。
布谷鸟搜索算法[19]是一种基于莱维飞行的优化算法,这种飞行模式可以扩大搜索范围,容易跳出局部最优,寻优能力更强。布谷鸟鸟巢的更新公式为:
$$ x_i^{\left( {t + 1} \right)} = x_i^{\left( t \right)} + \partial \oplus L(\beta ), {\rm{ }}i = 1, 2, \cdots, n $$ (42) 式中,$ x_i^{\left( {t + 1} \right)} $表示第i个鸟巢第t次迭代的位置;∂表示步长控制量;L(β)表示莱维飞行的路径。
$$ Le'vy \sim u = {t^{ - 1 - \beta }}, {\rm{ }}0 < \beta \le 2 $$ (43) 此时,布谷鸟的行走路径是一个随机游走过程,差的鸟巢位置则以抛弃概率P被抛弃,新的位置在游走过程中建立。
对次用户的功率资源进行优化分配,将次用户的功率资源看作是布谷鸟待选择的鸟巢位置,通过鸟巢位置的不断更新实现功率的优化分配。布谷鸟搜索算法进行功率分配步骤如下。
1) 随机产生一组鸟巢位置,即随机产生每个用户的功率。
2) 根据式(41) 计算每个鸟巢的适应度值。
3) 根据莱维飞行进行鸟巢位置的更新,根据式(41) 计算更新后的鸟巢适应度值。
4) 将步骤2) 和步骤3) 的适应度值合在一起进行比较,选择适应度值大的一半鸟巢位置的值保留。
5) 以抛弃概率P(一般设为0.25) 再次更新鸟巢位置,计算新的适应度值。
6) 迭代步骤4) 和步骤5),设置迭代门限,记录当前最优解。否则,返回步骤2)。
-
仿真中假设系统中有一个主用户,3个次级用户,发送端和接收端均配置6根天线,即M=N=6,信道是均值为0,方差为1的循环对称复高斯信道。每个次用户的自由度为2,即di=2。
图 2表示的是不同干扰对齐算法次用户的系统传输速率。由图可以看出,本文算法次用户传输速率优于其他算法,比最小化泄露功率干扰对齐算法(Min-INL)和最大化信噪比干扰对齐算法(Max-SINR)系统传输速率高约2 b·s-1·Hz-2。
图 3比较的是不同种群数时算法的收敛性。从图中可以看出,改善种群规模对布谷鸟算法的寻优精度的影响并不明显,体现出布谷鸟算法容易跳出局部最优的优点。
图 4为不同SNR下次用户的传输速率。由图 4可以看出,本文算法在迭代15次左右后收敛,SNR为0 dB时,次用户的系统传输速率可以达到3.8 b·s-1·Hz-2,SNR为5 dB时,次用户的系统传输速率可达8 b·s-1·Hz-2, SNR为15 dB时,次用户的系统传输速率可达12 b·s-1·Hz-2。
图 5所示是本文算法和文献[13]算法以及等功率分配算法时次用户系统传输速率的比较。从图中可以看出,本文算法和文献[13]算法都具有较好的收敛性,传输速率都优于等功率算法。与文献[13]算法比较,本文算法次用户的系统传输速率较高。
-
干扰对齐是一种有效消除干扰的方法,本文针对认知MIMO系统中用户之间的干扰,提出基于博弈论的干扰对齐算法。数值分析结果表明,该算法具有良好的收敛性能,消除了主次用户之间的干扰以及次用户相互之间的干扰。此外,采用布谷鸟搜索算法对功率资源进行优化分配后,次用户系统的传输速率比文献[13]约高3 b·s-1·Hz-2,有效地提高了次用户传输速率。本文算法对于实际环境的通信算法具有理论指导意义,针对实际信道环境的算法研究是下一步研究重点。
Interference Alignment for Cognitive Radio MIMO Cognitive System Based on Game Theory
-
摘要: 为消除用户间干扰,提高认知无线电多输入多输出(CR-MIMO)系统传输速率,给出一种基于博弈论的干扰对齐算法。该算法首先采用注水算法为主用户进行功率分配,同时设计次用户预编码使次用户信号落入主用户未分配功率的子信道。然后将次用户之间的多条干扰链路构成一个博弈群体进行求解,实现次用户之间的干扰对齐。此外,为最大化次用户传输速率,将次用户功率分配问题转换为布谷鸟鸟巢的选择问题,构造适应度函数,得到最优的功率分配方案。数值分析表明,该算法可以消除主次用户的干扰以及次用户之间的干扰,传输速率比最大信干噪比(Max-SINR)算法高2 b·s-1·Hz-2,同时,结合布谷鸟搜索算法进行功率分配后传输速率高于文献[
13 ]。Abstract: To eliminate interference and improve the transmission rate of cognitive radio multiple-input multiple-output (CR-MIMO) systems, an interference alignment algorithm based on game theory is proposed. The algorithm uses water-filling algorithm for maximum the transmission rate of primary user. Meanwhile, the pre-coding matrix of secondary users is designed for the secondary user signal to fall into free sub-channel of the primary user. Multiple interference links are constituted into a game group to achieve interference alignment of secondary users. Moreover, the power allocation of secondary users is formulated as selection problem of cuckoo's nests, the optimal power allocation is obtained according to the fitness function. Numerical simulation results show that this algorithm can eliminate the interference between the primary user and secondary users and the interference among secondary users. Compared with the maximize-signal-to-interference-plus-noise-ratio algorithm (Max-SINR), the interference alignment algorithm proposed can improve the transmission rate of secondary users about 2 b·s-1·Hz-2. Moreover, the transmission rate can also be improved by using cuckoo search algorithm for power distribution compared with the result presented elsewhere.-
Key words:
- cognitive radio /
- cuckoo search algorithm /
- game theory /
- interference alignment /
- secondary user
-
[1] NO E D. 03-322, notice of proposed rule making and order[J]. Federal Communications Commission, Adopted, 2003, 59(26):84-86. http://www.oalib.com/references/7767586 [2] Agency for Healthcare Research and Quality, Office for Civil Rights, HHS. Patient safety and quality improvement. Notice of proposed rulemaking[J]. Federal Register, 2008, 73(29):84-86. http://www.ncbi.nlm.nih.gov/pubmed/18677818 [3] TSINOS C G, BERBERIDIS K. Blind opportunistic interference alignment in MIMO cognitive radio systems[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2013, 3(4):626-639. doi: 10.1109/JETCAS.2013.2284611 [4] PERLAZA S M, DEBBAH M, LASAULCE S, et al. Opportunistic interference alignment in MIMO interference channels[C]//IEEE 19th International Symposium on.[S.l.]:IEEE, 2008:1-5. [5] REZAEI F, TADAION A. Interference alignment in cognitive radio networks[J]. Communications, IET, 2014, 8(10):1769-1777. doi: 10.1049/iet-com.2013.0731 [6] ZHOU H, RATNARAJAH T, LIANG Y C. On secondary network interference alignment in cognitive radio[C]//2011 IEEE Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN), [S.l.]:IEEE, 2011:637-641. [7] AMIR M, El-KEYI A, NAFIE M. Constrained interference alignment and the spatial degrees of freedom of MIMO cognitive networks[J]. IEEE Transactions on Information Theory, 2011, 57(5):2994-3004. doi: 10.1109/TIT.2011.2119770 [8] QU T, ZHAO N, YIN H, et al. Interference alignment for overlay cognitive radio based on game theory[C]//2012 IEEE 14th International Conference on Communication Technology (ICCT).[S.l.]:IEEE, 2012:67-72. [9] XU Y, MAO S. Stackelberg game for cognitive radio networks with MIMO and distributed interference alignment[J]. IEEE Transactions on Vehicular Technology, 2013, 63(2):879-892. doi: 10.1109/TVT.2013.2279761 [10] KOO B, PARK D. Interference alignment with cooperative primary receiver in cognitive networks[J]. IEEE Communications Letters, 2012, 16(7):1072-1075. doi: 10.1109/LCOMM.2012.051512.120719 [11] GULER B, YENER A. Selective interference alignment for MIMO cognitive femtocell networks[J]. IEEE Journal on Selected Areas in Communication, 2014, 32(3):439-450. doi: 10.1109/JSAC.2014.140306 [12] FADLALLAH Y, AMIS K, AÏSSA-El-BEY A, et al. Interference alignment for a multi-user SISO interference channel[J]. Eurasip Journal on Wireless Communications & Networking, 2014(1):1-13. doi: 10.1186/1687-1499-2014-79 [13] ZHAO F, WANG W, CHEN H, et al. Interference alignment and game-theoretic power allocation in MIMO heterogeneous sensor networks communications[J]. Signal Processing, 2016, 126(c):173-179. http://dl.acm.org/citation.cfm?id=2936023.2936161 [14] CASTANHEIRA D, SILVA A, GAMEIRO A. Set optimization for efficient interference alignment in heterogeneous networks[J]. IEEE Transactions on Wireless Communication, 2014, 13(10):5648-5660. doi: 10.1109/TWC.2014.2322855 [15] PERLAZA S M, DEBBAH M, LASAULCE S, et al. Opportunistic interference alignment in MIMO interference channels[C]//Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communication.[S.l.]:IEEE, 2008:1-5. [16] REZAEI F, TADAION A. Interference alignment in cognitive radio networks[J]. Iet Communications, 2014, 8(10):1769-1777. doi: 10.1049/iet-com.2013.0731 [17] MONDERER D, SHAPLEY L S. Potential games[J]. Games and Economic Behavior, 1996, 14(1):124-143. doi: 10.1006/game.1996.0044 [18] 章扬, 周正, 石磊, 等.基于严格势博弈的干扰对齐[J].北京邮电大学学报, 2013, 36(2):50-54. http://www.cnki.com.cn/Article/CJFDTOTAL-BJYD201302011.htm ZHANG Yang, ZHOU Zheng, SHI Lei, et al. Interference alignment based on exact potential game[J]. Journal of Beijing University of Posts and Telecommunication, 2013, 36(2):50-54. http://www.cnki.com.cn/Article/CJFDTOTAL-BJYD201302011.htm [19] BANERJEE S, CHATTOPADHYAY S. A novel asymmetric turbo code using cuckoo search algorithm[C]//India Conference (INDICON), 2014 Annual.[S.l.]:IEEE, 2014. -


 ISSN
ISSN 




 下载:
下载: