-
自从文献[1]发现单一波束产生的梯度力能够吸引介质微粒以来,激光对颗粒的捕获效应,即“光镊”技术,由于其在物理、机械、化学和生命等学科的潜在应用,引发了对光学操纵等的研究热潮。为了得到负的光学力,文献[2-3]通过设计特殊的贝塞尔光束或者通过如非磁各向异性介质、梯度折射率介质、增益介质和手征介质等特殊材料来实现。文献[4]给出了排列成螺旋形状的25个金属球所受光力的解析解,文献[5]讨论了光场施加在介电系数虚部为负数时增益材料负的辐射光压。而对于激光与增益手征介质相互作用的复杂机理尚需要进一步的研究。
增益材料包括固体、液体、气体和半导体等。有些增益材料是非手征的,有些增益材料具有手征性,如手征异向介质[5]、细胞中的绿色荧光蛋白[6]、碳纳米管[7]等。目前手征介质光学力的研究大部分采用Mie理论[8]或通过设计特殊的结构光束[9]。Mie理论尽管具有准确度高和速度快等优点,但是不适合于求解非球形粒子,且Mie理论是基于Bohren的波分解技术,无法实时计算手征介质的磁电耦合效应。
与解析解相比[8],时域有限差分方法(finite-difference time-domain, FDTD)作为一种计算简单、表达直观的数值方法[10-19],具有广泛的适用性,能够模拟任意形状手征介质随时间和空间变化的电磁场分布情况。与其他数值方法相比,FDTD方法可以模拟天然有机分子、人工玫瑰花型和等效色散的手征介质[11, 13]。除了基于与Mie理论类似的波场分解技术的BI-FDTD方法[10],色散的FDTD方法还可以直接处理本构关系为磁电耦合的手征介质[12]。麦克斯韦应力张量(Maxwell’s stress tensor)和洛伦兹力(Lorentz force)是常用的两种光学力计算方法,均基于微粒的电磁场分布。麦克斯韦应力张量的方法,是在包含所计算结构的任意闭合曲面S上对麦克斯应力张量做面积分,能够获取宽频段的光学力分布情况;而洛伦兹力方法可以基于所计算结构的时谐电磁场分布,提取结构中任意位置的光学力分布情况。文献[3]基于FDTD方法,计算了两个手征介质板之间的作用力,无须考虑电荷和磁荷密度对手征介质辐射光压的影响;此外,与一维情况相比,二维FDTD方法能够模拟电磁波斜入射时,复杂形状手征介质的电磁场和洛伦兹力分布情况。
本文基于FDTD方法模拟了电磁波在二维增益手征介质柱的波传播和洛伦兹力密度的分布情况。首先给出了基于辅助差分方程(auxiliary differential equation, ADE) FDTD方法中手征介质的电极化和磁极化强度,推导了计算手征介质的波方程和洛伦兹力密度。模拟了二维普通介质板的场和洛伦兹力密度的分布,验证了本文方法和程序的正确性。最后分析了手征介质柱的同极化和交叉极化力密度分布情况,讨论其潜在工程应用。
-
频域各向同性手征介质中的磁电耦合本构关系可表示为[18]:
$$\mathit{\boldsymbol{D}}(\omega ) = \varepsilon (\omega )\mathit{\boldsymbol{E}} + \left[ {\chi (\omega ) - {\rm{j}}\kappa (\omega )} \right]\sqrt {{\mu _0}{\varepsilon _0}} \mathit{\boldsymbol{H}}$$ (1) $$\mathit{\boldsymbol{B}}(\omega ) = \mu (\omega )\mathit{\boldsymbol{H}} + \left[ {\chi (\omega ) + {\rm{j}}\kappa (\omega )} \right]\sqrt {{\mu _0}{\varepsilon _0}} \mathit{\boldsymbol{E}}$$ (2) 式中,ε(ω)、μ(ω)、κ(ω)和χ(ω)分别是与频率相关的介电系数、磁导系数、手征参数和非互易参数。本文仅讨论纯手征介质的情况,即χ(ω)=0。绝大部分天然和人工手征介质的宏观等效介质参数[16-18]由其材料属性、物理几何结构和电磁波入射角度等决定。洛伦兹模型一般用来表征手征介质的介电系数和磁导系数,而Condon模型用来表示手征参数,即:
$$\varepsilon (\omega ) = {\varepsilon _\infty }{\varepsilon _0} + [({\varepsilon _s} - {\varepsilon _\infty }){\varepsilon _0}\omega _e^2]/(\omega _e^2 - {\omega ^2} + {\rm{j}}2{\xi _e}\omega )$$ (3) $$\mu (\omega ) = {\mu _\infty }{\mu _0} + [({\mu _s} - {\mu _\infty }){\mu _0}\omega _h^2]/(\omega _h^2 - {\omega ^2} + {\rm{j}}2{\xi _h}\omega )$$ (4) $$\;\kappa (\omega ) = {\tau _\kappa }\omega _\kappa ^2\omega /(\omega _\kappa ^2 - {\omega ^2} + {\rm{j}}2{\omega _\kappa }{\xi _\kappa }\omega )$$ (5) 式中,εs、μs、ε∞和μ∞分别表示频率为零和无穷时的相对介电系数和磁导系数;ωe、ωh和ωκ表示谐振角频率;ξe、ξh和ξκ表示阻尼系数;τκ表示表征手征介质旋光幅度的特征时间常数。人工和生物手征介质的手征参数受其几何尺寸,如螺旋半径、宽度、厚度、轮廓长度和俯仰角等的影响。
手征介质中感应电流密度J和磁流密度K,耦合电流密度Jc和磁流密度Kc为:
$$\mathit{\boldsymbol{J}}/{\rm{j}}\omega = [({\varepsilon _s} - {\varepsilon _\infty }){\varepsilon _0}\omega _e^2]\mathit{\boldsymbol{E}}/(\omega _e^2 - {\omega ^2} + {\rm{j}}2{\xi _e}\omega ) = \;{\mathit{\boldsymbol{P}}_e}$$ (6) $$\mathit{\boldsymbol{K}}/{\rm{j}}\omega = [({\mu _s} - {\mu _\infty }){\mu _0}\omega _h^2]\mathit{\boldsymbol{H}}/(\omega _h^2 - {\omega ^2} + {\rm{j}}2{\xi _h}\omega ) = {\mathit{\boldsymbol{M}}_n}$$ (7) $${\mathit{\boldsymbol{J}}_c}/{\rm{j}}\omega = {\rm{j}}{\tau _\kappa }\omega _\kappa ^2\omega \sqrt {{\mu _0}{\varepsilon _0}} \mathit{\boldsymbol{E}}{\rm{/(}}\omega _\kappa ^2 - {\omega ^2} + {\rm{j}}2{\omega _\kappa }{\xi _\kappa }\omega {\rm{)}} = {\mathit{\boldsymbol{P}}_c}$$ (8) $${\mathit{\boldsymbol{K}}_c}/{\rm{j}}\omega = - {\rm{j}}{\tau _\kappa }\omega _\kappa ^2\omega \sqrt {{\mu _0}{\varepsilon _0}} \mathit{\boldsymbol{H}}{\rm{/(}}\omega _\kappa ^2 - {\omega ^2} + {\rm{j}}2{\omega _\kappa }{\xi _\kappa }\omega {\rm{)}} = {\mathit{\boldsymbol{M}}_c}$$ (9) 式中,Pe为感应电极化强度;Pc为耦合电极化强度;Mn为感应磁极化强度;Mc为耦合磁极化强度。
与常规非色散介质、电或磁色散介质相比,含磁电耦合本构关系手征介质中的电极化强度P和磁极化强度M复杂很多。在手征介质中,P和M的为:
$$\mathit{\boldsymbol{P}} = {\varepsilon _0}({\varepsilon _\infty } - 1)\mathit{\boldsymbol{E}} + ({\mathit{\boldsymbol{P}}_e} + {\mathit{\boldsymbol{M}}_c})$$ (10) $$\mathit{\boldsymbol{M}} = {\mu _0}({\mu _\infty } - 1)\mathit{\boldsymbol{H}} + ({\mathit{\boldsymbol{M}}_n} + {\mathit{\boldsymbol{P}}_c})$$ (11) 式中,任意位置磁极化强度M是由手征介质中的感应磁极化强度Mn和耦合电极化强度Pc产生的。
如果考虑手征介质的增益损耗特性,无源手征介质的介电系数、磁导系数和手征参数满足如下条件[20]:
$$\begin{array}{c} {\mathop{\rm Im}\nolimits} [\varepsilon ] < 0,{\mathop{\rm Im}\nolimits} [\mu ] < 0,\\ {{\mathop{\rm Im}\nolimits} ^2}(\kappa ) < [{\mathop{\rm Im}\nolimits} (\varepsilon ){\mathop{\rm Im}\nolimits} (\mu ){\rm{/(}}{\varepsilon _0}{\mu _0}{\rm{)}}] \end{array}$$ (12) 如果介质参数不满足式中的任意一条,手征介质即变成有源增益材料。
利用式~式的时域表达式及麦克斯韦方程,可得出手征介质中传播模的方程为[3]:
$$\nabla \times \mathit{\boldsymbol{H}} = {\varepsilon _\infty }{\varepsilon _0}\partial \mathit{\boldsymbol{E}}{\rm{/}}\partial t + \mathit{\boldsymbol{J}} + {\mathit{\boldsymbol{K}}_c}$$ (13) $$\frac{{{\partial ^2}\mathit{\boldsymbol{J}}}}{{{\partial ^2}t}} + 2{\xi _e}\frac{{\partial \mathit{\boldsymbol{J}}}}{{\partial t}} + \omega _e^2\mathit{\boldsymbol{J}} = ({\varepsilon _s} - {\varepsilon _\infty }){\varepsilon _0}\omega _e^2\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial t}}$$ (14) $$\frac{{{\partial ^2}\mathit{\boldsymbol{K}}}}{{{\partial ^2}t}} + 2{\xi _h}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial t}} + \omega _h^2\mathit{\boldsymbol{K}} = ({\mu _s} - {\mu _\infty }){\mu _0}\omega _h^2\frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial t}}$$ (15) $$\nabla \times \mathit{\boldsymbol{E}} = - {\mu _\infty }{\mu _0}\frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial t}} - \mathit{\boldsymbol{K}} - {\mathit{\boldsymbol{J}}_c}$$ (16) $$\frac{{{\partial ^2}{\mathit{\boldsymbol{J}}_c}}}{{{\partial ^2}t}} + 2{\omega _\kappa }{\xi _\kappa }\frac{{\partial {\mathit{\boldsymbol{J}}_c}}}{{\partial t}} + \omega _\kappa ^2{\mathit{\boldsymbol{J}}_c} = {\tau _\kappa }\omega _\kappa ^2\sqrt {{\mu _0}{\varepsilon _0}} \frac{{{\partial ^2}\mathit{\boldsymbol{E}}}}{{{\partial ^2}t}}$$ (17) $$\frac{{{\partial ^2}{\mathit{\boldsymbol{K}}_c}}}{{{\partial ^2}t}} + 2{\omega _\kappa }{\xi _\kappa }\frac{{\partial {\mathit{\boldsymbol{K}}_c}}}{{\partial t}} + \omega _\kappa ^2{\mathit{\boldsymbol{K}}_c} = - {\tau _\kappa }\omega _\kappa ^2\sqrt {{\mu _0}{\varepsilon _0}} \frac{{{\partial ^2}\mathit{\boldsymbol{H}}}}{{{\partial ^2}t}}$$ (18) 二维情况下,各物理量与z无关。采用ADE-FDTD法可推导出无源色散手征介质中的迭代公式。鉴于篇幅原因,本文只给出TM极化波的Ez,Jz和Kcz的迭表示达式为:
$$\begin{array}{c} E_z^{n + 1}(i,j) = E_z^n(i,j) - \frac{{\Delta t}}{{{\varepsilon _\infty }{\varepsilon _0}}}\left[ {J_z^{n + \frac{1}{2}}(i,j)} \right. + \\ \left. {K_z^n\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)} \right] + \frac{{\Delta t}}{{{\varepsilon _\infty }{\varepsilon _0}}} \times \\ \left[ {\frac{{H_y^{n + \frac{1}{2}}\left( {i + \frac{1}{2},j} \right) - H_y^{n + \frac{1}{2}}\left( {i - \frac{1}{2},j} \right)}}{{\Delta x}}} \right. - \\ \left. {\frac{{H_x^{n + \frac{1}{2}}\left( {i,j + \frac{1}{2}} \right) - H_x^{n + \frac{1}{2}}\left( {i,j - \frac{1}{2}} \right)}}{{\Delta y}}} \right] \end{array}$$ (19) $$\begin{array}{c} J_z^{n + \frac{3}{2}}(i,j) = {a_x}J_z^{n + \frac{1}{2}}(i,j) + {\beta _x}J_z^{n - \frac{1}{2}}(i,j) + \\ {\gamma _x}\left[ {E_z^{n + 1}(i,j) - E_z^{n - 1}(i,j)} \right] \end{array}$$ (20) $$\begin{array}{c} K_{cz}^{n + 1}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right) = {\alpha _{\kappa cx}}K_{cz}^n\left( {i + \frac{1}{2},j + \frac{1}{2}} \right) + \\ {\beta _{\kappa cx}}K_{cz}^{n - 1}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right) + \;{\gamma _{\kappa cx}}H_z^{n + \frac{1}{2}}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right) + \\ {\gamma _{\kappa cx}}\left[ {\left. { - 2H_z^{n - \frac{1}{2}}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right) + H_z^{n - \frac{3}{2}}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)} \right]} \right. \end{array}$$ (21) 式中,有:
$$\begin{array}{l} \;{\alpha _x} = \frac{{2 - \omega _e^2\Delta {t^2}}}{{1 + {\xi _e}\Delta t}}{\rm{ }}\;{\alpha _{\kappa cx}} = \frac{{(2 - \omega _\kappa ^2\Delta {t^2})}}{{1 + {\omega _\kappa }{\xi _\kappa }\Delta t}}\\ {\gamma _x} = \frac{{({\varepsilon _s} - {\varepsilon _\infty }){\varepsilon _0}\omega _e^2\Delta t/2}}{{1 + {\xi _e}\Delta t}}{\rm{ }}{\beta _x} = \frac{{{\xi _e}\Delta t - 1}}{{1 + {\xi _e}\Delta t}}\;\\ {\beta _{\kappa cx}} = \frac{{{\omega _\kappa }{\xi _\kappa }\Delta t - 1}}{{1 + {\omega _\kappa }{\xi _\kappa }\Delta t}}{\rm{ }}{\gamma _{\kappa cx}} = - \frac{{{\tau _\kappa }\omega _\kappa ^2\sqrt {{\mu _0}{\varepsilon _0}} }}{{1 + {\omega _\kappa }{\xi _\kappa }\Delta t}} \end{array}$$ (22) -
色散手征介质的磁感应强度B为:
$$\mathit{\boldsymbol{B}} = {\mu _0}\mathit{\boldsymbol{H}} + \mathit{\boldsymbol{M}} = {\mu _\infty }{\mu _0}\mathit{\boldsymbol{H}} + ({\mathit{\boldsymbol{M}}_n} + {\mathit{\boldsymbol{P}}_c})$$ (23) 将式(23)代入麦克斯韦方程组中的磁感应强度散度和电场旋度方程,有:
$$\nabla \cdot \mathit{\boldsymbol{B}} = 0 = \nabla \cdot {\mu _0}\mathit{\boldsymbol{H}} + \mathit{\boldsymbol{M}})$$ (24) $$\begin{array}{c} \nabla \times \mathit{\boldsymbol{E}} = - \partial \mathit{\boldsymbol{B}}/\partial t = - {\mu _0}\partial \mathit{\boldsymbol{H}}/\partial t - \partial \mathit{\boldsymbol{M}}/\partial t = \\ - {\mu _0}{\mu _\infty }\partial \mathit{\boldsymbol{H}}/\partial t - \partial ({\mathit{\boldsymbol{M}}_n} + {\mathit{\boldsymbol{P}}_c})/\partial t \end{array}$$ (25) 式可重写为:
$$\begin{array}{c} - {\mu _0}\frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial t}} = \frac{{\nabla \times \mathit{\boldsymbol{E}} + \partial ({\mathit{\boldsymbol{M}}_n} + {\mathit{\boldsymbol{P}}_c})/\partial t}}{{{\mu _\infty }}}\\ \partial \mathit{\boldsymbol{M}}/\partial t = - {\mu _0}\partial \mathit{\boldsymbol{H}}/\partial t - \nabla \times \mathit{\boldsymbol{E}} \end{array}$$ (26) 根据束缚磁流密度定义并将式带入有:
$$\begin{array}{c} {\mathit{\boldsymbol{J}}_{{\rm{m\_bound}}}} = \partial \mathit{\boldsymbol{M}}/\partial t = - {\mu _0}\partial \mathit{\boldsymbol{H}}/\partial t - \nabla \times \mathit{\boldsymbol{E}} = \\ \frac{{\nabla \times \mathit{\boldsymbol{E}} + \partial ({\mathit{\boldsymbol{M}}_n} + {\mathit{\boldsymbol{P}}_c})/\partial t}}{{{\mu _\infty }}} - \nabla \times \mathit{\boldsymbol{E}} = \\ \frac{{\partial ({\mathit{\boldsymbol{M}}_n} + {\mathit{\boldsymbol{P}}_c})/\partial t}}{{{\mu _\infty }}} + \frac{{(1 - {\mu _\infty })\nabla \times \mathit{\boldsymbol{E}}}}{{{\mu _\infty }}} \end{array}$$ (27) 式中,束缚磁流密度由磁极化强度Mn和耦合电极化强度Pc决定。
束缚磁荷密度可定义为:
$${\rho _{{\rm{m\_bound}}}} = {\mu _0}\nabla \cdot \mathit{\boldsymbol{H}} = - \nabla \cdot \mathit{\boldsymbol{M}}$$ (28) 采用相似的推导过程,可以得到手征介质中束缚电荷密度ρe_bound和束缚电流密度Je_bound的表达式为:
$$\begin{array}{l} \quad \quad \quad {\rho _{{\rm{e\_bound}}}} = {\varepsilon _0}\nabla \cdot \mathit{\boldsymbol{E}} = - \nabla \cdot \mathit{\boldsymbol{P}}\\ {\mathit{\boldsymbol{J}}_{{\rm{e\_bound}}}}\, = \frac{{\partial ({\mathit{\boldsymbol{P}}_e} + {\mathit{\boldsymbol{M}}_c})/\partial t}}{{{\varepsilon _\infty }}} + \frac{{({\varepsilon _\infty } - 1)(\nabla \times \mathit{\boldsymbol{H}})}}{{{\varepsilon _\infty }}} \end{array}$$ (29) 电磁场、电荷和电流密度都是时间和空间坐标的函数。因此,施加在手征介质的光力可通过计算洛伦兹力密度的时均值而求得。
$$\begin{array}{c} \left\langle \mathit{\boldsymbol{F}} \right\rangle = (1/T) \times \\ \int_{{\rm{ }}0}^{{\rm{ }}T} {({\rho _{{\rm{e\_bound}}}}\mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{J}}_{{\rm{e\_bound}}}} \times {\mu _0}\mathit{\boldsymbol{H}} + } \\ {\rho _{{\rm{m\_bound}}}}\mathit{\boldsymbol{H}} - {\mathit{\boldsymbol{J}}_{{\rm{m\_bound}}}} \times {\varepsilon _0}\mathit{\boldsymbol{E}}){\rm{d}}t \end{array}$$ (30) 通过对含点频时谐电磁场、束缚电磁流和电磁荷的式在一个周期内进行积分和求平均,可以得到手征介质的时均洛伦兹力密度。
因为垂直于介质分界面的磁感应强度B⊥必须连续,即磁场H⊥是不连续的,所以束缚磁荷仅存在于两种相邻介质之间的表面上;束缚电荷同样适用于类似的边界条件。
电磁场施加在手征介质上与时间和空间相关的洛伦兹力密度F(r, t)[21]可表示为:
$$\begin{array}{c} \left\langle \mathit{\boldsymbol{F}} \right\rangle = (1/T)\int_{{\rm{ }}0}^{{\rm{ }}T} {({\rho _{{\rm{e\_bound}}}}\mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{J}}_{{\rm{e\_bound}}}} \times {\mu _0}\mathit{\boldsymbol{H}}} + \\ {\rho _{{\rm{m\_bound}}}}\mathit{\boldsymbol{H}} - {\mathit{\boldsymbol{J}}_{{\rm{m\_bound}}}} \times {\varepsilon _0}\mathit{\boldsymbol{E}}){\rm{d}}t \end{array}$$ (31) 将式进一步用Yee元胞进行数值离散,结合ADE-FDTD方法计算得到的电磁场,可求出单位周期内的时均洛伦兹力密度。
本文中,在不同介质的分界面处,采用平均的介质参数而不是平均的电磁场和电磁流等来计算介质分界面中的电磁场、电磁流和洛伦兹力密度。对于二维FDTD情况,$\partial /\partial z = 0$,即TM极化波包括Ez,Hx和Hy场分量,而TE极化波包括Hz,Ex和Ey场分量,利用二阶Mur吸收边界截断外向行波。
-
时间t=1 100Δt TE极化波Hz的场分布图如图 1所示,同时叠加了电场强度矢量(Ey, Ex)。激励源为连续波高斯波束s(t)=0.5sin(ω0t),波束的焦平面在图 1中总场左边界处,随空间变化为exp(-x2/w12),其中w1=0.9 μm,工作波长λ0=0.65 μm,介质板折射率n及相对介电常数εr分别为2和4。波的介质波长λd=0.5λ0,算例中距离和时间离散间隔分别取为δ=2λd/65和Δt=δ/2c。
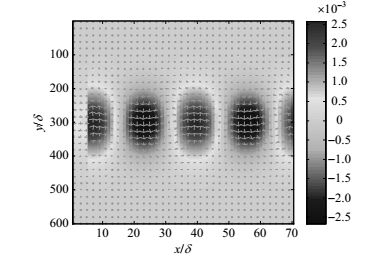
时间从t=1 165Δt到t=1 295Δt TE极化波入射时,介质板时均力密度Fx分量的分布图如图 2所示,同时叠加了矢量场(Fy, Fx)。高斯波束施加在图 2中半个介质板上的单位面积沿x轴积分的时均洛伦兹力密度为1.620 6 pN/m2,与文献p极化波结果1.657 7 pN/m2相比,相对误差为2.2%,且图 2中数值仿真结果与文献[18]中的p极化结果几乎完全一致,证明了本文ADE-FDTD和洛伦兹力密度方法和程序的正确性。
-
图 3给出了TM极化波垂直入射,半径为50 nm的手征介质柱的电磁场以及电磁荷和电磁流所贡献的洛伦兹力密度分布图。入射波工作频率选为f0为461.54 THz。式~式中手征介质板的介质参数分别为εs=1.1ε0,ε∞=ε0,μs=1.1μ0,μ∞=μ0,ωe=ωh=π× 500 THz,ωk=π×200 THz,ξe=1 500 ωe,ξh=1 500 ωh,ξk=3,τk=2.4×10-16。手征介质板与之相应的相对介电系数εr、磁导系数μr和手征参数κr在频率f0=461.54 THz时分别为1-j1.8×10-5、1-j1.8×10-5和-0.01-j0.016。计算频率对应的自由空间波长为λ0=650 nm。由于所选介质板介电系数和磁导率与自由空间非常接近,因此ADE-FDTD方法的Yee元胞空间尺寸选为δ=λ0/130=5 nm,时间步长Δt=δ/2c。
图 3给出了利用FDTD方法仿真的电磁波与手征介质柱的相互作用,同极化TM波和交叉极化TE波与手征介质相互作用产生的洛伦兹力分布情况。图 3给出平面波在自由空间中沿y方向的传播特性,整个模拟区域范围为(301δ, 296δ),手征介质柱的中心位置坐标为(x, y)=(139δ, 86δ)。图 3所示的数值结果中,时间范围是1 135~1 395Δt。电场幅度为1 000 V/m的TM极化平面波从上向下照射手征介质柱。如果扣除数值较小的手征参数,图 3中手征介质柱相对于背景介质真空是一个匹配的介质。从图 3a和图 3b中可以看出,手征介质柱对电磁波的反射很小;与同极化入射电场相比,耦合产生的交叉极化磁场幅度相对较小,手征介质柱手征参数引起的交叉极化TE波在手征介质柱中产生了一个会聚点。从图 3c和图 3e中可以看出,对于电流和磁流贡献的洛伦兹力密度而言,TM极化波在手征介质中靠近平面波入射波源方位一个周期内产生的时均力密度的绝对值较大;从图 3d和图 3f中可以看出,TE极化波在手征介质柱中距离入射波远的方位电流和磁流产生的捕获力较大。从图 3g~图 3j中可以看出,表面电荷和磁荷的洛伦兹力密度主要施加在手征介质柱偏左的部位,除TE极化波与手征介质柱表面电荷的洛伦兹力密度外,其他时均力密度整体均向左推手征介质柱。在一定条件下,入射的高斯波束可以对普通介质柱产生捕获力,而平面波入射对普通介质柱不能产生捕获力的效果。从时间t=1 135Δt开始的一个周期内,对TM和TE极化波电磁流施加在手征介质柱上的洛伦兹时均力密度进行积分,分别得到$\left( {\int {{F_{cox}}} (x,y)} \right.{\rm{d}}x{\rm{d}}y,$,$\left. {\int {{F_{coy}}} (x,y){\rm{d}}x{\rm{d}}y} \right)$=(-1.86×10-6,2.64×10-5) PN/m以及$\left( {\int {{F_{cox}}} (x,y){\rm{d}}x{\rm{d}}y,\int {{F_{coy}}} (x,y){\rm{d}}x{\rm{d}}y} \right)$=(-2.70×10-6,-3.62× 10-5) PN/m。
同极化TM和交叉极化TE波表面磁荷和电荷产生的力密度分别为(-2.75×10-5,2.1×10-8)PN/和(9.81×10-6,6.51×10-6) PN/m。平面波施加在手征介质柱上总的洛伦兹力密度为(-2.25×10-5,-3.29× 10-6) PN/m。可以看出平面入射波对手征介质柱产生捕获力,分析其根本原因是图 3模拟的手征介质为增益材料,满足Im2(κ) > [Im(ε)Im(μ)/ε0μ0],该捕获力主要由交叉极化波的电磁流密度贡献。
-
本文仿真了平面波照射下,色散手征介质柱的同极化和交叉极化电磁场和时均洛伦兹力密度分布。推导了模拟手征介质的ADE-FDTD方法和洛伦兹力密度公式。与文献中介质板的电磁场和洛伦兹力密度计算结果对比,验证了本文算法和程序的正确性。数值模拟结果表明,平面波入射时,耦合的交叉极化波在手征介质柱中产生了一个会聚点,从而捕获该色散增益的手征介质柱,该捕获力主要归因于交叉极化波电磁流的贡献。本文的研究工作可为光镊在生物大分子中的应用和手征参数的测量提供借鉴。宽频段手征介质的电磁波传播、散射以及光学力分布情况是下一步研究工作的重点。
Wave Propagation and the Lorentz Force Density of a Chiral Column Based on the FDTD Method
-
摘要: 基于辅助差分方程时域有限差分法,模拟了色散手征介质柱的电磁场和洛伦兹力密度分布。从本构关系出发,给出了手征介质中频域电、磁极化强度与感应电、磁极化强度和耦合电、磁极化强度之间的关系;并给出了波方程和电场的迭代公式。推导了手征介质中含束缚电荷、电流和束缚磁荷、磁流密度的时均洛伦兹力密度表达式。与相关文献结果进行了对比,验证了辅助差分方程时域有限差分法和洛伦兹力密度方法的正确性。仿真了增益手征介质柱的场和光力分布情况,讨论了电磁流和电磁荷对洛伦兹力密度的贡献,为手征介质在光镊和手征参数测量等工程应用提供了理论指导。Abstract: Based on the auxiliary differential equation (ADE) finite-difference time-domain (FDTD) method, distributions of electromagnetic fields and Lorentz force densities in a dispersive chiral column are simulated. Firstly, relationships between electromagnetic polarization densities and induced electromagnetic polarization densities, as well as coupled electromagnetic polarization densities of chiral media, are presented based on the constitutive relations. Wave equations and recurrence formula of electric are given. Secondly, the Lorentz force density in chiral media containing bound electric charge and electric current densities, as well as bound magnetic charge and magnetic current densities, is derived. Then, we verify the correctness of the ADE-FDTD method and the Lorentz force density method by comparing with literature's results. Finally, distributions of fields and optical forces for an active chiral cylinder are simulated. The contribution of electromagnetic current and electromagnetic charge densities to the Lorentz force density is discussed. The work in this paper provides some theoretical guidance for chiral media's potential engineering applications in optical tweezers and measurement of chiral parameter.
-
Key words:
- chiral media /
- dispersion /
- finite-difference time-domain method /
- force
-
[1] ASHKIN A, DZIEDZIC J M, BJORKHOLM J E, et al. Observation of a single-beam gradient force optical trap for dielectric particles[J]. Optical Letter, 1986, 11(5):288-290. doi: 10.1364/OL.11.000288 [2] GAO Dong-liang, NOVITSKY A, ZHANG Tian-hang, et al. Unveiling the correlation between non-diffracting tractor beam and its singularity in Poynting vector[J]. Laser & Photonics Reviews, 2015, 9(1):75-82. https://www.researchgate.net/publication/267875624_Unveiling_the... [3] WANG Mao-yan, LI Hai-long, GAO Dong-liang, et al. Radiation pressure of active dispersive chiral slabs[J]. Optics Express, 2015, 23(13):16546-6553. doi: 10.1364/OE.23.016546 [4] DING Kun, NG J, ZHOU Lei, et al. Realization of optical pulling forces using chirality[J]. Physical Review A, 2014, 89(6):063825. doi: 10.1103/PhysRevA.89.063825 [5] MIZRAHI A, FAINMAN Y. Negative radiation pressure on gain medium structures[J]. Optics Letters, 2010, 35(20):3405-3407. doi: 10.1364/OL.35.003405 [6] WANG Bing-nan, ZHOU Jiang-feng, KOSCHNY T, et al. Chiral metamaterials:Simulations and experiments[J]. Journal of Optics A:Pure and Applied Optics, 2009, 11(11):114003-1-114003-10. doi: 10.1088/1464-4258/11/11/114003 [7] GATHER M C, YUN S H. Single-cell biological lasers[J]. Nature Photonics, 2011, 5(7):406-410. doi: 10.1038/nphoton.2011.99 [8] LIU Hua-ping, NISHIDE D, TANAKA T, et al. Large-scale single-chirality separation of single-wall carbon nanotubes by simple gel chromatography[J]. Nature Communications, 2011, 2(5):309-1-309-8. http://www.nature.com/ncomms/foxtrot/svc/authoremailform?doi=10.1038/ncomms1313&file=/ncomms/journal/v2/n5/full/ncomms1313.html&title=Large-scale+single-chirality+separation+of+single-wall+carbon+nanotubes+by+simple+gel+chromatography&author=Hiromichi+Kataura [9] SHANG Qing-chao, WU Zhen-sen, QU Tan, et al. Analysis of the radiation force and torque exerted on a chiral sphere by a Gaussian beam[J]. Optics Express, 2013, 21(7):8677-8688. doi: 10.1364/OE.21.008677 [10] TKACHENKO G, BRASSELET E. Helicity-dependent three-dimensional optical trapping of chiral microparticles[J]. Natural Communication, 2014, 5(7):4491-1-4491-8. http://www.nature.com/ncomms/2014/140731/ncomms5491/fig_tab/ncomms5491_F5.html [11] AKYURTLU A, WERNER D H. BI-FDTD:a novel finite-difference time-domain formulation for modeling wave propagation in bi-isotropic media[J]. IEEE Trans Antennas and Propagation, 2004, 52(2):416-425. doi: 10.1109/TAP.2004.823956 [12] ZHENG Kui-song, MU Zong-min, LUO Huan, et al. Electromagnetic properties from moving dielectric in high speed with Lorentz-FDTD[J]. IEEE Antennas and Wireless Propagations Letters, 2016, 15(3):934-937. http://adsabs.harvard.edu/abs/2016IAWPL..15..934Z [13] PEREDA J A, GRANDE A, GONZÁLEZ O V et al. FDTD modeling of chiral media by using the mobius transformation technique[J]. IEEE Antennas and Wireless Propagation Letters, 2006, 5(3):327-330. https://www.infona.pl//resource/bwmeta1.element.ieee-art-000001665022 [14] WANG Mao-yan, LI Hai-long, DONG Yu-liang, et al. Propagation matrix method study on THz waves propagation in a dusty plasma sheath[J]. IEEE Trans Antennas Propagations and Propagation, 2016, 64(1):286-290. doi: 10.1109/TAP.2015.2496114 [15] 刘广东. Padé近似下模拟一般色散媒质的FDTD改进方案[J].电子科技大学学报, 2015, 44(6):845-850. http://manu50.magtech.com.cn/dzkjdx/CN/abstract/abstract189.shtml LIU Guang-dong. Simulation of general dispersive media in Padé approximation of the improved FDTD scheme[J]. Journal of University of Electronic Science and Technology of China, 2015, 44(6):845-850. http://manu50.magtech.com.cn/dzkjdx/CN/abstract/abstract189.shtml [16] 赖生建, 王秉中, 黄廷祝.共享内存系统中高效并行FDTD计算方案[J].电子科技大学学报, 2010, 39(5):680-683. http://manu50.magtech.com.cn/dzkjdx/CN/abstract/abstract1175.shtml LAI Sheng-jian, WANG Bing-zhong, HUANG Ting-zhu. Efficient parallel FDTD computing scheme in space shared memory system[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(5):680-683. http://manu50.magtech.com.cn/dzkjdx/CN/abstract/abstract1175.shtml [17] 刘瑜, 梁正, 杨梓强.混合并行技术在FDTD计算中的应用研究[J].电子科技大学学报, 2009, 38(2):222-226. http://manu50.magtech.com.cn/dzkjdx/CN/abstract/abstract860.shtml LIU Yu, LIANG Zheng, YANG Zi-qiang. Application of hybrid parallel technology in FDTD computing[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(2):222-226. http://manu50.magtech.com.cn/dzkjdx/CN/abstract/abstract860.shtml [18] ZAKHARIAN A R, MANSURIPUR M, MOLONEY J V. Radiation pressure and the distribution of electromagnetic force in dielectric media[J]. Optics Express, 2005, 13(7):2321-2336. doi: 10.1364/OPEX.13.002321 [19] DEMIR V, ELSHERBENI A Z, ARVAS E. FDTD formulation for dispersive chiral media using the Z transform method[J]. IEEE Trans Antennas and Propagation, 2005, 53(10):3374-3384. doi: 10.1109/TAP.2005.856328 [20] 葛德彪, 闫玉波.电磁波时域有限差分方法[M].第二版.西安:西安电子科技大学出版社, 2005. GE De-biao, YAN Yu-bo. Finite-difference time-domain method for electromagnetic waves[M]. 2nd Edition. Xi'an:Xidian University Press, 2005. [21] LINDELL V, SIHVOLA A H, TRETYAKOV S A, et al. Electromagnetic waves in chiral and bi-isotropic media[M]. Boston, USA:Artech House, 1994. [22] MANSURIPUR M, ZAKHARIAN A R. Maxwell's macroscopic equations, the energy-momentum postulates, and the Lorentz law of force[J]. Physical Review E, 2009, 79(2):026608-1-026608-11 doi: 10.1103/PhysRevE.79.026608 -


 ISSN
ISSN 




 下载:
下载: