-
对于精密传动系统,传动误差和侧隙是影响运动准确性的重要因素,而偏心是大周期传动误差和周期性侧隙的主要来源。由于齿轮传动中的偏心是不可避免的,因此研究考虑偏心作用下的齿轮传动误差有重要意义[1-4]。
目前在齿轮传动误差计算方法方面主要有几何解析法和啮合线增量法,如文献[5-6]采用几何学方法研究摆线轮的行星传动机构传动精度,但应用范围局限于摆线齿轮。文献[7]采用啮合线增量法等建立了多级传动误差耦合模型,研究了随机误差对行星齿轮传动误差的影响。文献[8-10]采用解析法计算分析了单偏心外啮合齿轮的传动误差。但在工程实际中,齿轮啮合副的两个齿轮通常均存在偏心误差。同时,传动误差啮合线增量计算法是一种近似计算方法,计算精度有限[11-12]。
本文采用精确的解析计算方法,建立存在双偏心的渐开线齿轮副传动误差解析计算模型,计算出双偏心齿轮的瞬时节点啮合轨迹,传动比误差和传动误差,应用RecurDyn软件验证了解析计算模型,并对啮合频率下的变负载动态传动误差进行仿真,建立了与理论传动误差的关系。同时针对已有偏心误差情况下,提出了齿轮偏心误差初始相位的优化配置方法,得到最小传动误差的初始相位调整方法,为精密传动系统的装配调整提供了理论指导。
-
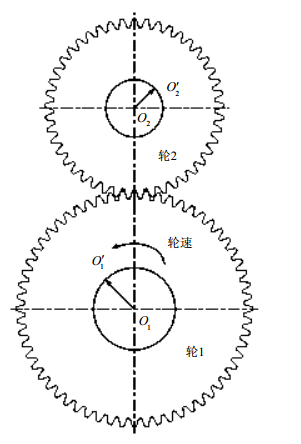
主动轮1和从动轮2为一对相啮合齿轮,如图 1所示。O1和O2分别为轮1、2的回转中心,O1′和O2′分别为轮1、2的基圆中心。在啮合过程中,O1′和O2′的轨迹分别是以O1和O2为圆心,偏心误差e1和e2为半径的圆。若O1′和O2′转动至O10和O20位置时,侧隙为零,P0为标准啮合时的节点,则O10P0和O20P0分别为轮1和轮2的分度圆半径R01和R02。
如图 2所示,O1′和O2′为任意位置,其中ψ1是轮1的任意时刻相对于初始时刻的转角,θ1是轮1初始时刻偏心e1与O1O2的夹角,ψ2是轮2的任意时刻相对于初始时刻的转角,θ2是轮2初始时刻偏心e2与O1O2的夹角。
在此瞬间,两齿轮基圆中心的连线为O1′O2′,两瞬时节圆的切点为P'。设PP'为此时两齿轮的瞬时啮合线,且与回转中心连线O1O2交于P点。
以轮2的旋转中心O2为原点,O1O2为y轴建立坐标系,基圆中心O1′的坐标(x1, y1)为:
$$ {x_1} =-{e_1}\sin ({\varphi _1} + {\theta _1}) $$ (1) $$ {y_1} =-{R_{02}}-{R_{01}}-{e_1} - {e_2} + {e_1}\cos ({\varphi _1} + {\theta _1}) $$ (2) 基圆中心O2′的坐标(x3, y3)为:
$$ {x_3} = {e_2}\sin ({\varphi _2} + {\theta _2}) $$ (3) $$ {y_3} = {e_2}\cos ({\varphi _2} + {\theta _2}) $$ (4) 瞬时节点P'的坐标(x2, y2)为:
$$ \begin{array}{c} {x_2} = {x_3}-\frac{{{R_{02}}}}{{{R_{02}} + {R_{01}}}}({x_3}-{x_1}) = \\ \frac{{{R_{01}}}}{{{R_{01}} + {R_{02}}}}{e_2}\sin ({\varphi _2} + {\theta _2})-\\ \frac{{{R_{02}}}}{{{R_{01}} + {R_{02}}}}{e_1}\sin ({\varphi _1} + {\theta _1}) \end{array} $$ (5) $$ \begin{array}{c} {y_2} = {y_3}- \frac{{{R_{02}}}}{{{R_{02}} + {R_{01}}}}({y_3}- {y_1}) = \\ \frac{{{R_{01}}}}{{{R_{01}} + {R_{02}}}}{e_2}\cos ({\varphi _2} + {\theta _2}) + \\ \frac{{{R_{02}}}}{{{R_{01}} + {R_{02}}}}[-{R_{02}}-{R_{01}}-{e_1} - {e_2} + {e_1}\cos ({\varphi _1} + {\theta _1})] \end{array} $$ (6) 以表 1中参数的为例,可描绘出具有双偏心的外啮合齿轮的瞬时节点轨迹如图 3所示。
表 1 偏心啮合齿轮副参数
偏心齿轮 半径/mm 偏心量/mm 转速/rad·s-1 初始相位/rad 压力角/(°) 轮1 60 0.04 π/3 7π/18 20 轮2 45 0.05 π/3 11π/18 20 由双偏心齿轮瞬时节点轨迹公式和图形可以看出,其轨迹由偏心值和半径决定而与齿轮转速无关,转速决定图形轨迹上的点的运动快慢。同时,由于偏心的影响,外啮合副齿轮的节点不再是一个固定的点,而是以原理想节点为中心,在其周围以一定的周期规律不停的波动。
-
在任意时刻时,齿轮啮合副的瞬时传动比为:
$$ {i'_{21}}{\rm{ = }}\frac{{{{R'}_1}}}{{{{R'}_2}}} $$ (7) 理论传动比为:
$$ {i_{21}}{\rm{ = }}\frac{{{R_{01}}}}{{{R_{02}}}} $$ (8) 传动比误差为:
$$ \begin{array}{c} \Delta {i_{21}}{\rm{ = }}\frac{{{{R'}_1}}}{{{{R'}_2}}}-\frac{{{R_{01}}}}{{{R_{02}}}} = \\ \frac{{{R_{02}} + {R_{01}} + {e_1} + {e_2}}}{{{{R'}_2}}}-\frac{{{R_{02}} + {R_{01}}}}{{{R_{02}}}} \end{array} $$ (9) 设线段O1′O2′的斜率为K1,PP'的斜率为K2,则:
$$ {K_1} = \frac{{{y_3}-{y_1}}}{{{x_3}-{x_1}}} $$ (10) $$ {K_2} = \frac{{1 + \tan \alpha {K_1}}}{{\tan \alpha-{K_1}}} $$ (11) 设$\lambda = \frac{{{R_{02}} + {R_{01}}}}{{{R_{02}}}}$,得P点的纵坐标y为:
$$ \begin{array}{c} y = {y_2}- {K_2}{x_2} = \\ \frac{1}{\lambda }[-y_1^2-(\lambda-2){y_1}{y_3} - \lambda {y_1}{x_3}\tan \alpha - \\ {x_1}^2 + \lambda {x_1}{y_3}\tan \alpha - (\lambda - 2){x_1}{x_3} + \\ (\lambda - 1)({x_3}^2 + {y_3}^2)]/[\tan \alpha ({x_1}-{x_3})-({y_1}-{y_3})] \end{array} $$ (12) 所以传动比误差为:
$$ \begin{array}{c} \Delta {i_{21}} = \frac{{{R_{02}} + {R_{01}} + {e_1} + {e_2}}}{{|y|}}-\frac{{{R_{02}} + {R_{01}}}}{{{R_{02}}}} = \\ \lambda \left\{ {\frac{{A + B + C}}{{{{(D-E)}^2} + F}}} \right\} \end{array} $$ (13) 式中,
$$ \begin{array}{c} A = [{R_{02}} + {R_{01}} + {e_1} + {e_2}-\\ {e_1}\cos ({\varphi _1} + {\theta _1})]{e_1}\cos ({\varphi _1} + {\theta _1}) - \\ [{R_{02}} + {R_{01}} + {e_1} + {e_2}-\\ {e_1}\cos ({\varphi _1} + {\theta _1})]{e_1}\sin ({\varphi _1} + {\theta _1})\tan \alpha \\ B = (\lambda - 1)[{R_{02}} + {R_{01}} + {e_1} + {e_2}-\\ {e_1}\cos ({\varphi _1} + {\theta _1})]{e_2}\cos ({\varphi _2} + {\theta _2}) + \\ [{R_{02}} + {R_{01}} + {e_1} + {e_2}-\\ {e_1}\cos ({\varphi _1} + {\theta _1})]{e_2}\sin ({\varphi _2} + {\theta _2})\tan \alpha \} \\ C = (\lambda -1){e_2}^2 + (\lambda -2){e_1}\sin ({\varphi _1} + {\theta _1}){e_2}\sin ({\varphi _2} + {\theta _2}) -\\ \lambda {e_1}\sin ({\varphi _1} + {\theta _1}){e_2}\cos ({\varphi _2} + {\theta _2})\tan \alpha - \\ {({e_1}\sin ({\varphi _1} + {\theta _1}))^2} + {e_1}\cos ({\varphi _1} + {\theta _1})\cos ({\varphi _2} + {\theta _2}) - \\ {e_1}\cos ({\varphi _1} + {\theta _1}){e_2}\sin ({\varphi _2} + {\theta _2})\tan \alpha - \\ {e_1}\cos ({\varphi _1} + {\theta _1}){e_1}\sin ({\varphi _1} + {\theta _1})\tan \alpha \\ D = {R_{02}} + {R_{01}} + {e_1} + {e_2} - {e_1}\cos ({\varphi _1} + {\theta _1})\\ E = \frac{{(\lambda - 2){e_2}\cos ({\varphi _2} + {\theta _2}) + \lambda {e_2}\sin ({\varphi _2} + {\theta _2})\tan \alpha }}{2}\\ F = {\left( {\frac{{(\lambda - 2){e_2}\cos {\varphi _2} + \lambda {e_2}\sin {\varphi _2}\tan \alpha }}{2}} \right)^2} - \\ (\lambda - 1){e_2}^2 - (\lambda - 2){e_1}\sin ({\varphi _1} + {\theta _1}){e_2}\sin ({\varphi _2} + {\theta _2}) + \\ \lambda {e_1}\sin ({\varphi _1} + {\theta _1}){e_2}\cos ({\varphi _2} + {\theta _2})\tan \alpha + \\ {({e_1}\sin ({\varphi _1} + {\theta _1}))^2} \end{array} $$ 由于${R_{01}}, {R_{02}} > > {e_1}, {e_2}$,所以将传动比误差简化为:
$$ \begin{array}{c} \Delta {i_{21}} \approx \lambda \frac{A}{{{D^2}}} + \lambda \frac{B}{{{D^2}}} \approx \\ \frac{{\cos ({\varphi _1} + {\theta _1} + \alpha )}}{{{R_{02}}\cos \alpha }} + \frac{{{R_{01}}}}{{{R_{02}}}}\frac{{\cos ({\varphi _2} + {\theta _2}-\alpha )}}{{{R_{02}}\cos \alpha }} \end{array} $$ (14) 以表 1的参数为例,代入上式方程,可得双齿轮偏心齿轮传动比误差曲线与简化后的曲线对比图 4。从图中可知,简化后的传动比误差与未简化的传动比误差几乎完全重合,两曲线差值的范围约在10-6内波动,与传动比误差本身差两个数量级,所以在一般情况下,计算传动误差时可采用简化后传动比误差公式。
-
一对相啮合的齿轮的理想传动比为:
$$ {i_{21}}{\rm{ = }}\frac{{{\rm{d}}{\varphi _2}}}{{{\rm{d}}{\varphi _1}}} $$ (15) 而实际传动比为:
$$ {i'_{21}}{\rm{ = }}\frac{{{\rm{d}}{{\varphi '}_2}}}{{{\rm{d}}{{\varphi '}_1}}} $$ (16) 式中,${\varphi _1}$是轮1的实际转角;${\varphi _2}$是轮2的理想转角;${\varphi '_2}$是轮2的实际转角。
所以传动比误差为:
$$ \Delta {i_{21}}{\rm{ = }}{i_{21}}-{i_{21}}{\rm{ = }}\frac{{{\rm{d}}{{\varphi '}_2}}}{{{\rm{d}}{\varphi _1}}}-\frac{{{\rm{d}}{\varphi _2}}}{{{\rm{d}}{\varphi _1}}} = \frac{{{\rm{d}}{{\varphi '}_2}-{\rm{d}}{\varphi _2}}}{{{\rm{d}}{\varphi _1}}} $$ (17) 因此轮2的转角误差为:
$$ \Delta {\varphi _2} = \int_{{\rm{ }}0}^{{\rm{ }}{\varphi _1}} {\Delta {i_{21}}} {\rm{d}}{\varphi _1} $$ (18) 在精密传动中,将上节所求得的精确传动比误差公式代入并通过计算机辅助积分即可得到理论精确的传动误差结果,如图 5所示。
在精度要求不是很高的情况下,为方便计算,本文将简化的传动比误差公式代入上式,可得到如下简化的传动误差公式:
$$ \begin{array}{c} \Delta {\varphi _2} = \int_{{\rm{ }}0}^{{\rm{ }}{\varphi _1}} {\Delta {i_{21}}} {\rm{d}}{\varphi _1} = \\ \frac{{{e_1}}}{{{R_{02}}\cos \alpha }}[{\rm{sin}}({\varphi _1} + {\theta _1} + \alpha )-{\rm{sin}}({\theta _1} + \alpha )] + \\ \frac{{{e_2}}}{{{R_{02}}\cos \alpha }}[{\rm{sin}}({\varphi _2} + {\theta _2}-\alpha )-{\rm{sin}}({\theta _2}-\alpha )] \end{array} $$ (19) 由所求得的简化的双偏心齿轮副传动误差公式可知,与啮合线向量法所求的结果一致,传动误差是两正弦函数和常数项构成的周期函数,幅值分别由主从轮的偏心值决定,频率分别是主从动轮的转频。由于外啮合副齿轮的从动轮转动方向与主动轮转动方向不同,所以双偏心齿轮传动误差计算中,不能将单偏心齿轮时计算所得传动误差直接简单叠加。
以表 1齿轮参数为例,代入上述传动误差公式,精确的传动误差和简化的传动误差对比如下:
从图中可知,简化后的传动误差与未简化的传动误差几乎完全重合,两曲线差值的范围约-6"~+1"内波动,与传动误差本身差1个数量级,所以在一般情况下,计算传动误差时可采用可简化后传动误差公式。
-
RecurDyn作为多体动力学分析软件,可以对齿轮的接触进行良好分析[13-15]。以图 1理论模型和表 1参数建立双偏心齿轮传动实体模型,如图 6所示,并对两偏心齿轮施加约束,设置接触参数以及添加驱动并设置驱动参数, 设定负载为恒定值。最后仿真曲线和理论曲线对比如图 7所示。
通过RecurDyn仿真的传动误差曲线与理论解析传动误差曲线对比可知,两曲线吻合良好,其中最大相差值占理论传动误差值的2.508 9%,并通过MALAB软件用理论公式拟合仿真数据曲线,决定系数高达0.991 6,从而验证了理论公式的正确性。仿真传动误差曲线相比理论传动误差曲线有一定微小量的向下偏移,是因为在仿真过程中,齿轮具有一定刚度、施加了一定的负载,且必须设置一定的穿透量。而刚度、负载和穿透量等因素相当于使齿轮在初始传动时有一定的微小侧隙,因此仿真的曲线整体向下微量偏移。
-
在实际工况下,负载为恒定值的情况非常少。因此,在上述仿真验证的基础上将RecurDyn中的恒定负载重新设定为啮合频率的变负载。在变负载的驱动下,从动轮将在齿隙间以负载变动的频率波动,仿真曲线如图 8所示。图中,动态传动误差的下轮廓线与理论传动误差重合,上轮廓线与理论传动误差叠加间隙曲线重合。可见,随着间隙量增大,动态传动误差与静态传动误差差值增大,因此间隙越大,动态冲击越大。
-
由于加工误差和装配误差的存在,齿轮偏心无可避免。但通过传动误差公式可以看出,在既定的偏心值下,调整偏心的初始相位,传动误差最值呈正弦函数变化。所以,为了尽可能减少偏心对传动误差的影响,调整齿轮偏心的初始相位非常有必要。
将传动误差公式分别对θ1和θ2求偏导:
$$ \begin{array}{c} \frac{{\partial \Delta {\varphi _2}}}{{\partial {\theta _1}}} = \\ \frac{\partial }{{\partial {\theta _1}}}\left\{ {\frac{{{e_1}}}{{{R_{02}}\cos \alpha }}} \right.[{\rm{sin}}({\varphi _1} + {\theta _1} + \alpha )-{\rm{sin}}({\theta _1} + \alpha )] + \\ \left. {\frac{{{e_2}}}{{{R_{02}}\cos \alpha }}[{\rm{sin}}({\varphi _2} + {\theta _2}-\alpha )-{\rm{sin}}({\theta _2}-\alpha )]} \right\} = 0\\ \frac{{\partial \Delta {\varphi _2}}}{{\partial {\theta _2}}} = \\ \frac{\partial }{{\partial {\theta _2}}}\left\{ {\frac{{{e_1}}}{{{R_{02}}\cos \alpha }}} \right.[{\rm{sin}}({\varphi _1} + {\theta _1} + \alpha )-{\rm{sin}}({\theta _1} + \alpha )] + \\ \left. {\frac{{{e_2}}}{{{R_{02}}\cos \alpha }}[{\rm{sin}}({\varphi _2} + {\theta _2}-\alpha )-{\rm{sin}}({\theta _2}-\alpha )]} \right\} = 0 \end{array} $$ 可得:
$$ {\theta _1}{\rm{ = }}-\alpha + n\pi, {\rm{ }}{\theta _2}{\rm{ = }}\alpha + n\pi $$ 传动误差值最小。
图 9为表 1数据的初始相位改变前后传动误差的对比。初始相位优化后,传动误差的最大幅值从-14分降低到最大幅值为6'左右,优化效果明显。
-
本文在考虑一对啮合的齿轮均有偏心的基础上,建立传动误差计算模型,用解析法推导了瞬时节点轨迹、传动比误差和传动误差公式,结果表明传动误差是两正弦函数和常数项构成的周期函数,幅值分别与主从轮的偏心值成正比,频率分别是主从动轮的转频。在外啮合齿轮副中,其传动误差并非分别两个单偏心齿轮时计算所得传动误差的直接简单叠加,其中的压力角相位主动轮为正,从动轮为负。通过与RecurDyn仿真传动误差曲线对比,两种方法推导的传动误差公式一致,验证了解析算法的正确性,并根据实际工况,在啮合频率变负载动态传动误差仿真的基础上,建立了与理论传动误差曲线的关系。最后在考虑齿轮几何偏心不变的情况下,分析初始相位对传动误差的影响,并给出了最佳初始相位,结果表明通过初始相位优化后,齿轮传动误差可以明显改善。
Research on Transmission Error of Dual-eccentric Gears
-
摘要: 采用解析法推导了存在双偏心误差的渐开线齿轮副的传动误差计算公式,建立了其传动误差解析计算模型,同时分析了齿轮副的瞬时节点、传动比误差以及传动误差之间的等价关系;应用RecurDyn软件验证了传动误差计算模型;在啮合频率变负载的动态传动误差仿真的基础上,建立了与理论计算的传动误差及其侧隙值间的关系;在此基础上,针对已有偏心误差情况下,提出齿轮偏心误差初始相位的优化配置方法,得到最小传动误差,为精密传动设备的装配调整提供理论指导。Abstract: A transmission error analytical mothed of dual-eccentric gears is proposed. The relation among instantaneous node, transmission ratio error, and transmission error is deduced. In order to demonstrate the validity of the analytical method, the solid model is constructed in the dynamics simulation software RecurDyn and the simulation transmission error is obtained. By comparison, the simulation transmission error curve agrees well with the analytical one. On this basis, dynamic transmission error under meshing frequency varying load is explored and the relation between dynamic transmission error, the theoretical transmission error and backlash is studied simultaneously. Finally, the optimum initial phase has been given to decrease the transmission error under the circumstance of fixed eccentricity
-
Key words:
- analytical method /
- eccentricity /
- RecurDyn /
- transmission error
-
表 1 偏心啮合齿轮副参数
偏心齿轮 半径/mm 偏心量/mm 转速/rad·s-1 初始相位/rad 压力角/(°) 轮1 60 0.04 π/3 7π/18 20 轮2 45 0.05 π/3 11π/18 20 -
[1] BRUYÈRE J, GU X, VELEX P H. On the analytical definition of profile modifications minimising transmission error variations in narrow-faced spur helical gears[J]. Mechanism and Machine Theory, 2015, 92:257-272. doi: 10.1016/j.mechmachtheory.2015.06.001 [2] JIANG Jin-ke, FANG Zong-de. Design and analysis of modified cylindrical gears with a higher-order transmission error[J]. Mechanism and Machine Theory, 2015, 88:141-152. doi: 10.1016/j.mechmachtheory.2015.02.006 [3] 王家序.滤波齿轮传动误差计算及分析[J].机械科学与技术, 2009, 28(11):1456-1459. doi: 10.3321/j.issn:1003-8728.2009.11.013 WANG Jia-xu. Calculation and analysis of filtering gear transmission error[J]. Mechanical Science and Technology, 2009, 28(11):1456-1459. doi: 10.3321/j.issn:1003-8728.2009.11.013 [4] 单丽君, 关天民.摆线针轮行星传动动态理论回转误差的计算与分析[J].机械传动, 2002, 26(2):29-31. http://www.cqvip.com/QK/92228A/200202/6530302.html SHAN Li-jun, GUAN Tian-min. Calculation and analysis of cycloid pin gear planetary gear dynamic theory[J]. Mechanical Transmission, 2002, 26(2):29-31. http://www.cqvip.com/QK/92228A/200202/6530302.html [5] BLANCHE J G, YANG D C H. Cycloid drives with machining tolerances[J]. Journal of Mechanisms, Transmissions, and Automation in Design, 1989, 111(9):337-344. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=JMTDDK000111000003000337000001&idtype=cvips&gifs=Yes [6] YANG D C H, BLANCHE J G. Design and application guidelines for cycloid drives with machining tolerances[J]. Mechanism and Machine Theory, 1990, 25(5):487-501. doi: 10.1016/0094-114X(90)90064-Q [7] 王朝兵.误差随机性对行星齿轮系统传动精度的影响特性[J].重庆大学学报, 2012, 35(9):41-47. doi: 10.11835/j.issn.1000-582X.2012.09.007 WANG Chao-bing. Random error of planetary gear transmission accuracy of the system characteristics[J]. Journal of Chongqing University, 2012, 35(9):41-47. doi: 10.11835/j.issn.1000-582X.2012.09.007 [8] 吴慈生.齿轮偏心误差所引起的传动误差[J].南京工学院学报, 1982(4):133-145. http://www.cqvip.com/QK/92228A/200003/4595896.html WU Ci-sheng. Research on transmission error by eccentric gear[J]. Journal of Nanjing Institute of Technology, 1982(4):133-145. http://www.cqvip.com/QK/92228A/200003/4595896.html [9] 韦杰, 侯秀菊.齿轮偏心误差所产生的传动比误差[J].本溪冶金高等专科学校学报, 2001, 3(2):29-32. http://www.cnki.com.cn/Article/CJFDTotal-GXJX201402058.htm WEI Jie, HOU Xiu-ju. Error in transmitting ratio caused by error in gear eccentricity[J]. Journal of Benxi College of Metallurgy, 2001, 3(2):29-32. http://www.cnki.com.cn/Article/CJFDTotal-GXJX201402058.htm [10] 张义正.齿轮偏心误差对空回的影响[J].长春光学精密机械学院学报, 1989, 12(2):70-73. http://www.irgrid.ac.cn/handle/1471x/603580 ZHANG Yi-zheng. Effects of gear eccentric error on backlash[J]. Journal of Changchun Institute of Optics and Fine Mechanics, 1989, 12(2):70-73. http://www.irgrid.ac.cn/handle/1471x/603580 [11] 柏永新.渐开线圆柱齿轮精度[M].西安:陕西科学技术出版社, 1988. BO Yong-xin. The accuracy of involute cylindrical gear[M]. Xi'an:Shanxi Science and Technology Press, 1988. [12] 张洁. RV减速器传动特性分析[D]. 天津: 天津大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10056-1013039820.htm ZHANG Jie. Analysis on the transmission characteristic of RV reducer[D]. Tianjin:Tianjin University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10056-1013039820.htm [13] 陆扬, 马星国, 舒启林.基于RecurDyn的行星轮系动力学仿真[J].沈阳理工大学学报, 2008, 27(4):76-79. http://www.cnki.com.cn/Article/CJFDTOTAL-LZGD201205009.htm LU Yang, MA Xing-guo, SHU Qi-lin. Dynamic simulation of planetary gear system based on recurdyn[J]. Transactions of Shenyang Ligong University, 2008, 27(4):76-79. http://www.cnki.com.cn/Article/CJFDTOTAL-LZGD201205009.htm [14] 周孔亢, 陆建辉, 侯永涛, 等.基于RecurDyn的钢板弹簧动力学模型的建立与参数辨识[J].机械工程学报, 2014, 50(4):128-134. http://www.cqvip.com/QK/90288X/201404/48989247.html ZHOU Kong-kang, LU Jian-hui, HOU Yong-tao, et al. Dynamics modeling and parameter identification of leaf spring based on recurdyn[J]. Journal of Mechanical Engineering, 2014, 50(4):128-134. http://www.cqvip.com/QK/90288X/201404/48989247.html [15] 李波, 张承宁, 李军求.基于RecurDyn和Simulink的电传动车辆转矩控制策略[J].农业机械学报, 2009, 40(7):1-5. http://www.cqvip.com/qk/90304X/200907/31185218.html LI Bo, ZHANG Cheng-ning, LI Jun-qiu. Torque control strategies base on recurdyn and simulink for electric drive tracked vehicle[J]. Transaction of the Chinese Society for Agricultural Machinery, 2009, 40(7):1-5. http://www.cqvip.com/qk/90304X/200907/31185218.html -


 ISSN
ISSN 




 下载:
下载: