-
传统PID控制、LQR控制(linear quadratic regulator)、模糊控制(fuzzy control)等控制策略多以车距控制作为主要目标,即重点考虑安全性而相对弱化舒适性等需求[1]。近年来,由于MPC模型预测控制采用预测模型、滚动在线优化以及反馈校正机制,具备同时兼顾系统I/O约束与过程状态约束,动态协调巡航过程中的多个控制目标等优势,使控制效果与鲁棒性皆能明显改善而被广泛应用[1]。
为了满足熟练驾驶群体的日常跟驰习惯,以及增强ACC(adaptive cruise control)系统对道路交通的良好适应性,多模式设计将有利于改善驾乘人员对量产ACC的接受度[2-5]。文献[2]将行车工况划分为巡航工况、跟随工况,并基于车距与相对车速的相位图确定出速度控制模式与间距控制模式的切换曲线。文献[3]根据期望加速度的幅值将跟随工况划分为:舒适、强减速、紧急制动,并利用混淆矩阵来确定模式切换逻辑。文献[4]根据跟车时距与碰撞时间(time to collision, TTC)倒数的相位图把跟随工况划分为:稳态跟随区、接近区、急加速区、强减速区、避撞区,并利用经验型TTC倒数来实现模式切换。文献[5]根据期望加速度幅值把跟随工况分为:稳态跟随、瞬态跟随(舒适跟随、安全跟随、紧急跟随),并通过受试驾驶群体的跟驰行为特性参数分布来界定过渡区域。
鉴于驾驶意图的主观性、不确定性,以及模式切换规则的模糊性、经验性,而模糊推理(fuzzy inference)在处理经验型模型决策问题上能够较好模拟人类思维方式[6]。基于此,本文发展了一种多目标自适应巡航控制算法,基于MPC模型预测控制理论,综合协调巡航过程中驾驶员期望响应、跟驰安全性、车辆自身物理限制等控制目标,同时采用模糊推理与加速度加权平均策略以实现工作模式最佳匹配与平稳过渡。
-
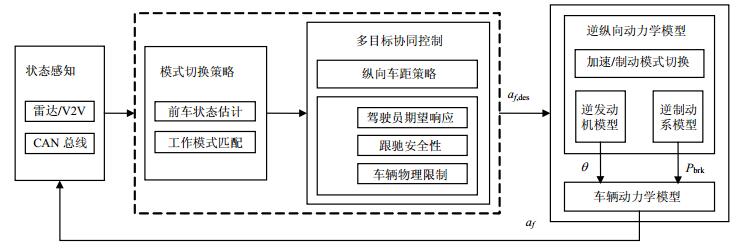
为实现多模式控制,应用有限状态机(finite state machine, FSM)原理,于决策层中增加模式切换部分,匹配当前最佳工作模式以提高ACC系统对道路交通的适应能力。多模式ACC分层化系统设计如图 1所示。
-
为平衡模式切换的逻辑复杂度与ACC系统对道路交通的适应能力,需合理定义纵向相对运动状态,本文设计的典型工况如图 2所示。工程上可用雷达技术[5]、V2V技术[7]对各工况予以辨识。
-
不同工况下,驾驶员期望响应不同,从而控制器的待优化目标、控制输入、约束条件不同。急加速工况下,对车距误差的合理约束,既可保证跟驰安全性,亦可避免邻道车辆的频繁切入,同时亦需兼顾对加速度与加速度变化率的限制以追求一定的驾乘舒适性、燃油经济性[8];而随着工况紧急程度的增加,对加速度与加速度变化率的约束变宽,而对车距误差与相对车速的约束变窄,即相对弱化舒适性与经济性而对安全性要求变严[5]。
因而,采用待优化目标与控制输入权重调校以及控制器工作域边界松弛的策略,将ACC系统划分出6种工作模式:定速巡航模式、稳态跟随模式、瞬态急加速模式、瞬态浅制动模式、瞬态深制动模式、瞬态紧急制动模式。
文献[9]给出稳态工况的评估方法:车辆加速度$a \in [ - 0.6, \;0.6] $ m/s2。基于此,本文的工况划分规则与相应工作模式如表 1所示。
表 1 典型工况划分与ACC工作模式
典型工况 前车加速度 ACC工作模式 定速巡航工况 — 定速巡航模式 稳态跟随工况 [-0.6, 0.6] 稳态跟随模式 瞬态急加速工况 (0.6, +∞) 瞬态急加速模式 瞬态浅制动工况 (-2, -0.6) 瞬态浅制动模式 瞬态深制动工况 (-4, -2] 瞬态深制动模式 瞬态紧急制动工况 (-∞, -4] 瞬态紧急制动模式 -
ACC系统的工作模式切换逻辑具有模糊性、经验性,故采用模糊推理来进行模式决策。建立两输入单输出的模糊推理机,选取车距误差Δd、相对车速Δv作为模糊推理机的输入,自车期望加速度${a_{f, {\rm{des}}}}$作为模糊推理机的输出。
1) 模糊化
定义描述输入的模糊集合皆为{负大,负中,零,正中,正大},描述输出的模糊集合为{---,--,-,0,+,++},且输入输出的模糊隶属度函数如图 3所示。
2) 知识库
基于驾驶群体跟驰行为习惯[10],建立模糊规则如表 2所示。
表 2 模糊规则表
Δv Δd 负大 负中 零 正中 正大 负大 --- -- - 0 + 负中 -- -- - + + 零 -- - 0 + ++ 正中 - - + ++ ++ 正大 - 0 + ++ ++ 3) 模糊决策
推理规则如下:
R1 : IF x is A1 and y is B1,THEN z is C1;
R2 : IF x is A2 and y is B2,THEN z is C2;
…
Rn : IF x is An and y is Bn,THEN z is Cn ;
先验知识:
x is A and y is B
推论结果:
$$ \begin{array}{c} C\;\; = \;\;(A\;\;\;{\rm{and}}\;\;\;B){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \circ {\kern 1pt} {\kern 1pt} {\kern 1pt} {R^ * }\\ {R^ * }\;\; = \;\;\bigcup\limits_{i = 1}^n {{R_i}} \\ {R_i}\; = \;\;({A_i}\;\;\;{\rm{and}}\;\;\;{B_i}) \to {C_i} \end{array} $$ 推理过程采用Larsen最大-乘积法,根据采样输入的模糊量与模糊规则进行判别决策。
4) 清晰化
由于模糊决策的推论结果是模糊集合,故需对输出进行清晰化处理,亦即反模糊化。常用的清晰化处理方法有:最大隶属度法、中位数法以及质心法。这里,清晰化处理选取质心法,即有:
$${z^*} = \frac{{\sum\limits_{z \in \mathit{\boldsymbol{{ Z}}}} {u(z){\kern 1pt} {\kern 1pt} z} }}{{\sum\limits_{z \in \mathit{\boldsymbol{{ Z}}}} {u(z)} }}$$ (1) 式中,z为论域元;u(z)反映z对模糊集合的隶属度分布情况;${z^*}$为清晰化值。
-
考虑到工作模式切换过程中容易出现加速度突变、频繁切换等系列问题,本文给出一种平稳过渡的参考设计,如图 4所示。
为了解决过渡区域加速度突变问题,采用加权平均处理方法以降低驾乘人员的敏感度。同时,为避免模式切换频繁,预设新模式连续判定阈值以防频繁切换带来的执行器物理磨损等切换开销。从而该策略下执行系的期望控制输入满足以下条件:
$$ {u^*} = \left\{ {\begin{array}{*{20}{l}} {{\omega _i}{\kern 1pt} u_i^*{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} }&{\;N \in [0, {N_1})}\\ {{\omega _i}{\kern 1pt} u_i^*{\kern 1pt} {\kern 1pt} + {\omega _j}{\kern 1pt} u_j^*}&{\;N \in [{N_1}, {N_2}]}\\ {{\omega _j}{\kern 1pt} u_j^*}&{\;N \in ({N_2}, \infty )} \end{array}} \right. $$ (2) 式中,$u_i^*{\kern 1pt} {\kern 1pt} {\kern 1pt} $、$u_j^*{\kern 1pt} $分别为当前工作模式i、新工作模式j的控制输入;${\rm{ }}{u^*} $为加权平均处理后的控制输入;$ {\omega _i}$、${\omega _j}\; $为相应模式的权重系数。
-
在ACC分层化设计中,上层是针对驾驶行为的决策,下层是针对执行系(油门、制动、档位)的控制。ACC纵向运动学关系如图 5所示。
期望车距采用固定时距(constant time headway, CTH)策略[11],即有:
$$ {d_{{\rm{des}}}} = ({\tau _h}{v_f} + {d_0}) $$ (3) 式中,${\tau _h} $为预设时距;${v_f}$为自车速度;$ {d_0}$为零速度车距。
由自车与前车纵向运动学特性、执行系的理想一阶惯性环节假设,建立离散时域关系为:
$$ \left\{ \begin{array}{l} \, \Delta d(k + 1) = \, \Delta d(k) + [\, \Delta v(k) - {\tau _h}{a_f}(k)]{T_s}\\ \, \, \Delta v(k + 1) = \, \Delta v(k) + [{a_p}(k) - {a_f}(k)]{T_s}\\ \, {a_f}(k + 1) = \left( {1 - \frac{{{T_s}}}{{{T_L}}}} \right){a_f}(k) + \frac{{{K_L}{T_s}}}{{{T_L}}}u(k)\\ \, j(k + 1) = \frac{{{K_L}}}{{{T_L}}}u(k) - \frac{1}{{{T_L}}}{a_f}(k) \end{array} \right. $$ (4) 式中,$\Delta d = d - {d_{{\rm{des}}}}$为车距误差;d为实际车距;${d_{{\rm{des}}}}$为期望车距;$\Delta v = {v_p} - {v_f}$为相对车速;${a_f}$为自车加速度;$ j = {\dot a_f}$为自车冲击度;${a_p}$为前车加速度;u为执行系输入;${K_L}$、${T_L}$分别为一阶惯性系统增益与时滞;${T_s} $为采样周期。
令$ \mathit{\boldsymbol{x}}(k) = {[\Delta d(k), \, \, \Delta v(k), \, \, {a_f}(k), \, \, j(k)]^{\rm{T}}}$,以$ \mathit{\boldsymbol{x}}(k)$作为状态向量,${a_p}(k) $作为系统扰动,$u(k) $作为控制输入,$\mathit{\boldsymbol{y}}(k) $作为系统输出,由式(4)可得ACC纵向运动学模型为:
$$ \mathit{\boldsymbol{x}}(k + 1|k) = \mathit{\boldsymbol{Ax}}(k) + \mathit{\boldsymbol{B}}u(k) + \mathit{\boldsymbol{G}}\varphi (k) $$ (5) 式中,$u(k) = {a_{f, {\rm{des}}}}(k) $;$\varphi (k) = {a_p}(k) $各系数矩阵满足:
$$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{{T_s}}&{ - {\tau _h}{T_s}}&0\\ 0&1&{ - {T_s}}&0\\ 0&0&{1 - {T_s}/{T_L}}&0\\ 0&0&{ - 1/{T_L}}&0 \end{array}} \right] $$ $$ \mathit{\boldsymbol{B}} = {\left[ {0, \, \, 0, \, \, {T_s}{K_L}/{T_L}, \, \, {K_L}/{T_L}} \right]^{\rm{T}}} $$ $$ \mathit{\boldsymbol{G}} = {\left[ {0, \, \, {T_s}, \, \, 0, \, \, 0} \right]^{\rm{T}}} $$ -
1) 驾驶员期望响应
关于追踪能力[12],当实际车距过小时会造成驾乘人员心理紧张不适,亦增加了追尾碰撞的潜在可能性,而当实际车距过大时不仅会降低道路容积率与吞吐量[13-14],还可能会诱发邻道车辆超车并线或变道强插等不文明事件,从而待优化目标为:
$$ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {\Delta d} \end{array}\;\; \to \;\;0\\ \begin{array}{*{20}{c}} {\Delta v} \end{array}\;\; \to \;\;0 \end{array} \right. $$ (6) 式中,$\Delta d$为车距误差;$\Delta v$为相对车速。
关于舒适体验[11],文献[3]通过对大量受试驾驶群体的调研分析得出结论,车辆加速度与加速度变化率幅值越小,驾乘舒适度越高,从而待优化目标为:
$$ \left\{ \begin{array}{l} {\rm{min}}\;\left| {{a_f}} \right|\\ {\rm{min}}\;\left| j \right| \end{array} \right. $$ (7) 式中,${a_f} $为自车加速度;j为加速度变化率,亦即自车冲击度。
关于燃油经济[15],亦可由式(7)来间接表征。
2) 跟驰安全性
ACC系统对安全性必须严格约束:
$$ d \ge {d_{{\rm{safe}}}} = \max \{ {t_{{\rm{TTC}}}}\Delta v, {d_s}\} $$ (8) 式中,碰撞时间${t_{{\rm{TTC}}}} $用于表示制动过程的安全性[11];d为实际车距;${d_{{\rm{safe}}}} $为安全跟车车距;$ {d_s}$为极限安全车距。
3) 车辆自身物理限制
除了对跟驰安全硬约束外,考虑到车辆自身物理限制,需对由控制输入、系统状态参数所构成的控制器工作域进行边界约束,即有:
$$\left\{ \begin{array}{l} {u_{{\rm{min}}}} \le u \le {u_{{\rm{max}}}}\\ \Delta {d_{{\rm{min}}}} \le \Delta d \le \Delta {d_{{\rm{max}}}}\\ \Delta {v_{{\rm{min}}}} \le \Delta v \le \Delta {v_{{\rm{max}}}}\\ {a_{f, {\rm{min}}}} \le {a_f} \le {a_{f, {\rm{max}}}}\\ {j_{{\rm{min}}}} \le j \le {j_{{\rm{max}}}} \end{array} \right.$$ (9) 综上,建立ACC系统待优化目标向量为:
$$ \mathit{\boldsymbol{y}}(k) = \mathit{\boldsymbol{Cx}}(k) $$ (10) 式中,$\mathit{\boldsymbol{C}} = {\rm{diag}}(1, 1, 1, 1) $。
考虑到舒适性、经济性等驾驶员期望需求,ACC系统动态响应曲线宜平滑些,故引入指数衰减函数[16]作为待优化目标向量的加权项,得到目标参考轨迹:
$$ {\mathit{\boldsymbol{y}}_{ref}}(k + i) = {\mathit{\boldsymbol{\xi }}^i}\mathit{\boldsymbol{y}}(k)\;\;\;\;\;i \in \;[1, p] $$ (11) 式中,$\xi = {\rm{diag}}({\xi _{\Delta d}}\;, \;{\xi _{\Delta v}}\;, \;{\xi _a}\;, \;{\xi _j}) $,${\xi _{\Delta d}}\;、\;{\xi _{\Delta v}}\;、\;{\xi _a}\;、{\xi _j} $分别为待优化目标向量$\mathit{\boldsymbol{y}}(k) $中相应元素的权系数,取值范围皆为(0, 1)。
-
为了改进ACC纵向运动学模型,引入反馈校正机制以提高模型的预测精度与鲁棒性[1, 16]。将式(5)改写为:
$$ \mathit{\boldsymbol{x}}(k + 1|k) = \mathit{\boldsymbol{Ax}}(k) + \mathit{\boldsymbol{B}}u(k) + \mathit{\boldsymbol{G}}\varphi (k) + \mathit{\boldsymbol{{\rm M}e}}(k) $$ (12) 式中,$\mathit{\boldsymbol{{ M}}} = {\rm{diag}}({m_1}, {m_2}, {m_3}) $为校正矩阵;$\mathit{\boldsymbol{e}}(k) = $ $\mathit{\boldsymbol{x}}(k) - \mathit{\boldsymbol{x}}(k|k - 1)$为误差修正项;$\mathit{\boldsymbol{x}}(k)$为k时刻的实际状态;$\mathit{\boldsymbol{x}}(k|k - 1)$为k-1时刻对k时刻的预测状态。
联立式(10)、式(12),得到ACC纵向运动学模型递推预测的离散状态空间方程:
$$ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}(k + 1|k) = \mathit{\boldsymbol{Ax}}(k) + \mathit{\boldsymbol{B}}u(k) + \mathit{\boldsymbol{G}}\varphi (k) + \mathit{\boldsymbol{{\rm M}e}}(k)\\ \mathit{\boldsymbol{y}}(k) = \mathit{\boldsymbol{Cx}}(k) \end{array} \right. $$ (13) 式(13)的可控阵为$[\mathit{\boldsymbol{B}}, \, \, \mathit{\boldsymbol{AB}}, \, \, {\mathit{\boldsymbol{A}}^2}\mathit{\boldsymbol{B}}, \, \, {\mathit{\boldsymbol{A}}^3}\mathit{\boldsymbol{B}}] $,当可控阵满秩时系统可控,即体现控制输入$ u(k)$对状态向量$ \mathit{\boldsymbol{x}}(k)$的控制能力。可观阵为${[\mathit{\boldsymbol{C}}, \, \, \mathit{\boldsymbol{CA}}, \, \, \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^2}, \, \, \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^3}]^{\rm{T}}} $,当可观阵满秩时系统可观,即体现输出$ \mathit{\boldsymbol{y}}(k)$对状态向量$ \mathit{\boldsymbol{x}}(k)$的反映能力。
假设当前时刻为k,预测时域为[k,k+p-1],由式(13)逐步迭代整理得到p(p≥1)步预测的离散状态空间方程:
$$ \left\{ \begin{array}{l} \mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{A}}_p}\mathit{\boldsymbol{x}}(k) + {\mathit{\boldsymbol{B}}_p}\mathit{\boldsymbol{U}} + {\mathit{\boldsymbol{G}}_p}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} + {\mathit{\boldsymbol{M}}_p}\mathit{\boldsymbol{e}}(k)\\ \mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{C}}_p}\mathit{\boldsymbol{X}} \end{array} \right. $$ (14) 式中,$ \mathit{\boldsymbol{X}} = {[\mathit{\boldsymbol{x}}(k + 1), \, \mathit{\boldsymbol{x}}(k + 2), \, \, \cdots \, , \, \mathit{\boldsymbol{x}}(k + p)]^{\rm{T}}}$为预测时域的状态序列;$ \mathit{\boldsymbol{U}} = {[u(k), \, u(k + 1), \, \cdots \, , \, u(k + p - 1)]^{\rm{T}}}$为预测时域的控制序列;$\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = [\varphi (k), \, \varphi (k + 1), \, \cdots \, , \, $ $ \varphi (k + p - 1){]^{\rm{T}}}$为预测时域的扰动序列;$\mathit{\boldsymbol{Y}} $为系统输出序列,各系数矩阵满足:
$$ \begin{array}{c} {\mathit{\boldsymbol{A}}_p} = {\left[ {\mathit{\boldsymbol{A}}, \, {\mathit{\boldsymbol{A}}^2}, \, \cdots \, , {\mathit{\boldsymbol{A}}^p}} \right]^T}\\ {\mathit{\boldsymbol{B}}_p} = {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{B}}&{\bf{0}}& \cdots &{\bf{0}}\\ {\mathit{\boldsymbol{AB}}}&\mathit{\boldsymbol{B}}& \cdots &{\bf{0}}\\ \vdots & \vdots & \ddots & \vdots \\ {{\mathit{\boldsymbol{A}}^{p - 1}}\mathit{\boldsymbol{B}}}&{{\mathit{\boldsymbol{A}}^{p - 2}}\mathit{\boldsymbol{B}}}& \cdots &\mathit{\boldsymbol{B}} \end{array}} \right]_{4p \times p}}\\ {\mathit{\boldsymbol{G}}_p} = {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{G}}&{\bf{0}}& \cdots &{\bf{0}}\\ {\mathit{\boldsymbol{AG}}}&\mathit{\boldsymbol{G}}& \cdots &{\bf{0}}\\ \vdots & \vdots & \ddots & \vdots \\ {{\mathit{\boldsymbol{A}}^{p - 1}}\mathit{\boldsymbol{G}}}&{{\mathit{\boldsymbol{A}}^{p - 2}}\mathit{\boldsymbol{G}}}& \cdots &\mathit{\boldsymbol{G}} \end{array}} \right]_{4p \times p}}\\ {\mathit{\boldsymbol{M}}_p} = {\left[ {\mathit{\boldsymbol{M}}, \, \mathit{\boldsymbol{AM}}, \, \, \cdots \, , {\mathit{\boldsymbol{A}}^{p - 1}}\mathit{\boldsymbol{M}}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{C}}_p} = {\rm{diag}}(\mathit{\boldsymbol{C}}, \mathit{\boldsymbol{C}}, \cdots , \mathit{\boldsymbol{C}}) \end{array} $$ -
为满足巡航过程中驾驶员的期望响应,基于MPC框架对多目标进行协调控制,建立预测时域为[k,k+p-1]的p步滚动优化目标函数:
$$ J\, = \sum {{{(\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{y}}_{{\rm{ref}}}})}^{\rm{T}}}\mathit{\boldsymbol{Q}}\;(\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{y}}_{{\rm{ref}}}})} \; + \;\sum {{u^{\rm{T}}}R\;u} $$ (15) 式中,$ \mathit{\boldsymbol{Q}}{\rm{ = diag}}({\omega _{\Delta d}}\;, \;{\omega _{\Delta v}}\;, \;{\omega _a}\;, \;{\omega _j})$为状态权系数矩阵;R为控制输入权系数。
-
由于硬约束条件易致MPC滚动优化过程中无可行解问题,故引入松弛向量对硬约束条件进行松弛化,以扩展求解可行域[11]。
考虑到3.2节中跟驰安全性的硬性约束要求,故仅对式(9)进行松弛化处理:
$$ \left\{ \begin{array}{l} {u_{{\rm{\min}} }} + {\varepsilon _1}\upsilon _{{\rm{\min}} }^u \le u \le {u_{{\rm{\max}} }} + {\varepsilon _1}\upsilon _{{\rm{\max}} }^u\\ \Delta {d_{{\rm{\min}} }} + {\varepsilon _2}\upsilon _{{\rm{\min}} }^{\Delta d} \le \Delta d \le \Delta {d_{{\rm{\max}} }} + {\varepsilon _2}\upsilon _{{\rm{\max}} }^{\Delta d}\\ \Delta {v_{{\rm{\min}} }} + {\varepsilon _3}\upsilon _{{\rm{\min}} }^{\Delta v} \le \Delta v \le \Delta {v_{{\rm{\max}} }} + {\varepsilon _3}\upsilon _{{\rm{\max}} }^{\Delta v}\\ {a_{f, {\rm{\min}} }} + {\varepsilon _4}\upsilon _{{\rm{\min}} }^a \le {a_f} \le {a_{f, {\rm{\max}} }} + {\varepsilon _4}\upsilon _{{\rm{\max}} }^a\\ {j_{{\rm{\min}} }} + {\varepsilon _5}\upsilon _{{\rm{\min}} }^j \le j \le {j_{{\rm{\max}} }} + {\varepsilon _5}\upsilon _{{\rm{\max}} }^j \end{array} \right. $$ (16) 式中,松弛因子满足${\varepsilon _1} \ge 0$、${\varepsilon _2} \ge 0$、${\varepsilon _3} \ge 0$、${\varepsilon _4} \ge 0$、${\varepsilon _5} \ge 0$;松弛系数满足$\upsilon _{{\rm{min}}}^u \le 0$、$\upsilon _{{\rm{min}}}^{\Delta d} \le 0$、$\upsilon _{{\rm{min}}}^{\Delta v} \le 0$、$\upsilon _{{\rm{min}}}^a \le 0$、 $\upsilon _{{\rm{min}}}^j \le 0 $、 $\upsilon _{{\rm{max}}}^u \ge 0$、$\upsilon _{{\rm{max}}}^{\Delta d} \ge 0$、$\upsilon _{{\rm{max}}}^{\Delta v} \ge 0$、$\upsilon _{{\rm{max}}}^a \ge 0$、$\upsilon _{{\rm{max}}}^j \ge 0$。
-
为抑制松弛因子对约束界的无限松弛能力,故于待优化目标函数中增加二次型惩罚项${\mathit{\boldsymbol{\varepsilon }}^{\rm{T}}}\mathit{\boldsymbol{\rho \varepsilon }} $,以便在控制器工作域具备合理性的条件下寻求可行解。
联立式(14)、式(15),并忽略常数项,整理得:
$$ \begin{array}{c} J(\mathit{\boldsymbol{y}}, u, \mathit{\boldsymbol{\varepsilon }}) = J + {\mathit{\boldsymbol{\varepsilon }}^{\rm{T}}}\mathit{\boldsymbol{\rho \varepsilon }} = \\ {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{U}}\\ \mathit{\boldsymbol{\varepsilon }} \end{array}} \right]^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{B}}_p^{\rm{T}}\mathit{\boldsymbol{C}}_p^{\rm{T}}{\mathit{\boldsymbol{Q}}_p}{\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{B}}_p} + \mathit{\boldsymbol{R}}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{\rho }} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{U}}\\ \mathit{\boldsymbol{\varepsilon }} \end{array}} \right] + \\ 2[({\mathit{\boldsymbol{x}}^{\rm{T}}}(k)(\mathit{\boldsymbol{A}}_p^{\rm{T}}\mathit{\boldsymbol{C}}_p^{\rm{T}} - {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{\xi }}_p^{\rm{T}}) + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{G}}_p^{\rm{T}}\mathit{\boldsymbol{C}}_p^{\rm{T}} + \\ {\mathit{\boldsymbol{e}}^{\rm{T}}}(k)\mathit{\boldsymbol{M}}_p^{\rm{T}}\mathit{\boldsymbol{C}}_p^{\rm{T}}){\mathit{\boldsymbol{Q}}_p}{\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{B}}_p}\;\;, \;\;{\bf{0}}]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{U}}\\ \mathit{\boldsymbol{\varepsilon }} \end{array}} \right] = \\ {{\mathit{\boldsymbol{\tilde U}}}^{\rm{T}}}\mathit{\boldsymbol{H\tilde U}} + 2{\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{\tilde U}} \end{array} $$ (17) 从而,在MPC框架下,多目标ACC控制算法最终转化成带有线性不等式组约束的二次规划问题,即有:
$$ \left\{ \begin{array}{l} {\rm{min}}\;\{ \;{{\mathit{\boldsymbol{\tilde U}}}^{\rm{T}}}\mathit{\boldsymbol{H\tilde U}} + 2{\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{\tilde U}}\;\} \\ {\rm{s}}{\rm{.t}}.\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varOmega} \tilde U}} \le \mathit{\boldsymbol{T}} \end{array} \right. $$ (18) 式中,有:
$$ \mathit{\boldsymbol{\tilde U}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{U}}\\ \mathit{\boldsymbol{\varepsilon }} \end{array}} \right] $$ $$ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{B}}_p^{\rm{T}}\mathit{\boldsymbol{C}}_p^{\rm{T}}{\mathit{\boldsymbol{Q}}_p}{\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{B}}_p} + \mathit{\boldsymbol{R}}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{\rho }} \end{array}} \right] $$ $$ \begin{matrix} \mathit{\boldsymbol{f}}=[({{\mathit{\boldsymbol{x}}}^{\rm{T}}}(k)(\mathit{\boldsymbol{A}}_{p}^{\rm{T}}\mathit{\boldsymbol{C}}_{p}^{\rm{T}}-{{\mathit{\boldsymbol{C}}}^{\rm{T}}}\mathit{\boldsymbol{ }}\!\!\xi\!\!\text{ }_{p}^{\rm{T}})+{{\mathit{\boldsymbol{ }}\!\!\mathit{\boldsymbol{ \Phi}}\!\!\text{ }}^{\rm{T}}}\mathit{\boldsymbol{G}}_{p}^{\rm{T}}\mathit{\boldsymbol{C}}_{p}^{\rm{T}}+ \\ {{\mathit{\boldsymbol{e}}}^{\rm{T}}}(k)\mathit{\boldsymbol{M}}_{p}^{\rm{T}}\mathit{\boldsymbol{C}}_{p}^{\rm{T}})\ {{\mathit{\boldsymbol{Q}}}_{p}}{{\mathit{\boldsymbol{C}}}_{p}}{{\mathit{\boldsymbol{B}}}_{p}}\ \ , \ \ \bf{0}{{]}^{\rm{T}}} \\ \end{matrix} $$ $$ \mathit{\boldsymbol{\varepsilon }}\!\!\!\!\text{ }={{[{{\varepsilon }_{1}}, {{\varepsilon }_{2}}, {{\varepsilon }_{3}}, {{\varepsilon }_{4}}, {{\varepsilon }_{5}}]}^{\text{T}}} $$ $$ \mathit{\boldsymbol{\rho }} = {\rm{diag}}({\rho _1}, {\rho _2}, {\rho _3}, {\rho _4}, {\rho _5}) $$ $$ \begin{array}{l} {\mathit{\boldsymbol{Q}}_p} = {\rm{diag}}(\mathit{\boldsymbol{Q}}, \mathit{\boldsymbol{Q}}, \cdots , \mathit{\boldsymbol{Q}})\\ \mathit{\boldsymbol{R}} = {\rm{diag}}(R, R, \cdots , R)\\ {\mathit{\boldsymbol{\xi }}_p} = {\left[ {{\mathit{\boldsymbol{\xi }}^1}, {\mathit{\boldsymbol{\xi }}^2}, \cdots , {\mathit{\boldsymbol{\xi }}^p}} \right]^{\rm{T}}} \end{array} $$ $$\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{E}}&{ - \mathit{\boldsymbol{\upsilon }}_{{\rm{max}}}^u}&{\bf{0}}\\ { - \mathit{\boldsymbol{E}}}&{\mathit{\boldsymbol{\upsilon }}_{{\rm{min}}}^u}&{\bf{0}}\\ {{\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{B}}_p}}&{\bf{0}}&{ - \mathit{\boldsymbol{V}}_{{\rm{max}}}^y}\\ { - {\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{B}}_p}}&{\bf{0}}&{\mathit{\boldsymbol{V}}_{{\rm{min}}}^y}\\ { - {\mathit{\boldsymbol{L}}_p}{\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{B}}_p}}&{\bf{0}}&{\bf{0}} \end{array}} \right]_{11p \times (p + 2)}} $$ $$ \mathit{\boldsymbol{{ T}}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}_{{\rm{max}}}}}\\ { - {\mathit{\boldsymbol{U}}_{{\rm{min}}}}}\\ {{\mathit{\boldsymbol{{ T}}}_1}}\\ {{\mathit{\boldsymbol{{ T}}}_2}}\\ {{\mathit{\boldsymbol{{ T}}}_3}} \end{array}} \right]_{11p \times 1}} $$ 其中,有:
$$ {\mathit{\boldsymbol{L}}_p} = {\rm{diag}}(\mathit{\boldsymbol{l}}, \, \mathit{\boldsymbol{l}}, \cdots \, , \, \mathit{\boldsymbol{l}})\;\;\;\mathit{\boldsymbol{l}} = \left[ {1\;, \;0\;, 0, 0} \right] $$ $$ \begin{array}{c} {\mathit{\boldsymbol{T}}_1} = {\mathit{\boldsymbol{Y}}_{{\rm{max}}}} - {\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{A}}_p}\mathit{\boldsymbol{x}}(k) - {\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{G}}_p}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - {\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{M}}_p}\mathit{\boldsymbol{e}}(k)\\ {\mathit{\boldsymbol{T}}_2} = - {\mathit{\boldsymbol{Y}}_{{\rm{min}}}} + {\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{A}}_p}\mathit{\boldsymbol{x}}(k) + {\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{G}}_p}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} + {\mathit{\boldsymbol{C}}_p}{\mathit{\boldsymbol{M}}_p}\mathit{\boldsymbol{e}}(k)\\ {\mathit{\boldsymbol{T}}_3} = - {\mathit{\boldsymbol{D}}_{{\rm{safe}}}} + {\mathit{\boldsymbol{D}}_{{\rm{des}}}} + {\mathit{\boldsymbol{L}}_p}{\mathit{\boldsymbol{C}}_p}[{\mathit{\boldsymbol{A}}_p}\mathit{\boldsymbol{x}}(k) + {\mathit{\boldsymbol{G}}_p}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} + {\mathit{\boldsymbol{M}}_p}\mathit{\boldsymbol{e}}(k)] \end{array} $$ $$ \begin{array}{c} {\mathit{\boldsymbol{D}}_{{\rm{safe}}}} = {\left[ {{d_{{\rm{safe}}}}(k), \, {d_{{\rm{safe}}}}(k)\, , \, \, \cdots \, , \, {d_{{\rm{safe}}}}(k)} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{D}}_{{\rm{des}}}} = {\left[ {{d_{{\rm{des}}}}(k), \, {d_{{\rm{des}}}}(k)\, , \, \cdots \, , \, {d_{{\rm{des}}}}(k)} \right]^{\rm{T}}} \end{array} $$ $$ \begin{array}{c} \mathit{\boldsymbol{\upsilon }}_{{\rm{\max}} }^u = {\left[ {\upsilon _{{\rm{\max}} }^u, \, \upsilon _{{\rm{\max}} }^u, \, \cdots \, , \, \upsilon _{{\rm{\max}} }^u} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{\upsilon }}_{{\rm{\min}} }^u = {\left[ {\upsilon _{{\rm{\min}} }^u, \, \upsilon _{{\rm{\min}} }^u, \, \cdots \, , \, \upsilon _{{\rm{\min}} }^u} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{V}}_{{\rm{\max}} }^y = {\left[ {\upsilon _{{\rm{\max}} }^y, \, \upsilon _{{\rm{\max}} }^y, \, \cdots , \, \upsilon _{{\rm{\max}} }^y} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{V}}_{{\rm{\min}} }^y = {\left[ {\upsilon _{{\rm{\min}} }^y, \, \upsilon _{{\rm{\min}} }^y, \, \cdots , \, \upsilon _{{\rm{\min}} }^y} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{\upsilon }}_{{\rm{\max}} }^y = {\left[ {\upsilon _{{\rm{\max}} }^{\Delta d}, \, \upsilon _{{\rm{\max}} }^{\Delta v}\, , \, \upsilon _{{\rm{\max}} }^a, \, \upsilon _{{\rm{\max}} }^j} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{\upsilon }}_{{\rm{\min}} }^y = {\left[ {\upsilon _{{\rm{\min}} }^{\Delta d}, \, \upsilon _{{\rm{\min}} }^{\Delta v}\, , \, \upsilon _{{\rm{\min}} }^a, \, \upsilon _{{\rm{\min}} }^j} \right]^{\rm{T}}} \end{array} $$ -
本文利用Matlab/Simulink搭建了多目标ACC车距控制模型、逆纵向动力学模型、车辆动力学模型,单模式仿真参数如表 3所示,多模式下目标向量与控制输入权重、约束边界以及松弛系数可调节。
表 3 单模式ACC仿真参数
参数 数值 Q diag(1, 1, 1, 1) R 1 ξ diag(0.94, 0.94, 0.94, 0.94) ρ diag(3, 3, 3, 3, 3) $ \mathit{\boldsymbol{\upsilon }}_{{\rm{max}}}^y$ [3, 0.9, 0.01, 0.01]T $ \mathit{\boldsymbol{\upsilon }}_{{\rm{min}}}^y$ [-3, 1, -0.1, -0.05]T $ \mathit{\boldsymbol{y }}_{{\rm{max}}}$ [5, 0.9, 0.6, 1]T $ \mathit{\boldsymbol{y }}_{{\rm{min}}}$ [-5, 1, -2.5, -1]T ${u_{{\rm{max}}}}$ 0.6 ${u_{{\rm{min}}}}$ -2.5 ${K_L}$ 1.0 ${T_L}$ 0.40 ${T_s}$ 0.1 ${t_{{\rm{TTC}}}} $ -3.0 ${d_0} $ 5 $ {d_s}$ 5 ${\tau _h}$ 1.5 p 5 $\upsilon _{{\rm{max}}}^u$ 0.01 $\upsilon _{{\rm{min}}}^u$ -0.1 前车紧急制动、邻道车辆强行并线是巡航过程中比较典型的紧急工况,为验证本文多模式设计与多目标控制算法的有效性与适应性,着重对紧急制动工况、强行并线工况进行仿真与探讨。
-
前车与自车初始速度皆为30 m/s,前车在10 s时刻以-4 m/s2的减速度紧急制动,速度降至10 m/s,多模式设计ACC与单模式设计ACC的系统响应曲线分别如图 6、图 7所示。
前车紧急制动工况下,多模式ACC工作于瞬态紧急制动模式。由图 6可知,该工况下,相对单模式ACC而言,多模式ACC对车距误差的约束能力较好,从而确保安全车距。由图 7可知,单模式ACC制动效果较差,减速不够及时,使得实际车距越过安全车距界限,易造成车辆追尾,且制动过程中产生较大的冲击度,影响驾乘舒适性。
-
自车以30 m/s的速度定速巡航,在10 s时刻前方50 m处位于邻道的前车以20 m/s的速度强行切入本道,并保持匀速前行,多模式设计ACC与单模式设计ACC的系统响应曲线分别如图 8、图 9所示。由运动学知识可知,此工况下,自车至少以3 m/s2的幅值进行减速才能保证实际车距不小于期望车距$ {d_{{\rm{des}}}}$,故多模式ACC将由定速巡航模式切换至瞬态深制动模式。
由图 8可知,前方邻道车辆强行并线时,单模式ACC对$\Delta d$负向边界的约束能力相对不足,导致实际车距相对偏小,存在潜在安全隐患。同样,由图 9可知,单模式ACC的制动效果、舒适性皆相对欠佳。
综上所述,多模式ACC对工况的适应性较好,有效地避免了单模式ACC应对紧急工况时响应滞后、制动能力不足的缺陷。
-
为增强量产ACC对前车驾驶意图的预判与自适应能力,提出了多模式控制策略、多目标控制算法,并设计了紧急制动工况、强行并线工况,对多模式多目标ACC工作性能进行了验证分析,主要结论如下。
1) 不同工况下,驾驶员期望响应不同,从而控制器的待优化目标、控制输入、约束条件不同。采用待优化目标与控制输入权重调校以及控制器工作域边界松弛的策略,将ACC系统划分出6种工作模式,同时采用模糊推理与加速度加权平均策略以实现工作模式最佳匹配与平稳过渡。
2) 建立闭环纵向跟驰模型,基于MPC模型预测控制理论,综合协调巡航过程中驾驶员期望响应、跟驰安全性、车辆自身物理限制等控制目标,并且引入松弛向量软化硬约束以确保可行解存在,从而实现ACC滚动在线优化控制。
3) 仿真结果表明,本文的多模式设计策略与多目标控制算法能够一定程度上提升ACC系统的适应性与友好性。
4) 建模时对车辆动力学系统进行了一阶惯性环节假设,弱化了复杂动力学系统的强非线性、时滞时变等特性;低速工况下可以忽略车辆稳定性控制等动力学问题,而高速工况下对车辆动力学(如质心侧偏角、轮胎侧偏角等)以及路面附着的约束将会变得严苛,后续研究中将进一步深入。
Multi-Objective Adaptive Cruise Control with Multi-Mode Strategy
-
摘要: 为增强量产ACC对前车驾驶意图的预判与自适应能力,发展了一种多目标自适应巡航控制算法,建立闭环纵向跟驰模型。基于模型预测控制理论,综合协调巡航过程中驾驶员期望响应、跟驰安全性、车辆自身物理限制等控制目标,并引入松弛向量以确保滚动在线优化存在可行解。采用待优化目标与控制输入权重调校以及控制器工作域边界松弛的策略,将ACC系统划分出6种工作模式,同时采用模糊推理与加速度加权平均策略,以实现工作模式最佳匹配与平稳过渡。仿真结果表明,多模式设计策略与多目标控制算法能够一定程度上提升ACC系统的适应性与友好性。Abstract: In order to prejudge driving intention of preceding car and enhance the adaptability of adaptive cruise control (ACC) against complex traffic scenarios simultaneously, a multi-objective adaptive cruise control algorithm considering multi-mode switching strategy is proposed. Based on the model predictive control (MPC) framework, it is hopeful to comprehensively coordinate various conflicting objectives such as driver's desired response, rear-end safety, and vehicular physical limits. Meanwhile, the slack variable vector is introduced to deal with non-feasible solution owing to hard constraints during online optimization. The desired response as well as constraint boundary varies with traffic scenarios, and consequently multiple ACC modes are designed by means of slightly adjusting weights of control objectives and system input, constraint boundary as well as slack relaxation. Further, we can obtain relatively suitable mode as well as smooth transition by fuzzy inference and the weighted average method. The simulations show that under emergent traffic scenarios, the multi-objective control algorithm together with multi-mode switching strategy is able to achieve good expectation during the car-following.
-
表 1 典型工况划分与ACC工作模式
典型工况 前车加速度 ACC工作模式 定速巡航工况 — 定速巡航模式 稳态跟随工况 [-0.6, 0.6] 稳态跟随模式 瞬态急加速工况 (0.6, +∞) 瞬态急加速模式 瞬态浅制动工况 (-2, -0.6) 瞬态浅制动模式 瞬态深制动工况 (-4, -2] 瞬态深制动模式 瞬态紧急制动工况 (-∞, -4] 瞬态紧急制动模式 表 2 模糊规则表
Δv Δd 负大 负中 零 正中 正大 负大 --- -- - 0 + 负中 -- -- - + + 零 -- - 0 + ++ 正中 - - + ++ ++ 正大 - 0 + ++ ++ 表 3 单模式ACC仿真参数
参数 数值 Q diag(1, 1, 1, 1) R 1 ξ diag(0.94, 0.94, 0.94, 0.94) ρ diag(3, 3, 3, 3, 3) $ \mathit{\boldsymbol{\upsilon }}_{{\rm{max}}}^y$ [3, 0.9, 0.01, 0.01]T $ \mathit{\boldsymbol{\upsilon }}_{{\rm{min}}}^y$ [-3, 1, -0.1, -0.05]T $ \mathit{\boldsymbol{y }}_{{\rm{max}}}$ [5, 0.9, 0.6, 1]T $ \mathit{\boldsymbol{y }}_{{\rm{min}}}$ [-5, 1, -2.5, -1]T ${u_{{\rm{max}}}}$ 0.6 ${u_{{\rm{min}}}}$ -2.5 ${K_L}$ 1.0 ${T_L}$ 0.40 ${T_s}$ 0.1 ${t_{{\rm{TTC}}}} $ -3.0 ${d_0} $ 5 $ {d_s}$ 5 ${\tau _h}$ 1.5 p 5 $\upsilon _{{\rm{max}}}^u$ 0.01 $\upsilon _{{\rm{min}}}^u$ -0.1 -
[1] 吴光强, 张亮修, 刘兆勇, 等.汽车自适应巡航控制系统研究现状与发展趋势[J].同济大学学报(自然科学版), 2017, 45(4):544-553. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tjdxxb201704012 WU Guang-qiang, ZHANG Liang-xiu, LIU Zhao-yong, et al. Research status and development trend of vehicle adaptive cruise control systems[J]. Journal of Tongji University (Natural Science), 2017, 45(4):544-553. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tjdxxb201704012 [2] FANCHER P, BAREKET Z. Evaluating headway control using range versus range-rate relationships[J]. Vehicle System Dynamics, 1994, 23(1):575-596. doi: 10.1080/00423119408969076 [3] MOON S, YI K. Human driving data-based design of a vehicle adaptive cruise control algorithm[J]. Vehicle System Dynamics, 2008, 46(8):661-690. doi: 10.1080/00423110701576130 [4] 裴晓飞, 刘昭度, 马国成, 等.汽车自适应巡航系统的多模式切换控制[J].机械工程学报, 2012, 48(10):96-102. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jxgcxb201210015 PEI Xiao-fei, LIU Zhao-du, MA Guo-cheng, et al. Multi-mode switching controller for vehicle adaptive cruise control system[J]. Journal of Mechanical Engineering, 2012, 48(10):96-102. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jxgcxb201210015 [5] 严伟. 仿驾驶员速度跟随行为的自适应巡航控制算法研究[D]. 长春: 吉林大学, 2016. YAN Wei. Study on adaptive cruise control algorithms imitating car-following behaviors of drivers[D]. Changchun: Jilin University, 2016. [6] WU H, LI Y, WU C. A longitudinal minimum safety distance model based on driving intention and fuzzy reasoning[C]//IEEE International Conference on Transportation Information and Safety. Alberta, Canada: IEEE, 2017: 158-162. [7] DARBHA S, KONDURI S, PAGILLA P R. Effects of V2V communication on time headway for autonomous vehicles[C]//American Control Conference. Seattle. USA: IEEE, 2017: 2002-2007. [8] 高振海, 严伟, 李红建, 等.基于模拟驾驶员多目标决策的汽车自适应巡航控制算法[J].汽车工程, 2015(6):667-673. http://www.cqvip.com/QK/91525X/201506/665237437.html GAO Zhen-hai, YAN Wei, LI Hong-jian, et al. A vehicle adaptive cruise control algorithm based on simulating driver's multi-objective decision making[J]. Automotive Engineering, 2015(6):667-673. http://www.cqvip.com/QK/91525X/201506/665237437.html [9] SULTAN B. The study of motorway operation using a microscopic simulation model[D]. Southampton: University of Southampton, 2000. [10] 章军辉, 李庆, 陈大鹏.基于BP神经网络的纵向避撞安全辅助算法[J].西安交通大学学报, 2017, 51(7):140-147. doi: 10.7652/xjtuxb201707020 ZHANG Jun-hui, LI Qing, CHEN Da-peng. Safety assistance algorithm of longitudinal collision avoidance safety assistance based on BP neural network[J]. Journal of Xi'an Jiaotong University, 2017, 51(7):140-147. doi: 10.7652/xjtuxb201707020 [11] LI S, LI K, RAJAMANI R, et al. Model Predictive multi-objective vehicular adaptive cruise control[J]. IEEE Transactions on Control Systems Technology, 2011, 19(3):556-566. doi: 10.1109/TCST.2010.2049203 [12] BAGESHWAR V L, GARRARD W L, RAJAMANI R. Model predictive control of transitional maneuvers for adaptive cruise control vehicles[J]. IEEE Transactions on Vehicular Technology, 2004, 53(5):1573-1585. doi: 10.1109/TVT.2004.833625 [13] FILHO C M, TERRA M H, WOLF D F. Safe optimization of highway traffic with robust model predictive control-based cooperative adaptive cruise control[J]. IEEE Transactions on Intelligent Transportation Systems, 2017(99):1-11. [14] TIENTRAKOOL P, HO Y C, MAXEMCHUK N F. Highway capacity benefits from using vehicle-to-vehicle communication and sensors for collision avoidance[C]//IEEE Vehicular Technology Conference. Budapest, Hungary: IEEE, 2011: 1-5. [15] ZHANG J, IOANNOU P A. Longitudinal control of heavy trucks in mixed traffic:Environmental and fuel economy considerations[J]. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(1):92-104. doi: 10.1109/TITS.2006.869597 [16] LUO L, LIU H, LI P, et al. Model predictive control for adaptive cruise control with multi-objectives:Comfort, fuel-economy, safety and car-following[J]. Journal of Zhejiang University, Science A(Applied Physics & Engineering), 2010, 11(3):191-201 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zjdxxb-e201003005 -


 ISSN
ISSN 




 下载:
下载: