-
针对各向异性媒质的光或者电磁散射特性研究一直都是物理界和工程界的研究热点,因为各向异性媒质在光学、生物学、医学以及纳米科学等领域都有着广泛而有前景的应用。文献[1]提出了均匀球形媒质对于平面波的散射理论,称之为Mie散射理论。随后许多研究者在Mie散射理论基础上对各向同性多层非均匀球体的电磁散射特性进行了研究[2-3]。除了对各向同性媒质散射特性的研究,研究者还根据Lorenz-Mie散射理论,应用不同的方法给出了各向异性媒质中电磁场的解析解,如:并矢格林函数结合变化的球矢量波函数的方法[4],应用球矢量波函数结合傅里叶变换的方法[5-6],T-矩阵方法[7-8]。近几年,学者们也提出了一些新的方法用于对各向异性媒质电磁特性的研究,如:使用频域鞍点估算法对外加单轴电各向异性涂层电大尺寸复杂目标散射场的计算[9],非均匀各向异性目标电磁散射的Nystom解[10],各向异性媒质的光学定理[11],尺度变换方法[12],应用状态空间法对双轴双各向异性媒质电磁特性的研究[13]。应用球矢量波函数结合傅里叶变换的方法对不同结构的球形等离子体的电磁散射特性进行了研究,包括:等离子各向异性球体[14],等离子各向异性球壳[15]以及等离子各向异性非均匀多层球壳[16]。文献[17]根据球矢量波函数的完备性与正交性给出了光各向异性磁性球体中电磁场的解析解,其方法避开了冗长而复杂的积分运算,在数值精度上有较大的优势。随后文献[18]将该方法应用在旋电各向异性球体的研究中,给出了完整的理论公式和数值结果。
本文将文献[17]的方法进行推广并用于研究径向非均匀多层旋磁介质球的电磁散射特性。具体地,根据Lorenz-Mie散射理论和球矢量波函数理论,多层球球心区域的电磁场被展开为第一类球矢量波函数的线性叠加,球壳区域电磁场展开为由第一类和第三类矢量波函数的线性叠加。而入射场和散射场分别由第一类和第三类球矢量波函数进行展开。最后在不连续表面匹配边界条件得到各个区域的展开系数以及散射系数。随后,计算了非均匀旋磁球体的双站雷达散射截面,并与有限元法得到的数值结果进行对比,结果吻合很好,验证了公式推导的正确性和有效性。最后给出了几个新的算例,用于分析旋磁各向异性多层球体的物理特性以及在减弱和加强雷达散射截面中可能的应用前景。
-
首先考虑旋磁各向异性球体,其电磁参数为标量电导率∈S和张量磁导率$\mathit{\boldsymbol{\bar \mu }}$,假设时谐因子为${{\rm{e}}^{ - {\rm{i}}\omega t}}$,$\mathit{\boldsymbol{\bar \mu }}$在直角坐标系下的表达式为:
$$\mathit{\boldsymbol{\bar \mu }} = {\mu _s}\left[ {\begin{array}{*{20}{c}} {{\mu _r}}&{ - {\rm{i}}{\mu _\kappa }}&0\\ {{\rm{i}}{\mu _\kappa }}&{{\mu _r}}&0\\ 0&0&1 \end{array}} \right]$$ (1) 根据文献[17],旋磁介质球中的电磁场在球坐标系下可以表达为具有不同特征值${k_l}$的球矢量波函数的线性叠加,具体的H和E的表达式为:
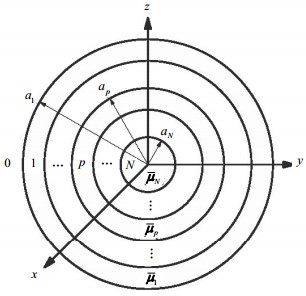
$$ \begin{array}{l} \mathit{\boldsymbol{H}} = - \sum\limits_{n,m} {{{\bar E}_{mn}}} \sum\limits_l {{\alpha _l}} \frac{{\omega {\varepsilon _s}}}{{{k_l}}}[{d_{mn,l}}\mathit{\boldsymbol{M}}_{mn}^{(1)}({k_l},\mathit{\boldsymbol{r}}) + \\ \;\;\;\;\;\;\;\;{c_{mn,l}}\mathit{\boldsymbol{N}}_{mn}^{(1)}({k_l},\mathit{\boldsymbol{r}}) + \frac{{{w_{mn,l}}}}{{{\lambda _l}}}\mathit{\boldsymbol{L}}_{mn}^{(1)}({k_l},\mathit{\boldsymbol{r}})] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_l {{\alpha _l}} \frac{{\omega {\varepsilon _s}}}{{{k_l}}}[\frac{{{w_{00,l}}}}{{{\lambda _l}}}\mathit{\boldsymbol{L}}_{00}^{(1)}({k_l},\mathit{\boldsymbol{r}})]\\ \mathit{\boldsymbol{E}} = - \sum\limits_{n,m} {{\rm{i}}{{\bar E}_{mn}}} \sum\limits_l {{\alpha _l}} [{c_{mn,l}}\mathit{\boldsymbol{M}}_{mn}^{(1)}({k_l},\mathit{\boldsymbol{r}}) + {d_{mn,l}}\mathit{\boldsymbol{N}}_{mn}^{(1)}({k_l},\mathit{\boldsymbol{r}})]{\rm{ }} \end{array} $$ (2) 将文献[17]用于研究径向多层结构的旋磁各向异性球体。图 1为径向多层非均匀球形结构的平面图。层数N可以取任意值。散射体置于自由空间中,球心与坐标原点重合。区域0为自用空间,其介电常数和磁导率分别为${\varepsilon _0}$和${\mu _0}$。而对于区域$p$,其电磁参数分别为${\varepsilon _{ps}}$和${\mathit{\boldsymbol{\bar \mu }}_p}$,其中${\mathit{\boldsymbol{\bar \mu }}_p}$表达式和$\mathit{\boldsymbol{\bar \mu }}$完全一致,除了用于标记区域的下标$p$,$p = 1,2, \cdots ,N$。
-
如图 1所示,在区域N($0 \le r \le {a_N}$),即多层球的球心区域,因为包括了原点,考虑到在电磁场在原点取值必须为有限值,所以这里只采用第一类矢量波函数对区域N的电磁场进行展开,其表达式与式(2)相同,并增加了区域下标N:
$$ \begin{array}{l} {\mathit{\boldsymbol{H}}_N} = - \sum\limits_{n,m} {{{\bar E}_{mn}}} \sum\limits_l {{\alpha _{Nl}}} \frac{{\omega {\varepsilon _{Ns}}}}{{{k_{Nl}}}}[d_{mn,l}^{(N)}\mathit{\boldsymbol{M}}_{mn}^{(1)}({k_{Nl}},\mathit{\boldsymbol{r}}) + \\ \;\;\;\;\;\;c_{mn,l}^{(N)}\mathit{\boldsymbol{N}}_{mn}^{(1)}({k_{Nl}},\mathit{\boldsymbol{r}}) + \frac{{w_{mn,l}^{(N)}}}{{{\lambda _{Nl}}}}\mathit{\boldsymbol{L}}_{mn}^{(1)}({k_{Nl}},\mathit{\boldsymbol{r}})] - \\ \;\;\;\;\;\;\;\;\sum\limits_l {{\alpha _{Nl}}} \frac{{\omega {\varepsilon _{Ns}}}}{{{k_{Nl}}}}[\frac{{w_{00,l}^{(N)}}}{{{\lambda _{Nl}}}}\mathit{\boldsymbol{L}}_{00}^{(1)}({k_{Nl}},\mathit{\boldsymbol{r}})]\\ {\mathit{\boldsymbol{E}}_N} = - \sum\limits_{n,m} {{\rm{i}}{{\bar E}_{mn}}} \sum\limits_l {{\alpha _{Nl}}} [c_{mn,l}^{(N)}\mathit{\boldsymbol{M}}_{mn}^{(1)}({k_{Nl}},\mathit{\boldsymbol{r}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;d_{mn,l}^{(N)}\mathit{\boldsymbol{N}}_{mn}^{(1)}({k_{Nl}},\mathit{\boldsymbol{r}})] \end{array} $$ (3) 在区域p(${a_{p + 1}} \le r \le {a_p}$,p=1, 2, …, N-1),因为不包括原点,第一类和第三类Bessel都为有限值,考虑到球矢量波函数的完备性,区域p中的电磁场需要展开为第一类和第三类球矢量波函数的叠加,具体表达式为:
$$ \begin{array}{l} {\mathit{\boldsymbol{H}}_p} = - \sum\limits_{n,m} {{{\bar E}_{mn}}} \sum\limits_{v = 1,3} {\sum\limits_l {\alpha _{pl}^{(v)}} \frac{{\omega {\varepsilon _{ps}}}}{{{k_{pl}}}}[d_{mn,l}^{(p)}\mathit{\boldsymbol{M}}_{mn}^{(v)}({k_{pl}},\mathit{\boldsymbol{r}})} + \\ \;\;\;\;\;\;\;c_{mn,l}^{(p)}\mathit{\boldsymbol{N}}_{mn}^{(v)}({k_{pl}},\mathit{\boldsymbol{r}}) + \frac{{w_{mn,l}^{(p)}}}{{{\lambda _{pl}}}}\mathit{\boldsymbol{L}}_{mn}^{(v)}({k_{pl}},\mathit{\boldsymbol{r}})] - \\ \;\;\;\;\;\;\;\;\sum\limits_{v = 1,3} {\sum\limits_l {\alpha _{pl}^{(v)}} \frac{{\omega {\varepsilon _{ps}}}}{{{k_{pl}}}}[\frac{{w_{00,l}^{(p)}}}{{{\lambda _{pl}}}}\mathit{\boldsymbol{L}}_{00}^{(v)}({k_{pl}},\mathit{\boldsymbol{r}})]} \\ {\mathit{\boldsymbol{E}}_p} = - \sum\limits_{n,m} {i{{\bar E}_{mn}}} \sum\limits_{v = 1,3} {\sum\limits_l {\alpha _{pl}^{(v)}} [c_{mn,l}^{(p)}\mathit{\boldsymbol{M}}_{mn}^{(v)}({k_{pl}},\mathit{\boldsymbol{r}}) + } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;d_{mn,l}^{(p)}\mathit{\boldsymbol{N}}_{mn}^{(v)}({k_{pl}},\mathit{\boldsymbol{r}})] \end{array} $$ (4) 因为$\mathit{\boldsymbol{\nabla}} \cdot {\mathit{\boldsymbol{L}}_{mn}} \ne 0$,可知$\mathit{\boldsymbol{\nabla}} \cdot {\mathit{\boldsymbol{H}}_p} \ne 0$,这与各向同性媒质中磁场散度为零不同,也体现了旋磁媒质特殊的电磁特性。
-
图 2为平面波照射到球体的球坐标系示意图。自由空间中的散射场$({\mathit{\boldsymbol{E}}_{{\rm{sca}}}},{\mathit{\boldsymbol{H}}_{{\rm{sca}}}})$与Mie理论中的表达式相同[19-20],根据矢量波函数理论,可将散射场展开为:
$$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{E}}_{{\rm{sca}}}} = \sum\limits_{n,m} {{\rm{i}}{{\bar E}_{mn}}} [{{\rm{a}}_{mn}}\mathit{\boldsymbol{N}}_{mn}^{(3)}({k_0},\mathit{\boldsymbol{r}}) + {b_{mn}}\mathit{\boldsymbol{M}}_{mn}^{(3)}({k_0},\mathit{\boldsymbol{r}})]\\ {\mathit{\boldsymbol{H}}_{{\rm{sca}}}} = \frac{{{k_0}}}{{\omega {\mu _0}}}\sum\limits_{n,m} {{{\bar E}_{mn}}} [{b_{mn}}\mathit{\boldsymbol{N}}_{mn}^{(3)}({k_0},\mathit{\boldsymbol{r}}) + {a_{mn}}\mathit{\boldsymbol{M}}_{mn}^{(3)}({k_0},\mathit{\boldsymbol{r}})] \end{array} \right. $$ (5) 式中,$k_0^2 = {\omega ^2}{\varepsilon _0}{\mu _0}$。波矢量为k0的平面波照射到多层球体结构,入射场$({\mathit{\boldsymbol{E}}_{{\rm{inc}}}},{\mathit{\boldsymbol{H}}_{{\rm{inc}}}})$的表达式为:
$$ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{E}}_{{\rm{inc}}}} = {E_0}({p_\theta }{{\mathit{\boldsymbol{\hat \theta }}}_k} + {p_\phi }{{\mathit{\boldsymbol{\hat \phi}}}_k}){{\rm{e}}^{{\rm{i}}{\mathit{\boldsymbol{k}}_0} \cdot \mathit{\boldsymbol{r}}}}}\\ {{\mathit{\boldsymbol{H}}_{{\rm{inc}}}} = \frac{{{k_0}}}{{\omega {\mu _0}}}{E_0}({p_\theta }{{\mathit{\boldsymbol{\hat \phi}}}_k} + {p_\phi }{{\mathit{\boldsymbol{\hat \theta }}}_k}){{\rm{e}}^{{\rm{i}}{\mathit{\boldsymbol{k}}_0} \cdot \mathit{\boldsymbol{r}}}}} \end{array}} \right. $$ (6) 式中,$\mathit{\boldsymbol{\hat p}} = ({p_\theta }{\mathit{\boldsymbol{\widehat \theta }}_k} + {p_\phi }{\mathit{\boldsymbol{\hat \phi}}_k})$为归一化复极化矢量;E0是入射场的幅度。同样的,根据矢量波函数理论[21],$({\mathit{\boldsymbol{E}}_{{\rm{inc}}}},{\mathit{\boldsymbol{H}}_{{\rm{inc}}}})$可以展开为:
$$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{E}}_{{\rm{inc}}}} = - \sum\limits_{n,m} {{\rm{i}}{{\bar E}_{mn}}} [{p_{mn}}\mathit{\boldsymbol{N}}_{mn}^{(1)}({k_0},\mathit{\boldsymbol{r}}) + {q_{mn}}\mathit{\boldsymbol{M}}_{mn}^{(1)}({k_0},\mathit{\boldsymbol{r}})]\\ {\mathit{\boldsymbol{H}}_{{\rm{inc}}}} = - \frac{{{k_0}}}{{\omega {\mu _0}}}\sum\limits_{n,m} {{{\bar E}_{mn}}} [{q_{mn}}\mathit{\boldsymbol{N}}_{mn}^{(1)}({k_0},\mathit{\boldsymbol{r}}) + {p_{mn}}\mathit{\boldsymbol{M}}_{mn}^{(1)}({k_0},\mathit{\boldsymbol{r}})]{\rm{ }} \end{array} \right. $$ (7) 式中,展开系数pmn和qmn可以在文献[17]中找到;双求和符号$\sum\limits_{n,m} {} $中的下标$n$的取值为1~${n_c}$ (截断常数);对应每个n,m的取值为-n~n。
-
入射场、散射场、以及球体内部各个区域场都已展开为球矢量波函数的叠加形式。下面通过匹配边界条件来确定各个内场区域的展开系数以及散射系数。在不连续表面$r = {a_p}$,根据电磁场切向连续性,可以得到:
$$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{E}}_{p - 1}} \times {\mathit{\boldsymbol{e}}_r} = {\mathit{\boldsymbol{E}}_p} \times {\mathit{\boldsymbol{e}}_r}\\ {\mathit{\boldsymbol{H}}_{p - 1}} \times {\mathit{\boldsymbol{e}}_r} = {\mathit{\boldsymbol{H}}_p} \times {\mathit{\boldsymbol{e}}_r} \end{array} \right. $$ (8) 式中$p = 2,3, \cdots ,N$。在球体的最外层表面$r = {a_1}$,边界条件为:
$$ \left\{ \begin{array}{l} ({\mathit{\boldsymbol{E}}_{{\rm{inc}}}} + {\mathit{\boldsymbol{E}}_{{\rm{sca}}}}) \times {\mathit{\boldsymbol{e}}_r} = {\mathit{\boldsymbol{E}}_1} \times {\mathit{\boldsymbol{e}}_r}\\ ({\mathit{\boldsymbol{H}}_{{\rm{inc}}}} + {\mathit{\boldsymbol{H}}_{{\rm{sca}}}}) \times {\mathit{\boldsymbol{e}}_r} = {\mathit{\boldsymbol{H}}_1} \times {\mathit{\boldsymbol{e}}_r} \end{array} \right. $$ (9) 将电磁场展开式(4)带入式(8),经过化简,并考虑等式两边对应分量相等,可以得到以下矩阵递推公式:
$$ {\mathit{\boldsymbol{\overline T}} _{p - 1,p}} \cdot {\mathit{\boldsymbol{X}}_{p - 1}} = {\mathit{\boldsymbol{\overline T}} _{p,p}} \cdot {\mathit{\boldsymbol{X}}_p} $$ (10) 式中,$p = 2,3, \cdots ,N$;$\mathit{\boldsymbol{T}}$矩阵具体表示为:
$$ \begin{array}{l} {\mathit{\boldsymbol{\overline T}} _{p,f}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{(p,f)}}}\\ {{\mathit{\boldsymbol{B}}^{(p,f)}}}\\ {{\mathit{\boldsymbol{C}}^{(p,f)}}}\\ {{\mathit{\boldsymbol{D}}^{(p,f)}}} \end{array}}&{\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\overline A}} }^{(p,f)}}}\\ {{{\mathit{\boldsymbol{\overline B}} }^{(p,f)}}}\\ {{{\mathit{\boldsymbol{\overline C}} }^{(p,f)}}}\\ {{{\mathit{\boldsymbol{\overline D}} }^{(p,f)}}} \end{array}} \end{array}} \right],\;\;{\mathit{\boldsymbol{X}}_p} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\alpha }}_p^{(1)}}\\ {\mathit{\boldsymbol{\alpha }}_p^{(3)}} \end{array}} \right]\\ \;\;{\mathit{\boldsymbol{\overline T}} _{N,f}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{(N,f)}}}\\ {{\mathit{\boldsymbol{B}}^{(N,f)}}}\\ {{\mathit{\boldsymbol{C}}^{(N,f)}}}\\ {{\mathit{\boldsymbol{D}}^{(N,f)}}} \end{array}} \right],\;\;{\mathit{\boldsymbol{X}}_N} = {\mathit{\boldsymbol{\alpha }}_N} \end{array} $$ (11) T中的矩阵元素具体为:
$$ \begin{array}{l} A_{mn,l}^{(p,f)} = \frac{{{k_0}}}{{{k_{pl}}}}\frac{{{{\psi '}_n}({k_{pl}}{a_f})}}{{{{\psi '}_n}({k_0}{a_f})}}d_{mn,l}^{(p)}\\ \bar A_{mn,l}^{(p,f)} = \frac{{{k_0}}}{{{k_{pl}}}}\frac{{{{\xi '}_n}({k_{pl}}{a_f})}}{{{{\psi '}_n}({k_0}{a_f})}}d_{mn,l}^{(p)}\\ B_{mn,l}^{(p,f)} = \frac{{{k_0}}}{{{k_{pl}}}}\frac{{{\psi _n}({k_{pl}}{a_f})}}{{{\psi _n}({k_0}{a_f})}}c_{mn,l}^{(p)}\\ \bar B_{mn,l}^{(p,f)} = \frac{{{k_0}}}{{{k_{pl}}}}\frac{{{\xi _n}({k_{pl}}{a_f})}}{{{\psi _n}({k_0}{a_f})}}c_{mn,l}^{(p)}\\ C_{mn,l}^{(p,f)} = \frac{{{\mu _0}{\lambda _{pl}}}}{{{\mu _{ps}}}}\frac{{{\psi _n}({k_{pl}}{a_f})}}{{{\psi _n}({k_0}{a_f})}}d_{mn,l}^{(p)}\\ \bar C_{mn,l}^{(p,f)} = \frac{{{\mu _0}{\lambda _{pl}}}}{{{\mu _{ps}}}}\frac{{{\xi _n}({k_{pl}}{a_f})}}{{{\psi _n}({k_0}{a_f})}}d_{mn,l}^{(p)}\\ D_{mn,l}^{(p,f)} = \frac{{{\mu _0}{\lambda _{pl}}}}{{{\mu _{ps}}}}\frac{{{{\psi '}_n}({k_{pl}}{a_f})}}{{{{\psi '}_n}({k_0}{a_f})}}c_{mn,l}^{(p)} + \frac{{{\mu _0}}}{{{\mu _{ps}}{k_{pl}}{a_f}}}\frac{{{\psi _n}({k_{pl}}{a_f})}}{{{\psi _n}({k_0}{a_f})}}w_{mn,l}^{(p)}\\ \bar D_{mn,l}^{(p,f)} = \frac{{{\mu _0}{\lambda _{pl}}}}{{{\mu _{ps}}}}\frac{{{{\xi '}_n}({k_{pl}}{a_f})}}{{{{\psi '}_n}({k_0}{a_f})}}c_{mn,l}^{(p)} + \frac{{{\mu _0}}}{{{\mu _{ps}}{k_{pl}}{a_f}}}\frac{{{\xi _n}({k_{pl}}{a_f})}}{{{\psi _n}({k_0}{a_f})}}w_{mn,l}^{(p)} \end{array} $$ (12) 式中,${\psi _n}(z) = z{j_n}(z)$和${\xi _n}(z) = zh_n^{(1)}(z)$分别为第一类和第三类球Riccati-Bessel函数。根据递推公式可以得到:
$$ {\mathit{\boldsymbol{X}}_1} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\alpha }}_1^{(1)}}\\ {\mathit{\boldsymbol{\alpha }}_1^{(3)}} \end{array}} \right] = \mathit{\boldsymbol{\overline T}} _{1,2}^{ - 1} \cdot {\mathit{\boldsymbol{\overline T}} _{2,2}} \cdots \mathit{\boldsymbol{\overline T}} _{N - 1,N}^{ - 1} \cdot {\mathit{\boldsymbol{\overline T}} _{N,N}}{\alpha _N} $$ (13) 在分界面$r = {a_1}$匹配边界条件,可以得到:
$$ \left\{ \begin{gathered} \left[ {\frac{{{{\xi '}_n}({x_1})}}{{{{\psi '}_n}({x_1})}}} \right]{a_{mn}} + \sum\limits_l {(A_{mn,l}^{(1,1)}\alpha _{1l}^{(1)} + \overline A _{mn,l}^{(1,1)}\alpha _{1l}^{(3)})} = {p_{mn}} \hfill \\ \left[ {\frac{{{\xi _n}({x_1})}}{{{\psi _n}({x_1})}}} \right]{b_{mn}} + \sum\limits_l {(B_{mn,l}^{(1,1)}\alpha _{1l}^{(1)} + \overline B _{mn,l}^{(1,1)}\alpha _{1l}^{(3)})} = {q_{mn}} \hfill \\ \left[ {\frac{{{\xi _n}({x_1})}}{{{\psi _n}({x_1})}}} \right]{a_{mn}} + \sum\limits_l {(C_{mn,l}^{(1,1)}\alpha _{1l}^{(1)} + \overline C _{mn,l}^{(1,1)}\alpha _{1l}^{(3)})} = {p_{mn}} \hfill \\ \left[ {\frac{{{{\xi '}_n}({x_1})}}{{{{\psi '}_n}({x_1})}}} \right]{b_{mn}} + \sum\limits_l {(D_{mn,l}^{(1,1)}\alpha _{1l}^{(1)} + \overline D _{mn,l}^{(1,1)}\alpha _{1l}^{(3)})} = {q_{mn}} \hfill \\ \end{gathered} \right. $$ (14) 式中,${x_1} = {k_0}{a_1}$,表示球体的电尺寸。
将式(13)代入式(14),并求解线性方程组,可以得到散射系数${a_{mn}},{b_{mn}}$以及球心区域展开系数${\alpha _N}$。根据递推关系式(10),当求得展开系数${\alpha _N}$后,可以采用由内向外递推的方式以获得区域$N - 1$到区域1的场展开系数。并且,根据已经求得的散射系数${a_{mn}}$、${b_{mn}}$,可以对雷达散射截面进行计算,其定义为[21]:
$$ \sigma = \mathop {\lim }\limits_{r \to \infty } 4{\rm{ \mathsf{ π} }}{r^2}\frac{{{{\left| {{\mathit{\boldsymbol{E}}_{{\rm{sca}}}}} \right|}^2}}}{{{{\left| {{\mathit{\boldsymbol{E}}_{{\rm{inc}}}}} \right|}^2}}} $$ (15) 当$r \to \infty $时,球矢量波函数在远场的近似表达式可以在文献[22]中找到。
-
通过数值计算对旋磁非均匀介质球的雷达散射截面进行分析和讨论。根据已经得到的公式,可以计算空间任意点的场值。对于入射场,假设其幅度为1,极化方向沿着$x$轴,传播方向为$z$轴正方向,即${E_0} = 1,{p_\theta } = 1,{p_\phi } = 0$。球体结构的大小由电尺寸所描述${x_p} = {k_0}{a_p} = 2{\rm{ \mathsf{ π} }}{a_p}/\lambda $,介电常数统一假定为${\varepsilon _{ps}} = {\varepsilon _0}$,其中$p = 1,2, \cdots ,N$。由Lorenz-Mie理论知道,线性展开式(3)和式(4)是收敛级数,因此可以对展开式进行截断以便于实际的计算。本文的截断常数为${n_c}$[17]:
$$ {n_c} = {x_1} + 4x_1^{1/3} + 2 $$ (16) 实际计算中,递推式中不同区域的矩阵$\mathit{\boldsymbol{T}}$需要有相同的维度,那么各个区域中电磁场展开式的截断系数${n_c}$应该具有相同的值,为了获得足够的精度,本文采用最大电尺寸${x_1}$计算截断常数${n_c}$。
为了验证本文公式的正确性和有效性,首先将2层旋电介质球雷达散射截面的数值结果同有限元仿真结果进行对比,观察到雷达散射截面在E面和H面都具有很好的吻合,如图 3所示。其中电尺寸为:${x_1} = 2{\rm{ \mathsf{ π} }}$, ${x_2} = 1.5{\rm{ \mathsf{ π} }}$;材料参数为${\mu _{1s}}$=${\mu _{2s}}$=${\mu _0}$, ${\mu _{1\kappa }}$=${\mu _{2\kappa }}$=2, ${\mu _{1r}}$= 3.14 + 2.0i,${\mu _{2r}}$ = 6.28 + 2.0i。这在一定程度上证明了公式的正确性和数值计算的有效性。下面给出3个新的算例研究该散射结构的远场特性,并分析材料参数${\mu _r}$和${\mu _\kappa }$的改变对雷达散射截面的影响。
图 4给出了3层单轴各向异性磁球在E面和H面的双站雷达散射截面图,电尺寸和材料参数为:${x_1} = {\rm{ \mathsf{ π} }}$, ${x_2} = 0.8{\rm{ \mathsf{ π} }}$, ${x_3} = 0.6{\rm{ \mathsf{ π} }}$, ${\mu _{1s}} = 5{\mu _0}$, ${\mu _{2s}} = 7{\mu _0}$, ${\mu _{3s}} = 9{\mu _0}$, ${\mu _{p\kappa }} = 0$($p$=1, 2, 3)。其中根据不同的${\mu _{ps}}{\mu _{pr}}$($p$= 1, 2, 3)画出了3条雷达散射截面曲线图。由图 4可以看出,当${\mu _{ps}}{\mu _{pr}}$的值从$5{\mu _0}$增加到$9{\mu _0}$时,E面的谐振角往左有明显的偏移,而在H面,谐振角往右有着明显偏移。
图 5给出了3层旋磁各向异性球在E面和H面的雷达散射截面图,该散射结构的电尺寸和图 4相同,${\mu _{1s}} = {\mu _0}$,${\mu _{2s}} = 3{\mu _0}$,${\mu _{3s}} = 5{\mu _0}$。对于每一层的电磁参数,${\mu _{ps}}{\mu _{pr}} = 3{\mu _0}$($p$=1, 2, 3),而${\mu _{ps}}{\mu _{p\kappa }}$选取了4组参数,变化范围为${\mu _0}$到$2.5{\mu _0}$。从图 5可以看出随着${\mu _{ps}}{\mu _{p\kappa }}$的增加,E面和H面的雷达散射截面有着不规则的变化。因此可以预见通过改变${\mu _{ps}}{\mu _{p\kappa }}$的值来对散射场进行控制有困难。
图 6给出了一个中等电尺寸的5层无耗旋磁媒质球在E面和H面的雷达散射截面,材料参数为表 1所示。从图 6可以看出,当电尺寸变大以后,雷达散射截面曲线变得十分振荡,这与图 4和图 5有所不同。同时也可以看出当入射波长和散射体大小相当时,雷达散射截面图的分布特性。
表 1 5层无耗旋磁各向异性球体的电尺寸以及材料参数
区域 x μs μs/μr μs/μk 1 2π μ0 3μ0 2μ0 2 1.7π 3μ0 3μ0 2μ0 3 1.4π 5μ0 3μ0 2μ0 4 1.1π 7μ0 3μ0 2μ0 5 0.8π 9μ0 3μ0 2μ0 -
本论文以T矩阵方法为基础,得到了旋磁各向异性非均匀球体散射特性的新的解析解。根据Lorenz- Mie散射理论,入射场、散射场以及球体内部各区域的场被展开为球矢量波函数的线性叠加形式。通过在非连续表面匹配边界条件得到各区域场的展开系数以及散射系数。通过与有限元法计算得到的雷达散射截面数值结果进行对比,很好地验证了本文公式的正确性和有效性。最后通过几个算例对该模型的电磁散射特性进行了详细分析和讨论。对于旋磁材料,利用球形多层非均匀结构,可以实现对雷达散射截面的增强或者减弱的优化设计。
Anisotropic Scattering Characteristics of an Inhomogeneous Gyromagnetic Sphere
-
摘要: 应用 T 矩阵方法推导了旋磁各向异性径向非均匀球体散射场的解析解。置于自由空间的球形结构被分为N个区域,每个区域的材料参数为标量电导率和旋磁张量磁导率。根据球矢量波函数理论将入射场,散射场以及球体内部各个区域的电磁场展开为球矢量波函数的线性叠加,最后通过匹配边界条件求得散射系数。雷达散射截面数值结果与有限元方法得到的数值结果有很好的吻合,验证了公式的正确性与有效性。最后给出几个新的算例分析了旋磁非均匀球体的散射特性。Abstract: In this paper, we present an analytical T -matrix solution of Mie type for electromagnetic (EM) scattering by a radially multilayered gyromagnetic anisotropic sphere. A sphere located in free space is divided into N regions, each region is characterized by scalar permittivity and gyromagnetic permeability tensor. Based on the vector spherical wave functions (VSWFs) theory, the incident field, scattered field, and the field inside the sphere are expanded as linear combination of VSWFs. The scattering coefficients and unknown expansion coefficients of each layer are calculated by matching the boundary conditions on the discontinuous surfaces. According to the derived formulations, the numerical results of radar cross sections (RCS) given by proposed analytical method is in good agreement with those computed by finite element method (FEM). Several calculation examples for some specific cases are also presented to investigate the EM scattering characteristic of multilayered gyromagnetic sphere.
-
Key words:
- anisotropic media /
- electromagnetic scattering /
- gyromagnetic media /
- Mie theory /
- vector wave functions
-
表 1 5层无耗旋磁各向异性球体的电尺寸以及材料参数
区域 x μs μs/μr μs/μk 1 2π μ0 3μ0 2μ0 2 1.7π 3μ0 3μ0 2μ0 3 1.4π 5μ0 3μ0 2μ0 4 1.1π 7μ0 3μ0 2μ0 5 0.8π 9μ0 3μ0 2μ0 -
[1] MIE G. Beiträge zur optik trüber Medien, speziell kolloidaler Metallösungen[J]. Ann Phys, 1908, 25:377-452. doi: 10.1002/andp.19083300302 [2] WU Z S, WANG Y P. Electromagnetic scattering for multilayered sphere:Recursive algorithms[J]. Radio Sci, 1991, 26(6):1393-1401. doi: 10.1029/91RS01192 [3] JOHNSON B R. Light scattering by a multilayer sphere[J]. Appl Opt, 1996, 35(18):3286-3296. doi: 10.1364/AO.35.003286 [4] QIU Cheng-wei, ZOUHDI S, RAZEK A. Modified spherical wave functions with anisotropy ratio:Application to the analysis of scattering by multilayered anisotropic shells[J]. IEEE Trans Antennas Propag, 2007, 55(12):3515-3523. doi: 10.1109/TAP.2007.910491 [5] GENG You-lin, WU Xin-bao, LI Le-wei, et al. Mie scattering by a uniaxial anisotropic sphere[J]. Phys Rev E, 2004, 70(5):056609. doi: 10.1103/PhysRevE.70.056609 [6] GENG You-lin, QIU Cheng-wei, YUAN Ning. Exact solution to electromagnetic scattering by an impedance sphere coated with a uniaxial anisotropic layer[J]. IEEE Trans Antennas Propag, 2009, 57(2):572-576. doi: 10.1109/TAP.2008.2011410 [7] KISELEV A D, RESHETNYAK V Y, SLUCKIN T J. Light scattering by optically anisotropic scatterers:T-matrix theory for radial and uniform anisotropies[J]. Phys Rev E, 2002, 65(5):056609. doi: 10.1103/PhysRevE.65.056609 [8] STOUT B, NEVIERE M, POPOV E. T matrix of the homogeneous anisotropic sphere:applications to orientation-averaged resonant scattering[J]. J Opt Soc Am A, 2007, 24(4):1120-1130. doi: 10.1364/JOSAA.24.001120 [9] YAO Jing-jing, HE Si-yuan, ZHANG Yun-hua, et al. Evaluation of scattering from electrically large and complex PEC target coated with uniaxial electric anisotropic medium layer based on asymptotic solution in spectral domain[J]. IEEE Trans Antennas and Propag, 2014, 62(4):2175-2186. doi: 10.1109/TAP.2014.2300537 [10] YANG Kuo, ZHOU Jia-cheng, SHENG Wei-tian, et al. Efficient nystrom solutions of electromagnetic scattering by composite objects with inhomogeneous anisotropic media[J]. IEEE Trans Antennas and Propag, 2013, 61(10):5328-5332. doi: 10.1109/TAP.2013.2272671 [11] MARENGO E A. A new theory of the generalized optical theorem in anisotropic media[J]. IEEE Trans. Antennas and Propag, 2013, 61(4):2164-2179. doi: 10.1109/TAP.2012.2233702 [12] LI Ying-le, LI Jin, DONG Qun-feng, et al. Internal and external electric fields for an anisotropic dielectric particle in electromagnetic beams[J]. IEEE Trans Antennas and Propag, 2013, 61(9):4754-4758. doi: 10.1109/TAP.2013.2265215 [13] ZARIFI D, SOLEIMANI M, ABDOLALI A. Electromagnetic characterization of biaxial bianisotropic media using the state space approach[J]. IEEE Trans Antennas and Propag, 2014, 62(3):1538-1542. doi: 10.1109/TAP.2013.2297166 [14] GENG You-lin, WU Xin-bao, LI Le-wei. Analysis of electromagnetic scattering by a plasma anisotropic sphere[J]. Radio Science, 2003, 38(6):1104. doi: 10.1029/2003RS002913 [15] GENG You-lin, WU Xin-bao, LI Le-wei. Characterization electromagnetic scattering by a plasma anisotropic spherical shell[J]. IEEE Antennas Wireless Propag Lett, 2004, 3(1):100-103. https://www.researchgate.net/publication/224748844_Characterization_of_electromagnetic_scattering_by_a_plasma_anisotropic_spherical_shell [16] GENG You-lin, WU Xin-bao, LI Le-wei, et al. Electromagnetic scattering by an inhomogeneous plasma anisotropic sphere of multilayers[J]. IEEE Trans Antennas Propag, 2005, 53(12):3982-3989. doi: 10.1109/TAP.2005.859903 [17] LIN Zhi-fang, CHUI S T. Electromagnetic scattering by optically anisotropic magnetic particle[J]. Phys Rev E, 2004, 69(5):056614. doi: 10.1103/PhysRevE.69.056614 [18] LI J L W, ONG W L. A new solution for characterizing electromagnetic scattering by a gyroelectric sphere[J]. IEEE Trans Antennas and Propag, 2011, 59(9):3370-3378. doi: 10.1109/TAP.2011.2161541 [19] STRATTON J A. Electromagnetic Theory[M]. New York:McGraw-Hill, 1941. [20] BOHREN C F, HUFFMAN D R. Absorption and scattering of light by small particles[M]. New York:John Wiley & Sons, 1998. [21] TSANG L, KONG J A, SHIN T S. Theory of microwave remote sensing[M]. New York:Wiley-Interscience, 1985. [22] XU Yu-lin. Electromagnetic scattering by an aggregate of spheres:Far field[J]. Appl Opt, 1997, 36(36):9496-9508. doi: 10.1364/AO.36.009496 -


 ISSN
ISSN 




 下载:
下载: