-
阵列天线具有增益高、波束控制灵活等优点,在现代无线通信和雷达系统中得到越来越广泛的应用。对于实际的阵列天线,其辐射特性受各种工程实现误差的影响,主要包括天线阵元的通道误差[1-2],即阵元的激励幅度和激励相位误差;阵元与阵元之间的耦合作用[3-6];阵元位置安装误差等。另外还有一些系统误差,如馈电时产生的误差、放大器、采样器等。这些误差一般具有一定的随机性,导致阵列天线某些重要性能指标的下降。深入研究这些随机误差对阵列辐射方向图的影响具有重要的意义[7-8]。
文献[1]研究了激励电流的随机幅度、相位和位置误差对方向图均值的影响。文献[2]在阵列天线出现激励幅度相位误差时,对线阵方向图的分布进行了概率分析。文献[3-6]考虑互耦时的随机幅相误差对天线方向图的影响进行了分析。文献[7]在出现激励幅度相位误差时对阵列方向图的主瓣增益和平均副瓣电平产生的影响进行了分析。文献[8]从理论角度对随机误差进行了数值分析并且导出两种评估随机误差所引起的副瓣电平的公式。文献[9]对幅度误差和相位误差多种组合的情况,分析了通道误差对波束方向图的影响。文献[10-13]对阵列误差的校正方法进行了研究。文献[14-15]将区间分析数学方法引入阵列天线领域,分析了含扰动的功率方向图的区间,为实际工程的实现提供了参考。
本文对阵列天线的通道实现误差和位置误差进行理论推导和分析,在高斯分布的假设下,分析了功率方向图的期望值,并推导了功率方向图方差的理论公式。进一步地,结合切比雪夫不等式,推导了在给定概率条件下功率方向图上、下边界的理论预测公式。最后,使用蒙特卡洛模拟,验证了本文理论推导的正确性和准确度。
-
考虑一个$N$元的线性阵列,波长为$\lambda $,对应第$n$个阵元的激励为${w_n}$(其中幅度表示为${I_n}$,相位表示为${\varphi _n}$,即${w_n} = {I_n}{{\rm{e}}^{{\rm{j}}{\varphi _n}}}$),对应$n$个在$Z$轴上排列的阵元位置${z_n}$,当不考虑耦合作用,阵列的方向图可以表示为:
$$f(\theta ) = \sum\limits_{n = 1}^N {{I_n}{{\rm{e}}^{{\rm{j}}{\varphi _n}}}{{\rm{e}}^{{\rm{j}}\beta {z_n}\cos \theta }}} $$ (1) 可以将上述方向图的进一步表示为:
$$f(\theta ) = \sum\limits_{n = 1}^N {{I_n}{{\rm{e}}^{{\rm{j}}{\varphi _n}}}{{\rm{e}}^{{\rm{j}}u{z_n}}}} $$ (2) 式中,$\beta = \frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }$;$u = \frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }cos\theta $。
假设理想的阵元激励幅度为${I_n}$,激励相位为${\varphi _n}$,位置为${z_n}$,当阵元的激励产生误差(即通道误差)和位置产生误差时,添加扰动之后的幅度、相位和位置分别设为${I_n}^e$、${\varphi _n}^e$和${z_n}^e$,加上误差之后的阵元的激励、相位和位置则可分别表示为:
$${I_n}^e = {I_n}(1 + \Delta {I_n})$$ (3) $${\varphi _n}^e = {\varphi _n} + \Delta {\varphi _n}$$ (4) $${z_n}^e = {z_n} + \Delta {z_n}$$ (5) 因为误差的产生是不确定因素,并不一定只存在单一类型的误差,有可能是阵元幅度、相位、位置同时存在误差,此时阵列的方向图就变为:
$${f^e}(\theta ) = \sum\limits_{n = 1}^N {{I_n}^e{{\rm{e}}^{{\rm{j}}{\varphi _n}^e}}{{\rm{e}}^{{\rm{j}}u{z_n}^e}}} $$ (6) -
阵列的通道误差可能是由于处理器配置时的不准确造成的,而位置误差是由于对阵元的位置配置不够精确导致。假设阵元的相对幅度误差$\Delta {I_n}$、相位误差$\Delta {\varphi _n}$、位置误差$\Delta {z_n}$都是随机变量,且服从统计独立、零均值的高斯分布,在此种假设下,对阵列的波束方向图进行分析。
实际波束功率方向图的期望值可以表示为:
$${\rm{E}}\left[ {{{\left| {{f^e}(\theta )} \right|}^2}} \right] = {\rm{E}}\left[ {\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^N {{I_n}^e{{\rm{e}}^{{\rm{j}}{\varphi _n}^e}}{{\rm{e}}^{{\rm{j}}u{z_n}^e}}} } {I_m}^e{{\rm{e}}^{{\rm{j}}{\varphi _m}^e}}{{\rm{e}}^{{\rm{j}}u{z_n}^e}}} \right]$$ (7) 可以将上述表达式转换为:
$$\begin{gathered} {\rm{E}}\left[ {{{\left| {{f^e}(\theta )} \right|}^2}} \right] = \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^N {{\rm{E}}[{I_n}(1 + \Delta {I_n}){I_m}(1 + \Delta {I_m})} } \times \\ {{\rm{e}}^{{\rm{j}}({\varphi _n} + \Delta {\varphi _n} - {\varphi _m} - \Delta {\varphi _m})}}{e^{ju({z_n} + \Delta {z_n} - {z_m} - \Delta {z_m})}}] \\ \end{gathered} $$ (8) 令:
$${\alpha _{mn}} = {\rm{E}}\left[ {(1 + \Delta {I_n})(1 + \Delta {I_m}){{\rm{e}}^{{\rm{j}}(\Delta {\varphi _n} - \Delta {\varphi _m})}}} \right]$$ (9) $${\rho _{mn}} = {\rm{E}}\left[ {{{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m})}}} \right]$$ (10) 当$m = n $时,则:
$${\alpha _{mn}} = {\rm{E}}\left[ {(1 + \Delta {I_n})(1 + \Delta {I_m})} \right] = \;1 + {\sigma _I}^2$$ (11) 当$ m \ne n$时,则:
$$\begin{gathered} {\alpha _{mn}} = {\rm{E}}\left[ {(1 + \Delta {I_n}){{\rm{e}}^{{\rm{j}}\Delta {\varphi _n}}}} \right]{\rm{E}}\left[ {(1 + \Delta {I_m}){{\rm{e}}^{ - {\rm{j}}\Delta {\varphi _m}}}} \right] = \\ {\rm{E}}[{{\rm{e}}^{{\rm{j}}\Delta {\varphi _n}}}]{\rm{E[}}{{\rm{e}}^{ - {\rm{j}}\Delta {\varphi _m}}}] \\ \end{gathered} $$ (12) 已知对X服从期望为0,方差为${\sigma ^2}$的高斯分布满足:
$${\rm{E}}[{{\rm{e}}^{{\rm{j}}kx}}] = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\int_{ - \infty }^{ + \infty } {{{\rm{e}}^{{\rm{j}}kx}}{{\rm{e}}^{ - \frac{{{x^2}}}{{2\sigma }}}}} {\rm{d}}x = {{\rm{e}}^{\frac{{ - {k^2}{\sigma ^2}}}{2}}}$$ (13) 所以,
$${\rm{E}}[{{\rm{e}}^{{\rm{j}}\Delta {\varphi _n}}}] = {\rm{E}}[{{\rm{e}}^{ - {\rm{j}}\Delta {\varphi _m}}}] = {{\rm{e}}^{\frac{{ - {\sigma _\varphi }^2}}{2}}}$$ (14) $${\alpha _{mn}} = \;{\rm{E}}[{{\rm{e}}^{{\rm{j}}\Delta {\varphi _n}}}]{\rm{E}}[{{\rm{e}}^{ - {\rm{j}}\Delta {\varphi _m}}}] = {{\rm{e}}^{ - {\sigma _\varphi }^2}}$$ (15) 综上可得:
$${\alpha _{mn}} = \left\{ \begin{gathered} {{\rm{e}}^{ - {\sigma _\varphi }^2}}\;\;\;{\rm{ }}\;m \ne n \hfill \\ 1 + {\sigma _I}^2{\rm{ }}\;m = n \hfill \\ \end{gathered} \right.$$ (16) 同理,
$${\rho _{mn}} = \left\{ \begin{gathered} {{\rm{e}}^{ - {\sigma _l}^2{u^2}}} = {{\rm{e}}^{ - {\sigma _\lambda }^2}}{\rm{ }}\;m \ne n \hfill \\ 1{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m = n \hfill \\ \end{gathered} \right.$$ (17) 式中,${\sigma _I}^2$为阵元激励幅度误差的方差;${\sigma _\varphi }^2$为阵元激励相位误差的方差;${\sigma _l}^2$为阵元位置误差的方差;${\sigma _\lambda }^2$是以波长的形式计算时对应的位置误差的方差。对应的实际波束功率方向图的期望值可以表示为:
$$\begin{array}{*{20}{c}} {{\rm{E}}\left[ {{{\left| {{f^e}(\theta )} \right|}^2}} \right] = \sum\limits_{n = 1, n \ne m}^N {\sum\limits_{m = 1}^N {{\rm{E}}[{I_n}{I_m}{{\rm{e}}^{{\rm{j}}({\varphi _n} - {\varphi _m})}}} } {{\rm{e}}^{{\rm{j}}u({z_n} - {z_m})}} \times }\\ {{{\rm{e}}^{ - ({\sigma _\varphi }^2 + {\sigma _\lambda }^2)}}] + \sum\limits_{n = 1}^N {(1{\rm{ + }}{\sigma _I}^2){I_n}^2}} \end{array} $$ (18) 若在式(18)中第一项加上$m = n$的结果${I_n}^2{e^{ - ({\sigma _\varphi }^2 + {\sigma _\lambda }^2)}}$,且在第二项中减去该项,则可将式(18)化简为:
$$\begin{gathered} {\rm{E}}\left[ {{{\left| {{f^e}(\theta )} \right|}^2}} \right] = {\left| {f(\theta )} \right|^2}{{\rm{e}}^{ - ({\sigma _\varphi }^2 + {\sigma _\lambda }^2)}} + \\ \sum\limits_{n = 1}^N {{I_n}^2\left[ {(1{\rm{ + }}{\sigma _I}^2) - {{\rm{e}}^{ - ({\sigma _\varphi }^2 + {\sigma _\lambda }^2)}}} \right]} \\ \end{gathered} $$ (19) 由上式看出,阵列实现过程中的随机误差会对阵列的方向图产生两种影响。第一种影响可以由式(19)的第一项看出,它表明加入了随机误差之后的波束方向图与理想的波束方向图会有一个统计偏差,实际的波束方向图对比理想波束方向图有均匀的衰减,导致阵列增益有所下降。一般而言,由于随机误差的方差比较小,这种增益的下降不会太大。从式(19)中第二项表明,在统计平均意义上,随机实现误差导致理想波束方向图的旁瓣电平抬升,这种抬升量在不同角度是均匀分布的。因此,对于阵列旁瓣电平有严格要求的应用场合,在阵列设计中考虑实际实现过程中的误差因素是非常重要的。
-
利用数理统计中的公式$D(X){\rm{ = E}}[{X^2}] - $ ${{\rm{\{ E}}[X]\} ^2}$,对应的功率方向图的方差值为:
$$D[|{f^e}(\theta ){|^2}] = {\rm{E}}[|{f^e}(\theta ){|^4}] - {\rm{E}}[|{f^e}(\theta ){|^2}]$$ (20) ${\rm{E}}[|{f^e}(\theta ){|^2}]$由式(19)已知,${\rm{E}}[|{f^e}(\theta ){|^4}]$推导如下:
$$\begin{array}{*{20}{c}} {{\rm{E}}\left[ {{{\left| {{f^e}(\theta )} \right|}^4}} \right] = {\rm{E}}\left[ {\sum\limits_{q = 1}^N {\sum\limits_{p = 1}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {I_n^e} } } } } \right.{{\rm{e}}^{{\rm{j}}\varphi _n^e}}{{\rm{e}}^{{\rm{j}}u{z_n}^e}}I_m^e{{\rm{e}}^{{\rm{j}}\varphi _m^e}}{{\rm{e}}^{{\rm{j}}u{z_m}^e}} \times}\\ {\left. { I_{\rm{p}}^{\rm{e}}{{\rm{e}}^{{\rm{j}}\varphi _p^e}}{{\rm{e}}^{{\rm{j}}u{z_p}^e}}I_{\rm{q}}^{\rm{e}}{{\rm{e}}^{{\rm{j}}\varphi _q^e}}{{\rm{e}}^{{\rm{j}}u{z_q}^e}}} \right] =}\\ {\sum\limits_{{\rm{q}} = 1}^N {\sum\limits_{p = 1}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{\rm{E}}[{I_n}(1 + \Delta {I_n}){I_m}(1 + \Delta {I_m})} } } } \times}\\ {{{\rm{e}}^{{\rm{j}}\left( {{\varphi _n} - {\varphi _m} + \Delta {\varphi _n} - \Delta {\varphi _m}} \right)}}{{\rm{e}}^{{\rm{j}}u({z_n} - {z_m} + \Delta {z_n} - \Delta {z_m})}} \times}\\ { {I_p}(1 + \Delta {I_p}){I_q}(1 + \Delta {I_q}) \times}\\ {{{\rm{e}}^{{\rm{j}}({\varphi _p} - {\varphi _q} + \Delta {\varphi _p} - \Delta {\varphi _q})}}{{\rm{e}}^{{\rm{j}}u({z_p} - {z_q}{\bf{ + }}\Delta {z_p} - \Delta {z_q})}}]} \end{array} $$ (21) 令:
$$\begin{gathered} {\alpha _{mnpq}} = {\rm{E}}[(1 + \Delta {I_n})(1 + \Delta {I_m})(1 + \Delta {I_p}) \times \\ (1 + \Delta {I_q}){{\rm{e}}^{{\rm{j}}(\Delta {\varphi _n} - \Delta {\varphi _m} + \Delta {\varphi _p} - \Delta {\varphi _q})}}] \\ \end{gathered} $$ (22) $${\rho _{{\rm{nmpq}}}} = {\rm{E}}[{{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m}{\bf{ + }}\Delta {z_p} - \Delta {z_q})}}]$$ (23) 根据n, m, p, q的关系,可以分为如下情况:
情况1):4个变量相同,对应的,
$${\alpha _n} = {\rm{E}}[{(\Delta {I_n} + 1)^4}] = 3{\sigma _I}^4 + 6{\sigma _I}^2 + 1$$ (24) $${\rho _n} = {\rm{E}}[{{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m} + \Delta {z_p} - \Delta {z_q})}}]{\rm{ = }}1$$ (25) $n = m = p = q$,对应的期望分量,
$${{\rm{E}}_A}{\rm{ = }}\sum\limits_{n = 1}^N {{I_n}^4(3{\sigma _I}^4 + 6{\sigma _I}^2 + 1)} $$ (26) 情况2):3个变量相同,对应的,
$$\begin{gathered} {\alpha _{nm}} = {\rm{E}}[{(1 + \Delta {I_n})^3}(1 + \Delta {I_m}){{\rm{e}}^{{\rm{j}}(\Delta {\varphi _n} - \Delta {\varphi _m})}}] = \\ (3{\sigma _I}^2 + 1){{\rm{e}}^{ - {\sigma _\varphi }^2}} \\ \end{gathered} $$ (27) $${\rho _{{\rm{nm}}}} = {\rm{E}}[{{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m} + \Delta {z_p} - \Delta {z_q})}}] = {{\rm{e}}^{ - {\sigma _\lambda }^2}}$$ (28) B1:$n = m = p \ne q$,对应的期望分量,
$${{\rm{E}}_{{\rm{B1}}}}{\rm{ = }}\sum\limits_{\begin{array}{*{20}{c}} {p = 1}\\ {p \ne q} \end{array}}^{N} {\sum\limits_{q = 1}^N {{I_{\rm{p}}}^3{I_q}(3{\sigma _I}^2 + 1)} } {{\rm{e}}^{ - ({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}({\varphi _{\rm{p}}} - {\varphi _{\rm{q}}})}}{{\rm{e}}^{{\rm{j}}u({z_p} - {z_q})}}$$ (29) B2:$n = m = q \ne p$,对应的期望分量,
$$ {{\rm{E}}_{{\rm{B}}2}}{\rm{ = }}\sum\limits_{\begin{array}{*{20}{c}} {p = 1}\\ {p \ne q} \end{array}}^{N} {\sum\limits_{p = 1}^N {{I_p}{I_q}^3(3{\sigma _I}^2 + 1)} } {{\rm{e}}^{ - ({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}({\varphi _{\rm{p}}} - {\varphi _{\rm{q}}})}}{{\rm{e}}^{{\rm{j}}u({z_p} - {z_q})}} $$ (30) B3:$n = p = q \ne m$,对应的期望分量${{\rm{E}}_{{\rm{B3}}}}$与B1情况的期望分量${{\rm{E}}_{{\rm{B1}}}}$相同,不再赘述。
B4:$m = p = q \ne n$,对应的期望分量${{\rm{E}}_{{\rm{B4}}}}$与B2情况的期望分量${{\rm{E}}_{{\rm{B2}}}}$相同。
由结果可以看出,${{\rm{E}}_{{\rm{B1}}}}{\rm{ = }}{{\rm{E}}_{{\rm{B3}}}}$,${{\rm{E}}_{{\rm{B2}}}}{\rm{ = }}{{\rm{E}}_{{\rm{B4}}}}$,且${{\rm{E}}_{{\rm{B1}}}}$与${{\rm{E}}_{{\rm{B2}}}}$,${{\rm{E}}_{{\rm{B3}}}}$与${{\rm{E}}_{{\rm{B4}}}}$构成共轭相位。
情况3):有2组2个变量相同,且2组相同变量均构成共轭相位项,对应的,
$${\alpha _{nm}} = {\rm{E}}[{(1 + \Delta {I_n})^2}{(1 + \Delta {I_m})^2}] = {(1 + {\sigma _I}^2)^2}$$ (31) $${\rho _{{\rm{nm}}}} = {\rm{E}}[{{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m} + \Delta {z_p} - \Delta {z_q})}}] = 1$$ (32) C1:$n = m \ne p = q$,对应的期望分量,
$${{\rm{E}}_{{\rm{C1}}}}{\rm{ = }}\sum\limits_{\begin{array}{*{20}{c}} {{\rm p} = 1}\\ {n \ne p} \end{array}}^{N}{\sum\limits_{n = 1}^N {{I_n}^2{I_{\rm{p}}}^2(1 + } } {\sigma _I}^2{)^2}$$ (33) C2:$n = q \ne m = p$,对应的期望分量${{\rm{E}}_{{\rm{C2}}}}$与C1情况的期望分量${{\rm{E}}_{{\rm{C1}}}}$相同。
情况4):有2组2个变量相同,且不构成共轭相位项。对应的,
$$\begin{gathered} {\alpha _{nm}} = {\rm{E}}[{(1 + \Delta {I_n})^2}{(1 + \Delta {I_m})^2}{{\rm{e}}^{{\rm{j}}(2\Delta {\varphi _n} - 2\Delta {\varphi _m})}}] = \\ {(1 + {\sigma _I}^2)^2}{{\rm{e}}^{ - 4{\sigma _\varphi }^2}} \\ \end{gathered} $$ (34) $${\rho _{{\rm{nm}}}} = {\rm{E}}[{{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m} + \Delta {z_p} - \Delta {z_q})}}] = {{\rm{e}}^{ - 4{\sigma _\lambda }^2}}$$ (35) D:$n = p \ne m = q$,对应的期望分量,
$${{\rm{E}}_{\rm{D}}}{\rm{ = }}\sum\limits_{\begin{array}{*{20}{c}} { m = 1 }\\ { n \ne m} \end{array}}^N {\sum\limits_{n = 1}^N {{I_n}^2{I_m}^2{{(1 + {\sigma _I}^2)}^2}} } {{\rm{e}}^{ - 4({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}2({\varphi _{\rm{n}}} - {\varphi _m})}}{{\rm{e}}^{{\rm{j}}2u({z_n} - {z_m})}}$$ (36) 情况5):有1组2个变量相同,且构成共轭相位项。对应的,
$$\begin{gathered} {\alpha _{nmp}} = {\rm{E}}[{(1 + \Delta {I_n})^2}(1 + \Delta {I_m})(1 + \Delta {I_p}){{\rm{e}}^{{\rm{j}}(\Delta {\varphi _p} - \Delta {\varphi _m})}}] = \\ (1 + {\sigma _I}^2){{\rm{e}}^{ - {\sigma _\varphi }^2}} \\ \end{gathered} $$ (37) $${\rho _{{\rm{nmp}}}} = {\rm{E}}[{{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m} + \Delta {z_p} - \Delta {z_q})}}] = {{\rm{e}}^{ - {\sigma _\lambda }^2}}$$ (38) E1:$n = m, {\rm{ }}n \ne p, {\rm{ }}n \ne q, {\rm{ }}p \ne q$,对应的期望分量,
$${{\rm{E}}_{{\rm{E1}}}}{\rm{ = }}\sum\limits_{\begin{array}{*{20}{c}} {q = 1 }\\ {q \ne p, }\\ {q \ne n, }\\ {n \ne p } \end{array}}^N {\sum\limits_{p = 1}^N {\sum\limits_{n = 1}^N {{I_n}^2{I_p}{I_q}(1 + {\sigma _I}^2)} } } {{\rm{e}}^{ - ({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}({\varphi _p} - {\varphi _q})}}{{\rm{e}}^{{\rm{j}}u({z_p} - {z_q})}}$$ (39) E2:$n = q, {\rm{ }}n \ne m, {\rm{ }}n \ne p, m \ne p$,对应的期望分量${{\rm{E}}_{{\rm{E2}}}}$与E3:$m = p{\rm{ }}, {\rm{ }}n \ne p, {\rm{ }}n \ne q, {\rm{ }}n \ne m$,对应的期望分量${{\rm{E}}_{{\rm{E3}}}}$,以及E4:$p = q, {\rm{ }}p \ne n, {\rm{ }}p \ne m, {\rm{ }}n \ne m$,对应的期望分量${{\rm{E}}_{{\rm{E4}}}}$的结果关系为:${{\rm{E}}_{{\rm{E1}}}}{\rm{ = }}{{\rm{E}}_{{\rm{E2}}}}{\rm{ = }}{{\rm{E}}_{{\rm{E3}}}}{\rm{ = }}$ ${{\rm{E}}_{{\rm{E4}}}}$。
情况6):有1组2个变量相同,且不构成共轭相位项。对应的,
$$\begin{array}{*{20}{c}} {{\alpha _{nmq}} = {\rm{E}}[{(1 + \Delta {I_n})^2}(1 + \Delta {I_m})(1 + \Delta {I_q}){{\rm{e}}^{{\rm{j}}(2\Delta {\varphi _p} - \Delta {\varphi _m} - \Delta {\varphi _q})}}]{\rm{ = }}}\\ {(1 + {\sigma _I}^2){{\rm{e}}^{ - 3{\sigma _I}^2}}} \end{array}$$ (40) $${\rho _{{\rm{nmq}}}} = E({{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m} + \Delta {z_p} - \Delta {z_q})}}) = {{\rm{e}}^{ - 3{\sigma _\lambda }^2}}$$ (41) F1:$n = p, {\rm{ }}n \ne m, {\rm{ }}n \ne q, {\rm{ }}m \ne q$,对应期望分量:
$$\begin{array}{*{20}{c}} {{{\rm{E}}_{{\rm{F1}}}}{\rm{ = }}\sum\limits_{\begin{array}{*{20}{c}} {q = 1 }\\ {q \ne m}\\ {q \ne n}\\ {n \ne m} \end{array}}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {} } } {I_n}^2{I_m}{I_q}(1 + {\sigma _I}^2){{\rm{e}}^{ - 3({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{j(2{\varphi _{\rm{n}}} - {\varphi _m} - {\varphi _q})}} \times}\\ {{{\rm{e}}^{{\rm{j}}u(2{z_n} - {z_m} - {z_q})}}} \end{array}$$ (42) F2:$m = q{\rm{ }}, n \ne m, {\rm{ }}n \ne p, {\rm{ }}p \ne q$,对应期望分量:
$$\begin{array}{*{20}{c}} {{{\rm{E}}_{{\rm{F2}}}}{\rm{ = }}\sum\limits_{\begin{array}{*{20}{c}} {p = 1 }\\ {p \ne m}\\ {p \ne n}\\ {n \ne m} \end{array}}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{I_n}{I_m}^2{I_p}(1 + {\sigma _I}^2){{\rm{e}}^{ - 3({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}({\varphi _{\rm{n}}} - 2{\varphi _m} + {\varphi _p})}}} } } \times}\\ {{{\rm{e}}^{{\rm{j}}u({z_n} - 2{z_m} + {z_p})}}} \end{array}$$ (43) 由结果可知,${{\rm{E}}_{F1}}$和${{\rm{E}}_{F2}}$构成共轭相位。
情况7):4个变量均不相等,对应的,
$$\begin{gathered} {\alpha _{nmpq}} = {\rm{E}}[(1 + \Delta {I_n})(1 + \Delta {I_m})(1 + \Delta {I_p})(1 + \Delta {I_q}) \times \\ {{\rm{e}}^{{\rm{j}}(\Delta {\varphi _n} - \Delta {\varphi _m})}}{{\rm{e}}^{{\rm{j}}(\Delta {\varphi _p} - \Delta {\varphi _q})}}] = {{\rm{e}}^{ - 2{\sigma _\varphi }^2}} \\ \end{gathered} $$ (44) $${\rho _{nmpq}} = {\rm{E}}[{{\rm{e}}^{{\rm{j}}u(\Delta {z_n} - \Delta {z_m} + \Delta {z_p} - \Delta {z_q})}}] = {{\rm{e}}^{ - 2{\sigma _\lambda }^2}}$$ (45) G:$n \ne m, {\rm{ }}n \ne p, {\rm{ }}n \ne q, {\rm{ }}m \ne p$,对应期望分量
$$\begin{array}{*{20}{c}} {{{\rm{E}}_{\rm{G}}}{\rm{ = }}\sum\limits_{\begin{array}{*{20}{c}} {q = 1 }\\ {q \ne p, }\\ {q \ne m }\\ {q \ne n, }\\ {p \ne m }\\ {p \ne n, }\\ {m \ne n } \end{array}}^N {\sum\limits_{p = 1}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{I_n}{I_m}} } } } {I_p}{I_q}{{\rm{e}}^{ - 2({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}({\varphi _{\rm{n}}} - {\varphi _m} + {\varphi _p} - {\varphi _q})}} \times}\\ {{{\rm{e}}^{{\rm{j}}u({z_n} - {z_m} + {z_p} - {z_q})}}} \end{array}$$ (46) 综合以上结果,得到:
$$\begin{array}{*{20}{c}} {{\rm{E}}[|{f^e}(\theta ){|^4}] = \sum\limits_{{\rm{q}} = 1}^N {\sum\limits_{p = 1}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{\rm{E}}[{I_n}(1 + \Delta {I_n})} } } } {I_m}(1 + \Delta {I_m}) \times}\\ {{{\rm{e}}^{{\rm{j}}({\varphi _n} - {\varphi _m} + \Delta {\varphi _n} - \Delta {\varphi _m})}}{{\rm{e}}^{{\rm{j}}u({z_n} - {z_m} + \Delta {z_n} - \Delta {z_m})}}{I_p}(1 + \Delta {I_p}){I_q}(1 + \Delta {I_q}) \times}\\ {{{\rm{e}}^{{\rm{j}}({\varphi _p} - {\varphi _q} + \Delta {\varphi _p} - \Delta {\varphi _q})}}{{\rm{e}}^{{\rm{j}}u({z_p} - {z_q} + \Delta {z_p} - \Delta {z_q})}}] =}\\ {\sum\limits_{n = 1}^N {{I_n}^4(3{\sigma _I}^4 + 6{\sigma _I}^2 + 1)} + 2\sum\limits_{\begin{array}{*{20}{c}} {m = 1 }\\ {n \ne m } \end{array}}^N {\sum\limits_{n = 1}^N {{I_n}^2{I_m}^2(1 + } } {\sigma _I}^2{)^2} + }\\ 2\sum\limits_{\begin{array}{*{20}{c}} {m = 1 }\\ {n \ne m } \end{array}}^N {\sum\limits_{n = 1}^N {{I_n}^3{I_m}(3{\sigma _I}^2 + 1)} } {{\rm{e}}^{ - ({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}u({z_n} - {z_m})}} + \\ 2\sum\limits_{\begin{array}{*{20}{c}} {m = 1 }\\ {n \ne m } \end{array}}^N {\sum\limits_{n = 1}^N {{I_n}{I_m}^3(3{\sigma _I}^2 + 1)} } {{\rm{e}}^{ - ({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}u({z_n} - {z_m})}} + \\ 4\sum\limits_{\begin{array}{*{20}{c}} {p = 1 }\\ {p \ne m}\\ {p \ne n}\\ {n \ne m} \end{array}}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{I_n}^2{I_m}{I_p}(1 + {\sigma _I}^2)} } } {{\rm{e}}^{ - ({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}({\varphi _p} - {\varphi _m})}}{{\rm{e}}^{{\rm{j}}u({z_p} - {z_m})}} + \\ \sum\limits_{\begin{array}{*{20}{c}} {m = 1 }\\ {n \ne m } \end{array}}^N {\sum\limits_{n = 1}^N {{I_n}^2{I_m}^2{{(1 + {\sigma _I}^2)}^2}} } {{\rm{e}}^{ - 4({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}2({\varphi _n} - {\varphi _m})}}{{\rm{e}}^{{\rm{j}}2u({z_n} - {z_m})}} + \\ \sum\limits_{\begin{array}{*{20}{c}} {q = 1 }\\ {q \ne m}\\ {q \ne n}\\ {n \ne m} \end{array}}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{I_n}^2{I_m}{I_q}(1 + {\sigma _I}^2){{\rm{e}}^{ - 3({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}} } } {{\rm{e}}^{{\rm{j}}(2{\varphi _n} - {\varphi _m} - {\varphi _q})}} \times \\ {{\rm{e}}^{{\rm{j}}u(2{z_n} - {z_m} - {z_q})}} + \sum\limits_{\begin{array}{*{20}{c}} {q = 1 }\\ {q \ne m}\\ {q \ne n}\\ {n \ne m} \end{array}}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{I_n}{I_m}^2{I_q}(1 + {\sigma _I}^2){{\rm{e}}^{ - 3({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}} } } \times \\ {{\rm{e}}^{{\rm{j}}(2{\varphi _n} - {\varphi _m} - {\varphi _q})}}{{\rm{e}}^{{\rm{j}}u(2{z_n} - {z_m} - {z_q})}} + \\ {\sum\limits_{\begin{array}{*{20}{c}} {q = 1 }\\ {q \ne p }\\ {q \ne m }\\ {q \ne n }\\ {p \ne m }\\ {p \ne n }\\ {m \ne n } \end{array}}^N {\sum\limits_{p = 1}^N {\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{I_n}{I_m}} } } } {I_p}{I_q}{{\rm{e}}^{ - 2({\sigma _\phi }^2 + {\sigma _\lambda }^2)}}{{\rm{e}}^{{\rm{j}}({\varphi _{\rm{n}}} - {\varphi _m} + {\varphi _p} - {\varphi _q})}} \times}\\ {{{\rm{e}}^{{\rm{j}}u({z_n} - {z_m} + {z_p} - {z_q})}}} \end{array}$$ (47) 由此,根据式(19)、式(20)和式(47)的推导,得到随机误差扰动的实际阵列功率方向图方差的理论值。由切比雪夫不等式:设随机变量$X$的数学期望${\rm{E}}(X)$和$D(X)$存在,则对任意常数$\varepsilon > 0$,有下列不等式成立:
$$P(|X - {\rm{E}}(X)| \geqslant \varepsilon ) \leqslant \frac{{D(X)}}{{{\varepsilon ^2}}}$$ (48) $$P(|X - {\rm{E}}(X)| < \varepsilon ) \geqslant 1 - \frac{{D(X)}}{{{\varepsilon ^2}}}$$ (49) 因此,根据推导的阵列功率方向图的期望和方差的理论值,再利用切比雪夫不等式,可以对功率方向图的扰动范围进行粗略估计。
-
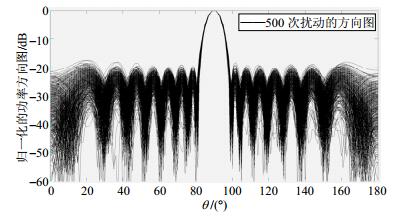
考虑某16元阵列,在理想情况下阵元均匀间隔半个波长,激励幅度对应副瓣电平为-25 dB的切比雪夫分布,激励相位由波束指向90°的相位聚焦条件确定。理想情况下的波束方向图如图 1中的虚线所示。分别在阵元激励的幅度加上均值为0,均方差为0.02的高斯随机误差;在阵元激励相位加上均值为0,均方差为5°的高斯随机误差;在阵元位置加入均值为0,均方差为0.01个波长的高斯随机误差。为统计分析,本文进行了500次的扰动。图 1显示了500次扰动功率方向图,图 2显示了本文推导的方向图期望的理论值,统计平均结果,无扰动的理想方向图以及利用文献[2]计算的期望结果。
从图 1、图 2可以看出,相比原来得到的最大副瓣电平值-25 dB,加入随机误差会导致副瓣电平抬升,最高超过了-20 dB,在实际应用中对系统产生较大的影响。本文理论预测的功率方向图期望值与文献[2]结果基本一致,且与500次统计平均值结果吻合,验证了式(18)的准确性。

图 2 理论期望、统计均值、无扰动的理想方向图、文献[2]的期望结果对比
将期望和方差结果用在切比雪夫不等式中:
$$P(|X - {\rm{E}}(X)| < 3\sigma ) \geqslant 1 - \frac{{{\sigma ^2}}}{{{{(3\sigma )}^2}}} \approx 0.90$$ (50) 以此概率得出扰动功率方向图的上、下界,当下界低于0时,取0为下界,归一化后如图 3所示。图 4显示了500次扰动在不同角度上超过边界的比例,约在3.5%以内,满足不超过10%的预测,验证了使用切比雪夫不等式预测的正确性。由于这种预测是在不确定功率方向图这种随机变量的实际分布类型的情况下进行的,预测边界较实际情况松弛。
-
本文对阵列天线方向图受位置、激励幅度和相位实现误差的影响进行了分析,推导了扰动功率方向图的理论期望和方差。并且利用期望和方差结果,结合切比雪夫不等式,得出了含扰动的功率方向图在给定概率下满足的上下边界。对所得结果进行了蒙特卡洛模拟分析,证明了本文理论预测的正确性和准确度。结果也显示,实际阵列中的随机实现误差通常会导致副瓣电平受到较大影响。若在阵列设计时对实现过程中的误差因素进行分析,则可以利用本文结果预测随机扰动方向图的期望、方差以及满足给定概率条件下的方向图边界,从而可以事先对工程中的实现误差所带来的阵列性能影响进行较为准确的预估。
值得说明的是,在本文推导过程中,采用了理想点源线性阵列的数学模型,如式(1)所述。对式(1)进行适当扩展,本文提出的理论推导方法可以适用于任意三维的点源阵列情况。并且,如果采用有源单元方向图取代理想点源模型,则本文方法可以进一步推广用于分析含耦合及平台影响的共形阵列受通道幅相的影响。另外,本文假定了随机实现误差满足高斯分布,因此所得结论适用于高斯误差的情况。当考虑误差为均匀随机分布时,可以借鉴本文所给的理论推导方法,在均匀随机误差模型下重新推导扰动功率方向图的期望及方差。
Analysis of Power Pattern Pertubations Due to Implementation Errors in Practical Antenna Arrays
-
摘要: 对阵列天线工程实现过程中的阵元位置、激励幅度和相位误差进行了分析,在假定各误差为高斯分布的情况下分析了阵列天线功率方向图的期望,并推导了功率方向图方差的理论公式。利用切比雪夫不等式,推导了在给定概率条件下功率方向图上、下边界的理论结果。使用蒙特卡洛模拟,验证了理论推导的正确性和准确度。利用该结果,可以较为准确地预测实际阵列天线中随机实现误差对阵列功率方向图的影响,对于阵列天线工程实践具有重要的指导意义。Abstract: The influence of amplitude, phase and position errors on the performance of an antenna array is analyzed and studied in this paper. On the assumption that each type of these random errors obeys the Gauss distribution, the expectation of the antenna array power pattern is analyzed, and the theoretical formula of variance is derived for the first time. In addition, theoretical upper and lower boundaries on which the power pattern falls on with a given probability are derived by using the Chebyshev's inequality. The effectiveness and accuracy of all the obtained theoretical equations are verified by Monte Carlo simulation. The simulation results show that the influence of the random implementation errors on the power pattern can be accurately predicted by using the proposed technique. Hence, it provides significant guidance for the practical array antenna design.
-
Key words:
- antenna arrays /
- Gaussian distribution /
- power pattern /
- random error
-
图 2 理论期望、统计均值、无扰动的理想方向图、文献[2]的期望结果对比
-
[1] SHIFRIN Y S, KORNIENKO L G. The State-of-The-Art of the statistical theory of antenna arrays[C]//6th International Symposium on Antennas, Propagation and EM Theory Proceedings. Beijing: [s.n.], 2003: 176-181. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1276657 [2] 向广志.超低副瓣阵列天线的公差分析[J].现代雷达, 1996(6):39-47. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199600826590 XIANG Guang-zhi. Analysis on the errors of an ultra-low sidelobe array antenna[J]. Modern Radar, 1996(6):39-47. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199600826590 [3] 杨志荣, 王建武, 傅文斌, 等.互耦和随机幅相误差对直线阵副瓣电平的影响[J].空军雷达学院学报, 2008, 22(2):94-96. doi: 10.3969/j.issn.1673-8691.2008.02.005 YANG Zhi-rong, WANG Jian-wu, FU Wen-bin, et al. Effects of mutual coupling and random amplitude-phase errors on sidelobe level of linear arrays[J]. Journal of Air Force Radar Academy, 2008, 22(2):94-96. doi: 10.3969/j.issn.1673-8691.2008.02.005 [4] SCHMID C, SCHUSTER S, FEGER R, et al. On the effects of calibration errors and mutual coupling on the beam pattern of an antenna array[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(8):4063-4071. doi: 10.1109/TAP.2013.2259455 [5] MOWLER M, LINDMARK B, LARSSON E G, et al. Joint estimation of mutual coupling, element factor and phase center in antenna arrays[J]. Eurasip Journal on Wireless Communications and Networking, 2007, 2007(1):10-10. https://www.researchgate.net/profile/Bjoern_Ottersten/publication/26488226_Joint_Estimation_of_Mutual_Coupling_Element_Factor_and_Phase_Center_in_Antenna_Arrays/links/0a85e53802a8e50bd9000000.pdf?inViewer=true&pdfJsDownload=true&disableCoverPage=true&origin=publication_detail [6] CHAKRAVORTY P, MANDAL D. Radiation pattern correction in mutually coupled antenna arrays using parametric assimilation technique[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(9):4092-4095 doi: 10.1109/TAP.2016.2578307 [7] JACOBS E. Phase error effects on gain and sidelobe level of a space-fed array[J]. IEEE Transactions on Antennas and Propagation, 1980, 28(2):243-246. doi: 10.1109/TAP.1980.1142319 [8] 冯雪勇, 杨林, 雷娟, 等.随机误差对雷达阵列天线低副瓣波束影响的分析[J].电波科学学报, 2015, 30(2):264-268. http://d.old.wanfangdata.com.cn/Periodical/dbkxxb201502010 FENG Xue-yong, YANG Lin, LEI Juan, et al. Analysis of effects of the random errors on the low side lobe of radar array antenna[J]. Chinese Journal of Radio Science. 2015, 30(2):264-268. http://d.old.wanfangdata.com.cn/Periodical/dbkxxb201502010 [9] 见伟, 张玉, 韩名权.阵列天线通道误差对波束性能的影响分析[J].无线电工程, 2014, 44(11):45-48. doi: 10.3969/j.issn.1003-3106.2014.11.13 XIAN Wei, ZHANG Yu, HAN Ming-quan. Analysis on impact of phased array antenna channel errors on beam forming[J]. Radio Engineering, 2014, 44(11):45-48. doi: 10.3969/j.issn.1003-3106.2014.11.13 [10] 鲁祖坤, 高鹰, 肖剑, 等.基于均匀圆阵的幅相误差自校正算法[J].火控雷达技术, 2013, 42(1):1-5. doi: 10.3969/j.issn.1008-8652.2013.01.001 LU Zu-kun, GAO Ying, XIAO Jian, et al. Amplitude and phase error auto-calibration algorithm based on uniform circular array[J]. Fire Control Radar Technology, 2013, 42(1):1-5. doi: 10.3969/j.issn.1008-8652.2013.01.001 [11] ZHANG Yu-feng, MA Hong, TAN Ping. A low complexity calibration method of gain and phase error for arrays with arbitrary geometry[C]//International Conference on Multimedia Technology. Hangzhou: [s.n.], 2011: 3342-3345. http://ieeexplore.ieee.org/document/6001803/ [12] 袁自月, 牛一鸣, 杨国, 等.一种阵列天线阵元幅相, 位置误差校正方法[J].电子与信息学报, 2014, 36(9):2232-2237. http://d.old.wanfangdata.com.cn/Periodical/dzkxxk201409031 YUAN Zi-yue, NIU Yi-ming, YANG Guo, et al. A calibration method for sensor gain/phase and position errors of array antenna[J]. Journal of Electronics & Information Technology, 2014, 36(9):2232-2237. http://d.old.wanfangdata.com.cn/Periodical/dzkxxk201409031 [13] ANSELMI N, MANICA L, ROCCA P, et al. Tolerance analysis of antenna arrays through Interval Arithmetic[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(11):5496-5507. doi: 10.1109/TAP.2013.2276927 [14] MASSA A, ROCCA P, GIACCAR E, et al. Tolerance analysis of antenna arrays through Interval Analysis[C]//2014 IEEE Radar Conference. Cincinnati, OH: IEEE, 2014: 0896-0899. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6875718 -


 ISSN
ISSN 




 下载:
下载: