-
能源的急速消耗和环境的日益污染严重限制了人类进一步的发展,而光伏发电因其安全性能好、运行与维护成本低、易于普及与发展范围广等优点被广泛应用,最影响新能源发电系统的因素是系统控制性能的优劣[1]。新能源并网发电系统一般采用两级式的功率变换拓扑形式[2-3]。常规的两级式光伏发电系统,前级是升压功能的Boost模块,可实现光伏发电系统的最大功率点追踪功能;后级是逆变功能的DC/AC模块,对逆变器进行优化控制,实现电网的并网逆变[4-6]。
目前,由于光伏并网逆变器中谐波的存在使并网电流发生畸变,造成并网控制器的设计困难。国内外学者在改善并网电流及其相关并网指标这一领域进行大量研究:文献[7]将自适应谐波补偿应用在逆变器中,对特征谐波进行检测并滤除进而消除谐波的影响。但该方法的基础不适用于两级式单相并网系统,提出的控制系统模型有待改良。文献[8]在推导出稳态时直流母线电压纹波与电压控制器的数学关系基础上,设计了一种2次谐波发生器补偿母线电压纹波,消除了母线电压纹波对逆变器的影响。然而该方法只对2次谐波进行了补偿,无法对其他低次谐波进行补偿。文献[9-10]运用神经网络对控制器进行优化,减小了谐波的影响。由于补偿增益难以精确整定,因此存在补偿精度不高,抗畸变能力弱等缺陷。文献[11-12]先通过单相d-q坐标变换将单相交流量转换为直流量,再通过PI控制实现无静差并网电流调节,但无法较好适应直流侧波动、电网电压谐波等原因造成的影响,使并网电流发生畸变。
本文针对以上方法的不足,构造了同步坐标系下附带谐波补偿环节的双环比例积分控制,根据LM-BP神经网络自适应调节谐波的补偿增益,使并网电流的波形更加优化,降低了系统中谐波造成的影响,利用MATLAB仿真研究以及实验验证,证明了该方法的可行性。
-
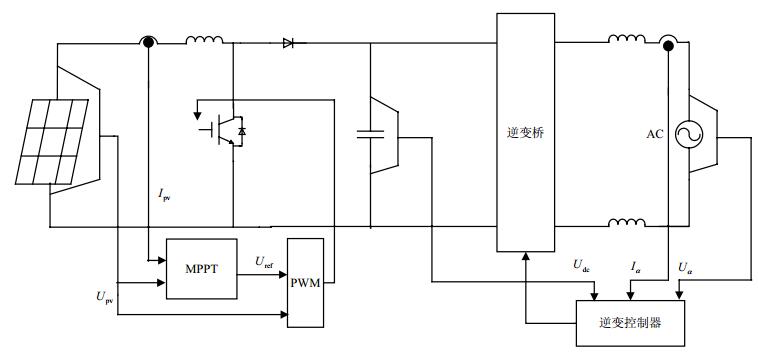
图 1所示为两级式单相光伏并网系统,图中Boost升压变换器在前级DC/DC模块中实现升压功能,并且对光伏阵列输出电压${U_{{\rm{pv}}}}$和光伏阵列输出电流${I_{{\rm{pv}}}}$进行采样,经过最大功率点跟踪(maximum power point tracking, MPPT)技术处理[8],采用扰动观察法得到参考电压${U_{{\rm{ref}}}}$。${U_{{\rm{ref}}}}$与${U_{{\rm{pv}}}}$进行比较产生脉宽调制PWM信号,实现光伏阵列的最大功率输出,同时把电压较低的${U_{{\rm{pv}}}}$升高为后级逆变系统所要求的工作电压。后级是全桥逆变电路组成的DC/AC逆变系统,可根据电网电压相关指标对前级电路直流电逆变的交流电进行调整,进而并入电网。
-
由于单相光伏并网系统中仅有一个交流量,不能直接实现Park变换,但首先可以构造一个与对应物理量相互垂直的虚拟变量组成两相静止坐标系,再进行坐标变换。
设${X_\alpha } = {X_R}$、${X_\beta } = {X_O}$,则单相坐标变换中静止坐标系到旋转坐标系$\alpha \beta /dq$变换公式为:
$$\left\{ \begin{array}{l} \left[ \begin{array}{l} {X_d}\\ {X_q} \end{array} \right] = \mathit{\boldsymbol{C}}\;\left[ \begin{array}{l} {X_\alpha }\\ {X_\beta } \end{array} \right]{\rm{ = }}{X_M}\left[ {\begin{array}{*{20}{c}} {\cos \varphi }\\ {\sin \varphi } \end{array}} \right]\\ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {\cos (\omega t)}&{\sin (\omega t)}\\ { - \sin (\omega t)}&{\cos (\omega t)} \end{array}} \right] \end{array} \right.$$ (1) 式中,${X_d}$为旋转坐标系中的d轴分量;${X_q}$为旋转坐标系中的q轴分量。${X_d}$和${X_q}$在旋转坐标下可以代表电压或者电流。由于${X_\beta }$是由${X_\alpha }$延迟四分之一个周期得到的,可只用${X_\alpha }$作为调制波。
-
逆变器控制系统将首先对电压电流进行坐标变换,对转换到旋转坐标系下的电压电流值分别进行双闭环比例积分控制[12],可得出系统在d-q坐标系下的状态方程为:
$$\left\{ \begin{gathered} \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{U_d}} \\ {{U_q}} \end{array}} \right] = \frac{1}{C}\left[ {\begin{array}{*{20}{c}} {{I_d}} \\ {{I_q}} \end{array}} \right] - \frac{1}{{RC}}\left[ {\begin{array}{*{20}{c}} {{U_d}} \\ {{U_q}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&\omega \\ { - \omega }&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{U_d}} \\ {{U_q}} \end{array}} \right] \hfill \\ \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{I_d}} \\ {{I_q}} \end{array}} \right] = \frac{{{U_{{\rm{di}}}}}}{L}\left[ {\begin{array}{*{20}{c}} {{D_d}} \\ {{D_q}} \end{array}} \right] - \frac{1}{L}\left[ {\begin{array}{*{20}{c}} {{U_d}} \\ {{U_q}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&\omega \\ { - \omega }&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_d}} \\ {{I_q}} \end{array}} \right] \hfill \\ \end{gathered} \right.$$ (2) 式中${I_d}$、${U_d}$为电流、电压的d轴分量;${I_q}$、${U_q}$为电流、电压的q轴分量。根据式(2)可得如图 2所示逆变器控制系统在旋转坐标下的等效模型。以d-q旋转坐标系为基础,可知系统的输出电流${I_d}$和${I_q}$不仅与控制量${D_d}{U_{{\rm{di}}}}$和${D_q}{U_{{\rm{di}}}}$有关,还与耦合电压$\omega L{I_d}$和$\omega L{I_q}$扰动以及输出电压${U_d}$和${U_q}$有关。
对单相逆变器模型进行输出电压和负载电流前馈解耦,得到电流控制方程为:
$$\left\{ \begin{gathered} {U_{{\rm{df}}}} = \left( {{K_{{\rm{ip}}}} + \frac{{{K_{{\rm{iv}}}}}}{s}} \right)({I_d} - {{I'}_d}) + {U_d} - \omega L{I_q} \hfill \\ {U_{{\rm{qf}}}} = \left( {{K_{{\rm{ip}}}} + \frac{{{K_{{\rm{iv}}}}}}{s}} \right)({I_q} - {{I'}_q}) + {U_q} + \omega L{I_d} \hfill \\ \end{gathered} \right.$$ (3) 式中,${U_{{\rm{df}}}}$、${U_{{\rm{qf}}}}$为逆变控制器的输出量;${K_{{\rm{ip}}}}$、${K_{{\rm{iv}}}}$为电流内环控制器的比例积分系数;${I'_d}$、${I'_q}$分别为电流内环给定值。
在控制系统中电流内环的给定值由电压外环经过运算处理得到。则根据式(2)得到电压控制方程为:
$$\left\{ \begin{gathered} {{I'}_d} = \left( {{K_{{\rm{op}}}} + \frac{{{K_{{\rm{oi}}}}}}{s}} \right)(U_d^* - {U_d}) \hfill \\ {{I'}_q} = \left( {{K_{{\rm{op}}}} + \frac{{{K_{{\rm{oi}}}}}}{s}} \right)(U_q^* - {U_q}) \hfill \\ \end{gathered} \right.$$ (4) 式中,${K_{{\rm{op}}}}$、${K_{{\rm{oi}}}}$为外环比例积分系数;$U_d^*$、$U_q^*$为电压外环给定值。将式(3)、式(4)带入式(2)后,可以得到光伏逆变器双闭环控制系统如图 3所示。电压外环分别对电压$U_d^*$、$U_q^*$进行PI控制,输出参考电流值${I'_d}$、${I'_q}$为电流内环所需的控制量;内环再依据外环给定的值对交流侧电流进行PI控制,图 3所示的控制器实现了对电压电流的解耦。
-
将所测谐波表达式展开成三角级数形式,即:
$$x(t) = \sum\limits_{l = 1, 3, \cdots }^N {[{A_l}\sin (l\omega t) + {B_l}\cos (l\omega t)]} $$ (5) 式中,$\omega $是基波角频率;${A_l} = {X_l}\cos {\phi _l}$,${B_l} = {X_l}\sin {\phi _l}$,${X_l}$和${\phi _l}$分别为第$l(l = 1, 3, \cdots , N)$次谐波的幅值和相角,各次谐波的幅值和相角分别为:
$$\left\{ \begin{gathered} {X_l} = \sqrt {A_l^2 + B_l^2} \hfill \\ {\phi _l} = \arctan \frac{{{B_l}}}{{{A_l}}} \hfill \\ \end{gathered} \right.$$ (6) 谐波前馈信号的检测采用全谐波补偿与特征谐波补偿两种方法。考虑到逆变器的限制因素,如果采用全谐波补偿进行优化处理,在高频区域内不但补偿效果差,还会增大相应的谐波含量及对系统的威胁。因此本文选择性补偿了阶数较低且含量较大的3、5、7、9次特征谐波。谐波检测系统如图 4所示,采用基于锁相环的幅相合成的方法。首先利用FFT变换求出并网电流${i_\alpha }$的三角级数形式,提取三角级数第$l$次分量,利用式(6)求出${\phi _l}$、${X_l}$与锁相环PLL所求出的$l$倍频$l\omega t$重新进行幅相合成,求出第$l$次谐波${i_{\alpha l}}$,从而达到特征谐波检测的要求。
-
根据谐波检测系统检测并网电流${i_\alpha }$得到$l$次谐波电流分量${i_{\alpha l}}$,然后静态阻抗$l\omega {L_f}$环节使谐波电流${i_{\alpha l}}$经过转换成为相应的电压信号,重新产生PWM调制波。由于实际工程中网侧电压变化以及消除特定频率的谐波会对相邻谐波产生放大作用,本文采用LM(Levenberg-Marquardt)算法对BP神经网络进行优化处理,以下简称LM-BP神经网络。谐波消除环节优化处理的原理如图 5所示。
LM-BP神经网络的工作原理是在误差反向传播学习的基础上,按照LM算法加快权向量收敛速度的同时避免了BP神经网络容易陷入局部最优的问题,以产生误差的均方差值最小为目标,对网络权值实现自适应调整。本文通过全谐波检测得到的并网电流值作为补偿系统的期望值,同时将实际补偿信号应用LM-BP神经网络对权值进行动态调整。权值调整达到补偿效果最优时收敛,则最优时的补偿信号可作为对总谐波电流的最小均方估计,使经过补偿的并网电流畸变率降为最低。鉴于${i_\beta }$是根据${i_\alpha }$延迟四分之一个周期得到的,它们的调整方法相同,因此这里只采用${i_\alpha }$作为说明。令广义坐标变换法检测到的各次谐波电流${i_{\alpha l}}$组成的输入向量为:
$${\mathit{\boldsymbol{X}}_\alpha } = {[{i_{\alpha 3}}, {i_{\alpha 5}}, {i_{\alpha 7}}, {i_{\alpha 9}}]^{\rm{{\rm T}}}}$$ (7) 所对应各次谐波动态补偿权值向量${W_\alpha }$,并将初值选为1,即:
$${\mathit{\boldsymbol{W}}_\alpha } = {[{a_3}, {a_5}, {a_7}, {a_9}]^{\rm{{\rm T}}}} = {[1, 1, 1, 1]^{\rm{{\rm T}}}}$$ (8) 期望值${i_{h\alpha }}$为并网电流${i_\alpha }$经过全谐波检测得到,同时将输入向量${\mathit{\boldsymbol{X}}_\alpha }$和权向量${\mathit{\boldsymbol{W}}_\alpha }$的乘积表示为LM-BP神经网络的输出${y_\alpha }$,于是得到误差${e_\alpha }$为:
$${e_\alpha } = {i_{h\alpha }} - {y_\alpha } = {i_{h\alpha }} - \mathit{\boldsymbol{W}}_\alpha ^{\rm{{\rm T}}}{\mathit{\boldsymbol{X}}_\alpha }$$ (9) 则神经网络第n个样本均方误差定义为:
$$\varepsilon (n) = \frac{1}{2}{({e_\alpha })^2} = \frac{1}{2}{({i_{h\alpha }} - {y_\alpha })^2}$$ (10) 在反向传播算法中,利用LM算法改进,求得误差函数的负梯度,依据它的方向对权值进行自适应调整,得到权向量权值变化量为:
$$\Delta \mathit{\boldsymbol{W}} = - {[{\nabla ^2}{e_\alpha }]^{ - 1}}[\nabla {e_\alpha }]$$ (11) 式中,${\nabla ^2}{e_\alpha }$是误差函数${e_\alpha }$的Hessian矩阵,可以用$\mathit{\boldsymbol{H}}(e)$表示;$\nabla e$是${e_\alpha }$的梯度,可以用$\mathit{\boldsymbol{G}}(e)$表示,分别为:
$$\left\{ \begin{array}{l} \mathit{\boldsymbol{H}}(e) = \left[ {\begin{array}{*{20}{c}} {\frac{{{\partial ^2}e}}{{\partial {a_3}\partial {a_3}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_3}\partial {a_5}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_3}\partial {a_7}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_3}\partial {a_9}}}}\\ {\frac{{{\partial ^2}e}}{{\partial {a_5}\partial {a_3}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_5}\partial {a_5}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_5}\partial {a_7}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_5}\partial {a_9}}}}\\ {\frac{{{\partial ^2}e}}{{\partial {a_7}\partial {a_3}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_7}\partial {a_5}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_7}\partial {a_7}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_7}\partial {a_9}}}}\\ {\frac{{{\partial ^2}e}}{{\partial {a_9}\partial {a_3}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_9}\partial {a_5}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_9}\partial {a_7}}}}&{\frac{{{\partial ^2}e}}{{\partial {a_9}\partial {a_9}}}} \end{array}} \right]\\ \mathit{\boldsymbol{G}}(e) = \left( {\frac{{\partial e}}{{\partial {a_3}}}, \frac{{\partial e}}{{\partial {a_5}}}, \frac{{\partial e}}{{\partial {a_7}}}, \frac{{\partial e}}{{\partial {a_9}}}} \right) \end{array} \right.$$ (12) 式中,$\frac{{\partial e}}{{\partial {a_l}}} = 2(y - {i_{h\alpha }})\frac{{\partial y}}{{\partial {a_l}}}$为$\mathit{\boldsymbol{G}}(e)$在连接权${a_l}$上的分梯度,通过反向传播算法求出。对该分梯度公式两边再次求偏导数得到:
$$\frac{{{\partial ^2}e}}{{\partial {a_l}\partial {a_h}}} = 2\left[ {\frac{{\partial y}}{{\partial {a_l}}}\frac{{\partial y}}{{\partial {a_{lh}}}} + (y - {i_{h\alpha }})\frac{{{\partial ^2}y}}{{\partial {a_l}\partial {a_h}}}} \right]$$ (13) 式中,$l$、$h \in (3, 5, 7, 9)$。因为误差之间相互独立,并且都服从$N(0, {\delta ^2})$分布,那么式(13)右侧第二项可以忽略,由此进一步化简,可以近似得到误差函数的Hessian矩阵$\mathit{\boldsymbol{H}}(e)$。考虑到Hessian矩阵的逆矩阵${\mathit{\boldsymbol{H}}^{ - 1}}(e)$可能奇异,引入一个衰变因子$\mu $,则式(11)可以写为:
$$\Delta \mathit{\boldsymbol{W}} = - {[\mathit{\boldsymbol{H}}(e) + \mu \mathit{\boldsymbol{I}}]^{ - 1}}[\nabla {e_\alpha }]$$ (14) 最终权向量迭代公式为:
$$\left\{ {\begin{array}{*{20}{l}} {{y_\alpha } = \mathit{\boldsymbol{W}}_\alpha ^{\rm{{\rm T}}}{\mathit{\boldsymbol{X}}_\alpha }}\\ {{e_\alpha } = {i_{h\alpha }} - \mathit{\boldsymbol{W}}_\alpha ^{\rm{{\rm T}}}{\mathit{\boldsymbol{X}}_\alpha }}\\ {{\mathit{\boldsymbol{W}}_\alpha }^{k + 1} = {\mathit{\boldsymbol{W}}_\alpha }^k + {{[\mathit{\boldsymbol{H}}(e) + \mu \mathit{\boldsymbol{I}}]}^{ - 1}}[\nabla {e_\alpha }]} \end{array}} \right.$$ (15) 式中,$\mu $为大于零的常数;I为单位矩阵。当系数$\mu $为0时,式(15)即为牛顿法;反之则使式(15)变为具有较小步长的梯度下降法,这样可以避免局部最优以及保证每次迭代时,权值调整的方向都为误差减小的方向。牛顿法改进神经网络在对并网电流进行优化时出现一定程度的畸变,不能很好改进并网电流波形,而LM-BP神经网络可以对并网电流进行更好的改善。
综上所述,将权值初始值设置为1可对系统权值进行自适应迭代运算。当LM-BP神经网络算法稳态收敛时,将此稳态调整后的权向量的权值,作为自适应调节系统对各次谐波的最佳补偿增益。
-
利用仿真软件MATLAB/Simulink搭建两级式单相并网逆变系统仿真模型,验证本文提出的自适应特征谐波补偿优化并网电流的方法,所用参数如表 1所示。
表 1 仿真参数
元件 参数 网侧电压${U_s}/{\rm{V}}$ 220 系统频率$f/{\rm{HZ}}$ 50 滤波电感${L_f}/{\rm{ \mathsf{ μ} H}}$ 800 滤波电容${C_f}/{\rm{ \mathsf{ μ} F}}$ 50 直流侧电容${C_{{\rm{dc}}}}/{\rm{ \mathsf{ μ} F}}$ 1 000 直流母线电压参考${U_{{\rm{dc}}}}/{\rm{V}}$ 400 -
在前级直流侧电压波动为6 V条件下,将牛顿法得出的结果与本文改进方法结果进行比较,得到如图 6所示的结果。
-
为了进一步验证本文电流跟踪优化方法的有效性,搭建了一套额定功率为2 kW的两级式单相光伏并网逆变器实验平台,波形采集装置为含数据采集卡的LABWINDOWS/CVI实验平台,逆变装置采用INF-50组件,DSP选用工作频率为2.5 ${\rm{GHZ}}$,芯片为AMD OPERATOR的DS1006,光伏发电装置采用BK_PVS60085MR组件,日照强度设置为1 000 W/m2,温度为25 ℃,实验参数与仿真一致,得到结果如图 7所示。
图 7中,由于死区时间、前级直流电压波动等造成的影响,在传统的双环PI控制方法中,单相光伏并网逆变系统的并网电流总畸变率(THD)达到3.52%,主要由3次、5次、7次、9次等谐波组合而成;而应用本文提出的基于LM-BP神经网络,将特征谐波消除策略应用于优化并网电流,选择性补偿了对电流畸变影响最大的3次、5次、7次、9次低频谐波,优化了电流波形,使THD降为1.32%。
比较图 7改进特征谐波消除法仿真与图 8实验图形,忽略实验平台由于死区时间、带宽限制、采样率低对波形造成的影响,观察并网电流波形,在并网电流波峰与波谷处有明显的畸变现象,仿真结果与实验结果一致。
-
本文在传统电压电流双闭环PI控制的基础上,研究了并网逆变器优化控制,并且针对需实时准确补偿谐波电流这一特点,提出一种基于LM-BP神经网络的自适应特征谐波消除方法,主要研究对低次特征谐波的补偿,运用LM-BP神经网络实现了对实时补偿增益的调整,通过MATLAB仿真及实验数据表明该方法能够优化并网电流波形,降低特征谐波对并网电流的影响实现自适应补偿。最后,本文提出的优化方法不仅适用于两级式单相光伏并网系统,同时在通用型逆变器的应用以及提高补偿性能等方面有一定参考价值。
Adaptive Current Control Strategy for Harmonic Compensation in Single Phase Solar Inverter
-
摘要: 针对两级式单相光伏并网逆变器由于死区时间、直流侧波动等原因造成并网电流畸变的严重现象,将特征谐波消除策略应用于并网逆变器,以优化并网电流波形、提高电流跟踪性能。首先通过Park变换实现单相d-q坐标下的电压电流双环比例积分控制(PI),再增加含动态增益的补偿环节,对PWM调制波进行重构,实现对谐波的补偿,利用莱文贝格-马夸特(LM)算法改进的BP神经网络提高前馈补偿的精度与对电压畸变的适应性。最后,MATLAB仿真研究以及实验验证了该方法的有效性与合理性。Abstract: In order to solve the current distortion phenomenon, which is caused by the dead-time effect and DC voltage fluctuation in the single-phase solar grid-connected inverter, this paper presents a selective characteristic harmonic elimination strategy to design a current controller for grid-connect inverter for optimizing current waveform and improving current tracking performance. The double loop proportional integral (PI) control of voltage and current is realized by adopting Park transformation. PWM is reconstructed to compensate harmonics by the harmonic compensation with dynamic gain. Levenberg-Marquardt (LM) algorithm is used to improve back propagation (BP) neural network, so as to increase the accuracy of feed-forward compensation and enhance the adaptability of voltage distortion. Finally, MATLAB simulation and experimental results verify the effectiveness and rationality of the proposed method.
-
表 1 仿真参数
元件 参数 网侧电压${U_s}/{\rm{V}}$ 220 系统频率$f/{\rm{HZ}}$ 50 滤波电感${L_f}/{\rm{ \mathsf{ μ} H}}$ 800 滤波电容${C_f}/{\rm{ \mathsf{ μ} F}}$ 50 直流侧电容${C_{{\rm{dc}}}}/{\rm{ \mathsf{ μ} F}}$ 1 000 直流母线电压参考${U_{{\rm{dc}}}}/{\rm{V}}$ 400 -
[1] XAVIER L S, CUPERTINO A F, MEDES V F, et al. Adaptive current control strategy for harmonic compensation in single-phase solar inventers[J]. Electric Power Systems Research, 2017, 142:84-95. doi: 10.1016/j.epsr.2016.08.040 [2] SAAD L M S, ABDESLAM D O. Direct neural method for harmonic currents estimation using adaptive linear element[J]. Electric Power Systems Research, 2017, 152:61-70. doi: 10.1016/j.epsr.2017.06.018 [3] KATOLE D N, DAIGAVANE M B, GAWANDE S P, et al. Analysis design and implementation of single phase SRF controller for dynamic voltage restorer under distorted supply condition[J]. Energy Procedia, 2017, 117:716-723. doi: 10.1016/j.egypro.2017.05.186 [4] HAO Xiang, YANG Xu, LIU Tao, et al. A sliding-mode controller with multiresonant sliding surface for single-phase grid-connected VSI with an LCL filter[J]. Power Electronics, 2013, 28(5):2259-2268. doi: 10.1109/TPEL.2012.2218133 [5] ARUN K, SELVAJYOTHI K. Observer based current controlled single phase grid connected[J]. Procedia Engineering, 2013, 64:367-376. doi: 10.1016/j.proeng.2013.09.109 [6] BOSE B K. Modern power electronics and AC drives[M]. New Jersey:Prentice Hall, 2002. [7] 刘景晖, 郑益慧, 姚钢, 等.自适应特征谐波消除策略的并网逆变器电流跟踪优化方法[J].电工技术学报, 2013, 28(9):120-128. doi: 10.3969/j.issn.1000-6753.2013.09.015 LIU Jing-hui, ZHENG Yi-hui, YAO Gang, et al. Optimized current tracking method for grid-connected inverter with adaptive characteristic harmonic elimination[J]. Transactions of China Electrotechnical Society, 2013, 28(9):120-128. doi: 10.3969/j.issn.1000-6753.2013.09.015 [8] 郭晓瑞, 王培良, 郭吉丰, 等.光伏并网逆变器母线电压纹波的分析与控制[J].电力自动化设备, 2017, 37(5):48-53. http://d.old.wanfangdata.com.cn/Periodical/dlzdhsb201705008 GUO Xiao-rui, WANG Pei-liang, GUO Ji-feng, et al. Analysis and control of bus voltage ripples for grid-connected photovoltaic inverter[J]. Electric Power Automation Equipment, 2017, 37(5):48-53. http://d.old.wanfangdata.com.cn/Periodical/dlzdhsb201705008 [9] CORONADO-MENDOZA A, PEREZ-CISNEROS M A, DOMINGUEZ-NAVARRO J A, et al. Dynamic phasors modeling for a single phase two stage inverter[J]. Electric Power Systems Research, 2016, 140:854-865. doi: 10.1016/j.epsr.2016.04.020 [10] FARAJI F, MMG S, HAJIRAYAT A, et al. Single-stage single-phase three-level neutral-point-clamped transformerless grid-connected photovoltaic inverters:Topology review[J]. Renewable and Sustainable Energy Review, 2017, 80:197-214. doi: 10.1016/j.rser.2017.05.181 [11] 孟建辉, 石新春, 付超, 等.新型高效率两级式单相光伏并网逆变系统的研究与应用[J].电力系统保护与控制, 2013, 41(20):87-92. doi: 10.7667/j.issn.1674-3415.2013.20.014 MENG Jian-hui, SHI Xin-chun, FU Chao, et al. Research and application of novel high efficiency two-stage single-phase photovoltaic grid-connected inverter system[J]. Power System Protection and Control, 2013, 41(20):87-92. doi: 10.7667/j.issn.1674-3415.2013.20.014 [12] 邓长吉, 刘向立, 胡永华, 等.基于dq坐标变换的单相逆变器控制技术研究[J].电气传动, 2015, 45(9):30-33. doi: 10.3969/j.issn.1001-2095.2015.09.007 DENG Chang-ji, LIU Xiang-li, HU Yong-hua, et al. Reaserch on control strategy of single-phase inverter based on dq coordinatetransfor[J]. Electric Drive, 2015, 45(9):30-33. doi: 10.3969/j.issn.1001-2095.2015.09.007 -


 ISSN
ISSN 




 下载:
下载: