-
随着电子技术的发展,低频电磁目标和小尺寸电子器件的数值仿真分析方法受到越来越多的关注。然而,在工程领域广泛使用的基于电场积分方程(EFIE)的矩量法(MoM)[1]在使用RWG基函数[2]时,必须使用高密度的剖分网格以精确模拟细微目标的结构。随着网格的不断缩小,方程中的矢量磁位贡献不断变小并被最终标量电位湮没,EFIE矩阵条件数不断上升,将最终陷入所谓的“低频崩溃”中[3-4]。
为了克服低频崩溃问题,学者们通常在RWG基函数的基础上采取loop-tree,loop-star分解的方法分离电和磁的物理贡献[5-6],并使用Calderón预条件以获得良好的矩阵形态[7-9]。然而使用loop-tree,loop-star方法不可避免地需要进行繁琐的loop基函数和tree基函数搜索,这种搜索在目标尺寸增大和含有分枝结构时变得十分困难。为了简化电和磁的分离过程,近年来学者们从分离电流和电荷的角度又取得了一系列成果。例如分离位积分方程(separated potential integral equation, SPIE)[10]、电流电荷积分方程(current and charge integral equation, CCIE)[11]、增量电场积分方程(AEFIE)[12]等均可以改善EFIE的低频崩溃问题。其中,AEFIE将电荷作为额外的未知量引入方程之中,通过强加电流连续性条件和频率缩放获得了稳定的系统方程,其阻抗矩阵为鞍点矩阵,可以通过专门的预条件加速迭代收敛速度,并且矩阵系统中有一半为稀疏矩阵,内存占用较低。
随着计算量的增加,诸多快速方法也被应用到AEFIE当中。如低频多层快速多极子算法(low- frequency multilevel fast multipole algorithm, LF-MLFMA)[13],积分方程快速傅里叶变换(integral equation fast Fourier transform, IE-FFT)[14],多层快速笛卡尔展开算法(multilevel accelerated cartesian expansion algorithm, MLACEA)[15-16],以及多层自适应交叉近似(multilevel adaptive cross approximation, MLACA)[17]等。其中前3种方法在计算电小问题时均可以获得O(N)量级的复杂度。最近,一种基于复源点(CSP)的方法应用在了电磁场分析中[18-19]。由于复源点波束是麦克斯韦方程的精确解,因此可以用定义在等效面上的复源点展开基函数与外界的互作用[20-21],并将基函数间的远场阻抗矩阵表示为这些复源点之间的相互作用。本文将使用多层复源波束(MLCSP)法加速AEFIE,并通过数值算例对低频问题的MLCSP方法进行分析和验证。
-
对处于自由空间的理想金属目标,利用目标表面的边界条件,可以得到其表面电流$\mathit{\boldsymbol{J}}(\mathit{\boldsymbol{r}}')$满足的电场积分方程:
$$ {\left. {\left\{ {{{\mathit{\boldsymbol{E}}}^i} + {\text{i}}{k_0}{\eta _0}\int_{{S_j}} {\left[{1 + \frac{1}{{k_0^2}}\nabla \nabla } \right]G(\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{r'}}){\mathit{\boldsymbol{J}}}(\mathit{\boldsymbol{r'}}){\text{d}}S'} } \right\}} \right|_t} = 0 $$ (1) 式中,$G(\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{r'}}) = \frac{{{{\text{e}}^{{\text{i}}{k_0}R}}}}{{4\pi R}}$;$R = \left| \mathit{\boldsymbol{r}}-\mathit{\boldsymbol{r'}} \right|$为自由空间中的标量格林函数;${k_0}$、${\eta _0}$分别是自由空间的波数和波阻抗;${\mathit{\boldsymbol{E}}^i}$表示入射电场;$\mathit{\boldsymbol{r}}$、$\mathit{\boldsymbol{r'}}$分别表示观察点和源点的位置。
由于前述原因,为了克服低频崩溃问题,需要在电场积分方程中引入表面电荷$\mathit{\Phi }(\mathit{\boldsymbol{r'}})$作为未知量,并使用脉冲基函数对其进行离散:
$$ {h_i}(\mathit{\boldsymbol{r}}) = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{{A_i}}}\;\;\;\;\;\mathit{\boldsymbol{r}} \in {T_i}}\\ {0\;\;\;\;\;\;\;\;\;\;{\rm{ 其他}}} \end{array}} \right. $$ (2) 式中,${A_i}$为电荷所在三角形面元${T_i}$的表面积。表面电流使用去除公共边长的归一化RWG基函数进行离散:
$$ {\mathit{\boldsymbol{\rho }}_i}(\mathit{\boldsymbol{r}}) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\frac{{\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{r}}_i^ + }}{{2A_i^ + }}\;\;\;\;\;\mathit{\boldsymbol{r}} \in T_i^ + }\\ {\frac{{\mathit{\boldsymbol{r}}_i^ - - \mathit{\boldsymbol{r}}}}{{2A_i^ - }}\;\;\;\;\mathit{\boldsymbol{r}} \in T_i^ - } \end{array}}\\ {0\;\;\;\;\;\;\;\;\;\;\;\, 其他} \end{array}} \right. $$ (3) 通过添加电流连续性关系,可以得到增量电场积分方程:
$$ \left[{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\overline V}} }&{{{\mathit{\boldsymbol{\overline D}} }^{\rm{T}}} \cdot \mathit{\boldsymbol{\overline P}} }\\ {\mathit{\boldsymbol{\overline D}} }&{k_0^2\mathit{\boldsymbol{\overline I}} } \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {{\rm{i}}{k_0}\mathit{\boldsymbol{J}}}\\ {{c_0}\mathit{\boldsymbol{\varphi }}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\eta _0^{-1}\mathit{\boldsymbol{b}}}\\ 0 \end{array}} \right] $$ (4) 其中,各矩阵向量的相应元素为:
$$ {\overline {\mathit{\boldsymbol{V}}} _{ij}} = \int_{{S_i}} {{{\mathit{\boldsymbol{\rho }}}_i}({\mathit{\boldsymbol{r}}}) \cdot \int_{{S_j}} {G(\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){{\mathit{\boldsymbol{\rho }}}_j}(\mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){\text{d}}S'{\text{d}}S} } $$ (5) $$ {\overline {\mathit{\boldsymbol{P}}} _{ij}} = \int_{{T_i}} {{h_i}({\mathit{\boldsymbol{r}}}) \cdot \int_{{T_j}} {G(\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){h_j}(\mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){\text{d}}S'{\text{d}}S} } $$ (6) $$ {{\mathit{\boldsymbol{b}}}_i} = \int_{{S_i}} {{{\mathit{\boldsymbol{g}}}_i}({\mathit{\boldsymbol{r}}}) \cdot {{\mathit{\boldsymbol{E}}}^i}{\text{d}}S} $$ (7) $$ {\mathit{\boldsymbol{\overline D}} _{ij}} = \left\{ {\begin{array}{*{20}{c}} {1\quad \;\;\;T_i^ + \in {S_j}}\\ { - 1\quad T_i^ - \in {S_j}}\\ {0\quad \;\;T_i^ \pm \notin {S_j}} \end{array}} \right. $$ (8) 式中,$\mathit{\boldsymbol{j}}$、$\mathit{\boldsymbol{\varphi}} $分别表示电流与电荷未知向量;${c_0}$表示自由空间中的光速;稠密矩阵$\mathit{\boldsymbol{\bar V}}$表示定义在表面电流所产生的磁矢量位的相互作用关系;$\mathit{\boldsymbol{\bar P}}$表示表面电荷所产生的电标量位的相互作用关系;稀疏矩阵$\mathit{\boldsymbol{\bar D}}$表示电流所在的三角形贴片对和电荷所在的三角形贴片之间的几何连接关系;$\mathit{\boldsymbol{\bar I}}$为单位矩阵。在上述AEFIE方程中,磁矢量位和电标量位被分离,并通过合适的频率缩放因子进行平衡,因此可以在低频时获得良好的矩阵形态。
-
同EFIE的复源点波束展开类似,AEFIE的复源点展开可以从电流产生的磁矢量位和电荷产生的电标量位进行等效开始:
$$ {{\mathit{\boldsymbol{V}}}_i}({\mathit{\boldsymbol{r}}}) = \int_{{S_i}} {G(\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){{\mathit{\boldsymbol{\rho }}}_i}(\mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){\text{d}}S'} $$ (9) $$ {P_j}({\mathit{\boldsymbol{r}}}) = \int_{{S_j}} {G(\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){h_j}(\mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){\text{d}}S'} $$ (10) 式中,${\mathit{\boldsymbol{\rho }}_i}(r')$、${h_j}(r')$分别是第$i$个归一化的RWG基函数和第$j$个脉冲基函数。利用复源点等效,上述位函数可以写作一系列复源点所产生的位函数的叠加:
$$ {\mathit{\boldsymbol{V}}_i}(\mathit{\boldsymbol{r}}) = \sum\limits_{q = 1}^Q {\tilde G(\mathit{\boldsymbol{r}}, {{\widetilde {\mathit{\boldsymbol{r'}}}}_q})(\hat xw_{q, i}^x + \hat yw_{q, i}^y + \hat zw_{q, i}^z)} $$ (11) $$ {P_j}(\mathit{\boldsymbol{r}}) = \sum\limits_{q = 1}^Q {\tilde G(\mathit{\boldsymbol{r}}, {{\widetilde {\mathit{\boldsymbol{r'}}}}_q})w_{q, j}^p} $$ (12) 式中,$Q$为等效CSP的数量;${{{\widetilde {\mathit{\boldsymbol{r'}}}}_q}}$为第$q$个等效CSP的复位置[21],$\tilde G\left( {\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\tilde r'}}} \right) = \frac{{{{\rm{e}}^{{\rm{i}}{k_0}\tilde R}}}}{{4\pi \tilde R}}\tilde R = \sqrt {{{\left| {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{\tilde r'}}} \right|}^2}} $为使用复位置时的标量格林函数;$\hat xw_{q,i}^x + \hat yw_{q,i}^y + \hat zw_{q,i}^z$为基函数${\mathit{\boldsymbol{\rho}} _i}(r)$向第$q$个CSP展开的矢量权值;$w_{q, j}^p$为基函数${h_j}(r)$向第$q$个CSP展开的标量权值。结合式(9)~式(11),并在远区点$\mathit{\boldsymbol{r}} = {\mathit{\boldsymbol{r}} _t}(t = 1, 2, \cdots, Q)$处作匹配,可以得到:
$$ \begin{gathered} \widehat v \cdot \sum\limits_{q = 1}^Q {\tilde G({{\mathit{\boldsymbol{r}}}_t}, {{{\widetilde {\mathit{\boldsymbol{r'}}}}_q}})} \widehat vw_{q, i}^v = \\ \widehat v \cdot \int_{{S_i}} {G({{\mathit{\boldsymbol{r}}}_t}\mathit{\boldsymbol{, }}{{\mathit{\boldsymbol{r'}}}}){{\mathit{\boldsymbol{\rho }}}_i}(\mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){\text{d}}S'} \quad (v = x, y, z) \\ \end{gathered} $$ (13) $$ \sum\limits_{q = 1}^Q {\tilde G({{\mathit{\boldsymbol{r}}}_t}, {\widetilde {\mathit{\boldsymbol{r'}}}})} w_{q, j}^p = \int_{{S_j}} {G({{\mathit{\boldsymbol{r}}}_t}, \mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){h_j}(\mathit{\boldsymbol{\mathit{\boldsymbol{r'}}}}){\text{d}}S'} $$ (14) 通过求解上述方程,可以得到相应基函数的CSP展开权值$w_{q, i}^x$、$w_{q, i}^y$、$w_{q, i}^z$和$w_{q, j}^p$。利用基函数的展开权值,组$m'$对应的等效CSP的矢量展开系数可以由组内的电流系数${\mathit{\boldsymbol{j}}_{m'}}$展开:
$$ \mathit{\boldsymbol{\bar s}}_{L, m'}^v = \left[{\mathit{\boldsymbol{s}}_{L, m'}^x, \mathit{\boldsymbol{s}}_{L, m'}^y, \mathit{\boldsymbol{s}}_{L, m'}^z} \right] = \left[{\mathit{\boldsymbol{W}}_{m'}^x, \mathit{\boldsymbol{W}}_{m'}^y, \mathit{\boldsymbol{W}}_{m'}^z} \right]{{\mathit{\boldsymbol{J}}}_{m'}} $$ (15) 标量展开系数可以由电荷系数${\mathit{\boldsymbol{\varphi }}_{m'}}$展开:
$$ \mathit{\boldsymbol{s}}_{L, m'}^p = \mathit{\boldsymbol{W}}_{m'}^p{{\mathit{\boldsymbol{\varphi }}}_{m'}} $$ (16) 式中,${[\mathit{\boldsymbol{W}}_{m'}^\nu]_{qi}} = w_{q, i}^v$;${[\mathit{\boldsymbol{W}}_{m'}^p]_{qj}} = w_{q, j}^p$;$L$表示该组位于八叉树分组的最细层。利用这些展开系数,可以将式(4)中的远区组$m$和组$m'$之间的矩矢相乘分别写作:
$$ {\overline {\mathit{\boldsymbol{V}}} _{mm'}} \cdot i{k_0}{{\mathit{\boldsymbol{J}}}_{m'}} = i{k_0} \cdot \sum\limits_{v = x, y, z} {{{(\mathit{\boldsymbol{W}}_m^v)}^{\text{T}}}{\mathit{\boldsymbol{T}}_{m, m'}}\mathit{\boldsymbol{W}}_{m'}^v{{\mathit{\boldsymbol{J}}}_{m'}}} $$ (17) $$ {\overline {\mathit{\boldsymbol{P}}} _{mm'}} \cdot {c_0}{{\mathit{\boldsymbol{\varphi }}}_{m'}} = {c_0} \cdot {(\mathit{\boldsymbol{W}}_m^{\text{d}})^{\text{T}}}{\mathit{\boldsymbol{T}}_{m, m'}}\mathit{\boldsymbol{W}}_{m'}^p{{\mathit{\boldsymbol{\varphi }}}_{m'}} $$ (18) 式中,T表示矩阵的转置运算;${\mathit{\boldsymbol{T}}_{m, m'}}$是组$m$和组$m'$之间的转移因子,其元素为:
$${\left[{{\mathit{\boldsymbol{T}}_{mm'}}} \right]_{qq'}} = \tilde G\left( {{\mathit{\boldsymbol{\tilde r}}}_m^q, {\widetilde {\mathit{\boldsymbol{r'}}}}_{m'}^{q'}} \right) $$ (19) 式中,${\mathit{\boldsymbol{\tilde r}}}_m^q, {\widetilde {\mathit{\boldsymbol{r'}}}}_{m'}^{q'}$分别表示这两个组的等效CSP的复位置。
以上给出了用于AEFIE-MoM远区的复源点加速方法,同MLFMA[22]等基于八叉树的多层算法类似,为了实现多层复源点算法,需要构建相关展开量在子-父层之间的递推关系。由于子层(第l+1层)第${q_{l + 1}}$个复源点所产生的矢量位函数和标量位函数分别为:
$$ {{\mathit{\boldsymbol{V}}}_{{q_{l + 1}}}}({\mathit{\boldsymbol{r}}}) = \tilde G({\mathit{\boldsymbol{r}}}, {{\widetilde {\mathit{\boldsymbol{r'}}}}_{{q_{l + 1}}}})(\hat xs_{{q_{l + 1}}}^x + \hat ys_{{q_{l + 1}}}^y + \hat zs_{{q_{l + 1}}}^z) $$ (20) $$ {{\mathit{\boldsymbol{P}}}_{{q_{l + 1}}}}({\mathit{\boldsymbol{r}}}) = \tilde G({\mathit{\boldsymbol{r}}}, {{\widetilde {\mathit{\boldsymbol{r'}}}}_{{q_{l + 1}}}})s_{{q_{l + 1}}}^p $$ (21) 利用类似式(9)~式(14)的方法,可以构建相似的方程组,矩阵形式为:
$$ {\mathit{\boldsymbol{G}}_l}{\mathit{\boldsymbol{A}}_l} = {{\mathit{\boldsymbol{P}}}_{l + 1}} $$ (22) 式中,${[{\mathit{\boldsymbol{G}}_l}]_{{t_l}{q_l}}} = \tilde G({\mathit{\boldsymbol{r}}_{{t_l}}},{\widetilde {\mathit{\boldsymbol{r'}}}_{ql}})$表示父层(第l层)CSP在远区点的位函数的匹配;${[{\mathit{\boldsymbol{P}}_{l + 1}}]_{{t_l}{q_{l + 1}}}} = \tilde G({\mathit{\boldsymbol{r}}_{{t_l}}},{\mathit{\boldsymbol{\tilde r}}_{{q_{l + 1}}}})$表示子层CSP在远区点的标量位函数。需要注意的是,此时对矢量位函数匹配的3个方程均和标量位函数的匹配式(22)一致。在求解完矩阵式(22)后,即可以获得聚合矩阵${\mathit{\boldsymbol{A}}_l}$,利用其可以实现子层CSP展开系数向父层的递推:
$$ \mathit{\boldsymbol{\bar s}}_{l, m'}^v = \left[{\mathit{\boldsymbol{s}}_{l, m'}^x, \mathit{\boldsymbol{s}}_{l, m'}^y, \mathit{\boldsymbol{s}}_{l, m'}^z} \right] = \sum\limits_{n' \in {\text{child}}(m')} {{\mathit{\boldsymbol{A}}_l}\mathit{\boldsymbol{\bar s}}_{l + 1, n'}^v} $$ (23) $$ \mathit{\boldsymbol{s}}_{l, m'}^p = \sum\limits_{n' \in {\text{child}}(m')} {{\mathit{\boldsymbol{A}}_l}\mathit{\boldsymbol{s}}_{l + 1, n'}^p} $$ (24) 最终使用MLCSP加速方程(4)中远区矩矢相乘可以写作:
$$ \begin{gathered} {\overline {\mathit{\boldsymbol{V}}} _{mm'}} \cdot i{k_0}{{\mathit{\boldsymbol{J}}}_{m'}} = \\ i{k_0} \cdot \sum\limits_{v = x, y, z} {{{(\mathit{\boldsymbol{W}}_m^v)}^{\text{T}}}\prod\limits_{l = 2}^{L - 1} {\mathit{\boldsymbol{A}}_{l, l + 1}^{\text{T}}} \mathit{\boldsymbol{T}}_{{m_2}, {{m'}_2}}^{}\prod\limits_{l = L - 1}^2 {{\mathit{\boldsymbol{A}}_{l, l + 1}}} \mathit{\boldsymbol{W}}_{m'}^v{{\mathit{\boldsymbol{J}}}_{m'}}} \\ \end{gathered} $$ (25) $$ \begin{gathered} {\overline {\mathit{\boldsymbol{P}}} _{mm'}} \cdot {c_0}{{\mathit{\boldsymbol{\varphi }}}_{m'}} = \\ {c_0} \cdot {(\mathit{\boldsymbol{W}}_m^d)^{\text{T}}}\prod\limits_{l = 2}^{L - 1} {\mathit{\boldsymbol{A}}_{l, l + 1}^{\text{T}}} \mathit{\boldsymbol{T}}_{{m_2}, {{m'}_2}}^{}\prod\limits_{l = L - 1}^2 {{\mathit{\boldsymbol{A}}_{l, l + 1}}} \mathit{\boldsymbol{W}}_{m'}^p{{\mathit{\boldsymbol{\varphi }}}_{m'}} \\ \end{gathered} $$ (26) 这里先将最细层的组$m$和$m'$的电流和电荷使用CSP展开;随后为了简单起见,上行过程直接将系数聚合至第2层,并在其位于第2层的父组${m_2}$和${m'_2}$之间进行转移;最后使用聚合和展开矩阵的转置进行下行和配置过程。
-
为了验证本文方法的正确性和性能,对低频金属目标的散射问题和电小电感模型进行计算,并简要分析了本文方法的精度和复杂度。
-
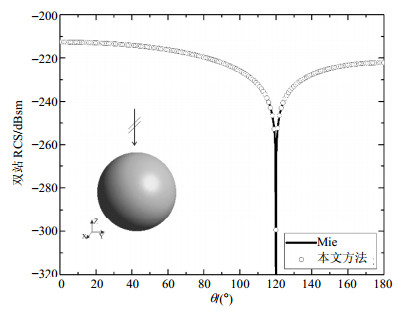
如图 1所示,本文首先计算了一个低频电小金属球的散射。球的半径为1 m,采用100 Hz平面波入射,(入射角为),电尺寸为$6.67 \times {10^{ - 7}}\lambda $。共剖分成1 764个三角形贴片,共有2 646个电流未知量和1 764个电荷未知量。使用本文方法进行多层分组,共分3层,最细层边长为$8.3 \times {10^{ - 8}}\lambda $。采用GMRES-30进行迭代求解,在使用文献[12]中的预条件时,仅80次迭代就可以收敛到${10^{ - 15}}$。图 1还给出了使用本文方法和使用Mie解析结果计算的的双站RCS结果,可以看到,两种方法的结果一致,并均在120°时出现零陷,与电小目标的散射理论一致。
-
由于常见的射频元件在其工作频率下均为电小目标,因此本文方法针对的低频问题也适于该类目标的求解。以电感为例,如图 2所示的电感模型被剖分成7 144个三角形贴片,共10 716个电流未知量和7 144个电荷未知量,采用Delta-Gap进行馈电端口的建模。为了对比本文方法对电小目标的低频稳定性,本文在400 MHz到7 GHz的频带范围内(每隔150 MHz,共45个频点)计算了其电感参数。其中,EFIE和AEFIE为了求解的稳定性,均使用了LU分解计算。本文方法将目标分为4层,每个最细层盒子约60个未知量;由于目标电尺寸极小,在计算时,每层的每个盒子使用的等效CSP数量不变,在本文中取82个;使用GMRES-30和文献[12]中的预条件进行迭代计算,并收敛到${10^{ - 3}}$。图 3给出了EFIE、AEFIE和本文方法计算出的电感值,可以看出本文方法同AEFIE方法获得的电感参数吻合良好,且在低频时趋于稳定的常数;在较高频率下,EFIE同前两者吻合较好,但随着频率的降低,EFIE开始出现明显的低频崩溃,无法计算出正确的结果。
为了详细考察本文方法的计算复杂度,本文在3 GHz时,对采用不同剖分网格的电感进行计算。这里,剖分Ⅱ到剖分Ⅳ是不断对前一个网格进行4次细分得到的,具体的MLCSP分层数和总未知量数目如表 1所示。可以看到随着未知量呈4倍的增加,填充时间、单次迭代时间和总内存占用也约呈4倍的增加。这表明本文方法的存储复杂度和矩矢相乘复杂度均为O(N)量级。
表 1 不同剖分大小时MLCSP的计算复杂度统计
剖分Ⅰ 剖分Ⅱ 剖分Ⅲ 剖分Ⅳ 总未知量数 4 465 17 860 71 440 285 760 分层数 3 4 5 6 最细层边长/λ 0.001 6 0.000 8 0.000 4 0.000 2 填充时间/s 0.3 1.1 4.2 16 单次迭代时间/s 0.06 0.23 0.92 3.6 总内存/MB 105.1 384.4 1 242.6 4 863.5 -
本文针对低频电磁问题的计算,提出了多层复源点方法来加速增量电场积分方程矩量法的远区计算。该方法首先将AEFIE的磁矢量位和电标量位用CSP进行展开;随后构建了子层CSP展开系数向父层递推的聚合矩阵;最后使用多层复源点方法来加速AEFIE的矩矢相乘。结果表明,本文方法的计算结果准确,并且时间和内存复杂度为O(N)量级。
A Multilevel Complex Source Point method for low-frequency problems
-
摘要: 该文将多层复源点(MLCSP)方法用于求解理想导体目标的增量电场积分方程(AEFIE)。AEFIE将待求问题的电流和电荷进行分离,使用合适的频率归一化因子来平衡电场积分方程(EFIE)的磁矢量位和电标量位,使之成为解决低频问题的一种有效手段。为了降低AEFIE-矩量法(MoM)的复杂度,使用复源点(CSP)分别展开AEFIE的磁矢量位和电标量位,并构造了用于MLCSP的聚合矩阵以加速其矩矢相乘。数值算例表明,在求解低频电磁散射问题及电路问题时,该方法计算结果准确,其计算量和计算机内存需求可降低至O(N)量级。Abstract: The multilevel complex source point (MLCSP) method is used to solve augmented electric field integral equation (AEFIE) for perfect electric conduct target. As an effective solution of the low-frequency problem, AEFIE separates current and charge to avoid the imbalance between the vector potential and the scalar potential in the conventional electric field integral equation (EFIE). In order to reduce the computational complexity of method of moment (MoM) for AEFIE, the vector potential and scalar potential are expanded by complex source point (CSP). Then, an aggregation operator is introduced to form a multilevel algorithm for acceleration the matrix-vector products. The numerical results showed that, the accuracy of the method is very high when solving low frequency electromagnetic scattering problems and circuit problems, while computational complexity can be reduced to O(N)level.
-
表 1 不同剖分大小时MLCSP的计算复杂度统计
剖分Ⅰ 剖分Ⅱ 剖分Ⅲ 剖分Ⅳ 总未知量数 4 465 17 860 71 440 285 760 分层数 3 4 5 6 最细层边长/λ 0.001 6 0.000 8 0.000 4 0.000 2 填充时间/s 0.3 1.1 4.2 16 单次迭代时间/s 0.06 0.23 0.92 3.6 总内存/MB 105.1 384.4 1 242.6 4 863.5 -
[1] HARRINGTON R F, HARRINGTON J L. Field computation by moment methods[M]. New York, USA:Oxford University Press, 1996. [2] RAO S, WILTON D, GLISSON A. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(3):409-418. doi: 10.1109/TAP.1982.1142818 [3] QIAN Z G, CHEW W C. A quantitative study on the low frequency breakdown of EFIE[J]. Microwave and Optical Technology Letters, 2008, 50(5):1159-1162. http://www.mendeley.com/research/quantitative-study-low-frequency-breakdown-efie/ [4] 王镇雷.中低频的电场积分方程矩量法研究[D].南京: 东南大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016215670.htm WANG Zhen-lei. Moment method for electric field integral equation in middle and low frequency[D]. Nanjing: Southeast University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016215670.htm [5] ANDRIULLI F P. Loop-star and loop-tree decompositions:analysis and efficient algorithms[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(5):2347-2356. doi: 10.1109/TAP.2012.2189723 [6] BOGDANOV F, ROMAN J, ANNA G. Application of loop-star and loop-tree basis functions to MoM solution of radiation and scattering problems on complicated surface and wire geometries from low to microwave frequencies[C]//2012 6th European Conference on Antennas and Propagation (EUCAP).[S.l.]: IEEE, 2012: 985-989. http://ieeexplore.ieee.org/document/6206152/ [7] STEPHANSON M B, LEE J F. Preconditioned electric field integral equation using Calderón identities and dual loop/star basis functions[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(4):1274-1279. doi: 10.1109/TAP.2009.2016173 [8] YAN S, JIN J M, NIE Z. EFIE analysis of low-frequency problems with loop-star decomposition and Calderón multiplicative preconditioner[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(3):857-867. doi: 10.1109/TAP.2009.2039336 [9] CHEN Y P, JIANG L, QIAN Z G. An augmented electric field integral equation for layered medium Green's function[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(3):960-968. doi: 10.1109/TAP.2010.2103042 [10] DAS A, GOPE D. Modified SPIE formulation for low-frequencystability of electric field integral equation[C]//Applied Electromagnetics Conference(AEMC) 2015.[S.l.]: IEEE, 2015: 1-2. http://ieeexplore.ieee.org/document/7509163/ [11] TASKINEN M, YLA-OIJALA P. Current and charge integral equation formulation[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(1):58-67. doi: 10.1109/TAP.2005.861580 [12] QIAN Z G, CHEW W C. Fast full-wave surface integral equation solver for multiscale structure modeling[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(11):3594-3601. doi: 10.1109/TAP.2009.2023629 [13] ZHAO J S, CHEW W C. Applying LF-MLFMA to solve complex PEC structures[J]. Microwave and Optical Technology Letters, 2001, 28(3):155-160. doi: 10.1002/(ISSN)1098-2760 [14] JIA M M, SUN S, LI Y. Acceleration of perturbation-based electric field integral equations using fast fourier transform[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(10):4559-4564. doi: 10.1109/TAP.2016.2593930 [15] 郑宇腾, 赵延文, 蔡强明, 等.笛卡尔展开算法高效求解增广电场积分方程[J].电波科学学报, 2014(6):1009-1015. http://d.old.wanfangdata.com.cn/Periodical/dbkxxb201406001 ZHENG Yu-teng, ZHAO Yan-wen, CAI Qian-ming. Efficient solution of augmented electric field integral equation using accelerated cartesian expansion algorithm[J]. Chinese Journal of Radio Science, 2014(6):1009-1015. http://d.old.wanfangdata.com.cn/Periodical/dbkxxb201406001 [16] ZHENG Y T, ZHAO Y W, NIE Z P. Full-wave fast solver for circuit devices modeling[J]. Applied Computational Electromagnetics Society Journal, 2015, 30(10):1115-1121. [17] DING D Z, SHI Y, JIANG Z N. Augmented EFIE with adaptive cross approximation algorithm for analysis of electromagnetic problems[J]. International Journal of Antennas and Propagation, 2013:e487276. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Doaj000002922196 [18] TAP K, PATHAK P H, BURKHOLDER R J. Complex source beam-moment method procedure for accelerating numerical integral equation solutions of radiation and scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(4):2052-2062. doi: 10.1109/TAP.2014.2298536 [19] FAN Z H, HU X, CHEN R S. Multilevel complex source beam method for electromagnetic scattering problems[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14:843-846. doi: 10.1109/LAWP.2014.2379927 [20] HANSEN T B, KAISER G. Huygens' principle for complex spheres[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(10):3835-3847. doi: 10.1109/TAP.2011.2163764 [21] TAP K, PATHAK P H, BURKHOLDER R J. Exact complex source point beam expansions for electromagnetic fields[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(9):3379-3390. doi: 10.1109/TAP.2011.2161438 [22] ERGÜL Ö, GÜREL L. The multilevel fast multipole algorithm (MLFMA) for solving large-scale computational electromagnetics problems[M]. New Jersey, USA:John Wiley & Sons, 2014. -


 ISSN
ISSN 




 下载:
下载: