-
近年来以页岩油气为代表的非常规油气资源日益成为能源焦点,其中岩性识别是页岩油气储层勘探开发的重要组成。根据取芯资料识别岩性最为直观准确,但受费用制约,推广受到极大限制[1]。由于常规测井资料连续性好、纵向分辨率高,且对岩性响应敏感,以常规测井曲线为特征输入,利用人工神经网络(artificial neural network, ANN)完成岩性识别的方法正引起国内外关注。文献[2]利用测井资料和神经网络对墨西哥海湾泥页岩岩性进行定量评价。文献[3]利用模糊神经网络,结合井段测井数据实现岩性分类。文献[4]通过优选测井曲线和BP神经网络实现岩性识别。以上研究均获得较好的应用效果,但仍存在不足:1) ANN受同步瞬时输入限制,无法体现测井连续信号的时间累积效应,影响岩性识别精度。而岩性识别主要依据各测井曲线的幅值特征的组合关系,因此测井曲线形态的准确提取是提高识别精度的关键,在本质上属于非线性时变系统分类问题。2)测井曲线的振幅、频率突变频繁,存在大量的奇异点,属于非平稳时变过程信号。ANN受激励函数限制,难于有效完成这种复杂奇异性信号的非线性映射。
过程神经元网络(process neural network, PNN)通过改进神经元聚合机制实现连续输入信号的处理,相继有正交基展开[5]、双并联[6]、离散[7]等模型提出,更加适用于非线性时变系统的逼近,但网络内部映射结构复杂,正交基展开参数成倍增长,PNN训练速度较慢,且训练收敛性存在很大的不足。2004年,文献[8]提出极限学习机(extreme learning machine, ELM)理论,通过理论分析和实验已证明可极大提高神经网络的学习速度[9]。截至目前以ELM为研究主题的文献共被SCI收录2 606篇,其中372篇为IEEE文献,在模式识别[10-11]、回归预测[12-14]、智能芯片[15-16]等领域都已成为国际研究热点。2016年,文献[17]根据PNN自身特性,融合ELM提出QE-DPNN,较大提高了PNN训练收敛能力。
综上所述,本文在前期工作的基础上,为提高岩性识别准确率,首先将脊波函数作为过程神经元的激励函数,提出一种脊波过程神经元网络(ridgelet process neural network, RPNN);其次结合极限学习机理论,提出基于满秩分解的极限学习算法E-RPNN;最后,引入Adaboost实施动态集成E-RPNN,构建集成型极限脊波过程神经网络AE-RPNN模型,通过弱分类器加权组合来构成强分类器。仿真实验以A区的B1和B2井为例验证了AE-RPNN模型在页岩的岩性识别中的有效性,识别准确率高于其他过程神经网络模型。
-
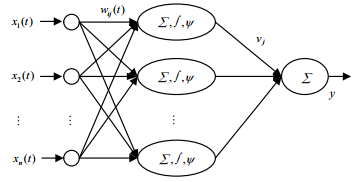
常规PNN模型对于测井曲线这种复杂奇异性时变信号,若满足精度要求,需增加隐层节点数或隐层数,影响模型泛化能力。近年来,脊波变换作为一种多尺度几何分析工具,可有效完成奇异性信号的逼近,目前已应用于图像处理[18]、函数逼近[19-20]中。本文针对测井曲线突变频繁的映射逼近问题,选用脊波变换作为过程神经元激励函数,记输入到隐层的连接权函数为$W(t) = \{ {w_1}(t),{w_2}(t), \cdots ,{w_n}(t)\} $,$\psi $为脊波函数,则单隐层RPNN结构如图 1所示。
RPNN的输出与输入间的关系为:
$$y = \sum\limits_{j = 1}^m {{v_j}\psi \left( {\left( {{u_j}\int_{{\rm{ }}0}^{{\rm{ }}T} {\sum\limits_{i = 1}^n {{\omega _{ij}}(t){x_i}(t)} {\rm{d}}t} - {b_j}} \right)/{a_j}} \right)} $$ (1) 式中,${w_{ij}}(t){x_i}(t)$是第$i$个输入${x_i}(t)$与${w_{ij}}(t)$的内积。
在输入函数空间中选取一组正交基函数${b_1}(t),{b_2}(t), \cdots ,{b_L}(t)$,对于输入函数和权函数在满足拟合精度的条件下进行展开:
$${x_i}{\text{(}}t{\text{)}} = \sum\limits_{l = 1}^L {c_i^{(l)}{b_l}(t)} ,\;\;{w_{ij}}{\text{(}}t{\text{)}} = \sum\limits_{k = 1}^L {w_{ij}^{(k)}{b_l}(t)} $$ (2) 按式(2),式(1)可重写为:
$$y = \sum\limits_{j = 1}^m {{v_j}\psi \left( {\frac{{{u_j}\sum\limits_{i = 1}^n {\sum\limits_{l = 1}^L {\sum\limits_{k = 1}^L {w_{ij}^{(k)}c_i^{(l)}} } } \int_0^T {{b_k}(t){b_l}(t){\text{d}}t} - {b_j}}}{{{a_j}}}} \right)} $$ 根据标准正交基的特性,
式(2)可整理为:
$$y = \sum\limits_{j = 1}^m {{v_j}\psi \left( {\frac{{{u_j}\sum\limits_{i = 1}^n {\sum\limits_{l = 1}^L {w_{ij}^{(l)}c_i^{(l)}} } - {b_j}}}{{{a_j}}}} \right)} $$ (3) 设样本为$({x_{k1}}(t),{x_{k2}}(t), \cdots ,{x_{kn}}(t),{d_k})$,$k = 1,2, \cdots ,K$,则RPNN的误差函数定义为:
$$ \begin{array}{c} E = \frac{1}{2}\sum\limits_{s = 1}^K {({y_k} - {d_k}} {)^2} = \\ \frac{1}{2}\sum\limits_{s = 1}^K {{{\left( {\sum\limits_{j = 1}^m {{v_j}\psi \left( {\frac{{{u_j}\sum\limits_{i = 1}^n {\sum\limits_{l = 1}^L {w_{ij}^{(l)}c_{i,l}^{(k)}} } - {b_j}}}{{{a_j}}}} \right)} - {d_k}} \right)}^2}} \end{array} $$ (4) -
由于正交基展开后的RPNN模型学习参数较多,传统的基于梯度信息的学习算法计算量较大,训练较为耗时。文献[1]利用SVD求解Moore-Penrose广义逆,较大提高了PNN训练速度。本文在此基础上,为进一步提高计算效率,根据满秩分解法求解广义逆,提出脊波PNN的极限学习算法E-RPNN,计算过程仅需矩阵初等行变换,因此计算量更小。
1) 计算隐层输出矩阵
对于给定的$K$个样本$\{ {x_k}(t),{d_k}\} _{k = 1}^K$,第$i$个脊波过程神经元对第$k$个样本的输出为:
$$\psi _j^{(k)}({u_j},{a_j},{b_j}) = \psi \left( {\frac{{{u_j}\sum\limits_{i = 1}^n {\sum\limits_{l = 1}^L {c_{i,l}^{(k)}w_{ij}^{(l)} - {b_j}} } }}{{{a_j}}}} \right)$$ (5) 则RPNN模型的隐层输出矩阵为:
$$\begin{gathered} \boldsymbol{H}{\text{ = }} \\ \left[ {\begin{array}{*{20}{c}} {\psi _1^{(1)}({u_1},{a_1},{b_1})}&{\psi _2^{(1)}({u_2},{a_2},{b_2})}& \cdots &{\psi _m^{(1)}({u_m},{a_m},{b_m})} \\ {\psi _1^{(2)}({u_1},{a_1},{b_1})}&{\psi _2^{(2)}({u_2},{a_2},{b_2})}& \cdots &{\psi _m^{(2)}({u_m},{a_m},{b_m})} \\ \vdots & \vdots & \ddots & \vdots \\ {\psi _1^{(K)}({u_1},{a_1},{b_1})}&{\psi _2^{(K)}({u_2},{a_2},{b_2})}& \cdots &{\psi _m^{(K)}({u_m},{a_m},{b_m})} \end{array}} \right] \\ \end{gathered} $$ (6) 根据ELM理论,对RPNN模型的正交基展开系数随机赋值后,模型的训练转化为输出权值的求解问题。记$\boldsymbol{O} = [{d_1},{d_2}, \cdots ,{d_K}]_{K \times 1}^{\text{T}}$为训练样本的期望输出,$\boldsymbol{V} = [{v_1},{v_2}, \cdots ,{v_m}]_{m \times 1}^{\text{T}}$为隐层输出权值,则RPNN模型的输入输出映射关系可写为:
$$\boldsymbol{HV} = \boldsymbol{O}$$ (7) 2) 求解$\boldsymbol{H}$的Moore-Penrose广义逆
按式(7)和Moore-Penrose广义逆,RPNN的隐层输出权值为:
$$\boldsymbol{V} = {\boldsymbol{H}^\dagger }\boldsymbol{O}$$ (8) 当矩阵${\boldsymbol{H}^{\text{T}}}\boldsymbol{H}$为非奇异矩阵时,式(8)可重写为:
$$\boldsymbol{V} = {({\boldsymbol{H}^{\text{T}}}\boldsymbol{H})^{ - {\text{1}}}}{\boldsymbol{H}^{\text{T}}}\boldsymbol{O}$$ (9) 当${\boldsymbol{H}^{\text{T}}}\boldsymbol{H}$为奇异矩阵时,无法直接求解${({\boldsymbol{H}^{\text{T}}}\boldsymbol{H})^{ - 1}}$。若${\boldsymbol{H}^{\text{T}}}\boldsymbol{H}$接近奇异矩阵时,直接求解逆矩阵也会引起计算结果不稳定,即${\boldsymbol{H}^{\text{T}}}\boldsymbol{H}$中微小扰动都会引起计算结果很大的变化。因此式(9)并不具有普适性。针对此问题,本文提出使用满秩分解法求解广义逆矩阵${\boldsymbol{H}^{\dagger }}$。首先对$\boldsymbol{H}$实施初等行变换,得到Hermite标准形$\boldsymbol{P}$,取$\boldsymbol{H}$第${j_1},{j_2}, \cdots ,{j_r}$列构成$K \times r$的矩阵$\boldsymbol{A}$,取$\boldsymbol{P}$的前$r$行构成$r \times m$的矩阵$\boldsymbol{B}$,则$\boldsymbol{H}$满秩分解为:
$$\boldsymbol{H} = \boldsymbol{AB}$$ (10) 记RPNN的隐层输出矩阵$\boldsymbol{H} \in \boldsymbol{C}_r^{K \times m}$,当$r < K$且$r < m$时,即矩阵$\boldsymbol{H}$不是行满秩矩阵,也不是列满秩矩阵,则Moore-Penrose广义逆矩阵${\boldsymbol{H}^\dagger }$为:
$${\boldsymbol{H}^\dagger } = {\boldsymbol{B}^{\text{T}}}{(\boldsymbol{B}{\boldsymbol{B}^{\text{T}}})^{ - 1}}{({\boldsymbol{A}^{\text{T}}}\boldsymbol{A})^{ - 1}}{\boldsymbol{A}^{\text{T}}}$$ (11) 当$r = K$,矩阵$\boldsymbol{H}$为行满秩矩阵时,矩阵$H$的满秩分解为$\boldsymbol{H} = {\boldsymbol{I}_K}\boldsymbol{H}$,则:
$${\boldsymbol{H}^\dagger } = {\boldsymbol{H}^{\text{T}}}{(\boldsymbol{H}{\boldsymbol{H}^{\text{T}}})^{ - 1}}$$ (12) 当$r = m$,矩阵$\boldsymbol{H}$是列满秩矩阵时,矩阵$H$的满秩分解为$\boldsymbol{H} = \boldsymbol{H}{\boldsymbol{I}_m}$,则:
$${\boldsymbol{H}^\dagger } = {({\boldsymbol{H}^{\text{T}}}\boldsymbol{H})^{ - 1}}{\boldsymbol{H}^{\text{T}}}$$ (13) -
AdaBoost算法是一种元算法集成框架,通过多个弱分类器的线性加权得到强分类器。本文为提高岩性识别精度,通过引入AdaBoost,将E-RPNN视为弱分类器,通过迭代学习不断提高识别错误样本的权值,减小识别误差大的弱分类器的权值,最终使用的投票机制完成强分类器的构建。为描述方便,记$N$个E-RPNN构成的弱分类器集合为:
$$\boldsymbol{F} = ({\delta _1}({X_i}(t)),{\delta _2}({X_i}(t)), \cdots ,{\delta _N}({X_i}(t)))$$ AE-PRNN学习算法如下:
1) 训练样本数据集的初始化权值分布为:
$$ {\boldsymbol{D}_1} = \{ \lambda _1^1,\lambda _2^1, \cdots ,\lambda _K^1\} ,\;\;\lambda _i^1 = \frac{1}{K},\;\;i = 1,2, \cdots ,K $$ (14) 2) 循环开始,计数器$r = 1$;
① 根据权值分布${\boldsymbol{D}_r}$的样本集,实施数据拟合后选取一组勒让德基函数,按式(2)对RPNN输入和权函数正交基展开,对基展开系数随机赋值;
② 按式(6)计算输出矩阵$\boldsymbol{H}$,根据${\text{rank}}(H)$对矩阵$\boldsymbol{H}$实施满秩分解,并计算广义逆矩阵${\boldsymbol{H}^\dagger }$,最后按式(8)求解RPNN隐层输出权值;
③ 用当前训练完成的弱分类器${\delta _r}$,对样本识别,并计算弱分类器${\delta _r}$的加权分类错误率:
$${\varepsilon _r} = \sum\limits_{k = 1}^K {\lambda _k^r} \times \left| {{d_k} - {\delta _r}({X_k}(t))} \right|$$ (15) ④ 计算弱分类器${\delta _r}$的权重${\eta _r}$和样本权重:
$${\eta _r} = \frac{1}{2}\ln \left( {\frac{{1 - {\varepsilon _r}}}{{{\varepsilon _r}}}} \right)$$ (16) $$\lambda _i^{r + 1} = \frac{{\lambda _i^r}}{{{B_r}}} \times \exp \left( { - {\eta _r} \times {d_i} \times {\delta _r}({X_i}(t))} \right)$$ (17) 式中,${B_r}$是弱分类器${\delta _r}$的规范化因子;
⑤ $r \leftarrow r + 1$,若$r < N$,转②,否则弱分类器训练结束,转③;
3) 对弱分类器,按各自权重加权线性组合,则最终的强分类器输出:
$$ h({X_i}(t)) = \sum\limits_{r = 1}^N {{\eta _r}} \cdot {\delta _r}({X_i}(t)) $$ (18) -
为验证本文所提AE-RPNN的有效性,与未使用AdaBoost的E-RPNN、文献[5]的OBPNN、文献[6]的双并联过程神经网络DPPNN、文献[7]的数值积分离散过程神经网络IPNN对比,同时也给出与普通神经网络BP-ANN和RBF进行对比。
岩性样本数据来源于A地区的8口页岩油井,常规测井资料包括自然伽马GR、中子CN、声波时差AC、密度DEN、自然电位SP、井陉CAL、深侧向电阻率RLLD、浅侧向电阻率RLLS。由于测井曲线是岩性的综合反映,选取测井曲线越多,越有利于提高岩性识别准确率。但当输入样本维数较多时,神经网络模型不仅计算效率低、收敛速度慢,而且还会因输入维数过高引起网络结构的复杂化,降低模型的泛化能力,因此本文使用主成分分析法PCA对所选测井曲线实施分析,表 1是部分样本的PCA统计分析结果,表 2为各主成分的方差及累积贡献率。
表 1 部分实测岩性和测井曲线特征数据及PCA主成分
岩性 实测岩性样本数据 主成分 DEN CN AC GR RLLD RLLS CAL SP X1 X2 X3 泥岩 2.53 16.32 75.61 81.8 19.70 16.52 10.21 30.29 1.22 -1.06 1.83 2.53 17.26 76.84 84.26 14.42 12.32 10.31 30.20 1.37 -0.33 1.23 2.53 19.28 77.86 88.90 11.81 10.20 10.32 30.11 1.29 0.17 0.74 2.53 21.14 78.85 92.36 10.59 9.18 10.27 30.04 1.23 0.42 0.55 2.53 22.82 79.24 94.75 9.77 8.50 10.20 29.98 1.19 0.57 0.46 2.53 24.20 79.36 96.05 8.97 7.86 10.13 29.93 1.17 0.70 0.37 2.53 24.98 79.44 94.19 8.61 7.57 10.13 29.89 1.15 0.75 0.34 … … … … … … … … … … … 2.54 25.61 78.81 85.62 8.34 7.38 10.27 29.83 0.50 0.99 -0.23 砂岩 2.53 31.59 84.67 89.40 7.15 6.09 9.87 34.75 0.51 0.99 -0.25 2.53 31.29 84.18 89.30 7.10 6.06 9.87 34.79 0.50 0.96 -0.23 2.52 30.85 83.35 88.89 7.12 6.09 9.86 34.82 0.52 0.92 -0.23 2.52 30.38 81.50 88.29 7.21 6.19 9.85 34.85 0.58 0.77 -0.15 2.52 29.95 80.15 87.70 7.57 6.52 9.84 34.88 0.62 0.72 -0.14 2.53 29.45 79.17 87.46 7.90 6.82 9.85 34.90 0.64 0.68 -0.10 2.54 29.17 78.40 87.70 8.2 7.10 9.86 34.91 0.66 0.67 -0.09 … … … … … … … … … … … 2.54 29.38 78.81 87.88 8.60 7.50 9.91 34.92 1.37 -0.33 1.23 表 2 测井曲线主成分统计分析
成分 特征根 方差贡献率/% 累积贡献率/% 1 1.887 5 52.674 8 52.674 8 2 0.801 1 22.357 6 75.032 4 3 0.581 3 16.221 5 91.253 9 4 0.234 9 6.555 3 97.809 3 5 0.061 3 1.711 4 99.520 7 6 0.010 2 0.283 3 99.804 0 7 0.004 1 0.114 6 99.918 7 8 0.002 9 0.081 3 100.000 0 主成分特征数量选择依据如下:1)受限于PNN模型的正交基展开结构限制,每增加一个输入节点,训练参数呈指数级增长,模型复杂度大大提高,降低了训练收敛率,从而影响模型的分类识别精度;2)前3个主成分的累积贡献率达到91.253 9%,已超过了85%。按照PCA分析原则,多个主成分累积贡献率超过85%时,即可代表原有的数据空间特征,因此最终选用前3个主成分来表示原数据集中的8条测井曲线;3)此外,为进一步说明主成分的选择依据,表 3为选择不同数量的主成分对应的模型训练和岩性识别结果,可明显看出随着主成分特征输入的增多,AE-RPNN的训练收敛率和岩性识别精度均有一定程度的降低。
表 3 不同主成分的模型训练与识别对比
主成分数量 模型训练时间/s 训练收敛率/% B1识别精度/% B2识别精度/% 2 62.39 88.56 79.67 76.53 3 78.66 90.67 90.05 88.49 4 91.82 84.52 86.79 85.55 5 99.64 80.46 85.83 81.72 -
1) 样本训练集和测试集:以A区8口页岩油井的人工解释320组样本为训练样本,泥岩、砂岩、灰岩、油页岩的样本数分别为60、90、70、100。其中对于过程神经网络模型,每个岩性样本用10个长度为3的离散序列描述。各种神经网络模型训练结束后分别对B1和B2的部分井段进行岩性识别。
2) 模型参数设置:根据所选数据集,输入样本拟合时选取勒让德基函数,满足精度条件下的基展开个数L=7,输入部分为3个节点,输出为1个节点,隐层节点为8个。参照文献[6],OBPNN、DPPNN、IPNN中的学习速度参数均设置为$\alpha = \beta = \gamma = 0.5$,惯性系数$\eta = 0.1$。此外,在AE-RPNN的隐层节点选择过程中,根据试探法,根据节点数目对模型训练时间和识别率来确定,具体如图 2所示。
为尽量减少实验结果的随机性,使用训练样本对每种模型各训练20次,每次训练结束后用测试样本集进行岩性识别测试,并取岩性识别结果的平均值作为最终岩性。参与对比的6个神经网络模型,岩性识别指标对比如表 2所示。岩性识别准确率从高到低依次AE-RPNN、DPPNN、E-RPNN、IPNN、OBPNN、BP-ANN。其中AE-RPNN的岩性识别能力明显优于其他模型。此外,AE-RPNN对B1井的岩性分布的纵向识别结果分别如图 3所示,结果表明AE-RPNN在页岩岩性识别问题中的适用性,较好地完成了A区地层岩性的垂向分布识别。
表 4 不同神经网络模型的页岩岩性识别结果对比
序号 模型 训练集 测试集(B1井) 测试集(B2井) 识别误差 识别率/% 训练时间/s 识别误差 识别率/% 识别误差 识别率/% 1 BP-ANN 0.138 9 80.02 34.56 0.275 4 71.89 0.283 4 69.86 2 RBF 0.130 6 82.73 48.52 0.251 0 76.97 0.259 1 74.77 3 OBPNN 0.112 7 91.90 97.37 0.225 2 78.68 0.236 8 77.71 4 IPNN 0.100 8 92.27 87.45 0.206 9 81.04 0.198 5 80.03 5 DPPNN 0.088 3 94.79 154.82 0.164 7 84.56 0.187 4 81.08 6 E-RPNN 0.092 4 93.52 13.31 0.185 8 82.33 0.190 3 80.25 7 AE-RPNN 0.056 7 97.45 78.66 0.136 3 90.05 0.155 1 88.43 -
测井曲线是地质岩性的综合反映,纵向分辨率高、连续性好,因此二者之间必然存在某种隐含的复杂非线性映射关系。而普通神经网络进行岩性识别时,对于随深度、时间连续变化的测井曲线输入,无法有效体现信号的时间累积关系。从地质理论上看,不能准确提取测井曲线形态与岩性间的映射关系,从而影响了识别精度。对于5种过程神经网络模型,模型内部计算均是利用正交基展开后的积分聚合机制,可以完成测井曲线连续输入信号的映射处理,因此识别精度高于普通神经网络BP和RBF。其中AE-RPNN高于其他4种PNN的原因如下:
1) 测井曲线突变频繁,具有奇异性特征,属于非平稳时变过程信号。AE-RPNN和E-RPNN选用脊波变换作为激励函数,通过调节位置、尺度和方向3组参数向量,在权函数正交基展开后,利用多组脊函数的叠加,能够更加有效完成这种复杂非线性映射的逼近。而OBPNN、DPPNN、IPNN的激励函数均为具有全局特性的Sigmoid函数,仅对于平稳的时变信号较为适用。这一点从E-RPNN高于OBPNN和IPNN的实验结果中可明显看出。
2) AE-RPNN模型通过AdaBoost元算法框架的加权投票策略,对多个E-RPNN弱分类器进行叠加,是“三个臭皮匠,赛过诸葛亮”的经验的实际应用。在具体实验中,若某个岩性样本被识别错误,则该样本会被赋予更大的权重,从而下一次迭代时使弱分类器更加关注该样本的识别,在同等情况下加大弱分类器针对错分岩性样本的参数修正概率,有效提高模型非线性映射能力。与此同时,每次迭代后的E-RPNN也根据分类识别率被赋予相应的权重,预测效果好的,权重越大,从而使AE-RPNN在岩性识别过程中,根据多组弱分类器的输出和加权投票策略,提升分类效果较优的弱分类器输出比重,弱化分类效果较差的弱分类器。因此,相对于其他监督学习模型,AE-RPNN学习过程增加了动态调整机制,通过样本和弱分类器的权重调节,有效提高模型的学习和岩性识别能力,此种机制是DPPNN与其他PNN所不具备的,DPPNN是双并联模型,其他PNN受限于每次训练的非线性映射过程,二者均缺少样本和模型的权重调整。
3) IPNN在处理测井曲线连续输入时,以多组离散数据向量直接作为模型特征输入,内部采用数值积分完成时域聚合,减少了样本拟合时所需的基函数展开和正交基项数的确定,因此识别精度优于OBPNN。但激励函数仍为Sigmoid函数,且缺少模型动态集成机制,直接构建岩性识别的强分类器难度依然较大。
4) 此外,过程神经网络在正交基展开后,传统的梯度下降或者进化算法训练的方式均存在学习速度较慢的不足,此时若直接使用AdaBoost集成,则学习时间则会非常耗时。本文的AE-RPNN内部的E-RPNN采用极限学习理论,通过满秩分解计算的Moore-Penrose广义逆求解隐层输出权值,算法训练速度较快,这一点从表 1中的E-RPNN的训练时间可以看出。该特性也为过程神经网络模型完成AdaBoost动态集成提供了很好的基础。
综上所述,AE-RPNN模型在页岩油测井评价的岩性识别问题中,具有较高的识别率,对于连续测井曲线的岩性识别问题具有较好的适用性。极限学习算法的提出也为构建集成型的PNN模型提供了训练基础。
-
岩性识别的关键问题在于测井曲线形态的准确完整的提取和突变奇异性的处理。本文所提的脊波过程神经网络RPNN模型利用PCA处理的测井曲线作为特征输入,内部通过积分完成时域聚合。同时针对测井曲线的连续变化和奇异性特征,首先选用过程神经网络作为岩性识别模型,并提出使用脊波变换作为过程神经元的激励函数,通过一组具有不同尺度、位置、方向的脊函数叠加完成测井信号的映射逼近;其次,为进一步提高岩性识别准确率,给出AdaBoost的模型的动态集成机制,完成模型和样本权值的动态调整。为避免模型训练时间过长,利用满秩分解计算隐层输出矩阵广义逆,有效解决过程神经网络训练速度慢的问题。通过岩性识别的仿真实验,AE-RPNN的提出对于提高页岩岩性的识别准确率具有较好的适用性,有效提高了传统PNN模型在处理该类问题时的逼近效率。
Extreme Learning Ridgelet Process Neural Network and Application
-
摘要: 为提高页岩的岩性识别精度,首先针对测井曲线连续变化、突变频繁的信号特征,利用脊波变换作为过程神经元的激励函数,提出一种脊波过程神经网络模型;其次通过AdaBoost的动态调整机制迭代调整模型和样本集权重,利用多个弱分类器的线性加权构建强分类器;最后为提高AdaBoost中的每个脊波过程神经网络模型的学习速度,提出一种基于满秩分解的极限学习算法,通过Moore-Penrose广义逆求解隐层输出权值。仿真实验以A区的B1井和B2井为例进行岩性识别,通过对比分析验证方法的有效性,识别效果优于其他过程神经网络模型,准确率最高可达90%左右。Abstract: To improve the accuracy about shale lithology identification, this paper proposes a ridgelet process neural network (RPNN) and selects the ridgelet transform as the active function of process neuron according to the signal characteristic of continuous and frequent variation about logging curve. RPNN uses the dynamic mechanism of AdaBoost to adjust iteratively weights of the models and the sample. In order to improve the RPNN learning speed in AdaBoost, an extreme learning algorithm based on full rank decomposition is proposed. The proposed method was applied to the lithology identification for B1 and B2 well in A area and its effectiveness was tested through comparison and analysis. The results show that the lithology identification result of RPNN is better than other process neural networks and the recognition accuracy of RPNN is up to about 90 per cent.
-
表 1 部分实测岩性和测井曲线特征数据及PCA主成分
岩性 实测岩性样本数据 主成分 DEN CN AC GR RLLD RLLS CAL SP X1 X2 X3 泥岩 2.53 16.32 75.61 81.8 19.70 16.52 10.21 30.29 1.22 -1.06 1.83 2.53 17.26 76.84 84.26 14.42 12.32 10.31 30.20 1.37 -0.33 1.23 2.53 19.28 77.86 88.90 11.81 10.20 10.32 30.11 1.29 0.17 0.74 2.53 21.14 78.85 92.36 10.59 9.18 10.27 30.04 1.23 0.42 0.55 2.53 22.82 79.24 94.75 9.77 8.50 10.20 29.98 1.19 0.57 0.46 2.53 24.20 79.36 96.05 8.97 7.86 10.13 29.93 1.17 0.70 0.37 2.53 24.98 79.44 94.19 8.61 7.57 10.13 29.89 1.15 0.75 0.34 … … … … … … … … … … … 2.54 25.61 78.81 85.62 8.34 7.38 10.27 29.83 0.50 0.99 -0.23 砂岩 2.53 31.59 84.67 89.40 7.15 6.09 9.87 34.75 0.51 0.99 -0.25 2.53 31.29 84.18 89.30 7.10 6.06 9.87 34.79 0.50 0.96 -0.23 2.52 30.85 83.35 88.89 7.12 6.09 9.86 34.82 0.52 0.92 -0.23 2.52 30.38 81.50 88.29 7.21 6.19 9.85 34.85 0.58 0.77 -0.15 2.52 29.95 80.15 87.70 7.57 6.52 9.84 34.88 0.62 0.72 -0.14 2.53 29.45 79.17 87.46 7.90 6.82 9.85 34.90 0.64 0.68 -0.10 2.54 29.17 78.40 87.70 8.2 7.10 9.86 34.91 0.66 0.67 -0.09 … … … … … … … … … … … 2.54 29.38 78.81 87.88 8.60 7.50 9.91 34.92 1.37 -0.33 1.23 表 2 测井曲线主成分统计分析
成分 特征根 方差贡献率/% 累积贡献率/% 1 1.887 5 52.674 8 52.674 8 2 0.801 1 22.357 6 75.032 4 3 0.581 3 16.221 5 91.253 9 4 0.234 9 6.555 3 97.809 3 5 0.061 3 1.711 4 99.520 7 6 0.010 2 0.283 3 99.804 0 7 0.004 1 0.114 6 99.918 7 8 0.002 9 0.081 3 100.000 0 表 3 不同主成分的模型训练与识别对比
主成分数量 模型训练时间/s 训练收敛率/% B1识别精度/% B2识别精度/% 2 62.39 88.56 79.67 76.53 3 78.66 90.67 90.05 88.49 4 91.82 84.52 86.79 85.55 5 99.64 80.46 85.83 81.72 表 4 不同神经网络模型的页岩岩性识别结果对比
序号 模型 训练集 测试集(B1井) 测试集(B2井) 识别误差 识别率/% 训练时间/s 识别误差 识别率/% 识别误差 识别率/% 1 BP-ANN 0.138 9 80.02 34.56 0.275 4 71.89 0.283 4 69.86 2 RBF 0.130 6 82.73 48.52 0.251 0 76.97 0.259 1 74.77 3 OBPNN 0.112 7 91.90 97.37 0.225 2 78.68 0.236 8 77.71 4 IPNN 0.100 8 92.27 87.45 0.206 9 81.04 0.198 5 80.03 5 DPPNN 0.088 3 94.79 154.82 0.164 7 84.56 0.187 4 81.08 6 E-RPNN 0.092 4 93.52 13.31 0.185 8 82.33 0.190 3 80.25 7 AE-RPNN 0.056 7 97.45 78.66 0.136 3 90.05 0.155 1 88.43 -
[1] 黎泽刚, 汪忠浩, 刘海军.基于常规测井资料的岩性识别方法优劣分析[J].工程地球物理学报, 2015, 12(1):77-82. doi: 10.3969/j.issn.1672-7940.2015.01.015 LI Ze-gang, WANG Zhong-hao, LIU Hai-jun. The comparative study of the lithologic identification based on conventional well logging information[J]. Chinese Journal of Engineering Geophysics, 2015, 12(1):77-82. doi: 10.3969/j.issn.1672-7940.2015.01.015 [2] YANG Y L, APLIN C, LARTER R. Quantitative assessment of mudstone lithology using geophysical wireline logs and artificial neural networks[J]. Petroleum Geoscience, 2004(10):141-151. http://171.67.120.59/content/10/2/141.short [3] HSIEH B Z, LEWIS C, LIN Z S. Lithology identification of aquifers from geophysical well logs and fuzzy logic analysis:Shui-Lin Area, Taiwan[J]. Computers & Geosciences, 2005(31):263-275. https://www.sciencedirect.com/science/article/pii/S0098300404001323 [4] MOAZZENI A, HAFFAR M A. Artificial intelligence for lithology identification through real-time drilling data[J]. Earth Science & Climatic Change, 2015, 6(3):1-6. [5] 许少华, 何新贵.基于函数正交基展开的过程神经网络学习算法[J].计算机学报, 2004, 27(5):645-650. doi: 10.3321/j.issn:0254-4164.2004.05.009 XU Shao-hua, HE Xin-gui. Learning algorithms of process neural networks based on orthogonal function basis expansion[J]. Chinese Journal of Computers, 2004, 27(5):645-650. doi: 10.3321/j.issn:0254-4164.2004.05.009 [6] DING G, ZHONG S. Time series prediction by parallel feedforward process neural network with time-varied input and output functions[J]. Neural Network World, 2005, 15(2):137-147. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f8ffc53d461f6d4a9345ce7c8dc0e89a [7] LI P C, SHI G Y. Numerical integration-based discrete process neural networks algorithm and applications[J]. System Engineering-Theory & Practice, 2013, 33(12):3216-3222. http://d.old.wanfangdata.com.cn/Periodical/xtgcllysj201312028 [8] HUANG G B, ZHU Q Y, SIEW C K, Extreme learning machine: a new learning scheme of feedforward neural networks[C]//Int Joint Conference on Neural Networks. Budapest: IEEE Press, 2004: 985-990. [9] HUANG G B. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, 2012, 42(2):513-516 http://www.ncbi.nlm.nih.gov/pubmed/21984515 [10] HUANG Z Y, YU Y L, GU J, et al. An efficient method for traffic sign recognition based on extreme learning machine[J]. IEEE Transactions on Cybernetics, 2017, 47(4):920-933. doi: 10.1109/TCYB.2016.2533424 [11] HUANG G, SONG S, GUPTA J N. Semi-supervised and unsupervised extreme learning machines[J]. IEEE Intelligent System, 2014, 44(12):2405-2417. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0234918494/ [12] KASUN L L C, ZHOU H M, HUANG G B. Representational learning with extreme learning machine for big data[J]. IEEE Intelligent System, 2013, 28(6):31-34 [13] HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B:Cybernetics, 2012, 42(2):513-529. doi: 10.1109/TSMCB.2011.2168604 [14] XU Y. A reliable intelligent system for real-time dynamic security assessment of power systems[J]. IEEE Transactions on Power Systems, 2012, 27(3):1235-1263. doi: 10.1109/TPWRS.2012.2183899 [15] CHEN Yi, YAO En-yi, BASU A. A 128 channel extreme learning machine based neural decoder for brain machine interface[J]. IEEE Transactions on Biomedical Circuits and Systems, 2015:arXiv:1509. 07450. http://arxiv.org/abs/1509.07450 [16] WANG Y, YU H, HUANG G B, et al. An energy-efficient nonvolatile in-memory computing architecture for extreme learning machine by domain-wall nanowire devices[J]. IEEE Transactions on Nanotechnologies, 2015, 14(6):998-1012. doi: 10.1109/TNANO.2015.2447531 [17] 刘志刚, 许少华, 李盼池.基于QPSO和极限学习的离散过程神经网络及学习算法[J].控制与决策, 2016, 31(12):2241-2247. http://d.old.wanfangdata.com.cn/Periodical/kzyjc201612018 LIU Zhi-gang, XU Shao-hua, LI Pan-chi. Discrete process neural networks and learning algorithms based on QPSO and extreme learning machine[J]. Control and Decision, 2016, 31(12):2241-2247 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201612018 [18] SAUDAGAR A K J, SYED A S. Image compression approach with ridgelet transformation using modified neuro modeling for biomedical images[J]. Neural Computing & Applications, 2014, 24(7-8):1725-1734. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0232804289/ [19] MARTIAS C. On the subexponentiality of the ridgelet transform[J]. Comptes Rendus Mathematique, 2014, 352(12):1029-1031. doi: 10.1016/j.crma.2014.06.012 [20] YANG S Y, WANG M, JIAO L C. Approximation of functions with spatial inhomogeneity based on true ortho-ridgelet neural network[J]. Applied Soft Computing, 2011, 11(2):2444-2451. https://www.sciencedirect.com/science/article/pii/S1568494610002504 -


 ISSN
ISSN 




 下载:
下载: