-
INS/GNSS组合导航系统充分利用惯性导航系统(INS)和全球卫星导航系统(GNSS)的优点,使导航精度与可靠性均优于各单个子系统,已在导航领域得到广泛应用[1-2]。组合导航系统多采用扩展卡尔曼滤波(EKF)融合算法,当组合导航数学模型和系统噪声的统计特性已知情况下,基于EKF的组合导航精度较高[3]。然而在实际导航应用中,多路径效应、卫星被遮挡和观测粗差等观测信息异常,以及数学模型与真实模型之间存在偏差等因素使得滤波结果出现较大误差甚至发散现象[4]。近年来学者先后提出抗差自适应EKF(robust adaptive EKF, RAEKF)[5-6],其思想为利用抗差估计理论抵抗粗差影响,利用自适应因子调节动力学模型误差影响[7-9]。目前自适应因子的计算多采用预测残差法,而当可见卫星数少于4颗或卫星几何机构分布不佳的情况下,该方法不能有效降低其对导航结果的影响。本文提出卫星少于4颗或卫星几何结构分布不佳时自适应因子计算方法,并利用一组实测车载导航实验验证了该方法的可行性。
-
INS/GNSS紧组合状态方程采用17维误差状态参数构成:
$$ \begin{gathered} {\mathit{\boldsymbol{X}}_t} = [\begin{array}{*{20}{c}} {\delta L}&{\delta \lambda }&{\delta h}&{\delta {v_E}}&{\delta {v_N}}&{\delta {v_U}}&{{\varphi _E}}&{{\varphi _N}} \end{array} \\ \begin{array}{*{20}{l}} {{\varphi _U}{\text{ }}{\varepsilon _x}}&{{\varepsilon _y}}&{{\varepsilon _z}}&{{\nabla _{bx}}}&{{\nabla _{by}}}&{{\nabla _{bz}}}&{\begin{array}{*{20}{c}} {\delta {t_u}}&{\delta {t_{{\text{ru}}}}} \end{array}} \end{array}{]^{\text{T}}} \\ \end{gathered} $$ (1) 式中,$\delta L、\delta \lambda、\delta h$为位置误差;$\delta {v_E}、\delta {v_N}、\delta {v_U}$为速度误差;${\varphi _E}、{\varphi _N}、{\varphi _U}$为姿态误差;${\varepsilon _x}、{\varepsilon _y}、{\varepsilon _z}$为三轴陀螺仪漂移误差;${\nabla _x}、{\nabla _y}、{\nabla _z}$为三轴加速度计零偏误差;$\delta {t_u}、\delta {t_{{\text{ru}}}}$分别为等效钟差距离误差和等效钟漂距离误差。
设i为地心惯性系,n为当地地理坐标系,e为地心地固坐标系。由于INS导航算法和惯性器件等误差的存在,实际计算的坐标系与理想的导航坐标系间存在微小姿态误差角${\mathit{\boldsymbol{\varphi }}^n}$,设其表达式为,则平台误差角的矢量表达式为:
$$ {\mathit{\boldsymbol{\dot \varphi }}^n} = \delta \omega _{ie}^n + \delta \omega _{en}^n - (\omega _{ie}^n + \omega _{en}^n){\mathit{\boldsymbol{\varphi }}^n} + \mathit{\boldsymbol{C}}_b^n{\varepsilon ^b} $$ (2) 速度误差定义为计算的速度与载体真实速度之差。其误差方程的矢量表达形式为:
$$ \begin{gathered} \delta {{\mathit{\boldsymbol{\dot V}}}^n} = {f^n}{\mathit{\boldsymbol{\varphi }}^n} - (2\delta \omega _{ie}^n + \delta \omega _{en}^n){\mathit{\boldsymbol{V}}^n} - \\ (2\omega _{ie}^n + \omega _{en}^n)\delta {\mathit{\boldsymbol{V}}^n} + \mathit{\boldsymbol{C}}_b^n{\nabla ^b} \\ \end{gathered} $$ (3) 位置误差为:
$$ \left\{ {\begin{array}{*{20}{l}} {\delta \dot L = \frac{{\delta {v_N}}}{{{R_M} + h}}} \\ {\delta \dot \lambda = \frac{{\delta {v_E}}}{{{R_N} + h}}\sec L + \frac{{{v_E}\sec L}}{{{R_N} + h}}\tan L\delta L} \\ {\delta \dot h = \delta {v_U}} \end{array}} \right. $$ (4) 式(2)~(4)中,$\mathit{\boldsymbol{C}}_b^n$为载体系到地理系的转换矩阵;$\omega _{ie}^n$、$\omega _{en}^n$分别为地球自转角速率在导航坐标系和导航系相对地球系在导航系下的分量;${f^n}$为加速度计测得的比力;${R_M}、{R_N}$分别为子午圈曲率半径和卯酉圈曲率半径。对于本文采用的LCI惯导,陀螺仪和加速度计误差模型可简化为:
$$ \left\{ {\begin{array}{*{20}{c}} {{{\dot \varepsilon }^b} = 0} \\ {{{\dot \nabla }^b} = 0} \end{array}} \right. $$ (5) 在紧组合中,GNSS接收机的等效时钟距离误差和等效钟漂距离误差为:
$$ \left\{ {\begin{array}{*{20}{l}} {\delta {{\dot t}_u} = \delta {t_{{\text{ru}}}} + {w_{{\text{ru}}}}} \\ {\delta {{\dot t}_{{\text{ru}}}} = - \frac{1}{T}\delta {t_{{\text{ru}}}} + {w_{{\text{tru}}}}} \end{array}} \right. $$ (6) 式中,T为相关时间;${w_{{\text{tu}}}}、{w_{{\text{tru}}}}$为对应噪声。
根据式(2)~式(6),可以得到INS/GNSS紧组合状态方程为:
$$ {\mathit{\boldsymbol{\dot X}}_t} = {\mathit{\boldsymbol{F}}_t}{\mathit{\boldsymbol{X}}_t} + {\mathit{\boldsymbol{G}}_t}{\mathit{\boldsymbol{W}}_t} $$ (7) 将状态方程离散化可得:
$$ {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k - 1}}{\mathit{\boldsymbol{W}}_{k - 1}} $$ (8) 式中,${\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}$为$k - 1$时刻到$k$时刻的系统一步转移矩阵;${\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k - 1}}$为系统噪声矩阵;${\mathit{\boldsymbol{W}}_{k - 1}}$为系统噪声。
-
紧组合采用惯导推算的伪距和伪距率与卫星测量的伪距和伪距率之差作为量测信息,有:
$$ \delta \rho = {\rho _I} - {\rho _G} = \mathit{\boldsymbol{E}}\delta \mathit{\boldsymbol{r}} - \delta {t_u} - {v_\rho } $$ (9) $$ \delta \dot \rho = {\dot \rho _I} - {\dot \rho _G} = \mathit{\boldsymbol{E}}\delta \mathit{\boldsymbol{v}} - \delta {t_{{\text{ru}}}} - {v_{\dot \rho }} $$ (10) 式中,$\mathit{\boldsymbol{E}}$为载体到卫星的方向余弦向量;${v_\rho }、{v_{\dot \rho }}$为观测噪声;$\delta \mathit{\boldsymbol{r}}$、$\delta \mathit{\boldsymbol{v}}$为地心地固坐标系下位置和速度误差向量。地心地固坐标系与导航坐标系之间的转换关系为:
$$ C_e^t = \left[ {\begin{array}{*{20}{c}} { - \sin \lambda }&{\cos \lambda }&0 \\ { - \sin L\cos \lambda }&{ - \sin L\sin \lambda }&{\cos L} \\ {\cos L\cos \lambda }&{\cos L\sin \lambda }&{\sin L} \end{array}} \right] $$ (11) 由式(9)和式(10)可得到紧组合离散化的量测方程为:
$$ {\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{V}}_k} $$ (12) 式中,${\mathit{\boldsymbol{H}}_k}$为量测矩阵;${\mathit{\boldsymbol{V}}_k}$为量测噪声。
-
GNSS/INS紧组合系统为非线性系统,EKF算法通过对非线性系统进行线性化可进一步提高导航解的精度。对于中低精度的惯性系统一般采用闭环校正方式,即在计算时每次校正后状态参数重新设置为零矢量。EKF的滤波方程可表示为:
$$ \left\{ {\begin{array}{*{20}{l}} {{{\hat X}_{k, k - 1}} = 0} \\ {{\mathit{\boldsymbol{P}}_{k, k - 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{P}}_{k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}^{\text{T}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k - 1}}{\mathit{\boldsymbol{Q}}_{K - 1}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k - 1}^{\text{T}}} \\ {{\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{k, k - 1}}\mathit{\boldsymbol{H}}_k^{\text{T}}{{({\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k, k - 1}}\mathit{\boldsymbol{H}}_k^{\text{T}} + {\mathit{\boldsymbol{R}}_k})}^{ - 1}}} \\ {{{\hat X}_k} = {{\hat X}_{k, k - 1}} + {\mathit{\boldsymbol{K}}_k}({\mathit{\boldsymbol{Z}}_k} - {\mathit{\boldsymbol{H}}_k}{{\hat X}_{k, k - 1}})} \\ {{\mathit{\boldsymbol{P}}_k} = (\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_k}){\mathit{\boldsymbol{P}}_{k, k - 1}}} \end{array}} \right. $$ (13) 式中,${\mathit{\boldsymbol{K}}_k}$为滤波增益矩阵;${\mathit{\boldsymbol{P}}_{k, k - 1}}$为状态一步预测协方差矩阵;${\mathit{\boldsymbol{P}}_k}$为状态估计协方差矩阵;${\mathit{\boldsymbol{Q}}_k}$和${\mathit{\boldsymbol{R}}_k}$分别为系统噪声和量测噪声的方差矩阵。
-
精确的滤波模型和误差统计特性是卡尔曼滤波最优估计的基础。而在实际的组合导航应用中,滤波模型与真实模型存在一定的偏差以及观测值受到外界条件的干扰使得观测粗差的存在不可避免,如果不处理直接进行卡尔曼滤波将会导致导航解次优甚至发散。所以本文采用抗差自适应EKF算法,其原理是利用抗差因子和自适应因子调节动力学模型信息和观测信息对滤波结果贡献的大小。即:
$$ \left\{ {\begin{array}{*{20}{l}} {{{\bar R}_k} = \frac{1}{{{r_k}}}{R_k}} \\ {{{\bar P}_{k, k - 1}} = \frac{1}{{{\alpha _k}}}{P_{k, k - 1}}} \end{array}} \right. $$ (14) 式中,${r_k}$为抗差因子;${\alpha _k}$为自适应因子。将式中${\bar R_k}、{\bar P_{k, k - 1}}$代替式(13)中的${R_k}、{P_{k, k - 1}}$即为抗差自适应EKF算法。
抗差等价权矩阵的构造主要有Huber法、丹麦法、IGG法。其中IGG法充分考虑到观测数据的实际情况,更适用于INS/GNSS组合导航系统,其函数表达式为[10]:
$$ {r_k} = \left\{ {\begin{array}{*{20}{l}} 1&{{v_k} \leqslant {k_0}} \\ {\frac{{{k_0}}}{{{v_k}}}\left[ {\frac{{{k_1} - {v_k}}}{{{k_1} - {k_0}}}} \right]}&{{k_0} < {v_k} \leqslant {k_1}} \\ {{{10}^{ - 30}}}&{{v_k} > {k_1}} \end{array}} \right. $$ (15) 式中,${k_0}、{k_1}$为阈值参数,可根据具体仪器参数通过实验选取相应值,通常${k_0}$取2.5~3.5,${k_1}$取3.5~4.5[10];${v_k}$为标准化残差。
利用预测残差法构造误差判别统计量和对应自适应因子为[11-12]:
$$ \Delta {\bar V_k} = {\left( {\frac{{\bar V_k^{\text{T}}{{\bar V}_k}}}{{{\text{tr}}({P_k})}}} \right)^{\frac{1}{2}}} $$ (16) $$ {\alpha _k} = \left\{ {\begin{array}{*{20}{c}} 1&{\left| {\Delta {{\bar V}_k}} \right| \leqslant c} \\ {\frac{c}{{\left| {\Delta {{\bar V}_k}} \right|}}}&{\left| {\Delta {{\bar V}_k}} \right| > c} \end{array}} \right. $$ (17) 式中,c为调整系数,其最优值为1。
基于预测残差法计算的自适应因子通过调整${\alpha _k}$的值,可减小因动力学模型扰动异常和观测精度较低对滤波结果的影响。而在车载组合导航实际应用中,卫星受建筑物和桥梁遮挡或干扰,使可见卫星数少于4颗或卫星空间几何结构不佳,使用预测残差法计算自适应因子将无法分辨出上述误差带来的影响。对自适应因子进行适当改进,以适应车载导航的实际情况:
$$ {\alpha _k} = \left\{ {\begin{array}{*{20}{c}} {\exp \left( {{{\left( {\frac{{{\text{PDOP}}}}{k}} \right)}^2} - 1} \right)}&{{\text{PDOP}} \geqslant k} \\ {\exp \left( {{{\left( {\frac{{{\text{PDO}}{{\text{P}}_{\max }}}}{k}} \right)}^2} - 1} \right)}&{n < 4} \end{array}} \right. $$ (18) 式中,$k$为PDOP的阈值,PDOP是衡量卫星空间几何分布对定位精度的影响,PDOP值越大说明观测卫星几何分布越不理想,通常认为PDOP小于4时卫星定位结果理想,所以本文取$k = 4$;$n$为可见卫星数。当可见卫星数$n \geqslant 4$且${\text{PDOP}} < k$时采用式(17),其他情况采用式(18)计算自适应因子。
-
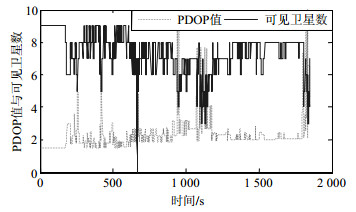
取一组采集于阜新市的NovAtel公司SPAN双频接收机INS/GNSS组合导航车载动态实验数据。INS采样频率为200 Hz,GNSS采集频率为1 Hz,组合周期为1 s。IMU性能如表 1所示。车载实验经过市区,车辆通过高楼和高架桥区域时,可见卫星数与PDOP值变化较大如图 1所示,在604~606 s、1 108~1 110 s、1 130~1 133 s和1 870~1 875 s 4个时段可见卫星数少于4颗,并在1 100 s卫星观测值基础上加入20 m的粗差。为验证RAEKF算法可行性与可靠性,实验数据通过Inertial Explorer(IE)软件差分后处理得到的高精度位置和速度信息作为参考基准,采用EKF算法和RAEKF算法计算的结果与其对比得到速度误差与位置误差曲线如图 2~5所示。误差统计结果如表 2和表 3所示。
表 1 IMU性能参数
参数名称 数值 陀螺常值漂移/°·h-1 1.0 角速率随机漂移 0.05°/$\sqrt h $ 陀螺刻度因子/deg·LSB-1 4×2-31 加速度计常值偏置/mg 1 加速度计随机偏差均方差/μg 10 加速度计刻度因子/m·s-1·LSB-2 2×2-31 表 2 基于EKF的紧组合误差数学特性
地理坐标系 均值 标准差 RMS 最大值 速度误差
/m·s-1E -0.040 0.050 0.068 -0.806 N 0.010 0.037 0.037 0.481 U -0.016 0.017 0.019 -0.378 位置误差
/mE -0.691 0.482 0.915 -3.542 N 0.528 0.401 1.285 2.125 U -0.581 0.929 1.436 -26.461 表 3 基于RAEKF的紧组合误差数学特性
地理坐标系 均值 标准差 RMS 最大值 速度误差
/m·s-1E -0.039 0.045 0.065 0.197 N 0.007 0.032 0.032 0.231 U -0.007 0.015 0.017 0.117 位置误差
/mE -0.607 0.434 0.910 -2.922 N 0.536 0.381 1.257 2.126 U -0.381 0.486 1.336 -7.505 由图 2和图 3可知,在PDOP值较小和可见卫星数较多的情况下,EKF紧组合速度精度优于0.2 m/s,位置精度优于3 m,但在可见卫星变化剧烈和PDOP值较大时间段内,如604~606 s、1 108~1 110 s、1 130~1 133 s和1 870~1 875 s 4个时段,速度和位置结果出现较大偏差。在1 100 s处引起天向26 m误差,说明利用标准EKF导航解不能有效抵抗粗差和由于外界观测条件变化对组合系统的干扰。
根据图 4和图 5,对照图 2和图 3可知,当卫星观测数目不足和卫星几何分布不佳状态下,如604~606 s、1 108~1 110 s、1 130~1 133 s时间段内,抗差自适应EKF算法通过调整增益矩阵和状态协方差矩阵来降低卫星观测数据的权重,使其更依赖于惯性导航结果,有效避免了粗差和观测异常对系统带来的影响。结合表 2和表 3可知,在1 100 s卫星观测值有20 m粗差时,RAEKF导航解在天向为7.5 m,对应EKF为26.5 m,表明RAEKF算法可有效抵抗粗差和观测异常对导航解的影响。
-
本文在分析EKF算法的基础上,针对GNSS观测值存在粗差和动力学模型异常扰动等因素影响,给出抗差自适应EKF计算方法及卫星少于4颗和卫星几何结构分布不佳时自适应因子的计算方法。通过车载组合导航实验对算法进行分析,结果表明,利用EKF算法计算的导航结果不能有效抵抗粗差和观测异常等因素对导航结果的影响,抗差自适应EKF算法可有效抵制粗差对导航结果的影响。在观测良好情况下,导航精度也得到进一步改善。
Application of Robust Adaptive EKF in INS/GNSS Tight Combination
-
摘要: 针对惯性/卫星紧组合导航中卫星观测数据存在粗差,影响组合导航系统定位精度,同时考虑到卫星少于4颗和卫星几何分布不佳对预测残差构造自适应因子的影响,提出了一种抗差自适应EKF紧组合算法。该算法给出惯性/卫星紧组合状态方程与观测方程,抗差等价权因子和预测残差法构造自适应因子的计算公式,并给出卫星少于4颗和卫星几何状态分布不佳情况下自适应因子的计算方法。通过车载实测数据对算法进行验证与分析,实验结果表明,基于抗差自适应EKF的惯性/卫星紧组合算法可有效削弱卫星粗差观测值的影响,在可见卫星数少于4颗和卫星几何分布不佳的状态下,依据该算法获取的系统导航精度得到进一步提高。Abstract: In inertial navigation system/global navigation satellite system (INS/GNSS) integrated navigation system, the positioning accuracy of integrated navigation solution will be degraded by the outliers of GNSS measurements. The predicted residuals and the setup of adaptive factors are affected if less than four satellites are observed and the satellite geometric distribution is poor. Therefore, a tightly coupled integration algorithm based on robust adaptive extend Kalman filter (EKF) is proposed in this paper. The state transition equation and observation equation of the tightly coupled INS/GNSS system are introduced. The equations of robust equivalent weight factor and adaptive factor constructed by using prediction residual method are derived. In addition, the adaptive factor calculation under the condition of less than four satellites and poor satellite geometric distribution is conducted. The proposed algorithm is verified and analyzed by using land vehicle test data, the experimental results show that the robust adaptive EKF INS/GNSS tightly integration method can effectively reduce the influence caused by satellite outliers. With the proposed algorithm, the navigation accuracy can be further improved under conditions of less than four satellites observable and poor satellite geometric distribution.
-
Key words:
- EKF /
- inertial navigation /
- integrated navigation /
- robust adaptive /
- satellite navigation
-
表 1 IMU性能参数
参数名称 数值 陀螺常值漂移/°·h-1 1.0 角速率随机漂移 0.05°/$\sqrt h $ 陀螺刻度因子/deg·LSB-1 4×2-31 加速度计常值偏置/mg 1 加速度计随机偏差均方差/μg 10 加速度计刻度因子/m·s-1·LSB-2 2×2-31 表 2 基于EKF的紧组合误差数学特性
地理坐标系 均值 标准差 RMS 最大值 速度误差
/m·s-1E -0.040 0.050 0.068 -0.806 N 0.010 0.037 0.037 0.481 U -0.016 0.017 0.019 -0.378 位置误差
/mE -0.691 0.482 0.915 -3.542 N 0.528 0.401 1.285 2.125 U -0.581 0.929 1.436 -26.461 表 3 基于RAEKF的紧组合误差数学特性
地理坐标系 均值 标准差 RMS 最大值 速度误差
/m·s-1E -0.039 0.045 0.065 0.197 N 0.007 0.032 0.032 0.231 U -0.007 0.015 0.017 0.117 位置误差
/mE -0.607 0.434 0.910 -2.922 N 0.536 0.381 1.257 2.126 U -0.381 0.486 1.336 -7.505 -
[1] 付心如, 徐爱功, 孙伟.抗差自适应UKF的INS/GNSS组合导航算法[J].导航定位学报, 2017, 5(2):111-116. doi: 10.3969/j.issn.2095-4999.2017.02.020 FU Xin-ru, XU Ai-gong, SUN Wei. An INS/GNSS integrated navigation algorithm based on robust adaptive UKF[J]. Journal of Navigation and Positioning, 2017, 5(2):111-116. doi: 10.3969/j.issn.2095-4999.2017.02.020 [2] 吴富梅. GNSS/INS组合导航误差补偿与自适应滤波理论的拓展[D].郑州: 解放军信息工程大学, 2011. WU Fu-mei. Error compensation and extension of adaptive filtering theory in gnss/ins integrated navigation[D]. Zhengzhou: The PLA Information Engineering University, 2011. [3] 苗岳旺, 孙付平, 李飞, 等.基于抗差EKF的INS/GNSS紧组合算法应用研究[J].大地测量与地球动力学, 2013, 33(3):97-101. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dkxbydz201303022 MIAO Yue-wang, SUN Fu-ping, LI Fei, et al. Research on application of tightly coupled INS/GNSS based on robust extended Kalman filter[J]. Journal of Geodesy and Geodynamics, 2013, 33(3):97-101. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dkxbydz201303022 [4] YANG Y X, HE H B, XU G C. Adaptively robust filtering for Kinematic geodetic positioning[J]. Journal of Geodesy, 2001, 75(2):109-116. doi: 10.1007-s001900000157/ [5] 高为广, 陈谷仓.结合自适应滤波和神经网络的GNSS/INS抗差组合导航算法[J].武汉大学学报·信息科学版, 2014, 39(11):1323-1328. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whchkjdxxb201411012 GAO Wei-guang, CHEN Gu-cang. Integrated GNSS/INS navigation algorithms combining adaptive filter with neural network[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11):1323-1328. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whchkjdxxb201411012 [6] 王坚, 刘超, 高井祥, 等.基于抗差EKF的GNSS/INS紧组合算法研究[J].武汉大学学报·信息科学版, 2011, 36(5):596-600. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dkxbydz201303022 WANG Jian, LIU Chao, GAO Jing-xiang, et al. GNSS/INS tightly coupled navigation model based on robust EKF[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5):596-600. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dkxbydz201303022 [7] 杨元喜, 高为广.两种渐消滤波与自适应抗差滤波的综合比较分析[J].武汉大学学报·信息科学版, 2006, 31(11):980-982. http://d.old.wanfangdata.com.cn/Periodical/whchkjdxxb200611010 YANG Yuan-xi, GAO Wei-guang. Comparison of two fading filters and adaptively robust filter[J]. Geomatics and Information Science of Wuhan University, 2006, 31(11):980-982. http://d.old.wanfangdata.com.cn/Periodical/whchkjdxxb200611010 [8] YANG Y X, GAO W G. An optimal adaptive Kalman filter[J]. Journal of Geodesy, 2006, 80(4):177-183. doi: 10.1007/s00190-006-0041-0 [9] RHUDY M, GU Y, GROSS J, et al. Sensitivity and robustness analysis of EKF and UKF design parameters for GPS/INS sensor fusion[J]. AIAA Journal of Aerospace Information Systems, 2013, 10(3):131-143. doi: 10.2514/1.54899 [10] 谭兴龙, 王坚, 韩厚增.支持向量回归辅助的GPS/INS组合导航抗差自适应算法[J].测绘学报, 2014, 43(6):590-597. http://www.cqvip.com/QK/90069X/201406/67728866504849524854484856.html TAN Xing-long, WANG Jian, HAN Hou-zeng. SVR aided adaptive robust filtering algorithm for GPS/INS integrated navigation[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6):590-597. http://www.cqvip.com/QK/90069X/201406/67728866504849524854484856.html [11] 吴富梅, 杨元喜, 崔先强.利用部分状态不符值构造的自适应因子在GPS/INS紧组合导航中的应用[J].武汉大学学报·信息科学版, 2010, 35(2):156-159. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whchkjdxxb201002007 WU Fu-mei, YANG Yuan-xi, CUI Xian-qiang. Application of adaptive factor based on partial state discrepancy in tight coupled GPS/INS integration[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2):156-159. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whchkjdxxb201002007 [12] 杨元喜, 任夏, 许艳.自适应抗差滤波理论及应用的主要进展[J].导航定位学报, 2013, 1(1):9-15. doi: 10.3969/j.issn.2095-4999.2013.01.003 YANG Yuan-xi, REN Xia, XU Yan. Main progress of adaptively robust filter with application in navigation[J]. Journal of Navigation and Positioning, 2013, 1(1):9-15. doi: 10.3969/j.issn.2095-4999.2013.01.003 -


 ISSN
ISSN 




 下载:
下载: