-
随着智能电网的不断发展和进化,传感器、计算机网络和通信技术已经与传统的电力输送网深度融合。信息技术被广泛地应用到智能电网的控制和维护等各个方面。为了保障电网运行的稳定性和安全性,电力系统状态评估(state estimation, SE)综合使用各种传感器和监测技术,通过采集电网各个单元的观测数据,来综合评估电网当前的运行状态。SE是智能电网中整个能量管理系统(energy management systems, EMS)的核心功能之一,对智能电网的正常运转起着至关重要的作用[1]。近年来的一些研究表明,由于存在不可预料的测量异常,比如传感器故障和网络恶意攻击等[2-3],使得智能电网所采集到观测数据中混杂着不良数据(bad data)和虚假数据(false data),这些数据的引入导致SE对电网状态的评估产生偏差,进而影响控制决策,产生不可估量的经济损失[4]。
为了保证智能电网的健康和稳定运行,从系统观测数据中监测和识别出不良数据和虚假数据具有非常重要的现实意义。已有的检测方法多是基于简单统计的方法,并且对检测算法的训练多使用单一来源的数据。对一个已经投入运行的智能电网来说,其运行是比较平滑和规则的,不良数据通常会产生一些波动和毛刺,使用较简单的统计方法有时也能识别。但是虚假数据由于多是人为注入的数据,具有伪装性,其不易被直接发现。
为了解决上述问题,本文提出一种基于多视角低秩分析的电力状态不良数据检测算法。该算法使用多个来源的数据进行综合分析,多个来源可能是来自单个节点的不同时期的观测数据,也可能是来自多个节点系统的观测数据。由于网络攻击通常表现出局部性,无论是空间的局部性还是时间的局部性,而正常的观测数据无论在空间上还是时间上都表现出相对的一致性,因此,多个来源或多个视角的观测综合分析有助于挖掘出其中的不良数据和虚假数据。在技术手段上,本文提出一种基于低秩表示[5-6](low-rank representation, LRR)的鲁棒的多视角学习[6](multi-view learning)算法。使用低秩结构表达来自多个视角的观测数据的共享因子——即正常数据,另外使用稀疏结构来表达来自不同视角的观测数据的异常因子,并从中发现不良数据和虚假数据。此外,本文还针对所提出的目标方程给出一种基于交叉迭代优化的解决方案。最后,在多个IEEE节点系统上验证本文算法的有效性和先进性。
-
在电力系统中,控制中心通过观测所在节点的电压相位角来实时地对电力系统的运行状态进行评估。但是在现实中,由于电压相位角比较难获取,因此通常使用线路中的有功功率(active power)代替评估系统状态[7]。在控制中心的观测可以表达为:
$$ \boldsymbol{x} = H\theta + \boldsymbol{u} $$ (1) 式中,$\boldsymbol{x} = {[{z_1}, {z_2}, \cdots , {z_M}]^{\rm{T}}}$是测量向量;$\boldsymbol{\theta} = [{\theta _1}, $ ${\theta _2}, \cdots , {\theta _M}{]^{\rm{T}}}$是状态向量;$\boldsymbol{u} = {[{u_1}, {u_2}, \cdots , {u_M}]^{\rm{T}}}$是高斯噪声;H是一个雅可比矩阵(Jacobian Matrix)。式(1)是一个相对比较理想的状态,在现实系统中,由于可能受到来自网络攻击和系统异常产生的注入数据和不良数据的污染,因此测量值可以进一步表达为:
$$ \tilde {\mathit{\boldsymbol{x}}} = \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{H\theta}} + \mathit{\boldsymbol{e}} $$ (2) 式中,$ \mathit{\boldsymbol{e}} = {[{e_1}, {e_2}, \cdots , {e_M}]^{\rm{T}}}$表示注入数据或不良数据。
-
近年来,低秩表示[5-6](low-rank representation, LRR)在计算机视觉和数据挖掘等领域取得了广泛的应用。低秩表示可以用于从受污染的数据中分离出干净的数据。低秩表示的一个代表性工作是鲁棒主成分分析[8](robust PCA)。低秩表示的一般形式为:
$$ \mathop {\min }\limits_z {\rm{rank}}( \mathit{\boldsymbol{Z}}), {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{AZ}} $$ (3) 式中,$X$是观测到的数据样本;$A$是一个字典;$Z$是系数矩阵;rank(·)表示一个矩阵的秩。
-
多视角学习是机器学习领域非常重要的一类研究方向。在自然界中,一个相同的语义信息可以被表达为多种各异的形态。如,同一个人的人脸图像随着拍摄角度和拍摄时间的不同在表现形态上就有差异,但其语义信息始终是一致的。来自于多个视角或者多个形态的观察往往具有相互补充的作用,因此多视角学习在解决很多机器学习问题时能表现出比单视角学习更优异的性能。
通常,多视角学习的主要技术手段有协同训练(co-training)、多核学习(multiple kernel learning)和子空间学习(subspace learning)3种。本文提出的算法属于子空间学习类别。假设来自于多个视角的观测数据共享一个低秩的子空间,在该子空间中去挖掘不同视角之间的共享因子以及视角特有的观测信息。
-
假设使用x表达某一时刻电力控制中心得到的一个观测数据向量,在一个时间序列中所有的观测数据向量将形成一个矩阵,不妨将其表示为$X$。假设从V个视角观测数据,则有多视角样本集可以表达为$\mathit{\boldsymbol{X}} = \{ {X^{(1)}}, {X^{(2)}}, \cdots , {X^{(V)}}\} $,假设存在一个合适的字典A,则来自于每一个视角的数据都可以表示为:
$$ {\mathit{\boldsymbol{X}}^{(v)}} = {\mathit{\boldsymbol{A}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} + {\mathit{\boldsymbol{E}}^{(v)}} $$ (4) 式中,${\mathit{\boldsymbol{Z}}^{(v)}}$是一个系数矩阵,${\mathit{\boldsymbol{E}}^{(v)}}$用于表达噪声信息。由于多个视角的信息之间存在共享的语义信息,因此将设多个不同视角之间的共享因子潜伏在同一个子空间当中,则${\mathit{\boldsymbol{Z}}^{(v)}}$应该是一个低秩结构的块矩阵。同时,考虑到${\mathit{\boldsymbol{Z}}^{(v)}}$是表达共享因子的,因此不同的${\mathit{\boldsymbol{Z}}^{(v)}}$之间应该尽可能相似。另一方面,由于不良数据和虚假数据都是突发性质的,并且在空间和时间上表现出一定的局部性,因此这些信息会被排除在共享因子之外。由于观测数据被分解成了两部分,一部分是共享因子,另一部分是噪声数据,因此,从噪声数据中可以发现不良数据和虚假数据。同时,相对于整个观测值的数量而言,噪声数据和虚假数据的数量是有限的,在数据矩阵上表现为稀疏性。基于此,使用${\mathit{\boldsymbol{L}}_1}$范数(norm)对噪声数据建模,从而得到目标方程为:
$$ \mathop {\min }\limits_{{\mathit{\boldsymbol{Z}}^{(v)}}, {\mathit{\boldsymbol{E}}^{(v)}}} \sum\limits_{v = 1}^V {(rank({\mathit{\boldsymbol{Z}}^{(v)}}) + \alpha ||{\mathit{\boldsymbol{E}}^{(v)}}|{|_1})} + \beta \sum\limits_{v = 1}^V {\sum\limits_{j = v + 1}^V {||{\mathit{\boldsymbol{Z}}^{(v)}} - { \mathit{\boldsymbol{Z}}^{(j)}}||_F^2} } , \\ \;\;\;\;{\rm s.t.}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{X}}^{(v)}} = {\mathit{\boldsymbol{A}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} + {\mathit{\boldsymbol{E}}^{(v)}}, v = 1, 2, \cdots , V $$ (5) 式中,$|| \cdot |{|_1}$表示${\mathit{\boldsymbol{L}}_1}$范数,$|| \cdot |{|_F}$表示弗罗贝尼乌斯范数(Frobenius norm);$\alpha > 0$和$\beta > 0$是两个平衡参数。式(5)的前半部分用于对各个视角的观测数据进行低秩约束和稀疏约束,后半部分用于对各个视角共享因子的相似性进行约束。由于秩最小化是一个非常困难的问题,因此在实际应用中,经常使用最小化矩阵的核范数(nuclear norm)作为最小化秩的近似替代。另一方面,由于$\mathit{\boldsymbol{A}}$在目标方程中是未知的,文献[7]将$\mathit{\boldsymbol{A}}$直接初始化为$\mathit{\boldsymbol{X}}$,将(5)写为如下的等价问题:
$$ \mathop {\min }\limits_{{\mathit{\boldsymbol{Z}}^{(v)}}, {\mathit{\boldsymbol{E}}^{(v)}}} \sum\limits_{v = 1}^V {(||{\mathit{\boldsymbol{Z}}^{(v)}}|{|_ * } + \alpha ||{\mathit{\boldsymbol{E}}^{(v)}}|{|_1})} + \beta \sum\limits_{v = 1}^V {\sum\limits_{j = v + 1}^V {||{\mathit{\boldsymbol{Z}}^{(v)}} - {\mathit{\boldsymbol{Z}}^{(j)}}|{|_F}} } , \\ \;\;\;\;{\rm s.t.}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{X}}^{(v)}} = {\mathit{\boldsymbol{A}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} + {\mathit{\boldsymbol{E}}^{(v)}}, v = 1, 2, \cdots , V $$ (6) 式中,$||{\mathit{\boldsymbol{Z}}^{(v)}}|{|_ * }$表示${\mathit{\boldsymbol{Z}}^{(v)}}$的核范数。
-
为了表达的简洁和便于理解,在本文仅考虑只有两个视角(即V=2)的情形对目标方程进行优化,本文的方法可非常容易扩展到V > 2的情况。首先,给出V=2时式(6)的形式:
$$ \mathop {\min }\limits_{{\mathit{\boldsymbol{Z}}^{(1)}}, { \mathit{\boldsymbol{E}}^{(1)}}, {\mathit{\boldsymbol{Z}}^{(2)}}, { \mathit{\boldsymbol{E}}^{(2)}}} \sum\limits_{v = 1}^2 {(||{\mathit{\boldsymbol{Z}}^{(v)}}|{|_ * } + \alpha ||{\mathit{\boldsymbol{E}}^{(v)}}|{|_1})} + \beta ||{\mathit{\boldsymbol{Z}}^{(1)}} - {\mathit{\boldsymbol{Z}}^{(2)}}||_F^2, \\ \qquad {\rm s.t.}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{X}}^{(v)}} = {\mathit{\boldsymbol{A}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} + {\mathit{\boldsymbol{E}}^{(v)}}, v = 1, 2, $$ (7) 由于${\mathit{\boldsymbol{Z}}^{(v)}}$有低秩约束,并且出现在限制条件中,因此首先引入松弛变量J,将式(7)写为如下的等价形式:
$$ \mathop {\min }\limits_{{\mathit{\boldsymbol{Z}}^{(1)}}, {\mathit{\boldsymbol{E}}^{(1)}}, {\mathit{\boldsymbol{Z}}^{(2)}}, {\mathit{\boldsymbol{E}}^{(2)}}} \sum\limits_{v = 1}^2 {(|||{\mathit{\boldsymbol{J}}^{(v)}}|{|_ * } + \alpha |{\mathit{\boldsymbol{E}}^{(v)}}|{|_1})} + \beta ||{\mathit{\boldsymbol{Z}}^{(1)}} - {\mathit{\boldsymbol{Z}}^{(2)}}||_F^2, \\ {\rm s.t.}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{X}}^{(v)}} = {\mathit{\boldsymbol{A}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} + {\mathit{\boldsymbol{E}}^{(v)}}, {\mathit{\boldsymbol{Z}}^{(v)}} = {\mathit{\boldsymbol{J}}^{(v)}}, v = 1, 2 $$ (8) 式(8)所示的最优化问题可以通过增广拉格朗日方法[9](augmented Lagrange multiplier, ALM)求解。首先得到式(8)的增广拉格朗日方程:
$$ \begin{gathered} \sum\limits_{v = 1}^2 {(||{\mathit{\boldsymbol{J}}^{(v)}}|{|_ * } + \alpha ||{\mathit{\boldsymbol{E}}^{(v)}}|{|_1})} + \beta ||{\mathit{\boldsymbol{Z}}^{(1)}} - {\mathit{\boldsymbol{Z}}^{(2)}}||_F^2{\rm{ + }} \\ \sum\limits_{v = 1}^2 {\left( \begin{gathered} \langle \mathit{\boldsymbol{Y}}_1^{(v)}, {\mathit{\boldsymbol{X}}^{(v)}} - {\mathit{\boldsymbol{X}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} - {\mathit{\boldsymbol{E}}^{(v)}}\rangle + \langle \mathit{\boldsymbol{Y}}_2^{(v)}, {\mathit{\boldsymbol{Z}}^{(v)}} - {\mathit{\boldsymbol{J}}^{(v)}}\rangle + \\ 2/\mu (||{\mathit{\boldsymbol{X}}^{(v)}} - {\mathit{\boldsymbol{X}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} - {\mathit{\boldsymbol{E}}^{(v)}}||_F^2 + ||{\mathit{\boldsymbol{Z}}^{(v)}} - {\mathit{\boldsymbol{J}}^{(v)}}||_F^2) \\ \end{gathered} \right)} \\ \end{gathered} $$ (9) 式中,< > 表示矩阵相乘的迹;$\mathit{\boldsymbol{Y}}_1^{(v)}$和$\mathit{\boldsymbol{Y}}_2^{(v)}$是拉格朗日乘子;$\mu > 0$是一个平衡参数。通过交替方向乘子法[10](alternating direction method of multipliers, ADMM)来优化式(9)。
S1:首先优化变量${\mathit{\boldsymbol{J}}^{(v)}}$,将式(9)中除${\mathit{\boldsymbol{J}}^{(v)}}$外的其他变量作为常数,对${\mathit{\boldsymbol{J}}^{(v)}}$求偏导,可以得到${\mathit{\boldsymbol{J}}^{(v)}}$的优化方程为:
$$ \begin{gathered} {\mathit{\boldsymbol{J}}^{(v)}} = \\ \arg {\kern 1pt} {\kern 1pt} \mathop {\min }\limits_{{\mathit{\boldsymbol{J}}^{(v)}}} \sum\limits_{v = 1}^2 {(1/\mu ||{\mathit{\boldsymbol{J}}^{(v)}}|{|_ * } + 1/2||{\mathit{\boldsymbol{J}}^{(v)}} - {\mathit{\boldsymbol{Z}}^{(v)}} - \mathit{\boldsymbol{Y}}_2^{(v)}/\mu ||_F^2)} \\ \end{gathered} $$ (10) 问题式(10)可通过奇异值阈值方法[11](singular value thresholding, SVT)求解。
S2:将式(9)中除${\mathit{\boldsymbol{Z}}^{(1)}}$外的变量看作常数,对${\mathit{\boldsymbol{Z}}^{(1)}}$求偏导,并令偏导为0,可以得到${\mathit{\boldsymbol{Z}}^{(1)}}$的解为:
$$ \begin{gathered} {\mathit{\boldsymbol{Z}}^{(1)}} = \\ (2 \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{X}}^{(1){\rm T}}}{\mathit{\boldsymbol{X}}^{(1)}})\left( \begin{gathered} {\mathit{\boldsymbol{X}}^{(1){\rm T}}}({\mathit{\boldsymbol{X}}^{(1)}} - {\mathit{\boldsymbol{E}}^{(1)}}) + {\mathit{\boldsymbol{J}}^{(1)}} + \\ {\mathit{\boldsymbol{Z}}^{(2)}} + \frac{{{\mathit{\boldsymbol{X}}^{(1){\rm T}}}\mathit{\boldsymbol{Y}}_1^{(1)} - \mathit{\boldsymbol{Y}}_2^{(1)} + \beta {\mathit{\boldsymbol{Z}}^{(2)}}}}{\mu } \\ \end{gathered} \right) \\ \end{gathered} $$ (11) S3:同理,可以得到${\mathit{\boldsymbol{Z}}^{(2)}}$的解为:
$$ \begin{gathered} {\mathit{\boldsymbol{Z}}^{(2)}} = \\ (2 \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{X}}^{(2){\rm T}}}{\mathit{\boldsymbol{X}}^{(2)}})\left( \begin{gathered} {\mathit{\boldsymbol{X}}^{(2){\rm T}}}({\mathit{\boldsymbol{X}}^{(2)}} - {\mathit{\boldsymbol{E}}^{(2)}}) - {\mathit{\boldsymbol{J}}^{(2)}} + \\ {\mathit{\boldsymbol{Z}}^{(1)}} + \frac{{{\mathit{\boldsymbol{X}}^{(1){\rm T}}}\mathit{\boldsymbol{Y}}_1^{(2)} - \mathit{\boldsymbol{Y}}_2^{(2)} + \beta {\mathit{\boldsymbol{Z}}^{(1)}}}}{\mu } \\ \end{gathered} \right) \\ \end{gathered} $$ (12) S4:变量${\mathit{\boldsymbol{E}}^{(v)}}$可以通过如下的方程优化:
$$ \begin{gathered} {\mathit{\boldsymbol{E}}^{(v)}} = \\ \arg {\kern 1pt} {\kern 1pt} \mathop {\min }\limits_{{\mathit{\boldsymbol{E}}^{(v)}}} \sum\limits_{v = 1}^2 {\left( \begin{array} [c]{l} \alpha /\mu ||{\mathit{\boldsymbol{E}}^{(v)}}|{|_{2, 1}} + \\ 1/2||{\mathit{\boldsymbol{E}}^{(v)}} - ({\mathit{\boldsymbol{X}}^{(v)}} - {\mathit{\boldsymbol{X}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} + \mathit{\boldsymbol{Y}}_1^{(v)}/\mu )||_F^2 \\ \end{array} \right)} \\ \end{gathered} $$ (13) S5:依次更新拉格朗日乘子
$$ \mathit{\boldsymbol{Y}}_1^{(v)} = \mathit{\boldsymbol{Y}}_1^{(v)} + \mu ({\mathit{\boldsymbol{X}}^{(v)}} - {\mathit{\boldsymbol{X}}^{(v)}}{\mathit{\boldsymbol{Z}}^{(v)}} - {\mathit{\boldsymbol{E}}^{(v)}}) $$ (14) $$ \mathit{\boldsymbol{Y}}_2^{(v)} = \mathit{\boldsymbol{Y}}_2^{(v)} + \mu ({\mathit{\boldsymbol{Z}}^{(v)}} - {\mathit{\boldsymbol{J}}^{(v)}}) $$ (15) 式(9)的优化可以通过不断迭代更新S1~S5,每次更新完之后检查收敛条件,如果收敛或者达到最大更新次数,则停止更新,否则进行下一轮迭代,直到满足条件为止。通过优化式(9),可以得到${\mathit{\boldsymbol{Z}}^{(v)}}$和${\mathit{\boldsymbol{E}}^{(v)}}$。如果第$i$个观测数据是正常数据,那么不同的$\mathit{\boldsymbol{Z}}_i^{(v)}$非常相似,导致不同$\mathit{\boldsymbol{Z}}_i^{(v)}$的乘积数值较大,同时不同视角的$\mathit{\boldsymbol{E}}_i^{(v)}$的乘积也会比较小,反之会有截然不同的值。所以,最后通过测量$\mathit{\boldsymbol{Z}}_i^{(v)}$和$\mathit{\boldsymbol{E}}_i^{(v)}$即可检测出观测数据中的不良数据和虚假数据。
-
将本文算法在电力潮流数据中进行测试,所采用的实验数据来自于IEEE 57节点系统和IEEE 118节点系统。IEEE 57节点系统和IEEE 118节点系统都是公开的被广泛使用的电力测试系统。假设电力系统中每个母线节点上的负载都是均匀分布在相对于基本负载的50%~150%之间的。当电力状态估计数据被收集以后,根据文献[12]中所示的攻击方法向其中注入一定比例的不良数据和虚假数据。
在实验结果上,本文使用被广泛使用的受试者工作特征曲线(receiver operating characteristic, ROC)作为评价指标,该指标反映了正确率和误报率之间的关系,同时报告曲线下的面积(area under ROC curve,AUC),该指标也是系统评估领域最广泛使用的指标之一。
-
首先,为了直观验证多视角学习的有效性,本文设置不同范围的注入数据比例,同时将信噪比SNR设置为10 dB。比较多视角算法相对于单视角在不良数据检测中的效果。其中,对于单视角任务,使用鲁棒PCA作为对比算法。鲁棒PCA和本文算法的共同特点是均使用了低秩约束,因此实验结果的比较会相对公正。该实验将来自IEEE 57节点系统的数据作为视角一,来自IEEE 118节点系统的数据作为视角二。实验结果如表 1所示。
表 1 不同不良值比例下单视角学习与多视角学习算法对比
注入数据比例/% IEEE 57鲁棒PCA IEEE 118鲁棒PCA 多视角本文算法 5 0.93 0.95 0.99 10 0.91 0.94 0.98 15 0.86 0.89 0.95 20 0.77 0.81 0.93 通过表 1所示实验结果可以看出,与单视角学习算法相比较,多视角算法有着明显的性能优势。当不良数据的比例比较小的时候,使用了低秩表示的鲁棒PCA表现出较好的性能。但是随着不良数据比例的增加,鲁棒PCA的性能逐步下降,并且下降速度增快。与此形成明显对比的是,多视角算法由于多个视角之间数据的相互补充,在不良数据比例增加时虽然性能受到影响,但依然表现比较稳定。实验结果不仅充分说明了多视角学习相对于单视角学习的性能优势,也验证了本文的基本假设。
为了进一步验证本文算法的有效性,将该算法与其他多视角算法进行对比。其中对比算法有双约束多视角异常检测算法[13](dual-regularized multi- view outlier detection, DMOD)以及低秩判别嵌入算法(low-rank discriminate embedding for multi-view learning, LRDE),实验结果如表 2所示。
表 2 不同不良值比例下多视角学习算法对比
注入数据比例/% DMOD LRDE 本文算法 5 0.97 0.96 0.99 10 0.95 0.95 0.98 15 0.91 0.93 0.95 20 0.86 0.89 0.93 从表 2所示实验结果可以进一步看出,多视角学习算法的性能往往优于单视角学习算法。DMOD同时考虑了系数约束和样本约束两种约束条件,使其不仅能检测到属性不良数据,也能检测到样本不良数据。在异常数据的比例相对比较小时,DMOD对异常非常敏感,可以正确检测出其中大部分不良数据。但是随着不良数据比例的增加,由于DMOD在鲁棒性方面比较欠缺,因此性能逐渐下滑。LRDE和本文算法一样,也使用了低秩约束,因此鲁棒性较好,在不良数据的比例增加时仍能保持较好的性能。最后,本文算法在所有测试中都表现出明显的优势,验证了本文模型对电力系统不良数据的准确建模。
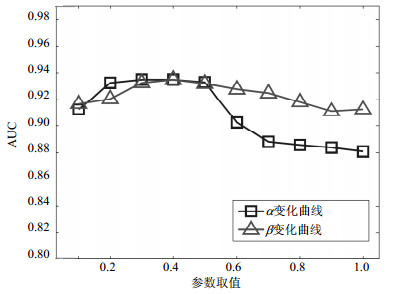
图 1给出了参数α和β取不同值时对算法性能的影响。图 2报告了算法的相对错误率随迭代次数的变化,反映了算法的收敛情况。
从图 1可以看出,算法对参数的选择不是特别敏感。在实际应用中,建议使用交叉验证方法来选择最优参数。图 2说明算法在一定的迭代次数后,可以顺利收敛。
-
电力系统状态评估是电网运维的重要部分,评估所需要的观测数据中可能会混入不良数据,这些数据的混入将影响评估结果,进而导致决策失误。为了应对这一问题,本文提出一种基于多视角低秩分析的电力状态不良数据检测算法,该算法使用来自多个观测节点的数据共同分析,从而有效检测出观测中混杂的不良数据。在IEEE 57和IEEE 118节点系统上的实验结果验证了本文算法的有效性和先进性。实验结果显示,本文算法不仅比单视角算法表现出明显的优势,在电力状态不良数据检测中,也比最新的多视角学习算法更有优势。
An Approach for Detecting Band Data in Smart Grid Based on Low-Rank Multi-View Analysis
-
摘要: 随着信息化技术在智能电网的应用逐步深入,在智能电网的运维中能及时自动检测到不良数据,如网络攻击数据和设备故障数据,对电网的稳定和持续运行有着重要意义。该文提出一种基于多视角低秩分析的电力状态不良数据检测算法。该算法使用来自多个观测源的观测数据综合估计电力系统的状态,算法使用低秩模型挖掘出来自多个观测源数据间的共享本真数据,同时使用稀疏模型对不良数据建模。针对所提出的目标方程,给出了一种基于交叉迭代的优化算法。最后,在IEEE多个节点测试系统上的实验证明了该算法相对于已有算法的先进性。Abstract: With the widely deployment of information techniques in smart grid, it is quite important to automatically detect the bad data, e.g., malicious injection data and unfunctional sensor data, from daily observations. In this paper, we propose a novel approach for bad data detection in smart grid based on multi-view low-rank analysis. Specifically, the proposed method estimates the grid state by analyzing the data collected from multiple sources. A low-rank function is learned to unveil the shared true data from observations, and the sparsity of data is applied to formulate bad data. Furthermore, an iterative optimization algorithm is proposed to solve the objective function. At last, extensive experiments on several IEEE bus systems verify the superiority of the proposed method.
-
表 1 不同不良值比例下单视角学习与多视角学习算法对比
注入数据比例/% IEEE 57鲁棒PCA IEEE 118鲁棒PCA 多视角本文算法 5 0.93 0.95 0.99 10 0.91 0.94 0.98 15 0.86 0.89 0.95 20 0.77 0.81 0.93 表 2 不同不良值比例下多视角学习算法对比
注入数据比例/% DMOD LRDE 本文算法 5 0.97 0.96 0.99 10 0.95 0.95 0.98 15 0.91 0.93 0.95 20 0.86 0.89 0.93 -
[1] 陈树勇, 宋书芳, 李兰欣, 等.智能电网技术综述[J].电网技术, 2009(8):1-7. http://d.old.wanfangdata.com.cn/Periodical/zgdjgcxb201307005 CHEN Shu-yong, SONG Shu-fang, LI Lan-xin, et al. A survey on smart grid[J]. Power System Technology, 2009, 33(8):1-7. http://d.old.wanfangdata.com.cn/Periodical/zgdjgcxb201307005 [2] CUI Shu-guang, HAN Zhu, KAR S, et al. Coordinated data-injection attack and detection in the smart grid:a detailed look at enriching detection solutions[J]. IEEE Signal Processing Magazine, 2012, 29(5):106-115. doi: 10.1109/MSP.2012.2185911 [3] HUANG Yi, MOHAMMAD E, NGUYEN H, et al. Bad data injection in smart grid:attack and defense mechanisms[J]. IEEE Communications Magazine, 2013, 51(1):27-33. doi: 10.1109/MCOM.2013.6400435 [4] MOHAMMAD E, HAN Zhu, SONG Ling-yang. Effect of stealthy bad data injection on network congestion in market based power system[C]//Wireless Communications and Networking Conference. Shanghai, China: IEEE, 2012: 2468-2472. https://www.researchgate.net/publication/261638198_Effect_Of_Stealthy_Bad_Data_Injection_On_Network_Congestion_In_Market_Based_Power_System [5] LIU Guang-can, LIN Zhou-chen, YAN Shui-cheng, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1):171-184. doi: 10.1109/TPAMI.2012.88 [6] LI Jing-jing, WU Yue, ZHAO Ji-dong, et al. Low-rank discriminant embedding for multiview learning[J]. IEEE Transactions on Cybernetics, 2017, 47(11):3516-3529. doi: 10.1109/TCYB.2016.2565898 [7] LIU Lan-chao, ESMALIFALAK M, HAN Zhu. Detection offalse data injection in power grid exploiting low rank and sparsity[C]//2013 IEEE International Conference on Communications. Budapest, Hungary: IEEE, 2013: 4461-4465. https://www.researchgate.net/publication/261279057_Detection_of_false_data_injection_in_power_grid_exploiting_low_rank_and_sparsity [8] JOHN W, GANESH A, RAO S, et al. Robust principal component analysis: exact recovery of corrupted low-rank matrices via convex optimization[R]. Urbana-Champaign: Coordinated Science Laboratory, University of Illinois, 2009. https://arxiv.org/pdf/0905.0233v1.pdf [9] LIN Zhou-chen, CHEN Min-ming, MA Yi. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[R]. Urbana-Champaign: Coordinated Science Laboratory, University of Illinois, 2009. [10] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3(1):1-122. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3e990a176868f2d25550830e52a96572 [11] CAI Jian-feng, CANDES E, SHEN Zuo-wei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4):1956-1982. doi: 10.1137/080738970 [12] OLIVER K, JIA Li-yan, THOMAS R, et al. Malicious data attacks on the smart grid[J]. IEEE Transaction on Smart Grid, 2011, 2(4):645-658. doi: 10.1109/TSG.2011.2163807 [13] ZHAO Han-dong, FU Yun. Dual-regularized multi-view outlier detection[C]//International Conference on Artificial Intelligence. Buenos Aires, Argentina: AAAI Press, 2015: 4077-4083. https://www.ijcai.org/Proceedings/15/Papers/572.pdf -


 ISSN
ISSN 




 下载:
下载: