-
近年复数域神经网络在联想记忆、优化问题求解、图像处理等多个领域得到了越来越多的应用[1],因此受到学者们的广泛关注。复值神经网络平衡点的动态行为研究是其应用的前提条件,如对于联想记忆问题,要求人工神经网络的多个平衡点都是稳定的,即分析该系统平衡点的多稳定性[2]或Lagrange稳定性[3]。对于优化问题求解,要求系统存在唯一的平衡点,且分析该平衡点的指数稳定性[4]或者渐近稳定性[5]。文献[6]运用同胚映射原理,建立了确保一类时滞复值神经网络平衡点存在性和唯一性的判定条件,并通过构造合适的Lyapunov-Krasovskii泛函和矩阵不等式,建立了时间标度上的复值神经网络平衡点全局稳定性的充分条件。文献[7]研究了一类具有的变时滞的中立性复数域神经网络的全局Lagrange稳定性。关于复数域神经网络的动态行为研究的其他成果见文献[8-12]。文献[2-5, 7, 9]所考虑的复值神经网络都是确定型系统,未考虑不确定性因素。学者们在研究实数域神经网络的动态行为时,引入了脉冲干扰[13]、反应扩散[14]、随机干扰[15]等实际系统中存在的不确定性因素,并研究了相关系统的平衡点的稳定性问题。文献[6, 8, 10]在复数域神经网络模型中引入脉冲干扰,研究了系统的动态行为。在物理学、生物学等多学科中,存在着一些具有如下行为的系统:该系统是与时间有关的一个系统,如果已知系统在现在的状态,则此系统的过去状态与将来状态是(条件)独立的,这个特性称为Markova性。在人工神经网络系统中,这种模型允许神经网络具有有限多个模式,不同的模式在一条马尔可夫链的驱动下进行切换,使运用神经网络时更符合实际,因此研究具有Markova跳变参数的复数域神经网络的动态行为具有一定的实际意义。目前学者们对具有Markova跳变参数的神经网络平衡点的动态行为进行了大量研究[16-20],但取得的研究成果均针对实数域神经网络系统进行展开的,尚未在复数域神经网络模型中考虑Markova跳变参数。
基于以上分析,本文在一类变时滞复数域神经网络模型中考虑Markova跳变参数,利用矢量Lyapunov函数法,研究该系统在不同模式下的平衡点的动态行为。
-
首先定义一些记号。令$C$和$R$分别为复数集和实数集。对于复数$z$,令$|z| = \sqrt {{{(\operatorname{Re} (z))}^2} + {{(\operatorname{Im} (z))}^2}} $表示复数$z$的模,$\operatorname{Re} (z)$和$\operatorname{Im} (z)$分别表示$z$的实部和虚部。对于复数向量${\mathit{\boldsymbol{z}}} \in { \mathit{\boldsymbol{C}}^n}$,令$|{\mathit{\boldsymbol{z}}}| = {(|{z_1}|, |{z_2}|, \cdots , |{z_n}|)^{\rm{T}}}$表示向量${\mathit{\boldsymbol{z}}}$的模,${( \cdot )^{\rm{T}}}$表示向量${\mathit{\boldsymbol{z}}}$的转置。令$||{\mathit{\boldsymbol{z}}}|{|_\infty } = {\max _{1 \leqslant i \leqslant n}}\{ |{z_i}|\} $和$||{\mathit{\boldsymbol{z}}}|{|_1} = \sum\limits_{i = 1}^n {|{z_i}|} $分别表示向量${\mathit{\boldsymbol{z}}}$的无穷范数和1-范数。令$(F, {\rm P})$表示表示全概率空间,且滤波器${\{ {F_t}\} _{t \geqslant 0}}$是有连续函数并包含P-null集合。令$r(t)$,$t \geqslant 0$表示在有限空间$S = \{ 1, 2, \cdots , N\} $中取值的右连续马尔可夫过程,且满足下面转换规律:
$$ {P}\{ r(t + \Delta t) = m|r(t) = k\} = \left\{ {\begin{array}{*{20}{c}} {{\pi _{km}}\Delta t + { O}(\Delta t)\quad \;\;k \ne m} \\ {1 + {\pi _{kk}}\Delta t + { O}(\Delta t)\;\;k = m\;} \end{array}} \right. $$ (1) 式中,$\Delta t > 0$,$\mathop {\lim }\limits_{\Delta t \to 0} { O}(\Delta t)/\Delta t = 0$;${\pi _{km}} > 0$表示从模式k转换到m的概率,且满足${\pi _{kk}} = - \sum\limits_{m = 1, \, m \ne k}^N {{\pi _{km}}} $。令${\rm{{\rm E}}}\{ \cdot \} $代表与给定概率测度P相关的数学期望。
假设神经元状态、关联矩阵和激活函数定义在复数域下,并且自反馈系数和关联矩阵具有Markova性的情况下,本文考虑一类具有变时滞和Markova跳变参数的复数域区间神经网络,其模型为:
$$ \begin{gathered} \frac{{\operatorname{d} {z_i}(t)}}{{\operatorname{d} t}} = - {d_i}(r(t)){z_i}(t) + \\ \sum\limits_{j = 1}^n {[{a_{ij}}(r(t)){f_j}({z_j}(t))} {\rm{ + }}{b_{ij}}(r(t)){f_j}({z_j}(t - {\tau _{ij}}(t)))] + {J_i}(t) \\ \end{gathered} $$ (2) 式中,${z_i} \in C$代表神经元状态;$n$表示神经元的个数。${\mathit{\boldsymbol{A}}}(r(t)) = {({a_{ij}}(r(t)))_{n \times n}}$和${\mathit{\boldsymbol{B}}}(r(t)) = {({b_{ij}}(r(t)))_{n \times n}}$是定义在复数域下的连接加权矩阵;${\mathit{\boldsymbol{J}}}(t) = {({J_1}(t), {J_2}(t), \cdots , {J_n}(t))^{\rm T}} \in $${ \mathit{\boldsymbol{C}}^n}$是外部输入向量;${d_i}(r(t)) > 0$为自反馈连接系数;${f_j}({z_j}(t))$表示复数域激活函数;${\tau _{ij}}(t)$$(i, j = 1, 2, \cdots , n)$为有界连续函数且满足$\tau = {\max _{1 \leqslant i, j \leqslant n}}{\sup _{t \geqslant 0}}{\tau _{ij}}(t)$。
对于任意模式$k$($k \in S$),定义如下记号:
$$ {\mathit{\boldsymbol{A}}}(k) = {\mathit{\boldsymbol{A}}}(r(t) = k) = {[{a_{ij}}(r(t) = k)]_{n \times n}} = {(a_{ij}^k)_{n \times n}} $$ $$ {\mathit{\boldsymbol{B}}}(k) = {\mathit{\boldsymbol{B}}}(r(t) = k) = {[{b_{ij}}(r(t) = k)]_{n \times n}} = {(b_{ij}^k)_{n \times n}} $$ $$ {\mathit{\boldsymbol{D}}}(k) = {\mathit{\boldsymbol{D}}}(r(t) = k) = {\rm diag}{[{d_i}(r(t) = k)]_{n \times n}} = {\rm diag}{(d_i^k)_{n \times n}} $$ 令$|{\mathit{\boldsymbol{A}}}|$表示矩阵${\mathit{\boldsymbol{A}}} = {({a_{ij}})_{n \times n}} \in $${ \mathit{\boldsymbol{C}}^{n \times n}}$的模,即$|{\mathit{\boldsymbol{A}}}| = {(|{a_{ij}}|)_{n \times n}} \in {R^{n \times n}}$,其中$|{a_{ij}}| = $ $\sqrt {{{[{\rm Re}({a_{ij}})]}^2} + {{[{\rm Im}({a_{ij}})]}^2}} $。在系统式(2)中,复数域区间加权矩阵定义为:
$$ \boldsymbol{A}_{I}(k)=\left\{|\boldsymbol{A}(k)|=\left(\left|a_{i j}^{k}\right|\right)_{n \times n} :|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\boldsymbol{A}}(k)| \leqslant|\boldsymbol{A}(k)| \leqslant\right.\\ |\tilde{\boldsymbol{A}}(k)|, \quad \text { i.e. }\left|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{a}_{i j}^{k}\right| \leqslant\left|a_{i j}^{k}\right| \leqslant\left|\tilde{a}_{i j}^{k}\right|, i, j=1,2, \cdots, n \} $$ $$ \boldsymbol{B}_{I}(k)=\left\{|\boldsymbol{B}(k)|=\left(\left|b_{i j}^{k}\right|\right)_{n \times n} :|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\boldsymbol{B}}(k)| \leqslant|\boldsymbol{B}(k)| \leqslant\right.\\ |\tilde{\boldsymbol{B}}(k)|, \quad \text { i.e. }\left|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{b}_{i j}^{k}\right| \leqslant\left|b_{i j}^{k}\right| \leqslant\left|\tilde{b}_{i j}^{k}\right|, i, j=1,2, \cdots, n \} $$ 对于系统式(2)的每一个固定模式下,${{\mathit{\boldsymbol{A}}}_I}(k)$和${{\mathit{\boldsymbol{B}}}_I}(k)$是常值区间矩阵。
假设系统式(2)的初始条件为${z_i}(s) = {\varphi _i}(s)$,其中${\varphi _i}(s)$在区间${\rm{[}} - \tau , 0]$上是有界和连续函数,$i = 1, 2, \cdots , n$。
文献[17]研究了一类具有Markova跳变参数的变时滞神经网络的动态行为。文献[17]建立的神经网络模型式(1)是定义在实数域下的。本文研究的神经网络模型式(2)定义在复数域下,并且每种模式下的加权矩阵为区间复数域关联矩阵。本文系统式(2)的模型包含文献[17]的系统式(1),所得结论推广了现有成果。
令${{\mathit{\boldsymbol{z}}}^\# }$$ = {(z_1^\# , z_2^\# , \cdots , z_n^\# )^{\rm T}} \in {\mathit{\boldsymbol{C}}^n}$表示系统式(2)的平衡点。
定义1 对于任意系统模式k,若存在常数${M_{}}(k) > 0$($k \in S$)和$\lambda > 0$,使得对所有的${\mathit{\boldsymbol{A}}}(k) \in {{\mathit{\boldsymbol{A}}}_I}(k)$和${\mathit{\boldsymbol{B}}}(k) \in {{\mathit{\boldsymbol{B}}}_I}(k)$,不等式:
$$ \begin{array} [c]{c} {\rm E}\{ ||{\mathit{\boldsymbol{z}}}(t) - {{\mathit{\boldsymbol{z}}}^\# }, r(t) = k||\} \leqslant \\ M(k)E\{ {\sup _{s \in [ - \tau , 0]}}||{\mathit{\boldsymbol{\varphi }}}(s) - {{\mathit{\boldsymbol{z}}}^\# }||\} \exp( - \lambda t) \end{array} $$ 是成立的,$t \geqslant 0$,那么系统式(2)的平衡点${{\mathit{\boldsymbol{z}}}^\# }$是随机指数鲁棒稳定的。
在文献[2, 9-10]中,令复值激活函数可分解成实部部分和虚部部分,并要求其偏导数满足有界性和解析性。根据Liouville’s定理可知,同时满足有界性和光滑性的复值激活函数必为复值常数,显然对复数域激活函数的假设限制了对人工复数域神经网络设计时对它的选取。
为便于复值激活函数的选择,对激活函数作如下假设。
假设1 假设激活函数${f_i}( \cdot )$满足全局Lipschitz条件,即存在Lipschitz常数${l_i} > 0$,使得对所有${u_i}(t), \;{v_i}(t) \in {\rm{C}}$,有$|{f_i}({u_i}(t)) - {f_i}({v_i}(t))| \leqslant $ ${l_i}|{u_i}(t) - {v_i}(t)|$成立,$i = 1, 2, \cdots , n$。令${\mathit{\boldsymbol{L}}} = {\rm diag}({l_1}, {l_2}, \cdots , {l_n})$。
引理1 [8] 若${\mathit{\boldsymbol{H}}}({\mathit{\boldsymbol{z}}})$是${\mathit{\boldsymbol{C}}^n}$上的连续函数,且满足如下条件:1) ${\mathit{\boldsymbol{H}}}({\mathit{\boldsymbol{z}}})$在${\mathit{\boldsymbol{C}}^n}$是单叶映射;2) ${\lim _{||{\mathit{\boldsymbol{z}}}|| \to \infty }}||{\mathit{\boldsymbol{H}}}({\mathit{\boldsymbol{z}}})|| \to \infty $,则${\mathit{\boldsymbol{H}}}({\mathit{\boldsymbol{z}}})$在${\mathit{\boldsymbol{C}}^n}$是同胚映射。
引理2 [8] 对于矩阵${\mathit{\boldsymbol{A}}} = {({a_{ij}})_{n \times n}} \in {R^{n \times n}}$,如果所有非对角元素${a_{ij}} \leqslant 0$,$i \ne j$,则下面陈述是等价成立的:1) ${\mathit{\boldsymbol{A}}}$是M矩阵;2) ${\mathit{\boldsymbol{A}}}$的各阶顺序主子式均为正;3)存在${\mathit{\boldsymbol{\xi }}} \in {R^n} > 0$,使得${\mathit{\boldsymbol{A\xi }}} > 0$;4) ${\mathit{\boldsymbol{A}}}$的所有特征根的实部为正。
-
下面给出判定系统式(2)的平衡点的随机指数稳定的充分条件。
定理1 在假设1成立的情况下,对于任意输入${\mathit{\boldsymbol{J}}}$$ \in {\mathit{\boldsymbol{C}}^n}$,若存在正数$T \geqslant 1$使得矩阵${\mathit{\boldsymbol{Q}}}(k) = {(q_{ij}^k)_{n \times n}}$为M矩阵,其中$q_{ii}^k = d_i^k - \left( {\sum\limits_{m = 1, {\kern 1pt} m \ne k}^N {{\pi _{km}}T} + {\pi _{kk}}} \right)$;$q_{ij}^k = - $ $\sum\limits_{j = 1}^n {\sqrt T {l_j}(|\tilde a_{ij}^k| + |\tilde b_{ij}^k|)} $,$k \in S$,$\;i, j = 1, 2, \cdots , n$,则系统式(2)存在唯一平衡点${{\mathit{\boldsymbol{z}}}^\# }$,且该平衡点${{\mathit{\boldsymbol{z}}}^\# }$是随机指数鲁棒稳定的。
证明 令:
$$ {V_i}(t, {z_i}(t) - z_i^\# , r(t) = k) = \omega _i^k\exp(\lambda t)|{z_i}(t) - z_i^\# {|^2} $$ (3) 式中,$\omega _i^k$($i = 1, 2, \cdots , n$,$k \in S$)是一系列正数。假设${w^k} \leqslant \omega _i^k \leqslant {W^k}$,定义${w_{\min }} = {\min _{1 \leqslant k \leqslant N}}\{ {w^k}\} $和${W_{\max }} = $ ${\max _{1 \leqslant k \leqslant N}}\{ {W^k}\} $,令$T = {W_{\max }}/{w_{\min }} \geqslant 1$。
首先证明系统式(2)存在唯一的平衡点${{\mathit{\boldsymbol{z}}}^\# }$。
定义与系统式(2)相关的一个${{\mathit{\boldsymbol{H}}}^k}({\mathit{\boldsymbol{z}}}) = {[H_1^k({\mathit{\boldsymbol{z}}}), \;H_2^k({\mathit{\boldsymbol{z}}}), \; \cdots \;, H_n^k({\mathit{\boldsymbol{z}}})]^{\rm T}}$,其中,
$$ H_i^k({\mathit{\boldsymbol{z}}}) = - d_i^k{z_i} + \sum\limits_{j = 1}^n {(a_{ij}^k + b_{ij}^k)} {f_j}({z_j}) + {J_i}\\ \qquad i = 1, 2, \cdots , n, \;\;k \in S $$ (4) 若${{\mathit{\boldsymbol{H}}}^k}({\mathit{\boldsymbol{z}}})$是${{\mathit{\boldsymbol{C}}}^n}$的同胚映射,那么显然系统式(2)具有唯一的平衡点${{\mathit{\boldsymbol{z}}}^\# }$。
1) 根据引理1,首先证明在假设1的情况下${{\mathit{\boldsymbol{H}}}^k}({\mathit{\boldsymbol{z}}})$为${\mathit{\boldsymbol{C}}^n}$上的单叶映射。
由于矩阵${\mathit{\boldsymbol{Q}}}(k)$是M矩阵,那么明显$\underline{\mathit{\boldsymbol{Q}}}(k)=\left(\underline{q}_{i j}^{k}\right)_{n \times n}$亦为M矩阵,其中$\underline{q} _{ii}^k = d_i^k$;$\underline{q} _{ij}^k = - $ $\sum\limits_{j = 1}^n {{l_j}(|\tilde a_{ij}^k| + |\tilde b_{ij}^k|)} $。根据引理2可知,存在正向量${\mathit{\boldsymbol{\xi }}}(k)$使得下面的不等式成立:
$$ - d_i^k\xi _i^k + \sum\limits_{j = 1}^n {\xi _j^k \cdot {l_j}(|\tilde a_{ij}^k| + |\tilde b_{ij}^k|)} < 0\\ \qquad i = 1, 2, \cdots , n, \;\;k \in S $$ (5) 进而,根据不等式(5),显然存在一个充分小的正数$\varepsilon {\rm{ > }}0$,使得:
$$ d_i^k\xi _i^k - \sum\limits_{j = 1}^n {\xi _j^k \cdot {l_j}(|\tilde a_{ij}^k| + |\tilde b_{ij}^k|)} \geqslant \varepsilon > 0 \\ \qquad i = 1, 2, \cdots , n, \;\;k \in S $$ (6) 假设存在${\mathit{\boldsymbol{u}}}, {\mathit{\boldsymbol{v}}}$$ \in {\mathit{\boldsymbol{C}}^n}$且${\mathit{\boldsymbol{u}}} \ne {\mathit{\boldsymbol{v}}}$,使得$H_i^k({\mathit{\boldsymbol{u}}}) = H_i^k({\mathit{\boldsymbol{v}}})$,即:
$$ \begin{array} [c]{c} - d_i^k{u_i} + \sum\limits_{j = 1}^n {(a_{ij}^k + b_{ij}^k)} {f_j}({u_j}) =-d_{i}^{k} v_{i}+\sum\limits_{j=1}^{n}\left(a_{i j}^{k}+b_{i j}^{k}\right) f_{j}\left(v_{j}\right)\\ i = 1, 2, \cdots , n, \;\; k \in S \end{array} $$ (7) 考虑到假设1,有
$$ d_i^k|{u_i} - {v_i}| \leqslant \sum\limits_{j = 1}^n {{l_j}(|\tilde a_{ij}^k| + |\tilde b_{ij}^k|)} |{u_j} - {v_j}| \\ \qquad i = 1, 2, \cdots , n, \;\;k \in S $$ (8) 不等式(8)可改写为$\underline {\mathit{\boldsymbol{Q}}} (k){\mathit{\boldsymbol{|u}}} - {\mathit{\boldsymbol{v|}}} \leqslant 0$。由于$\underline{\mathit{\boldsymbol{Q} }}(k)$是M矩阵,可知$\det \underline{\mathit{\boldsymbol{Q} }}(k) > 0$且$\underline{\mathit{\boldsymbol{Q} }}{(k)^{ - 1}}$存在。进而可以得到${\mathit{\boldsymbol{|u}}} - {\mathit{\boldsymbol{v|}}} = 0$,即${\mathit{\boldsymbol{u}}}{\rm{ = }}{\mathit{\boldsymbol{v}}}$。这与假设${\mathit{\boldsymbol{u}}} \ne {\mathit{\boldsymbol{v}}}$是矛盾的。因此,映射${{\mathit{\boldsymbol{H}}}^k}({\mathit{\boldsymbol{z}}})$是${\mathit{\boldsymbol{C}}^n}$上的单叶映射,$k \in S$,$i = 1, 2, \cdots , n$。
2) 下面将证明$\mathop {\rm lim}\limits_{||{\mathit{\boldsymbol{z}}}|| \to \infty } ||{{\mathit{\boldsymbol{H}}}^k}({\mathit{\boldsymbol{z}}})|| \to \infty $成立。
令$\tilde H_i^k({\mathit{\boldsymbol{z}}}) = H_i^k({\mathit{\boldsymbol{z}}}) - H_i^k(0)$,$k \in S$,$i = 1, 2, \cdots , n$,即:
$$ \tilde H_i^k({\mathit{\boldsymbol{z}}}) = - d_i^k{z_i} + \sum\limits_{j = 1}^n {(a_{ij}^k} + b_{ij}^k)[{f_j}({z_j}) - {f_j}(0)] \\ \qquad k \in S , \;\;i = 1, 2, \cdots , n $$ (9) 在式(9)两边同时乘以${z_i}$的共轭复数$\bar z_i^{}$,有:
$$ \tilde H_i^k(z){\bar z_i} = - d_i^k{z_i}{\bar z_i} + {\bar z_i}\sum\limits_{j = 1}^n {(a_{ij}^k + b_{ij}^k)[{f_j}({z_j}) - {f_j}(0)]} \\ \qquad k \in S, \;\;i = 1, 2, \cdots , n $$ (10) 在式(10)两边同时取共轭运算,有:
$$ \bar{\tilde H}_i^k(\mathit{\boldsymbol{z}}){z_i} = - d_i^k{\bar z_i}{z_i} + {z_i}\sum\limits_{j = 1}^n {(\bar a_{ij}^k} + \bar b_{ij}^k)[{\bar f_j}({z_j}) - {\bar f_j}(0)] \\ \qquad k \in S, \;\;i = 1, 2, \cdots , n $$ (11) 将式(10)和式(11)合并,并考虑到假设1,有:
$$ \begin{array} [c]{c} \operatorname{Re} [\tilde H_i^k({{\boldsymbol{\rm z}}}){\bar z_i}] = \\ - d_i^k|{z_i}{|^2} + \operatorname{Re} \{ {\bar z_i}\sum\limits_{j = 1}^n {(a_{ij}^k + b_{ij}^k)[{f_j}({z_j}) - {f_j}(0)]} \} \leqslant \\ - d_i^k|{z_i}{|^2} + |{\bar z_i}|\sum\limits_{j = 1}^n {{l_j}(|\tilde a_{ij}^k| + |\tilde b_{ij}^k|)|{z_j}|}\\ k \in S, \;\;i = 1, 2, \cdots , n \end{array} $$ (12) 在式(12)两边同时乘以$\xi _i^k$ ($i = 1, 2, \cdots , n$,$k \in S$)并求和,有下面的不等式成立:
$$ \begin{array} [c]{c} \sum\limits_{i = 1}^n {\xi _i^k\operatorname{Re} [\tilde H_i^k({\mathit{\boldsymbol{z}}}){{\bar z}_i}]} \leqslant \\ \sum\limits_{i = 1}^n {\xi _i^k|{z_i}|} [ - d_i^k + \sum\limits_{j = 1}^n {{l_j}(|\tilde a_{ij}^k| + |\tilde b_{ij}^k|)} ]|{z_j}| \end{array} $$ 考虑到不等式(6),有$\sum\limits_{i = 1}^n {\xi _i^k\operatorname{Re} [\tilde H_i^k({\mathit{\boldsymbol{z}}}){{\bar z}_i}]} \leqslant $ $ - \varepsilon \sum\limits_{i = 1}^n {|{z_i}|} \cdot \sum\limits_{j = 1}^n {|{z_j}|} $$k \in S$。进而,可得$\varepsilon \sum\limits_{i = 1}^n {|{z_i}|} \times $ $\sum\limits_{j = 1}^n {|{z_j}|} < - $$\sum\limits_{i = 1}^n {\xi _i^k\operatorname{Re} [\tilde H_i^k({\mathit{\boldsymbol{z}}}){{\bar z}_i}]} $$ \leqslant {\max _{1 \leqslant i \leqslant \leqslant n}}\{ \xi _i^k\} \times $ $\sum\limits_{i = 1}^n {|\tilde H_i^k({\mathit{\boldsymbol{z}}})|} \sum\limits_{i = 1}^n {|{z_i}|} $,即$\varepsilon ||{\mathit{\boldsymbol{z}}}|{|_1}$$ \leqslant {\max _{1 \leqslant i \leqslant n}}\{ \xi _i^k\} \times $ $||{{\mathit{\boldsymbol{\tilde H}}}^k}({\mathit{\boldsymbol{z}}})|{|_1}$。也即不等式$||{\mathit{\boldsymbol{z}}}|{|_1} \leqslant {\varepsilon ^{ - 1}}{\max _{1 \leqslant i \leqslant n}}\{ \xi _i^k\} \times $ $||{\mathit{\boldsymbol{\tilde H}}}_{}^k({\mathit{\boldsymbol{z}}})|{|_1}$成立。根据范数等价原则,有当$||{\mathit{\boldsymbol{z}}}|| \to \infty $,$||{{\mathit{\boldsymbol{\tilde H}}}^k}({\mathit{\boldsymbol{z}}})|| \to \infty $,即当$||{\mathit{\boldsymbol{z}}}|| \to \infty $,有$||{{\mathit{\boldsymbol{H}}}^k}({\mathit{\boldsymbol{z}}})|| \to \infty $成立。
综合1)和2)可知${{\mathit{\boldsymbol{H}}}^k}({\mathit{\boldsymbol{z}}})$是${\mathit{\boldsymbol{C}}^n}$上的同胚映射,$k \in S$。因此,系统式(2)具有唯一平衡点${{\mathit{\boldsymbol{z}}}^\# }$。
接下来利用矢量Lyapunov函数法证明平衡点${{\mathit{\boldsymbol{z}}}^\# }$是随机指数鲁棒稳定的。为便于分析,对系统式(2)进行坐标变换。令${\mathit{\boldsymbol{\tilde z}}}(t) = {\mathit{\boldsymbol{z}}}(t) - {{\mathit{\boldsymbol{z}}}^\# }$,进而系统式(2)可转换为:
$$ \begin{array} [c]{c} \frac{{\operatorname{d} {{\tilde z}_i}(t)}}{{\operatorname{d} t}} = - d_i^{}(r(t)){{\tilde z}_i}(t) + \\ \sum\limits_{j = 1}^n {[a_{ij}^{}(r(t)){g_j}({{\tilde z}_j}(t)) + } b_{ij}^{}(r(t)){g_j}({{\tilde z}_j}(t - {\tau _{ij}}(t))){\rm{]}} \\ \end{array} $$ (13) 式中,${g_j}({\tilde z_j}{\rm{(}}t{\rm{)}}) = {f_j}({\tilde z_j}(t) + z_j^\# ) - {f_j}(z_j^\# )$,$i{\rm{, }}\;j = $ $1, 2, \cdots , n$。令系统式(13)的初始条件为${\psi _i}(s) = {\varphi _i}(s) - z_i^\# $,$i = 1, 2, \cdots , n$,$ - \tau \leqslant s \leqslant 0$。显然,系统式(13)的零解的随机指数鲁棒稳定性与系统式(2)的平衡点的随机指数鲁棒稳定性是等价的。
由于${\mathit{\boldsymbol{Q}}}(k) = {(q_{ij}^k)_{n \times n}}$是M矩阵,根据引理2可知存在正向量${\mathit{\boldsymbol{\zeta }}}(k) = {(\zeta _1^k, \zeta _2^k, \cdots , \zeta _n^k)^{\rm T}}$使得对于所有$k \in S$,$i = 1, 2, \cdots , n$,不等式$\left[ { - 2d_i^k + \left( {\sum\limits_{m = 1, {\kern 1pt} m \ne k}^N {{\pi _{km}}T} + {\pi _{kk}}} \right)} \right]\zeta _i^k + $$2\sum\limits_{j = 1}^n {\sqrt T {l_j}\zeta _j^k{\rm{(|}}\tilde a_{ij}^k| + } $$|\tilde b_{ij}^k|{\rm{)}} < 0$成立。
构造如下函数${F_i}(\alpha , k)$,$k \in S$,$i = 1, 2, \cdots , n$:
$$ \begin{array}[c]{c} {F_i}(\alpha , k) = \left[ { - 2d_i^k + \alpha + \left( {\sum\limits_{m = 1, {\kern 1pt} m \ne k}^N {{\pi _{km}}T} + {\pi _{kk}}} \right)} \right]\zeta _i^k + \\ \sum\limits_{j = 1}^n {\sqrt T {l_j}\zeta _j^k{\rm{[|}}\tilde a_{ij}^k| + \exp(0.5\alpha \tau )|\tilde b_{ij}^k|{\rm{]}}} \\ \end{array} $$ 由于${F_i}(0, k) = \left[ { - 2d_i^k + } \right.\left( {\sum\limits_{m = 1, {\kern 1pt} m \ne k}^N {{\pi _{km}}T} + } \right.$$\left. {\left. {\sum\limits_{}^{} {} {\pi _{kk}}} \right)} \right]\zeta _i^k + $ $2\sum\limits_{j = 1}^n {\sqrt T {l_j}\zeta _j^k(|\tilde a_{ij}^k| + |\tilde b_{ij}^k|)} < 0$,显然,存在$\lambda > 0$使得:
$$ \begin{array} [c]{c} {F_i}(\lambda , k) = \left[ { - 2d_i^k + \lambda + \left( {\sum\limits_{m = 1, {\kern 1pt} m \ne k}^N {{\pi _{km}}T} + {\pi _{kk}}} \right)} \right]\zeta _i^k + \\ 2\sum\limits_{j = 1}^n {\sqrt T {l_j}\zeta _j^k\left[ {|\tilde a_{ij}^k| + \exp(0.5\lambda \tau )|\tilde b_{ij}^k|} \right]} < 0 \end{array} $$ (14) 在不引起混淆的情况下,并考虑到${\tilde z_i}(t) = {z_i}(t) - z_i^\# $,记${V_i}(t, k) = {V_i}(t, {\tilde z_i}(t), r(t) = k) = $ $\omega _i^k\exp(\lambda t)|{\tilde z_i}(t){|^2}$,$i = 1, 2, \cdots , n$,$k \in S$。令${\operatorname{L} _{(13)}}{V_i}(t, k)$表示${V_i}(t, k)$沿系统式(13)解的弱算子,其中$i = 1, 2, \cdots , n$,$k \in S$,具体定义如下:
$$ \begin{array} [c]{c} {\operatorname{L} _{(13)}}{V_i}(t, k) = \mathop {\lim }\limits_{\Delta \to {0^ + }} \frac{1}{\Delta }\{ \operatorname{E} \{ {V_i}(t + \Delta , r(t + \Delta ))\left| {t, r(t) = k} \right.\} - \\ \operatorname{E} \{ {V_i}(t, r(t) = k)\} \} \end{array} $$ (15) 考虑到式(1)及Markova随机过程的性质,将式(15)改写为${\operatorname{L} _{(13)}}{V_i}(t, k) = \sum\limits_{m = 1}^N {{\pi _{km}}{V_i}(\, t, m)} + {\operatorname{D} ^ + }{V_i}(t, \, k)$,$i = 1, 2, \cdots , n$,$k \in S$。计算${V_i}(t, \, k)$沿着系统式(13)的零解的右上导数${\operatorname{D} ^ + }{V_i}(t, \, k)$,有:
$$ \begin{matrix} {{\text{L}}_{(13)}}{{V}_{i}}(t,k)=\sum\limits_{m=1}^{N}{{{\pi }_{km}}}{{V}_{i}}(t,m)+{{\text{D}}^{+}}{{V}_{i}}(t,k)= \\ \exp(\lambda t)\left\{ \sum\limits_{m=1}^{N}{\omega _{i}^{m}{{(\omega _{i}^{k})}^{-1}}{{\pi }_{km}}}\omega _{i}^{k}|{{{\tilde{z}}}_{i}}(t){{|}^{2}}\text{+} \right. \\ \left. \omega _{i}^{k}\text{ }\!\![\!\!\text{ }\lambda |{{{\tilde{z}}}_{i}}(t){{|}^{2}}+2\operatorname{Re}({{{\bar{\tilde{z}}}}_{i}}(t){{{\dot{\tilde{z}}}}_{i}}(t))\text{ }\!\!]\!\!\text{ } \right\}\le \\ \exp(\lambda t)\left\{ \sum\limits_{m=1}^{N}{T{{\pi }_{km}}}\omega _{i}^{k}|{{{\tilde{z}}}_{i}}(t){{|}^{2}}+\lambda \omega _{i}^{k}|{{{\tilde{z}}}_{i}}(t){{|}^{2}}\text{+} \right. \\ 2|{{{\bar{\tilde{z}}}}_{i}}(t)|\{-d_{i}^{k}\omega _{i}^{k}|{{{\tilde{z}}}_{i}}(t)|+ \\ \left. \sum\limits_{j=1}^{n}{\omega _{i}^{k}{{l}_{j}}[|\tilde{a}_{ij}^{k}||{{{\tilde{z}}}_{j}}(t)|+|}\tilde{b}_{ij}^{k}||{{{\tilde{z}}}_{j}}(t-{{\tau }_{ij}}(t))|\} \right\}\le \\ \sqrt{\omega _{i}^{k}}\exp(\lambda t)\text{ }\!\!|\!\!\text{ }{{{\tilde{z}}}_{i}}(t)|\left\{ \sum\limits_{m=1}^{N}{T{{\pi }_{km}}}\sqrt{\omega _{i}^{k}}|{{{\tilde{z}}}_{i}}(t\text{) }\!\!|\!\!\text{ }+ \right. \\ \lambda \sqrt{\omega _{i}^{k}}|{{{\tilde{z}}}_{i}}(t)|+\{-2d_{i}^{k}\sqrt{\omega _{i}^{k}}|{{{\tilde{z}}}_{i}}(t)|+ \\ \left. 2\sum\limits_{j=1}^{n}{\sqrt{T}\sqrt{\omega _{j}^{k}}{{l}_{j}}[|\tilde{a}_{ij}^{k}||{{{\tilde{z}}}_{j}}(t)|+|}\,\tilde{b}_{ij}^{k}||{{{\tilde{z}}}_{j}}(t-{{\tau }_{ij}}(t))|]\} \right\}\le \\ \sqrt{{{V}_{i}}(t)}\left\{ [-2d_{i}^{k}+\sum\limits_{m=1}^{N}{T{{\pi }_{km}}}+\lambda ]\sqrt{{{V}_{i}}(t)}+ \right. \\ \left. 2\sum\limits_{j=1}^{n}{{{l}_{j}}\sqrt{T}[|\tilde{a}_{ij}^{k}|\sqrt{{{V}_{j}}(t)}+}|\tilde{b}_{ij}^{k}|\exp(0.5\lambda \tau )\sqrt{{{V}_{j}}(t-{{\tau }_{ij}}(t))}] \right\} \\ \end{matrix} $$ (16) 不等式(16)两边同时计算数学期望,有:
$$ \begin{array}[c]{c} \operatorname{E} \{ {\operatorname{L} _{(13)}}{V_i}(t, k)\} \leqslant \\ \operatorname{E} \{ \sqrt {{V_i}(t)} \} \{ [ - 2d_i^k + \sum\limits_{m = 1}^N {T{\pi _{km}}} + \lambda ]\operatorname{E} \{ \sqrt {{V_i}(t)} \} + \\ 2\sum\limits_{j = 1}^n {{l_j}\sqrt T [|\tilde a_{ij}^k|\operatorname{E} \{ \sqrt {{V_j}(t)} \} + } \\ |\tilde b_{ij}^k|\exp(0.5\lambda \tau )E\{ \sqrt {{V_j}(t - {\tau _{ij}}(t))} \} ] \\ \end{array} $$ (17) 定义曲线${\mathit{\boldsymbol{\zeta }}}(k) = \{ \gamma (\chi , k):\;{\gamma _i} = {(\zeta _i^k)^2}\chi , $ $\chi > 0, $ ${\kern 1pt} \, \;k \in S, \;\;i = 1, 2, \cdots , n\} $及集合$\varOmega (\gamma ) = \{ y:0 \leqslant y \leqslant \gamma , $ $\gamma \in \zeta (k), $ $k \in S\} $。当$\chi > \chi '$,显然有$\varOmega (\gamma (\chi )) \supset $ $\varOmega (\gamma (\chi '))$成立。令$\zeta _{\max }^k = {\max _{1 \leqslant i \leqslant n}}\{ \zeta _i^k\} $,$\zeta _{\min }^k = $ ${\min _{1 \leqslant i \leqslant n}}\{ \zeta _i^k\} $,${\chi _0}(k) = \frac{{{W^k}E\{ ||{\mathit{\boldsymbol{\psi }}}(s)|{|^2}\} }}{{{{(\zeta _{\min }^k)}^2}}}$,则有:$\;\left\{ {\operatorname{E} \{ V(k)\} :\operatorname{E} \{ {V_i}(s, k)} \right.{\rm{\} }} = \exp {\rm{(}}\lambda {\rm{s)}}\omega _i^k\operatorname{E} \{ |{\varphi _i}(s){|^2}\} , \, - \tau \leqslant $ $\left. {s \leqslant 0, \;\;1 \leqslant i \leqslant n, \;\;k \in S} \right\} \subset \varOmega (\gamma ({\chi _0}(k), k))$,即不等式$\exp {\rm{(}}\lambda {\rm{s)}}\omega _i^k\operatorname{E} \{ |{\varphi _i}(s){|^2}\} < {(\zeta _i^k)^2}{\chi _0}(k)$成立,$ - \tau \leqslant $ $s \leqslant 0$,$i = 1, 2, \cdots , n$,$k \in S$。
根据以上分析有$\operatorname{E} \{ {V_i}(t, k)\} \leqslant {(\zeta _i^k)^2}{\chi _0}(k)$成立,$i = 1, 2, \cdots , n$,$k \in S$,$t \geqslant 0$。若该不等式不成立,则必然存在$i' \in {\rm{\{ 1, 2, }} \cdots {\rm{, }}n{\rm{\} }}$以及时刻${t^ * }$$({t^ * } > 0)$使得$\operatorname{E} \{ {V_{i'}}({t^ * }, k)\} = {(\zeta _{i'}^k)^2}{\chi _0}(k)$,$\operatorname{E} \{ {\operatorname{L} _{(13)}}{V_{i'}}({t^*}, k)\} \geqslant 0$且$\operatorname{E} \{ {V_j}(t, k)\} \leqslant {(\zeta _j^k)^2}{\chi _0}(k)$,${t^ * } - \tau < t \leqslant {t^ * }$,$j = 1, 2, \cdots , n$,$k \in S$。将其代入到不等式(17),并考虑到不等式(14),有$\operatorname{E} \{ {\operatorname{L} _{(13)}}{V_{i'}}({t^ * }, k)\} \leqslant \zeta _{i'}^k{\chi _0}(k) \times $$\{ [ - 2d_{i'}^k + {\rm{ }}\sum\limits_{m = 1}^N {T{\pi _{km}}} + {\rm{ }}\lambda ]\zeta _{i'}^k{\rm{ }} + $$2\sum\limits_{j = 1}^n {{l_j}{\rm{ }}\zeta _j^k{\rm{ }}\sqrt T {\rm{ }}[|\tilde a_{i'j}^k| + } $$\sum {|\tilde b_{i'j}^k|\exp(0.5\lambda \tau )]\} } $ < 0,$k \in S$,$\;i = 1, 2, \cdots , n$。这显然与假设$\operatorname{E} \{ {\operatorname{L} _{(13)}}{V_{i'}}({t^ * }, k)\} \geqslant 0$是矛盾的。因此,对所有$k \in S$,$\;i = 1, 2, \cdots , n$,不等式$\operatorname{E} \{ {V_i}({t^ * }, k)\} < $ ${(\zeta _i^k)^2}{\chi _0}(k)$成立,也即$|{\tilde z_i}(t)| < \exp( - 0.5\lambda t)\frac{{\zeta _i^k}}{{\sqrt {\omega _i^k} }} \times $ $\sqrt {{\chi _0}(k)} = $$\exp( - 0.5\lambda t)\frac{{{W^k}\zeta _i^k\sqrt {E\{ ||{\mathit{\boldsymbol{\psi }}}(s)|{|^2}\} } }}{{\zeta _{\min }^k\sqrt {\omega _i^k} }}$。
令$M(k) = \frac{{{W^k}\zeta _i^k}}{{\zeta _{\min }^k\sqrt {\omega _i^k} }}$,$k \in S$。显然$M(k) \geqslant 1$,$k \in S$。根据定义1可知系统式(13)的零解是随机指数鲁棒稳定的,即系统式(2)的平衡点${{\mathit{\boldsymbol{z}}}^\# }$是随机指数鲁棒稳定的。证毕
当系统式(2)中没有Markova跳变参数时,此时系统模型为:
$$ \begin{array}[c]{c} \frac{{\operatorname{d} {z_i}(t)}}{{\operatorname{d} t}} = - {d_i}{z_i}(t) + \\ \sum\limits_{j = 1}^n {[{a_{ij}}{f_j}({z_j}(t))} {\rm{ + }}{b_{ij}}{f_j}({z_j}(t - {\tau _{ij}}(t)))] + {J_i}(t) \\ i = 1, 2, \cdots , n \end{array} $$ (18) 根据定理1可得到确保系统式(18)的平衡点稳定性的充分条件。
推论1 在假设1成立的情况下,对于任意输入${\mathit{\boldsymbol{J}}}$$ \in {\mathit{\boldsymbol{C}}^n}$,若矩阵${\mathit{\boldsymbol{Q}}} = {(q_{ij}^{})_{n \times n}}$为M矩阵,其中$q_{ii}^{} = d_i^{}$,$q_{ij}^{} = - \sum\limits_{j = 1}^n {{l_j}(|\tilde a_{ij}^{}| + |\tilde b_{ij}^{}|)} $,$\;i = 1, 2, \cdots , n$,则该系统式(18)存在唯一的平衡点${{\mathit{\boldsymbol{z}}}^\# }$,且该平衡点${{\mathit{\boldsymbol{z}}}^\# }$是指数鲁棒稳定的。
在系统式(2)中,复数域加权矩阵假设为区间矩阵。若矩阵${\mathit{\boldsymbol{A}}}(r(t))$和${\mathit{\boldsymbol{B}}}(r(t))$在每种固定模式下是常值复数域矩阵,根据定理1同样可得到确保系统式(2)的平衡点稳定性的充分条件。具体如下:
推论2 在假设1成立的情况下,对于任意输入${\mathit{\boldsymbol{J}}}$$ \in {\mathit{\boldsymbol{C}}^n}$,若存在正数$T \geqslant 1$使得矩阵${\mathit{\boldsymbol{Q}}}(k) = {(q_{ij}^k)_{n \times n}}$为M矩阵,其中$q_{ii}^k = d_i^k - \left( {\sum\limits_{m = 1, {\kern 1pt} m \ne k}^N {{\pi _{km}}T} + {\pi _{kk}}} \right)$;$q_{ij}^k = - \sum\limits_{j = 1}^n {\sqrt T {l_j}\left( {|a_{ij}^k| + |b_{ij}^k|} \right)} $,$k \in S$,$\;i, j = 1, 2, \cdots , n$,则系统式(2)存在唯一平衡点${{\mathit{\boldsymbol{z}}}^\# }$,且该平衡点${{\mathit{\boldsymbol{z}}}^\# }$是随机指数稳定的。
-
下面利用定理1判定如下具有3种模式的二维变时滞复数域区间神经网络的随机指数鲁棒稳定性。
$$\left\{ \begin{array}[c]{c} \frac{{\operatorname{d} {z_1}(t)}}{{\operatorname{d} t}} = - {d_1}(r(t)){z_1}(t) + \sum\limits_{j = 1}^2 {[{a_{1j}}(r(t)){f_j}({z_j}(t))} {\rm{ + }}{b_{1j}}(r(t)){f_j}({z_j}(t - 0.5{\rm{|}}\sin {\rm{t|}}))] + {J_1}(t) \\ \frac{{\operatorname{d} {z_2}(t)}}{{\operatorname{d} t}} = - {d_2}(r(t)){z_2}(t) + \sum\limits_{j = 1}^2 {[{a_{2j}}(r(t)){f_j}({z_j}(t))} {\rm{ + }}{b_{2j}}(r(t)){f_j}({z_j}(t - (1 - 0.4cost)))] + {J_2}(t) \\ \end{array} \right.$$ (19) 系统式(19)中,假设复数域区间加权矩阵为:
$$\begin{array}[c]{c} {{\mathit{\boldsymbol{A}}}_I}(r(t)) = \\ \left[ {\begin{array}{*{20}{c}} {[ - 1, 1.5] + [0.5, 1.3]{\rm i}}&{[0.8, 1.1] + [ - 0.1, 0.5]{\rm i}} \\ {[0, 1.4] + [ - 0.3, 0.9]{\rm i}}&{[0, 0.7] + [ - 0.1, \sqrt 2 ]{\rm i}} \end{array}} \right] \\ \end{array} $$ $$\begin{array}[c]{c} {{\mathit{\boldsymbol{B}}}_I}(r(t)) = \\ \left[ {\begin{array}{*{20}{c}} {[ - 0.5, 0.6] + [0.6, 0.9]{\rm i}}&{[ - 1, 1] + [0.7, 1]{\rm i}} \\ {[0.5, 0.8] + [ - 0.4, 0.7]{\rm i}}&{[ - 0.4, 0.5] + [0.9, 1.2]{\rm i}} \end{array}} \right] \\ \end{array} $$ 此外,令$T = 3$,$d_1^{}(1) = 9$,$d_2^{}(1) = 8$,$d_1^{}(2) = 10$,$d_2^{}(2) = 9$,$d_1^{}(3) = 7$,$d_2^{}(3) = 8$;令激活函数为${f_1}({z_1}(t)) = \frac{{1 - \exp ( - {{\bar z}_1}(t))}}{{1 + \exp ( - {{\bar z}_1}(t))}}$,${f_2}({z_2}(t)) = \frac{3}{{1 + \exp ( - {{\bar z}_2}(t))}}$;令初始条件为${z_1}(s) = 0.7 + 1.5i$, ${z_2}(s) = - 2.5 - 0.8i$, $s \in [ - 1.4, \;0]$;令跳变转移概率分别为$\pi {}_{11}{\kern 1pt} = - 1/2$,$\pi {}_{12}{\kern 1pt} = 1/6$,$\pi {}_{13}{\kern 1pt} = 1/3$,$\pi {}_{21}{\kern 1pt} = 1/8$,$\pi {}_{22}{\kern 1pt} = - 1/2$,$\pi {}_{23}{\kern 1pt} = 3/8$,$\pi {}_{31}{\kern 1pt} = 1/5$,$\pi {}_{32}{\kern 1pt} = 3/10$,$\pi {}_{33}{\kern 1pt} = - 1/2$。
经过计算有:${l_1} = 0.5$,${l_2} = 0.7$,$\left| {{\mathit{\boldsymbol{\tilde A}}}} \right| = $ ,。进而,可以得到,,。根据引理2可知,矩阵${\mathit{\boldsymbol{Q}}}(1)$,${\mathit{\boldsymbol{Q}}}(2)$和${\mathit{\boldsymbol{Q}}}(3)$均为M矩阵。根据定理1可以得出结论:系统式(19)存在唯一平衡点,且该平衡点是随机指数鲁棒稳定的。
下面对该系统进行数值仿真。仿真时:
模式1取:,${\mathit{\boldsymbol{B}}}(1) = $ ,${J_1}(t){\rm{ = }}2{\rm{ + }}3{\rm{i}}$,${J_2}(t){\rm{ = }} - {\rm{0}}{\rm{.5 + 2i}}$。
模式2取:,${\mathit{\boldsymbol{B}}}(2) = $ ,${J_1}(t){\rm{ = 1 + 2i}}$,${J_2}(t){\rm{ = 0}}{\rm{.5}} - {\rm{0}}{\rm{.5i}}$。
模式3取:,${\mathit{\boldsymbol{B}}}(3) = $ ,${J_1}(t){\rm{ = }}2{\rm{ + i}}$,${J_2}(t){\rm{ = }} - {\rm{0}}{\rm{.5 + 2i}}$。
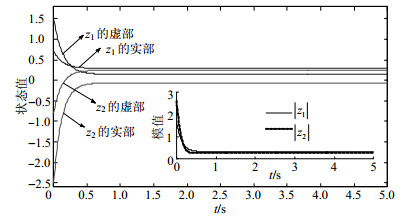
仿真结果如图 1~图 3所示。图 1~图 3分别给出了3种模式下系统式(19)的状态曲线。由仿真结果可知该系统的平衡点是稳定的,该结果进一步验证了定理1的正确性。
-
在假定复数域激活函数仅满足Lipchitz条件的情况下,针对具有Markova跳变参数和变时滞的复数域区间神经网络,利用M矩阵理论、同胚映射原理以及向量Lyapunov函数法,得到了确保该系统平衡点存在性、唯一性,并对随机指数鲁棒稳定性进行了分析。所建立的稳定性判据是显示判据,且形式简单易验证。通过数值算例表明该结论的可行性,同时仿真结果也验证了结论的正确性。
Stochastic Exponential Robust Stability of a Class of Complex-Valued Neural Networks
-
摘要: 为分析Markova跳变参数对系统的影响,研究了一类具有Markova跳变参数和变时滞的复数域区间神经网络的动态行为。在假定复数域激活函数仅满足Lipchitz条件的情况下,首先利用M矩阵理论和同胚映射相关原理,研究了该系统平衡点的存在性和唯一性。然后利用矢量Lyapunov函数法分析了不同模式下平衡点的随机指数鲁棒稳定性。建立的稳定性条件推广了现有结论,并且容易验证。最后,通过一个数值仿真算例验证了所得结论的可行性。
-
关键词:
- 复数域 /
- Markova跳变参数 /
- 神经网络 /
- 随机指数鲁棒稳定性 /
- 变时滞 /
- 矢量Lyapunov函数法
Abstract: In order to analyze the influence of the Markova jumping parameters on the system, this paper deals with dynamic behavior analysis for a class of interval neural networks defined in complex number domain with Markova jumping parameters and time-varying delays. It is assumed that the activation functions defined in complex number domain satisfy Lipschitz condition. Firstly, the existence and uniqueness of the equilibrium point of the addressed system are studied by employing the M-matrix theory and the homeomorphism mapping theory. Then, the stochastic exponential robust stability of the equilibrium point is analyzed based on the idea of the vector Lyapunov function method. The presented stability analysis is the generalization of existing ones not only, but also easy to be verified in the practice applications. Finally, a numerical example with several simulation results is given to illustrate the feasibility of the obtained results in this paper. -
[1] HIROSE A. Recent progress in applications of complex-valued neural networks[C]//Proceedings of 10th International Conference on Artificial Intelligence Soft Computing Ⅱ. Zakopane, Poland: Springer-Verlag Berlin, 2010: 42-46. doi: 10.1007/978-3-642-13232-2_6 [2] HUANG Yu-jiao, ZHANG Hua-guang, WANG Zhan-shan. Multistability of complex-valued recurrent neural networks with real-imaginary-type activation functions[J]. Applied Mathematics and Computation, 2014, 229:187-200. doi: 10.1016/j.amc.2013.12.027 [3] JIAN Ji-gui, WAN Peng. Lagrange α-exponential stability and α-exponential convergence for fractional-order complex-valued neural networks[J]. Neural Networks, 2017, 91(7):1-10. https://www.sciencedirect.com/science/article/pii/S0893608017300679 [4] 徐晓惠, 张继业, 赵玲.一类混合时滞复值神经网络的动态行为分析[J].西南交通大学学报, 2014, 49(3):470-476. doi: 10.3969/j.issn.0258-2724.2014.03.016 XU Xiao-hui, ZHANG Ji-ye, ZHAO Ling. Dynamic behaviors analysis of a class of complex-valued neural networks with mixed delays[J]. Journal of Southwest Jiaotong University, 2014, 49(3):470-476. doi: 10.3969/j.issn.0258-2724.2014.03.016 [5] ZHANG Zheng-qiu, YU Sheng-hua. Global asymptotic stability for a class of complex-valued Cohen-Grossberg neural networks with time delays[J]. Neurocomputing, 2016, 171(1):1158-1166. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a8ade5c38047d690ff2c37ec1a806998 [6] 闫欢, 宋乾坤, 赵振江.时间标度上时滞脉冲复值神经网络的全局稳定性[J].应用数学和力学, 2015, 36(11):1191-1203. doi: 10.3879/j.issn.1000-0887.2015.11.007 YAN Huan, SONG Qian-kun, ZHAO Zhen-jiang. Global stability of impulsive complex-valued neural networks with time delay on time scales[J]. Applied mathematics and Mechanics, 2015, 36(11):1191-1203. doi: 10.3879/j.issn.1000-0887.2015.11.007 [7] TU Zheng-wen, CAO Jin-de, ALSAEDI A, et al. Global lagrange stability of complex-valued neural networks of neutral type with time-varying delays[J]. Complexity, 2017, 21(s2):438-450. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=51e5b7427a5571e1fe8b8cbb55a6a698 [8] 徐晓惠, 张继业, 施继忠, 等.脉冲干扰时滞复值神经网络的稳定性分析[J].哈尔滨工业大学学报, 2016, 48(3):166-170. http://d.old.wanfangdata.com.cn/Periodical/hebgydxxb201603028 XU Xiao-hui, ZHANG Ji-ye, SHI Ji-zhong, et al. Stability analysis of delayed complex-valued neural networks with impulsive disturbances[J]. Journal of Harbin Institute of Technology, 2016, 48(3):166-170. http://d.old.wanfangdata.com.cn/Periodical/hebgydxxb201603028 [9] LIANG Jin-ling, GONG Wei-qiang, HUANG Ting-wen. Multistability of complex-valued neural networks with discontinuous activation functions[J]. Neural Networks, 2016, 84:125-142. doi: 10.1016/j.neunet.2016.08.008 [10] RAKKIYAPPAN R, VELMURUGAN G, LI Xiao-di. Complete stability analysis of complex-valued neural networks with time delays and impulses[J]. Neural Process Letter, 2015, 41(3):435-468. doi: 10.1007/s11063-014-9349-6 [11] LIU Dan, ZHU Song, YE Er. Synchronization stability of memristor-based complex-valued neural networks with time delays[J]. Neural Networks, 2017, 96:115-127. doi: 10.1016/j.neunet.2017.09.008 [12] GUO Run-an, ZHANG Zi-ye, LIU Xiao-ping, et al. Existence, uniqueness, and exponential stability analysis for complex-valued memristor-based BAM neural networks with time delays[J]. Applied Mathematics and Computation, 2017, 311:100-117. doi: 10.1016/j.amc.2017.05.021 [13] WAN Peng, JIAN Ji-gui. Global convergence analysis of impulsive inertial neural networks with time-varying delays[J]. Neurocomputing, 2017, 245:68-76. doi: 10.1016/j.neucom.2017.03.045 [14] WANG Ling, ZHAO Hong-yong. Synchronized stability in a reaction-diffusion neural network model[J]. Physics Letters A, 2014, 378(48):3586-3599. doi: 10.1016/j.physleta.2014.10.019 [15] HUANG Ting-wen, LI Chuan-dong, DUAN Shu-kai, et al. Robust exponential stability of uncertain delayed neural networks with stochastic perturbation and impulse effects[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(6):866-875. doi: 10.1109/TNNLS.2012.2192135 [16] ZHANG Chun-mei, LI Wen-xue, SU Huan, et al. A graph-theoretic approach to boundedness of stochastic Cohen-Grossberg neural networks with Markovian switching[J]. Applied Mathematics and Computation, 2013, 219(17):9165-9173. doi: 10.1016/j.amc.2013.03.048 [17] ZHONG Qi-shui, CHENG Jun, ZHAO Yu-qing. Delay-dependent finite-time boundedness of a class of Markovian switching neural networks with time-varying delays[J]. ISA Transactions, 2015, 57:43-50. doi: 10.1016/j.isatra.2015.01.001 [18] LI Qian, ZHU Qing-xin, ZHONG Shou-ming, et al. State estimation for uncertain Markovian jump neural networks with mixed delays[J]. Neurocomputing, 2016, 182:82-93. doi: 10.1016/j.neucom.2015.11.083 [19] LI Zhi-hong, LIU Lei, ZHU Quan-xin. Mean-square exponential input-to-state stability of delayed Cohen-Grossberg neural networks with Markovian switching based on vector Lyapunov functions[J]. Neural Networks, 2016, 84:39-46. doi: 10.1016/j.neunet.2016.08.001 [20] CHEN Guo-liang, XIA Jian-wei, ZHUANG Guang-ming. Delay-dependent stability and dissipativity analysis of generalized neural networks with Markovian jump parameters and two delay components[J]. Journal of the Franklin Institute, 2016, 353(9):2137-2158. doi: 10.1016/j.jfranklin.2016.02.020 -


 ISSN
ISSN 




 下载:
下载: