脉冲干扰是指将干扰能量集中在一个脉冲周期的某一段时间内发射的干扰样式。射频脉冲干扰信号可表示为：

式中，${f_0}$为期望信号中心频率；${P_J}$为干扰功率；${f_J}$为干扰频偏；$\varphi $为干扰相位；$p(t)$为基带脉冲信号，常见为矩形脉冲，其时域和频域的表达式分别为：

式中，$\tau $和$T$分别为脉宽和脉冲重复周期。

压制干扰对GPS接收机捕获、载波跟踪和数据解调的影响可统一归结到对干扰等效载噪比的计算上，而对码跟踪的影响却不能单纯用干扰等效载噪比来表征，因此，兼顾采用干扰等效载噪比和码跟踪误差作为干扰效果的评估指标。由于$\tau $和$T$的取值没有一个相对固定的范围，且两者之间存在一定的依赖关系，还有可能对${f_J}$的最佳设置造成影响，因此，本文只分析不同脉冲干扰参数取值对离散谱C/A码信号和连续谱M码信号产生的干扰效果，以求揭示出脉冲干扰参数的影响本质，从而设置参数取值范围，提高干扰利用效率。

脉冲干扰经过离散谱C/A码解扩解调后的频域形式为：

式中，${S_{{\rm{C/A}}}}(f)$为用来解扩的C/A码频谱；$\hat \tau $为码相位估计误差；${f_d}$为多普勒频移。将式(3)通过一个冲激响应$h(t) = {1 \mathord{\left/ {\vphantom {1 {{T_d}}}} \right. } {{T_d}}}$($ - {{{T_d}} \mathord{\left/ {\vphantom {{{T_d}} 2}} \right. } 2} \leqslant t \leqslant {{{T_d}} \mathord{\left/ {\vphantom {{{T_d}} 2}} \right. } 2}$)的低通滤波器后可得：

式中，$P_{矩形n}$和${C_k}$分别为$S_{矩形}$和${S_{{\rm{C/A}}}}(f)$各离散谱线的傅里叶系数；${N_c}$为C/A码码长；${T_c}$为C/A码码宽；$l$为最靠近${f_J}$的C/A码谱线序号；$\Delta {f_J}$为${f_J}$与第$l$条C/A码谱线的频差($\left| {\Delta {f_J}} \right| < {1 \mathord{\left/ {\vphantom {1 {(2{N_c}{T_c})}}} \right. } {(2{N_c}{T_c})}}$)；${T_d}$为相关积分时间；$\hat \theta $为本地载波的相位估计。鉴于C/A码周期为1 ms，因此，可将$T$分为$T \ll 1{\rm{ ms}}$、$T \gg 1{\rm{ ms}}$和$T = 1{\rm{ ms}}$这3种情况进行干扰效能讨论^[5]。

当$T \ll 1{\rm{ ms}}$时，相关器输出的干扰等效载噪比为：

式中，${R_0}( \bullet )$为伪码带限自相关函数。设${f_d} = 0$，${f_J}$与C/A码的第$l$条谱线重合，当$T \ll 1{\rm{ ms}}$时，相关器输出处的干扰分量为常数，将式(4)变换到时域可表示为：

式中，${\alpha _l} = {\rm{angle}}({C_l})$。经过非相干超前减滞后功率(noncoherent early-late processing, NELP)处理后可得到：

式中，$d$为早迟码间距(码片)；$\theta $为载波相位；$X = \sqrt {{{{P_J}} \mathord{\left/ {\vphantom {{{P_J}} {{P_s}}}} \right. } {{P_s}}}} \left| {{P_{矩形0}}{C_l}} \right|$。由于$\varphi $和$\theta $都在$[0, 2{\rm{ \mathsf{ π} }}]$间独立随机取值，因此，$ - 2{\rm{ \mathsf{ π} }}\hat \tau {l \mathord{\left/ {\vphantom {l {({N_c}{T_c})}}} \right. } {({N_c}{T_c})}} + \varphi - \theta - {\alpha _l}$的主值也任意分布在$[0, 2{\rm{ \mathsf{ π} }}]$之间，令其等于$\phi $。根据码跟踪环的鉴相过程，可得：

式(8)中由于$\phi $的存在，可考虑干扰影响最严重时的情况，求解${{\partial {{\hat \tau }_{{\rm{NEL}}{{\rm{P}}_{({\rm{C/A}})}}}}} \mathord{\left/ {\vphantom {{\partial {{\hat \tau }_{{\rm{NEL}}{{\rm{P}}_{({\rm{C/A}})}}}}} {\partial \phi }}} \right. } {\partial \phi }} = 0$并证明${{{\partial ^2}{{\hat \tau }_{{\rm{NEL}}{{\rm{P}}_{({\rm{C/A}})}}}}} \mathord{\left/ {\vphantom {{{\partial ^2}{{\hat \tau }_{{\rm{NEL}}{{\rm{P}}_{({\rm{C/A}})}}}}} {\partial {\phi ^2}}}} \right. } {\partial {\phi ^2}}}$在${{\partial {{\hat \tau }_{{\rm{NEL}}{{\rm{P}}_{({\rm{C/A}})}}}}} \mathord{\left/ {\vphantom {{\partial {{\hat \tau }_{{\rm{NEL}}{{\rm{P}}_{({\rm{C/A}})}}}}} {\partial \phi }}} \right. } {\partial \phi }} = 0$的点不为零，即可得到$\hat \tau _{{\rm{NEL}}{{\rm{P}}_{({\rm{C/A}})}}}^{\max }$：

由式(5)和式(9)可以看出，此时只有$n = 0$($0 < \left| {{P_{矩形0}}} \right| < 1$)的中心干扰谱线进入到接收机的中频带宽内，干扰效果较差。

当$T \gg 1{\rm{ ms}}$时，相关器输出的干扰等效载噪比为：

$M$的大小由$T$和${T_d}$共同确定，同理可得：

式中，${\beta _{矩形n}} = {\rm{angle}}({P_{矩形n}})$。对比式(11)和式(6)容易发现，式(9)对此种情况同样适用。由于$P_{矩形n}$为实数，因此，主瓣内的谱线相位为零，而脉冲干扰的能量主要就集中在主瓣内，则此时$X$为：

由式(10)和式(12)可以看出，$T \gg 1{\rm{ ms}}$时有包含脉冲干扰中心谱线在内的多条谱线会对C/A码信号产生作用。另外，由于式(10)和式(12)都只与$\left| {{C_l}} \right|$有关，因此，$T \gg 1{\rm{ ms}}$时的脉冲干扰${f_J}$设置与单频干扰类似。

当$T = 1{\rm{ ms}}$时，相关器输出的干扰等效载噪比为：

该情况下对应的式(4)的时域形式为：

式中，

这种情况下主瓣内的所有干扰谱线不再受${T_d}$的限制而都能产生作用。由于式(13)和式(15)的计算涉及到${C_{l - n}}$和${C_{l + n}}$，因此，${f_J}$的设置与单频干扰有所差异。

由于M码周期长、码速率快，其频谱近乎连续，可通过计算$\int_{{\rm{ }} - \infty }^{{\rm{ }}\infty } {{G_{矩形}}(f){G_{\rm{M}}}(f){\rm{d}}f} $($G(f)$为功率谱密度函数)得到脉冲干扰下M码信号的干扰等效载噪比：

式中，${T_{c1}}$和${f_s}$分别为M码的码宽和副载频；$\left\lfloor \bullet \right\rfloor $和$\left\lceil \bullet \right\rceil $分别表示向下和向上取整。可以看出，式(16)与$T = 1{\rm{ ms}}$脉冲干扰下的C/A码信号情况类似，即${T_d}$对$T$的取值没有影响，$T$越大，产生作用的干扰项和信号项越多。当脉冲间隔$T - \tau $远远超过GPS接收机的最大导航数据更新周期时(飞行器一般为1 000 ms^[12])，接收机可通过AGC电路对占空比很小的突发强脉冲进行检测和接收信号消零^[13]，在剩余时间内，接收机还是能够正常工作(除非造成接收机前端饱和)，因此，可将$T \leqslant 1{\rm{ }}000{\rm{ ms}}$作为对M码信号脉冲干扰$T$取值的约束条件。

由于M码信号频谱近乎连续，对于脉冲干扰可看作是由${{2T} \mathord{\left/ {\vphantom {{2T} \tau }} \right. } \tau }$个相互独立的窄带干扰的合成，而每一个窄带干扰满足相关输出干扰分量服从零均值高斯分布的假设^[9-10]，因此，脉冲干扰下M码信号NELP处理码跟踪误差为：

式中，${B_n}$为码环噪声带宽；${\beta _r}$为接收机前端等效预相关带宽；${T_d}$为相关积分时间。

通过仿真分析不同脉冲干扰参数取值下的干扰等效载噪比和码跟踪误差，对GPS信号的脉冲干扰参数进行设置。

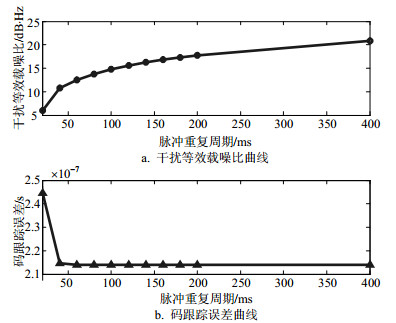
仅对$T \gg 1{\rm{ ms}}$和$T = 1{\rm{ ms}}$时的干扰效能进行仿真分析比较。以PRN16# C/A码为干扰对象，令${{{P_J}} \mathord{\left/ {\vphantom {{{P_J}} {{P_s}}}} \right. } {{P_s}}} = 15{\rm{ dB}}$，${T_d} = 20{\rm{ ms}}$，$d = 1$，$\hat \tau = {d \mathord{\left/ {\vphantom {d 6}} \right. } 6}$，$T \gg 1{\rm{ ms}}$下脉冲干扰${f_J}$设置参照单频干扰，根据式(10)、式(12)和式(9)可得此时造成干扰等效载噪比最小和码跟踪误差最大的${f_J}$分别为154 KHz和261 KHz(在干信比小于16 dB时，造成码跟踪误差最大的${f_J}$位置几乎不变)，在各自最佳${f_J}$下，$\tau $=20 ms和占空比${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$=0.2时，干扰等效载噪比和码跟踪误差随$T$的变化情况如图 1和图 2所示。

图  1  $T \gg 1{\rm{ ms}}$，$\tau $一定时，干扰效果评估指标随$T$变化曲线

图  2  $T \gg 1{\rm{ ms}}$，${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$一定时，干扰效果评估指标随$T$变化曲线

在$T = 1{\rm{ ms}}$下干扰谱线的数量会对最佳${f_J}$产生影响，设${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$分别为0.05、0.1、0.2和0.5，不同${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$下干扰等效载噪比和码跟踪误差随${f_J}$的变化情况如图 3和图 4所示。

图  3  $T = 1{\rm{ ms}}$时不同${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$下干扰等效载噪比随${f_J}$变化曲线

图  4  $T = 1{\rm{ ms}}$时不同${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$下码跟踪误差随${f_J}$变化曲线

对比图 1、图 2、图 3和图 4可得到脉冲干扰参数设置影响C/A码信号干扰效能的普适性结论：1) ${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$减小会使得干扰等效载噪比明显上升，尽管此时进入到接收机中频带宽内的干扰谱线增多，但连续脉冲渐变成突发脉冲，致使在较长时间段内干扰信号的瞬时幅度很小，干扰有效平均功率下降，这说明在影响接收机捕获、载波跟踪和数据解调功能上，长脉冲更具干扰优势，$T$不宜取值过大或$\tau $不易取值过小；2) ${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$减小对$T \gg 1{\rm{ ms}}$脉冲干扰下的码跟踪误差的影响比$T = 1{\rm{ ms}}$小，这是因为$T \gg 1{\rm{ ms}}$下的干扰谱线都与最佳${f_J}$下的$\left| {{C_l}} \right|$相乘，在$\tau $取值与${T_d}$相等时，通过增大$T$使${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$减小，会导致干扰谱线更为集中，滤波器对其的衰减作用减弱，谱线幅度加权和基本保持不变，从而码跟踪误差也无明显变化，而$T = 1{\rm{ ms}}$时干扰谱线分散在最佳${f_J}$下的$\left| {{C_l}} \right|$两侧，通过减小$\tau $使${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$减小，会导致中心干扰谱线幅度减小，与$\left| {{C_{l - n}}} \right|$相乘的干扰谱线数量增多，从而码跟踪误差会持续减小；3)在${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$一定的情况下，干扰效果会随着$T$的增加而提升，但当$\tau > {T_d}$时，这种提升作用明显下降，即$T \gg 1{\rm{ ms}}$时干扰优势要受到${T_d}$取值的制约，在获得相同干扰效果下，图 3和图 4仿真条件下的脉冲干扰主瓣带宽约为图 2仿真条件下的50倍，因此，尽管$T \gg 1{\rm{ ms}}$的干扰效果有时要好于$T = 1{\rm{ ms}}$，但增加了被频域滤波抑制的风险；4)在$T = 1{\rm{ ms}}$的脉冲干扰下，${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$增加会减弱干扰效果评估指标随${f_J}$变化曲线的波动性，从而可降低对最佳${f_J}$设置的要求，$\tau $不再受${T_d}$限制而可以更加灵活地取值，$\tau $趋近于0时能获得类似宽带噪声的干扰效果，$\tau $趋近于1 ms时能获得类似单频的干扰效果。

基于上述仿真分析，可以在获得C/A码PRN#信息的情况下，设置脉冲干扰$T$为1 ms，$\tau $可在0.01~0.05 ms范围内取值(为确保干扰效果，$\tau $也不宜过小)，${f_J}$可根据不同PRN# C/A码谱线特征预先计算比较得到，这时在相同干扰效果下的${f_J}$设置范围比单频干扰大，提高了对${f_J}$设置偏差的容忍度。另外，在降低频域滤波抑制作用的同时，还可采取提高脉冲幅度来增加${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$下的干扰有效平均功率。

设${{{P_J}} \mathord{\left/ {\vphantom {{{P_J}} {{P_s}}}} \right. } {{P_s}}} = 40{\rm{ dB}}$，${\beta _r} = 30{\rm{ MHz}}$，${B_n}{\rm{ = 2 Hz}}$，${T_d} = 20{\rm{ ms}}$，$d = {1 \mathord{\left/ {\vphantom {1 8}} \right. } 8}$，$\hat \tau = {d \mathord{\left/ {\vphantom {d 6}} \right. } 6}$，$T$取10 ms，${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$取0.000 1，脉冲幅度取100(保证脉冲干扰谱线的功率和为1)，脉冲干扰下的M码信号干扰等效载噪比和码跟踪误差随${f_J}$的变化情况如图 5所示。

图  5  M码信号干扰效果评估指标随${f_J}$变化曲线

由图 5可以看出，尽管此时干扰谱线间隔为100 Hz，脉冲主瓣宽度为2 MHz，但对M码信号脉冲干扰的最佳${f_J}$仍与单频干扰几乎相同，且在单频干扰几乎无效的${f_J}$下也能对期望信号造成一定影响，这同样是由于干扰谱线的数量“稀释”了对${f_J}$选择的敏感性。

${f_J}$取9.77 MHz(不同干扰效果评估指标最佳${f_J}$的均值)，其他仿真参数同图 5，在$\tau $取0.1 ms和${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$取0.000 1的情况下，M码信号干扰等效载噪比和码跟踪误差随$T$的变化情况如图 6和图 7所示。

图  6  $\tau $一定时M码信号干扰效果评估指标随$T$变化曲线

图  7  ${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$=0.000 1时，M码信号干扰效果评估指标随$T$变化曲线

由图 6可以看出，$\tau $一定时，M码信号脉冲干扰效果会随着$T$的增加而下降，且当$T$在10~100 ms范围内增加时，干扰效果下降明显。尽管此时干扰谱线数量增多，且越来越集中于最佳${f_J}$附近，但由于M码信号频谱近乎连续且带宽较大，使得在距离最佳${f_J}$很宽的范围内信号功率谱值差异都很小，因此，干扰效果受脉冲干扰平均功率的影响较大，即长脉冲对M码信号的干扰优势比C/A码信号更加明显，通过提高脉冲幅度使干扰谱线的功率和保持为1时，干扰效果几乎不发生变化。

由图 7可以看出，${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$一定时，M码信号脉冲干扰效果几乎不随$T$的增加而变化，这与C/A码信号有所不同。由于脉冲干扰主瓣内的谱线都可轻易落入到M码信号功率谱的带宽内，因此，干扰效果只受主瓣谱线功率的影响，而与主瓣宽窄关系不大。

由于${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$一定时长周期脉冲对干扰效果几乎没有提升作用，同时为了降低宽带期望信号下频域滤波的影响，$\tau $不宜取值过大，因此，应通过减小$T$以及提高脉冲幅度来确保干扰效果。

在$T$=10 ms情况下，其他仿真参数同图 6，M码信号干扰等效载噪比和码跟踪误差随${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$的变化情况如图 8所示。

图  8  $T$=10 ms时，M码信号干扰效果评估指标随${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$变化曲线

图 8实质上也是反映了脉冲干扰平均功率是对频谱近乎连续的GPS伪码信号干扰效果影响的主要因素。当$T$一定时，脉冲干扰效果会随着${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$的增加而提升，但当${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T} > 0.01$时，这种提升作用明显减弱，这同样是由于M码信号频谱近乎连续而使得脉冲主瓣带宽在压缩到一定程度后对干扰效果的提升十分有限，考虑到带宽较窄或脉冲幅度较大易被接收机频域滤波或AGC电路减轻甚至消除，因此，$T$固定下的${\tau \mathord{\left/ {\vphantom {\tau T}} \right. } T}$可在0.002~0.005取值。

脉冲干扰通过参数设置可让多根干扰谱线同时进入GPS接收机以增大有效干扰能量，并且易让功率最强的中心谱线对准期望信号的最佳干扰频偏位置。这样对于离散谱特征的C/A码信号，能更好地利用最强谱线的易感优势，设置脉冲重复周期为1 ms，脉宽可在0.01~0.05 ms取值，干扰频偏可根据C/A码PRN#信息预先计算比较得到；对于连续谱特征的M码信号，能使功率较大的干扰谱线分布在最佳干扰频偏周围，可通过减小脉冲重复周期和提高脉冲幅度(使干扰谱线功率和接近于1)来确保干扰效果，在脉冲重复周期固定时，占空比可在0.002~0.005取值，干扰频偏可依据单频干扰频偏设置预先计算平均得到。